Experimental and Simulation Study on Welding Characteristics and Parameters of Gas Metal Arc Welding for Q345qD Thick-Plate Steel
Abstract
:1. Introduction
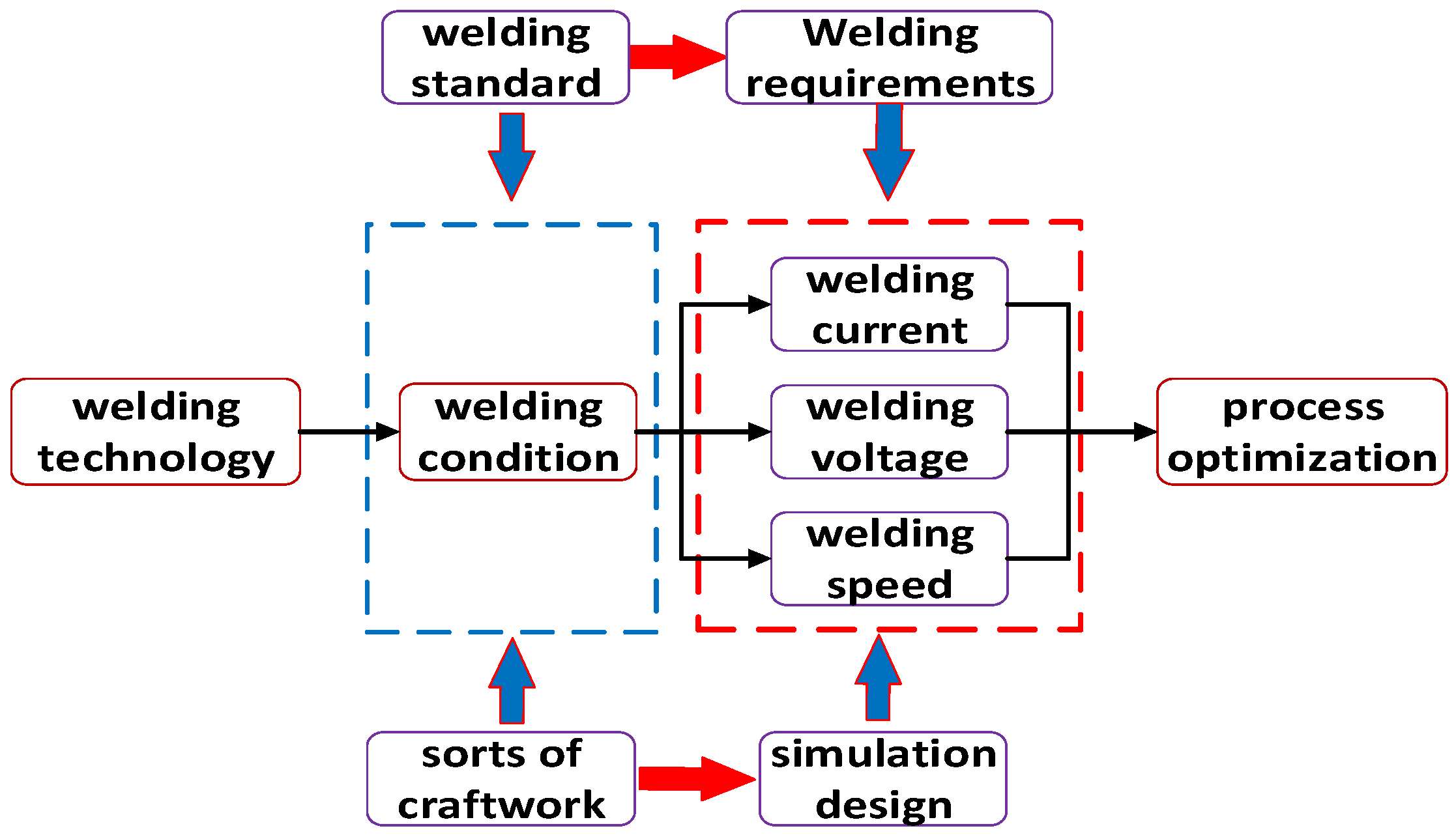
2. Material and Research Method
2.1. Definition of Welding Process Parameters
2.2. Methodology
2.3. Specification of Parameters
3. Numerical Analysis
3.1. Thermal–Mechanical Coupling
- The material yield follows the von Mises yield criterion.
- The elastic strain and plastic strain of the materials can be separated from the temperature strain.
- The mechanical properties of the materials depend on temperature changes.
- The behavior of the material in the plastic zone after yielding follows the plastic-flow criterion and strengthening criterion.
- Based on the small-time increment, the mechanical properties, stress, and strain of materials show linear changes.
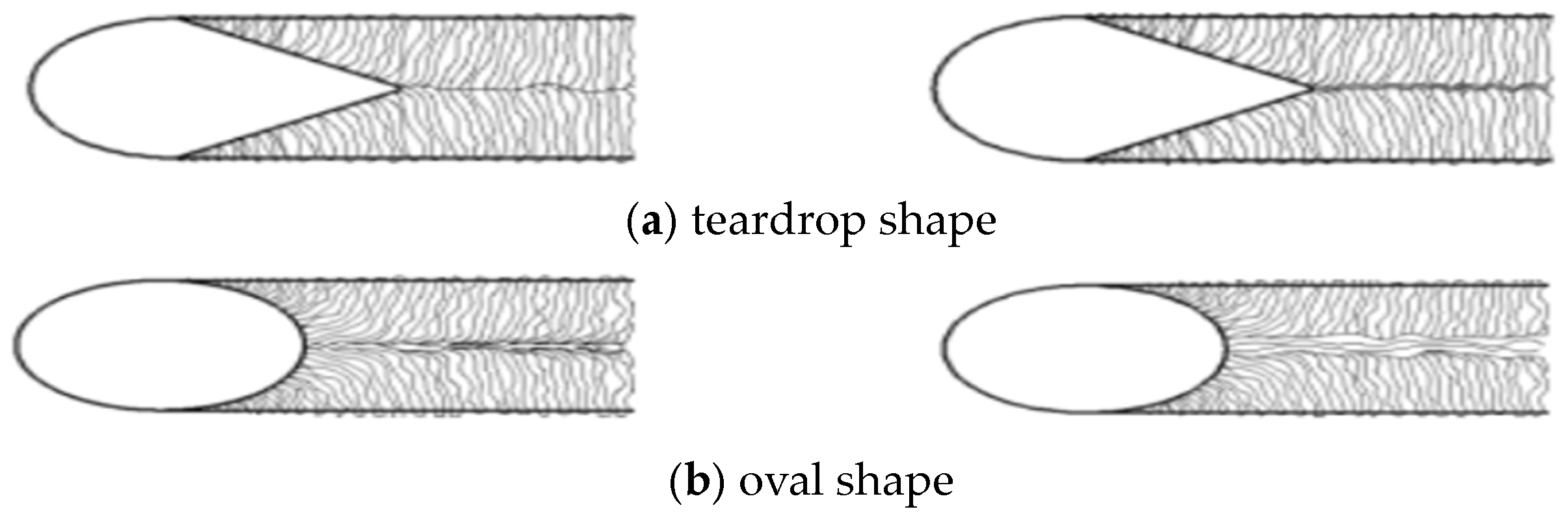
3.2. Welding Heat Source
3.3. Secondary Development of Heat Source Model Subroutine
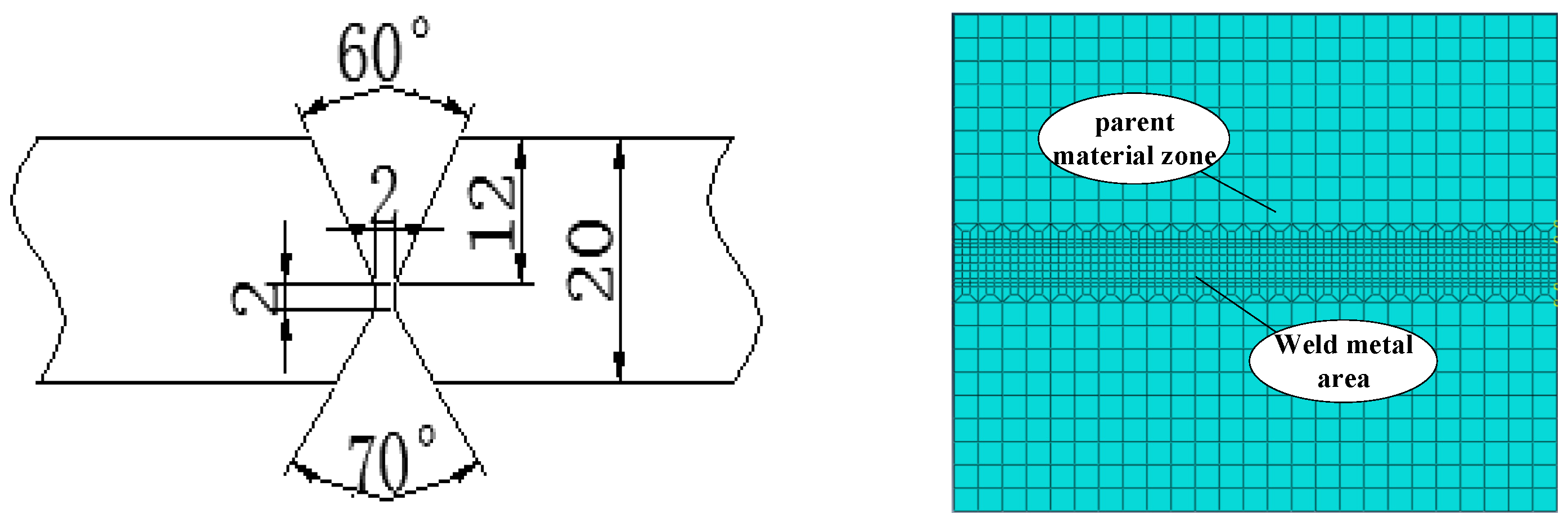
3.4. Numerical Modelling
3.5. Boundary Conditions
4. Simulation Results
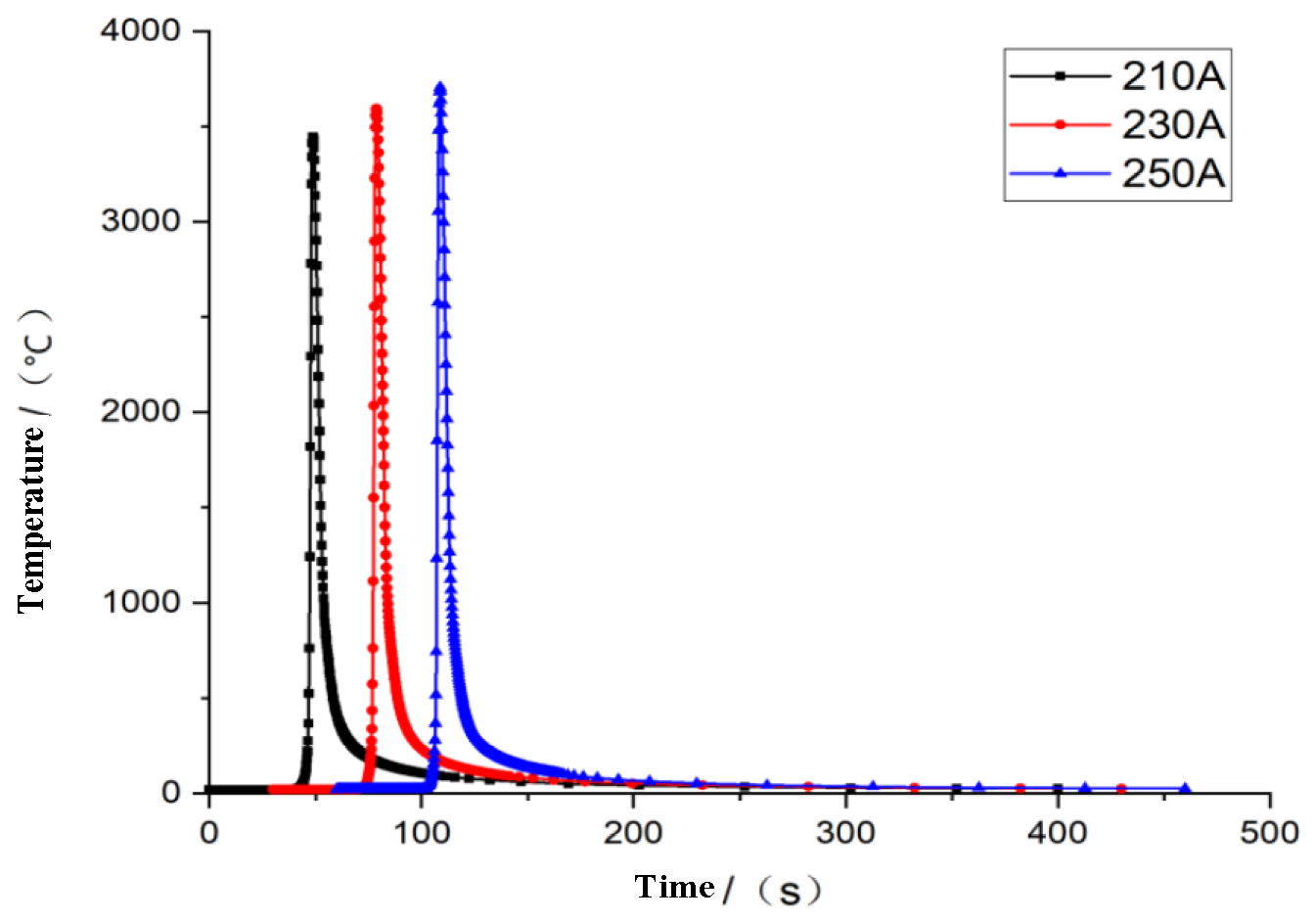
4.1. Effect of Welding Current
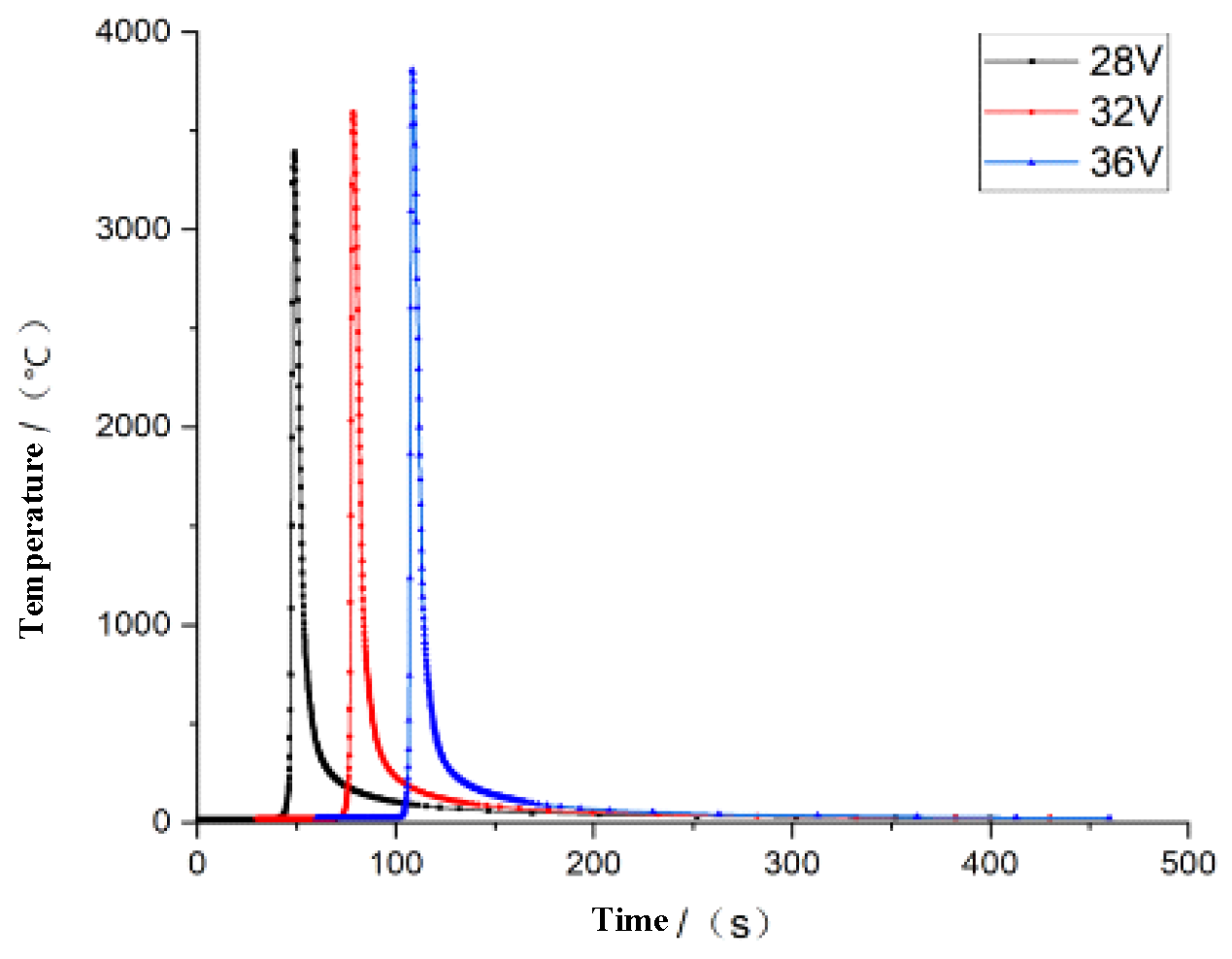
4.2. Effect of Welding Voltage
4.3. Effect of Welding Speed
5. Optimization Analysis and Experiment
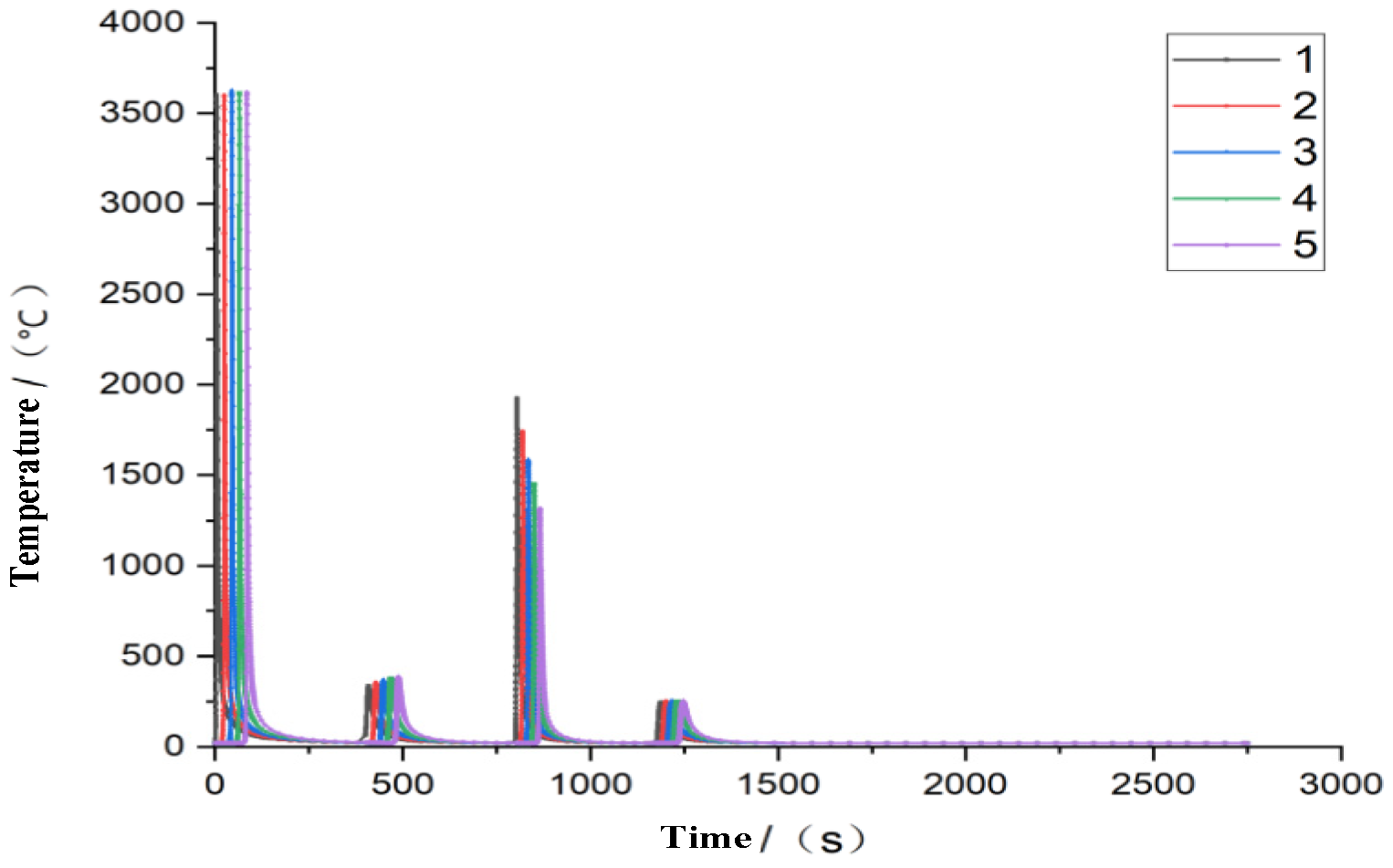
5.1. Results of Temperature Field
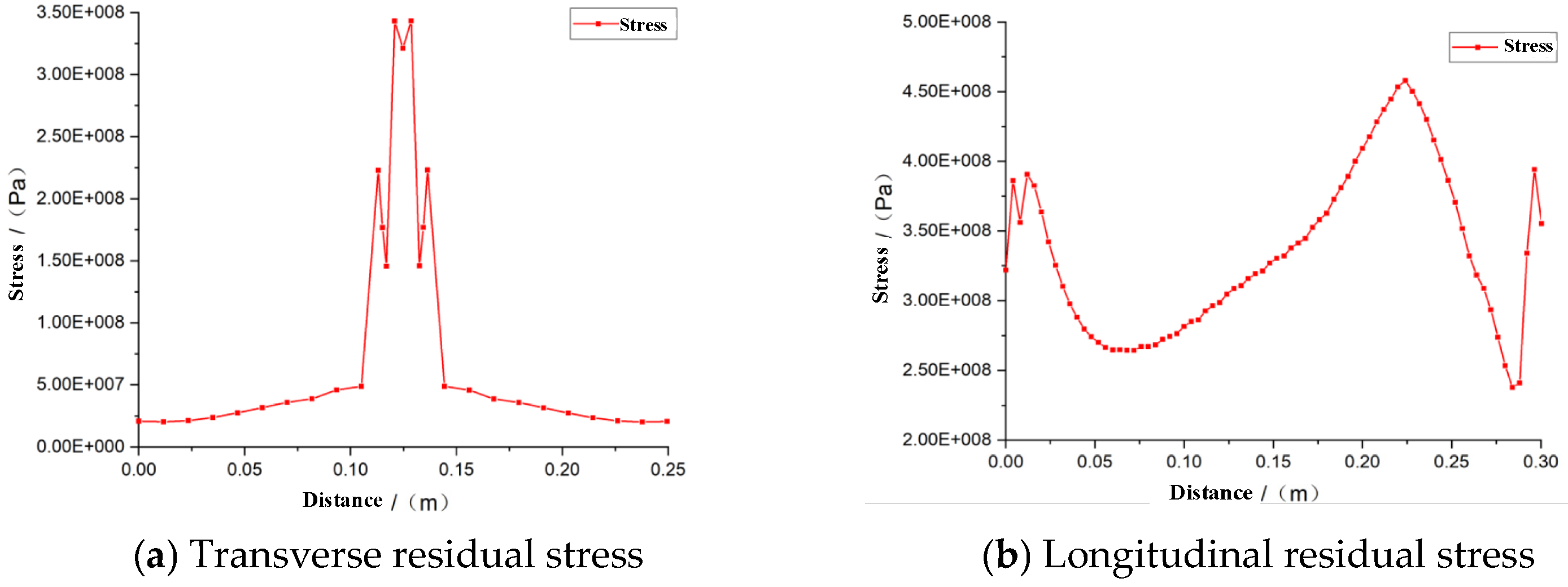
5.2. Results of Stress Field
5.3. Results of Strain Field
5.4. Welding Test Detection
- The average tensile strength and yield strength of the weld zone are 565.5 MPa and 404 MPa, respectively, meaning that the test results show that the tensile properties of the welded joints are excellent, and meet the welding standards.
- There is no crack in the welded joint, and it has an excellent plastic toughness, which meets the toughness requirements, and there are no pores, residues, cracks, or pits at the welded joints.
- The highest hardness of HAZ is 194.8 HV; the average hardness is 188.525 HV. The hardness is lower than HV380, and meets the welding standard.
- The welded plate has no significant deformation or distortion; the maximum deformation is 0.6 mm.
6. Conclusions
- Based on the welding quality requirements of Q345qD for thick-plate bridge steel, the technical route of the GMAW welding process is established, and its parameters are studied. According to thermal–elastic–plastic analysis, the optimal welding parameters are utilized.
- As results show that, with the gradual increase in the welding current, the maximum welding temperature can reach 3706 °C, the optimal welding current is 230 A, the optimal welding voltage is 32 V, and the optimal welding speed is 0.003 m/s.
- According to the simulation analysis of single welding process parameters, the welding residual stress is mainly distributed in the weld zone; its value increases closer to the weld, reaching the maximum peak value in the middle position. The maximum residual stress is 345 MPa.
- According to the experimental results, the average tensile strength and yield strength in the weld zone are 565.5 MPa and 404 MPa, indicating that the welded joint has excellent tensile properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, J.; Jiang, M.; Hao, Y. Welding crack control measures for thick steel structures. China Met. Bull. 2019, 20, 274–276. [Google Scholar] [CrossRef]
- Zhang, J. Manufacturing processes and deformation control for large-scale welding H-steel. Eng. Mach. 2013, 44, 48–52. [Google Scholar]
- Jose, B.; Manoharan, M.; Natarajan, A.; Muktinutalapati, N.R.; Reddy, G.M. Development of a low heat-input welding technique for joining thick plates of 250 grade maraging steel to fabricate rocket motor casings. Mater. Lett. 2022, 326, 132984. [Google Scholar] [CrossRef]
- Samadi, F.; Mourya, J.; Wheatley, G.; Khan, M.N.; Nejad, R.M.; Branco, R.; Macek, W. An investigation on residual stress and fatigue life assessment of T-shape welded joints. Eng. Fail. Anal. 2022, 141, 106685. [Google Scholar] [CrossRef]
- Kumaresan, A.; Sundar, A.; Annamalai, A.; Ramesh, G.; Chandaragiri Baskar, S.; Ramachandran, D.; Sajja Rama, K.R. Effect of welding current on properties of activated gas tungsten arc super duplex stainless steel welds. Mater. Test. 2022, 64, 1242–1253. [Google Scholar] [CrossRef]
- Thien, N.T.; Thang, Q.T.; Hau, T.N. Effect of Orbital Welding Parameters on the Weld Geometry. Mater. Sci. Forum 2022, 116, 6604. [Google Scholar]
- Kumar, D.; Biswas, A.; Mandal, A.; Kumar, R. Improvement of Welding Performance on Mild Steel by a Hybrid TIG-MAG Welding Technique. Int. J. Steel Struct. 2023, 23, 993–1004. [Google Scholar] [CrossRef]
- John, M.; Diaz, O.; Esparza, A.; Fliegler, A.; Ocenosak, D.; Van Dorn, C.; Bhat, K.U.; Menezes, P.L. Welding Techniques for High Entropy Alloys: Processes, Properties, Characterization, and Challenges. Materials 2022, 15, 2273. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Vora, J.; Patel, V.; Bogum, S. Experience with advanced welding techniques (RMD & P-GMAW) with seamless metal cored wire for Oil & Gas pipeline industries. J. Phys. Conf. Ser. 2021, 1950, 012043. [Google Scholar]
- Larin, M.; Pevzner, Y.; Shalnova, S.; Petrovskiy, P. Laser Welding Modes Optimization of the Selective Laser Melted Ti-6Al-4V Thin-Thickness Parts with Complex Shape. Metals 2021, 11, 2013. [Google Scholar] [CrossRef]
- Barot, R.S.; Patel, V.J. Process monitoring and internet of things feasibility for submerged arc welding: State of art. Mater. Today Proc. 2021, 45, 4441–4446. [Google Scholar] [CrossRef]
- Aravind, A.P.; Suryaprakash, S.; Vishal, S.; Sethuraman, M.; Kannan, T.D.B.; Umar, M.; Rajak, S. Optimization of welding parameters in CMT welding of Al 5083 alloys using VIKOR optimization method. IOP Conf. Ser. Mater. Sci. Eng. 2020, 912, 032035. [Google Scholar] [CrossRef]
- Frango, T.L.; Prabhakaran, M.; Sivakandhan, C.; Babu, K.V.; Vairamuthu, J. Enhancement of welding strength on Eglin steel using MIG welding process. Mater. Today Proc. 2020, 33, 4617–4620. [Google Scholar] [CrossRef]
- Tarık, H.S.; Gürel, Ç. Multi-pass butt welding of thick AISI 316L plates by gas tungsten arc welding: Microstructural and mechanical characterization. Int. J. Press. Vessel. Pip. 2022, 200, 104842. [Google Scholar]
- Kanakavalli, B.P.; Babu, N.B.; Sai, V.C. A hybrid methodology for optimizing MIG welding process parameters in joining of dissimilar metals. Mater. Today Proc. 2020, 23 Pt 3, 507–512. [Google Scholar] [CrossRef]
- Zhu, Q.; Jia, C.; Gou, G.; Chen, H.; Li, P. Ameliorated Longitudinal Critically Refracted Attenuation Velocity Method for Welding Residual Stress Measurement. J. Mater. Process. Technol. 2017, 246, 267–275. [Google Scholar] [CrossRef]
- Rizvi, S.A.; Ali, W. Optimization of Welding Parameters and Microstructure and Fracture Mode Characterization of GMA Welding by Using Taguchi Method on SS304H Austenitic Steel. Mech. Mech. Eng. 2020, 22, 1121–1131. [Google Scholar] [CrossRef]
- Ma, F. Study on Numerical Simulation of Welding Deformation and Residual Stress of Aluminum Alloy Based on ABAQUS. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2016. [Google Scholar]
- Li, X. Numerical simulation of welding temperature field of Q345 steel plate based on different heat source models. Weld. Technol. 2020, 49, 19–21. [Google Scholar]






| Number of Beads | Welding Process | Protective Gas Flow Rate (l/min) | Electric Current (A) | Voltage (V) | Welding Speed (m/s) |
|---|---|---|---|---|---|
| 1~2 | GMAW | 10~15 | 210~250 | 28~36 | 0.0026~0.0043 |
| 3~4 | SAW | -- | 560~660 | 33~37 | 0.003~0.0046 |
| Sequence of Weld Paths | (m) | b (m) | c (m) | |
|---|---|---|---|---|
| 1 | 0.012 | 0.0036 | 0.006 | 0.007 |
| 2 | 0.006 | 0.0018 | 0.003 | 0.0045 |
| 3 | 0.011 | 0.003 | 0.005 | 0.003 |
| 4 | 0.016 | 0.0048 | 0.008 | 0.004 |
| C | Mn | Si | V | Nb | Ti | Cr | Ni | |
|---|---|---|---|---|---|---|---|---|
| Standard | ≤0.18 | ≤1.6 | ≤0.55 | 0.010~0.080 | 0.005~0.060 | 0.006~0.030 | ≤0.30 | ≤0.30 |
| Certificate | 0.16 | 1.48 | 0.21 | 0.010 | 0.0055 | 0.0067 | 0.20 | 0.10 |
| Number of Plies | Welding Process | Protective Gas-Flow Rate (l/min) | Electric Current (A) | Voltage (V) | Welding Speed (m/s) |
|---|---|---|---|---|---|
| 1 | GMAW | 10 | 230 | 32 | 0.003 |
| 2 | GMAW | 10 | 230 | 32 | 0.003 |
| 3 | SAW | -- | 600 | 35 | 0.004 |
| 4 | SAW | -- | 600 | 35 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, R.; Yang, S.; Zhan, L.; Xiong, M.; Wang, B.; Zhang, J. Experimental and Simulation Study on Welding Characteristics and Parameters of Gas Metal Arc Welding for Q345qD Thick-Plate Steel. Materials 2023, 16, 5944. https://doi.org/10.3390/ma16175944
Zhang H, Li R, Yang S, Zhan L, Xiong M, Wang B, Zhang J. Experimental and Simulation Study on Welding Characteristics and Parameters of Gas Metal Arc Welding for Q345qD Thick-Plate Steel. Materials. 2023; 16(17):5944. https://doi.org/10.3390/ma16175944
Chicago/Turabian StyleZhang, Hui, Rong Li, Shuxuan Yang, Liebang Zhan, Ming Xiong, Ban Wang, and Juyong Zhang. 2023. "Experimental and Simulation Study on Welding Characteristics and Parameters of Gas Metal Arc Welding for Q345qD Thick-Plate Steel" Materials 16, no. 17: 5944. https://doi.org/10.3390/ma16175944
APA StyleZhang, H., Li, R., Yang, S., Zhan, L., Xiong, M., Wang, B., & Zhang, J. (2023). Experimental and Simulation Study on Welding Characteristics and Parameters of Gas Metal Arc Welding for Q345qD Thick-Plate Steel. Materials, 16(17), 5944. https://doi.org/10.3390/ma16175944






