A Review of Computational Approaches to the Microstructure-Informed Mechanical Modelling of Metals Produced by Powder Bed Fusion Additive Manufacturing
Abstract
1. Introduction
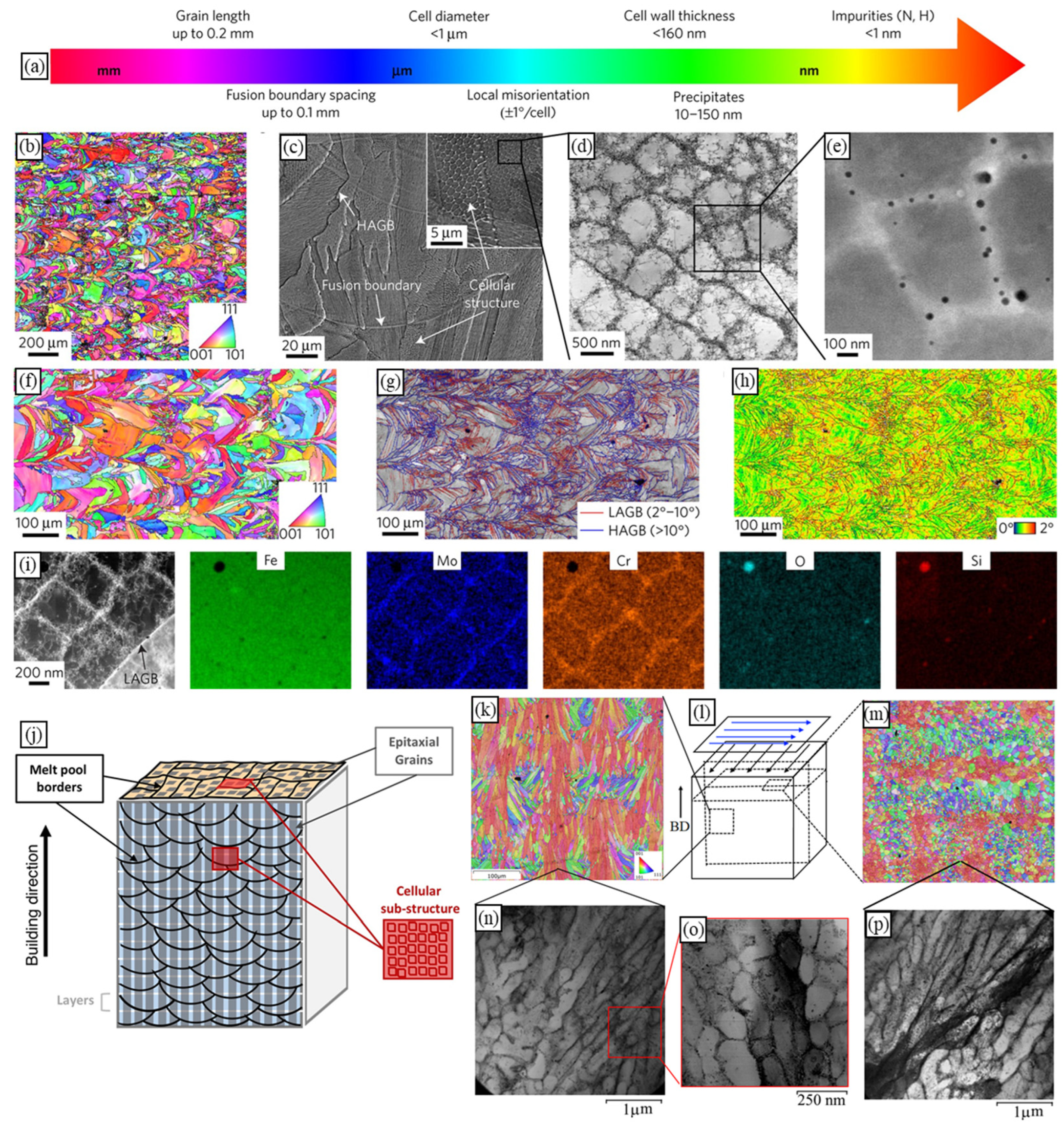
2. Microstructural Features of Materials Fabricated by PBF
2.1. Melt Pool Pattern
2.2. Grains

2.3. Cellular–Dendritic Substructure
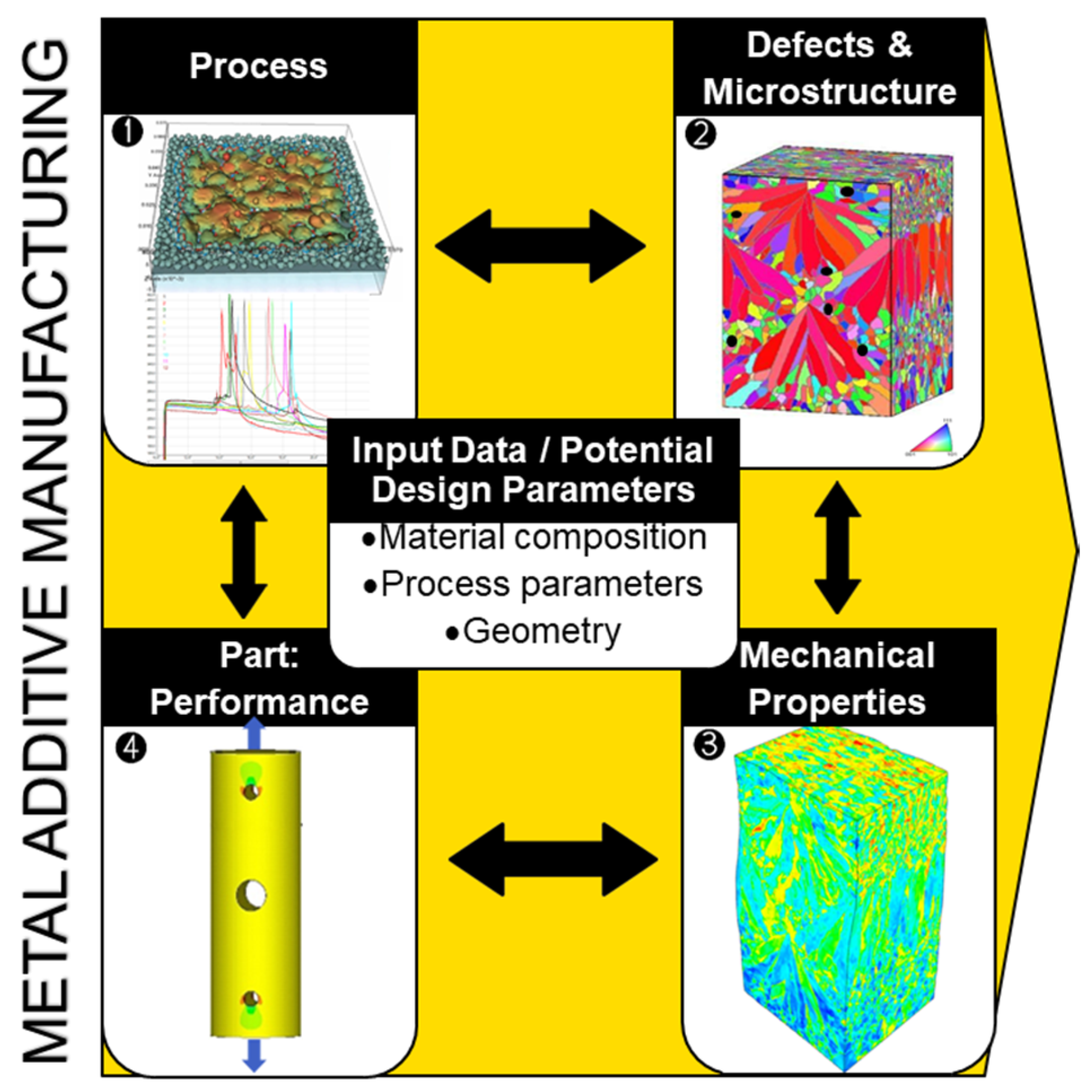
3. Process-Structure-Properties-Performance Concept
4. Microstructure Modelling in AM
4.1. Physically Based Microstructure Modelling

4.2. Geometrically Based Microstructure Modelling and Image Reconstruction

5. BVP Formulation for Microstructure-Based Mechanical Simulations of Additively Manufactured Metallic Materials
5.1. FE Implementation of a Boundary-Value Problem
5.2. Kinematics and Constitutive Laws
5.3. Constitutive Models of the Plastic Behaviour of Grains
5.4. Description of Hardening Mechanisms in PBF-Produced Materials
6. Microstructure-Informative Mechanical Simulations of Additively Manufactured Metallic Materials
6.1. Two-Dimensional Microstructure-Based Mechanical Simulations
6.2. Three-Dimensional Mechanical Simulations for Synthetic Microstructures
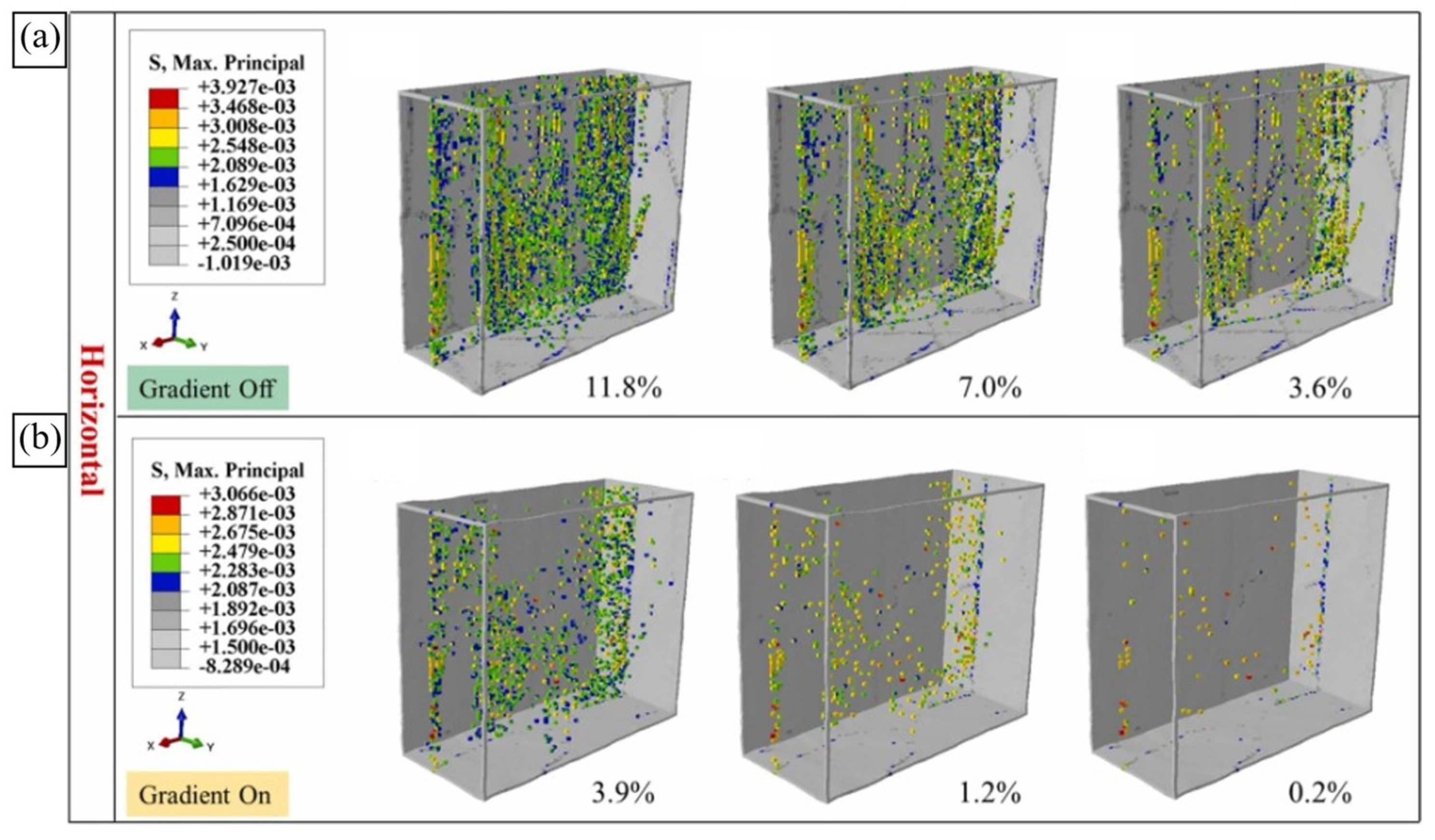
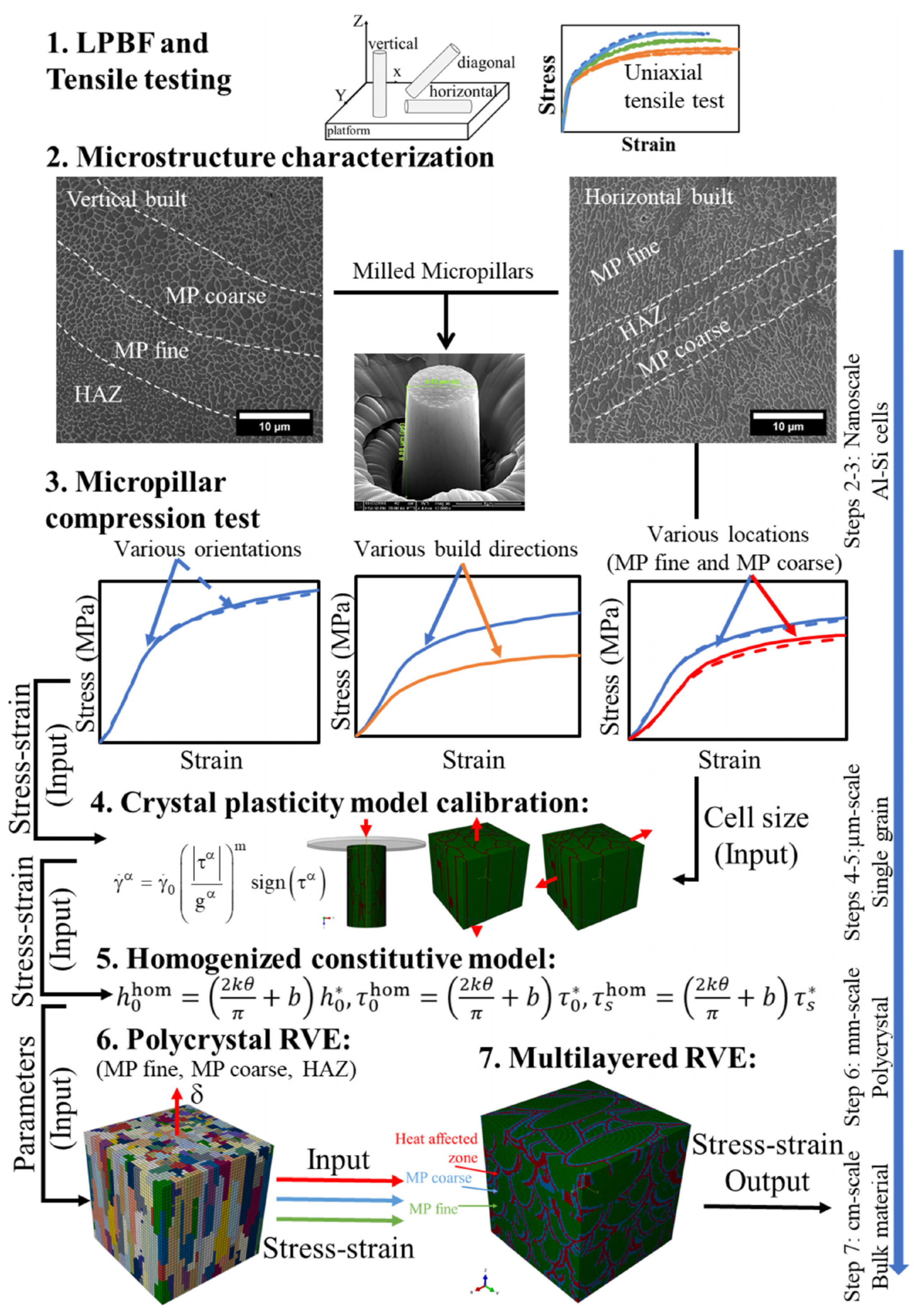
6.3. Process–Structure–Property–Performance Computational Analysis
7. Summary and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yadroitsev, I.; Yadroitsava, I.; du Plessis, A.; MacDonald, E. (Eds.) Fundamentals of Laser Powder Bed Fusion of Metals; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128240908. [Google Scholar]
- Francois, M.M.; Sun, A.; King, W.E.; Henson, N.J.; Tourret, D.; Bronkhorst, C.A.; Carlson, N.N.; Newman, C.K.; Haut, T.; Bakosi, J.; et al. Modeling of Additive Manufacturing Processes for Metals: Challenges and Opportunities. Curr. Opin. Solid State Mater. Sci. 2017, 21, 198–206. [Google Scholar] [CrossRef]
- Kotadia, H.R.; Gibbons, G.; Das, A.; Howes, P.D. A Review of Laser Powder Bed Fusion Additive Manufacturing of Aluminium Alloys: Microstructure and Properties. Addit. Manuf. 2021, 46, 102155. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive Manufacturing of Metallic Components—Process, Structure and Properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Fernandez-Zelaia, P.; Kirka, M.M.; Dryepondt, S.N.; Gussev, M.N. Crystallographic Texture Control in Electron Beam Additive Manufacturing via Conductive Manipulation. Mater. Des. 2020, 195, 109010. [Google Scholar] [CrossRef]
- Gokcekaya, O.; Ishimoto, T.; Hibino, S.; Yasutomi, J.; Narushima, T.; Nakano, T. Unique Crystallographic Texture Formation in Inconel 718 by Laser Powder Bed Fusion and Its Effect on Mechanical Anisotropy. Acta Mater. 2021, 212, 116876. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Yadroitsava, I. A Step-by-Step Guide to the L-PBF Process. In Fundamentals of Laser Powder Bed Fusion of Metals; Yadroitsev, I., Yadroitsava, I., du Plessis, A., MacDonald, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 39–77. [Google Scholar]
- Fotovvati, B.; Rauniyar, S.; Jobe, A.A.; Chou, K. Experimental, Computational, and Data-Driven Study of the Effects of Selective Laser Melting (SLM) Process Parameters on Single-Layer Surface Characteristics. Int. J. Adv. Manuf. Technol. 2022, 123, 119–144. [Google Scholar] [CrossRef]
- Rehme, O.; Emmelmann, C. Reproducibility for Properties of Selective Laser Melting Products. In Proceedings of the Third International WLT-Conference on Lasers in Manufacturing, Munich, Germany, 13–16 June 2005; Beyer, E., Ed.; AT-Verlag: Stuttgart, Germany, 2005; pp. 1–6. [Google Scholar]
- Kahlen, F.-J.; Kar, A. Tensile Strengths for Laser-Fabricated Parts and Similarity Parameters for Rapid Manufacturing. J. Manuf. Sci. Eng. 2001, 123, 38–44. [Google Scholar] [CrossRef]
- Samuel, M.P.; Mishra, A.K.; Mishra, R.K. Additive Manufacturing of Ti-6Al-4V Aero Engine Parts: Qualification for Reliability. J. Fail. Anal. Prev. 2018, 18, 136–144. [Google Scholar] [CrossRef]
- Lowther, M.; Louth, S.; Davey, A.; Hussain, A.; Ginestra, P.; Carter, L.; Eisenstein, N.; Grover, L.; Cox, S. Clinical, Industrial, and Research Perspectives on Powder Bed Fusion Additively Manufactured Metal Implants. Addit. Manuf. 2019, 28, 565–584. [Google Scholar] [CrossRef]
- DebRoy, T.; Mukherjee, T.; Milewski, J.O.; Elmer, J.W.; Ribic, B.; Blecher, J.J.; Zhang, W. Scientific, Technological and Economic Issues in Metal Printing and Their Solutions. Nat. Mater. 2019, 18, 1026–1032. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Balokhonov, R. Predictive Simulation of Microstructural Pattern in AM for Metals in Powder Bed Fusion. In Quality Analysis of Additively Manufactured Metals; Kadkhodapour, J., Schmauder, S., Sajadi, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Wang, F.; Williams, S.; Rush, M. Morphology Investigation on Direct Current Pulsed Gas Tungsten Arc Welded Additive Layer Manufactured Ti6Al4V Alloy. Int. J. Adv. Manuf. Technol. 2011, 57, 597–603. [Google Scholar] [CrossRef]
- Garibaldi, M.; Ashcroft, I.; Simonelli, M.; Hague, R. Metallurgy of High-Silicon Steel Parts Produced Using Selective Laser Melting. Acta Mater. 2016, 110, 207–216. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Balokhonov, R. Effects of Scanning Pattern on the Grain Structure and Elastic Properties of Additively Manufactured 316L Austenitic Stainless Steel. Mater. Sci. Eng. A 2022, 832, 142447. [Google Scholar] [CrossRef]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T.; et al. Additively Manufactured Hierarchical Stainless Steels with High Strength and Ductility. Nat. Mater. 2018, 17, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Sun, J.; Berto, F.; Wang, X.; Qian, G. Fatigue and Fracture Behavior of AlSi10Mg Manufactured by Selective Laser Melting: A Review. Phys. Mesomech. 2023, 26, 367–390. [Google Scholar] [CrossRef]
- Mukherjee, T.; DebRoy, T. A Digital Twin for Rapid Qualification of 3D Printed Metallic Components. Appl. Mater. Today 2019, 14, 59–65. [Google Scholar] [CrossRef]
- Wei, H.L.; Mukherjee, T.; Zhang, W.; Zuback, J.S.; Knapp, G.L.; De, A.; DebRoy, T. Mechanistic Models for Additive Manufacturing of Metallic Components. Prog. Mater. Sci. 2021, 116, 100703. [Google Scholar] [CrossRef]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser Powder Bed Fusion Additive Manufacturing of Metals; Physics, Computational, and Materials Challenges. Appl. Phys. Rev. 2015, 2, 41304. [Google Scholar] [CrossRef]
- Gunasegaram, D.R.; Murphy, A.B.; Barnard, A.; DebRoy, T.; Matthews, M.J.; Ladani, L.; Gu, D. Towards Developing Multiscale-Multiphysics Models and Their Surrogates for Digital Twins of Metal Additive Manufacturing. Addit. Manuf. 2021, 46, 102089. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I.; Kondratyev, N.S.; Yants, A.Y. Multilevel Models in Physical Mesomechanics of Metals and Alloys: Results and Prospects. Phys. Mesomech. 2021, 24, 391–417. [Google Scholar] [CrossRef]
- Costas, M.; Morin, D.; de Lucio, M.; Langseth, M. Testing and Simulation of Additively Manufactured AlSi10Mg Components under Quasi-Static Loading. Eur. J. Mech. A/Solids 2020, 81, 103966. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, W.; Behera, A.; Thompson, S.; To, A.C. Mean-Field Polycrystal Plasticity Modeling with Grain Size and Shape Effects for Laser Additive Manufactured FCC Metals. Int. J. Solids Struct. 2017, 112, 35–42. [Google Scholar] [CrossRef]
- Gribov, D.S.; Trusov, P.V. Three-Level Dislocation-Based Model for Describing the Deformation of Polycrystals: Structure, Implementation Algorithm, Examples for Studying Nonproportional Cyclic Loading. Phys. Mesomech. 2022, 25, 557–567. [Google Scholar] [CrossRef]
- Babu, B.; Lundbäck, A.; Lindgren, L.-E. Simulation of Ti-6Al-4V Additive Manufacturing Using Coupled Physically Based Flow Stress and Metallurgical Model. Materials 2019, 12, 3844. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Zinovieva, O.; Emelianova, E.; Dymnich, E.; Pisarev, M.; Zinoviev, A. Micromechanical Simulations of Additively Manufactured Aluminum Alloys. Comput. Struct. 2021, 244, 106412. [Google Scholar] [CrossRef]
- Romanova, V.; Zinovieva, O.; Balokhonov, R.; Dymnich, E.; Moskvichev, E.; Filippov, A.; Lychagin, D. Effects of the Grain Shape and Crystallographic Texture on the Grain-Scale Mechanical Behavior of Additively Manufactured Aluminum Alloys. Addit. Manuf. 2021, 48, 102415. [Google Scholar] [CrossRef]
- Kergaßner, A.; Mergheim, J.; Steinmann, P. Modeling of Additively Manufactured Materials Using Gradient-Enhanced Crystal Plasticity. Comput. Math. Appl. 2019, 78, 2338–2350. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Ploshikhin, V.; Romanova, V.; Balokhonov, R. Strategy of Computational Predictions for Mechanical Behaviour of Additively Manufactured Materials. Mater. Sci. Technol. 2018, 34, 1591–1605. [Google Scholar] [CrossRef]
- Bagheri, A.; Yadollahi, A.; Mahtabi, M.J.; Paudel, Y.; Vance, E.; Shamsaei, N.; Horstemeyer, M.F. Microstructure-Based Multistage Fatigue Modeling of NiTi Alloy Fabricated via Direct Energy Deposition (DED). J. Mater. Eng. Perform. 2022, 31, 4761–4775. [Google Scholar] [CrossRef]
- Wu, S.; Song, H.Y.; Peng, H.Z.; Hodgson, P.D.; Wang, H.; Wu, X.H.; Zhu, Y.M.; Lam, M.C.; Huang, A.J. A Microstructure-Based Creep Model for Additively Manufactured Nickel-Based Superalloys. Acta Mater. 2022, 224, 117528. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Emelianova, E.; Zinovieva, O.; Zinoviev, A. Microstructure-Based Simulations of Quasistatic Deformation Using an Explicit Dynamic Approach. Facta Univ. Ser. Mech. Eng. 2019, 17, 243–254. [Google Scholar] [CrossRef]
- Somlo, K.; Poulios, K.; Funch, C.V.; Niordson, C.F. Anisotropic Tensile Behaviour of Additively Manufactured Ti-6Al-4V Simulated with Crystal Plasticity. Mech. Mater. 2021, 162, 104034. [Google Scholar] [CrossRef]
- Saeb, S.; Steinmann, P.; Javili, A. Aspects of Computational Homogenization at Finite Deformations: A Unifying Review from Reuss’ to Voigt’s Bound. Appl. Mech. Rev. 2016, 68, 050801. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Ge, P. A Review on Modelling and Simulation of Laser Additive Manufacturing: Heat Transfer, Microstructure Evolutions and Mechanical Properties. Coatings 2022, 12, 1277. [Google Scholar] [CrossRef]
- Tan, Z.; Li, J.; Zhang, Z. Experimental and Numerical Studies on Fabrication of Nanoparticle Reinforced Aluminum Matrix Composites by Friction Stir Additive Manufacturing. J. Mater. Res. Technol. 2021, 12, 1898–1912. [Google Scholar] [CrossRef]
- Gatsos, T.; Elsayed, K.A.; Zhai, Y.; Lados, D.A. Review on Computational Modeling of Process–Microstructure–Property Relationships in Metal Additive Manufacturing. JOM 2020, 72, 403–419. [Google Scholar] [CrossRef]
- Zhao, L.; Song, L.; Santos Macías, J.G.; Zhu, Y.; Huang, M.; Simar, A.; Li, Z. Review on the Correlation between Microstructure and Mechanical Performance for Laser Powder Bed Fusion AlSi10Mg. Addit. Manuf. 2022, 56, 102914. [Google Scholar] [CrossRef]
- Bajaj, P.; Hariharan, A.; Kini, A.; Kürnsteiner, P.; Raabe, D.; Jägle, E.A. Steels in Additive Manufacturing: A Review of Their Microstructure and Properties. Mater. Sci. Eng. A 2020, 772, 138633. [Google Scholar] [CrossRef]
- Karthik, G.M.; Kim, H.S. Heterogeneous Aspects of Additive Manufactured Metallic Parts: A Review. Met. Mater. Int. 2021, 27, 1–39. [Google Scholar] [CrossRef]
- Tonelli, L. Revealing the Hierarchical Microstructure of Innovative Additively Manufactured Metal Parts with Conventional Light Microscopy. Metallogr. Microstruct. Anal. 2021, 10, 278–282. [Google Scholar] [CrossRef]
- Haines, M.P.; Rielli, V.V.; Primig, S.; Haghdadi, N. Powder Bed Fusion Additive Manufacturing of Ni-Based Superalloys: A Review of the Main Microstructural Constituents and Characterization Techniques. J. Mater. Sci. 2022, 57, 14135–14187. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Balokhonov, R.; Emelyanova, T. A Review of Microstructure and Mechanical Properties of Additively Manufactured Aluminum Alloys. AIP Conf. Proc. 2020, 2310, 020364. [Google Scholar] [CrossRef]
- Yin, Y.; Tan, Q.; Bermingham, M.; Mo, N.; Zhang, J.; Zhang, M.-X. Laser Additive Manufacturing of Steels. Int. Mater. Rev. 2022, 67, 487–573. [Google Scholar] [CrossRef]
- Delahaye, J.; Tchuindjang, J.T.; Lecomte-Beckers, J.; Rigo, O.; Habraken, A.M.; Mertens, A. Influence of Si Precipitates on Fracture Mechanisms of AlSi10Mg Parts Processed by Selective Laser Melting. Acta Mater. 2019, 175, 160–170. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, H.; Qi, T.; Hu, Z.; Zeng, X. Selective Laser Melting of High Strength Al–Cu–Mg Alloys: Processing, Microstructure and Mechanical Properties. Mater. Sci. Eng. A 2016, 656, 47–54. [Google Scholar] [CrossRef]
- Karayagiz, K.; Johnson, L.; Seede, R.; Attari, V.; Zhang, B.; Huang, X.; Ghosh, S.; Duong, T.; Karaman, I.; Elwany, A.; et al. Finite Interface Dissipation Phase Field Modeling of Ni–Nb under Additive Manufacturing Conditions. Acta Mater. 2020, 185, 320–339. [Google Scholar] [CrossRef]
- Vrancken, B.; Thijs, L.; Kruth, J.P.; Van Humbeeck, J. Microstructure and Mechanical Properties of a Novel β Titanium Metallic Composite by Selective Laser Melting. Acta Mater. 2014, 68, 150–158. [Google Scholar] [CrossRef]
- Sato, K.; Takagi, S.; Ichikawa, S.; Ishimoto, T.; Nakano, T. Microstructure and Solute Segregation around the Melt-Pool Boundary of Orientation-Controlled 316L Austenitic Stainless Steel Produced by Laser Powder Bed Fusion. Materials 2023, 16, 218. [Google Scholar] [CrossRef]
- Wei, H.L.; Mazumder, J.; Debroy, T. Evolution of Solidification Texture during Additive Manufacturing. Sci. Rep. 2015, 5, 16446. [Google Scholar] [CrossRef]
- Pantawane, M.V.; Sharma, S.; Dasari, S.; Mantri, S.A.; Sharma, A.; Banerjee, R.; Banerjee, S.; Dahotre, N.B. Spatial Variation of Thermokinetics and Associated Microstructural Evolution in Laser Surface Engineered IN718: Precursor to Additive Manufacturing. Metall. Mater. Trans. A 2021, 52, 2344–2360. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; van Humbeeck, J.; Kruth, J.P. A Study of the Microstructural Evolution during Selective Laser Melting of Ti-6Al-4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Liu, J.; Zhang, A.; Zhou, Y.; Wei, Q.; Yan, C.; Shi, Y. Effect of Heat Treatment on AlSi10Mg Alloy Fabricated by Selective Laser Melting: Microstructure Evolution, Mechanical Properties and Fracture Mechanism. Mater. Sci. Eng. A 2016, 663, 116–125. [Google Scholar] [CrossRef]
- Okugawa, M.; Ohigashi, Y.; Furishiro, Y.; Koizumi, Y.; Nakano, T. Equiaxed Grain Formation by Intrinsic Heterogeneous Nucleation via Rapid Heating and Cooling in Additive Manufacturing of Aluminum-Silicon Hypoeutectic Alloy. J. Alloys Compd. 2022, 919, 165812. [Google Scholar] [CrossRef]
- Liu, Y.J.; Liu, Z.; Jiang, Y.; Wang, G.W.; Yang, Y.; Zhang, L.C. Gradient in Microstructure and Mechanical Property of Selective Laser Melted AlSi10Mg. J. Alloys Compd. 2018, 735, 1414–1421. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Y.; Luo, H.; Zhou, B.; Liang, Y.; Liang, Y. Effect of the Boundary Orientation of Melt Pool on Mechanical Property and Fracture Path in Selective-Laser-Melted AlSi10Mg Alloy. Met. Mater. Int. 2022, 28, 2934–2946. [Google Scholar] [CrossRef]
- Shifeng, W.; Shuai, L.; Qingsong, W.; Yan, C.; Sheng, Z.; Yusheng, S. Effect of Molten Pool Boundaries on the Mechanical Properties of Selective Laser Melting Parts. J. Mater. Process Technol. 2014, 214, 2660–2667. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Liu, S.L.; Li, S.F.; Shi, Y.; Yang, Y.F.; Misra, R.D.K. Role of Melt Pool Boundary Condition in Determining the Mechanical Properties of Selective Laser Melting AlSi10Mg Alloy. Mater. Sci. Eng. A 2019, 740–741, 148–156. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, P.; Mooraj, S.; Chen, W. Printability of Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 Metallic Glass on Steel by Laser Additive Manufacturing: A Single-Track Study. Surf. Coat. Technol. 2021, 428, 127882. [Google Scholar] [CrossRef]
- Kudzal, A.; McWilliams, B.; Hofmeister, C.; Kellogg, F.; Yu, J.; Taggart-Scarff, J.; Liang, J. Effect of Scan Pattern on the Microstructure and Mechanical Properties of Powder Bed Fusion Additive Manufactured 17-4 Stainless Steel. Mater. Des. 2017, 133, 205–215. [Google Scholar] [CrossRef]
- Antonysamy, A.A.; Meyer, J.; Prangnell, P.B. Effect of Build Geometry on the β-Grain Structure and Texture in Additive Manufacture of Ti6Al4V by Selective Electron Beam Melting. Mater. Charact. 2013, 84, 153–168. [Google Scholar] [CrossRef]
- Ghorbanpour, S.; Alam, M.E.; Ferreri, N.C.; Kumar, A.; McWilliams, B.A.; Vogel, S.C.; Bicknell, J.; Beyerlein, I.J.; Knezevic, M. Experimental Characterization and Crystal Plasticity Modeling of Anisotropy, Tension-Compression Asymmetry, and Texture Evolution of Additively Manufactured Inconel 718 at Room and Elevated Temperatures. Int. J. Plast. 2020, 125, 63–79. [Google Scholar] [CrossRef]
- Koepf, J.A.; Gotterbarm, M.R.; Markl, M.; Körner, C. 3D Multi-Layer Grain Structure Simulation of Powder Bed Fusion Additive Manufacturing. Acta Mater. 2018, 152, 119–126. [Google Scholar] [CrossRef]
- Raghavan, N.; Dehoff, R.; Pannala, S.; Simunovic, S.; Kirka, M.; Turner, J.; Carlson, N.; Babu, S.S. Numerical Modeling of Heat-Transfer and the Influence of Process Parameters on Tailoring the Grain Morphology of IN718 in Electron Beam Additive Manufacturing. Acta Mater. 2016, 112, 303–314. [Google Scholar] [CrossRef]
- Guan, K.; Wang, Z.; Gao, M.; Li, X.; Zeng, X. Effects of Processing Parameters on Tensile Properties of Selective Laser Melted 304 Stainless Steel. Mater. Des. 2013, 50, 581–586. [Google Scholar] [CrossRef]
- Yin, Y.J.; Sun, J.Q.; Guo, J.; Kan, X.F.; Yang, D.C. Mechanism of High Yield Strength and Yield Ratio of 316 L Stainless Steel by Additive Manufacturing. Mater. Sci. Eng. A 2019, 744, 773–777. [Google Scholar] [CrossRef]
- Andreau, O.; Koutiri, I.; Peyre, P.; Penot, J.D.; Saintier, N.; Pessard, E.; De Terris, T.; Dupuy, C.; Baudin, T. Texture Control of 316L Parts by Modulation of the Melt Pool Morphology in Selective Laser Melting. J. Mater. Process Technol. 2019, 264, 21–31. [Google Scholar] [CrossRef]
- Niendorf, T.; Leuders, S.; Riemer, A.; Richard, H.A.; Tröster, T.; Schwarze, D. Highly Anisotropic Steel Processed by Selective Laser Melting. Metall. Mater. Trans. B 2013, 44B, 794–796. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Zhou, Z.; Wang, K.; Zhan, Q.; Xiao, X. Grain Refinement and Crack Inhibition of Selective Laser Melted AA2024 Aluminum Alloy via Inoculation with TiC–TiH2. Mater. Sci. Eng. A 2021, 813, 141171. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Zhou, Z.; Luo, W.; Zeng, Z. Enhanced Printability and Strength of Unweldable AA2024-Based Nanocomposites Fabricated by Laser Powder Bed Fusion via Nano-TiC-Induced Grain Refinement. Mater. Sci. Eng. A 2022, 856, 144010. [Google Scholar] [CrossRef]
- Tarafder, P.; Rock, C.; Horn, T. Quasi-Static Tensile Properties of Unalloyed Copper Produced by Electron Beam Powder Bed Fusion Additive Manufacturing. Materials 2021, 14, 2932. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Tan, Q.; Yin, Y.; Liu, S.; Li, M.; Li, M.; Liu, Q.; Zhou, Y.; Wu, T.; et al. Additive Manufacturing of High Strength Copper Alloy with Heterogeneous Grain Structure through Laser Powder Bed Fusion. Acta Mater. 2021, 220, 117311. [Google Scholar] [CrossRef]
- Ramirez, D.A.; Murr, L.E.; Martinez, E.; Hernandez, D.H.; Martinez, J.L.; MacHado, B.I.; Medina, F.; Frigola, P.; Wicker, R.B. Novel Precipitate–Microstructural Architecture Developed in the Fabrication of Solid Copper Components by Additive Manufacturing Using Electron Beam Melting. Acta Mater. 2011, 59, 4088–4099. [Google Scholar] [CrossRef]
- Raffeis, I.; Adjei-Kyeremeh, F.; Vroomen, U.; Westhoff, E.; Bremen, S.; Hohoi, A.; Bührig-Polaczek, A. Qualification of a Ni-Cu Alloy for the Laser Powder Bed Fusion Process (LPBF): Its Microstructure and Mechanical Properties. Appl. Sci. 2020, 10, 3401. [Google Scholar] [CrossRef]
- Sun, S.H.; Koizumi, Y.; Kurosu, S.; Li, Y.P.; Chiba, A. Phase and Grain Size Inhomogeneity and Their Influences on Creep Behavior of Co–Cr–Mo Alloy Additive Manufactured by Electron Beam Melting. Acta Mater. 2015, 86, 305–318. [Google Scholar] [CrossRef]
- Chae, H.; Huang, E.W.; Woo, W.; Kang, S.H.; Jain, J.; An, K.; Lee, S.Y. Unravelling Thermal History during Additive Manufacturing of Martensitic Stainless Steel. J. Alloys Compd. 2021, 857, 157555. [Google Scholar] [CrossRef] [PubMed]
- Piette, T.D.; Warren, R.J.; Spangenberger, A.G.; Hummelt, E.J.; Lados, D.A. Microstructure Evolution, Fatigue Crack Growth, and Ultrasonic Fatigue in As-Fabricated Laser Powder Bed and Conventionally Cast Al–10Si-0.4Mg: A Mechanistic Understanding and Integrated Flaw-Sensitive Fatigue Design Methods. Mater. Sci. Eng. A 2021, 825, 141892. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Li, X. An Overview of Residual Stresses in Metal Powder Bed Fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Salmi, A.; Atzeni, E. History of Residual Stresses during the Production Phases of AlSi10Mg Parts Processed by Powder Bed Additive Manufacturing Technology. Virtual Phys. Prototyp. 2017, 12, 153–160. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.Y.; Fang, X.Y.; Guo, Y.B. Residual Stress in Metal Additive Manufacturing. Procedia CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Tradowsky, U.; White, J.; Ward, R.M.; Read, N.; Reimers, W.; Attallah, M.M. Selective Laser Melting of AlSi10Mg: Influence of Post-Processing on the Microstructural and Tensile Properties Development. Mater. Des. 2016, 105, 212–222. [Google Scholar] [CrossRef]
- Liu, M.; Wada, T.; Suzuki, A.; Takata, N.; Kobashi, M.; Kato, M. Effect of Annealing on Anisotropic Tensile Properties of Al-12%Si Alloy Fabricated by Laser Powder Bed Fusion. Crystals 2020, 10, 1007. [Google Scholar] [CrossRef]
- Chen, S.; Tan, Q.; Gao, W.; Wu, G.; Fan, J.; Feng, Z.; Huang, T.; Godfrey, A.W.; Zhang, M.; Huang, X. Effect of Heat Treatment on the Anisotropy in Mechanical Properties of Selective Laser Melted AlSi10Mg. Mater. Sci. Eng. A 2022, 858, 144130. [Google Scholar] [CrossRef]
- Ch, S.R.; Raja, A.; Nadig, P.; Jayaganthan, R.; Vasa, N.J. Influence of Working Environment and Built Orientation on the Tensile Properties of Selective Laser Melted AlSi10Mg Alloy. Mater. Sci. Eng. A 2019, 750, 141–151. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Scudino, S.; Klauss, H.J.; Surreddi, K.B.; Löber, L.; Wang, Z.; Chaubey, A.K.; Kühn, U.; Eckert, J. Microstructure and Mechanical Properties of Al–12Si Produced by Selective Laser Melting: Effect of Heat Treatment. Mater. Sci. Eng. A 2014, 590, 153–160. [Google Scholar] [CrossRef]
- Popovich, V.A.; Borisov, E.V.; Popovich, A.A.; Sufiiarov, V.S.; Masaylo, D.V.; Alzina, L. Functionally Graded Inconel 718 Processed by Additive Manufacturing: Crystallographic Texture, Anisotropy of Microstructure and Mechanical Properties. Mater. Des. 2017, 114, 441–449. [Google Scholar] [CrossRef]
- Shamsujjoha, M.; Agnew, S.R.; Fitz-Gerald, J.M.; Moore, W.R.; Newman, T.A. High Strength and Ductility of Additively Manufactured 316L Stainless Steel Explained. Metall. Mater. Trans. A 2018, 49A, 3011–3027. [Google Scholar] [CrossRef]
- Maeshima, T.; Oh-ishi, K. Solute Clustering and Supersaturated Solid Solution of AlSi10Mg Alloy Fabricated by Selective Laser Melting. Heliyon 2019, 5, e01186. [Google Scholar] [CrossRef]
- Zyguła, K.; Pasiowiec, H.; Nosek, B.; Szysiak, N. Mechanical Properties and Microstructure of AlSi10Mg Alloy Obtained by Casting and SLM Technique. World Sci. News 2018, 104, 462–472. [Google Scholar]
- Ghassemali, E.; Riestra, M.; Bogdanoff, T.; Kumar, B.S.; Seifeddine, S. Hall-Petch Equation in a Hypoeutectic Al-Si Cast Alloy: Grain Size vs. Secondary Dendrite Arm Spacing. Procedia Eng. 2017, 207, 19–24. [Google Scholar] [CrossRef]
- Riemer, A.; Leuders, S.; Thöne, M.; Richard, H.A.; Tröster, T.; Niendorf, T. On the Fatigue Crack Growth Behavior in 316L Stainless Steel Manufactured by Selective Laser Melting. Eng. Fract. Mech. 2014, 120, 15–25. [Google Scholar] [CrossRef]
- Saeidi, K.; Gao, X.; Zhong, Y.; Shen, Z.J. Hardened Austenite Steel with Columnar Sub-Grain Structure Formed by Laser Melting. Mater. Sci. Eng. A 2015, 625, 221–229. [Google Scholar] [CrossRef]
- Kong, D.; Dong, C.; Ni, X.; Zhang, L.; Yao, J.; Man, C.; Cheng, X.; Xiao, K.; Li, X. Mechanical Properties and Corrosion Behavior of Selective Laser Melted 316L Stainless Steel after Different Heat Treatment Processes. J. Mater. Sci. Technol. 2019, 35, 1499–1507. [Google Scholar] [CrossRef]
- Tolosa, I.; Garciandía, F.; Zubiri, F.; Zapirain, F.; Esnaola, A. Study of Mechanical Properties of AISI 316 Stainless Steel Processed by “Selective Laser Melting”, Following Different Manufacturing Strategies. Int. J. Adv. Manuf. Technol. 2010, 51, 639–647. [Google Scholar] [CrossRef]
- Bayat, M.; Zinovieva, O.; Ferrari, F.; Ayas, C.; Langelaar, M.; Spangenberg, J.; Salajeghe, R.; Poulios, K.; Mohanty, S.; Sigmund, O.; et al. Holistic Computational Design within Additive Manufacturing through Topology Optimization Combined with Multiphysics Multi-Scale Materials and Process Modelling. Prog. Mater. Sci. 2023, 138, 101129. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, F.; Huang, Z.; Jia, M.; Chen, G.; Ye, Y.; Lin, Y.; Liu, W.; Chen, B.; Shen, Q.; et al. Additive Manufacturing of Functionally Graded Materials: A Review. Mater. Sci. Eng. A 2019, 764, 138209. [Google Scholar] [CrossRef]
- Reichardt, A.; Shapiro, A.A.; Otis, R.; Dillon, R.P.; Borgonia, J.P.; Mcenerney, B.W.; Hosemann, P.; Beese, A.M. Advances in Additive Manufacturing of Metal-Based Functionally Graded Materials. Int. Mater. Rev. 2021, 66, 1–29. [Google Scholar] [CrossRef]
- Fomin, V.M.; Malikov, A.G.; Golyshev, A.A.; Bulina, N.V.; Ancharov, A.I.; Vitoshkin, I.E.; Brusentseva, T.A.; Filippov, A.A. In-Situ Reactions during Direct Laser Deposition of a Functionally Gradient Ti64-B Composite. Phys. Mesomech. 2022, 25, 505–513. [Google Scholar] [CrossRef]
- Wu, X.; Su, Y.; Shi, J. Perspective of Additive Manufacturing for Metamaterials Development. Smart Mater. Struct. 2019, 28, 093001. [Google Scholar] [CrossRef]
- Li, Z.; Gao, W.; Yu Wang, M.; Luo, Z. Design of Multi-Material Isotropic Auxetic Microlattices with Zero Thermal Expansion. Mater. Des. 2022, 222, 111051. [Google Scholar] [CrossRef]
- Siddique, S.H.; Hazell, P.J.; Wang, H.; Escobedo, J.P.; Ameri, A.A.H. Lessons from Nature: 3D Printed Bio-Inspired Porous Structures for Impact Energy Absorption—A Review. Addit. Manuf. 2022, 58, 103051. [Google Scholar] [CrossRef]
- Islam, M.K.; Hazell, P.J.; Escobedo, J.P.; Wang, H. Biomimetic Armour Design Strategies for Additive Manufacturing: A Review. Mater. Des. 2021, 205, 109730. [Google Scholar] [CrossRef]
- Seifi, M.; Shamsaei, N. Perspectives on Advancing Qualification and Certification for Additive Manufacturing. In Proceedings of the International Conference on Materials for Advanced Technologies 2023, Singapore, 26–30 June 2023. [Google Scholar]
- Pauza, J.; Rollett, A. Simulation Study of Hatch Spacing and Layer Thickness Effects on Microstructure in Laser Powder Bed Fusion Additive Manufacturing Using a Texture-Aware Solidification Potts Model. J. Mater. Eng. Perform. 2021, 30, 7007–7018. [Google Scholar] [CrossRef]
- Yan, W.; Lian, Y.; Yu, C.; Kafka, O.L.; Liu, Z.; Liu, W.K.; Wagner, G.J. An Integrated Process–Structure–Property Modeling Framework for Additive Manufacturing. Comput. Methods Appl. Mech. Eng. 2018, 339, 184–204. [Google Scholar] [CrossRef]
- Romanova, V.; Mohebbi, M.S.; Dymnich, E.; Balokhonov, R.; Ploshikhin, V. A Physically-Based Computational Approach for Processing-Microstructure-Property Linkage of Materials Additively Manufactured by Laser Powder Bed Fusion. Int. J. Mech. Sci. 2022, 219, 107103. [Google Scholar] [CrossRef]
- Raabe, D.; Roters, F.; Barlat, F.; Chen, L. (Eds.) Continuum Scale Simulation of Engineering Materials; Wiley: Hoboken, NJ, USA, 2004; ISBN 9783527307609. [Google Scholar]
- Horstemeyer, M.F. Integrated Computational Materials Engineering (ICME) for Metals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 9781118342664. [Google Scholar]
- Schmauder, S.; Schäfer, I. (Eds.) Multiscale Materials Modeling. Approaches to Full Multiscaling; De Gruyter: Berlin, Germany, 2016; ISBN 9783110412451. [Google Scholar]
- Kwon, Y.W. Multiphysics and Multiscale Modeling; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9780429154423. [Google Scholar]
- Ghafouri, M.; Amraei, M.; Gopaluni, A.; Piili, H.; Björk, T.; Hämäläinen, J. Simulation and Its Use in Additive Manufacturing. In Impact of Scientific Computing on Science and Society; Neittaanmäki, P., Rantalainen, M.-L., Eds.; Springer: Cham, Switzerland, 2023; Volume 58, pp. 111–126. [Google Scholar]
- Lammens, N.; Gallego-Bordallo, F.; Ni, J.; Zinoviev, A.; de Weer, T.; Erdelyi, H. The Role of Simulation in the Industrialization of Additive Manufacturing. Procedia Struct. Integr. 2021, 34, 247–252. [Google Scholar] [CrossRef]
- Wimler, D.; Käsznar, K.; Musi, M.; Breuning, C.; Markl, M.; Keckes, J.; Clemens, H.; Körner, C.; Mayer, S. How Electron Beam Melting Tailors the Al-Sensitive Microstructure and Mechanical Response of a Novel Process-Adapted γ-TiAl Based Alloy. Mater. Des. 2021, 212, 110187. [Google Scholar] [CrossRef]
- Gouge, M.; Denlinger, E.; Irwin, J.; Li, C.; Michaleris, P. Experimental Validation of Thermo-Mechanical Part-Scale Modeling for Laser Powder Bed Fusion Processes. Addit. Manuf. 2019, 29, 100771. [Google Scholar] [CrossRef]
- Roehling, J.D.; Khairallah, S.A.; Shen, Y.; Bayramian, A.; Boley, C.D.; Rubenchik, A.M.; DeMuth, J.; Duanmu, N.; Matthews, M.J. Physics of Large-Area Pulsed Laser Powder Bed Fusion. Addit. Manuf. 2021, 46, 102186. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Balokhonov, R. Predictive Simulation of Microstructural Pattern in Additively Manufactured Metallic Materials. In Quality Analysis of Additively Manufactured Metals; Kadkhodapour, J., Schmauder, S., Sajadi, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 547–582. [Google Scholar]
- Tunay, M.; Baykasoğlu, C.; Akyildiz, O.; To, A.C. A Fully Coupled Thermal–Microstructural–Mechanical Finite Element Process Model for Directed Energy Deposition Additive Manufacturing of Ti–6Al–4V. Sci. Technol. Weld. Join. 2023, 28, 118–127. [Google Scholar] [CrossRef]
- Malmelöv, A.; Lundbäck, A.; Lindgren, L.-E. History Reduction by Lumping for Time-Efficient Simulation of Additive Manufacturing. Metals 2019, 10, 58. [Google Scholar] [CrossRef]
- Körner, C.; Attar, E.; Heinl, P. Mesoscopic Simulation of Selective Beam Melting Processes. J. Mater. Process Technol. 2011, 211, 978–987. [Google Scholar] [CrossRef]
- Haeri, S.; Wang, Y.; Ghita, O.; Sun, J. Discrete Element Simulation and Experimental Study of Powder Spreading Process in Additive Manufacturing. Powder Technol. 2017, 306, 45–54. [Google Scholar] [CrossRef]
- Megahed, M.; Mindt, H.-W.; Duan, H.; Desmaison, O. Metal Additive-Manufacturing Process and Residual Stress Modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef]
- Bayat, M.; Dong, W.; Thorborg, J.; To, A.C.; Hattel, J.H. A Review of Multi-Scale and Multi-Physics Simulations of Metal Additive Manufacturing Processes with Focus on Modeling Strategies. Addit. Manuf. 2021, 47, 102278. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Ploshikhin, V. Three-Dimensional Modeling of the Microstructure Evolution during Metal Additive Manufacturing. Comput. Mater. Sci. 2018, 141, 207–220. [Google Scholar] [CrossRef]
- Rodgers, T.M.; Moser, D.; Abdeljawad, F.; Jackson, O.D.U.; Carroll, J.D.; Jared, B.H.; Bolintineanu, D.S.; Mitchell, J.A.; Madison, J.D. Simulation of Powder Bed Metal Additive Manufacturing Microstructures with Coupled Finite Difference-Monte Carlo Method. Addit. Manuf. 2021, 41, 101953. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser Powder-Bed Fusion Additive Manufacturing: Physics of Complex Melt Flow and Formation Mechanisms of Pores, Spatter, and Denudation Zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef]
- Zakirov, A.; Belousov, S.; Bogdanova, M.; Korneev, B.; Stepanov, A.; Perepelkina, A.; Levchenko, V.; Meshkov, A.; Potapkin, B. Predictive Modeling of Laser and Electron Beam Powder Bed Fusion Additive Manufacturing of Metals at the Mesoscale. Addit. Manuf. 2020, 35, 101236. [Google Scholar] [CrossRef]
- Dorussen, B.J.A.; Geers, M.G.D.; Remmers, J.J.C. An Efficient Ray Tracing Methodology for the Numerical Analysis of Powder Bed Additive Manufacturing Processes. Addit. Manuf. 2023, 73, 103706. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J.H. A Systematic Investigation of the Effects of Process Parameters on Heat and Fluid Flow and Metallurgical Conditions during Laser-Based Powder Bed Fusion of Ti6Al4V Alloy. Int. J. Heat. Mass. Transf. 2019, 139, 213–230. [Google Scholar] [CrossRef]
- Zhavoronok, S.I.; Kurbatov, A.S.; Rabinskiy, L.N.; Solyaev, Y.O. Recent Problems of Heat-Transfer Simulation in Technological Processes of Selective Laser Melting and Fusion. High Temp. 2019, 57, 916–943. [Google Scholar] [CrossRef]
- Keller, T.; Lindwall, G.; Ghosh, S.; Ma, L.; Lane, B.M.; Zhang, F.; Kattner, U.R.; Lass, E.A.; Heigel, J.C.; Idell, Y.; et al. Application of Finite Element, Phase-Field, and CALPHAD-Based Methods to Additive Manufacturing of Ni-Based Superalloys. Acta Mater. 2017, 139, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.X.; Sridhar, N.; Zhang, Y.W. Phase Field Simulation of Powder Bed-Based Additive Manufacturing. Acta Mater. 2018, 144, 801–809. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Yan, W. Phase-Field Modeling of Grain Evolutions in Additive Manufacturing from Nucleation, Growth, to Coarsening. NPJ Comput. Mater. 2021, 7, 56. [Google Scholar] [CrossRef]
- Agius, D.; O’Toole, P.; Wallbrink, C.; Sterjovski, Z.; Wang, C.-H.; Schaffer, G.B. Integrating Phase Field and Crystal Plasticity Finite Element Models for Simulations of Titanium Alloy Ti-5553. J. Phys. Mater. 2021, 4, 44014. [Google Scholar] [CrossRef]
- Akram, J.; Chalavadi, P.; Pal, D.; Stucker, B. Understanding Grain Evolution in Additive Manufacturing through Modeling. Addit. Manuf. 2018, 21, 255–268. [Google Scholar] [CrossRef]
- Zinoviev, A.; Zinovieva, O.; Ploshikhin, V.; Romanova, V.; Balokhonov, R. Evolution of Grain Structure during Laser Additive Manufacturing. Simulation by a Cellular Automata Method. Mater. Des. 2016, 106, 321–329. [Google Scholar] [CrossRef]
- Mohebbi, M.S.; Ploshikhin, V. Implementation of Nucleation in Cellular Automaton Simulation of Microstructural Evolution during Additive Manufacturing of Al Alloys. Addit. Manuf. 2020, 36, 101726. [Google Scholar] [CrossRef]
- Rodgers, T.M.; Madison, J.D.; Tikare, V. Simulation of Metal Additive Manufacturing Microstructures Using Kinetic Monte Carlo. Comput. Mater. Sci. 2017, 135, 78–89. [Google Scholar] [CrossRef]
- Körner, C.; Markl, M.; Koepf, J.A. Modeling and Simulation of Microstructure Evolution for Additive Manufacturing of Metals: A Critical Review. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2020, 51, 4970–4983. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Romanova, V.; Balokhonov, R. Three-Dimensional Analysis of Grain Structure and Texture of Additively Manufactured 316L Austenitic Stainless Steel. Addit. Manuf. 2020, 36, 101521. [Google Scholar] [CrossRef]
- Wang, X.; Chou, K. Electron Backscatter Diffraction Analysis of Inconel 718 Parts Fabricated by Selective Laser Melting Additive Manufacturing. JOM 2017, 69, 402–408. [Google Scholar] [CrossRef]
- Choi, J.P.; Shin, G.H.; Yang, S.; Yang, D.Y.; Lee, J.S.; Brochu, M.; Yu, J.H. Densification and Microstructural Investigation of Inconel 718 Parts Fabricated by Selective Laser Melting. Powder Technol. 2017, 310, 60–66. [Google Scholar] [CrossRef]
- Parimi, L.L.; Ravi, G.; Clark, D.; Attallah, M.M. Microstructural and Texture Development in Direct Laser Fabricated IN718. Mater. Charact. 2014, 89, 102–111. [Google Scholar] [CrossRef]
- Taheri Andani, M.; Ghodrati, M.; Karamooz-Ravari, M.R.; Mirzaeifar, R.; Ni, J. Damage Modeling of Metallic Alloys Made by Additive Manufacturing. Mater. Sci. Eng. A 2019, 743, 656–664. [Google Scholar] [CrossRef]
- Charmi, A.; Falkenberg, R.; Ávila, L.; Mohr, G.; Sommer, K.; Ulbricht, A.; Sprengel, M.; Saliwan Neumann, R.; Skrotzki, B.; Evans, A. Mechanical Anisotropy of Additively Manufactured Stainless Steel 316L: An Experimental and Numerical Study. Mater. Sci. Eng. A 2021, 799, 140154. [Google Scholar] [CrossRef]
- Yeratapally, S.R.; Lang, C.G.; Cerrone, A.R.; Niebur, G.L.; Cronberger, K. Effect of Defects on the Constant-Amplitude Fatigue Behavior of as-Built Ti-6Al-4V Alloy Produced by Laser Powder Bed Fusion Process: Assessing Performance with Metallographic Analysis and Micromechanical Simulations. Addit. Manuf. 2022, 52, 102639. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R. A Method of Step-by-Step Packing and Its Application in Generating 3D Microstructures of Polycrystalline and Composite Materials. Eng. Comput. 2021, 37, 241–250. [Google Scholar] [CrossRef]
- Mandal, S.; Lao, J.; Donegan, S.; Rollett, A.D. Generation of Statistically Representative Synthetic Three-Dimensional Microstructures. Scr. Mater. 2018, 146, 128–132. [Google Scholar] [CrossRef]
- Dionyssopoulos, C.; Wallbrink, C.; Agius, D.; Qiu, D.; Easton, M.; Barter, S.; Das, R. A Comparison of Length Scale Dependent Classical Crystal Plasticity Models for Modelling the Deformation of Additively Manufactured Ti-6Al-4V. In Proceedings of the AIAC 2023: 20th Australian International Aerospace Congress, Engineers Australia, Melbourne, Australia, 27 February–1 March 2023; pp. 266–271. [Google Scholar]
- Tang, H.; Huang, H.; Liu, C.; Liu, Z.; Yan, W. Multi-Scale Modelling of Structure-Property Relationship in Additively Manufactured Metallic Materials. Int. J. Mech. Sci. 2021, 194, 106185. [Google Scholar] [CrossRef]
- Wang, P.; Lei, H.; Zhu, X.; Chen, H.; Fang, D. Influence of Manufacturing Geometric Defects on the Mechanical Properties of AlSi10Mg Alloy Fabricated by Selective Laser Melting. J. Alloys Compd. 2019, 789, 852–859. [Google Scholar] [CrossRef]
- Dymnich, E.; Romanova, V.A.; Balokhonov, R.R.; Zinovieva, O.S.; Zinoviev, A.V. A Numerical Study of the Stress-Strain Behavior of Additively Manufactured Aluminum-Silicon Alloy at the Scale of Dendritic Structure. Phys. Mesomech. 2021, 24, 51–60. [Google Scholar] [CrossRef]
- Cocke, C.K.; Rollett, A.D.; Lebensohn, R.A.; Spear, A.D. The AFRL Additive Manufacturing Modeling Challenge: Predicting Micromechanical Fields in AM IN625 Using an FFT-Based Method with Direct Input from a 3D Microstructural Image. Integr. Mater. Manuf. Innov. 2021, 10, 157–176. [Google Scholar] [CrossRef]
- Furushima, T.; Masuda, T.; Manabe, K.; Alexandrov, S. Prediction of Free Surface Roughening by 2D and 3D Model Considering Material Inhomogeneity. J. Solid Mech. Mater. Eng. 2011, 5, 978–990. [Google Scholar] [CrossRef][Green Version]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.-O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for Modeling Multi-Physics Crystal Plasticity, Thermal, and Damage Phenomena from the Single Crystal up to the Component Scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Romanova, V.A.; Balokhonov, R.R.; Batukhtina, E.E.; Emelianova, E.S.; Sergeev, M.V. On the Solution of Quasi-Static Micro- and Mesomechanical Problems in a Dynamic Formulation. Phys. Mesomech. 2019, 22, 296–306. [Google Scholar] [CrossRef]
- Balokhonov, R.; Romanova, V.; Batukhtina, E.; Martynov, S.; Zinoviev, A.; Zinovieva, O. A Mesomechanical Analysis of the Stress–Strain Localisation in Friction Stir Welds of Polycrystalline Aluminium Alloys. Meccanica 2016, 51, 319–328. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Prediction of Flow Stress and Surface Roughness of Stainless Steel Sheets Considering an Inhomogeneous Microstructure. Mater. Sci. Eng. A 2016, 678, 377–388. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile Deformation. Trans. AIME 1945, 112, 268. [Google Scholar]
- Sufiiarov, V.S.; Orlov, A.V.; Borisov, E.V.; Polozov, I.A.; Popovich, A.A.; Chukovenkova, M.O.; Soklakov, A.V.; Mikhaluk, D.S. Computer Modelling of Uniaxial Tension of Functionally Gradient Material Produced by Additive Manufacturing. Tech. Phys. 2021, 66, 23–27. [Google Scholar] [CrossRef]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.A.; Schaedler, T.A.; Pollock, T.M. 3D Printing of High-Strength Aluminium Alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef]
- Hofer, A.K.; Kocjan, A.; Bermejo, R. High-Strength Lithography-Based Additive Manufacturing of Ceramic Components with Rapid Sintering. Addit. Manuf. 2022, 59, 103141. [Google Scholar] [CrossRef]
- Ng, C.H.; Bermingham, M.J.; Yuan, L.; Dargusch, M.S. Towards β-Fleck Defect Free Additively Manufactured Titanium Alloys by Promoting the Columnar to Equiaxed Transition and Grain Refinement. Acta Mater. 2022, 224, 117511. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Zinoviev, A.; Nekhorosheva, O.; Balokhonov, R. Elastic Properties of Additively Manufactured Steel Produced with Different Scan Strategies. Int. J. Mech. Sci. 2023, 244, 108089. [Google Scholar] [CrossRef]
- Musienko, A. Plasticité Cristalline En Présence de Grandes Déformations et D’endommagement. Ph.D. Thesis, Centre des Matériaux P.M. FOURT de l’Ecole des Mines de Paris, Evry, France, 2005. [Google Scholar]
- Motaman, S.A.H.; Roters, F.; Haase, C. Anisotropic Polycrystal Plasticity Due to Microstructural Heterogeneity: A Multi-Scale Experimental and Numerical Study on Additively Manufactured Metallic Materials. Acta Mater. 2020, 185, 340–369. [Google Scholar] [CrossRef]
- Kalidindi, S.R. Incorporation of Deformation Twinning in Crystal Plasticity Models. J. Mech. Phys. Solids 1998, 46, 267–290. [Google Scholar] [CrossRef]
- Ji, H.; Song, Q.; Wang, R.; Cai, W.; Liu, Z. Evaluation and Prediction of Pore Effects on Single-Crystal Mechanical and Damage Properties of Selective Laser Melted Inconel-718. Mater. Des. 2022, 219, 110807. [Google Scholar] [CrossRef]
- Prithivirajan, V.; Sangid, M.D. The Role of Defects and Critical Pore Size Analysis in the Fatigue Response of Additively Manufactured IN718 via Crystal Plasticity. Mater. Des. 2018, 150, 139–153. [Google Scholar] [CrossRef]
- Cheng, J.; Fernandez-Zelaia, P.; Hu, X.; Kirka, M. Effect of Microstructure on Fatigue Crack Propagation in Additive Manufactured Nickel-Based Superalloy Haynes 282: An Experiment and Crystal Plasticity Study. J. Mater. Sci. 2022, 57, 9741–9768. [Google Scholar] [CrossRef]
- Cailletaud, G.; Chaboche, J.-L.; Forest, S.; Rémy, L. On the Design of Single Crystal Turbine Blades. Rev. Métallurgie 2003, 100, 165–172. [Google Scholar] [CrossRef]
- Yalcinkaya, T. Microstructure Evolution in Crystal Plasticity: Strain Path Effects and Dislocation Slip Patterning. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2011. [Google Scholar]
- Lindroos, M.; Pinomaa, T.; Antikainen, A.; Lagerbom, J.; Reijonen, J.; Lindroos, T.; Andersson, T.; Laukkanen, A. Micromechanical Modeling Approach to Single Track Deformation, Phase Transformation and Residual Stress Evolution during Selective Laser Melting Using Crystal Plasticity. Addit. Manuf. 2021, 38, 101819. [Google Scholar] [CrossRef]
- Hadadzadeh, A.; Baxter, C.; Amirkhiz, B.S.; Mohammadi, M. Strengthening Mechanisms in Direct Metal Laser Sintered AlSi10Mg: Comparison between Virgin and Recycled Powders. Addit. Manuf. 2018, 23, 108–120. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Tuck, C.; Ashcroft, I.; Maskery, I.; Everitt, N.M. On the Precipitation Hardening of Selective Laser Melted AlSi10Mg. Metall. Mater. Trans. A 2015, 46, 3337–3341. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An Analysis of Nonuniform and Localized Deformation in Ductile Single Crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Taheri Andani, M.; Karamooz-Ravari, M.R.; Mirzaeifar, R.; Ni, J. Micromechanics Modeling of Metallic Alloys 3D Printed by Selective Laser Melting. Mater. Des. 2018, 137, 204–213. [Google Scholar] [CrossRef]
- Anand, L.; Kothari, M. A Computational Procedure for Rate-Independent Crystal Plasticity. J. Mech. Phys. Solids 1996, 44, 525–558. [Google Scholar] [CrossRef]
- Besson, J.; Foerch, R. Object-Oriented Programming Applied to the Finite Element Method Part I. General Concepts. Rev. Eur. Éléments Finis 1998, 7, 535–566. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, J.; Xu, M.; Zhao, H.; Wang, M.; Wang, M.; Zhang, A. The Preparation of H13 Steel for TBM Cutter and the Performance Test Close to Working Condition. Appl. Sci. 2018, 8, 1877. [Google Scholar] [CrossRef]
- Song, D.; Xiao, X.; Xue, J.; Chu, H.; Duan, H. Mechanical Properties of Irradiated Multi-Phase Polycrystalline BCC Materials. Acta Mech. Sin. 2015, 31, 191–204. [Google Scholar] [CrossRef]
- Monnet, G.; Vincent, L.; Gélébart, L. Multiscale Modeling of Crystal Plasticity in Reactor Pressure Vessel Steels: Prediction of Irradiation Hardening. J. Nucl. Mater. 2019, 514, 128–138. [Google Scholar] [CrossRef]
- Ozturk, T.; Rollett, A.D. Effect of Microstructure on the Elasto-Viscoplastic Deformation of Dual Phase Titanium Structures. Comput. Mech. 2018, 61, 55–70. [Google Scholar] [CrossRef]
- Facchini, L.; Magalini, E.; Robotti, P.; Molinari, A. Microstructure and Mechanical Properties of Ti-6Al-4V Produced by Electron Beam Melting of Pre-alloyed Powders. Rapid Prototyp. J. 2009, 15, 171–178. [Google Scholar] [CrossRef]
- Zhang, X.X.; Andrä, H. Crystal Plasticity Simulation of the Macroscale and Microscale Stress–Strain Relations of Additively Manufactured AlSi10Mg Alloy. Comput. Mater. Sci. 2021, 200, 110832. [Google Scholar] [CrossRef]
- Zhang, X.X.; Lutz, A.; Andrä, H.; Lahres, M.; Gan, W.M.; Maawad, E.; Emmelmann, C. Evolution of Microscopic Strains, Stresses, and Dislocation Density during in-Situ Tensile Loading of Additively Manufactured AlSi10Mg Alloy. Int. J. Plast. 2021, 139, 102946. [Google Scholar] [CrossRef]
- Song, L.; Yuan, S.; Zhao, L.; Zhu, Y.; Liang, S.; Huang, M.; Simar, A.; Li, Z. Deciphering Phase Stress Partition and Its Correlation to Mechanical Anisotropy of Laser Powder Bed Fusion AlSi10Mg. Addit. Manuf. 2023, 71, 103594. [Google Scholar] [CrossRef]
- Song, L.; Zhao, L.; Ding, L.; Zhu, Y.; Huang, M.; Simar, A.; Li, Z. Microstructure and Loading Direction Dependent Hardening and Damage Behavior of Laser Powder Bed Fusion AlSi10Mg. Mater. Sci. Eng. A 2022, 832, 142484. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the Abaqus Finite Element Program; Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- Han, C.S.; Gao, H.; Huang, Y.; Nix, W.D. Mechanism-Based Strain Gradient Crystal Plasticity—I. Theory. J. Mech. Phys. Solids 2005, 53, 1188–1203. [Google Scholar] [CrossRef]
- Kuo, C.N.; Chua, C.K.; Peng, P.C.; Chen, Y.W.; Sing, S.L.; Huang, S.; Su, Y.L. Microstructure Evolution and Mechanical Property Response via 3D Printing Parameter Development of Al-Sc Alloy. Virtual Phys. Prototyp. 2019, 15, 120–129. [Google Scholar] [CrossRef]
- Leicht, A.; Rashidi, M.; Klement, U.; Hryha, E. Effect of Process Parameters on the Microstructure, Tensile Strength and Productivity of 316L Parts Produced by Laser Powder Bed Fusion. Mater. Charact. 2020, 159, 110016. [Google Scholar] [CrossRef]
- Zinovieva, O.; Romanova, V.; Balokhonov, R. Effect of Hatch Distance on the Microstructure of Additively Manufactured 316 L Steel. AIP Conf. Proc. 2020, 2310, 020363. [Google Scholar] [CrossRef]
- Patel, M.N.; Qiu, D.; Wang, G.; Gibson, M.A.; Prasad, A.; StJohn, D.H.; Easton, M.A. Understanding the Refinement of Grains in Laser Surface Remelted Al–Cu Alloys. Scr. Mater. 2020, 178, 447–451. [Google Scholar] [CrossRef]
- Gong, X.; Lydon, J.; Cooper, K.; Chou, K. Beam Speed Effects on Ti–6Al–4V Microstructures in Electron Beam Additive Manufacturing. J. Mater. Res. 2014, 29, 1951–1959. [Google Scholar] [CrossRef]
- Cao, M.; Liu, Y.; Dunne, F.P.E. A Crystal Plasticity Approach to Understand Fatigue Response with Respect to Pores in Additive Manufactured Aluminium Alloys. Int. J. Fatigue 2022, 161, 106917. [Google Scholar] [CrossRef]
- Balokhonov, R.R.; Zinovyev, A.V.; Romanova, V.A.; Bakeev, R.A.; Zinovyeva, O.S. Numerical Simulation of Deformation and Fracture of a Material with a Polysilazane-Based Coating. Phys. Mesomech. 2016, 19, 430–440. [Google Scholar] [CrossRef]
- Konovalenko, I.S.; Shilko, E.V.; Sharkeev, Y.P. Computer-Aided Study of the Mechanical Behavior of the Porous Ceramic Based Composite with Plastic Pore Filler. AIP Conf. Proc. 2018, 2051, 020130. [Google Scholar] [CrossRef]
- Rodgers, T.M.; Bishop, J.E.; Madison, J.D. Direct Numerical Simulation of Mechanical Response in Synthetic Additively Manufactured Microstructures. Model. Simul. Mat. Sci. Eng. 2018, 26, 055010. [Google Scholar] [CrossRef]
- Li, P.; Kim, Y.; Bobel, A.C.; Hector, L.G.; Sachdev, A.K.; Kumar, S.; Bower, A.F. Microstructural Origin of the Anisotropic Flow Stress of Laser Powder Bed Fused AlSi10Mg. Acta Mater. 2021, 220, 117346. [Google Scholar] [CrossRef]
- Herriott, C.; Li, X.; Kouraytem, N.; Tari, V.; Tan, W.; Anglin, B.; Rollett, A.D.; Spear, A.D. A Multi-Scale, Multi-Physics Modeling Framework to Predict Spatial Variation of Properties in Additive-Manufactured Metals. Model. Simul. Mat. Sci. Eng. 2019, 27, 025009. [Google Scholar] [CrossRef]
- Upadhyay, M.V.; Capek, J.; Van Petegem, S.; Lebensohn, R.A.; Van Swygenhoven, H. Intergranular Strain Evolution during Biaxial Loading: A Multiscale FE-FFT Approach. JOM 2017, 69, 839–847. [Google Scholar] [CrossRef]
- Loginova, I.S.; Bykovskiy, D.P.; Solonin, A.N.; Prosviryakov, A.S.; Cheverikin, V.V.; Pozdniakov, A.V.; Petrovskiy, V.N. Peculiarities of the Microstructure and Properties of Parts Produced by the Direct Laser Deposition of 316L Steel Powder. Russ. J. Non-Ferr. Met. 2019, 60, 87–94. [Google Scholar] [CrossRef]
- Mendagaliev, R.V.; Evdokimov, D.D.; Firsov, A.M.; Vildanov, A.M.; Evstifeev, A.D.; Maksimochkin, V.I.; Grachev, R.A.; Dubinin, O.N.; Evlashin, S.A.; Klimova-Korsmik, O.G. Direct Laser Deposition of Austenitic and Martensitic Steel Gradient Layers. Met. Mater. Int. 2023, 29, 1555–1562. [Google Scholar] [CrossRef]
- Eliseeva, O.V. Utilizing the Structure-Property Relationship of Porosity and Composition in Additively Manufactured Metallic Systems. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]


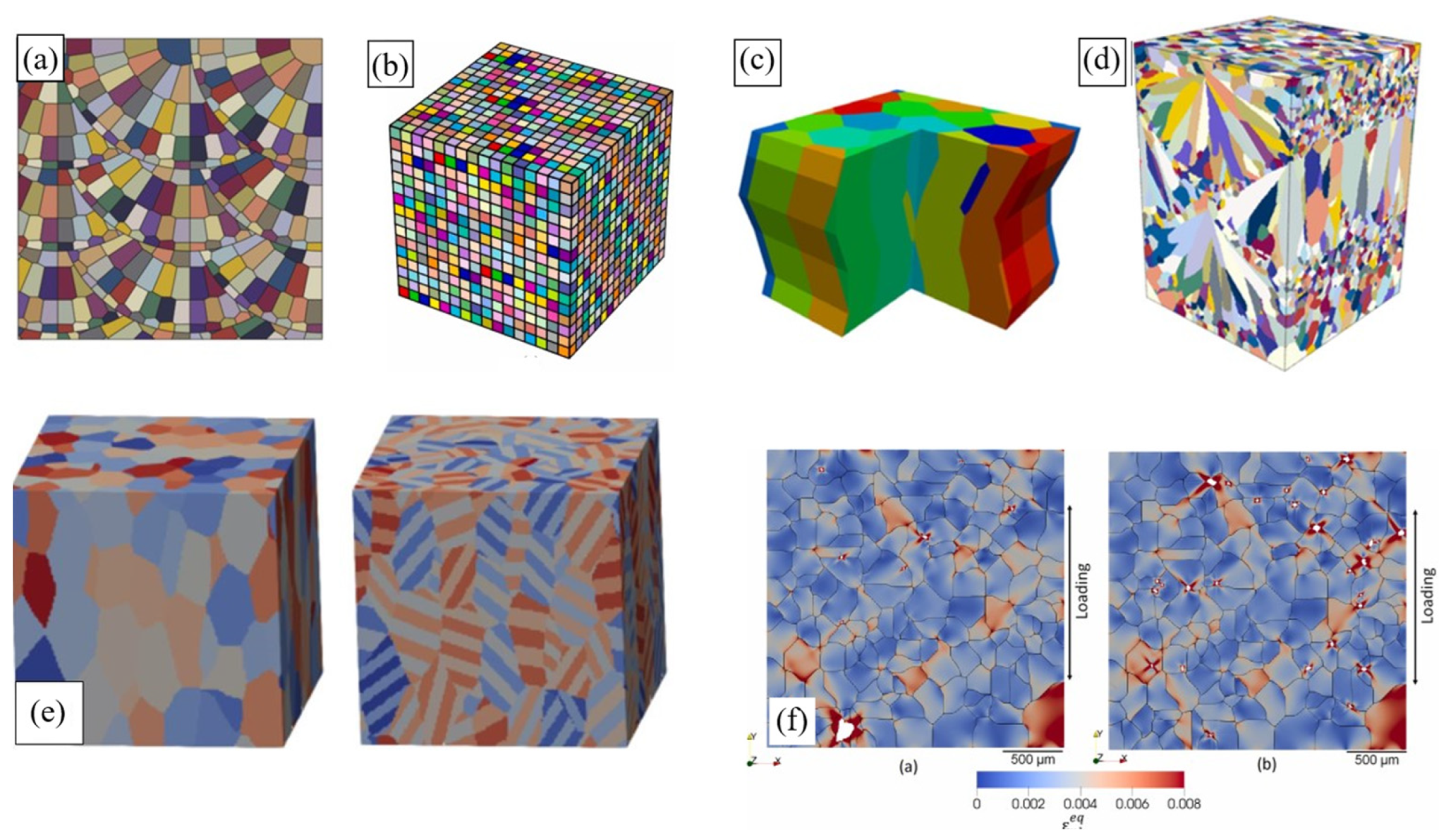
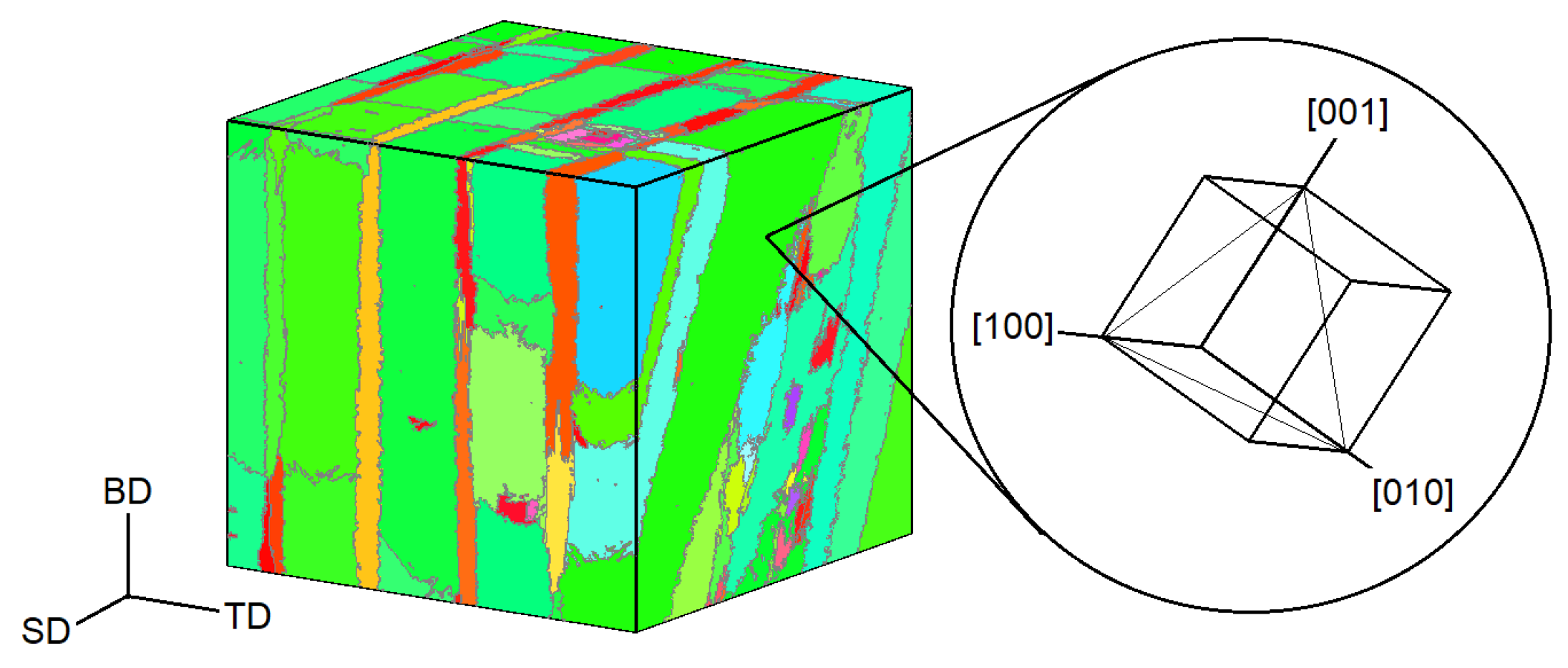
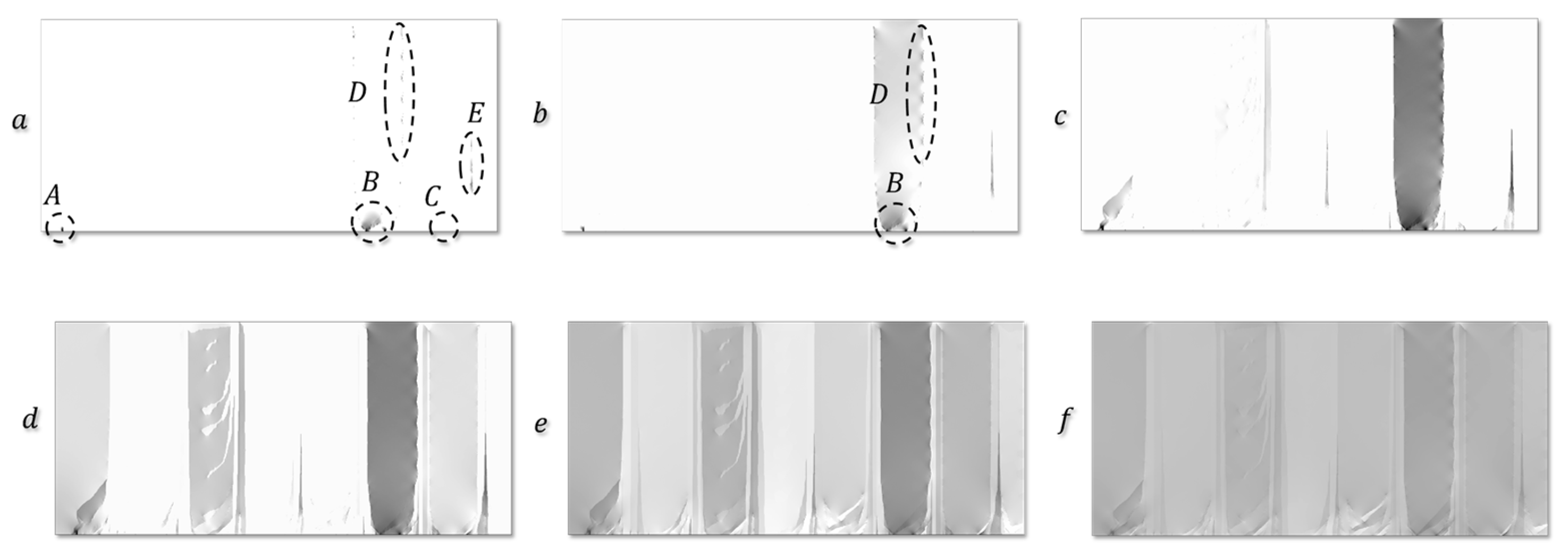
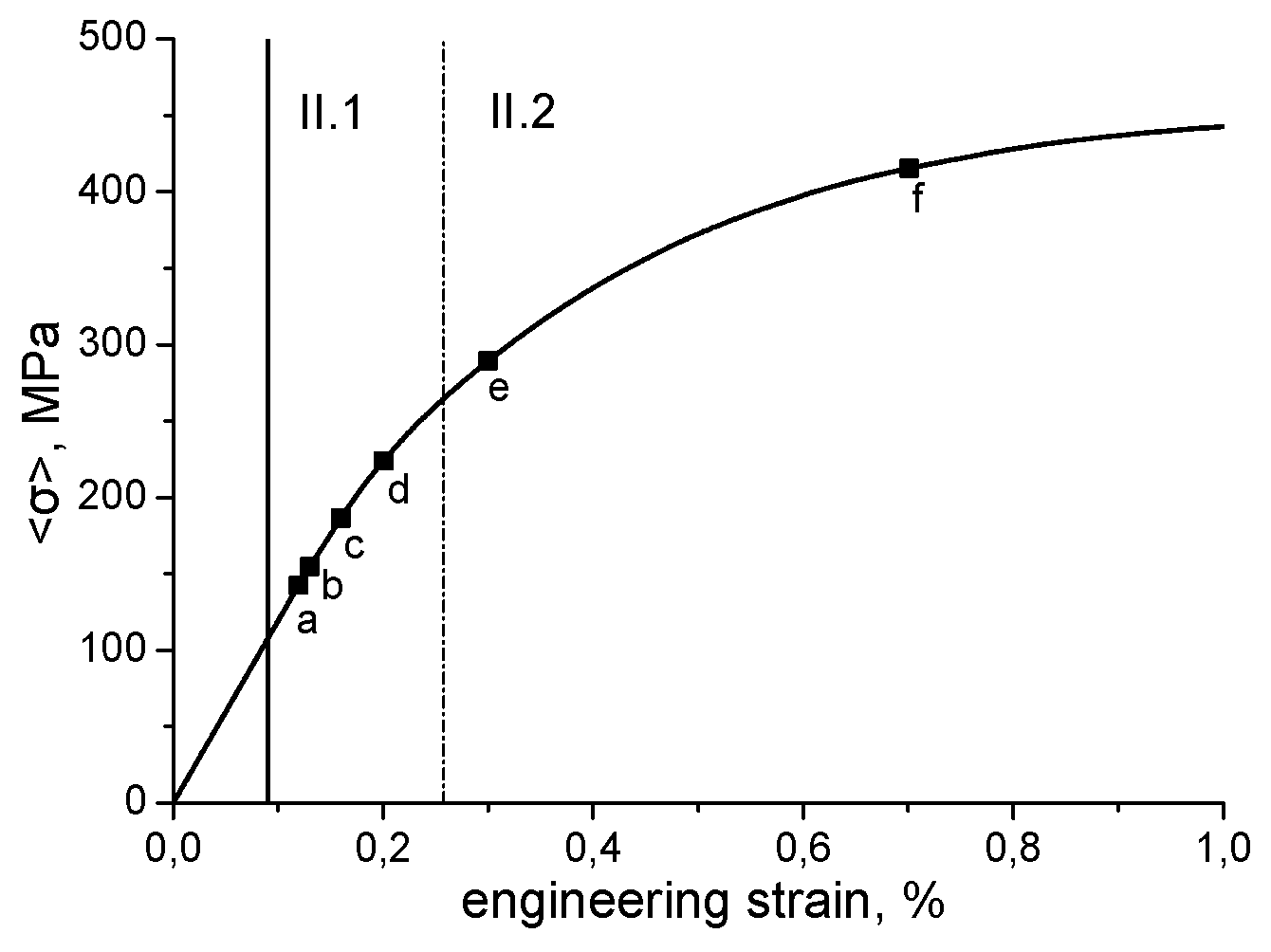

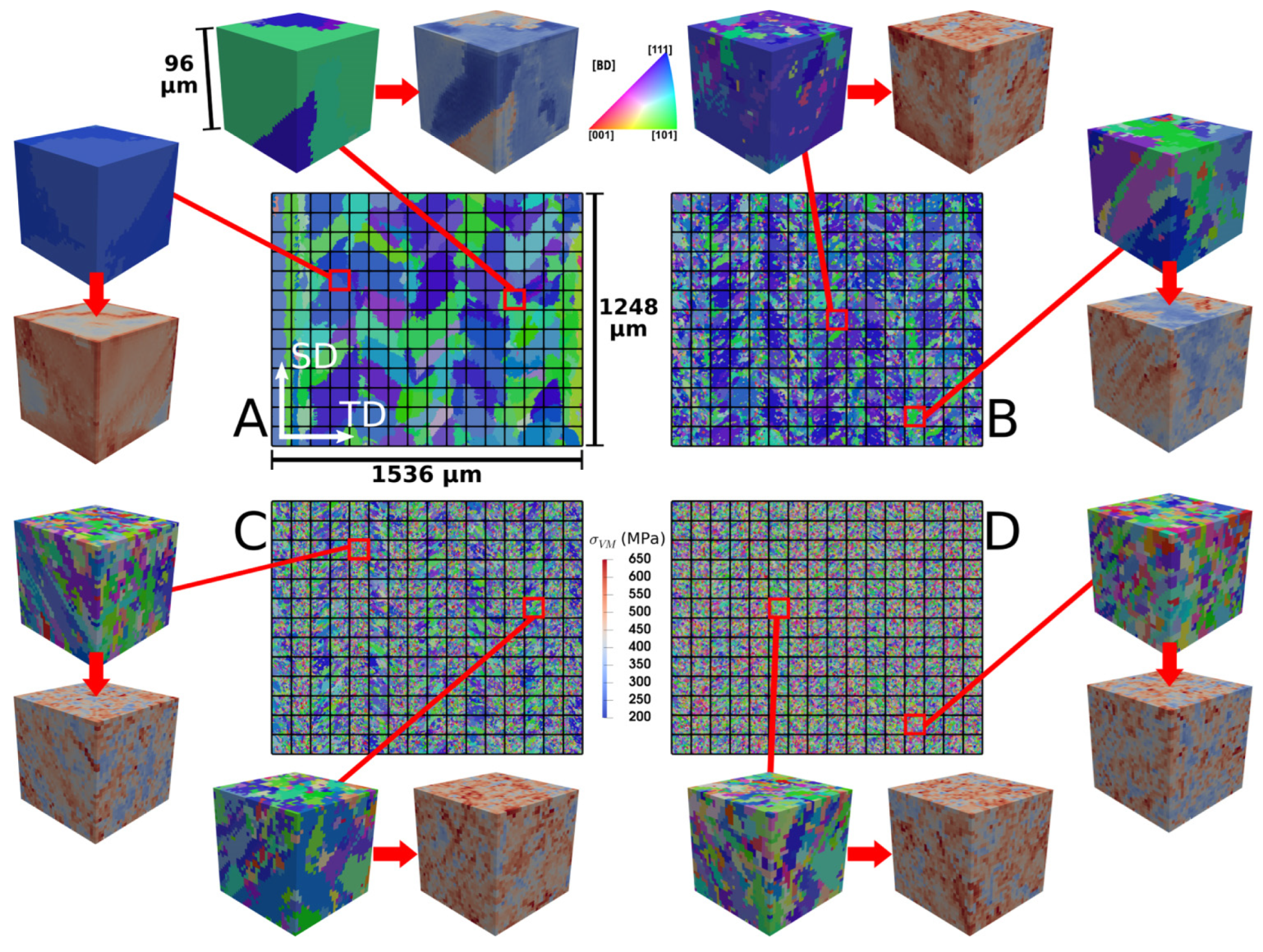
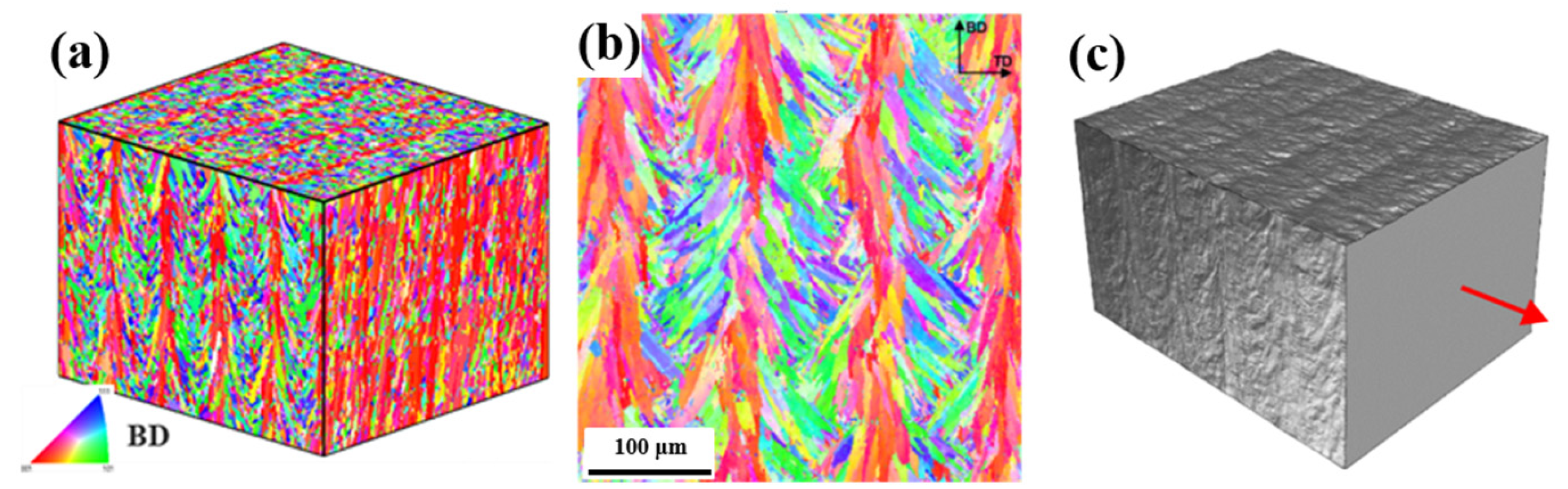

| Topic, Reference | Highlights | Hardening Law |
|---|---|---|
| Damage modelling of alloys produced by LPBF [146] | Two-dimensional FE structure–property model developed for uniaxial tensile loading of as-built LPBF 316L steel. Incorporates a simplistic synthetic grain structure that fits a melt pool (Figure 7a). Implemented in the FE commercial software Abaqus using a user material (UMAT) subroutine. Compared with an experimental stress–strain curve of the as-built LPBF 316L steel. | . (20) Here, areare the hardening moduli, including (no sum on ) and () which denote self and latent hardening moduli, respectively, as introduced by Peirce et al. [178], , . Here, is the initial hardening modulus; stands for accumulated shear strain; is the saturation stress; is the initial stress and denotes the ratio of latent to self-hardening. Latent hardening represents the increment of flow stress on the slip system due to a shear increment on the slip system . As pointed out by Peirce et al. [178], the components of the hardening matrix represent ‘the most elusive parameters’ in the constitutive equations. In a later study [179], Taheri Andani and coworkers adapted the model proposed in [180] where they considered the slip system hardening model as (no sum on ), where a single slip hardening rate ; is the Kronecker delta; and ; , are the slip system hardening parameters which were set to be identical for all slip systems. |
| Micromechanical modelling of single track deformation, phase transformation and residual stress evolution during laser surface remelting [175] | Two-dimensional FE structure–property model developed to estimate residual stresses that are formed due to the laser surface remelting of H13 tool steel. Incorporates a simplistic synthetic equiaxed grain structure and takes into account martensitic and austenitic phases. Implemented in the FE software Zset [181]. When determining single crystal model parameters, the authors compared a calculated macroscopic stress–strain curve with an experimental one for H13 samples that were cast and heat-treated [182]. | Martensite: . (21) Here, the self-hardening resistance which is usually defined as a constant, are considered. Here, is the hardening coefficient characterising the dislocation network interactions [183]; stands for the minimum length of the screw segment. is the effective stress, i.e., mean stress driving dislocation motion; the line tension model goes to the classical formulation proposed by Taylor. The average obstacle strength is a function of the densities of different defects, are the planar densities of carbides and solute clusters, respectively. A similar hardening model was adapted for austenite: . (22) Here, is the Hall–Petch term. Dislocation density evolution is estimated using a classical equation which describes the evolving mean free path during the accumulation of dislocations. The model is largely adopted from [184]. |
| Microstructural effects on the elasto-viscoplastic deformation of dual-phase Ti-6Al-4V produced by PBF [185] | laths. Equation (23) is calibrated with the experimental stress–strain curve of the as-built EPBF Ti-6Al-4V [186]. | A modified version of the Voce hardening model , (23) stands for the back-extrapolated CRSS. |
| CP modelling of the anisotropic tensile behaviour of LPBF Ti-6Al-4V [36] | laths. Implemented in the FFT software DAMASK [157]. Equation (24) is calibrated with experimental the stress–strain curves of the heat-treated LPBF Ti-6Al-4V ELI. | The slip resistance , (24) denotes the saturation value of the slip resistance. |
| CP modelling of the structure–property relationship in LPBF Ti-6A-4V [152] | ’ laths. Implemented in Abaqus using a UMAT subroutine. The results are compared with the experimental stress–strain curves obtained under tension, compression, and cyclic loading along the BD of LPBF Ti-6Al-4V. | , where (25) stands for CRSS. |
| Macroscale and microscale stress–strain relations of LPBF AlSi10Mg alloy [187] | Three-dimensional FFT structure–property model developed for the uniaxial tensile loading of as-built LPBF AlSi10Mg. Incorporates a synthetic grain structure (columnar or equiaxed), Si particles, and the porosity with a prescribed volume fraction. Implemented in DAMASK [157]. Compared the computationally obtained stress–strain curves with the experimental one from the in situ synchrotron X-ray diffraction experiment [188]. | (26) stands for the initial slip resistance. |
| Phase stress partition and its correlation with the mechanical anisotropy of LPBF AlSi10Mg [189] | Three-dimensional FE structure–property models developed for uniaxial tensile loading of the as-built LPBF AlSi10Mg in two different directions. Incorporate a synthetic Al-Si cellular substructure. Implemented in Abaqus using a UMAT subroutine. The results are compared with the experimental stress–strain curves obtained under tension along the BD and TD of LPBF AlSi10Mg [190]. | The traditional CP model 191 and the mechanism-based strain gradient crystal plasticity model (MSG-CP) [192] were employed. The former considered the hardening law suggested by Peirce et al. [178], as described in Equation (20). The MSG-CP defined the effective slip resistance following the Taylor hardening relation: , (27) ), in Equation (13). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zinovieva, O.; Romanova, V.; Dymnich, E.; Zinoviev, A.; Balokhonov, R. A Review of Computational Approaches to the Microstructure-Informed Mechanical Modelling of Metals Produced by Powder Bed Fusion Additive Manufacturing. Materials 2023, 16, 6459. https://doi.org/10.3390/ma16196459
Zinovieva O, Romanova V, Dymnich E, Zinoviev A, Balokhonov R. A Review of Computational Approaches to the Microstructure-Informed Mechanical Modelling of Metals Produced by Powder Bed Fusion Additive Manufacturing. Materials. 2023; 16(19):6459. https://doi.org/10.3390/ma16196459
Chicago/Turabian StyleZinovieva, Olga, Varvara Romanova, Ekaterina Dymnich, Aleksandr Zinoviev, and Ruslan Balokhonov. 2023. "A Review of Computational Approaches to the Microstructure-Informed Mechanical Modelling of Metals Produced by Powder Bed Fusion Additive Manufacturing" Materials 16, no. 19: 6459. https://doi.org/10.3390/ma16196459
APA StyleZinovieva, O., Romanova, V., Dymnich, E., Zinoviev, A., & Balokhonov, R. (2023). A Review of Computational Approaches to the Microstructure-Informed Mechanical Modelling of Metals Produced by Powder Bed Fusion Additive Manufacturing. Materials, 16(19), 6459. https://doi.org/10.3390/ma16196459