Assessing Effects of van der Waals Corrections on Elasticity of Mg3Bi2−xSbx in DFT Calculations
Abstract
:1. Introduction
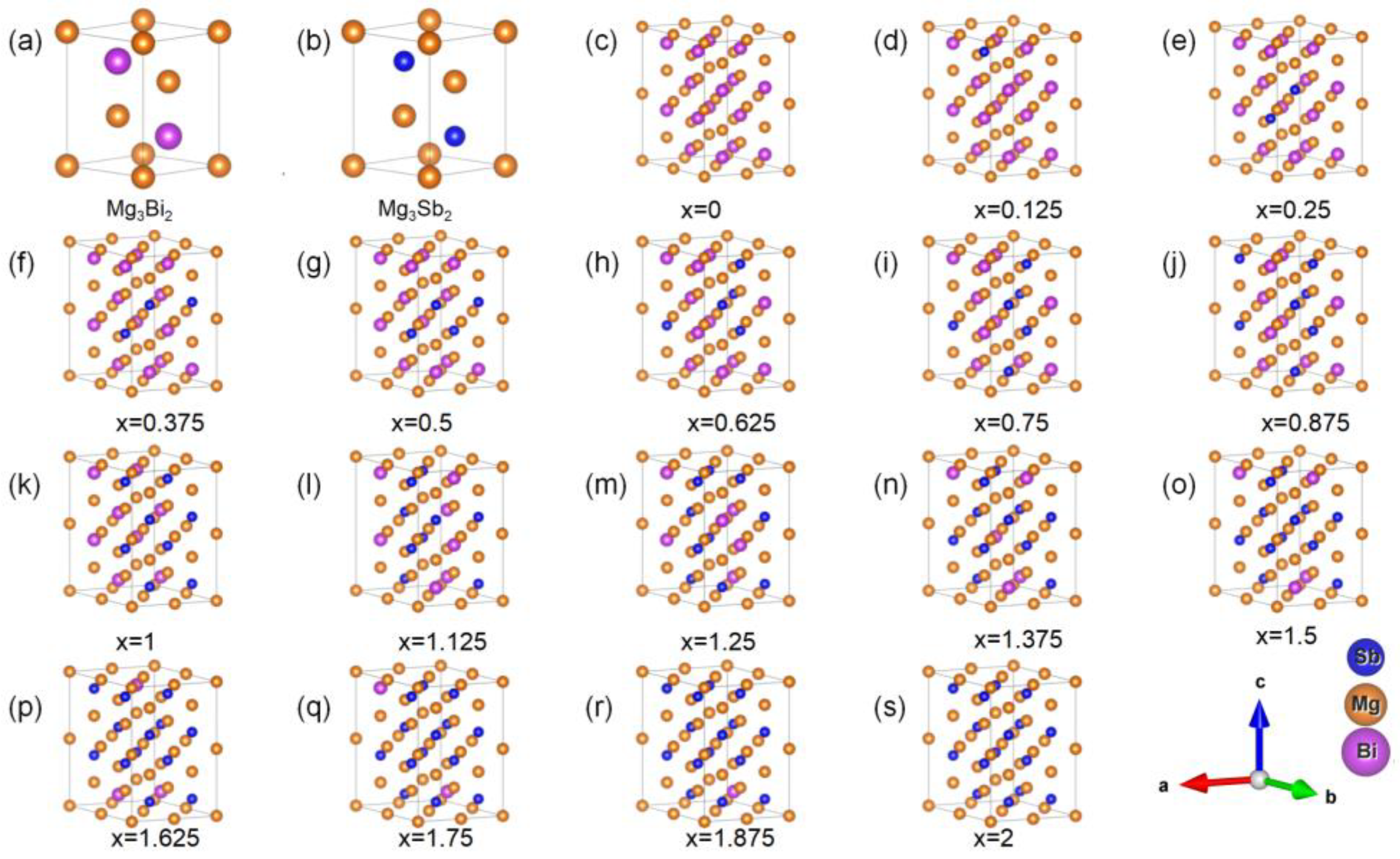
2. Materials and Methods
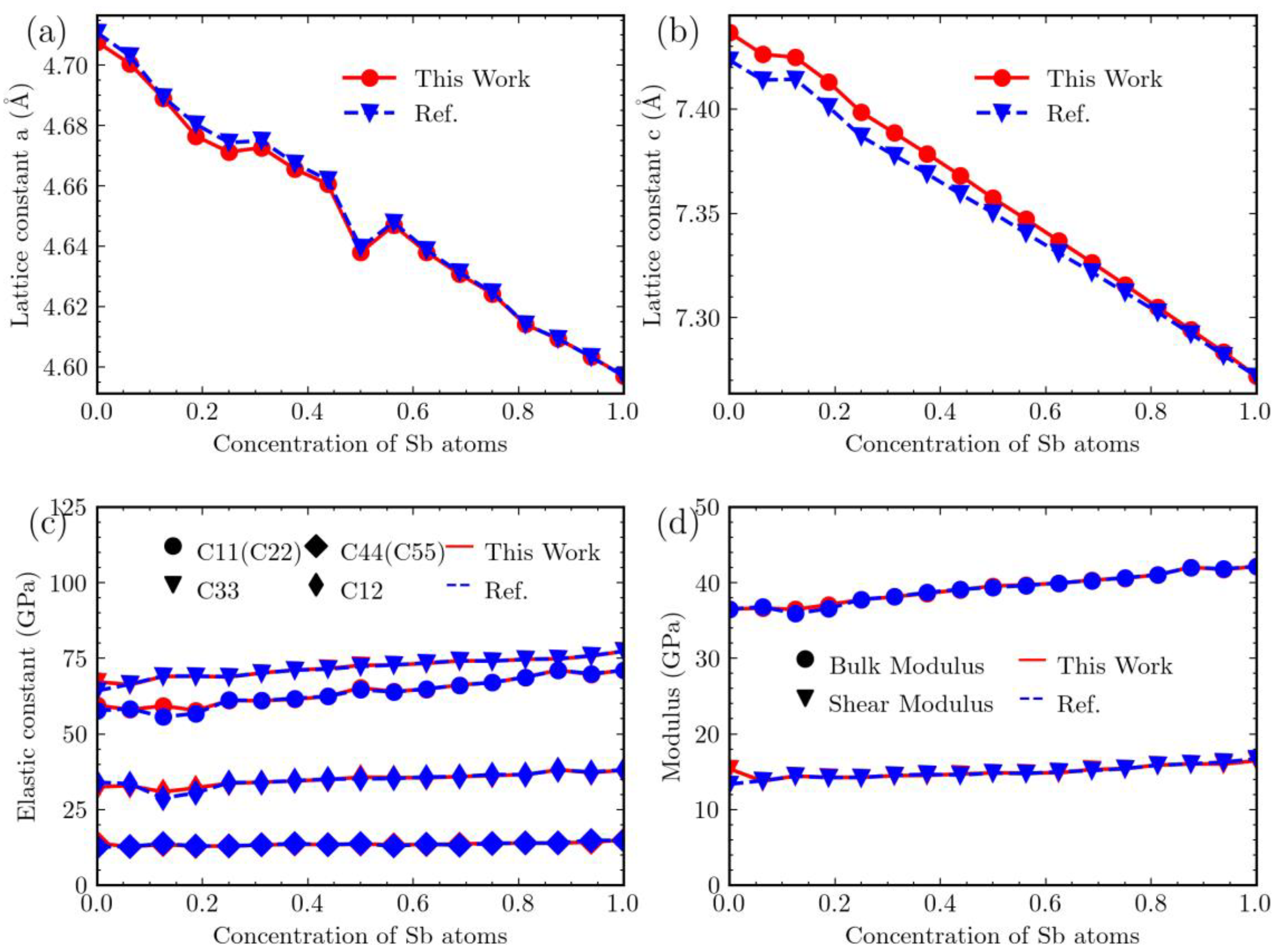
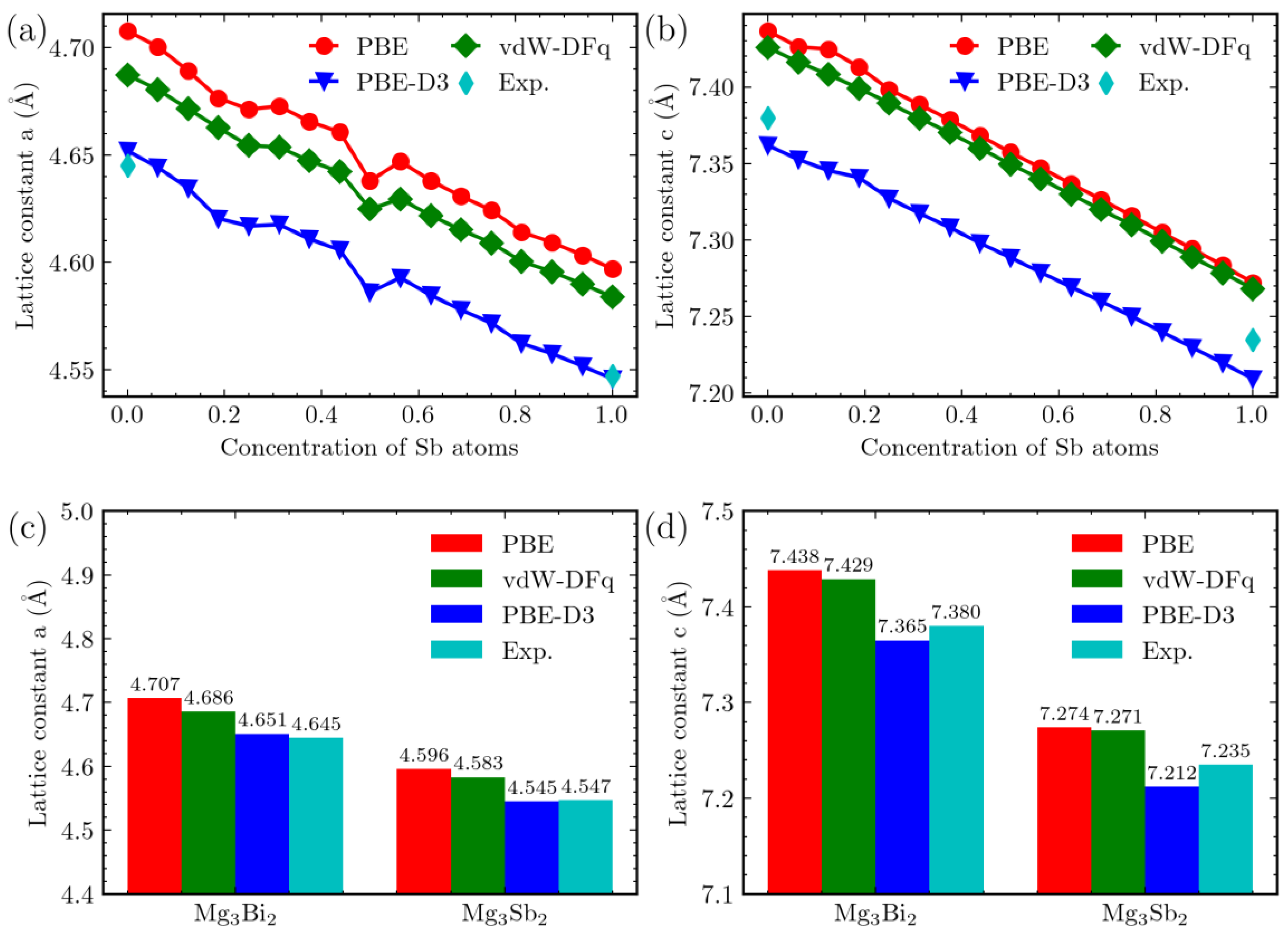
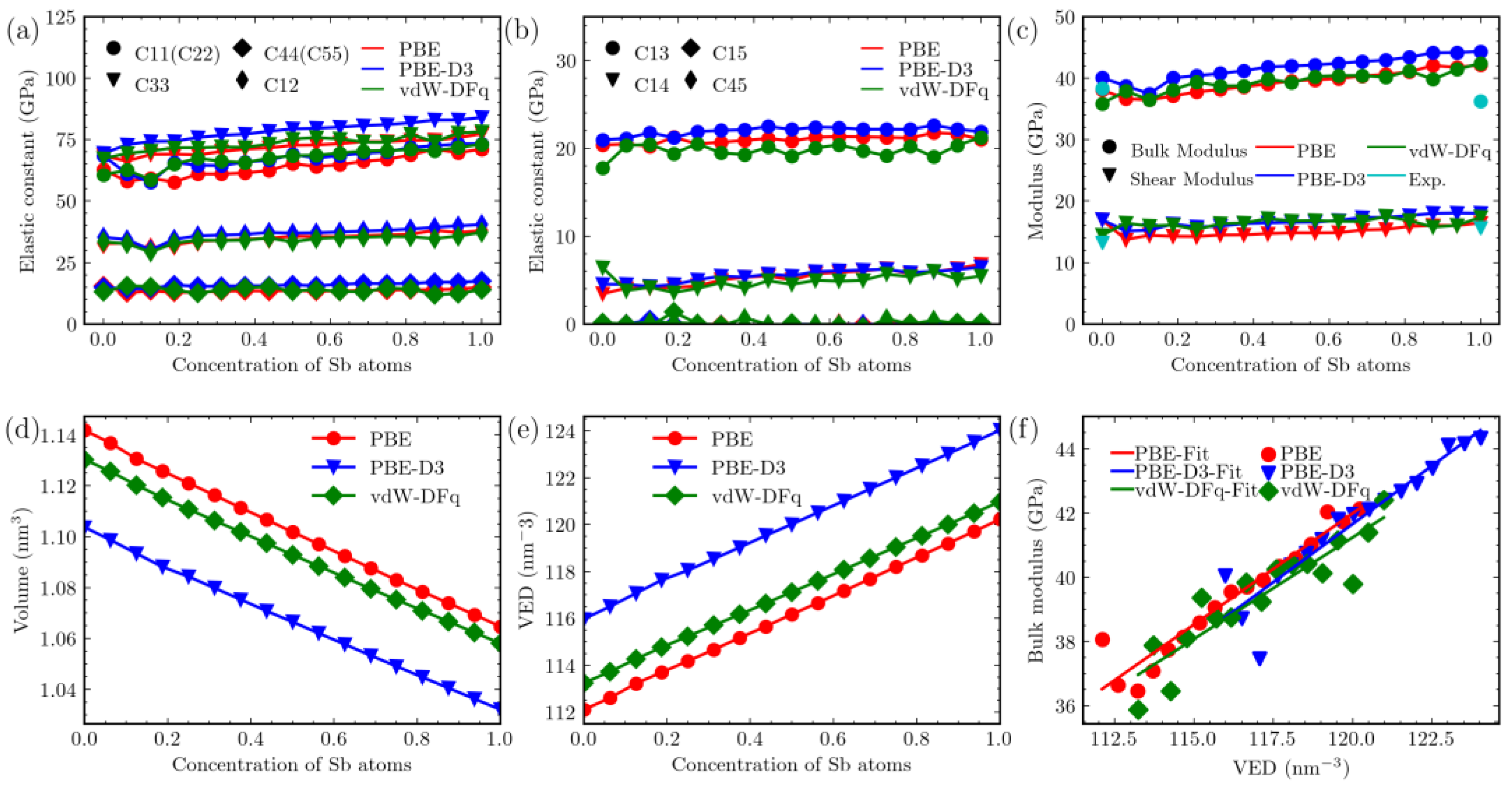
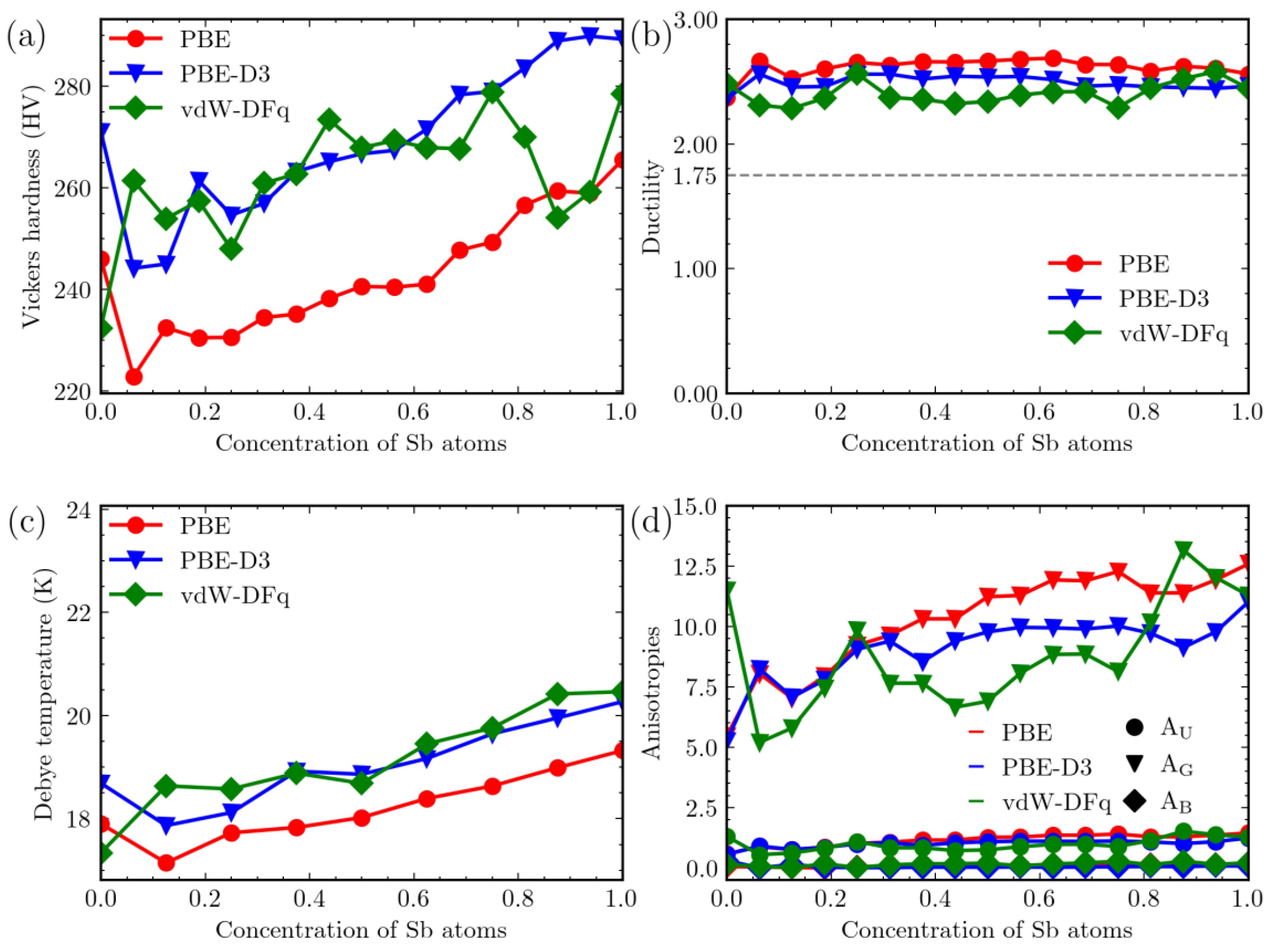
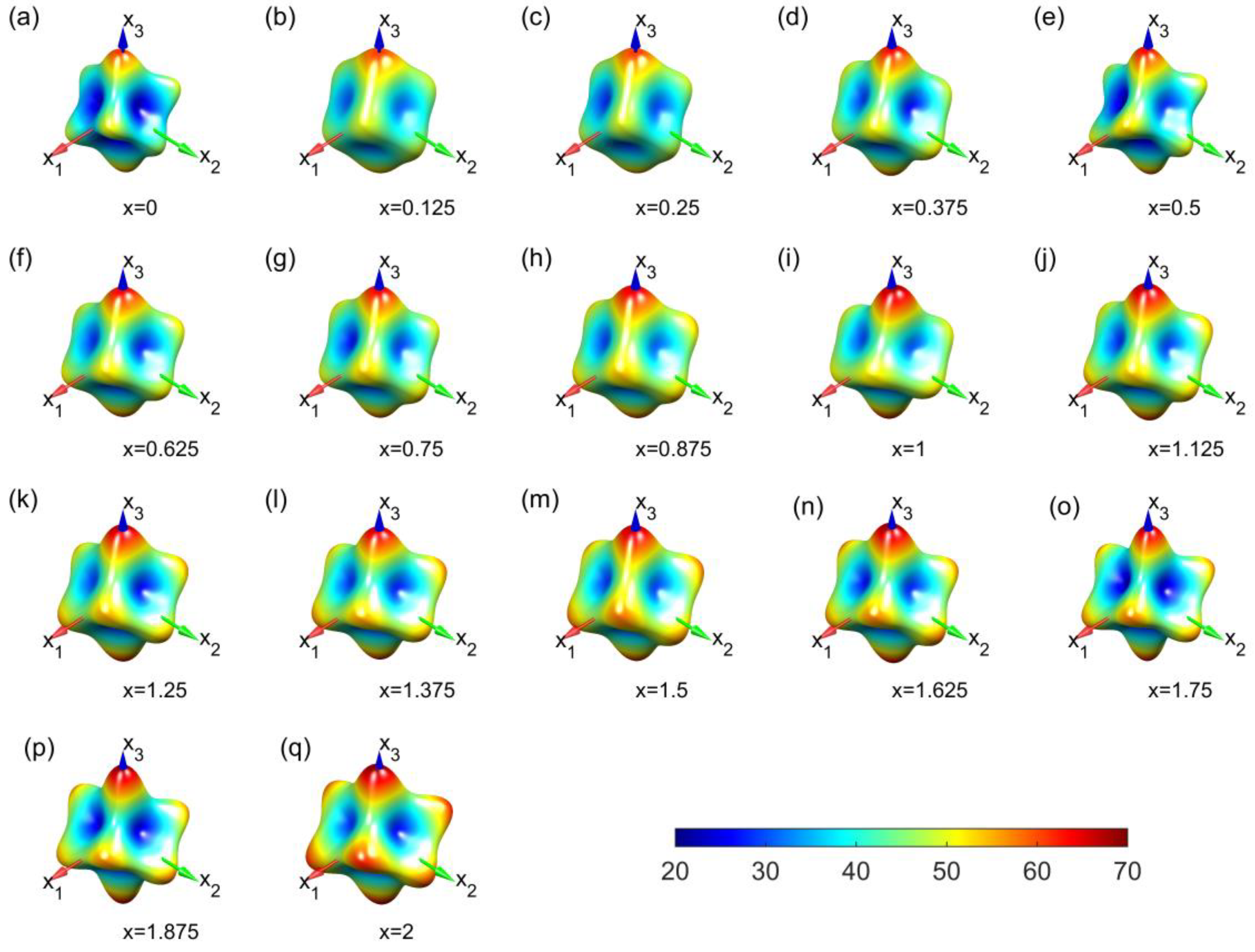
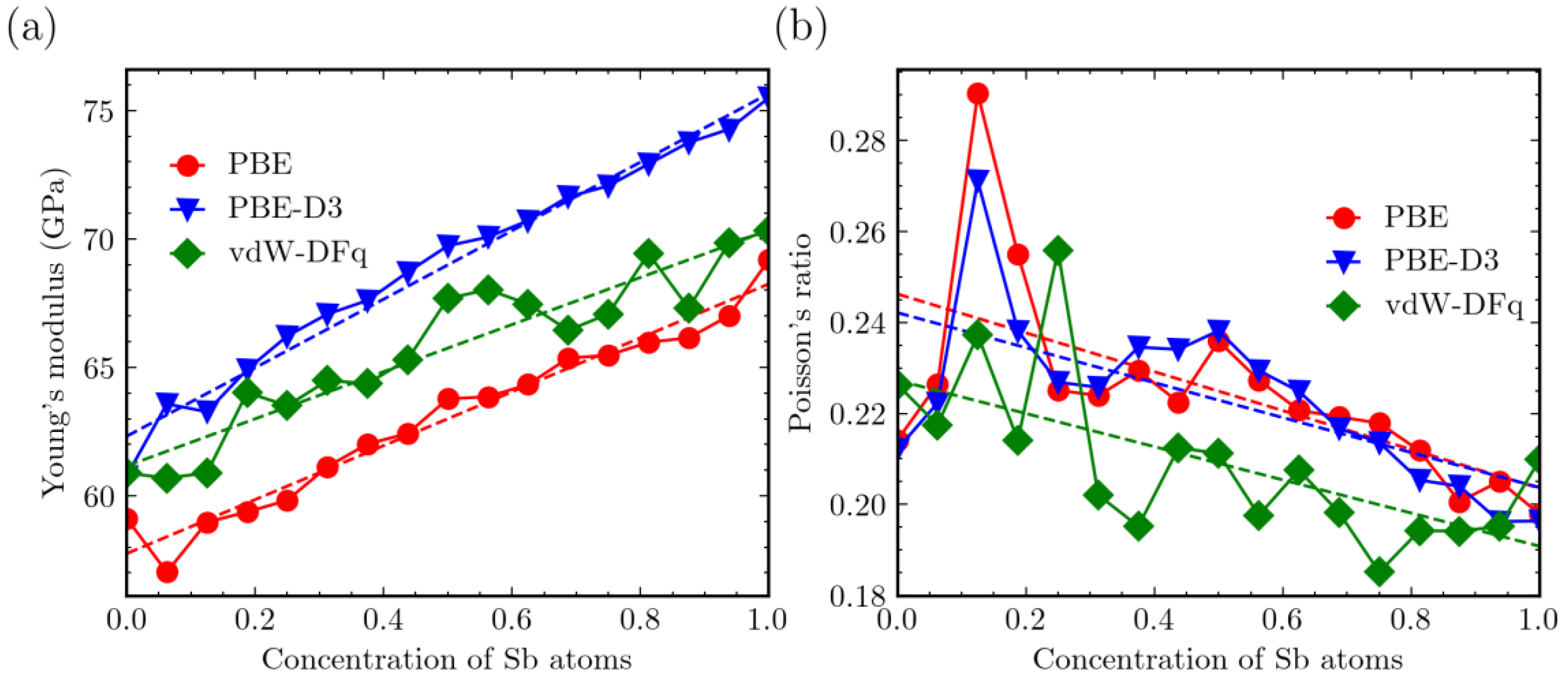
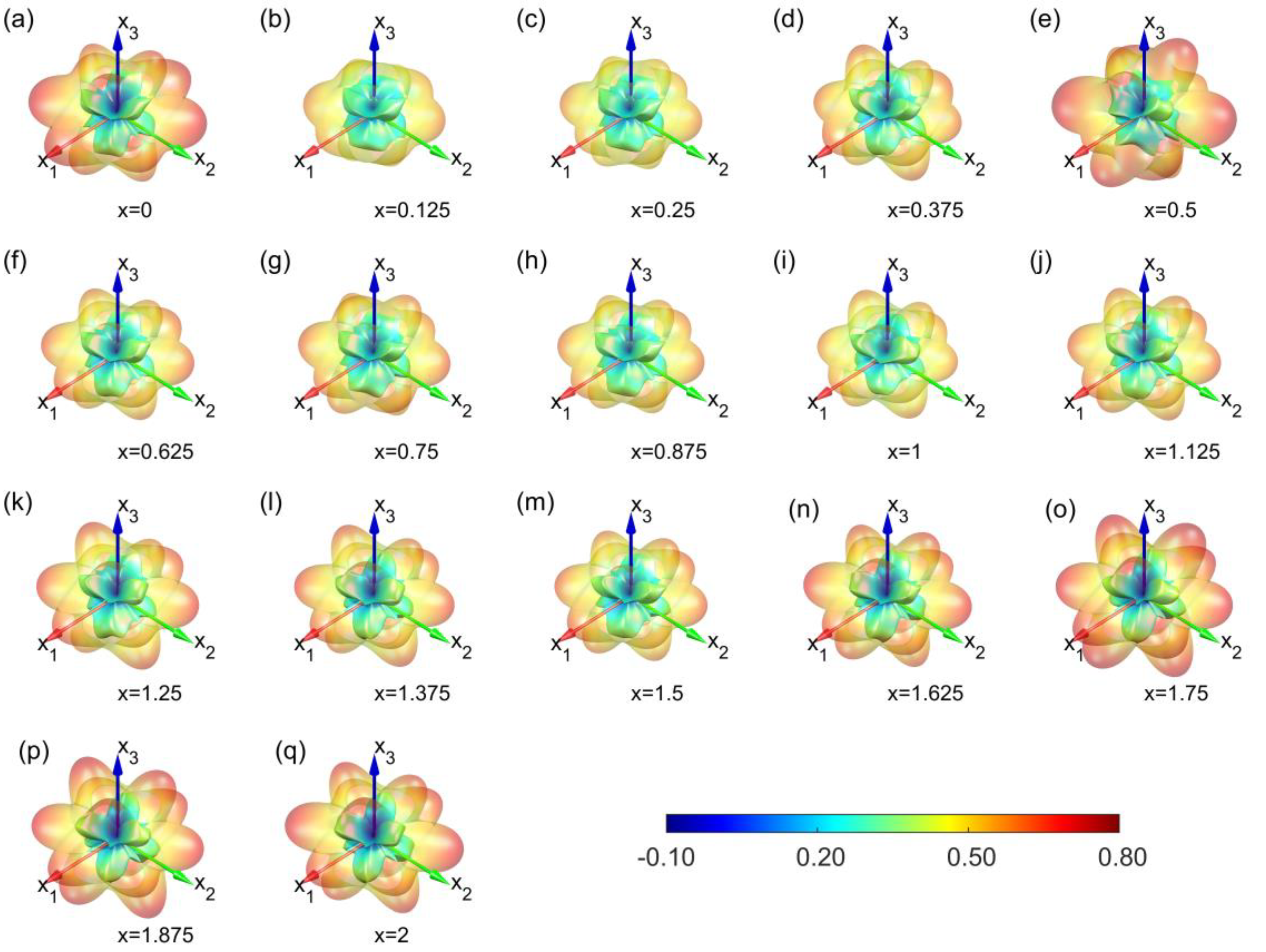
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Disalvo, F.J. Thermoelectric cooling and power generation. Science 1999, 285, 703–706. [Google Scholar] [CrossRef] [PubMed]
- Bell, L.E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Chen, C.; Yao, H.; Bai, F.; Yin, L.; Li, X.; Li, S.; Xue, W.; Wang, Y.; Cao, F.; et al. High-Performance N-type Mg3Sb2 towards Thermoelectric Application near Room Temperature. Adv. Funct. Mater. 2020, 30, 1906143. [Google Scholar] [CrossRef]
- Imasato, K.; Kang, S.D.; Ohno, S.; Snyder, G.J. Band engineering in Mg3Sb2 by alloying with Mg3Bi2 for enhanced thermoelectric performance. Mater. Horiz. 2018, 5, 59–64. [Google Scholar] [CrossRef]
- Shi, X.; Sun, C.; Bu, Z.; Zhang, X.; Wu, Y.; Lin, S.; Li, W.; Faghaninia, A.; Jain, A.; Pei, Y. Revelation of Inherently High Mobility Enables Mg3Sb2 as a Sustainable Alternative to n-Bi2Te3 Thermoelectrics. Adv. Sci. 2019, 6, 1802286. [Google Scholar] [CrossRef]
- Zhang, J.; Song, L.; Pedersen, S.H.; Yin, H.; Hung, L.T.; Iversen, B.B. Discovery of high-performance low-cost n-type Mg3Sb2-based thermoelectric materials with multi-valley conduction bands. Nat. Commun. 2017, 8, 13901. [Google Scholar] [CrossRef]
- Imasato, K.; Kang, S.D.; Snyder, G.J. Exceptional thermoelectric performance in Mg3Sb0.6Bi1.4 for low-grade waste heat recovery. Energy Environ. Sci. 2019, 12, 965–971. [Google Scholar] [CrossRef]
- Imasato, K.; Wood, M.; Kuo, J.J.; Snyder, G.J. Improved stability and high thermoelectric performance through cation site doping in n-type La-doped Mg3Sb1.5Bi0.5. J. Mater. Chem. A 2018, 6, 19941–19946. [Google Scholar] [CrossRef]
- Wood, M.; Kuo, J.J.; Imasato, K.; Snyder, G.J. Improvement of Low-Temperature zT in a Mg3Sb2–Mg3Bi2 Solid Solution via Mg-Vapor Annealing. Adv. Mater. 2019, 31, 1902337. [Google Scholar] [CrossRef]
- Zhang, J.; Song, L.; Iversen, B.B. Insights into the design of thermoelectric Mg3Sb2 and its analogs by combining theory and experiment. Npj Comput. Mater. 2019, 5, 76. [Google Scholar] [CrossRef]
- Pan, Y.; Yao, M.; Hong, X.; Zhu, Y.; Zhu, Y.; Fan, F.; Imasato, K.; He, Y.; Hess, C.; Fink, J.; et al. Mg3(Bi,Sb)2single crystals towards high thermoelectric performance. Energy Environ. Sci. 2020, 13, 1717–1724. [Google Scholar] [CrossRef]
- Tamaki, H.; Sato, H.K.; Kanno, T. Isotropic Conduction Network and Defect Chemistry in Mg3+δSb2-Based Layered Zintl Compounds with High Thermoelectric Performance. Adv. Mater. 2016, 28, 10182–10187. [Google Scholar] [CrossRef] [PubMed]
- Ao, D.W.; Liu, W.; di Chen, Y.X.; Wei, M.; Jabar, B.; Li, F.; Shi, X.L.; Zheng, Z.H.; Liang, G.X.; Zhang, X.H.; et al. Novel Thermal Diffusion Temperature Engineering Leading to High Thermoelectric Performance in Bi2Te3-Based Flexible Thin-Films. Adv. Sci. 2022, 9, 2103547. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, S.; Qiu, P.; Peng, L.; Wei, T.-R.; Zhang, Z.; Shi, X.; Chen, L. Flexible thermoelectrics based on ductile semiconductors. Science 2022, 377, 854–858. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Fang, Z.; Dai, X.; Weng, H. Topological nodal line semimetals predicted from first-principles calculations. Front. Phys. 2017, 12, 1–14. [Google Scholar] [CrossRef]
- Teshome, T.; Datta, A. Topological Phase Transition in Mg3Sb2 Assisted by Strain. ACS Omega 2019, 4, 8701–8706. [Google Scholar] [CrossRef]
- Li, S.; Yu, Z.M.; Liu, Y.; Guan, S.; Wang, S.S.; Zhang, X.; Yao, Y.; Yang, S.A. Type-II nodal loops: Theory and material realization. Phys. Rev. B 2017, 96, 081106. [Google Scholar] [CrossRef]
- Chen, W.; Lu, H.Z.; Zilberberg, O. Weak localization and antilocalization in nodal-line semimetals: Dimensionality and topological effects. Phys. Rev. Lett. 2019, 122, 196603. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J.; Wei, B.; Xu, S.; Song, Y.; Wang, X.; Xia, T.-L.; Chen, J.; Snyder, G.J.; Hong, J. Giant phonon anharmonicity driven by the asymmetric lone pairs in Mg3Bi2. Mater. Today Phys. 2022, 27, 100791. [Google Scholar] [CrossRef]
- Xin, J.; Li, G.; Auffermann, G.; Borrmann, H.; Schnelle, W.; Gooth, J.; Zhao, X.; Zhu, T.; Felser, C.; Fu, C. Growth and transport properties of Mg3X2 (X = Sb, Bi) single crystals. Mater. Today Phys. 2018, 7, 61–68. [Google Scholar] [CrossRef]
- Agne, M.T.; Imasato, K.; Anand, S.; Lee, K.; Bux, S.K.; Zevalkink, A.; ERettie, A.J.; Young Chung, D.; Kanatzidis, M.G.; Jeffrey Snyder, G. Heat capacity of Mg3Sb2, Mg3Bi2, and their alloys at high temperature. Mater. Today Phys. 2018, 6, 83–88. [Google Scholar] [CrossRef]
- Ding, J.; Lanigan-Atkins, T.; Calderón-Cueva, M.; Banerjee, A.; Abernathy, D.L.; Said, A.; Zevalkink, A.; Delaire, O. Soft anharmonic phonons and ultralow thermal conductivity in Mg3 (Sb, Bi)2 thermoelectrics. Sci. Adv. 2021, 7, eabg1449. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Petretto, G.; Rignanese, G.M.; Hautier, G.; Zevalkink, A. An Unlikely Route to Low Lattice Thermal Conductivity: Small Atoms in a Simple Layered Structure. Joule 2018, 2, 1879–1893. [Google Scholar] [CrossRef]
- Gooth, J.; Schierning, G.; Felser, C.; Nielsch, K. Quantum materials for thermoelectricity. MRS Bull. 2018, 43, 187–192. [Google Scholar] [CrossRef]
- Li, M.; Chen, G. Thermal transport for probing quantum materials. MRS Bull. 2020, 45, 348–356. [Google Scholar] [CrossRef]
- Barati, S.; Abedinpour, S.H. Thermoelectric response of nodal-line semimetals: Probing the Fermi surface topology. Phys. Rev. B 2020, 102, 125139. [Google Scholar] [CrossRef]
- Hosoi, M.; Tateishi, I.; Matsuura, H.; Ogata, M. Thin Films of Topological Nodal Line Semimetals as a Candidate for Efficient Thermoelectric Converters. Phys. Rev. B 2022, 105, 085406. [Google Scholar] [CrossRef]
- Kanno, T.; Tamaki, H.; Yoshiya, M.; Uchiyama, H.; Maki, S.; Takata, M.; Miyazaki, Y. High-Density Frenkel Defects as Origin of N-Type Thermoelectric Performance and Low Thermal Conductivity in Mg3Sb2-Based Materials. Adv. Funct. Mater. 2021, 31, 2008469. [Google Scholar] [CrossRef]
- Peng, Q.; Zhao, S.; Yuan, X.; Chen, X.J. Elasticity of Mg3Bi2-xSbx. Materials 2022, 15, 7161. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, G.; Liu, G.R.; De, S. Van der Waals density functional theory vdW-DFq for semihard materials. Crystals 2019, 9, 243. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, Y.; Peng, Q.; Yang, Y.; Li, Y.; Wen, X. Active learning to overcome exponential-wall problem for effective structure prediction of chemical-disordered materials. NPJ Comput. Mater. 2023, 9, 12. [Google Scholar] [CrossRef]
- Peng, Q.; Yuan, X.; Zhao, S.; Zhou, Y.; Wen, X.; Chen, X.J. Active-learning search for unitcell structures: A case study on Mg3Bi2-xSbx. Comput. Mater. Sci. 2023, 226, 112260. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects*. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmiiller, B.J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 24. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillonin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Z.; Zhao, X.; Song, J.; Zhang, M.; Liu, H. MatCloud: A high-throughput computational infrastructure for integrated management of materials simulation, data and resources. Comput. Mater. Sci. 2018, 146, 319–333. [Google Scholar] [CrossRef]
- Zhou, D.W.; Liu, J.S.; Xu, S.H.; Peng, P. Thermal stability and elastic properties of Mg3Sb2 and Mg3Bi2 phases from first-principles calculations. Phys. B Condens. Matter 2010, 405, 2863–2868. [Google Scholar] [CrossRef]
- Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Teubner: Leipzig, Germany, 1908. [Google Scholar]
- Isotta, E.; Peng, W.; Balodhi, A.; Zevalkink, A. Elastic Moduli: A Tool for Understanding Chemical Bonding and Thermal Transport in Thermoelectric Materials. Angew. Chem. Int. Ed. 2023, 62, e202213649. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Khare, S.V.; Gall, D. Valence electron concentration as an indicator for mechanical properties in rocksalt structure nitrides, carbides and carbonitrides. Acta Mater. 2018, 152, 175–185. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, C.; Ma, Z.; Li, L.; Li, S.; Wang, J. Improved thermoelectric performance of n-type Mg3Sb2–Mg3Bi2 alloy with Co element doping. Curr. Appl. Phys. 2021, 21, 25–30. [Google Scholar] [CrossRef]
- Jiang, X.; Zhao, J.; Wu, A.; Bai, Y.; Jiang, X. Mechanical and electronic properties of B12-based ternary crystals of orthorhombic phase. J. Phys. Condens. Matter 2010, 22, 315503. [Google Scholar] [CrossRef]
- Pugh, S. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids Pergamon Press. 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Chen, H.; Cao, Y.; Liu, K.; Tao, X.; Zhou, Y.; Ouyang, Y.; Gao, F.; Du, Y.; Peng, Q. Stability and physical properties tuning via interstitials chemical engineering of Zr5Sn3: A first-principles study. J. Mater. Sci. 2019, 54, 10284–10296. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Q.; Ma, X.; Yang, X.; Zhao, S.; Yuan, X.; Chen, X. Assessing Effects of van der Waals Corrections on Elasticity of Mg3Bi2−xSbx in DFT Calculations. Materials 2023, 16, 6482. https://doi.org/10.3390/ma16196482
Peng Q, Ma X, Yang X, Zhao S, Yuan X, Chen X. Assessing Effects of van der Waals Corrections on Elasticity of Mg3Bi2−xSbx in DFT Calculations. Materials. 2023; 16(19):6482. https://doi.org/10.3390/ma16196482
Chicago/Turabian StylePeng, Qing, Xinjie Ma, Xiaoyu Yang, Shuai Zhao, Xiaoze Yuan, and Xiaojia Chen. 2023. "Assessing Effects of van der Waals Corrections on Elasticity of Mg3Bi2−xSbx in DFT Calculations" Materials 16, no. 19: 6482. https://doi.org/10.3390/ma16196482
APA StylePeng, Q., Ma, X., Yang, X., Zhao, S., Yuan, X., & Chen, X. (2023). Assessing Effects of van der Waals Corrections on Elasticity of Mg3Bi2−xSbx in DFT Calculations. Materials, 16(19), 6482. https://doi.org/10.3390/ma16196482






