Study of the Effect of Carbon Black Filling on the Mechanical Behavior of Rubber Hyper-Elasticity
Abstract
:1. Introduction
2. Constitutive Models
3. Experimental Setup
3.1. Experimental Materials
3.2. Sample Preparation and Test
4. Experimental Result and Discussion
4.1. The Uniaxial Tensile Tests Results
4.2. Discussion
5. Conclusions
- (1)
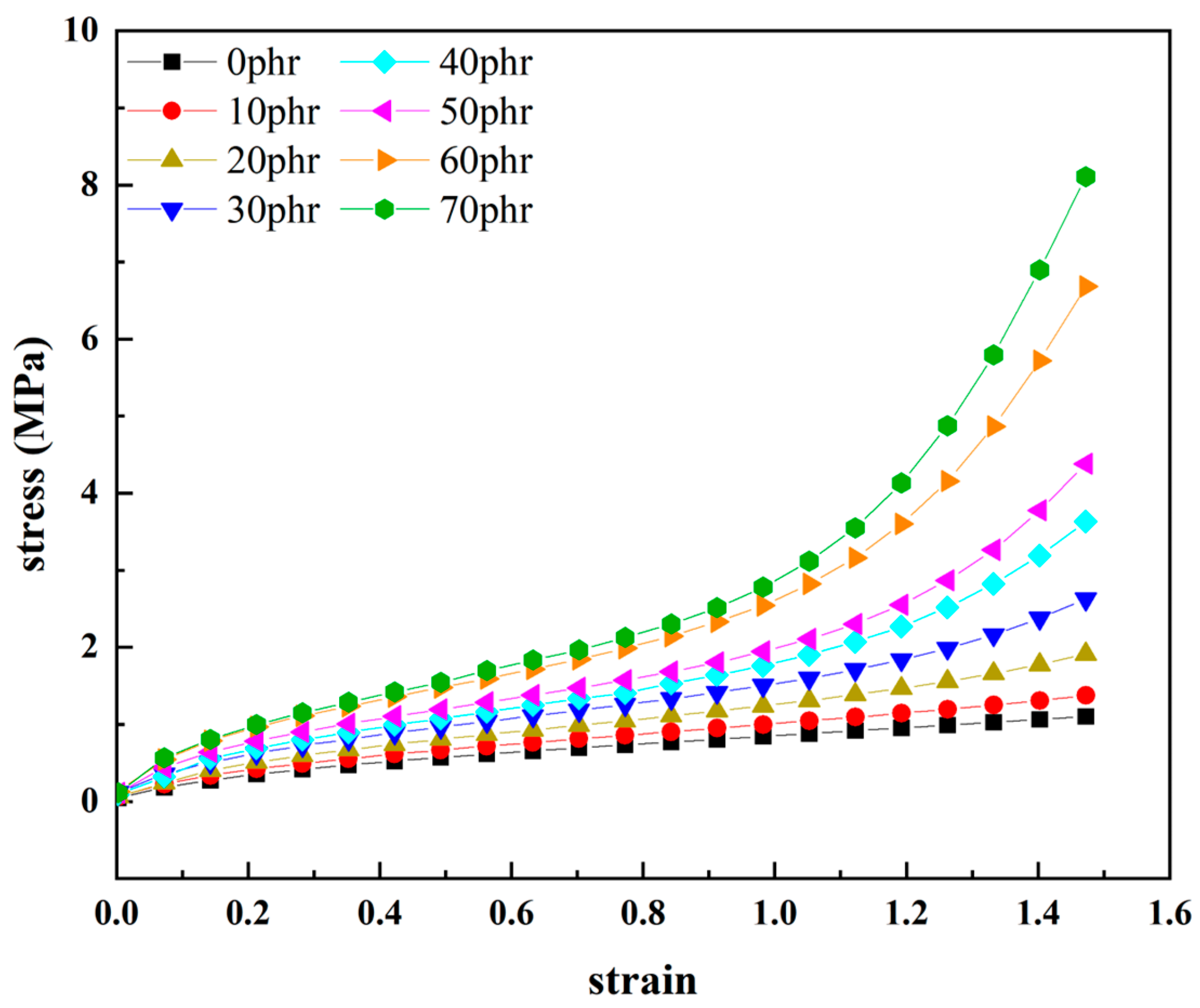
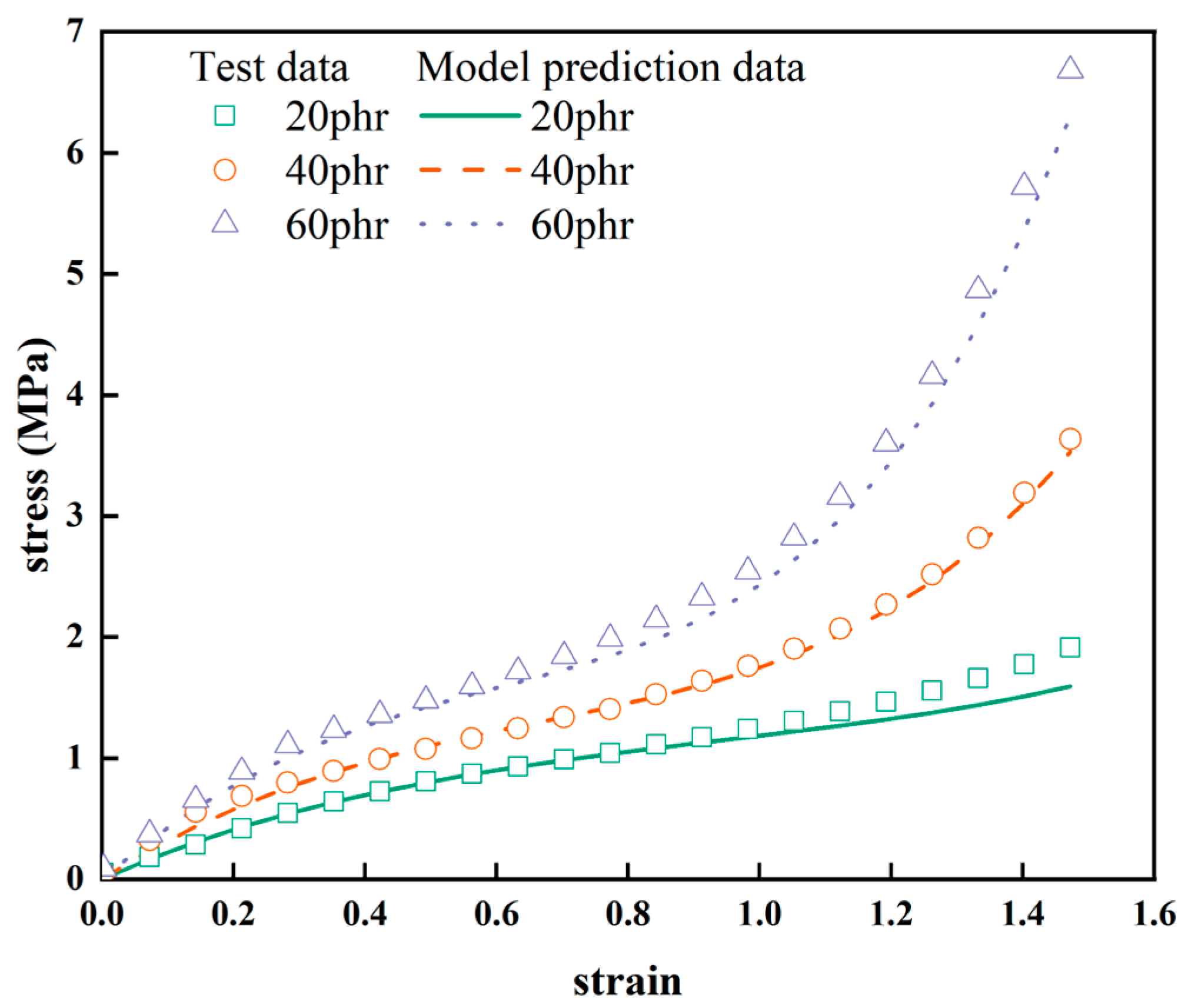
- Through uniaxial tensile tests on the natural rubber with varying levels of carbon black filling contents at a significant deformation range (150% elongation), the correlation between the hyper-elastic properties of natural rubber and the carbon black filling was revealed. The stress-strain curves of natural rubber became steeper with an increasing carbon black filling content, indicating that natural rubber gradually becomes “stiffer” as the filling with carbon black increases. The “S”−shaped nonlinearity in the stress-strain curve also became increasingly prominent.
- (2)
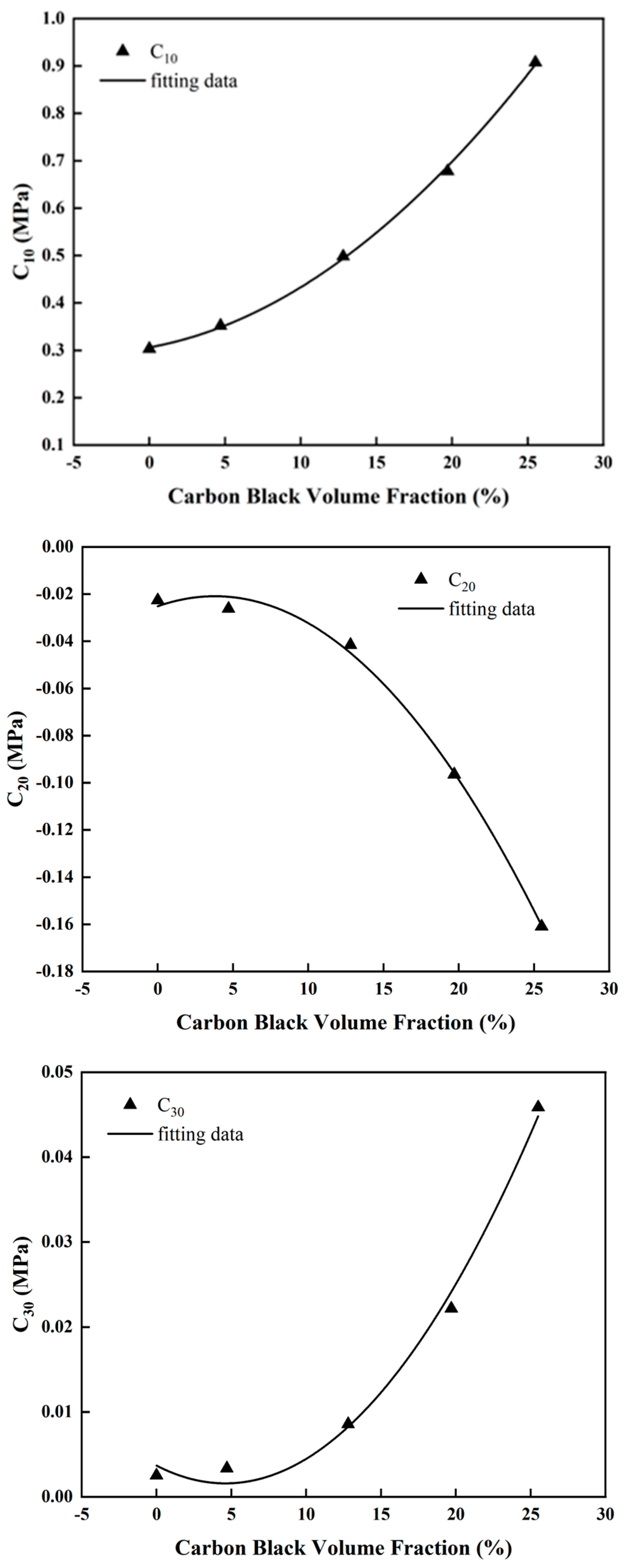
- A quantitative relationship between the Yeoh constitutive model and the volume fraction of carbon black filling was established. It explicitly characterizes the correlation between the hyper-elastic mechanical behavior of the rubber material and the carbon black filling. This further extends the applicability of the Yeoh constitutive model and allows for the prediction of the correlation between the hyper-elastic properties of natural rubber and the carbon black filling. During different stages of deformation in the tensile process, the degree of enhancement of natural rubber by the carbon black filling varies. This is reflected in the non-linear change in the stress of the rubber material with increasing tensile strain, showing a pattern of initially decreasing and then increasing over the increase in strain. Furthermore, as the carbon black filling amount increases, the nonlinear change characterized by an initial decrease followed by an increase becomes more pronounced.
- (3)
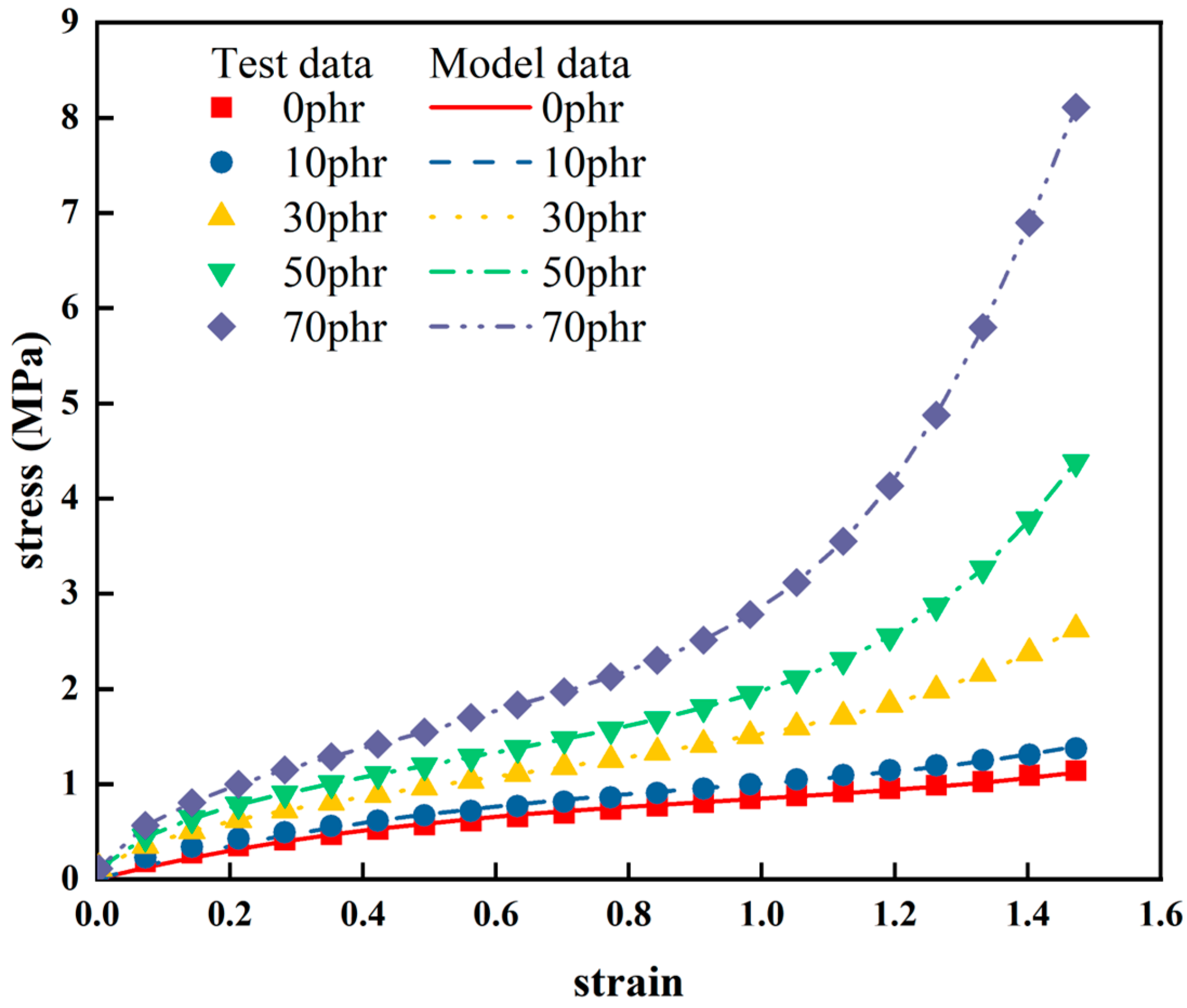
- The Yeoh constitutive model, which explicitly represents the volume fraction of carbon black filling, accurately captures the stress enhancement phenomenon under different levels of carbon black filling and different constant elongation ratios. This indicates that the effect of the carbon black filling on the performance of natural rubber, essentially making it progressively “stiffer”, is significant. The degree of enhancement increases as the volume fraction of carbon black filling increases. When conducting tests on certain rubber materials with higher costs, once the mechanical performance on rubber samples within a specific range of carbon black filling was determined, the Yeoh constitutive model, which explicitly represents the volume fraction of carbon black filling, could be used to predict the performance of other rubber formulations within a certain range of deformations. This approach offers a highly practical and viable method for real-world applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, X.; Li, L. State of the art of constitutive relations of hyperelastic materials. Chin. J. Theo-Retical Appl. Mech. 2020, 52, 1221–1232. [Google Scholar]
- Ding, F.; Zhang, H.; Ding, M. −M.; Shi, T.F.; Li, Y.Q.; An, L.J. Theoretical Models for Stress-Strain Curves of Elastomer Materials. ACTA Polym. Sin. 2019, 50, 1357–1366. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications Inc.: Mineola, NY, USA, 1997. [Google Scholar]
- Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: A review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Koprowski-Theiss, N.; Johlitz, M.; Diebels, S. Characterizing the time dependence of filled EPDM. Rubber Chem. Technol. 2011, 84, 147–165. [Google Scholar] [CrossRef]
- Mansouri, M.; Darijani, H. Constitutive modeling of isotropic hyperelastic materials in an exponential framework using a self-contained approach. Int. J. Solids Struct. 2014, 51, 4316–4326. [Google Scholar] [CrossRef]
- Zhao, Z.; Mu, X.; Du, F. Modeling and verification of a new hyperelastic model for rubber-like materials. Math. Probl. Eng. 2019, 2019, 2832059. [Google Scholar] [CrossRef]
- Poomuthu, A.; Stoček, R.; Chattopadhyay, S.; Khastgir, D.; Kaliske, M.; Özenç, K.; Sekar, P. Understanding fracture of a carbon black filled rubber compound using material force theory. Theor. Appl. Fract. Mech. 2020, 108, 102649. [Google Scholar] [CrossRef]
- El Yaagoubi, M.; Meier, J.; Juhre, D. Lifetime prediction of carbon black filled elastomers based on the probability distribution of particle using an inelastic and hyperelastic material model. Eng. Fail. Anal. 2020, 118, 104943. [Google Scholar] [CrossRef]
- Gudsoorkar, U.; Bindu, R. Computer simulation of hyper elastic re-treaded tire rubber with ABAQUS. Mater. Today Proc. 2021, 43, 1992–2001. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A comparative study of 85 hyperelastic constitutive models for both unfilled rubber and highly filled rubber nanocomposite material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Theory of the elastic properties of rubber. J. Chem. Phys. 1943, 11, 455–481. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos. Trans. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1948, 240, 459–490. [Google Scholar]
- GB/T 9869-2014; Rubber-Measurement of Vulcanization Characteristics with the Oscillating Disc Curemeter. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, and the Standardization Administration of China: Beijing, China, 2014.
- ISO 37:2017 (E); Rubber, Vulcanized or Thermoplastic—Determination of Tensile Stress-Strain Properties. ISO: Geneva, Switzerland, 2017.
- Fukahori, Y. The mechanics and mechanism of the carbon black reinforcement of elastomers. Rubber Chem. Technol. 2003, 76, 548–566. [Google Scholar] [CrossRef]
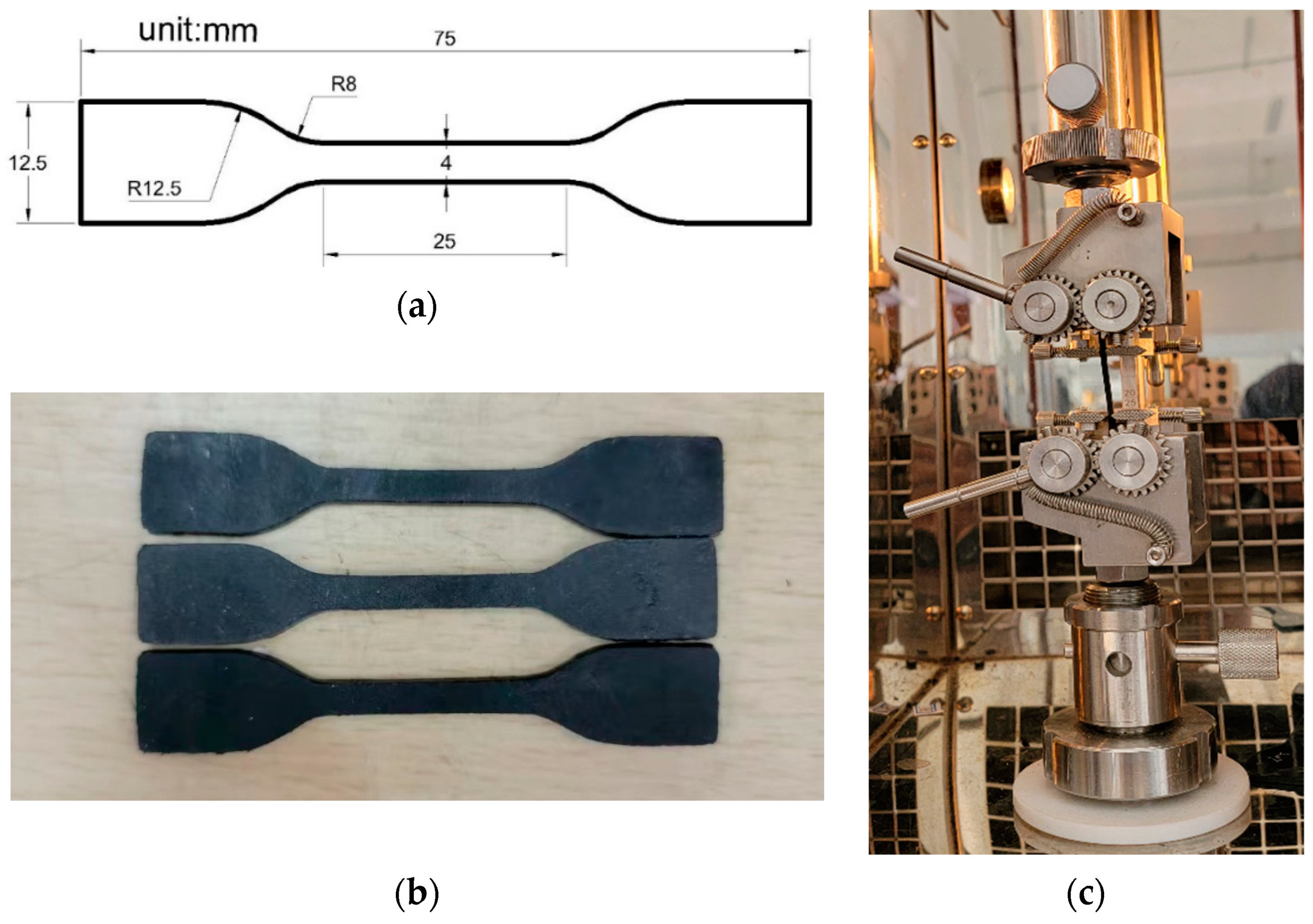
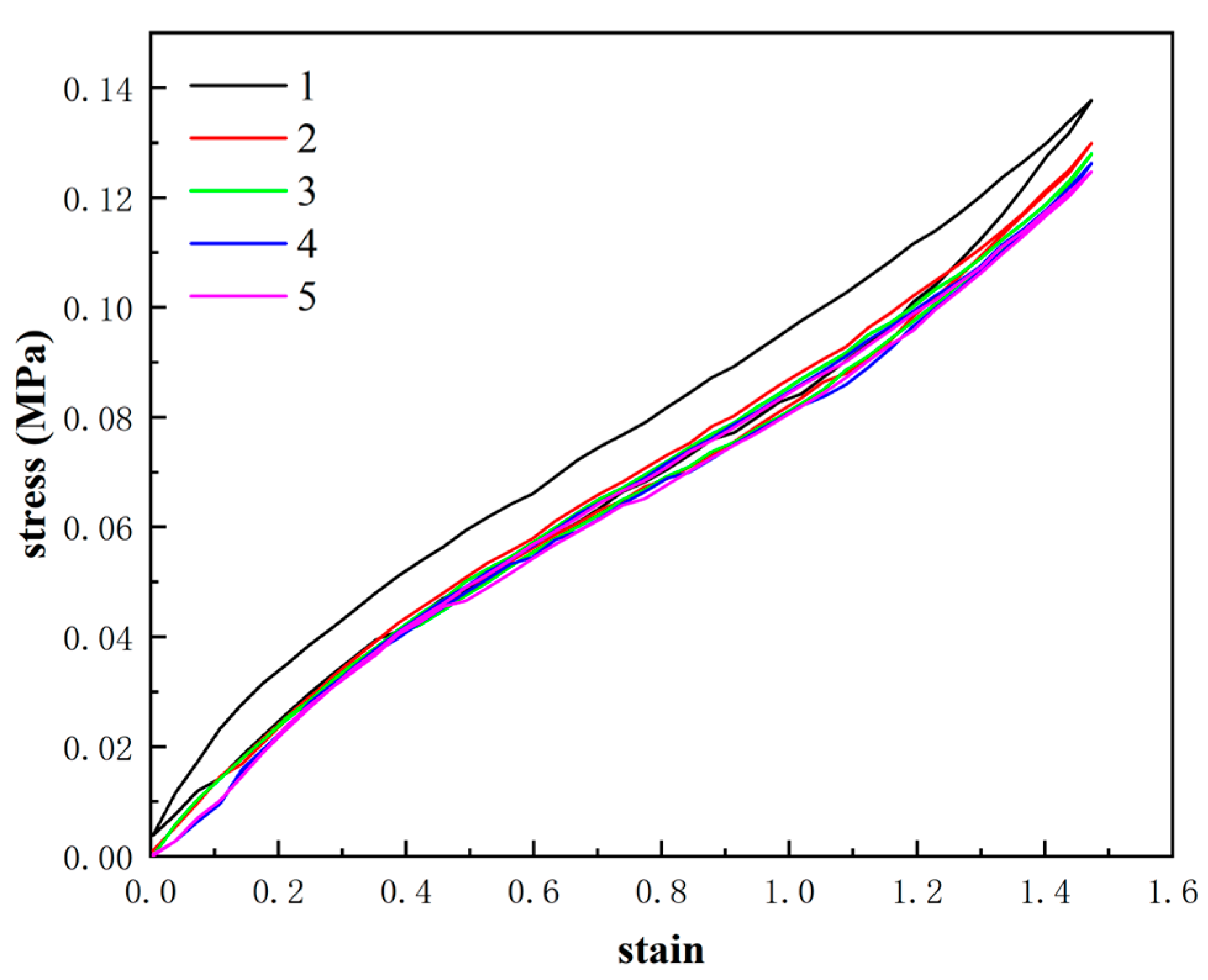



| Material Name | Specification | Manufacturers |
|---|---|---|
| NR | Shandong Haoshun Chemical Co., Ltd., Jinan, Shandong, China | |
| CB | N220 | Tianjin Zhengning New Materials Co., Ltd., Tianjin, China |
| Stearic acid | Industrial-grade | |
| Zinc oxide | Industrial-grade | |
| Sulfur | Industrial-grade | |
| Accelerator NS | Industrial-grade | |
| Antioxidant | 4020 | Industrial-grade |
| Specimen Code | NR | CB N220 | Zinc Oxide | Stearic Acid | Sulfur | Accelerator NS | Antioxidant 4020 | Total | CB Volume Fraction (%) |
|---|---|---|---|---|---|---|---|---|---|
| NR-0 | 100 | 0 | 5 | 3 | 2 | 1 | 1.2 | 112.2 | 0 |
| NR-1 | 100 | 10 | 5 | 3 | 2 | 1 | 1.2 | 122.2 | 4.7 |
| NR-2 | 100 | 20 | 5 | 3 | 2 | 1 | 1.2 | 132.2 | 8.9 |
| NR-3 | 100 | 30 | 5 | 3 | 2 | 1 | 1.2 | 142.2 | 12.8 |
| NR-4 | 100 | 40 | 5 | 3 | 2 | 1 | 1.2 | 152.2 | 16.4 |
| NR-5 | 100 | 50 | 5 | 3 | 2 | 1 | 1.2 | 162.2 | 19.7 |
| NR-6 | 100 | 60 | 5 | 3 | 2 | 1 | 1.2 | 172.2 | 22.7 |
| NR-7 | 100 | 70 | 5 | 3 | 2 | 1 | 1.2 | 182.2 | 25.5 |
| CB (phr) | CB (vol.%) | C10 | C20 | C30 | R2 |
|---|---|---|---|---|---|
| 0 | 0 | 0.30318 | −0.02264 | 0.00254 | 0.996 |
| 10 | 4.7 | 0.3521 | −0.0262 | 0.00337 | 0.992 |
| 30 | 12.8 | 0.4981 | −0.0415 | 0.008581 | 0.998 |
| 50 | 19.7 | 0.6781 | −0.09644 | 0.02217 | 0.998 |
| 70 | 25.5 | 0.9073 | −0.1609 | 0.04587 | 0.999 |
| Model Parameter | Characterization Parameters | R2 | ||
|---|---|---|---|---|
| C10 | A0 = 0.30622 | A1 = 0.00576 | A2 = 6.91 × 10−4 | 0.99991 |
| C20 | B0 = −0.02518 | B1 = 0.00225 | B2 = −2.06 × 10−4 | 0.99884 |
| C30 | C0 = 0.0037 | C1 = −9.12 × 10−4 | C2 = 9.90 × 10−5 | 0.99642 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yao, X.; Hu, F.; Ma, C.; Li, X.; Miao, Z.; Song, J.; Ma, L.; Li, W. Study of the Effect of Carbon Black Filling on the Mechanical Behavior of Rubber Hyper-Elasticity. Materials 2023, 16, 6561. https://doi.org/10.3390/ma16196561
Wang Z, Yao X, Hu F, Ma C, Li X, Miao Z, Song J, Ma L, Li W. Study of the Effect of Carbon Black Filling on the Mechanical Behavior of Rubber Hyper-Elasticity. Materials. 2023; 16(19):6561. https://doi.org/10.3390/ma16196561
Chicago/Turabian StyleWang, Zepeng, Xiulong Yao, Fangru Hu, Chuanxiang Ma, Xinyan Li, Zhanli Miao, Junping Song, Lianxiang Ma, and Wei Li. 2023. "Study of the Effect of Carbon Black Filling on the Mechanical Behavior of Rubber Hyper-Elasticity" Materials 16, no. 19: 6561. https://doi.org/10.3390/ma16196561





