Lone-Pair-Enabled Polymorphism and Photostructural Changes in Chalcogenide Glasses
Abstract
:1. Introduction
2. Simulation Details
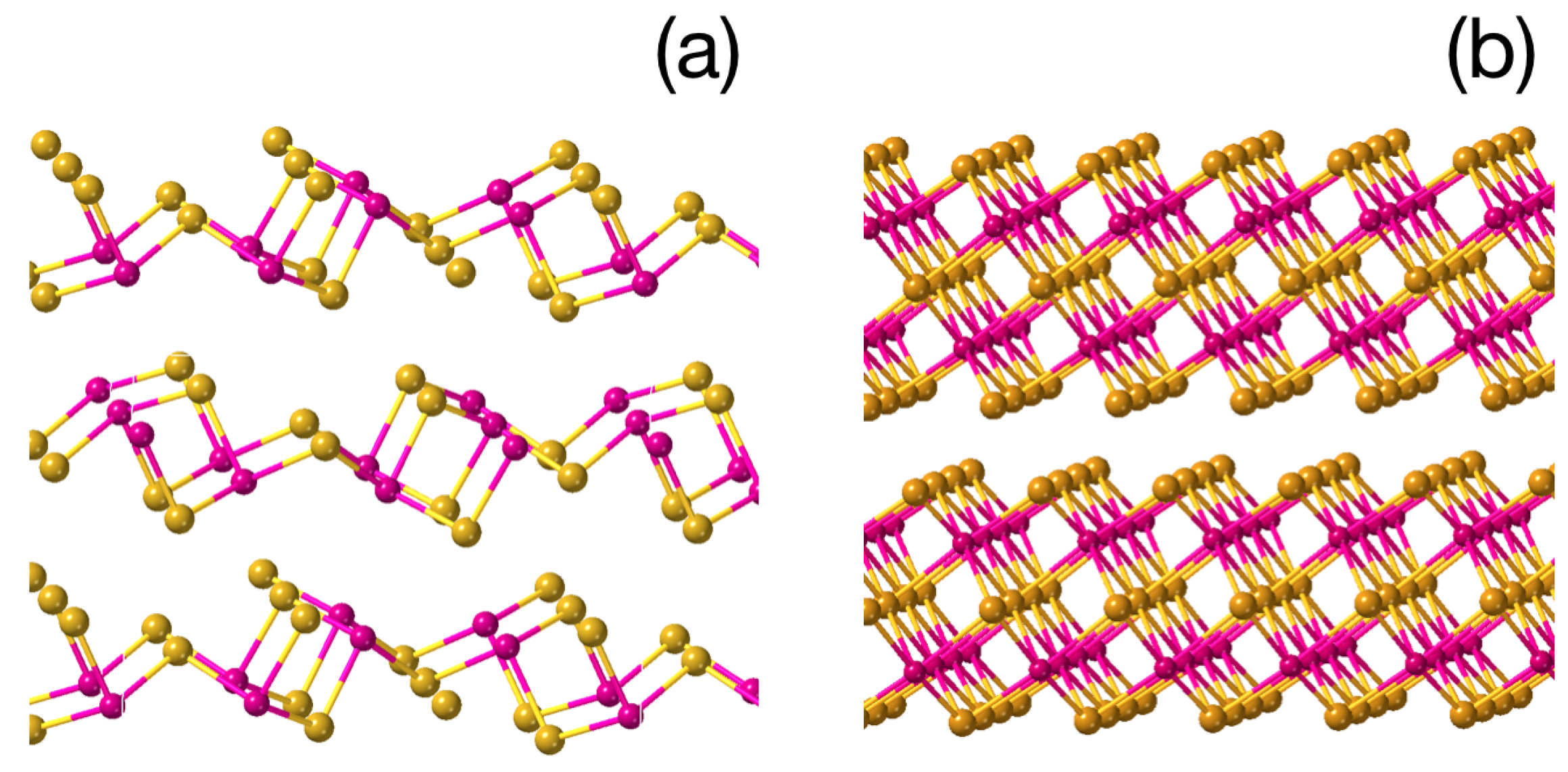
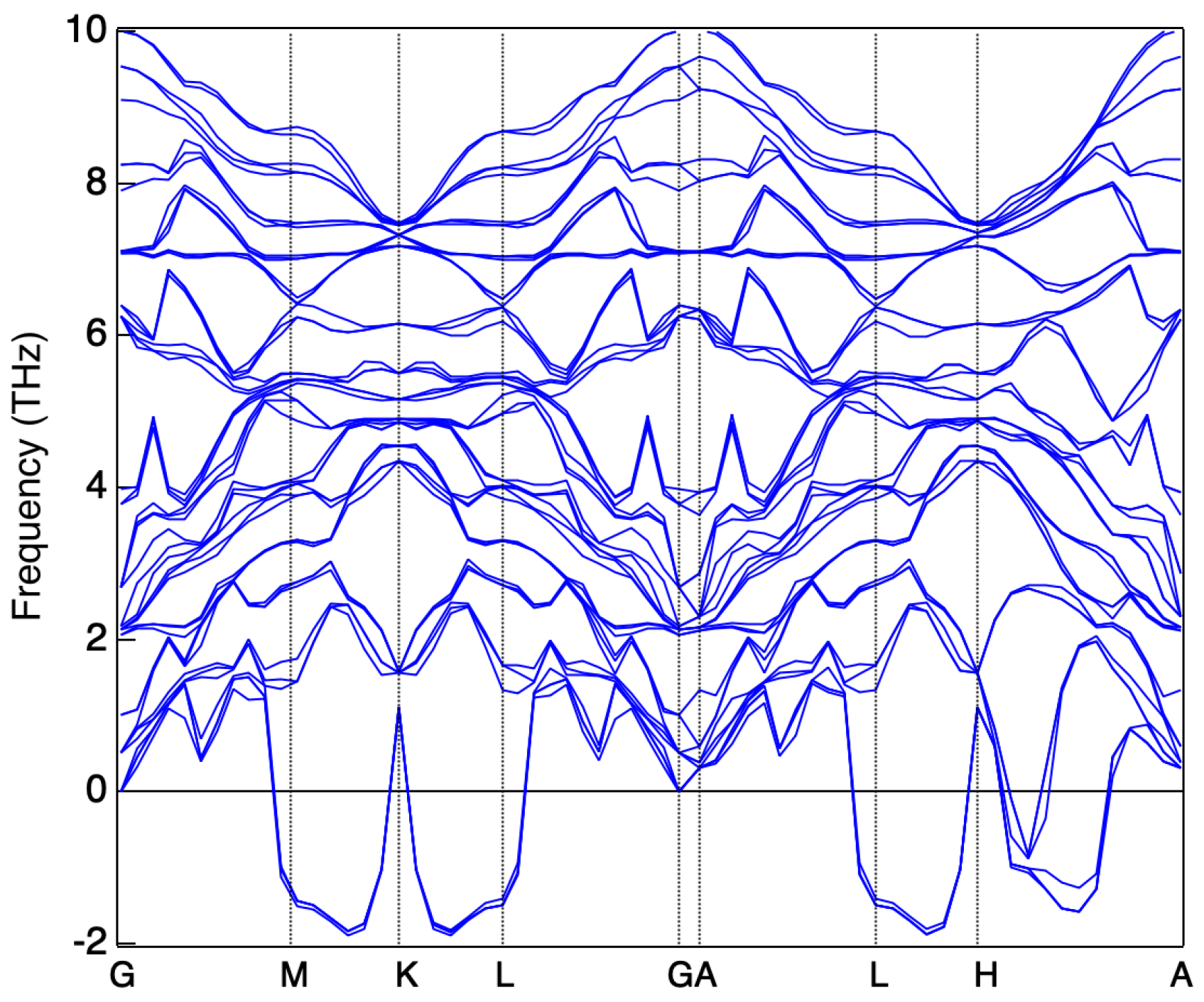
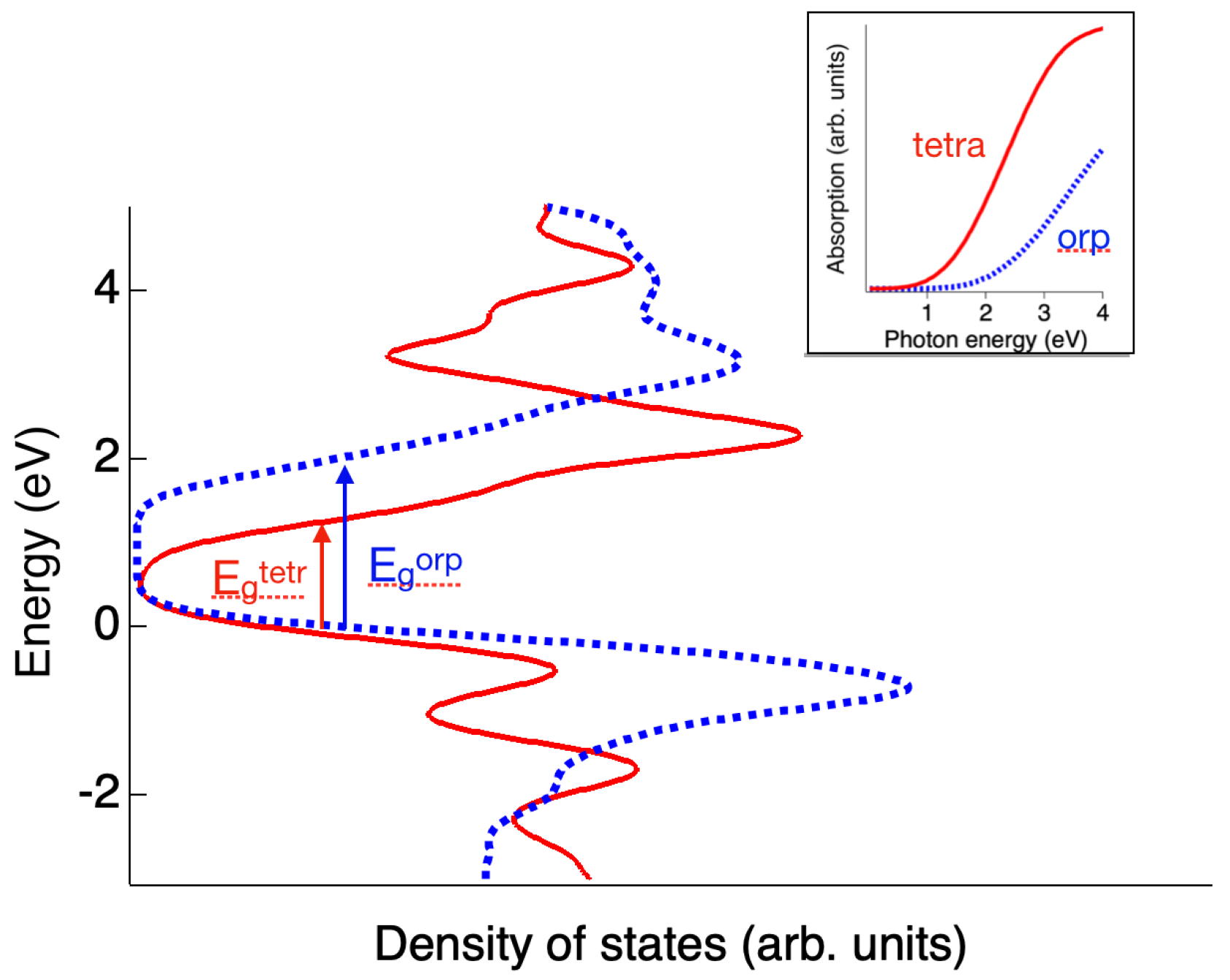
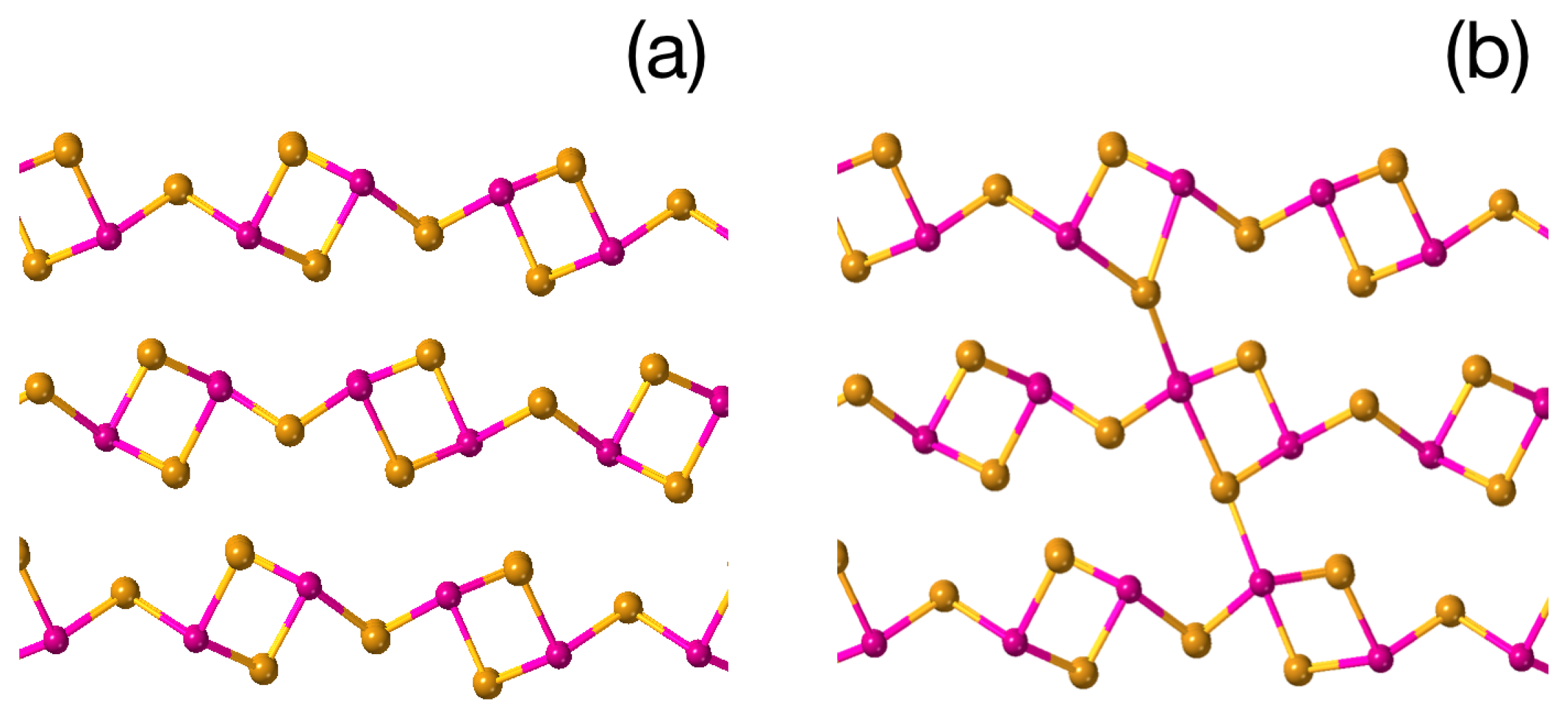
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kolobov, A.V. Photo-Induced Metastability in Amorphous Semiconductors; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tanaka, K.; Shimakawa, K. Amorphous Chalcogenide Semiconductors and Related Materials; Springer: New York, NY, USA, 2011. [Google Scholar]
- Frumar, M.; Firth, A.P.; Owen, A.E. Reversible photodarkening and structural changes in As2S3 thin films. Philos. Mag. B 1984, 50, 463–475. [Google Scholar] [CrossRef]
- Tanaka, K. Reversible photoinduced change in intermolecular distance in amorphous As2S3 network. Appl. Phys. Lett. 1975, 26, 243–245. [Google Scholar] [CrossRef]
- Kolobov, A.V.; Oyanagi, H.; Tanaka, K.; Tanaka, K. Structural study of amorphous selenium by in situ EXAFS: Observation of photoinduced bond alternation. Phys. Rev. B 1997, 55, 726–734. [Google Scholar] [CrossRef]
- Chen, G.; Jain, H.; Khalid, S.; Li, J.; Drabold, D.A.; Elliott, S.R. Study of structural changes in amorphous As2Se3 by EXAFS under in situ laser irradiation. Solid State Commun. 2001, 120, 149–153. [Google Scholar] [CrossRef]
- Berkes, J.S.; Ing, S.W.; Hillegas, W.J. Photodecomposition of amorphous As2Se3 and As2S3. J. Appl. Phys. 1971, 42, 4908–4916. [Google Scholar] [CrossRef]
- Gurevich, S.B.; Ilyashenko, N.N.; Kolomiets, B.T.; Lyubin, V.M.; Shilo, V.P. Photostimulated changes of optical properties and structure of amorphous Se-As films. Phys. Stat. Sol. A 1974, 26, K127–K130. [Google Scholar] [CrossRef]
- Tanaka, K. Photoexpansion in As2S3 glass. Phys. Rev. B 1998, 57, 5163. [Google Scholar] [CrossRef]
- Hisakuni, H.; Tanaka, K. Giant photoexpansion in As2S3 glass. Appl. Phys. Lett. 1994, 65, 2925–2927. [Google Scholar] [CrossRef]
- Lyubin, V.M.; Tikhomirov, V.K. Novel photo-induced effects in chalcogenide glasses. J. Non-Cryst. Solids 1991, 135, 37–48. [Google Scholar] [CrossRef]
- Lyubin, V.M.; Tikhomirov, V.K. Photodarkening and photoinduced anisotropy in chalcogenide vitreous semiconductor films. J. Non-Cryst. Solids 1989, 114, 133. [Google Scholar] [CrossRef]
- Delullier, P.; Druart, G.; De La Barrière, F.; Calvez, L.; Lancry, M. Femtosecond Laser Direct Writing of Gradient Index Fresnel Lens in GeS2-Based Chalcogenide Glass for Imaging Applications. Appl. Sci. 2022, 12, 4490. [Google Scholar] [CrossRef]
- D’amico, C.; Martin, G.; Troles, J.; Cheng, G.; Stoian, R. Multiscale laser written photonic structures in bulk chalcogenide glasses for infrared light transport and extraction. Photonics 2021, 8, 211. [Google Scholar] [CrossRef]
- Ivliev, N.A.; Khonina, S.N.; Podlipnov, V.V.; Karpeev, S.V. Holographic Writing of Forked Diffraction Gratings on the Surface of a Chalcogenide Glass Semiconductor. Photonics 2023, 10, 125. [Google Scholar] [CrossRef]
- Le, S.D.; Nguyen, D.M.; Thual, M.; Bramerie, L.; Silva, M.C.; Lenglé, K.; Gay, M.; Chartier, T.; Brilland, L.; Méchin, D.; et al. Efficient four-wave mixing in an ultra-highly nonlinear suspended-core chalcogenide As38Se62 fiber. Opt. Express 2011, 19, B653–B660. [Google Scholar] [CrossRef]
- Asobe, M.; Kobayashi, H.; Itoh, H.; Kanamori, T. Laser-diode-driven ultrafast all-optical switching by using highly nonlinear chalcogenide glass fiber. Opt. Lett. 1993, 18, 1056–1058. [Google Scholar] [CrossRef]
- Viens, J.F.; Meneghini, C.; Villeneuve, A.; Galstian, T.V.; Knystautas, E.J.; Duguay, M.A.; Richardson, K.A.; Cardinal, T. Fabrication and Characterization of Integrated Optical Waveguides in Sulfide Chalcogenide Glasses. J. Lightwave Technol. 1999, 17, 1184. [Google Scholar] [CrossRef]
- Meneghini, C.; Villeneuve, A. As2S3 photosensitivity by two-photon absorption: Holographic gratings and self-written channel waveguides. J. Opt. Soc. Am. B 1998, 15, 2946–2950. [Google Scholar] [CrossRef]
- Song, S.; Howard, S.S.; Liu, Z.; Dirisu, A.O.; Gmachl, C.F.; Arnold, C.B. Mode tuning of quantum cascade lasers through optical processing of chalcogenide glass claddings. Appl. Phys. Lett. 2006, 89, 041115. [Google Scholar] [CrossRef]
- Nesterov, S.; Boyko, M.; Krbal, M.; Kolobov, A. On the ultimate resolution of As2S3-based inorganic resists. J. Non-Cryst. Solids 2021, 563, 120816. [Google Scholar] [CrossRef]
- Palka, K.; Slang, S.; Vlcek, M. High-Resolution Photoresists; World Scientific: Singapore, 2021. [Google Scholar]
- Ikeda, Y.; Shimakawa, K. In situ simultaneous measurements of photoinduced volume and bandgap changes in amorphous As2S3 films. Chalcogenide Lett. 2005, 2, 127–132. [Google Scholar]
- Moreno, T.V.; Zanuto, V.S.; Astrath, N.G.; Silva, G.R.; Fonseca, E.J.; Souza, S.T.; Zhao, D.; Jain, H.; Malacarne, L.C. In situ measurements of photoexpansion in As2S3 bulk glass by atomic force microscopy. Opt. Mater. 2019, 94, 9–14. [Google Scholar] [CrossRef]
- Achimova, E.; Stronski, A.; Abaskin, V.; Meshalkin, A.; Paiuk, A.; Prisacar, A.; Oleksenko, P.; Triduh, G. Direct surface relief formation on As2S3–Se nanomultilayers in dependence on polarization states of recording beams. Opt. Mater. 2015, 47, 566–572. [Google Scholar] [CrossRef]
- Messaddeq, S.H.; Dumont, A.; Douaud, A.; El-Amraoui, M.; Messaddeq, Y. Formation of cross-superposed LIPSSs on bulk chalcogenide glasses using fs-laser. Adv. Opt. Technol. 2018, 7, 311–319. [Google Scholar] [CrossRef]
- Yu, X.; Qi, D.; Wang, H.; Zhang, Y.; Wang, L.; Zhang, Z.; Dai, S.; Shen, X.; Zhang, P.; Xu, Y. In situ and ex-situ physical scenario of the femtosecond laser-induced periodic surface structures. Opt. Express 2019, 27, 10087–10097. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Q.; Qi, D.; Tang, S.; Dai, S.; Zhang, P.; Xu, Y.; Shen, X. Femtosecond laser-induced large area of periodic structures on chalcogenide glass via twice laser direct-writing scanning process. Opt. Laser Technol. 2020, 124, 105977. [Google Scholar] [CrossRef]
- Elliott, S.R. A unified model for reversible photostructural effects in chalcogenide glasses. J. Non-Cryst. Solids 1986, 81, 71–98. [Google Scholar] [CrossRef]
- Klinger, M.I.; Taraskin, S.N. Theory of electron two-band self-trapping in atomic soft configurations: Hybridization of states, formation of negative-U centers, and anharmonic atomic dynamics. Phys. Rev. B 1995, 52, 2557. [Google Scholar] [CrossRef]
- Li, J.; Drabold, D.A. Direct Calculation of Light-Induced Structural Change and Diffusive Motion in Glassy As2Se3. Phys. Rev. Lett. 2000, 85, 2785–2788. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles calculations uning CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Vadnerbuilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B. 1990, 41, 7892–7895. [Google Scholar]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Baroni, S.; de Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Refson, K.; Tulip, P.R.; Clark, S.J. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Phys. Rev. B 2006, 73, 155114. [Google Scholar] [CrossRef]
- Caravati, S.; Bernasconi, M.; Kühne, T.D. Krack, M.; Parrinello, M. Coexistence of tetrahedral-and octahedral-like sites in amorphous phase change materials. Appl. Phys. Lett 2007, 91, 171906. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab-Initio Molecular-Dynamics Simulation of the Liquid-Metal Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Bloechl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Mott, N.F. Elecrtrons in glass. Science 1978, 201, 871–875. [Google Scholar] [CrossRef]
- Ioffe, A.F. Unsolved problems of the semiconductor theory. Izv. Akad. Nauk. SSSR Ser. Fiz. 1951, 15, 477. [Google Scholar]
- Zachariasen, W. The atomic arrangement in glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
- Seki, T.; Sakurada, K.; Muromoto, M.; Ito, H. Photoinduced single-crystal-to-single-crystal phase transition and photosalient effect of a gold(i) isocyanide complex with shortening of intermolecular aurophilic bonds. Chem. Sci. 2015, 6, 1491–1497. [Google Scholar] [CrossRef] [PubMed]
- Buron-Le Cointe, M.; Hébert, J.; Baldé, C.; Moisan, N.; Toupet, L.; Guionneau, P.; Létard, J.F.; Freysz, E.; Cailleau, H.; Collet, E. Intermolecular control of thermoswitching and photoswitching phenomena in two spin-crossover polymorphs. Phys. Rev. B 2012, 85, 064114. [Google Scholar] [CrossRef]
- Zallen, R. The Physics of Amorphous Solids; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Mott, N.F. Electrons in disordered structures. Adv. Phys. 1967, 16, 49–144. [Google Scholar] [CrossRef]
- Xu, M.; Cheng, Y.; Sheng, H.; Ma, E. Nature of Atomic Bonding and Atomic Structure in the Phase-Change Ge2Sb2Te5 Glass. Phys. Rev. Lett. 2009, 103, 195502. [Google Scholar] [CrossRef] [PubMed]
- Kolobov, A.V.; Fons, P.; Tominaga, J. p-Type conductivity of GeTe: The role of lone-pair electrons. Phys. Stat. Sol. B 2012, 249, 1902–1906. [Google Scholar] [CrossRef]
- Lucovsky, G.; White, R.M. Effects of Resonance Bonding on the Properties of Crystalline and Amorphous Semiconductors. Phys. Rev. B 1973, 8, 660–667. [Google Scholar] [CrossRef]
- Shportko, K.; Kremers, S.; Woda, M.; Lencer, D.; Robertson, J.; Wuttig, M. Resonant bonding in crystalline phase-change materials. Nature Mater. 2008, 7, 653–658. [Google Scholar] [CrossRef]
- Lee, T.H.; Elliott, S.R. Multi-Center Hyperbonding in Phase-Change Materials. Phys. Stat. Sol. RRL 2021, 15, 2000516. [Google Scholar] [CrossRef]
- Dembovsky, S.A.; Chechetkina, E.A. Glass Formation; Nauka: Moscow, Russia, 1990. [Google Scholar]
- Lyubin, V.M.; Tikhomirov, V.K. Photoinduced optical anisotropy in the chalcogenide glass As2S3. Sov. J. Exp. Theor. Phys. Lett. 1990, 51, 587. [Google Scholar]
- Dembovsky, S.A.; Chechetkina, E.A. Hypervalent Bonds as Active Centers Providing Photo-Induced Transformations in Glasses; Wiley: Hoboken, NJ, USA, 2003; pp. 299–309. [Google Scholar]
- Skoug, E.J.; Morelli, D.T. Role of lone-pair electrons in producing minimum thermal conductivity in nitrogen-group chalcogenide compounds. Phys. Rev. Lett. 2011, 107, 235901. [Google Scholar] [CrossRef] [PubMed]
- Kolobov, A.V.; Fons, P.; Tominaga, J.; Ovshinsky, S.R. Vacancy-mediated three-center four-electron bonds in GeTe-Sb2Te3 phase-change memory alloys. Phys. Rev. B 2013, 87, 165206. [Google Scholar] [CrossRef]
- Kolobov, A.V.; Tominaga, J. Chalcogenides: Metastability and Phase Change Phenomena; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kolobov, A.V.; Krbal, M.; Fons, P.; Tominaga, J.; Uruga, T. Distortion-triggered loss of long-range order in solids with bonding energy hierarchy. Nat. Chem. 2011, 3, 311–316. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Robertson, J. Bonding origin of optical contrast in phase-change memory materials. Phys. Rev. B 2010, 81, 081204. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolobov, A.V.; Kuznetsov, V.G.; Krbal, M.; Zabotnov, S.V. Lone-Pair-Enabled Polymorphism and Photostructural Changes in Chalcogenide Glasses. Materials 2023, 16, 6602. https://doi.org/10.3390/ma16196602
Kolobov AV, Kuznetsov VG, Krbal M, Zabotnov SV. Lone-Pair-Enabled Polymorphism and Photostructural Changes in Chalcogenide Glasses. Materials. 2023; 16(19):6602. https://doi.org/10.3390/ma16196602
Chicago/Turabian StyleKolobov, Alexander V., Vladimir G. Kuznetsov, Milos Krbal, and Stanislav V. Zabotnov. 2023. "Lone-Pair-Enabled Polymorphism and Photostructural Changes in Chalcogenide Glasses" Materials 16, no. 19: 6602. https://doi.org/10.3390/ma16196602
APA StyleKolobov, A. V., Kuznetsov, V. G., Krbal, M., & Zabotnov, S. V. (2023). Lone-Pair-Enabled Polymorphism and Photostructural Changes in Chalcogenide Glasses. Materials, 16(19), 6602. https://doi.org/10.3390/ma16196602







