Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear
Abstract
:1. Introduction
2. Finite Element Theory and Modeling of Die Quenching
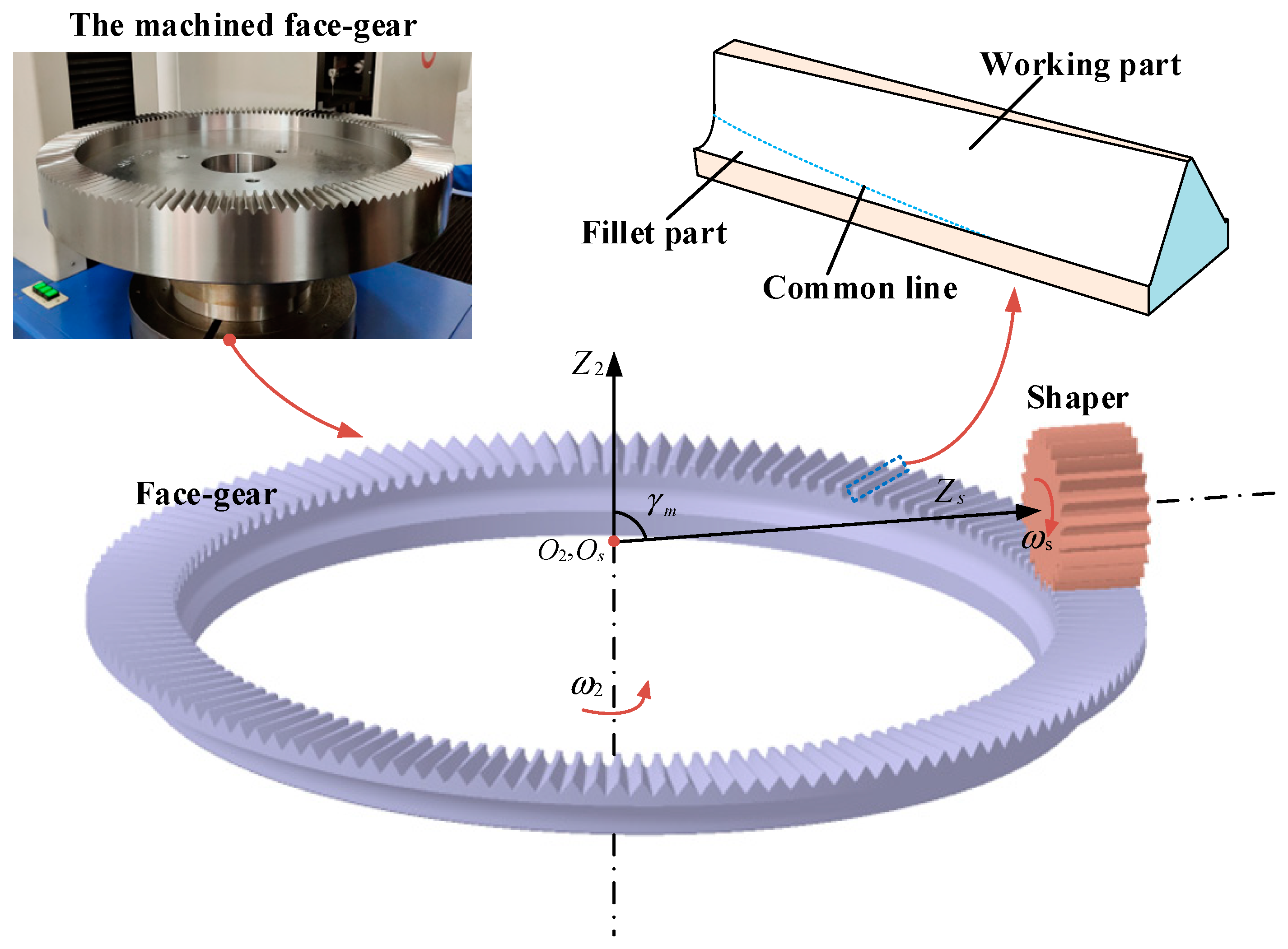
2.1. Modeling of Face Gear
2.2. Numerical Theoretical Model for Heat Treatment
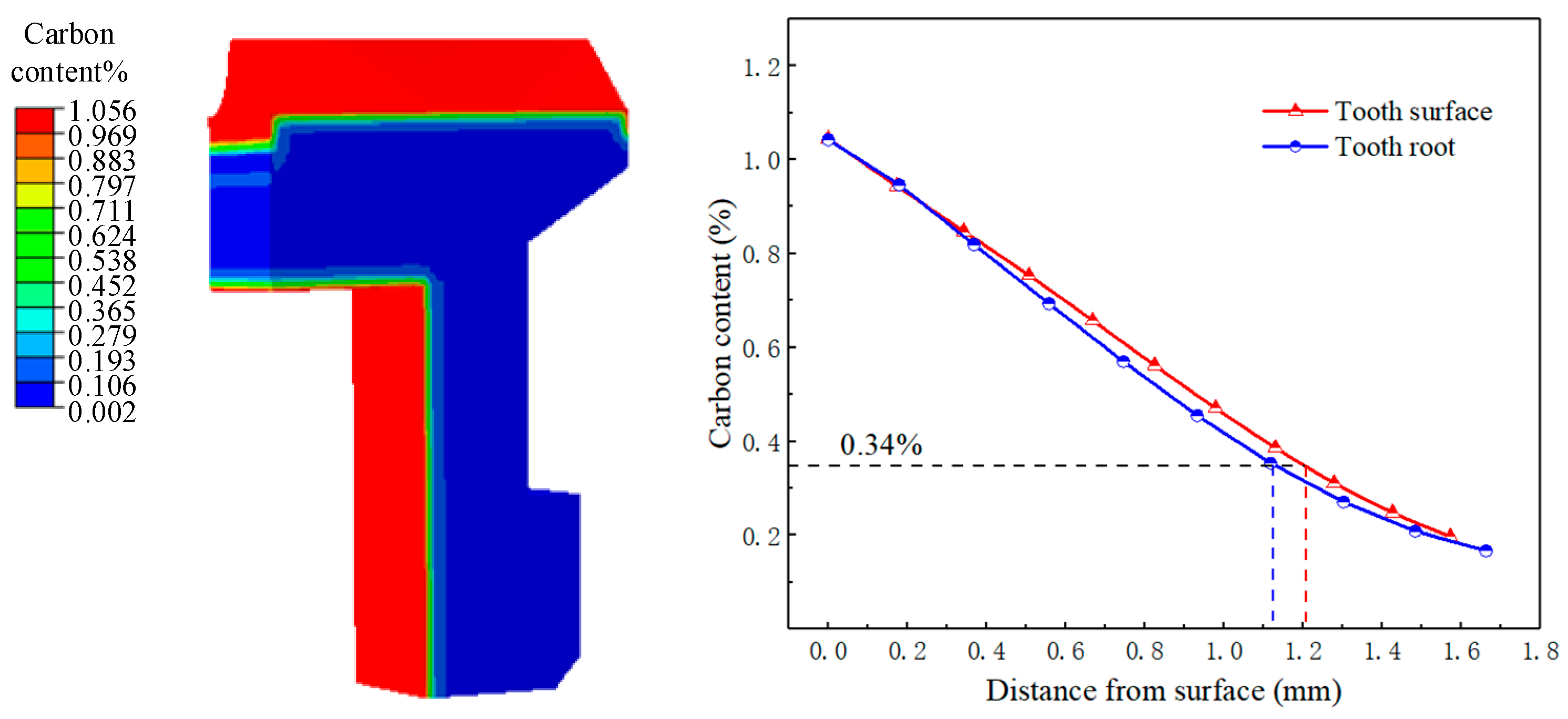
2.2.1. Carbon Diffusion Model
2.2.2. Temperature Calculation Model
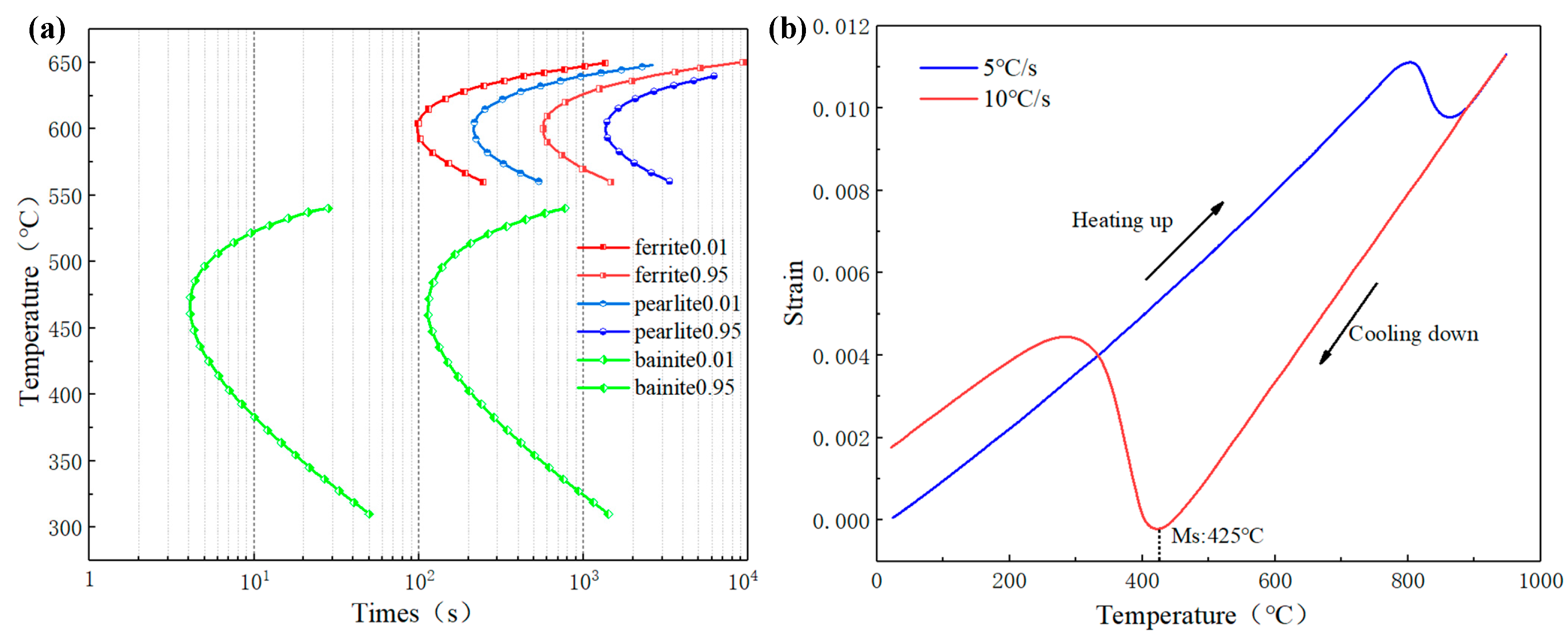
2.2.3. Kinetic Model of Phase Transformation
2.2.4. Mechanical Model
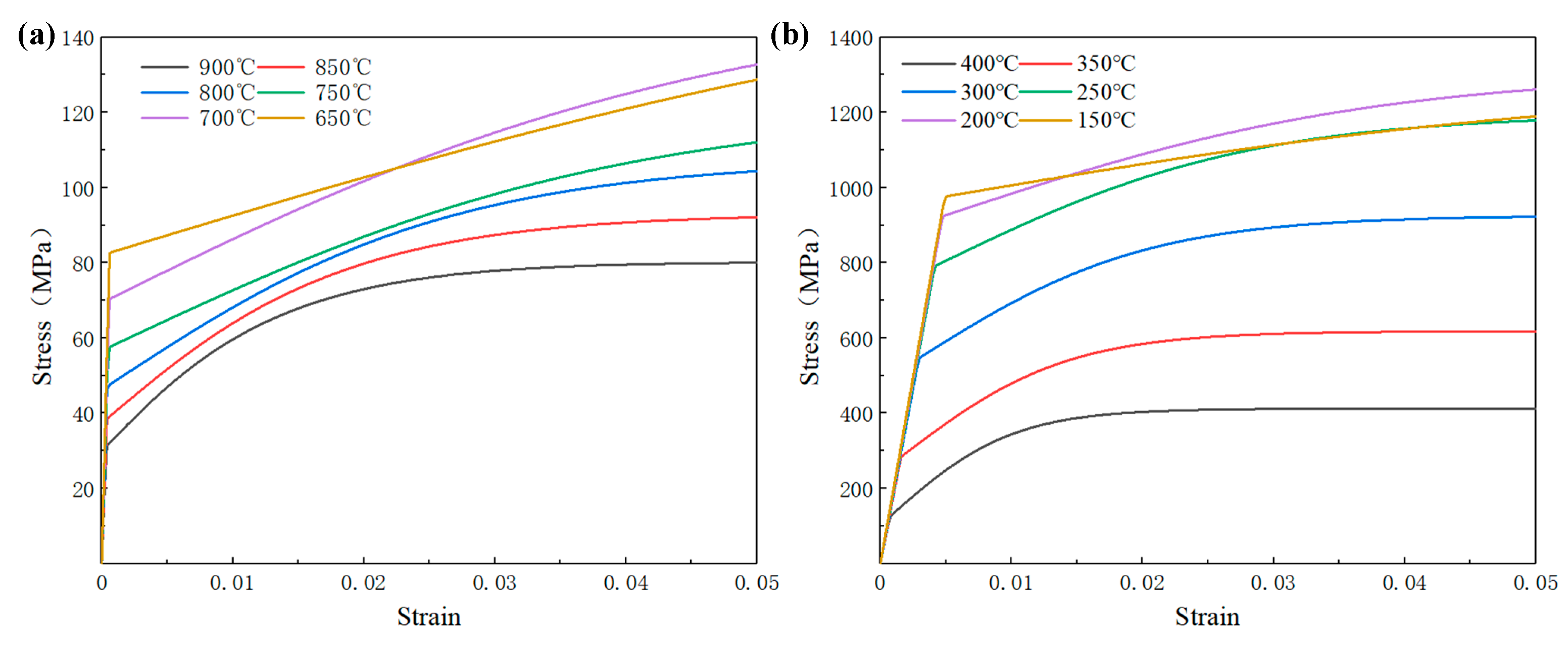
2.3. Material Properties of 9310
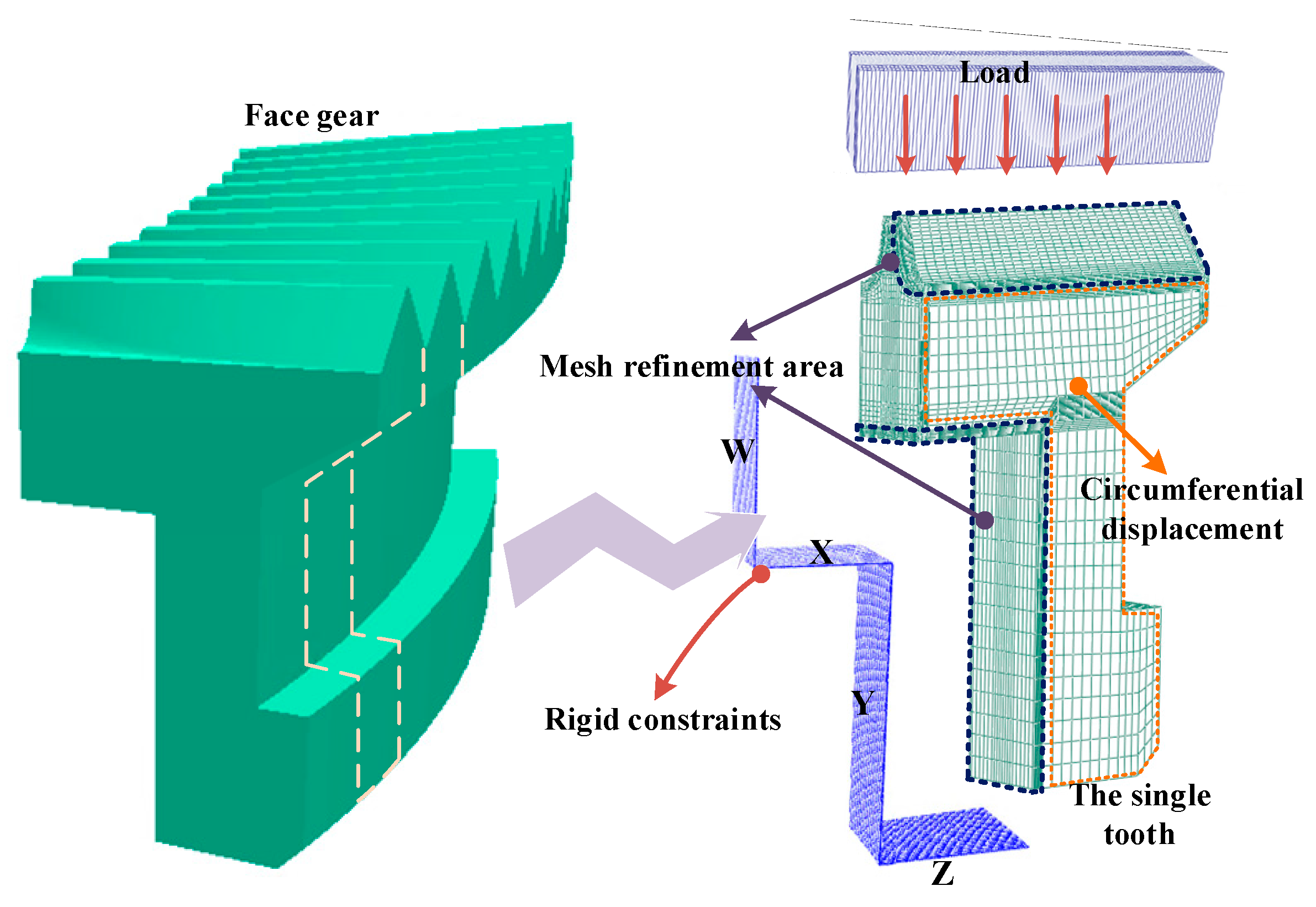
2.4. Finite Element Modeling of Die Quenching
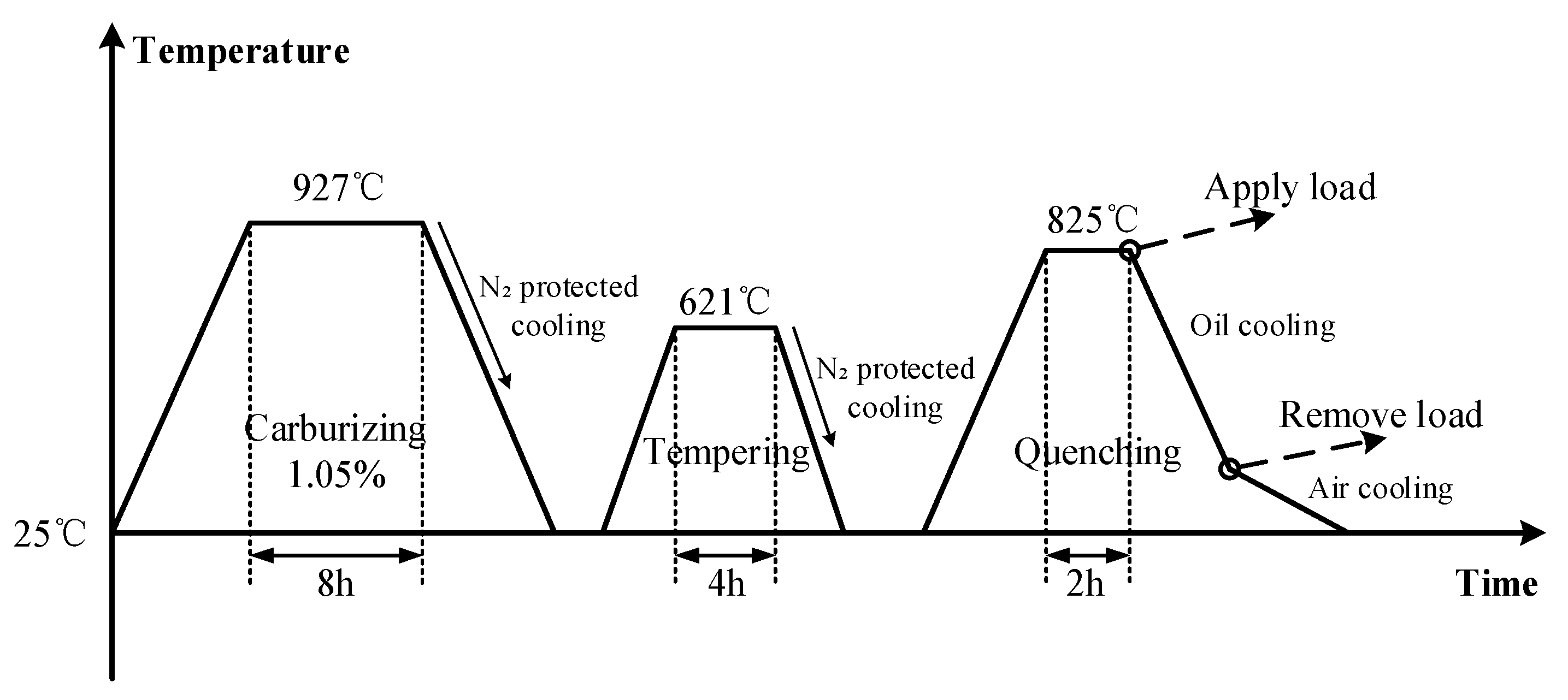
2.4.1. Parameters of the Die Quenching Model
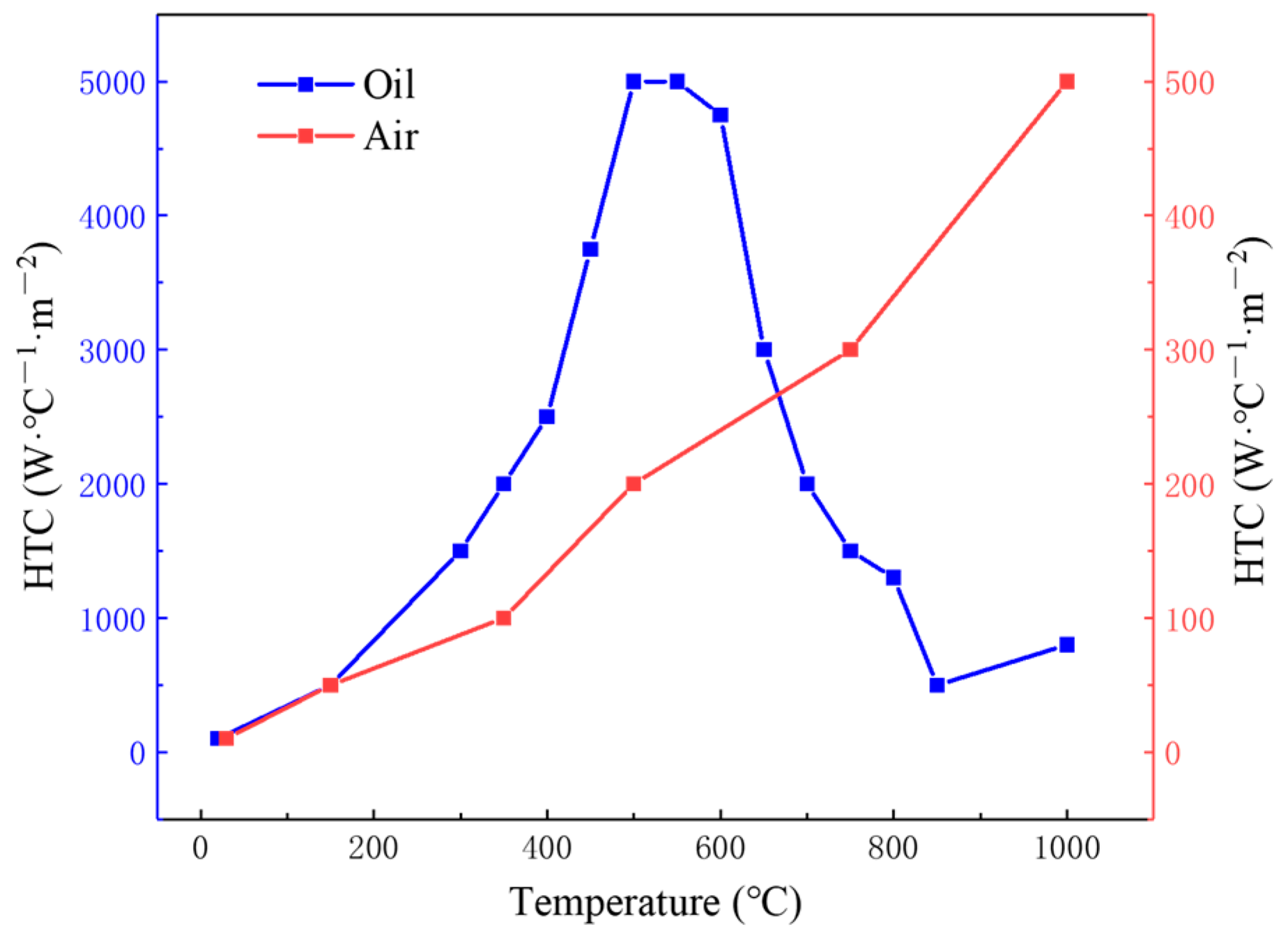
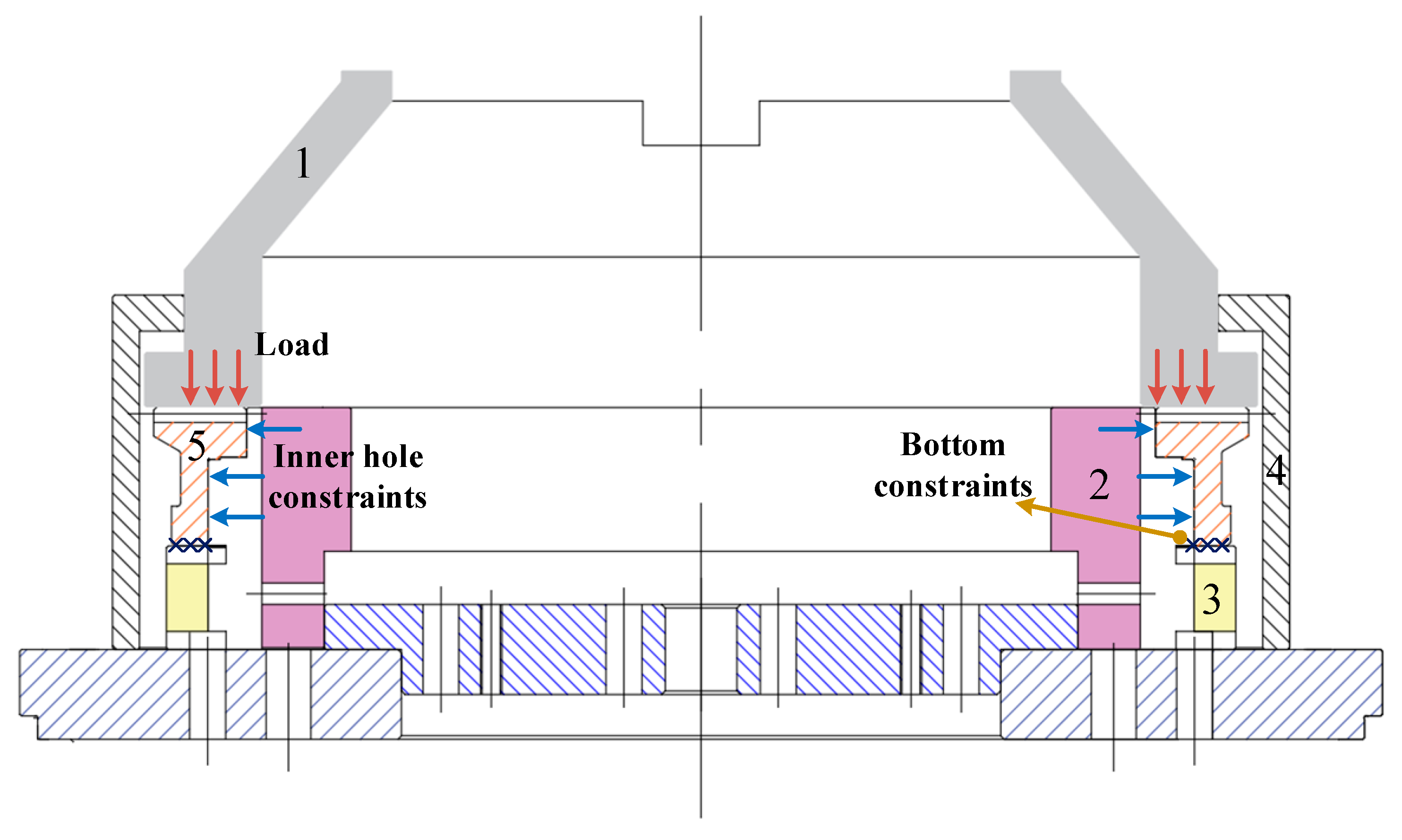
2.4.2. Boundary Conditions for Quenching
3. Results and Discussion
3.1. Deformation of Gear Die Quenching
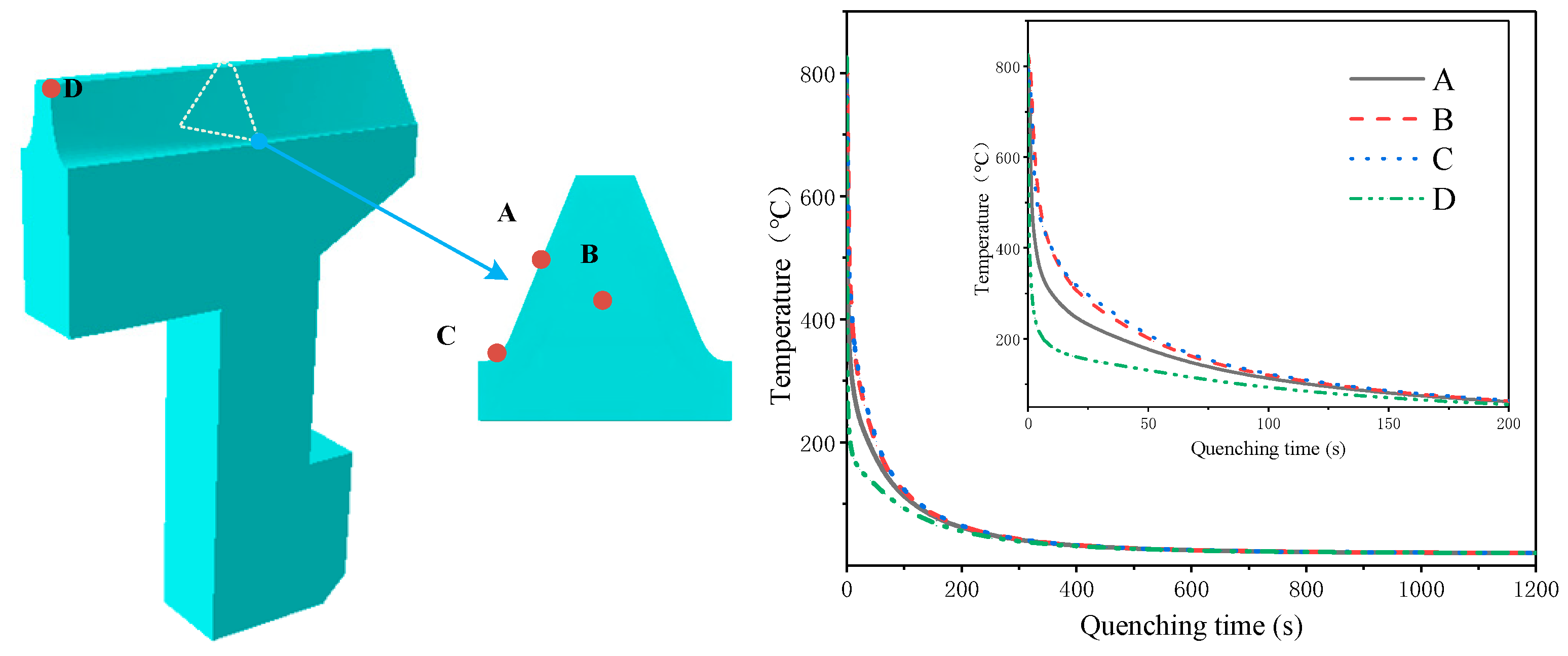
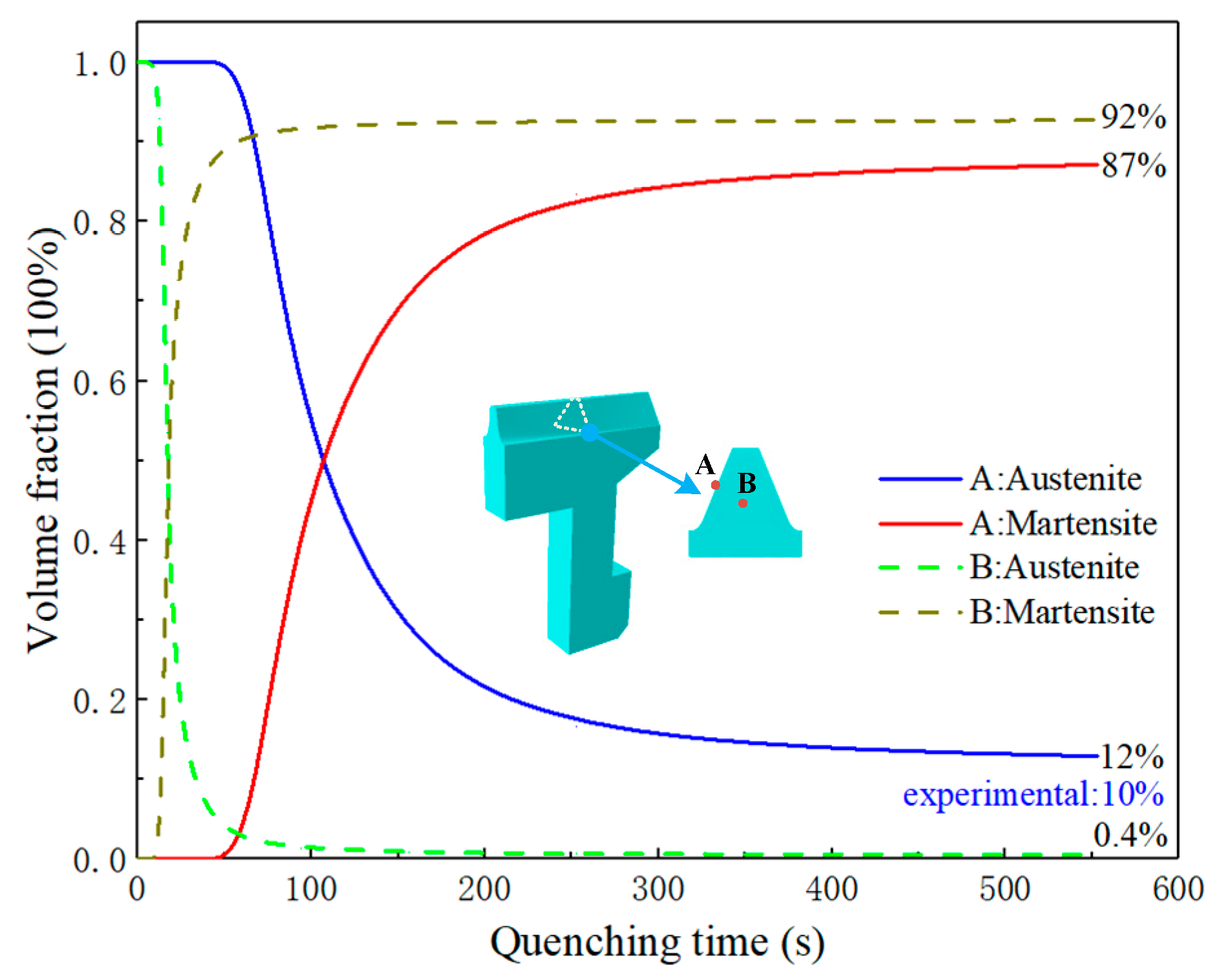
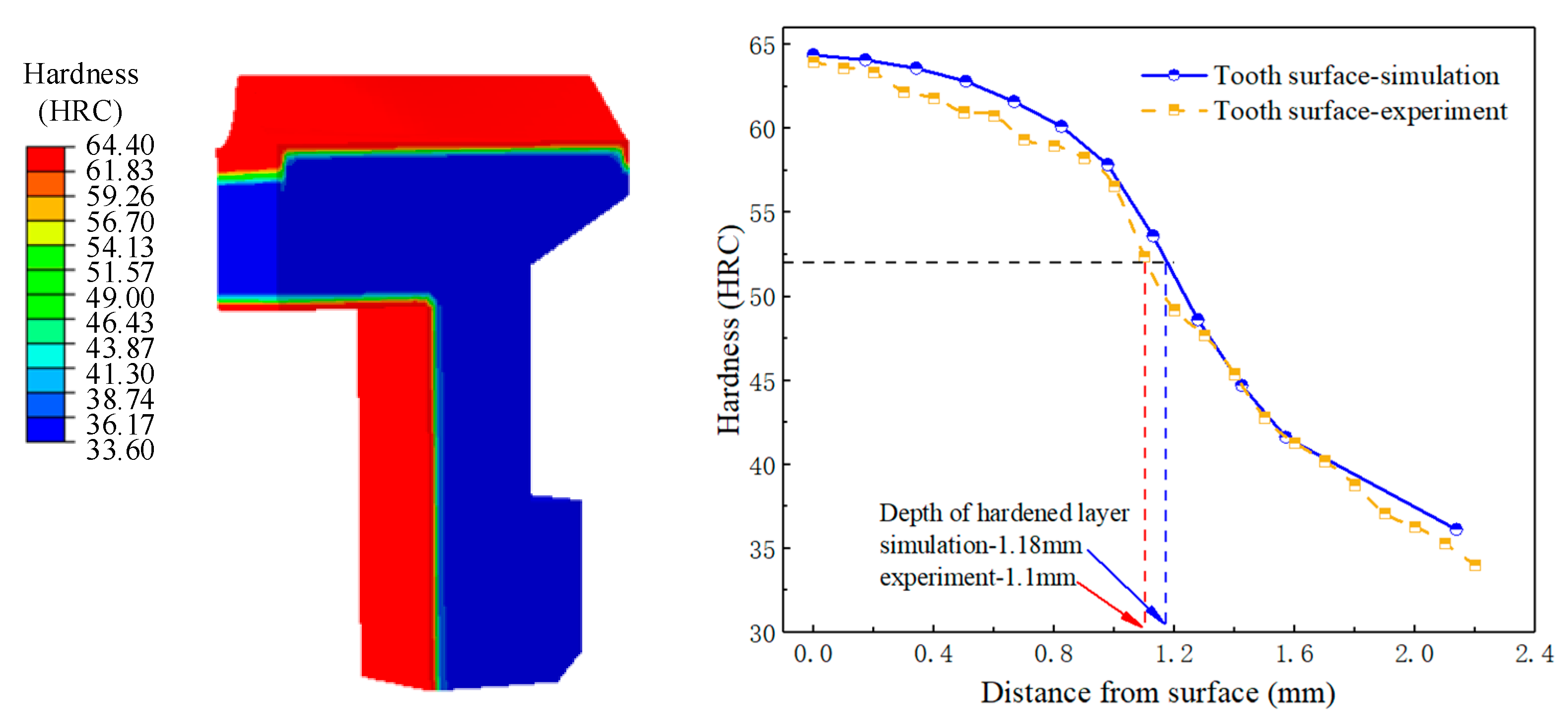
3.1.1. Temperature History and Microstructure Transformation
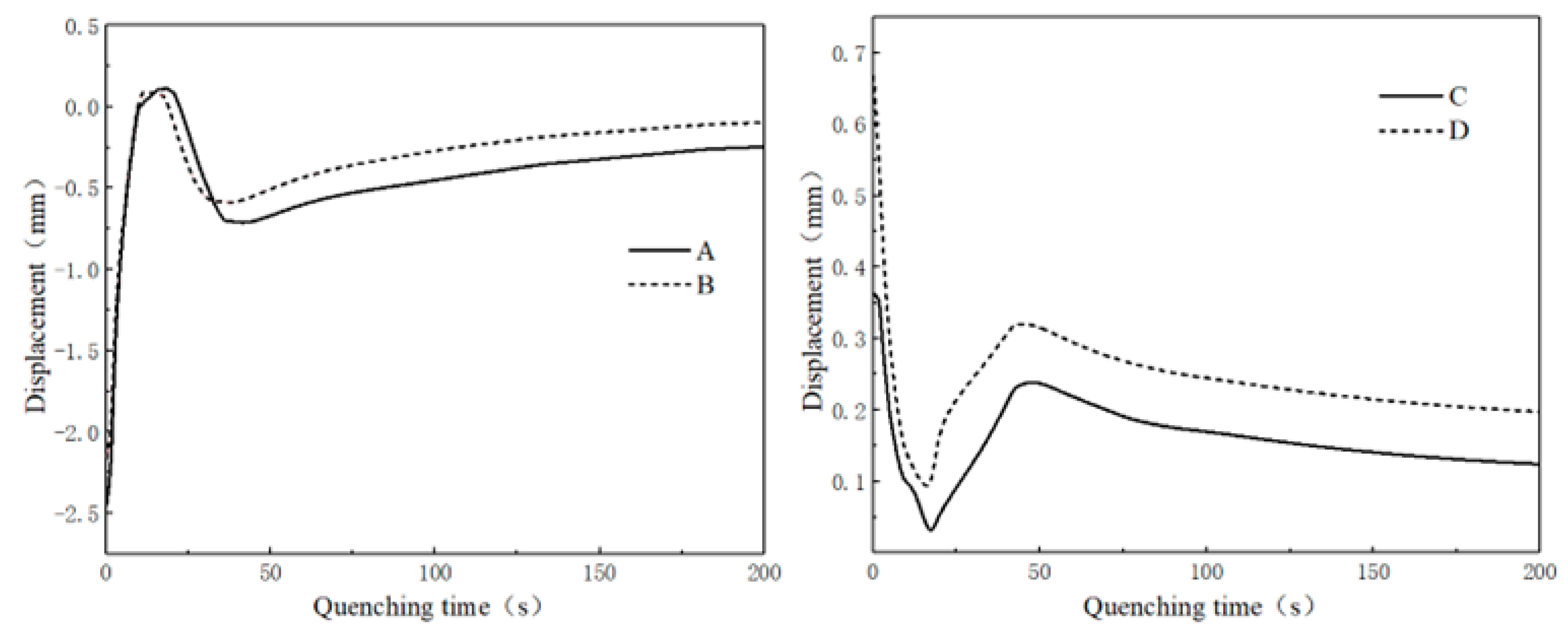
3.1.2. Gear Deformation of Die Quenching
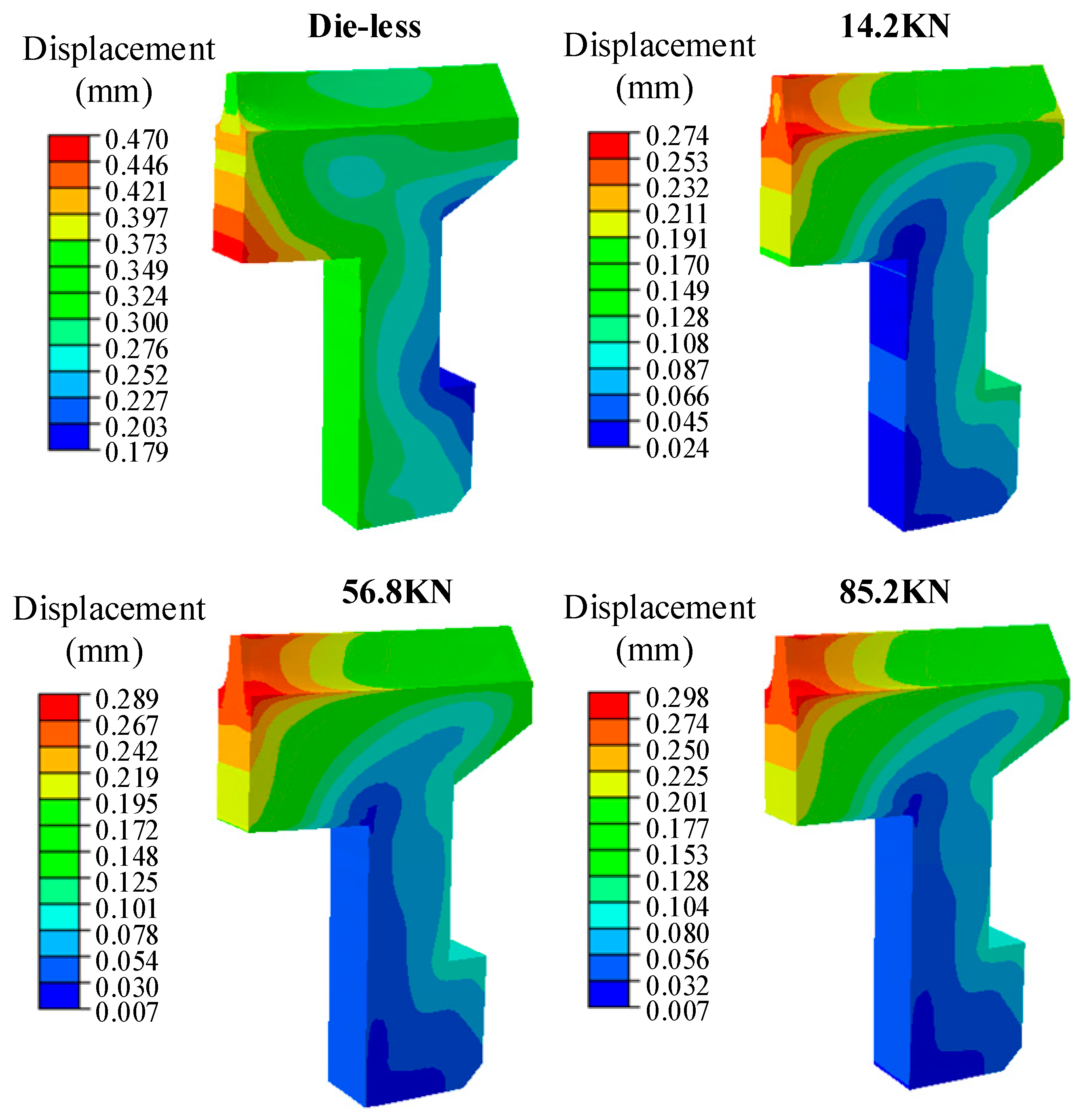
3.2. Influence of Load on Gear Deformation
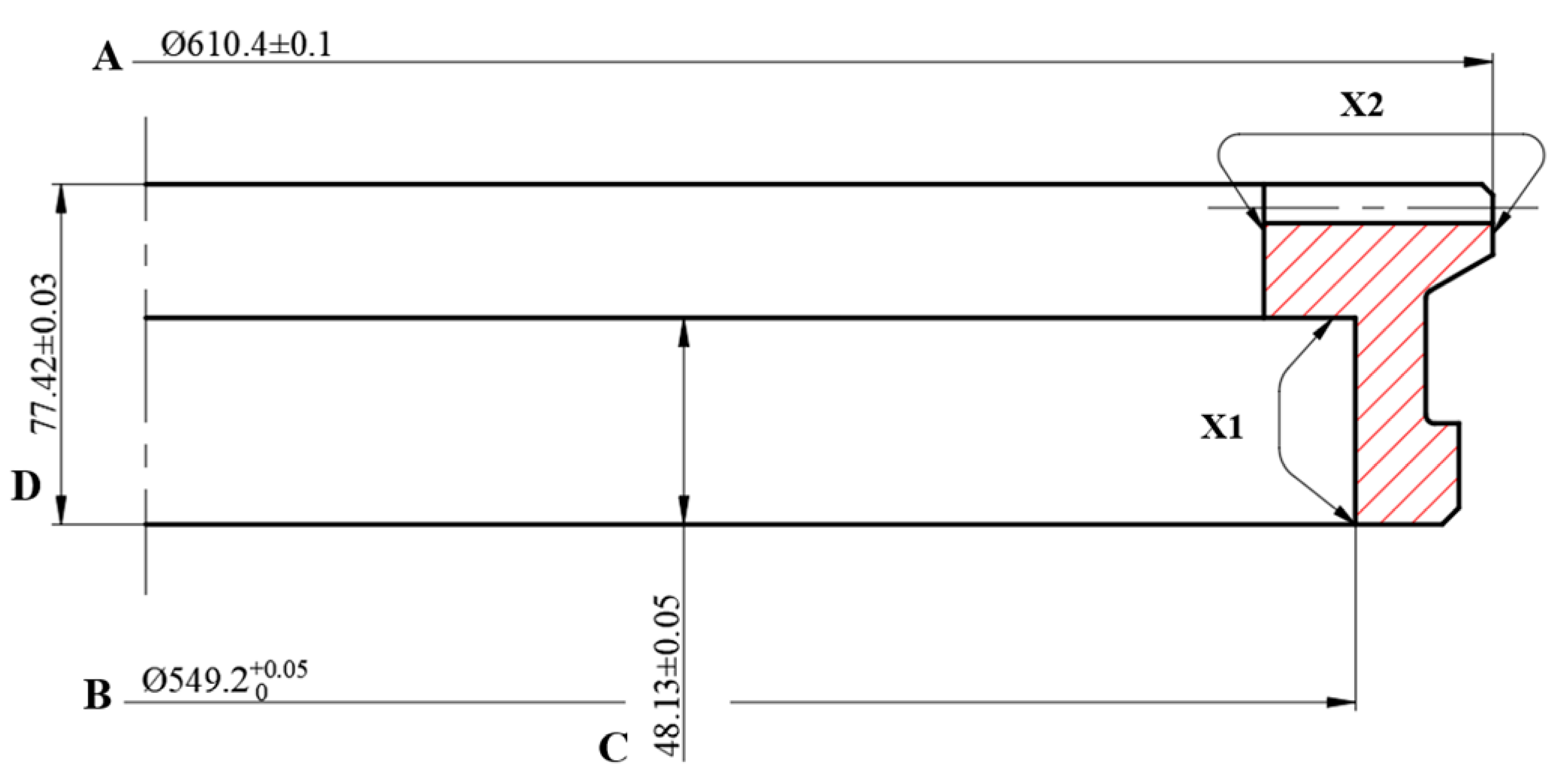
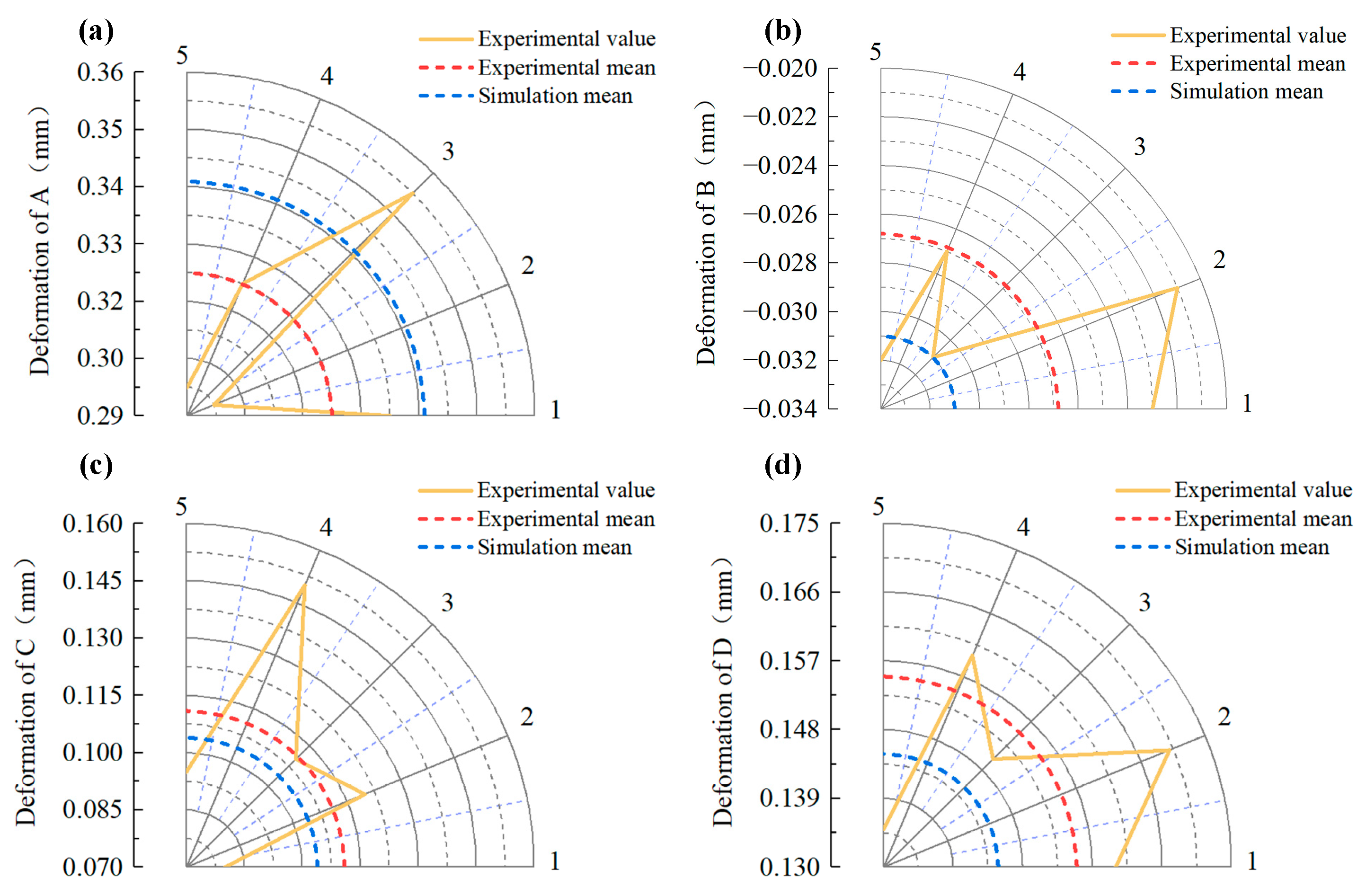
4. Experimental Verification of Die Quenching
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Wu, Y.; Wang, L.; Tang, J.; Ouyang, H. A new closed-form calculation of envelope surface for modeling face gears. Mech. Mach. Theory 2019, 137, 211–226. [Google Scholar] [CrossRef]
- Pietzsch, R.; Brzoza, M.; Kaymak, Y.; Specht, E.; Bertram, A. Simulation of the Distortion of Long Steel Profiles During Cooling. J. Appl. Mech. 2007, 74, 427–437. [Google Scholar] [CrossRef] [Green Version]
- Amey, C.M.; Huang, H.; Rivera-Diaz-Del-Castillo, P.E.J. Distortion in 100Cr6 and nanostructured bainite. Mater. Des. 2012, 35, 66–71. [Google Scholar] [CrossRef]
- Kim, N.-K.; Bae, K.-Y. Analysis of deformation in the carburizing-quenching heat treatment of helical gears made of SCM415H steel. Int. J. Precis. Eng. Manuf. 2015, 16, 73–79. [Google Scholar] [CrossRef]
- Yan-Zhong, W.; Zhou, L.; Liang-Wei, H.; Hong-Pu, Z.; Yang, Z. Heat treatment process optimization for face gears based on deformation and residual stress control. J. Chongqing Univ. (Engl. Ed.) 2015, 14, 10. [Google Scholar]
- Nie, Z.; Wang, G.; Lin, Y.; Rong, Y.K. Precision Measurement and Modeling of Quenching-Tempering Distortion in Low-Alloy Steel Components with Internal Threads. J. Mater. Eng. Perform. 2015, 24, 4878–4889. [Google Scholar] [CrossRef]
- Srinivasan, V.; Moon, K.-M.; Greif, D.; Wang, D.M.; Kim, M.-H. Numerical simulation of immersion quenching process of an engine cylinder head. Appl. Math. Model. 2009, 34, 2111–2128. [Google Scholar] [CrossRef] [Green Version]
- Dybowski, K.; Sawicki, J.; Kula, P.; Januszewicz, B.; Lipa, S. The Effect of the Quenching Method on the Deformations Size of Gear Wheels after Vacuum Carburizing. Arch. Metall. Mater. 2016, 61, 1057–1062. [Google Scholar] [CrossRef]
- Heuer, V.; Löser, K.; Faron, D.R.; Bolton, D. Low Distortion Heat Treatment of Transmission Components; American Gear Manufacturers Association Fall Technical Meeting 2010; AGMA American Gear Manufacturers Association: Cincinnati, OH, USA, 2010; pp. 38–53. [Google Scholar]
- Husson, R.; Baudouin, C.; Bigot, R.; Sura, E. Consideration of residual stress and geometry during heat treatment to decrease shaft bending. Int. J. Adv. Manuf. Technol. 2014, 72, 1455–1463. [Google Scholar] [CrossRef] [Green Version]
- Pang, Z.; Yu, S.; Xu, J. Study of Effect of Quenching Deformation Influenced by 17CrNiMo6 Gear Shaft of Carburization. Phys. Procedia 2013, 50, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Brinksmeier, E.; Th, L.; Fritsching, U.; Cui, C.; Slter, J. Distortion minimization of disks for gear manufacture. Int. J. Mach. Tools Manuf. 2011, 51, 331–338. [Google Scholar] [CrossRef]
- Cho, J.R.; Kang, W.J.; Kim, M.G.; Lee, J.H.; Lee, Y.S.; Bae, W.B. Distortions induced by heat treatment of automotive bevel gears. J. Mater. Process. Technol. 2004, 153–154, 476–481. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, D.W.; Zhang, J.G. Induction hardening and deformation control of rail components for high-speed railway turnout. Heat Treat. Met. 2011, 36, 103–105. [Google Scholar]
- Wang, J.; Zhang, W.L.; Wang, Z.J.; Li, X.J.; Wu, X.L. Deformation control of finish-rolled screw-thread steel bars during induction quenching. Heat Treat. Met. 2011, 36, 97–100. [Google Scholar]
- Committee, A.; Dossett, J.L.; Totten, G.E. Steel Heat Treating Fundamentals and Processes; ASM International: Novelty, OH, USA, 2013. [Google Scholar]
- Wang, H.M.; Ma, X.C.; Wang, X.J. Effect of Heat Treatment Process on Gear Distortion. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2010. [Google Scholar]
- Li, Z.; Freborg, A.M.; Ferguson, B.L.; Ding, P.; Hebbes, M. Press quench process design for a bevel gear using computer modeling. In Proceedings of the 23rd IFHTSE Congress, Savannah, GA, USA, 18–21 April 2016. [Google Scholar]
- Zhang, Y.; Wang, G.; Shi, W.; Yang, L.; Li, Z. Modeling and Analysis of Deformation for Spiral Bevel Gear in Die Quenching Based on the Hardenability Variation. J. Mater. Eng. Perform. 2017, 26, 3034–3047. [Google Scholar] [CrossRef]
- Reardon, A.C. Press Quenching and Effects of Prior Thermal History on Distortion during Heat Treatment. Gear Technol. 2014, 31, 50–53. [Google Scholar]
- Knauf, S.; Buchner, K.; Jenne, R. Gearbox Production Using Distortion Controlled Inductive Fixture Hardening*. HTM J. Heat Treat. Mater. 2022, 77, 70–85. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Tang, Z.W.; Shi, X.L.; Tang, J.Y.; Li, Z.M.Q. Efficient and accurate worm grinding of spur face gears according to an advanced geometrical analysis and a closed-loop manufacturing process. J. Cent. South Univ. 2022, 29, 1–13. [Google Scholar] [CrossRef]
- Rohde, J.; Jeppsson, A. Literature review of heat treatment simulations with respect to phase transformation, residual stresses and distortion. Scand. J. Metall. 2000, 29, 47–62. [Google Scholar] [CrossRef]
- Tibbetts, G.G. Diffusivity of carbon in iron and steels at high temperatures. J. Appl. Phys. 1980, 51, 4813–4816. [Google Scholar] [CrossRef]
- Kim, D.-W.; Cho, Y.-G.; Cho, H.-H.; Kim, S.-H.; Lee, W.-B.; Lee, M.-G.; Han, H.N. A numerical model for vacuum carburization of an automotive gear ring. Met. Mater. Int. 2011, 17, 885–890. [Google Scholar] [CrossRef]
- Liu, L.; Qiang, L.; Liu, X.; Gao, Y.; Ren, X.; Bo, L.; Yang, Q. Stress field simulation of carburized specimens with different carbon content during quenching process. Mater. Lett. 2007, 61, 1251–1255. [Google Scholar] [CrossRef]
- Leblond, J.-B.; Mottet, G.; Devaux, J.J.-C. Mathematical models of anisothermal phase transformations in steels, and predicted plastic behaviour. Mater. Sci. Technol. 1985, 1, 815–822. [Google Scholar] [CrossRef]
- Liu, C.; Ju, D.Y.; Inoue, T. A Numerical Modeling of Metallo-thermo-mechanical Behavior in Both Carburized and Carbonitrided Quenching Processes. ISIJ Int. 2002, 42, 1125–1134. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Scheil, E. Anlaufzeit der austenitumwandlung. Arch. Eisenhüttenwesen 1935, 8, 565–567. [Google Scholar] [CrossRef]
- Hsu, T. Additivity hypothesis and effects of stress on phase transformations in steel. Curr. Opin. Solid State Mater. Sci. 2005, 9, 256–268. [Google Scholar]
- Li, Z.C.; Ferguson, B.L.; Sims, J.; Yu, T. Sources of Distortion Study during Quench Hardening using Computer Modeling. In Proceedings of the Heat Treat 2017: 29th ASM Heat Treating Society Conference, Columbus, OH, USA, 20 October 2017. [Google Scholar]
- Koistinen, D.P.; Marburger, R.E. A general equation prescribing the extent of the austenite-martensite transformation in pure iron-carbon alloys and plain carbon steels. Acta Metall. 1959, 7, 59–60. [Google Scholar] [CrossRef]
- Prantil, V.; Callabresi, M.; Lathrop, J.; Ramaswamy, G.; Lusk, M. Simulating distortion and residual stresses in carburized thin strips. J. Eng. Mater. Technol. 2003, 125, 116–124. [Google Scholar] [CrossRef]
- Nallathambi, A.K.; Kaymak, Y.; Specht, E.; Bertram, A. Sensitivity of material properties on distortion and residual stresses during metal quenching processes. J. Mater. Process. Technol. 2010, 210, 204–211. [Google Scholar] [CrossRef]
- Shi, W.; Nie, Z.G. Experiment and modeling of stress affected bainitic transformation. In Proceedings of the 20th IFHTSE, Beijing, China, 23–25 October 2012; pp. 864–867. [Google Scholar]
- Greenwood, G.W.; Johnson, R.H. The deformation of metals under small stresses during phase transformations. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1965, 283, 403–422. [Google Scholar]
- Abrassart, F. Stress-induced γ→α martensitic transformation in two carbon stainless steels. Appl. Trip Steels. Metall. Mater. Trans. B 1973, 4, 2205–2216. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lee, Y.-K. Finite element simulation of quench distortion in a low-alloy steel incorporating transformation kinetics. Acta Mater. 2008, 56, 1482–1490. [Google Scholar] [CrossRef]
- Zordão, L.H.P.; Oliveira, V.A.; Totten, G.E.; Canale, L.C. Quenching power of aqueous salt solution. Int. J. Heat Mass Transf. 2019, 140, 807–818. [Google Scholar] [CrossRef]
- Manjunatha, L.; Lokesha, M.; Ajaykumar, B. A review: Mechanical Properties of HSS Steel by deep Cryo-Treatment. IOP Conf. Ser. Mater. Sci. Eng. 2018, 376, 012098. [Google Scholar]





| Transformation | ||
|---|---|---|
| Austenite to ferrite | 0.360 | 3.468 |
| Austenite to pearlite | 0.360 | 3.468 |
| Austenite to bainite | 0.697 | 0.243 |
| Transformation | ||||
|---|---|---|---|---|
| Austenite to martensite | 0.061 | 0.855 | 0.657 | 0.200 |
| Material Type | C | Mn | Ni | Cr | Cr | Mo | P | Si | Cu |
|---|---|---|---|---|---|---|---|---|---|
| 9310 | 0.1 | 0.58 | 3.33 | 0.570 | 1.31 | 0.1 | 0.0026 | 0.20 | 0.015 |
| Phase | Thermal Conductivity/(J/m/°C) | Specific Heat/(J/kg/°C) |
|---|---|---|
| Austenite | 16.0 + 1.3 × 10−2 T | 365.0 + 0.2938 T |
| Martensite | 25.0 + 3.0 × 10−3 T | 450.0 + 0.3875 T |
| Samples | A/mm | B/mm | C/mm | D/mm | Surface Hardness /HRC | Core Hardness /HRC |
|---|---|---|---|---|---|---|
| 1 | 610.73 | 549.207 | 48.21 | 77.58 | 64 | 33.5 |
| 2 | 610.7 | 549.209 | 48.25 | 77.59 | 62.5 | 34 |
| 3 | 610.75 | 549.199 | 48.24 | 77.57 | 64 | 33.5 |
| 4 | 610.72 | 549.203 | 48.28 | 77.58 | 62.5 | 34 |
| 5 | 610.7 | 549.198 | 48.225 | 77.555 | 64 | 33.5 |
| Average | 610.72 | 549.203 | 48.241 | 77.575 | 63.4 | 33.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhao, J.; Tang, J.; Shao, W.; Sun, B. Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear. Materials 2023, 16, 690. https://doi.org/10.3390/ma16020690
Liu H, Zhao J, Tang J, Shao W, Sun B. Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear. Materials. 2023; 16(2):690. https://doi.org/10.3390/ma16020690
Chicago/Turabian StyleLiu, Huaming, Jiuyue Zhao, Jinyuan Tang, Wen Shao, and Beier Sun. 2023. "Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear" Materials 16, no. 2: 690. https://doi.org/10.3390/ma16020690
APA StyleLiu, H., Zhao, J., Tang, J., Shao, W., & Sun, B. (2023). Simulation and Experimental Verification of Die Quenching Deformation of Aviation Carburized Face Gear. Materials, 16(2), 690. https://doi.org/10.3390/ma16020690







