The Influence of Materials on Footwear Behaviour: A Finite Element Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Equipment
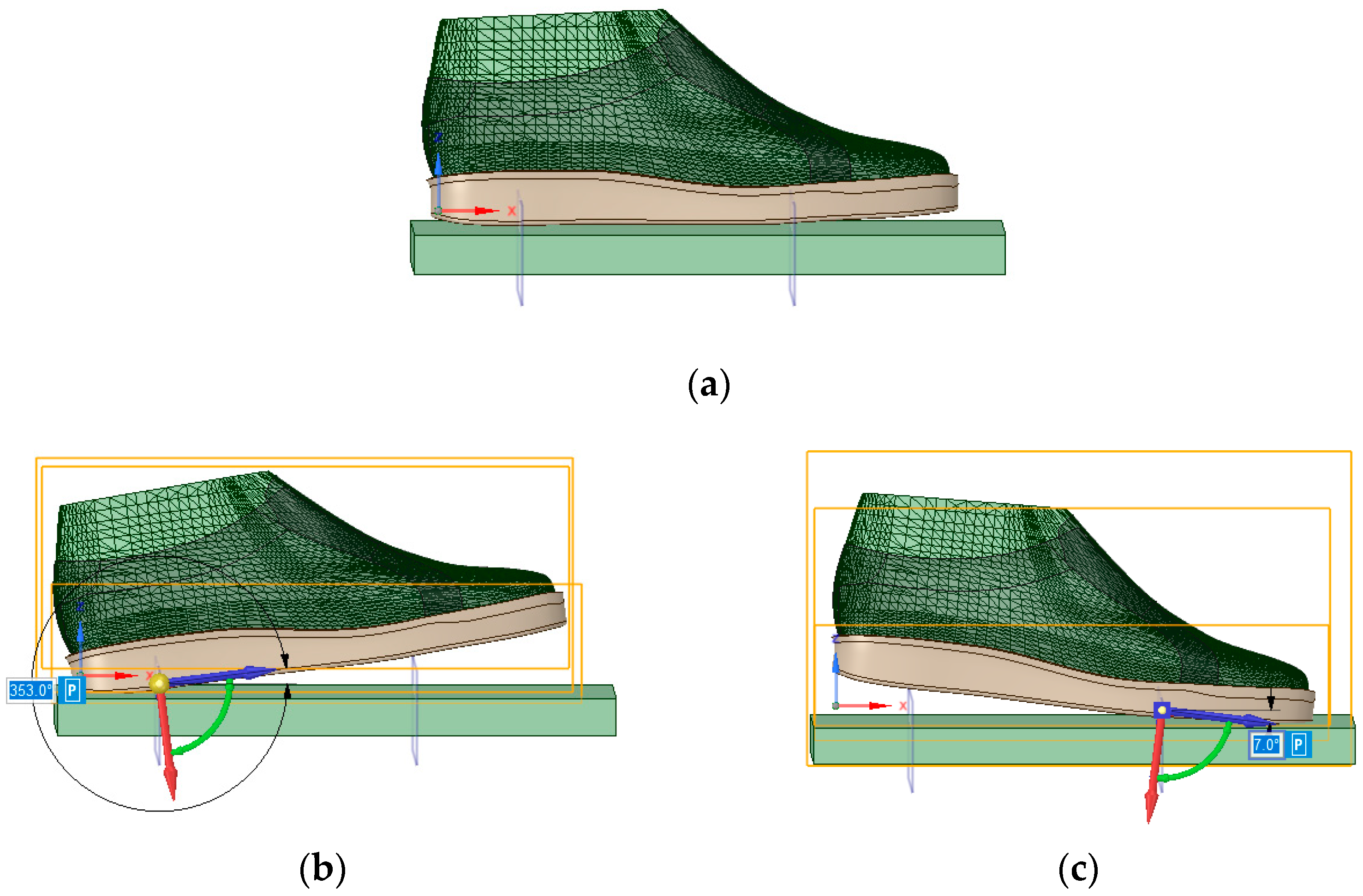
2.2. Three-Dimensional (3D) Model Creation and Editing
2.3. Properties of Materials
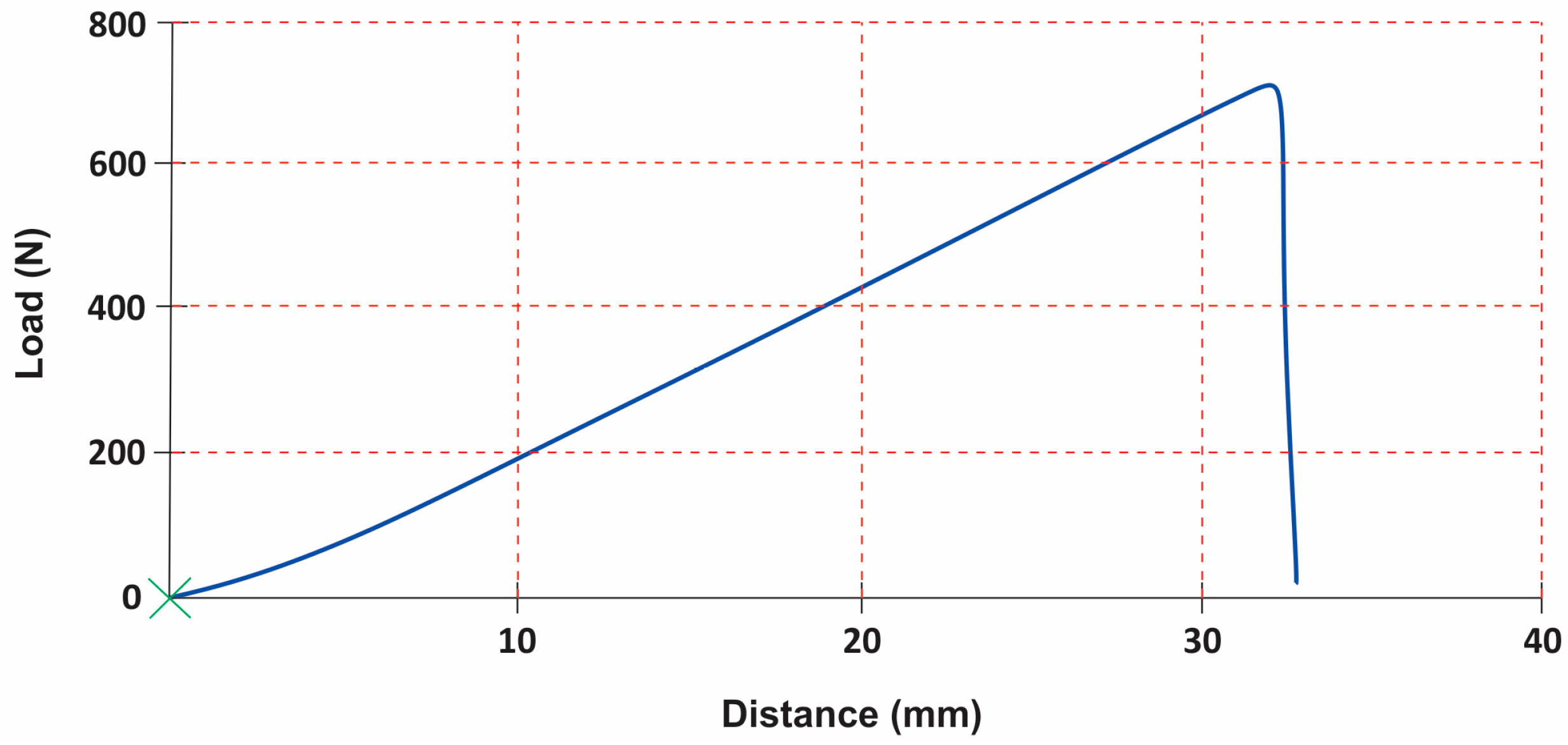
2.4. Setting Analysis Conditions
2.5. Setting the Parameters to Evaluate
3. Results and Discussion
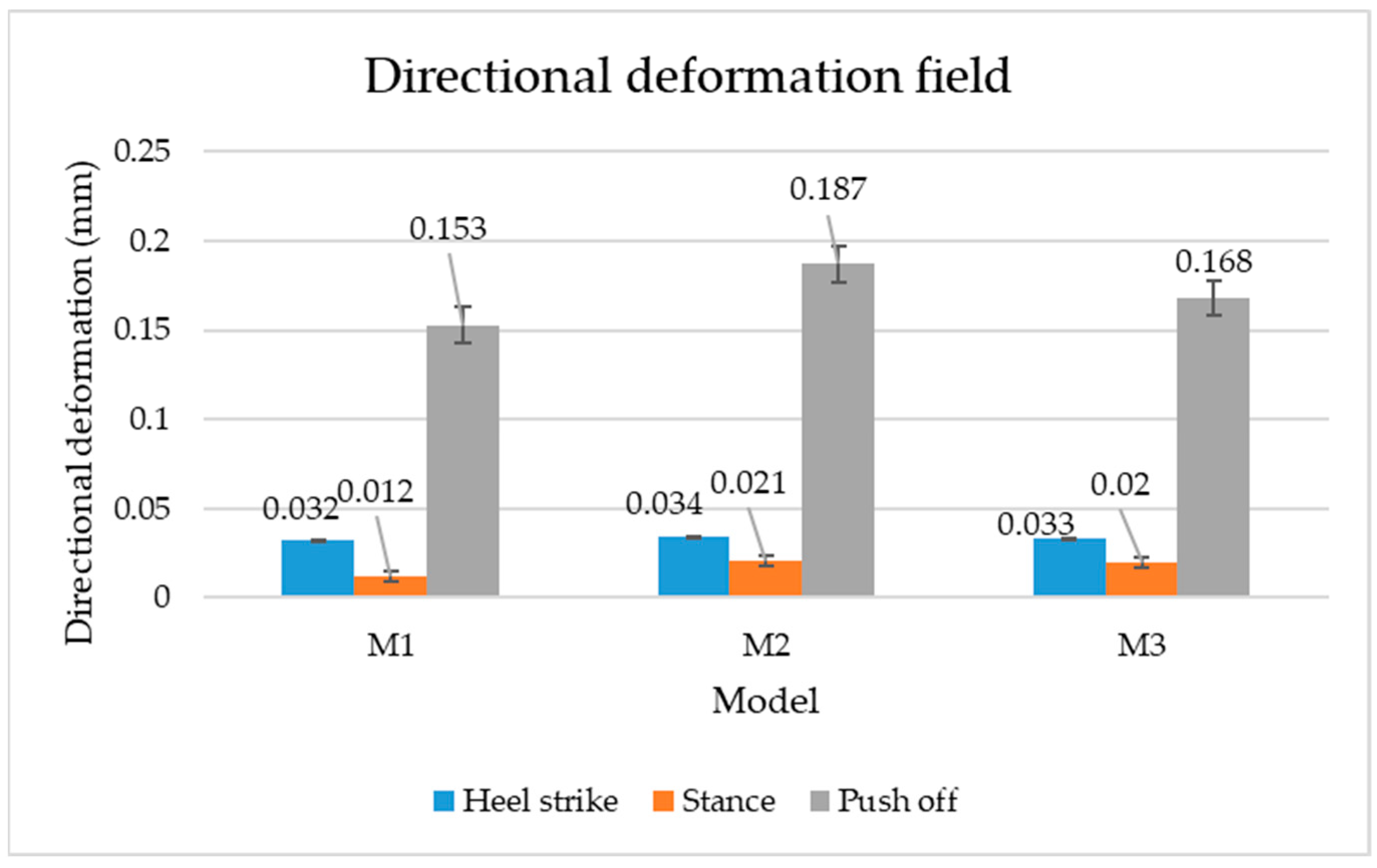
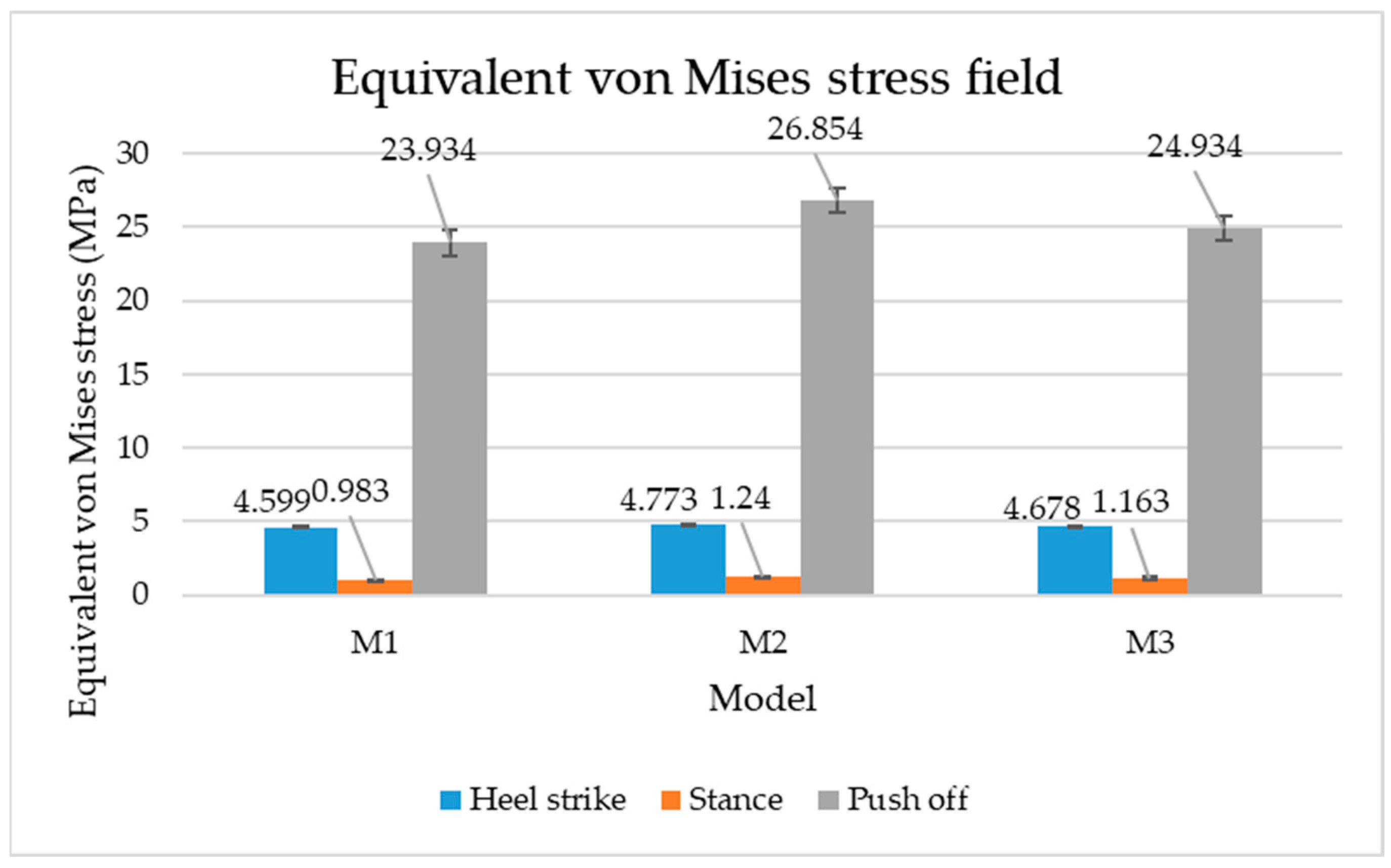
3.1. Results
3.2. Discussion
3.3. Validation of the Model Based on Biomechanical Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Willwacher, S.; König, M.; Braunstein, B.; Goldmann, J.P.; Brüggemann, G.P. The gearing function of running shoe longitudinal bending stiffness. Gait Posture 2014, 40, 386–390. [Google Scholar] [CrossRef] [PubMed]
- Chambon, N.; Delattre, N.; Guéguen, N.; Berton, E.; Rao, G. Is midsole thickness a key parameter for the running pattern? Gait Posture 2014, 40, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Wunsch, T.; Kroll, J.; Stoggl, T.; Schwameder, H. Effects of a structured midsole on spatio-temporal variables and running economy in overground running. Eur. J. Sport Sci. 2016, 17, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.W.; Lee, Y.H.; Lin, C.J.; Li, K.W.; Chen, C.Y. Shoe Sole Tread Designs and Outcomes of Slipping and Falling on Slippery Floor Surfaces. PLoS ONE 2013, 8, e68989. [Google Scholar] [CrossRef] [PubMed]
- Onodera, A.N.; Gavião Neto, W.P.; Roveri, M.I.; Oliveira, W.R.; Sacco, I.C. Immediate effects of EVA midsole resilience and upper shoe structure on running biomechanics: A machine learning approach. PeerJ 2017, 5, e3026. [Google Scholar] [CrossRef]
- Onodera, A.N.; Roveri, M.I.; Oliveira, W.R.; Sacco, I.C.N. The influence of shoe upper construction on the plantar pressure distribution during running. Footwear Sci. 2015, 7, 81–82. [Google Scholar] [CrossRef]
- Sun, X.; Lam, W.K.; Zhang, X.; Wang, J.; Fu, W. Systematic review of the role of footwear constructions in running biomechanics: Implications for running-related injury and performance. J. Sports Sci. Med. 2020, 19, 20–37. [Google Scholar]
- Azariadis, P. Finite Element Analysis Methods in Footwear Design. In The Science of Footwear, 1st ed.; Goonetilleke, R., Ed.; Taylor & Francis Group: Abingdon, UK, 2010; Chapter 15; pp. 321–340. [Google Scholar]
- Shih, K.S.; Jhou, S.Y.; Hsu, W.C.; Hsu, C.C.; Chen, J.W.; Yeh, J.C.; Hung, Y.C. A Biomechanical Investigation of Athletic Footwear Traction Performance: Integration of Gait Analysis with Computational Simulation. Appl. Sci. 2020, 10, 1672. [Google Scholar] [CrossRef]
- Qian, Z.; Ren, L.; Ding, Y.; Hutchinson, J.R.; Ren, L. A Dynamic Finite Element Analysis of Human Foot Complex in the Sagittal Plane during Level Walking. PLoS ONE 2013, 8, e79424. [Google Scholar] [CrossRef]
- Costa, C.A.; Lain, V.V.; Godoy-Santos, A.L.; Antoni, V.G.; Linzmaier, P.R.; Costa, F.A. Analysis of pressure distribution in the foot using finite elements. J. Foot Ankle 2020, 14, 197–200. [Google Scholar] [CrossRef]
- Luximon, Y.; Luximon, A.; Yu, J.; Zhang, M. Biomechanical evaluation of heel elevation on load transfer—Experimental measurement and finite element analysis. Acta Mech. Sin. 2012, 28, 232–240. [Google Scholar] [CrossRef]
- Yu, J.; Wong, D.; Zhang, H.; Luo, Z.; Zhang, M. The influence of high-heeled footwear on strain and tension force of the anterior talofibular ligament and plantar fascia during balanced standing and walking. Med. Eng. Phys. 2016, 38, 1152–1156. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V. Novel insole design for diabetic foot ulcer management. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Antunes, P.J.; Dias, G.R.; Coelho, A.T.; Rebelo, F.; Pereira, T. Non-linear finite element modelling of anatomically detailed 3D foot model. Rep. Pap. 2008, 1, 1–11. [Google Scholar]
- Ghazali, M.J.; Ren, X.; Rajabi, A.; Zamri, W.F.H.W.; Mohd Mustafah, N.; Ni, J. Finite Element Analysis of Cushioned Diabetic Footwear Using Ethylene Vinyl Acetate Polymer. Polymers 2021, 13, 2261. [Google Scholar] [CrossRef]
- Papagiannis, P.; Azariadis, P.; Papanikos, P. Evaluation and optimization of footwear comfort parameters using finite element analysis and a discrete optimization algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 162010. [Google Scholar] [CrossRef]
- Kropidłowska, P.; Irzmańska, E.; Gołębiowski, Ł.; Jurczyk-Kowalska, M.; Boczkowska, A. Analysis of the Impact Resistance of Toecaps by the Finite Element Method: Preliminary Studies. Int. J. Environ. Res. Public Health 2023, 20, 152. [Google Scholar] [CrossRef]
- Covill, D.; Guan, Z.W.; Bailey, M.; Raval, H. Development of Thermal Models of Footwear Using Finite Element Analysis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 268–281. [Google Scholar] [CrossRef]
- Song, Y.; Shao, E.; Bíró, I.; Baker, J.S.; Gu, Y. Finite element modelling for footwear design and evaluation: A systematic scoping review. Heliyon 2022, 8, e10940. [Google Scholar] [CrossRef]
- Rupérez, M.J.; Monserrat, C.; Alcañiz, M. Simulation of the deformation of materials in shoe uppers in gait. Force distribution using finite elements. Int. J. Interact. Des. Manuf. 2008, 2, 59–68. [Google Scholar] [CrossRef]
- Rupérez, M.J.; Giner, E.; Monserrat, C.; Montiel, E. Simulation of the behavior of the calfskin used as shoe upper material in footwear CAD. Comput.-Aided Des. 2012, 44, 1205–1216. [Google Scholar] [CrossRef]
- Song, Y.; Cen, X.; Zhang, Y.; Bíró, I.; Ji, Y.; Gu, Y. Development and Validation of a Subject-Specific Coupled Model for Foot and Sports Shoe Complex: A Pilot Computational Study. Bioengineering 2022, 9, 553. [Google Scholar] [CrossRef] [PubMed]
- Blaga, M.; Marmaralı, A.; Mihai, A. Functional Knitted Fabrics for Footwear Linings. Tekst. Kon-Feksiyon 2011, 21, 30–35. [Google Scholar]
- Serweta, W.; Olejniczak, Z.; Matusiak, M. Improve of Footwear Comfort Sensation with Material Packages and Knitted Fabrics. Fibers Text. East. Eur. 2019, 27, 85–90. [Google Scholar] [CrossRef]
- Blaga, M.; Ciobanu, A.; Marmaralı, A.; Ertekin, G.; Celik, P. Investigation of the physical and thermal comfort characteristics of knitted fabrics used for shoe linings. Tekst. Konfeksiyon 2015, 25, 111–118. [Google Scholar]
- Huffa, B.; Huffa, C. System and Method for Knitting Shoe Uppers; States Fabdesigns, Inc.: Malibu, CA, USA, 2019. [Google Scholar]
- Cai, Y.; Yu, W.; Chen, L. Finite element modeling of bra fitting. In Advances in Women’s Intimate Apparel Technology; Woodhead Publishing: Sawston, UK, 2016; pp. 147–168. [Google Scholar] [CrossRef]
- Sun, Y.; Yick, K.; Yu, W.; Chen, L.; Lau, N.; Jiao, W.; Zhang, S. 3D bra and human interactive modelling using finite element method for bra design. Comput.-Aided Des. 2019, 114, 13–27. [Google Scholar] [CrossRef]
- Ghorbani, E.; Hasani, H.; Nedoushan, R.J.; Jamshidi, N. Finite Element Modeling of the Compression Garments Structural Effect on the Pressure Applied to Leg. Fibers Polym. 2020, 21, 636–645. [Google Scholar] [CrossRef]
- Horiba, Y.; Amano, T.; Inui, S.; Yamada, T. Proposal of Method for Estimating Clothing Pressure of Tight-Fitting Garment Made from Highly Elastic Materials: Hybrid Method Using Apparel CAD and Finite Element Analysis Software. J. Fiber Sci. Technol. 2021, 77, 76–87. [Google Scholar] [CrossRef]
- Costea, M.; Mihai, A.; Seul, A. 3D Modelling of Customized Lasts Based on Anthropometric Data Acquired from 3D Foot Scanning—One Case Study. Leather Footwear J. 2022, 22, 87–100. [Google Scholar] [CrossRef]
- Seul, A.; Viziteu, D.-R.; Mihai, A.; Curteza, A.; Costea, M. Computer-Generated Shoe Lasts Using 3D Scanned Data And Anthropometric Measurements. In Proceedings of the 16th International Conference Interdisciplinarity in Engineering, Targu Mures, Romania, 6–7 October 2022. [Google Scholar]
- Cheung, J.T.; Zhang, M. Finite Element Modeling of the Human Foot and Footwear. ABAQUS Users Conf. 2006, 20, 145–159. [Google Scholar]
- Yu, J.; Cheung, J.T.; Wong, D.W.; Cong, Y.; Zhang, M. Biomechanical simulation of high-heeled shoe donning and walking. J. Biomech. 2013, 46, 2067–2074. [Google Scholar] [CrossRef] [PubMed]
- Ashby, M.F.; Gibson, U.W. The mechanical properties of natural materials. Material property charts. Math. Phys. Sci. 1995, 450, 123–140. [Google Scholar]
- Karimi, A.; Razaghi, R.; Sumikura, A. A 3-dimensional finite element model of a newly designed adjustable high-heeled shoe. Int. J. Ind. Ergon. 2018, 68, 304–310. [Google Scholar] [CrossRef]
- Mihai, A.; Seul, A.; Curteza, A.; Costea, M. Mechanical Parameters of Leather in Relation to Technological Processing of the Footwear Uppers. Materials 2022, 15, 5107. [Google Scholar] [CrossRef] [PubMed]
- Jinyun, Z.; Yi, L.; Lam, J. The Poisson Ratio and Modulus of Elastic Knitted Fabrics. Text. Res. 2010, 80, 1965–1969. [Google Scholar] [CrossRef]
- Seul, A.; Mihai, A.; Curteza, A.; Costea, M.; Sarghie, B. Biomechanical parameters characterising the foot during normal gait. Leather Footwear J. 2021, 21, 87–104. [Google Scholar] [CrossRef]
- Sanchis, E.; Sancho, J.L.; Roda, A.; Pascual, J. Kinematics and kinetics analysis of midfoot joints of 30 normal subjects during walking. Rev. Española Podol. 2016, 27, 6–12. [Google Scholar] [CrossRef]
- Balaramakrishnan, T.M.; Natarajan, S. Roll-over shape of a prosthetic foot: A finite element evaluation and experimental validation. Med. Biol. Eng. Comput. 2020, 58, 2259–2270. [Google Scholar] [CrossRef]
- Perttunen, J. Foot Loading in Normal and Pathological Walking; University of Jyväskylä: Jyväskylä, Finland, 2002. [Google Scholar]
- Yuk-Ming, T.; Kin-Chuen, H. Human foot modeling towards footwear design. Comput. Des. 2011, 43, 1841–1848. [Google Scholar]
- Jordan, C.; Bartlett, R. Pressure distribution and perceived comfort in casual footwear. Gait Posture 1995, 3, 215–220. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Ghasemi, H. Quantifying the uncertainties in modeling soft composites via a multiscale approach. Int. J. Solids Struct. 2022, 256, 111959. [Google Scholar] [CrossRef]





| Foot | Leather (Upper) | Knitted Fabric (Uppers) | Rubber (Bottom) | Concrete (Support) | |
|---|---|---|---|---|---|
| Young modulus (MPa) | 4.47 | 20 | 0.0025 | 1000 | 90,000 |
| Poisson coefficient | 0.45 | 0.4 | 0.43 | 0.42 | 0.18 |
| Gait Phase | Model M1 | Model M2 | Model M3 | |||
|---|---|---|---|---|---|---|
| Maximum Value (mm) | Maximum Value (mm) | Maximum Value (mm) | ||||
| Heel strike | 0.032 |  | 0.034 |  | 0.033 |  |
| Stance | 0.012 |  | 0.021 |  | 0.020 |  |
| Push-off | 0.153 |  | 0.187 |  | 0.168 |  |
| Gait Phase | Model M1 | Model M2 | Model M3 | |||
|---|---|---|---|---|---|---|
| Maximum Value (MPa) | Maximum Value (MPa) | Maximum Value (MPa) | ||||
| Heel strike | 4.599 |  | 4.773 |  | 4.678 |  |
| Stance | 0.983 |  | 1.240 |  | 1.163 |  |
| Push-off | 23.934 |  | 26.854 |  | 24.934 |  |
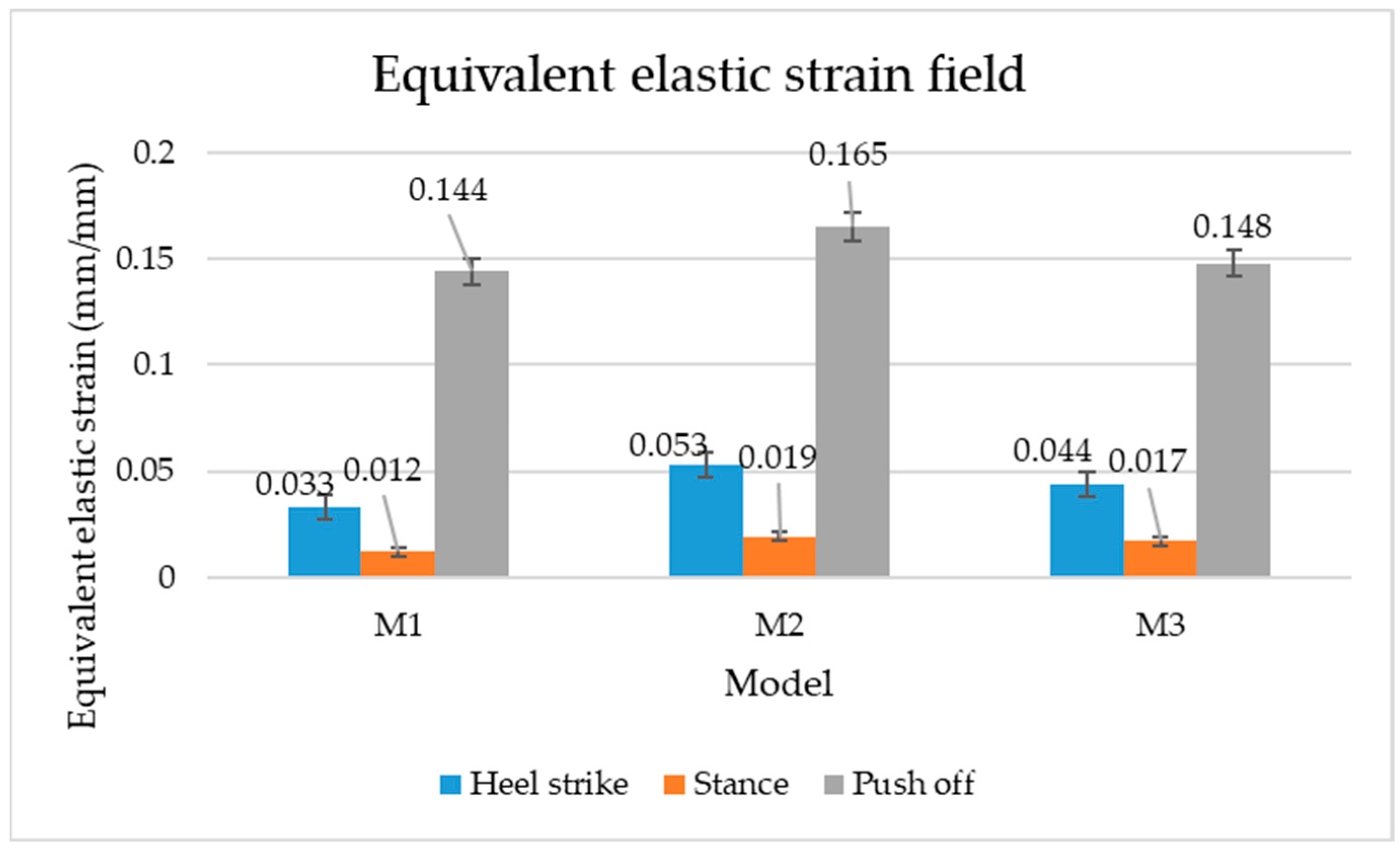
| Gait Phase | Model M1 | Model M2 | Model M3 | |||
|---|---|---|---|---|---|---|
| Maximum Value (mm/mm) | Maximum Value (mm/mm) | Maximum Value (mm/mm) | ||||
| Heel strike | 0.033 |  | 0.053 |  | 0.044 |  |
| Stance | 0.012 |  | 0.019 |  | 0.017 |  |
| Push-off | 0.144 |  | 0.165 |  | 0.148 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seul, A.; Mihai, A.; Costea, M.; Bodoga, A.; Curteza, A. The Influence of Materials on Footwear Behaviour: A Finite Element Simulation Study. Materials 2023, 16, 7203. https://doi.org/10.3390/ma16227203
Seul A, Mihai A, Costea M, Bodoga A, Curteza A. The Influence of Materials on Footwear Behaviour: A Finite Element Simulation Study. Materials. 2023; 16(22):7203. https://doi.org/10.3390/ma16227203
Chicago/Turabian StyleSeul, Arina, Aura Mihai, Mariana Costea, Alexandra Bodoga, and Antonela Curteza. 2023. "The Influence of Materials on Footwear Behaviour: A Finite Element Simulation Study" Materials 16, no. 22: 7203. https://doi.org/10.3390/ma16227203






