The Mechanism of Deformation Compatibility of TA2/Q345 Laminated Metal in Dynamic Testing with Split-Hopkinson Pressure Bar
Abstract
:1. Introduction
2. Material and Methods
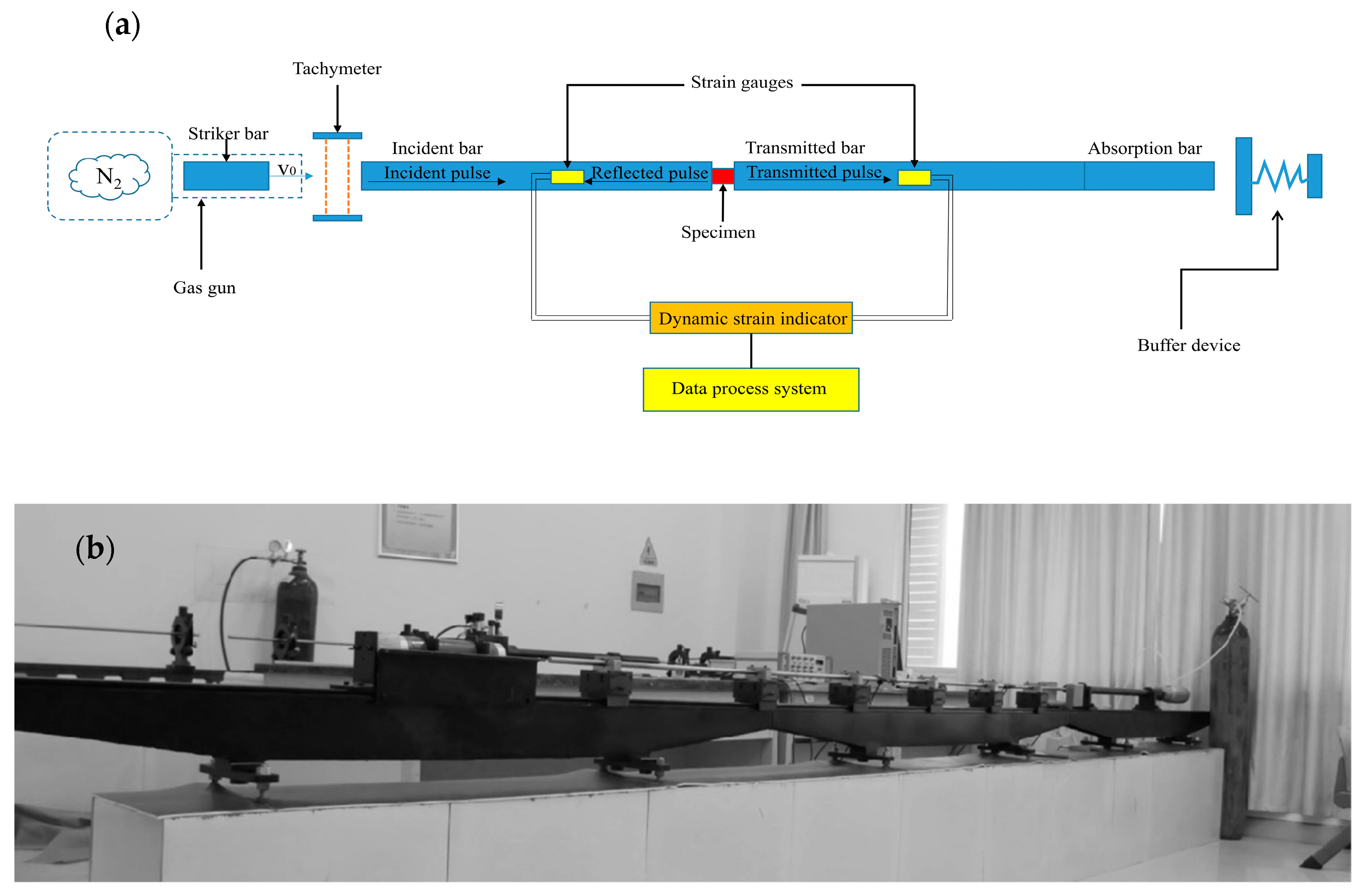
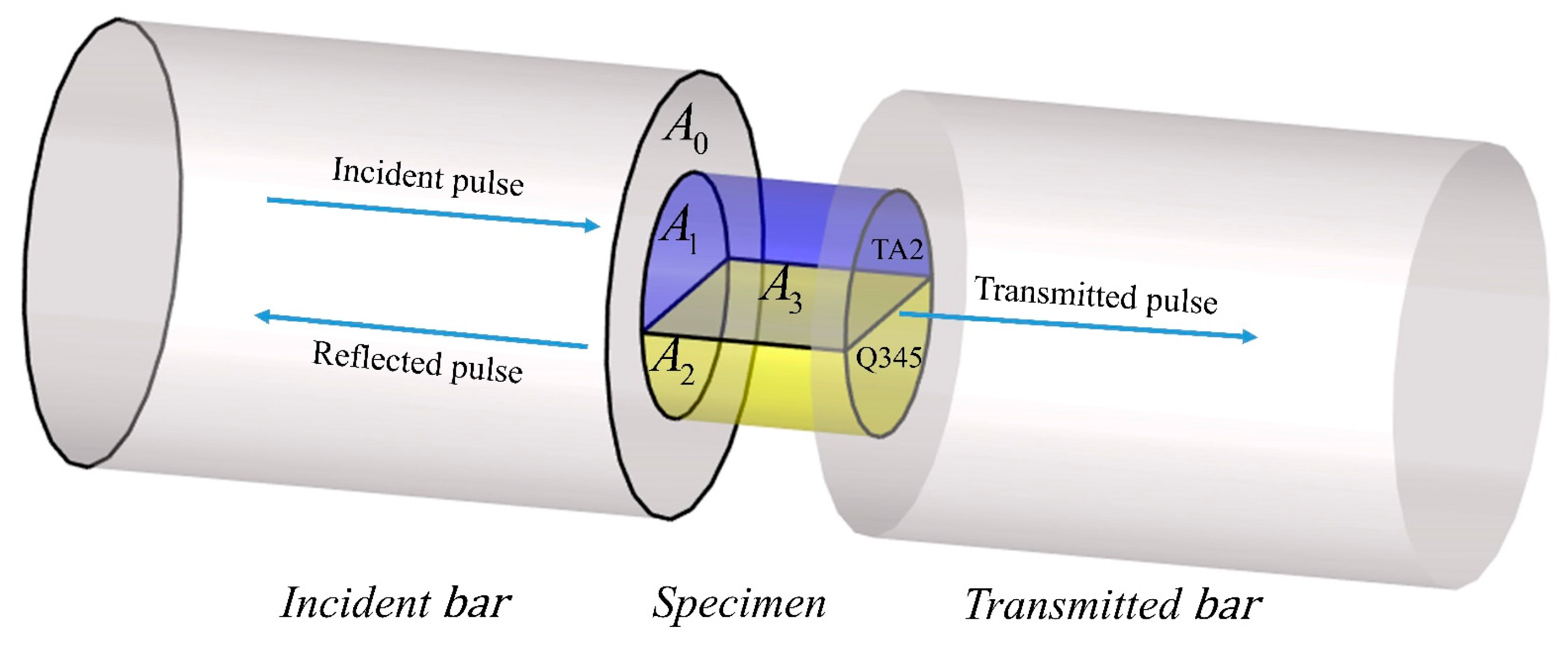
2.1. Experimental Setup
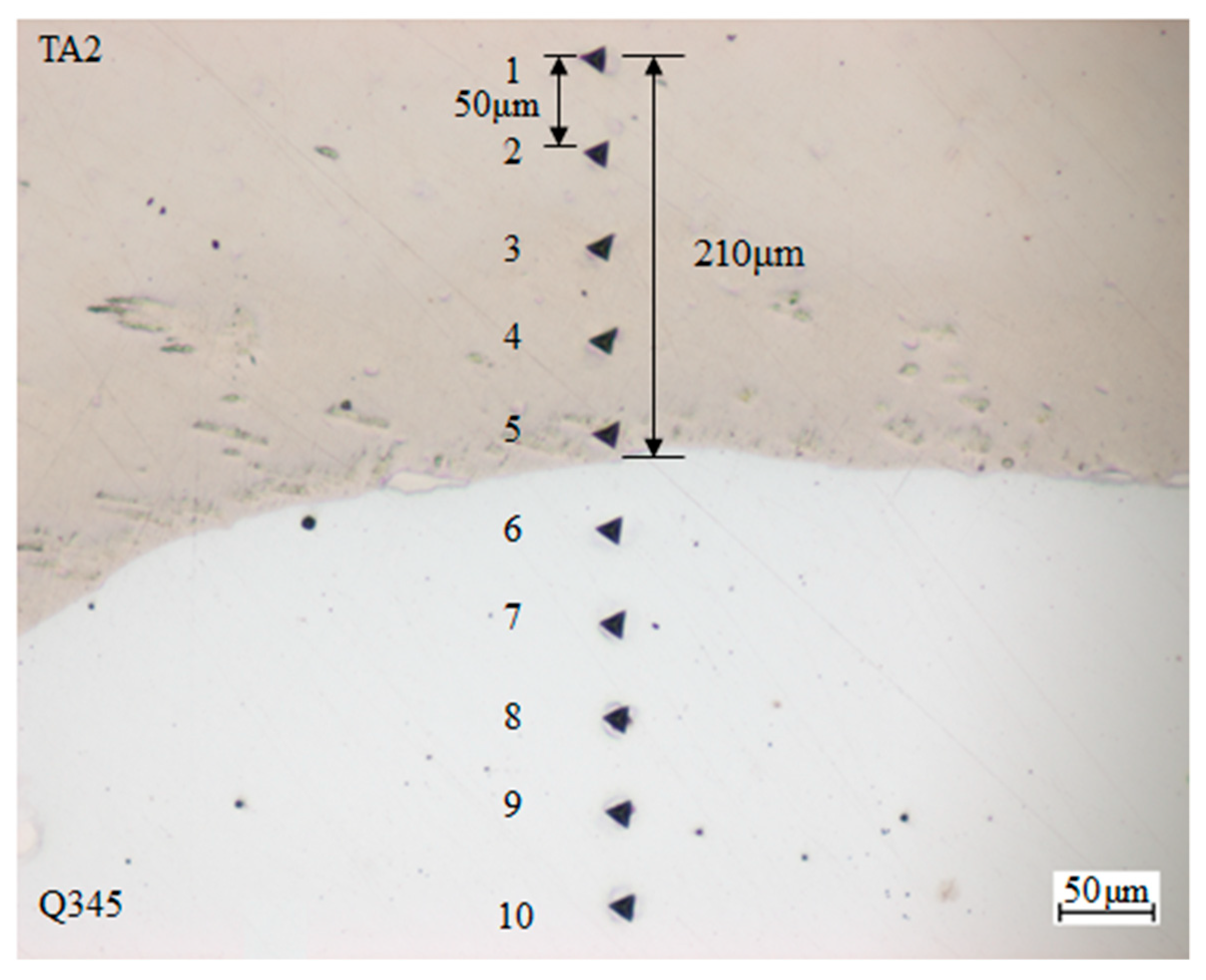
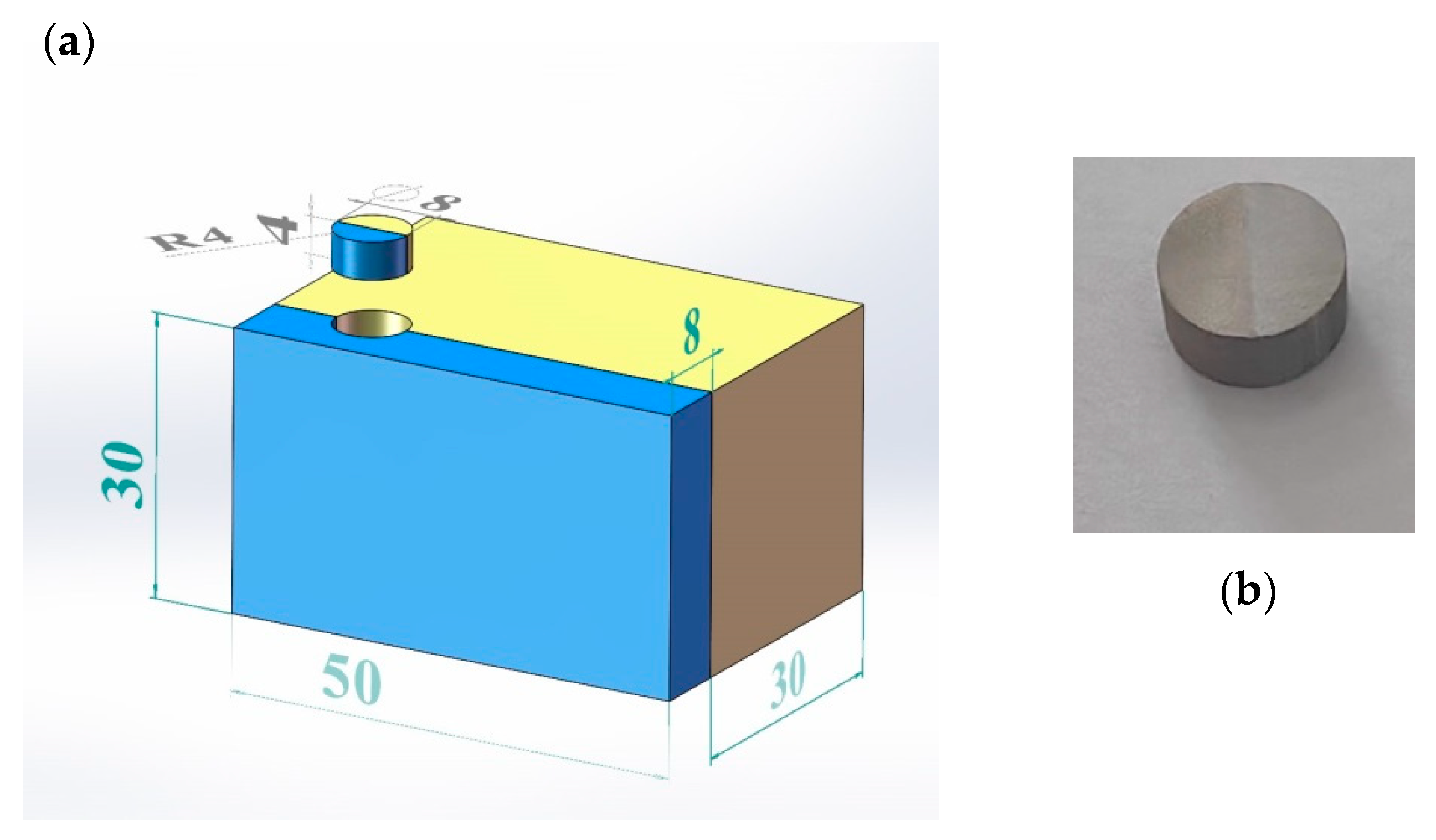
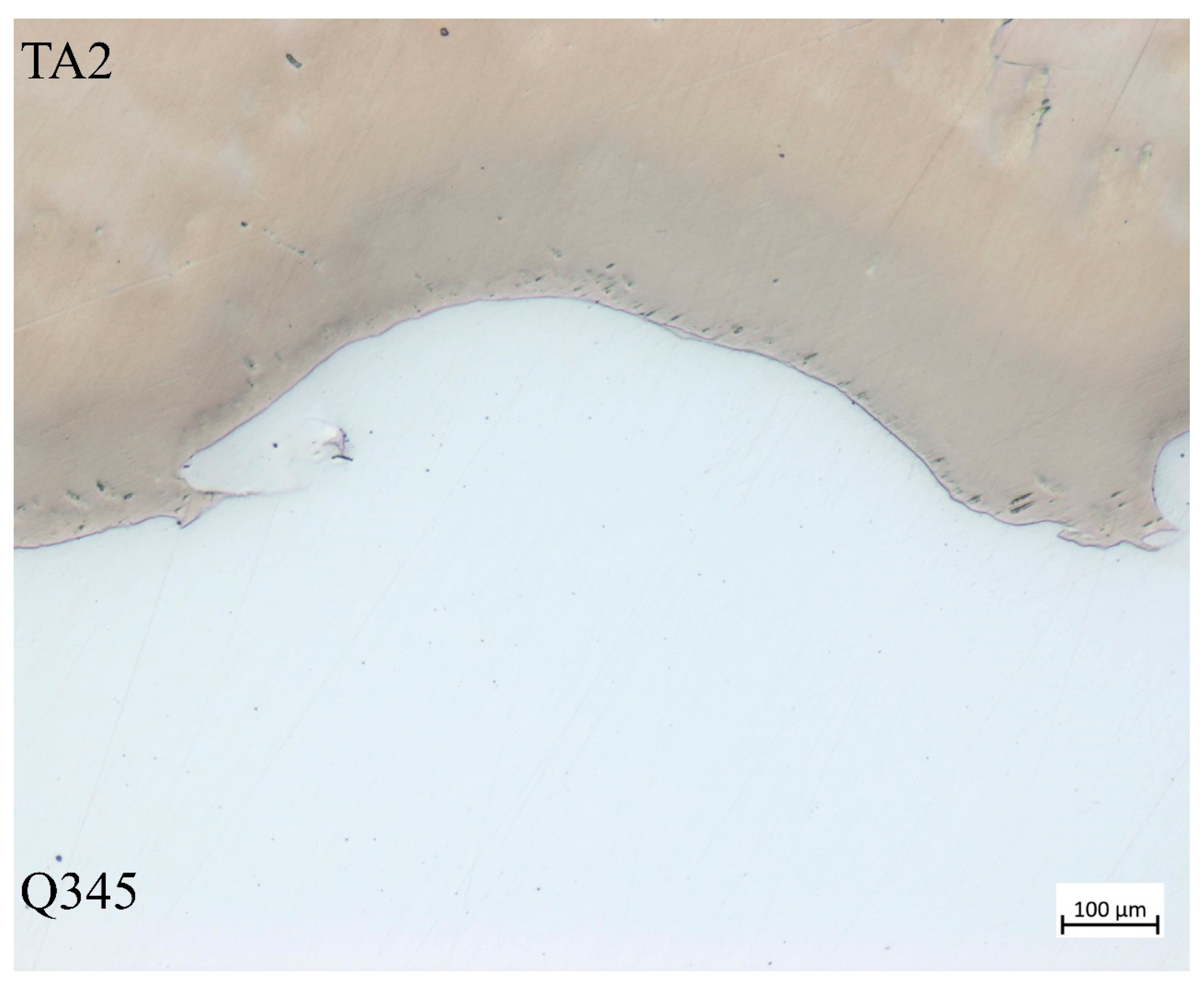
2.2. Specimen Preparations
3. Results and Discussion
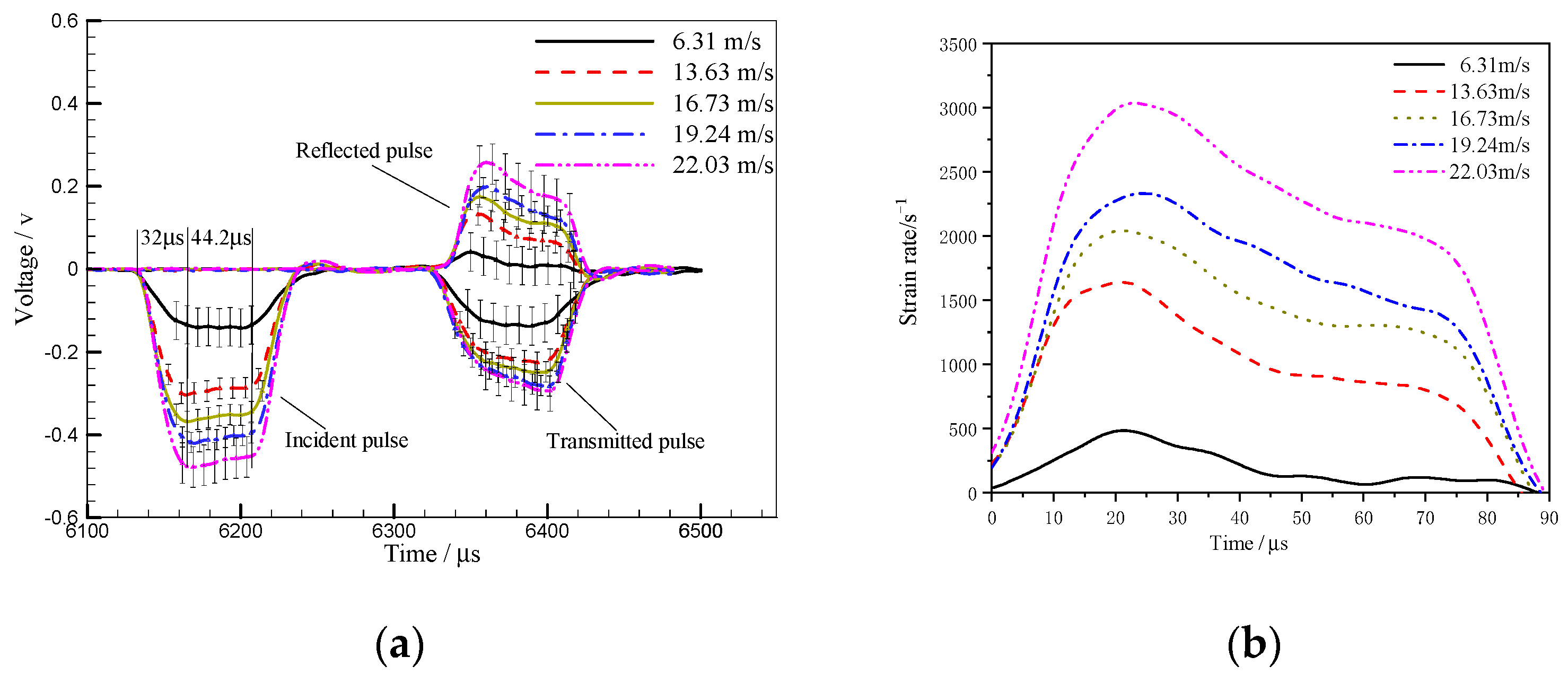
3.1. Typical Waveform of SHPB Tests of TA2/Q345
3.2. Verification of No-Slip Condition at Welding Interface
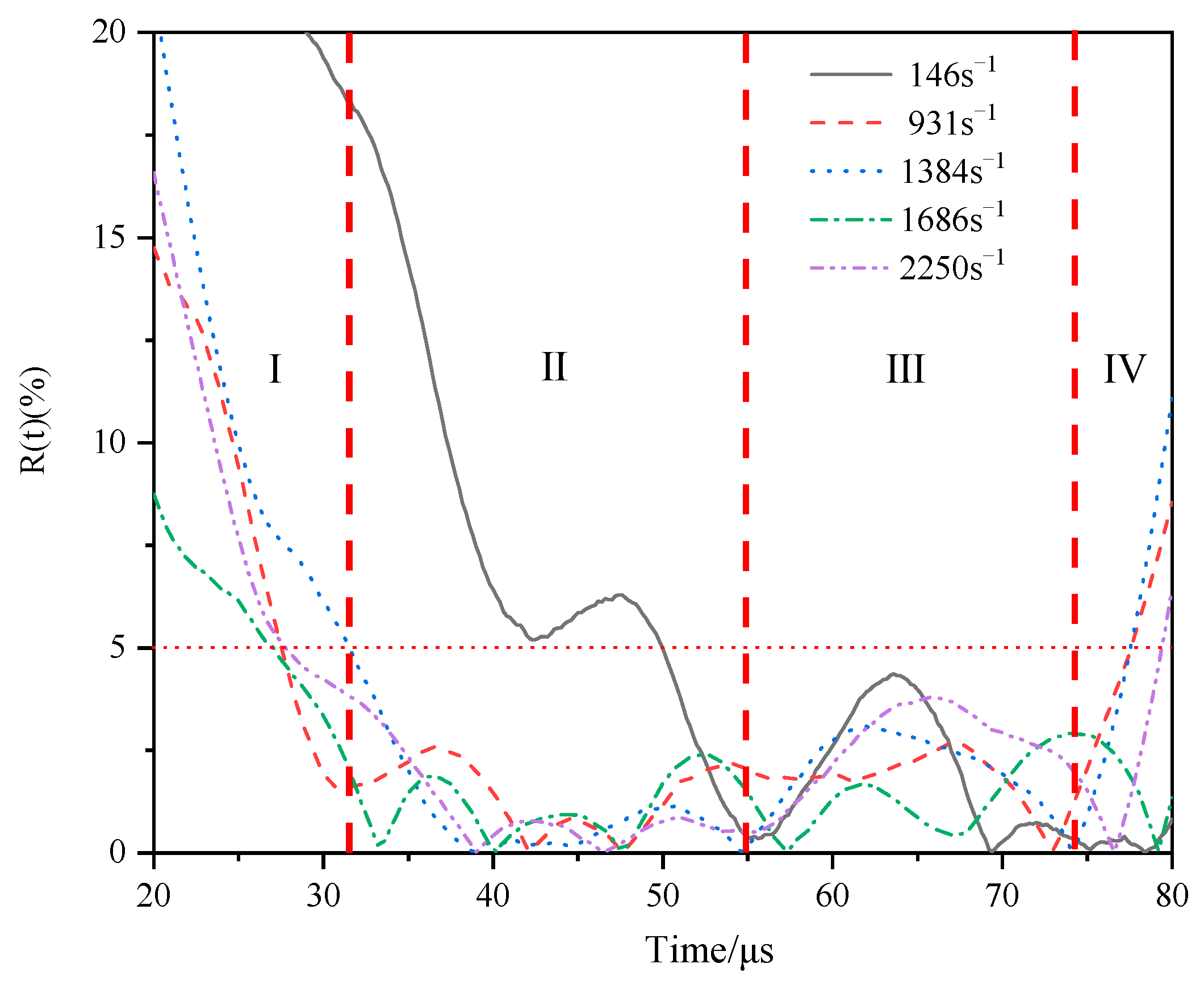
3.3. Verification of the Specimen Stress Uniformity
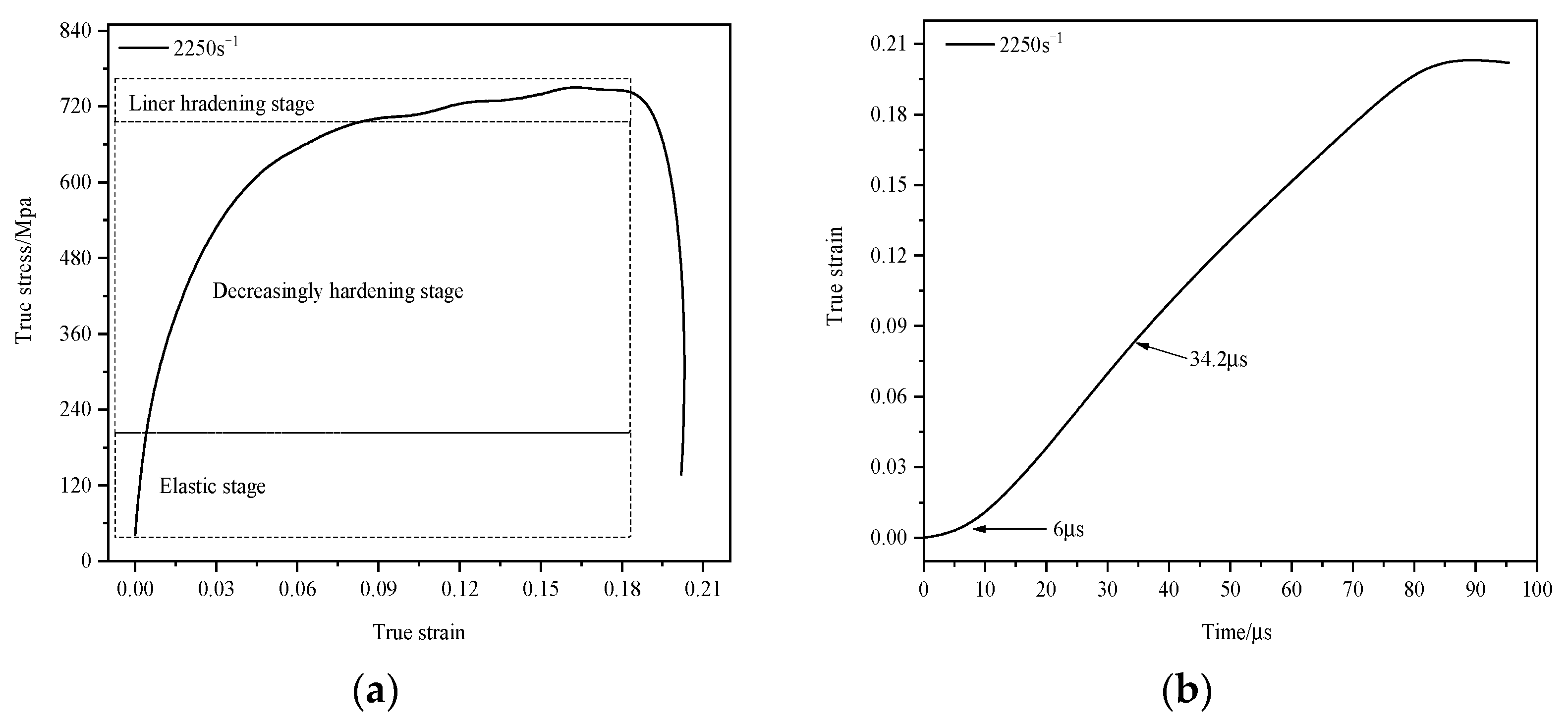
3.4. Four Deformation Stages during the Dynamic Response Process
3.4.1. Elastic Deformation Stage
3.4.2. Plastic Modulus Compatibility Deformation Stage
3.4.3. Uniform Plastic Deformation Stage
3.4.4. Non-Uniform Plastic Deformation Stage

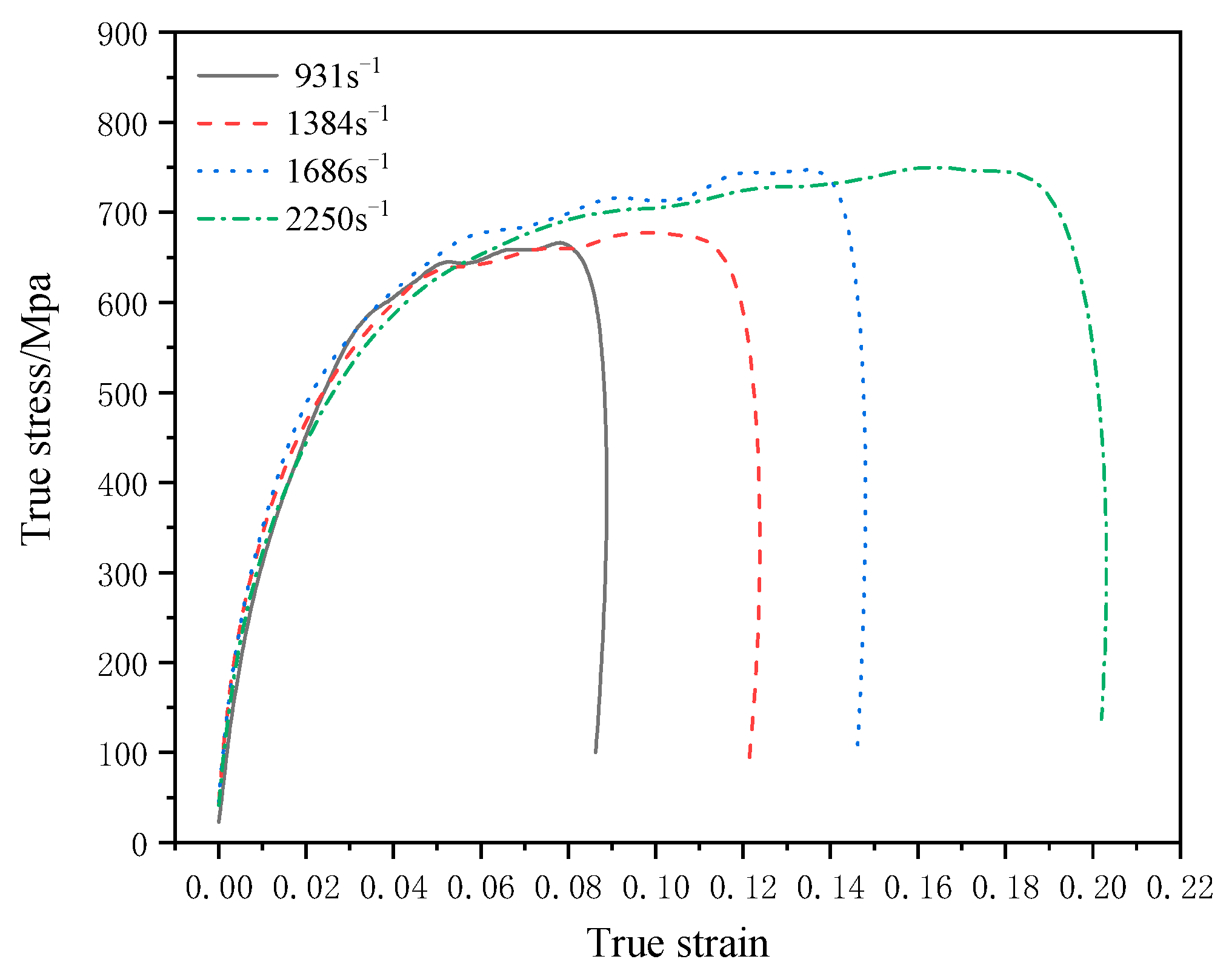
3.5. Dynamic Compressive Mechanical Response of TA2/Q345
4. Conclusions
- The relative non-uniformity of the internal stress is lower than 5% when the strain rates are in range of 931–2250 s−1, indicating that the stress–strain relationships of the parallel structure specimens are reliable. The experimental results are real and effective. When the strain rate is at a relatively low level, i.e., strain rate is 146 s−1, the one-dimensional stress wave hypothesis and the stress uniformity hypothesis are not satisfied until the latter half of the effective loading time of the incident wave.
- There exist four deformation stages of the parallel structure TA2/Q345 laminated material under the dynamic compression loading condition, namely, the elastic deformation stage, the plastic modulus compatible deformation stage, the uniform plastic deformation stage and the non-uniform plastic deformation stage. During the whole loading process, the proportion of the elastic deformation stage is only 7.5%. The plastic modulus compatible deformation stage accounts for 15.0%, mainly depending on the stress wave propagating in the specimen. The uniform plastic deformation stage accounts for the highest proportion of 53.7%, which is the primary stage in the process. The non-uniform plastic deformation stage happened with obvious characteristic of failure welding interface.
- The plastic modulus-compatible deformation stage is characterized by the decreasing hardening phenomenon, while the uniform plastic deformation stage is characterized by the linear hardening of the plastic modulus. In the non-uniform plastic deformation stage, adiabatic temperature dominates the material behavior, leading to the specimen softening effect.
- The parallel structure TA2/Q345 composites exhibit strain rate hardening effect, strain rate strengthening effect and strain rate plasticizing effect under 931 s−1–2250 s−1 strain rate dynamic compression load, which can be utilized in protective structure in electronic packaging, vehicle collision avoidance system et al.
Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hui, D.; Dutta, P.K. A new concept of shock mitigation by impedance-graded materials. Compos. Part B-Eng. 2011, 42, 2181–2184. [Google Scholar] [CrossRef]
- Corigliano, P.; Crupi, V.; Guglielmino, E.; Sili, A.M. Full-field analysis of AL/FE explosive welded joints for shipbuilding applications. Mar. Struct. 2018, 57, 207–218. [Google Scholar] [CrossRef]
- Sudha, J.; Vasumathi, M.; Archiana, P.; Balakumar, M.; Jaidah, M. Low velocity impact and axial loading response of hybrid fibre aluminium laminates. J. Mech. Sci. Technol. 2021, 35, 4925–4930. [Google Scholar] [CrossRef]
- Boggarapu, V.; Gujjala, R.; Ojha, S.; Acharya, S.; Venkateswara Babu, P.; Chowdary, S.; Gara, D.K. State of the art in functionally graded materials. Compos. Struct. 2021, 262, 113596. [Google Scholar] [CrossRef]
- Bruck Hugh, A. A one-dimensional model for designing functionally graded materials to manage stress waves. Int. J. Solids Struct. 2000, 37, 6383–6395. [Google Scholar] [CrossRef]
- Tasdemirci, A.; Hall, I.W. The effects of plastic deformation on stress wave propagation in multi-layer materials. Int. J. Impact Eng. 2007, 34, 1797–1813. [Google Scholar] [CrossRef]
- Fernando, P.L.N.; Mohotti, D.; Remennikov, A. Behaviour of explosively welded impedance-graded multi-metal composite plates under near-field blast loads. Int. J. Mech. Sci. 2019, 163, 105124. [Google Scholar] [CrossRef]
- Gladkovsky, S.V.; Kuteneva, S.V.; Sergeev, S.N. Microstructure and mechanical properties of sandwich cooper/steel composites produced by explosive welding. Mater. Charact. 2019, 154, 294–303. [Google Scholar] [CrossRef]
- Markovsky, P.E.; Janiszewski, J.; Savvakin, D.G.; Stasiuk, O.O.; Cieplak, K.; Baranowski, P.; Prikhodko, S.V. Mechanical behavior of bilayer structures of Ti64 alloy and its composites with TiC or TiB under quasi-static and dynamic compression. Mater. Des. 2022, 223, 111205. [Google Scholar] [CrossRef]
- Zemani, K.; May, A.; Gilson, L.; Tria, D. Numerical investigation of the dynamic behavior of a Ti/TiB functionally graded material using Split Hopkinson Pressure Bar test. J. Compos. Mater. 2022, 57, 1053–1070. [Google Scholar] [CrossRef]
- Samal, M.K.; Sharma, S. A new procedure to evaluate parameters of Johnson-Cook Elastic-Plastic material model from varying strain rate Split Hopkinson Pressure Bar tests. J. Mater. Eng. Perform. 2021, 30, 8500–8514. [Google Scholar] [CrossRef]
- Zhang, P.L.; Gong, Z.Z.; Tian, D.B.; Song, G.M.; Wu, Q.; Cao, Y.; Xu, K.; Li, M. Comparison of shielding performance of Al/Mg impedance-graded-material enhanced and aluminum Whipple shields. Int. J. Impact Eng. 2019, 126, 101–108. [Google Scholar] [CrossRef]
- Davies, E.; Hunter, S. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar. J. Mech. Phys. Solids 1963, 11, 155–179. [Google Scholar] [CrossRef]
- Jankowiak, T.; Rusinek, A.; Voyiadjis, G. Modeling and design of SHPB to characterize brittle materials under compression for high strain rates. Materials 2020, 13, 2191. [Google Scholar] [CrossRef]
- Panowicz, R.; Konarzewski, M. Infulence of imperfect position of a striker and input bar on wave propagation in a split Hopkinson pressure bar setup with a pulse-shape technique. Appl. Sci. 2020, 10, 2423. [Google Scholar] [CrossRef]
- Jang, T.; Yoon, J.; Kim, J. Determination of Johnson-Cook constitutive model coefficients considering initial gap between contact faces in SHPB test. J. Mater. Res. Technol. 2023, 24, 7242–7257. [Google Scholar] [CrossRef]
- Challita, G.; Othman, R. Finite-element analysis of SHPB tests on double-lap adhesive joints. Int. J. Adhes. Adhes. 2010, 30, 236–244. [Google Scholar] [CrossRef]
- Hopkinson, B. A method of measuring the pressure in the deformation of high explosives or by the impact of bullets. Philos. Trans. R. Soc. 1914, 213, 437–452. [Google Scholar]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Tasdemirci, A.; Hall, I.W.; Gama, B.A. Stress wave propagation effects in two and three-layered composite materials. J. Compos. Mater. 2004, 38, 995–1009. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, P.; Arab, A.; Zhou, Q.; Mahmood, Y. High strain rate deformation of explosion-welded Ti6Al4V/pure titanium. Def. Technol. 2020, 16, 678–688. [Google Scholar] [CrossRef]
- Wang, W.; Yang, J.; Deng, G.; Chen, X. Theoretical analysis of stress equilibrium of linear hardening plastic specimen during SHPB tests. Exp. Mech. 2023, 63, 1353–1369. [Google Scholar] [CrossRef]
- Bendarma, A.; Jankowiak, T.; Rusinek, A.; Lodygowski, T.; Jia, B.; Miguélez, M.H.; Klosak, M. Dynamic behavior of Aluminum Alloy Aw 5005 undergoing interfacial friction and specimen configuration in Split Hopkinson pressure bar system at high strain rates and temperatures. Materials 2020, 13, 4614. [Google Scholar] [CrossRef] [PubMed]
- Lifshitz, J.M.; Leber, H. Data processing in the split Hopkinson pressure bar tests. Int. J. Impact Eng. 1994, 15, 723–733. [Google Scholar] [CrossRef]
- Negger, J.; Hoefnagels, J.; Van Der Sluis, O.; Geers, M. Multi-scale experimental analysis of rate dependent metal-elastomer interface mechanics. J. Mech. Phys. Solids 2015, 80, 26–36. [Google Scholar] [CrossRef]
- Vecchio, K.S.; Jiang, F. Improved Pulse Shaping to achieve constant strain rate and stress equilibrium in Split-Hopkinson pressure bar testing. Metall. Mater. Trans. A 2007, 38, 2655–2665. [Google Scholar] [CrossRef]
- Ravichandran, G.; Subhash, G. Critical appraisal of limiting st rain rates for compression testing of ceramics in a split Hopkinson pressure bar. J. Am. Ceram. Soc. 2010, 77, 263–267. [Google Scholar] [CrossRef]
- Zhou, F.H.; Wang, L.L.; Hu, S.S. On the effect of stress non-uniformness in polymer specimen of SHPB tests. J. Exp. Mech. 1992, 7, 23–29. [Google Scholar]
- Lee, W.-S.; Liu, C.-Y. The effects of temperature and strain rate on the dynamic flow behaviour of different steels. Mater. Sci. Eng. A 2006, 426, 101–113. [Google Scholar] [CrossRef]
- Zhou, T.; Wu, J.; Che, J.; Wang, Y.; Wang, X. Dynamic shear characteristics of titanium alloy Ti-6Al-4V at large strain rates by the split Hopkinson pressure bar test. Int. J. Impact Eng. 2017, 109, 167–177. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; Liu, W.; Li, S.; Zhang, L.; He, H. Development of adiabatic shearing bands in 7003-T4 aluminum alloy under high strain rate impacting. Mater. Sci. Eng. A 2018, 732, 91–98. [Google Scholar] [CrossRef]

| Cases | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Velocity of striker bar (m/s) | 6.31 | 13.63 | 16.73 | 19.24 | 22.03 |
| Emission pressure (MPa) | 0.22 | 0.25 | 0.35 | 0.48 | 0.60 |
| Density (g/cm3) | Hardness HV | Elasticity Modulus (GPa) | Elastic Wave Velocity (m/s) | Poisson Ratio | |
|---|---|---|---|---|---|
| Q345 | 7.83 | ≥160 | 246.18 | 5607.2 | 0.3 |
| TA2 | 4.51 | ≥140 | 132.82 | 5426.8 | 0.33 |
| SHPB bars | 7.69 | ≥500 | 200 | 5100.0 | 0.3 |
| Strain Rate (s−1) | Yield Strength (Mpa) | Yield Strain (10–3) | Yield Time (μs) | Initial Stress of Strain Hardening Effect (Mpa) | Initial Time of Linear Hardening (μs) |
|---|---|---|---|---|---|
| 931 | 141.26 | 2.98 | 6.2 | 597.92 | 29.2 |
| 1384 | 169.47 | 2.56 | 5.8 | 638.56 | 33.2 |
| 1686 | 179.78 | 2.95 | 6 | 673.37 | 32 |
| 2250 | 204.87 | 4.22 | 6 | 695.33 | 34.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Chen, S.; Zhao, P.; Ye, X. The Mechanism of Deformation Compatibility of TA2/Q345 Laminated Metal in Dynamic Testing with Split-Hopkinson Pressure Bar. Materials 2023, 16, 7659. https://doi.org/10.3390/ma16247659
Fu Y, Chen S, Zhao P, Ye X. The Mechanism of Deformation Compatibility of TA2/Q345 Laminated Metal in Dynamic Testing with Split-Hopkinson Pressure Bar. Materials. 2023; 16(24):7659. https://doi.org/10.3390/ma16247659
Chicago/Turabian StyleFu, Yanshu, Shoubo Chen, Penglong Zhao, and Xiaojun Ye. 2023. "The Mechanism of Deformation Compatibility of TA2/Q345 Laminated Metal in Dynamic Testing with Split-Hopkinson Pressure Bar" Materials 16, no. 24: 7659. https://doi.org/10.3390/ma16247659
APA StyleFu, Y., Chen, S., Zhao, P., & Ye, X. (2023). The Mechanism of Deformation Compatibility of TA2/Q345 Laminated Metal in Dynamic Testing with Split-Hopkinson Pressure Bar. Materials, 16(24), 7659. https://doi.org/10.3390/ma16247659




