Drag Reduction Technology of Water Flow on Microstructured Surfaces: A Novel Perspective from Vortex Distributions and Densities
Abstract
:1. Introduction
2. Experimental Devices
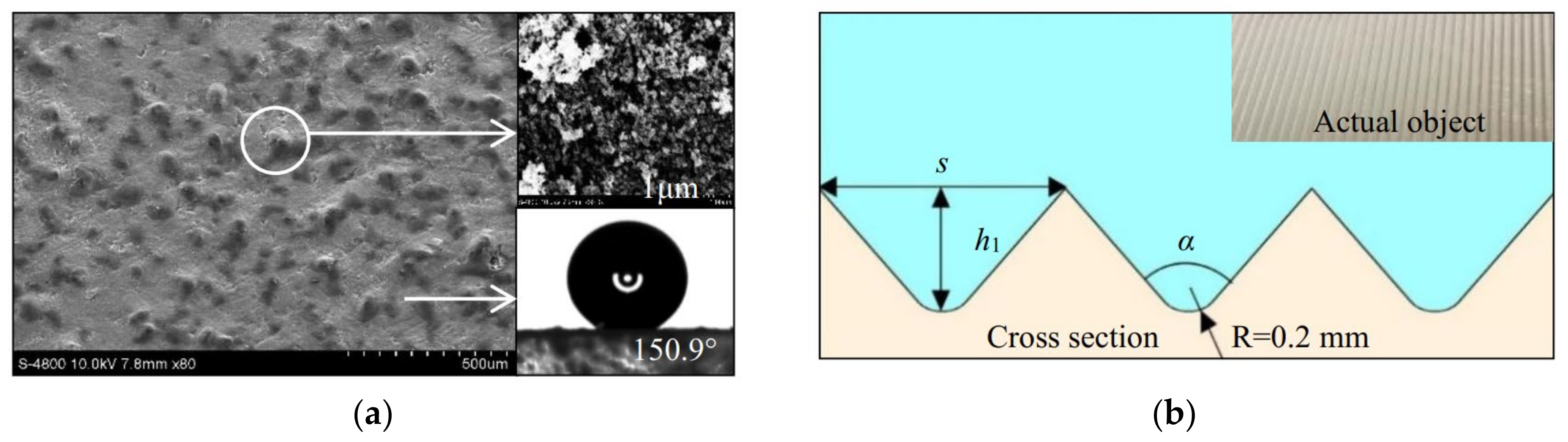
2.1. Experimental Materials
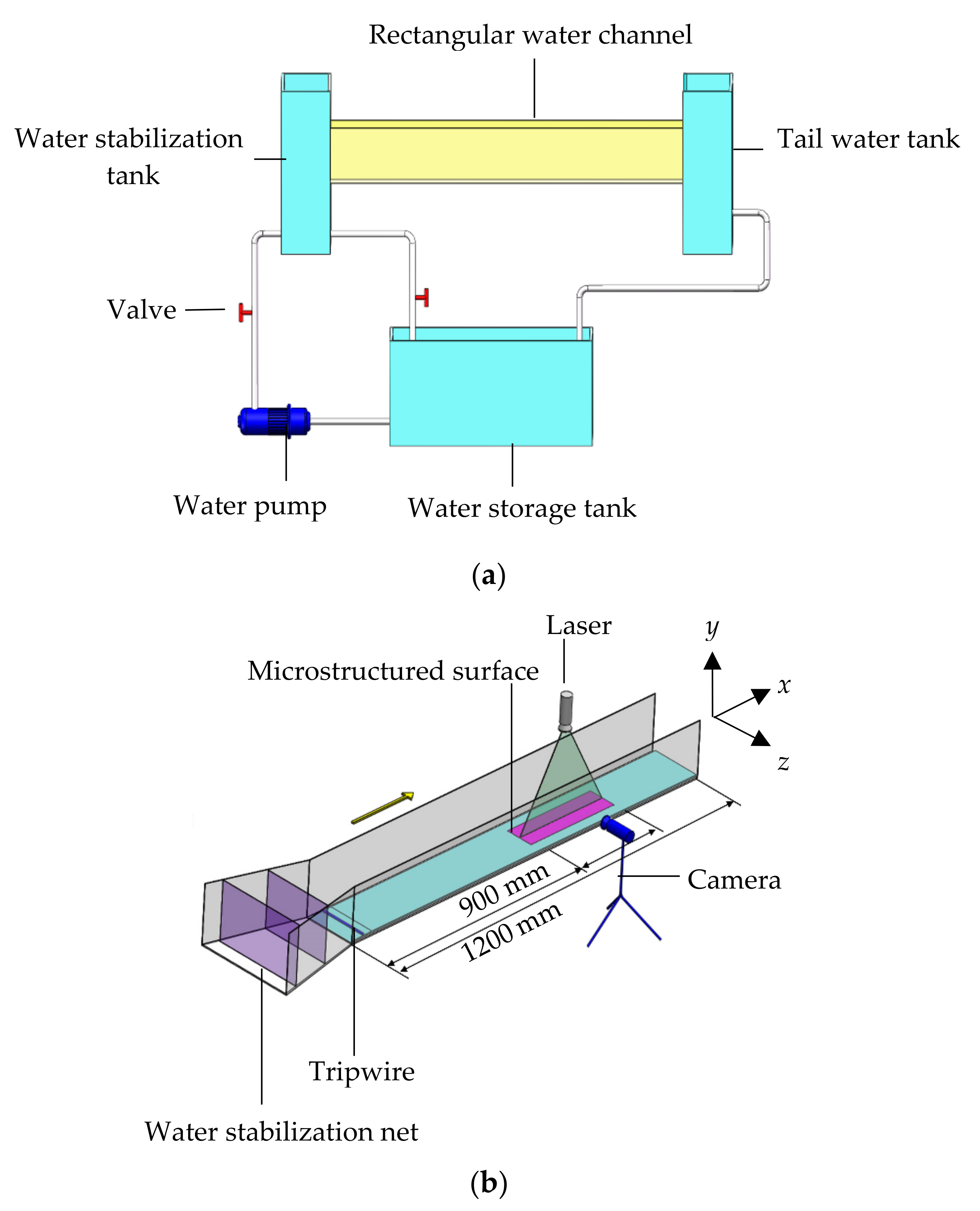
2.2. Experimental Design
2.3. Statistical Analyses
3. Modification of Ω Method
4. Results and Discussion
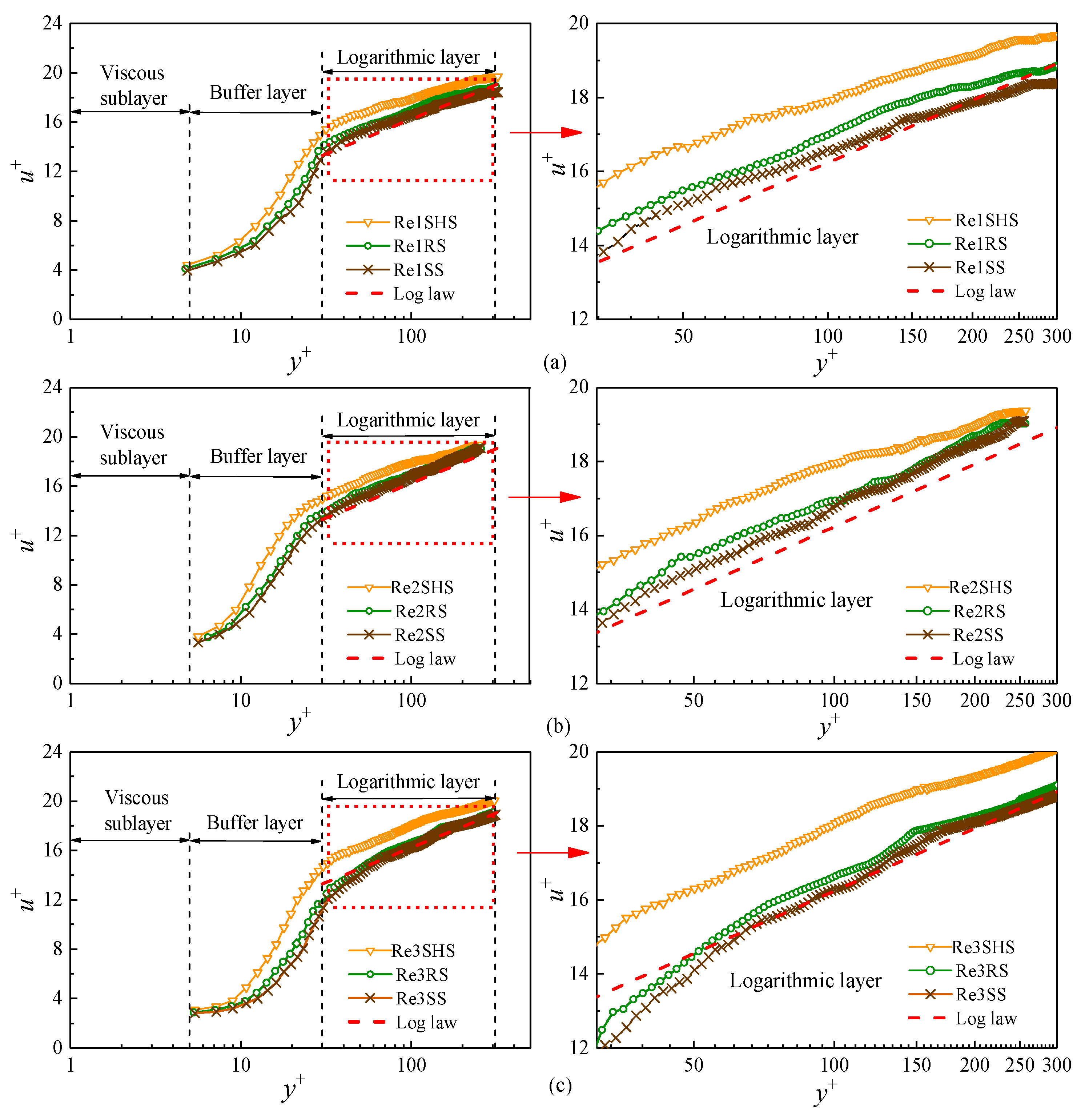
4.1. Average Velocity Distribution
4.2. Reynolds Shear Stress
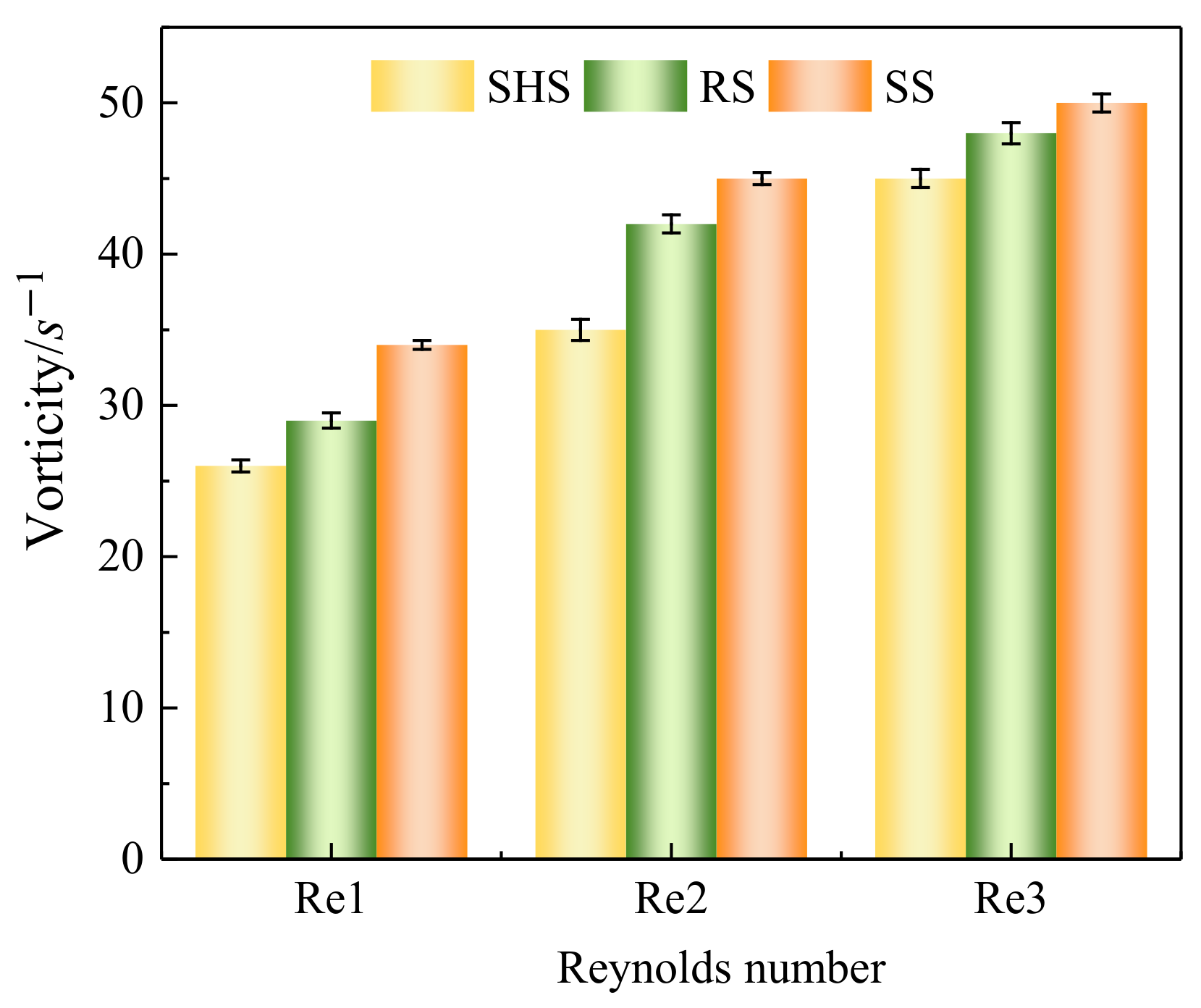
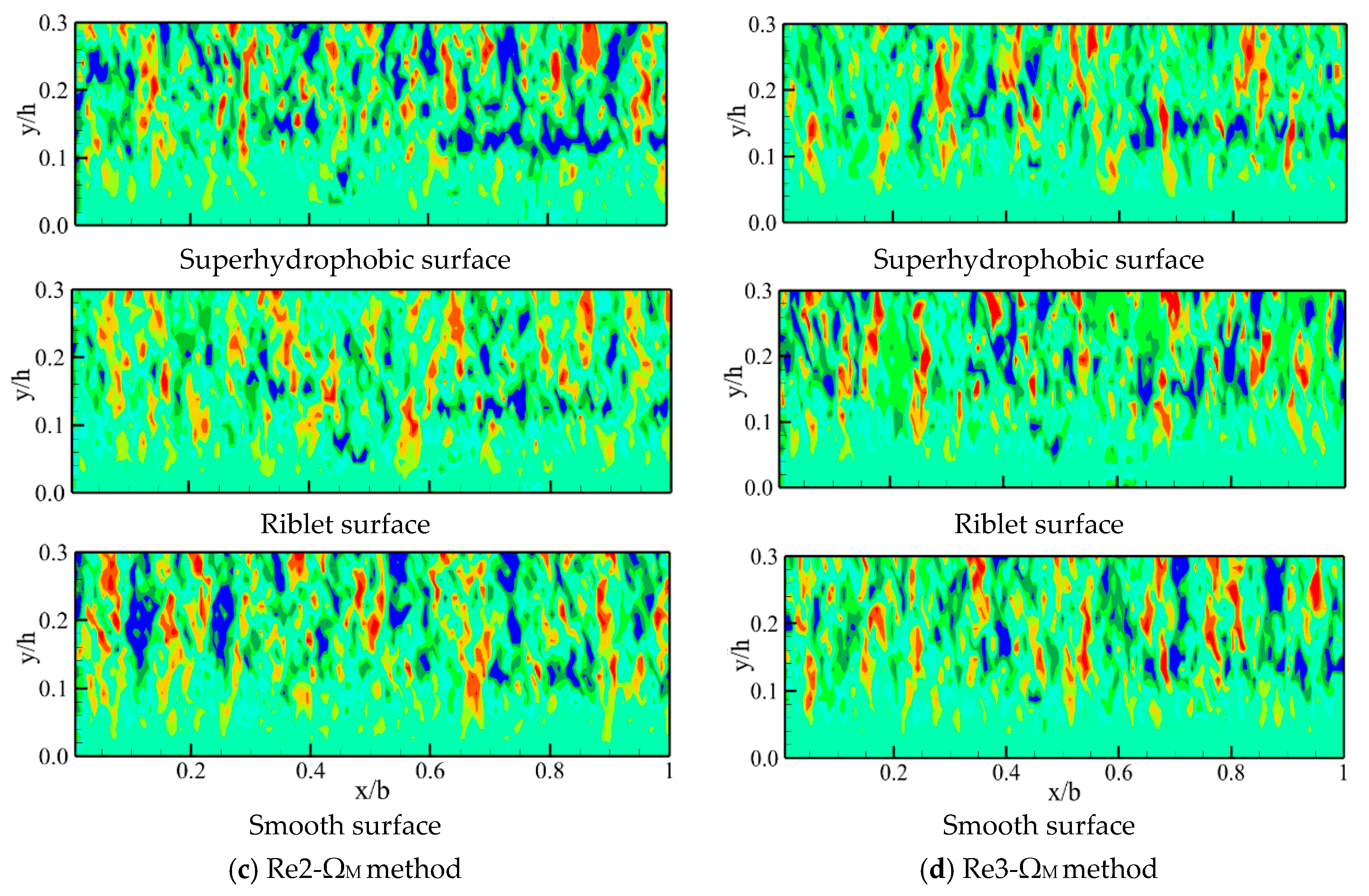
4.3. Vortex Distribution
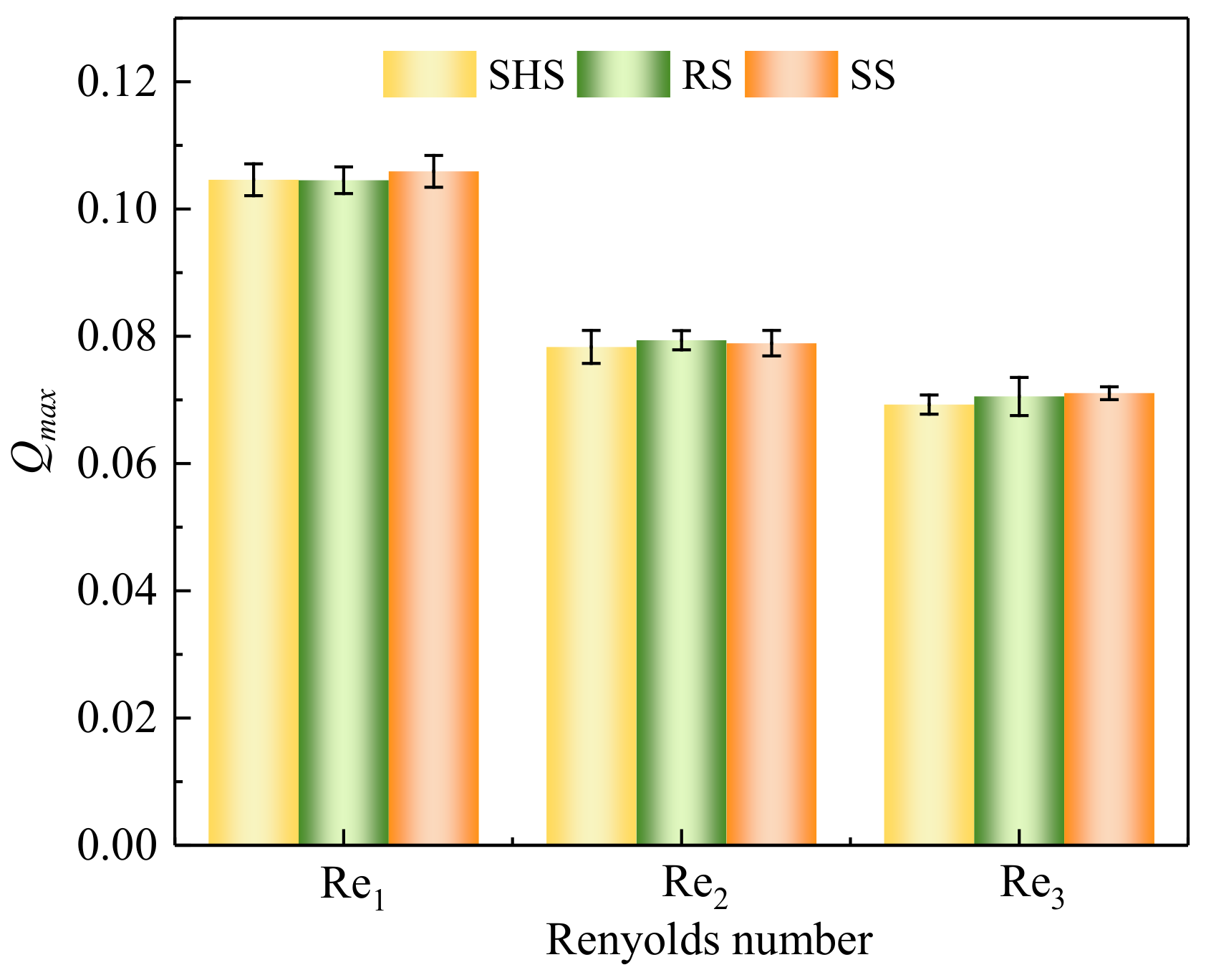
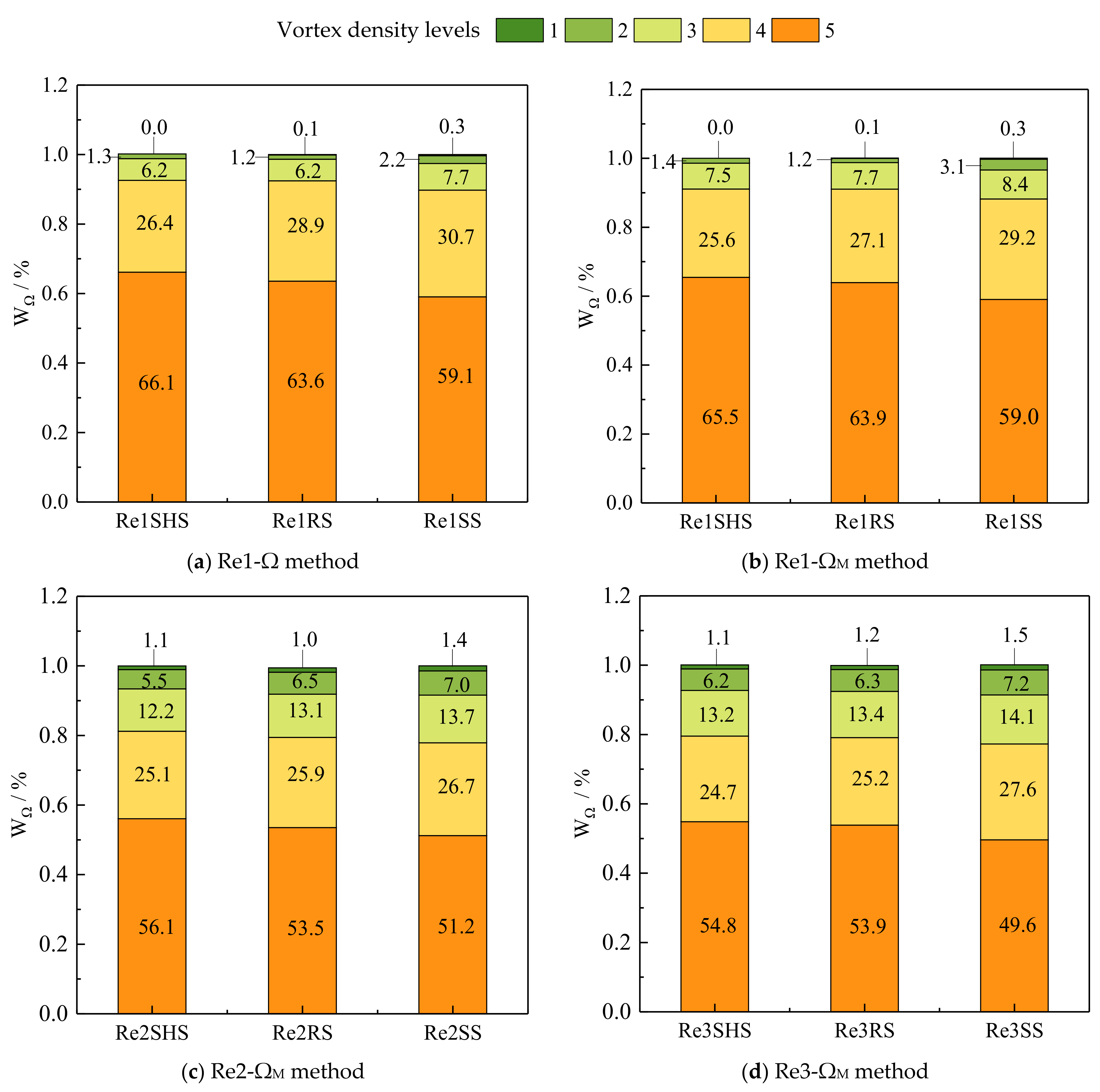
4.3.1. Reliability Analysis of the ΩM Method
4.3.2. Vortex Structures on Drag Reduction Effects
5. Drag Reduction Rate
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PIV | particle image velocimetry |
| SHS | superhydrophobic surface |
| RS | riblet surface |
| SS | smooth surface |
| Re | Reynolds number |
| u | flow velocity (m⋅s−1) |
| L | length (m) |
| ν | kinematic viscosity (m2⋅s−1) |
| ‖‖F | Frobenius two-norm of the matrix |
| dimensionless Reynolds shear stress | |
| ρ | water density (kg⋅m−3) |
| u′ | fluctuation velocity of streamwise (m⋅s−1) |
| B | antisymmetric tensor |
| A | symmetric tensor |
| ε | a positive parameter |
| Qmax | maximum value of the Q vortex method |
| U | dimensionless flow velocity |
| SΩ | total number of a strength vortex |
| S | total number of all strength vortices |
| u+ | dimensionless velocity |
| y+ | normal dimensionless position |
| κ | Karman constant |
| u* | wall friction velocity (m⋅s−1) |
| y | normal distance (m) |
| τ | frictional resistance of the microstructured surface (N⋅m−2) |
| τ0 | frictional resistance of the smooth surface (N⋅m−2) |
| v′ | fluctuation velocity of normal (m⋅s−1) |
| u∞ | free flow velocity (m⋅s−1) |
| DR | drag reduction rate (%) |
References
- Wang, Y.; Wang, Y.; Su, X.; Qi, L.; Liu, M. Evaluation of the comprehensive carrying capacity of interprovincial water resources in China and the spatial effect. J. Hydrol. 2019, 575, 794–809. [Google Scholar] [CrossRef]
- Fu, Z.; Zhao, H.; Wang, H.; Lu, W.; Wang, J.; Guo, H. Integrated planning for regional development planning and water resources management under uncertainty: A case study of Xining, China. J. Hydrol. 2017, 554, 623–634. [Google Scholar] [CrossRef]
- Wu, T.; Chen, W.; Zhao, A.; He, P.; Chen, H. A comprehensive investigation on micro-structured surfaces for underwater drag reduction. Ocean Eng. 2020, 218, 107902. [Google Scholar] [CrossRef]
- NBSPRC. Statistics on the Length of Water Supply Pipes; National Bureau of Statistics: Beijing, China, 2020.
- Wu, H.; Yue, Q.; Guo, P.; Pan, Q.; Guo, S. Sustainable regional water allocation under water-energy nexus: A chance-constrained possibilistic mean-variance multi-objective programming. J. Clean. Prod. 2021, 313, 127934. [Google Scholar] [CrossRef]
- Gu, Y.; Yu, S.; Mou, J.; Wu, D.; Zheng, S. Research progress on the collaborative drag reduction effect of polymers and surfactants. Materials 2020, 13, 444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bai, H.; Zhang, L.; Gu, D. Micrometer-sized spherulites as building blocks for lotus leaf-like superhydrophobic coatings. Appl. Surf. Sci. 2018, 459, 54–62. [Google Scholar] [CrossRef]
- Wang, P.; Qiu, R.; Zhang, D.; Lin, Z.; Hou, B. Fabricated super-hydrophobic film with potentiostatic electrolysis method on copper for corrosion protection. Electrochim. Acta 2010, 56, 517–522. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.; Latthe, S.S.; Gao, L.; An, S.; Yoon, S.S.; Liu, B.; Xing, R. Self-cleaning transparent superhydrophobic coatings through simple sol–gel processing of fluoroalkylsilane. Appl. Surf. Sci. 2015, 351, 897–903. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, Z.; Chen, T.; Xi, Y.; Zhang, J. Fabrication of superhydrophobic surface with desirable anti-icing performance based on micro/nano-structures and organosilane groups. Appl. Surf. Sci. 2020, 501, 144165. [Google Scholar] [CrossRef]
- Park, H.; Choi, C.-H.; Kim, C.-J. Superhydrophobic drag reduction in turbulent flows: A critical review. Exp. Fuids 2021, 62, 229. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Yan, Y.; Han, Z.; Ren, L. Anti-icing performance of superhydrophobic aluminum alloy surface and its rebounding mechanism of droplet under super-cold conditions. Surf. Coat. Tech. 2017, 331, 7–14. [Google Scholar] [CrossRef]
- Woolford, B.; Jeffs, K.; Maynes, D.; Webb, B. Laminar fully-developed flow in a microchannel with patterned ultrahydrophobic walls. In Proceedings of the Heat Transfer Summer Conference, San Francisco, CA, USA, 17–22 July 2005. [Google Scholar]
- Ren, W.; Chen, Y.; Mu, X.; Khoo, B.; Zhang, F.; Xu, Y. Heat transfer enhancement and drag reduction in transverse groove-bounded microchannels with offset. Int. J. Therm. Sci. 2018, 130, 240–255. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bruse, M.; Hage, W.V.; Van Der Hoeven, J.T.; Hoppe, G. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- Sharma, V.; Dutta, S. Experimental investigation of flow characteristics over a surface-modified structured torpedo model. J. Wind Eng. Ind. Aerod. 2022, 230, 105196. [Google Scholar] [CrossRef]
- Martin, S.; Bhushan, B. Modeling and optimization of shark-inspired riblet geometries for low drag applications. J. Colloid Interface Sci. 2016, 474, 206–215. [Google Scholar] [CrossRef]
- Daniello, R.J.; Waterhouse, N.E.; Rothstein, J. Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 2009, 21, 085103. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Liu, J.M.; Gao, Y.S.; Wang, Y.Q.; Liu, C.Q. Objective omega vortex identification method. J. Hydrodyn. 2019, 31, 455–463. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, C. Rortex and comparison with eigenvalue-based vortex identification criteria. Phys. Fluids 2018, 30, 085107. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.R.; Gao, Y.S.; Liu, C.Q. New normalized Rortex/vortex identification method. Phys. Fluids 2019, 31, 011701. [Google Scholar] [CrossRef]
- Flack, K.A.; Schultz, M.P.; Barros, J.M.; Kim, Y.C. Skin-friction behavior in the transitionally-rough regime. Int. J. Heat Fluid Flow 2016, 61, 21–30. [Google Scholar] [CrossRef]
- Lee, C.; Lee, G.W.; Choi, W.; Yoo, C.H.; Chun, B.; Lee, J.S.; Lee, J.H.; Jung, H.W. Pattern flow dynamics over rectangular Sharklet patterned membrane surfaces. Appl. Surf. Sci. 2020, 514, 145961. [Google Scholar] [CrossRef]
- Adrian, R.J.; Meinhart, C.D.; Tomkins, C. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 2000, 422, 1–54. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.D.; Choi, K.S.; Chun, H. Direct intervention of hairpin structures for turbulent boundary-layer control. Phys. Fluids 2008, 20, 101517. [Google Scholar] [CrossRef]
- Deng, S.C.; Pan, C.; Wang, J.J.; He, G.S. On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number. J. Fluid Mech. 2018, 844, 635–668. [Google Scholar] [CrossRef]
- Hwang, J.; Sung, H.J. Wall-attached clusters for the logarithmic velocity law in turbulent pipe flow. Phys. Fluids 2019, 31, 055109. [Google Scholar]
- Womack, K.M.; Meneveau, C.; Schultz, M.P. Comprehensive shear stress analysis of turbulent boundary layer profiles. J. Fluid Mech. 2019, 879, 360–389. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.Q.; Chen, X.P.; Dong, Y.L.; Zhang, Y.N.; Liu, C.Q. Determination of epsilon for Omega vortex identification method. J. Hydrodyn. 2018, 30, 541–548. [Google Scholar] [CrossRef]
- Haynes, P.H.; Mcintyre, M.E. On the evolution of vorticity and potential vorticity in the presence of diabatic heating and frictional or other forces. J. Atmos. Sci. 1987, 44, 828–840. [Google Scholar] [CrossRef]
- Choi, K.S. Near-wall structure of a turbulent boundary layer with riblets. J. Fluid Mech. 1989, 208, 417–458. [Google Scholar] [CrossRef]
- Wang, J.J.; Lan, S.L.; Chen, G. Experimental study on the turbulent boundary layer flow over riblets surface. Fluid Dyn. Res. 2000, 27, 217–229. [Google Scholar] [CrossRef]
- Xu, M.; Grabowski, A.; Yu, N.; Kerezyte, G.; Lee, J.W.; Pfeifer, B.R. Superhydrophobic drag reduction for turbulent flows in open water. Phys. Rev. Appl. 2020, 13, 034056. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, S. Flow field analysis of a turbulent boundary layer over a riblet surface. Exp. Fuids 2001, 30, 153–166. [Google Scholar] [CrossRef]
- Saltar, G.; Araya, G. Reynolds shear stress modeling in turbulent boundary layers subject to very strong favorable pressure gradient. Comput. Fluids 2020, 202, 104494. [Google Scholar] [CrossRef]
- Liu, H.Y.; Bo, T.L.; Wang, G.H.; Zheng, X.J. The analysis of turbulence intensity and Reynolds shear stress in wall-bounded turbulent flows at high Reynolds numbers. Bound.-Layer Meteorol. 2014, 150, 33–47. [Google Scholar] [CrossRef]
- Boomsma, A.; Sotiropoulos, F. Direct numerical simulation of sharkskin denticles in turbulent channel flow. Phys. Fluids 2016, 28, 035106. [Google Scholar] [CrossRef]
- Nezu, L. Turbulence intensities in open channel flows. In Proceedings of the Japan Society of Civil Engineers; Japan Society of Civil Engineers: Tokyo, Japan, 1977. [Google Scholar]
- Yang, S.F.; Zhang, P.; Hu, J.; Li, W.J.; Chen, Y. Distribution and motion characteristics of Q-events for open-channel uniform flow Advances in water Science. Acta Mech. Sin. 2016, 27, 430–438. [Google Scholar]
- Martin, S.; Bhushan, B. Fluid flow analysis of continuous and segmented riblet structures. J. Colloid Interface Sci. 2016, 6, 10962–10978. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, H.; Yao, Z.; Hao, P.; Jiang, N. Mechanisms of drag reduction of superhydrophobic surfaces in a turbulent boundary layer flow. Exp. Fluids 2015, 56, 179. [Google Scholar] [CrossRef]
- Ricco, P.; Skote, M.; Leschziner, M.A. A review of turbulent skin-friction drag reduction by near-wall transverse forcing. Prog. Aerosp. Sci. 2021, 123, 100713. [Google Scholar] [CrossRef]
- Martell, M.; Rothstein, J.P.; Perot, J.B. An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 2010, 22, 065102. [Google Scholar] [CrossRef] [Green Version]
- Riahi, D.N. Boundary wave-vortex interaction in channel flow with a wavy wall at high Reynolds numbers. Fluid Dyn. Res. 1999, 25, 129. [Google Scholar] [CrossRef]
- Dean, B.; Bhushan, B. The effect of riblets in rectangular duct flow. Appl. Surf. Sci. 2012, 258, 3936–3947. [Google Scholar] [CrossRef]
- Cabal, A.; Szumbarski, J.; Floryan, J.M. Stability of flow in a wavy channel. J. Fluid Mech. 2002, 457, 191–212. [Google Scholar] [CrossRef]
- Gogte, S.; Vorobieff, P.; Truesdell, R.; Mammoli, A.; Van Swol, F.; Shah, P.; Brinker, C.J. Effective slip on textured superhydrophobic surfaces. Phys. Fluids 2005, 17, 051701. [Google Scholar] [CrossRef] [Green Version]


| Experimental Treatments | Reynolds Number | Experimental Surface | Experimental Treatments | Reynolds Number | Experimental Surface | Experimental Treatments | Reynolds Number | Experimental Surface |
|---|---|---|---|---|---|---|---|---|
| Re1SHS | 85,900 | SHS | Re2SHS | 120,260 | SHS | Re3SHS | 137,440 | SHS |
| Re1RS | 85,900 | RS | Re2RS | 120,260 | RS | Re3RS | 137,440 | RS |
| Re1SS | 85,900 | SS | Re2SS | 120,260 | SS | Re3SS | 137,440 | SS |
| Experimental Treatments | R/% | Experimental Treatments | R/% | Experimental Treatments | R/% | |||
|---|---|---|---|---|---|---|---|---|
| Re1SHS | 1.84 | −9.8 | Re2SHS | 2.02 | −14.0 | Re3SHS | 2.38 | −15.9 |
| Re1RS | 1.98 | −2.9 | Re2RS | 2.28 | −3.1 | Re3RS | 2.73 | −3.5 |
| Re1SS | 2.04 | 0 | Re2SS | 2.35× | 0 | Re2SS | 2.83 | 0 |
| Treatments | Friction Shear Stress τ (kg/ms−2) | Drag Reduction Rate (%) |
|---|---|---|
| Re1SHS | 0.025 | 9.48 |
| Re1RS | 0.027 | 4.93 |
| Re1SS | 0.028 | 0.00 |
| Re2SHS | 0.034 | 8.58 |
| Re2RS | 0.036 | 4.50 |
| Re2SS | 0.037 | 0.00 |
| Re3SHS | 0.053 | 7.80 |
| Re3RS | 0.055 | 4.35 |
| Re3SS | 0.058 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wang, W.; Hu, X.; Liu, F. Drag Reduction Technology of Water Flow on Microstructured Surfaces: A Novel Perspective from Vortex Distributions and Densities. Materials 2023, 16, 1838. https://doi.org/10.3390/ma16051838
Liu C, Wang W, Hu X, Liu F. Drag Reduction Technology of Water Flow on Microstructured Surfaces: A Novel Perspective from Vortex Distributions and Densities. Materials. 2023; 16(5):1838. https://doi.org/10.3390/ma16051838
Chicago/Turabian StyleLiu, Chunye, Wene Wang, Xiaotao Hu, and Fulai Liu. 2023. "Drag Reduction Technology of Water Flow on Microstructured Surfaces: A Novel Perspective from Vortex Distributions and Densities" Materials 16, no. 5: 1838. https://doi.org/10.3390/ma16051838







