Shape Adjustment and Experimental Study of a Shape Memory Cable (SMC) Structure
Abstract
1. Introduction
2. Materials and Methods
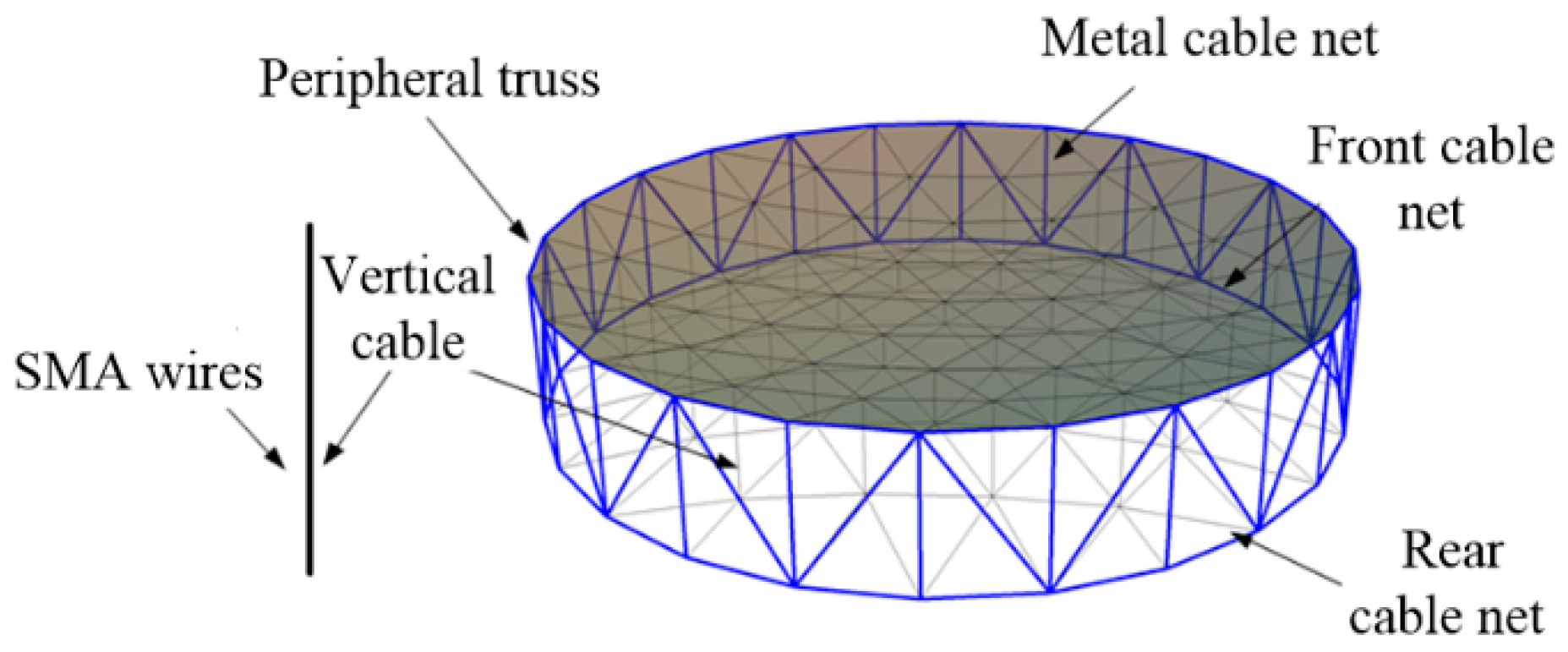
2.1. Model of the SMC Structure
2.1.1. Constitutive Model
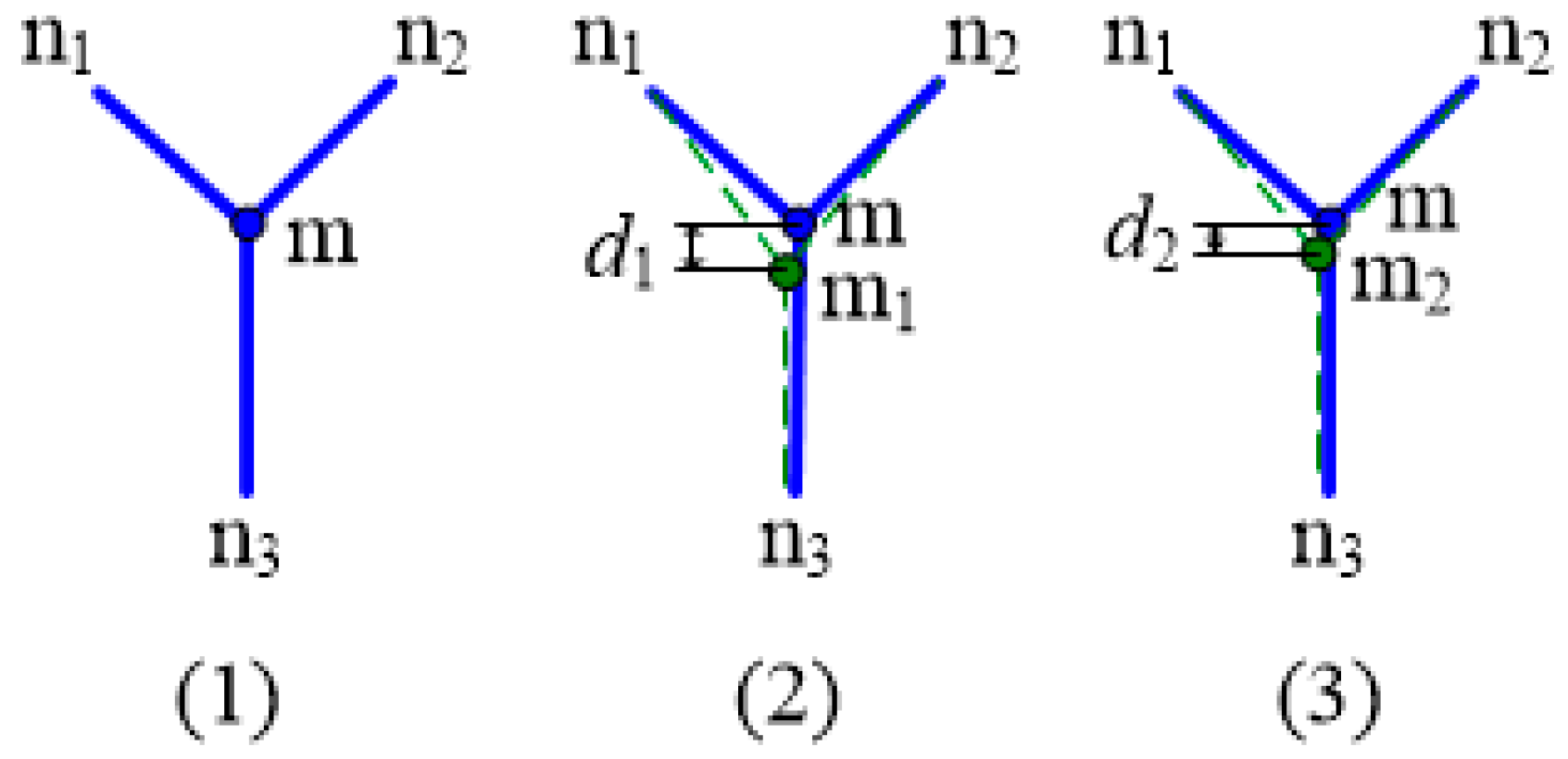
2.1.2. Reflector Adjustment Method
2.2. Model Parameters
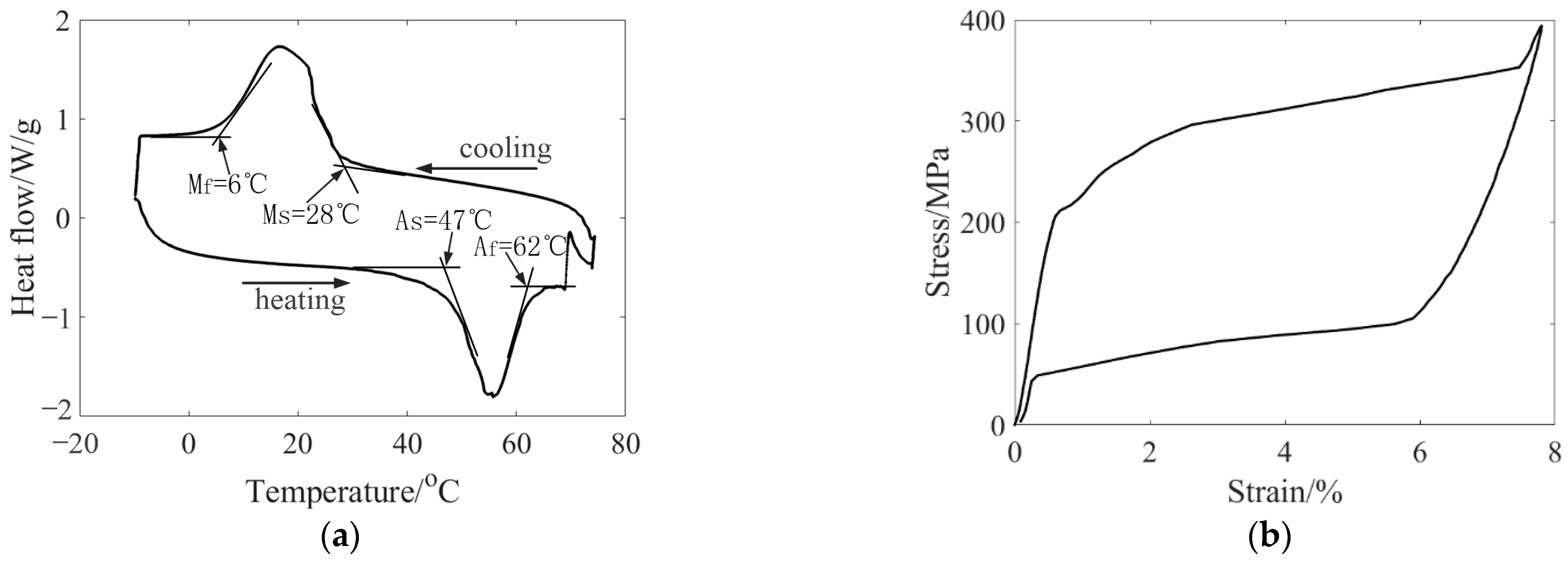
2.2.1. Material Parameters
2.2.2. Structural Parameters
3. Active Adjustment of the SMC Structure at Room Temperature
3.1. Normal Temperature Protocol
3.2. Analysis of Normal Temperature Test Results
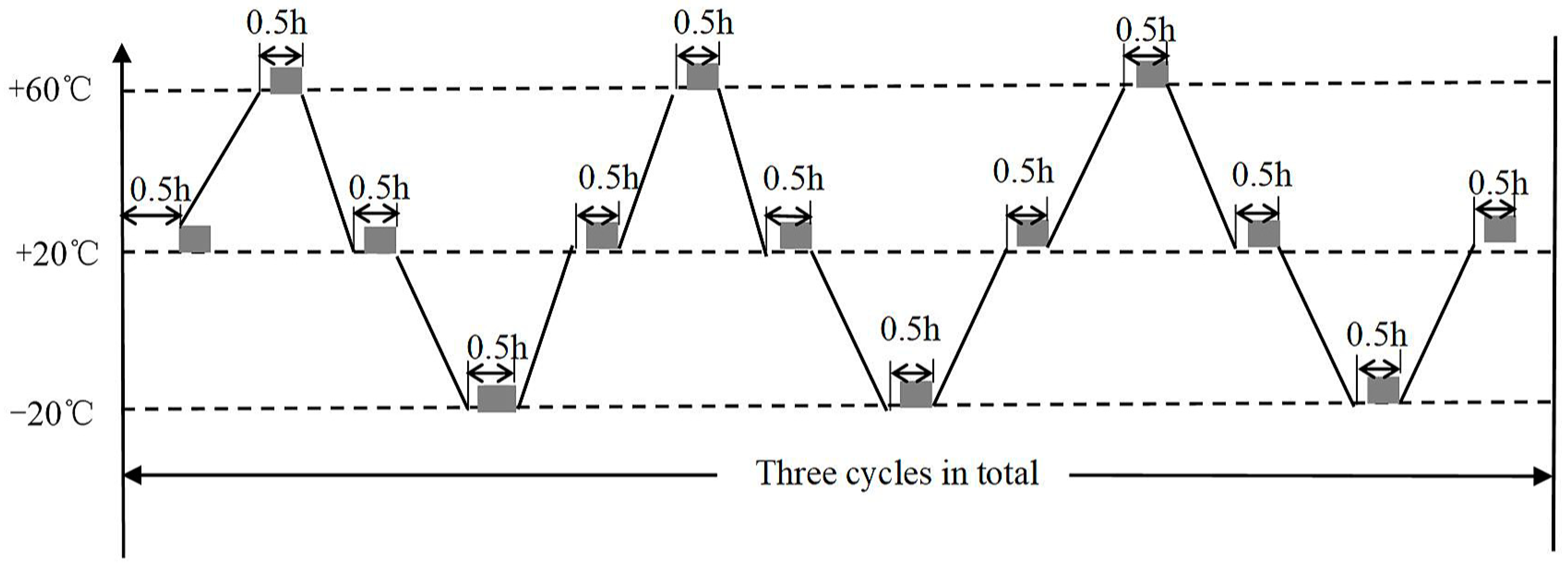
4. Experiment of SMC Structure under High and Low Temperatures
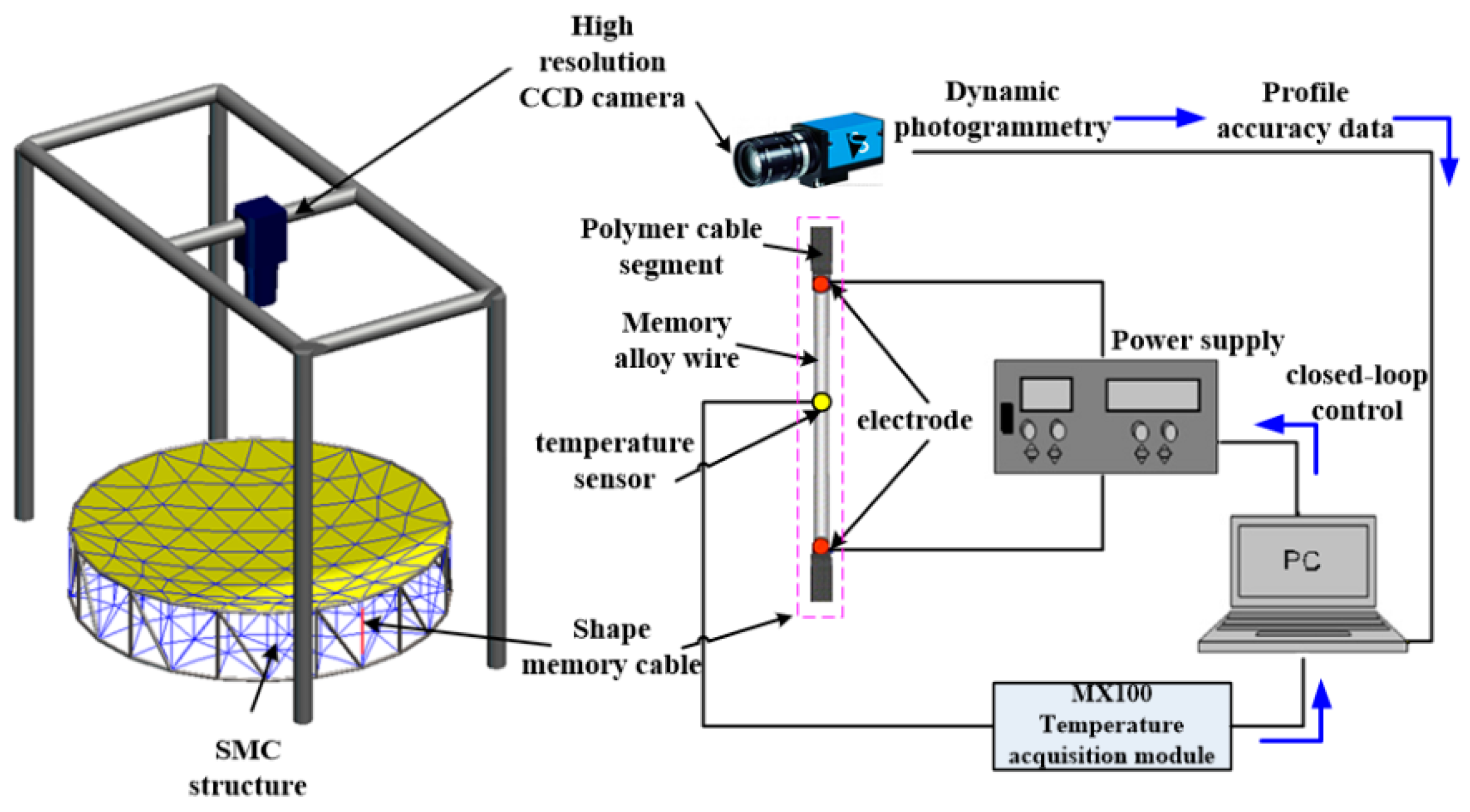
4.1. High and Low Temperature Experimental Scheme
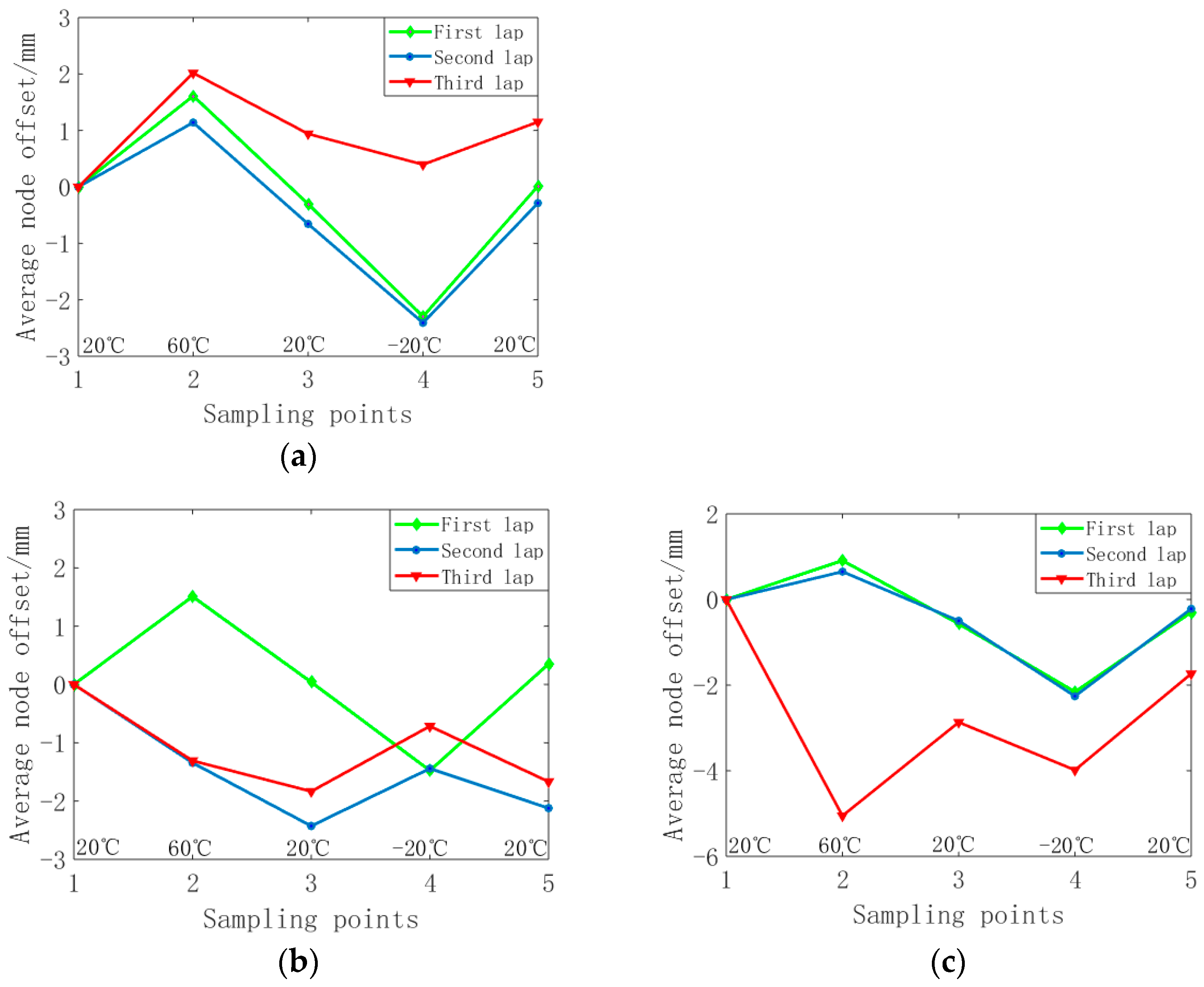
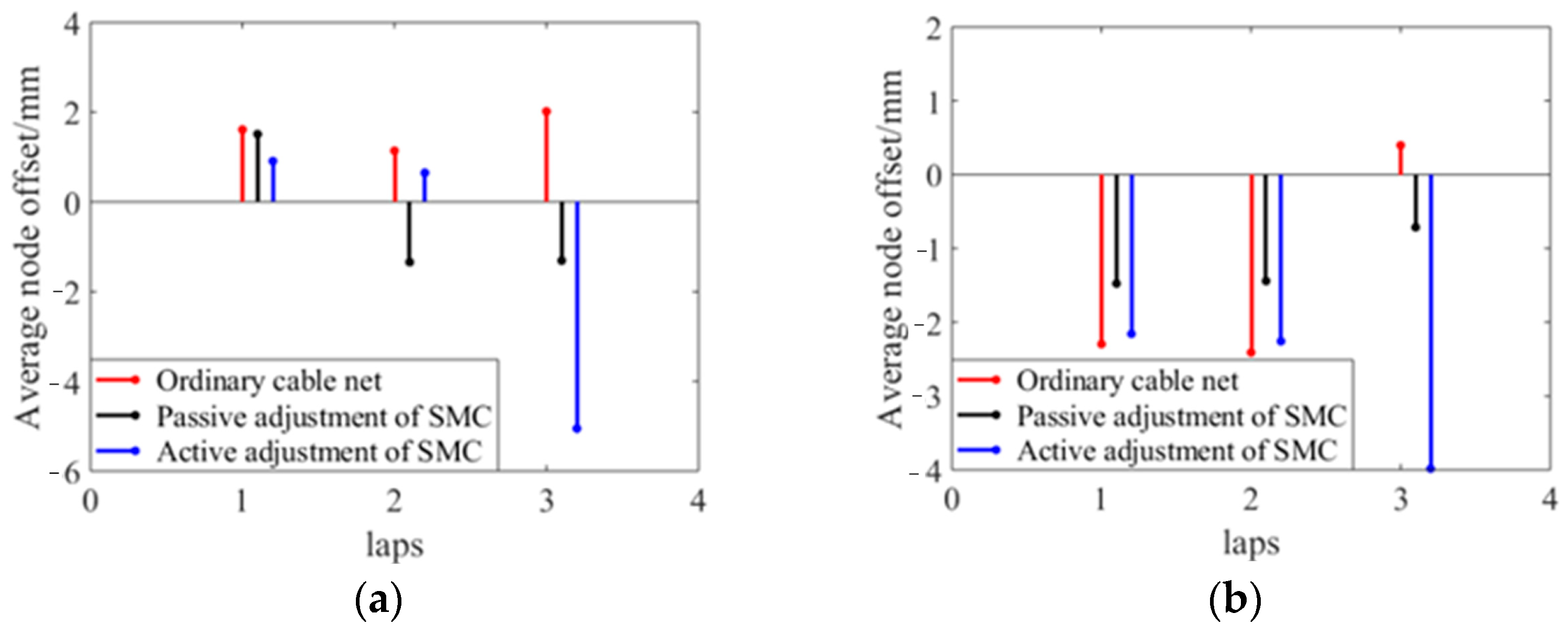
4.2. Analysis of Experimental Results
- (1)
- At 60 °C, the error of the reflective surface of the ordinary cable net increases obviously. Due to the creep effect of the high- and low-temperature environment on the polymer cable, the precision of the common cable net profile does not return to the initial state when the temperature cycle returns to 20 °C. Its surface accuracy increased from the initial 3.50 mm to 4.38 mm at most.
- (2)
- The surface accuracy of the shape memory cable net structure is relatively stable, and the variation is small when it is adjusted passively. The initial surface accuracy is 3.49 mm, and it becomes 3.36 mm at the end of a cycle.
- (3)
- When the shape memory cable net structure is actively adjusted, the surface accuracy is significantly improved at both 60 °C and −20 °C. The initial surface accuracy is 3.52 mm, which becomes 2.33 mm at 60 °C and 2.40 mm at −20 °C under active adjustment. The surface accuracy at the end of one cycle becomes 3.22 mm.
- (4)
- At 60 °C, compared to ordinary cable net structures, the passive adjustment improves the surface accuracy by 19.6%, while the active adjustment improves it by 44.4%. At −20 °C, compared to ordinary cable net structures, the passive adjustment improves the surface accuracy by 20.1%, while the active adjustment improves it by 45.2%.
5. Conclusions
- (1)
- The change in stress and strain during the phase transformation of the shape memory alloy wire can adjust the surface accuracy of the cable net structure.
- (2)
- In normal temperature and high- and low-temperature environments, the surface accuracy of the cable net structure has been improved through the adjustment of the shape memory alloy wire. Compared with ordinary cable net, at 60 °C and −20 °C, surface accuracy of SMC structure has improved by 44.4% and 45.2%, respectively.
- (3)
- Compared with passive adjustment, active adjustment has a larger adjustable amount of surface accuracy. The applicable temperature range is larger, but an external power supply is needed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Lian, P.Y.; Zhang, S.X.; Xiang, B.B.; Xu, Q. Effect of facet displacement on radiation field and its application for panel adjustment of large reflector antenna. CJME 2017, 30, 578–586. [Google Scholar] [CrossRef]
- Shively, J.; Miglionnico, C.; Roybal, R.; King, T.; Stein, C. Combined Effects of the Low-Earth-Orbit Environment on Polymeric Materianls. ASTM Spec. Tech. Publ. 1997, 1302, 20. [Google Scholar]
- Li, J.L.; Yan, S.Z. Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit. Appl. Therm. Eng. 2014, 71, 419–432. [Google Scholar] [CrossRef]
- Shen, Z.X.; Li, H.J.; Liu, X.N.; Hu, G.K. Thermal-structural dynamic analysis of a satellite antenna with the cable-network and hoop-truss supports. J. Therm. Stress. 2019, 42, 1339–1356. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.; Mei, Q.; Wang, Y.; Song, S.; Yu, F. On-orbit thermal deformation prediction for a high-resolution satellite camera. Appl. Therm. Eng. 2021, 195, 117152. [Google Scholar] [CrossRef]
- Du, J.; Bao, H.; Cui, C. Shape adjustment of cable mesh reflector antennas considering modeling uncertainties. Acta Astronaut. 2014, 97, 164–171. [Google Scholar] [CrossRef]
- Guo, W.; Li, Y.; Li, Y.-Z.; Tian, S.; Wang, S. Thermal–structural analysis of large deployable space antenna under extreme heat loads. J. Therm. Stress. 2016, 39, 887–905. [Google Scholar] [CrossRef]
- Yang, G.G.; Tang, A.F.; Yuan, Z.Y.; Yang, Z.; Li, S.; Li, Y. Surface shape stability design of mesh reflector antennas considering space thermal effects. IEEE Access 2020, 8, 89071–89083. [Google Scholar] [CrossRef]
- Nie, R.; He, B.Y.; Yan, S.Z.; Ma, X.F. Optimization design method for mesh reflector antennas considering the truss deformation and thermal effects. Eng. Struct. 2020, 208, 110253. [Google Scholar] [CrossRef]
- Nie, R.; He, B.Y.; Yan, S.Z.; Ma, X.F. Design optimazation of mesh antennas for on-orbit thermal effects. Int. J. Mech. Sci. 2020, 175, 105547. [Google Scholar] [CrossRef]
- Rodriguez NE, N.; Collado, M.; Cabas, R. New development mechanisms based on SMA technology for space Application. J. Mater. Eng. Perform. 2014, 23, 2712–2718. [Google Scholar]
- Godard, O.J.; Lagoudas, M.Z.; Lagoudas, D.C. Design of space systems using shape memory alloys. In Proceedings of the SPIE, Smart Structures and Materials, San Diego, CA, USA, 5 August 2003; Volume 5056, pp. 545–558. [Google Scholar]
- Webb, G.V.; Lagoudas, D.C.; Kurdila, A.J. Hysteresis modeling of SMA actuators for control applications. J. Intel. Mat. Syst. Str. 1998, 9, 432–448. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Shu, S.G. Residual deformation of active structures with SMA actuators. Int. J. Mech. Sci. 1999, 41, 595–619. [Google Scholar] [CrossRef]
- Yoon, H.S. Design, Modeling and Optimization of a Mechanically Reconfigurable Smart Reflector Antenna System. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2002. [Google Scholar]
- Saravanan, U.; Sivakumar, S.M.; Kalyanaraman, V. A study on the design and behavior of smart antenna. Smart Mater. Struct. 2001, 10, 580–598. [Google Scholar] [CrossRef]
- Peng, F.; Jiang, X.X.; Hu, Y.R.; Ng, A. Actuation precision control of SMA actuators used for shape control of inflatable SAR antenna. Acta Astronaut. 2008, 63, 578–585. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E. SMAs for aerospace, recent developments, and new applications: A short review. Materials 2020, 13, 1856. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Zhao, H.; Luo, X.D.; Huang, Z.Y. Membrane-constrained acoustic metamaterials for low frequency sound insulation. APL 2016, 108, 041905. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.; Sarsen, A.; Alu, A. Angular Memory of Photonic Metasurfaces. IEEE Trans. Antennas Propag. 2021, 69, 7720–7728. [Google Scholar] [CrossRef]
- Marinopoulou, E.; Katakalos, K. Thermomechanical Fatigue Testing on Fe-Mn-Si Shape Memory Alloys in Prestress Conditions. Materials 2022, 16, 237. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.W.; Li, T.; Cao, Y. Active shape adjustment of cable net structures with PZT actuators. Aerosp. Sci. Technol. 2013, 26, 160–168. [Google Scholar] [CrossRef]
- Song, X.S.; Tan, S.J.; Wang, E.M.; Wu, S.; Wu, Z. Active shape control of an antenna reflector using piezoelectric actuators. J. Intell. Mater. Syst. Struct. 2019, 30, 2733–2747. [Google Scholar] [CrossRef]
- Jiang, X.J.; Pan, F.Q.; Fan, Y.S.; Zhu, M.B.; Chen, Z. Active adjustment of surface accuracy for a large cable-net structure by SMA. Materials 2019, 12, 2619. [Google Scholar] [CrossRef] [PubMed]
- Pan, F.Q.; Jiang, X.J.; Dong, X.K.; Du, J.L.; Wang, Y.P. Optimization design of surface accuracy of SMC structure driven by space thermal radiation. J. Intell. Mater. Syst. Struct. 2023, 34, 279–291. [Google Scholar] [CrossRef]
- Furuya, H.; Haftka, R.T. Static shape control of space trusses with partial measurements. J. Spacecr. Rocket. 1995, 32, 856–865. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of SMAs: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]




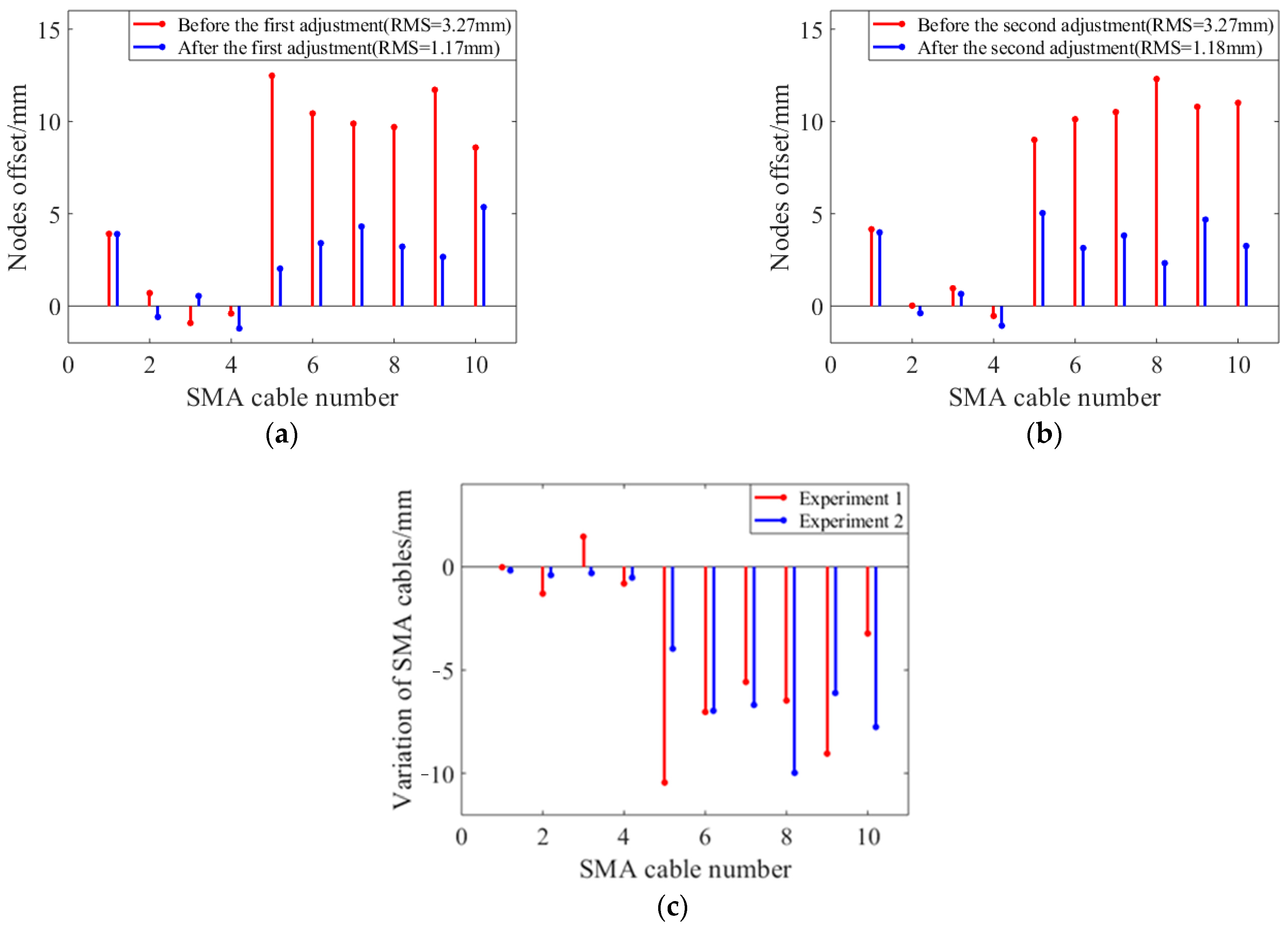
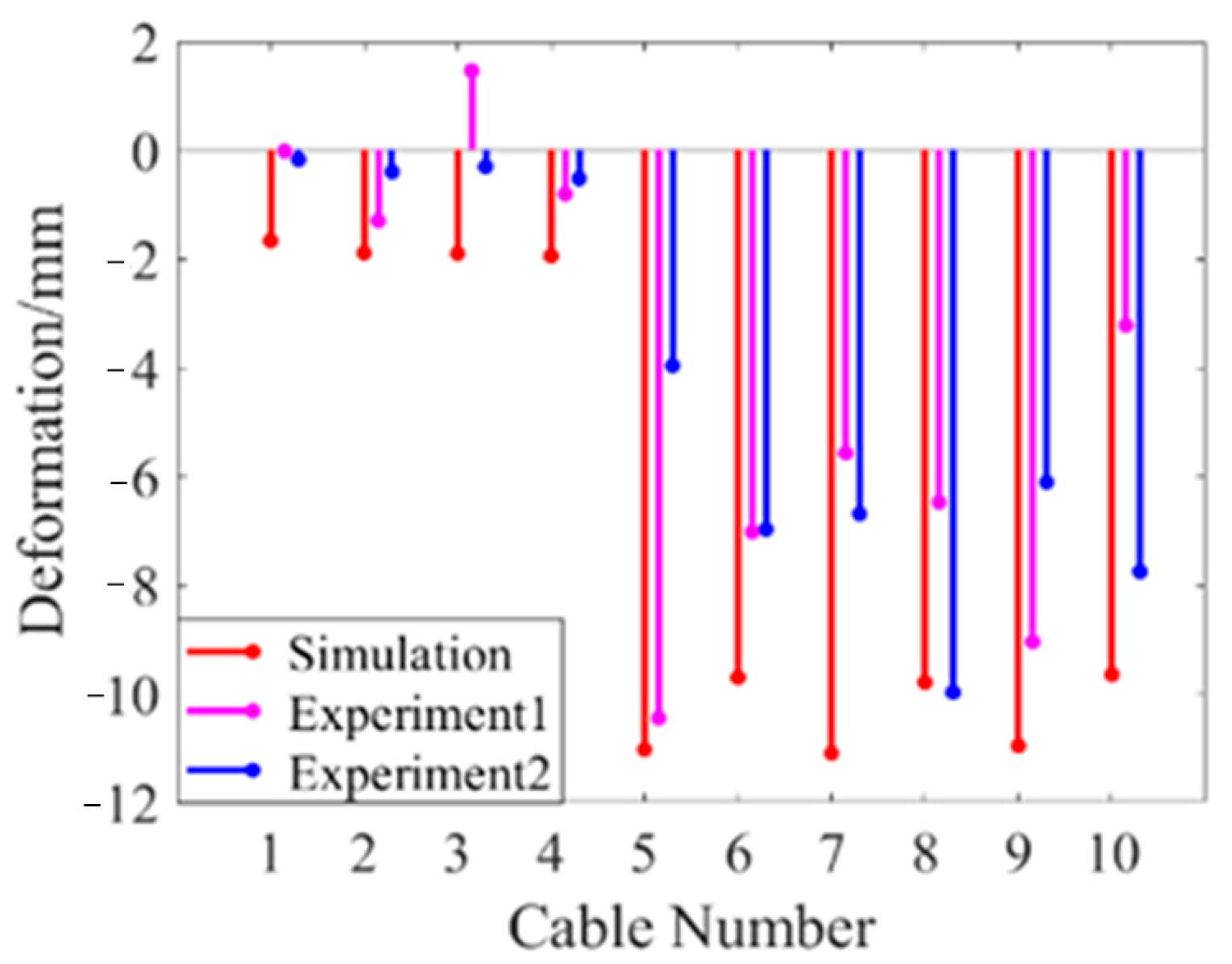
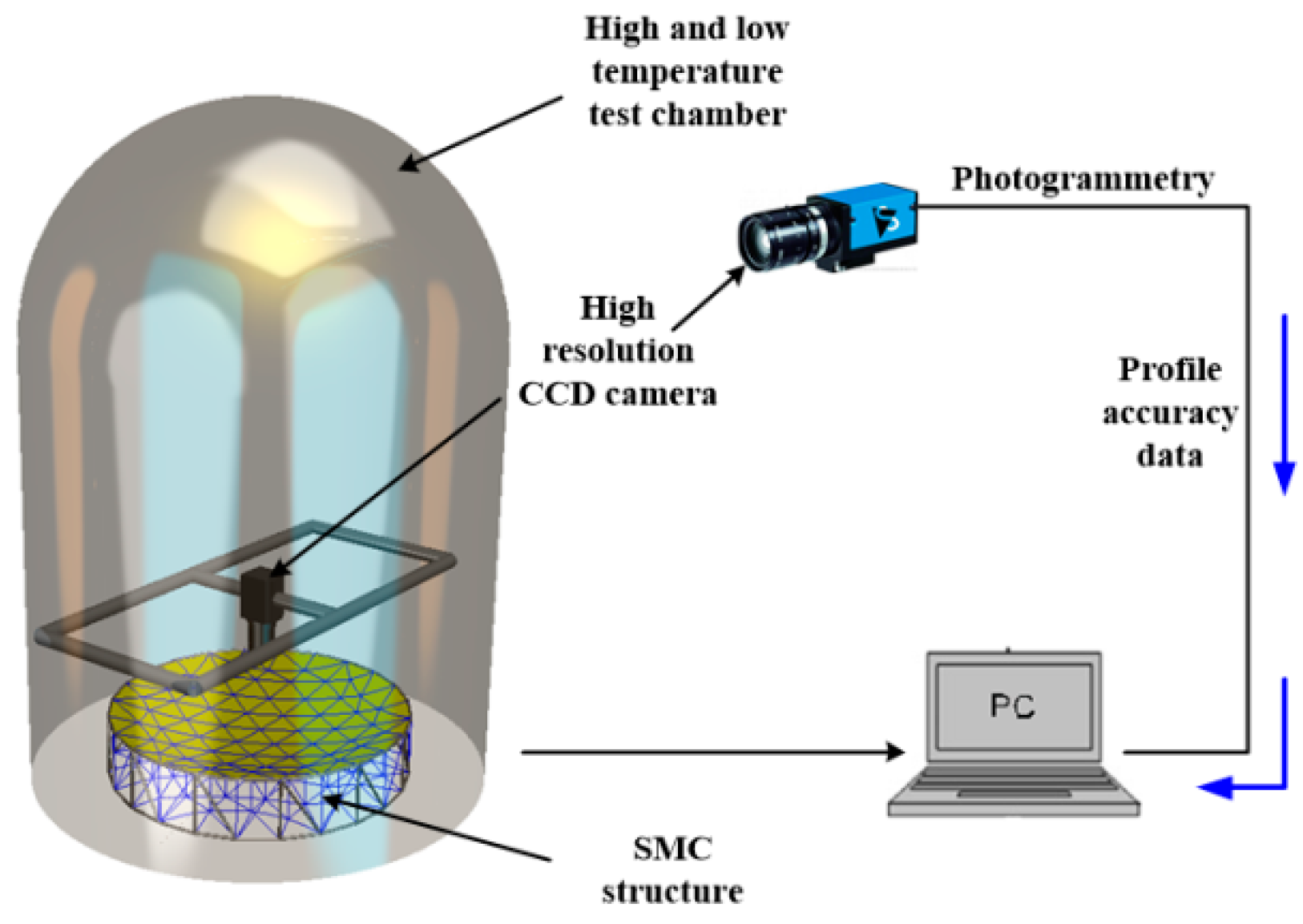


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| /°C | 28 | /°C | 47 |
| /°C | 6 | /°C | 62 |
| /GPa | 16.98 | /GPa | 45.32 |
| /MPa/°C | 8.14 | /MPa/°C | 11.27 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Diameter/mm | 2200 | Elastic modulus of polymer cables/GPa | 20 |
| Number of polymer cables | 88 | Diameter of polymer cables/mm | 1 |
| Number of free nodes | 20 | Number of SMA cables | 10 |
| Number of fixed nodes | 24 | Diameter of SMA cables/mm | 0.25 |
| Items | Initial RMS/mm | Optimized RMS/mm | Initial Average Deviation/mm | Optimized Average Deviation/mm |
|---|---|---|---|---|
| Simulation | 3.278 | 1.177 | 6.764 | 1.948 |
| Experiment 1 | 3.275 | 1.170 | 6.607 | 2.358 |
| Experiment 2 | 3.273 | 1.181 | 6.831 | 2.542 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, F.; Jiang, X.; Du, J.; Liu, J.; Fan, Y.; Zou, W. Shape Adjustment and Experimental Study of a Shape Memory Cable (SMC) Structure. Materials 2023, 16, 3476. https://doi.org/10.3390/ma16093476
Pan F, Jiang X, Du J, Liu J, Fan Y, Zou W. Shape Adjustment and Experimental Study of a Shape Memory Cable (SMC) Structure. Materials. 2023; 16(9):3476. https://doi.org/10.3390/ma16093476
Chicago/Turabian StylePan, Fengqun, Xiangjun Jiang, Jingli Du, Jia Liu, Yesen Fan, and Wusong Zou. 2023. "Shape Adjustment and Experimental Study of a Shape Memory Cable (SMC) Structure" Materials 16, no. 9: 3476. https://doi.org/10.3390/ma16093476
APA StylePan, F., Jiang, X., Du, J., Liu, J., Fan, Y., & Zou, W. (2023). Shape Adjustment and Experimental Study of a Shape Memory Cable (SMC) Structure. Materials, 16(9), 3476. https://doi.org/10.3390/ma16093476







