Determining the Hot Workability and Microstructural Evolution of an Fe-Cr-Mo-Mn Steel Using 3D Processing Maps
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Flow Characteristics and Deformation Mechanisms of Fe-Cr-Mo-Mn Steel
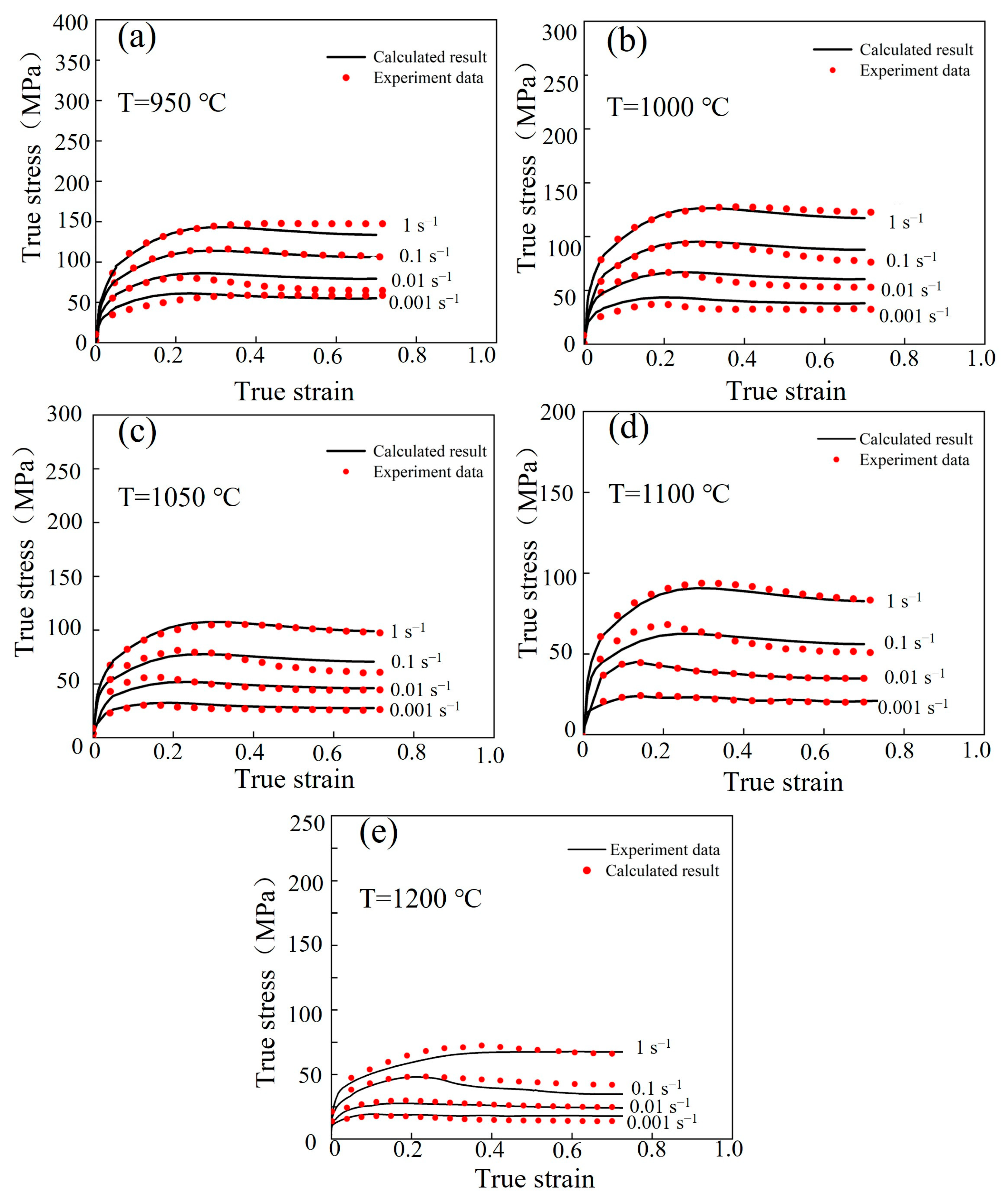
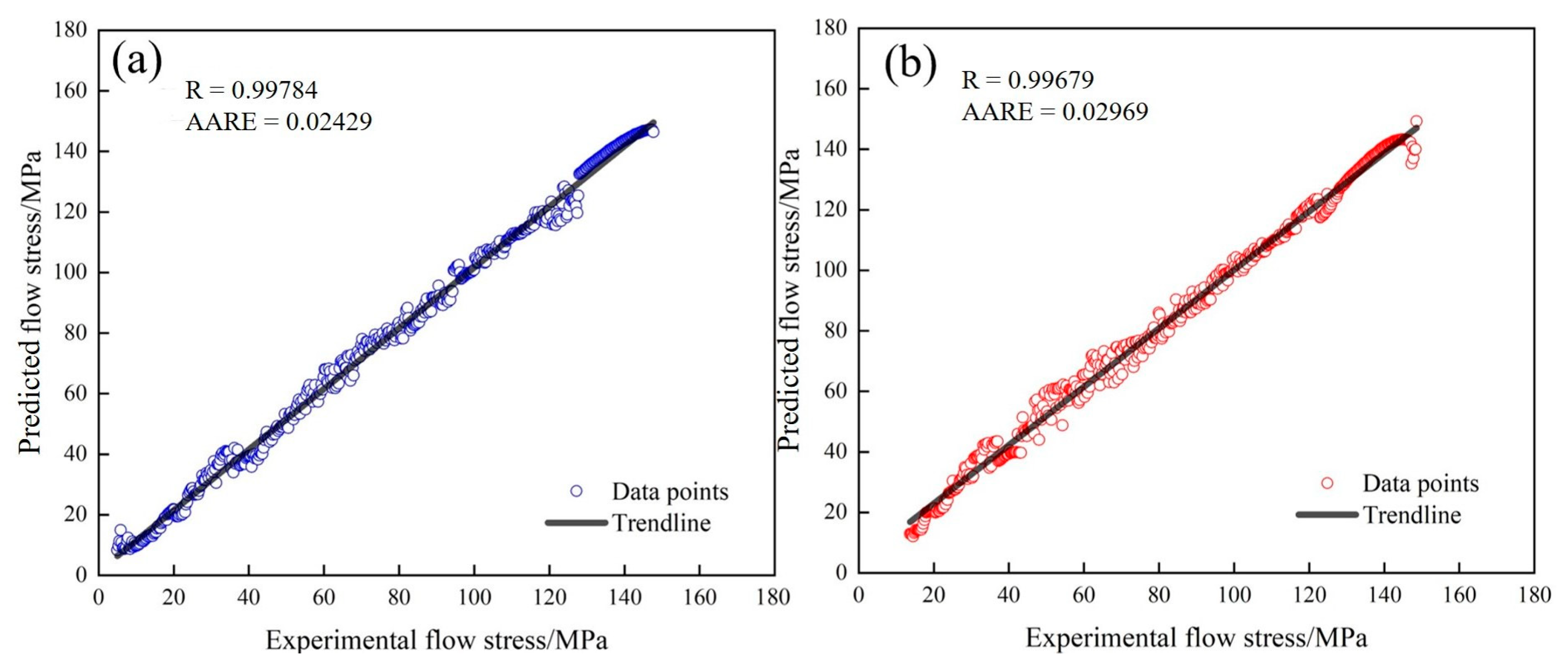
3.2. Construction of the Arrhenius Model
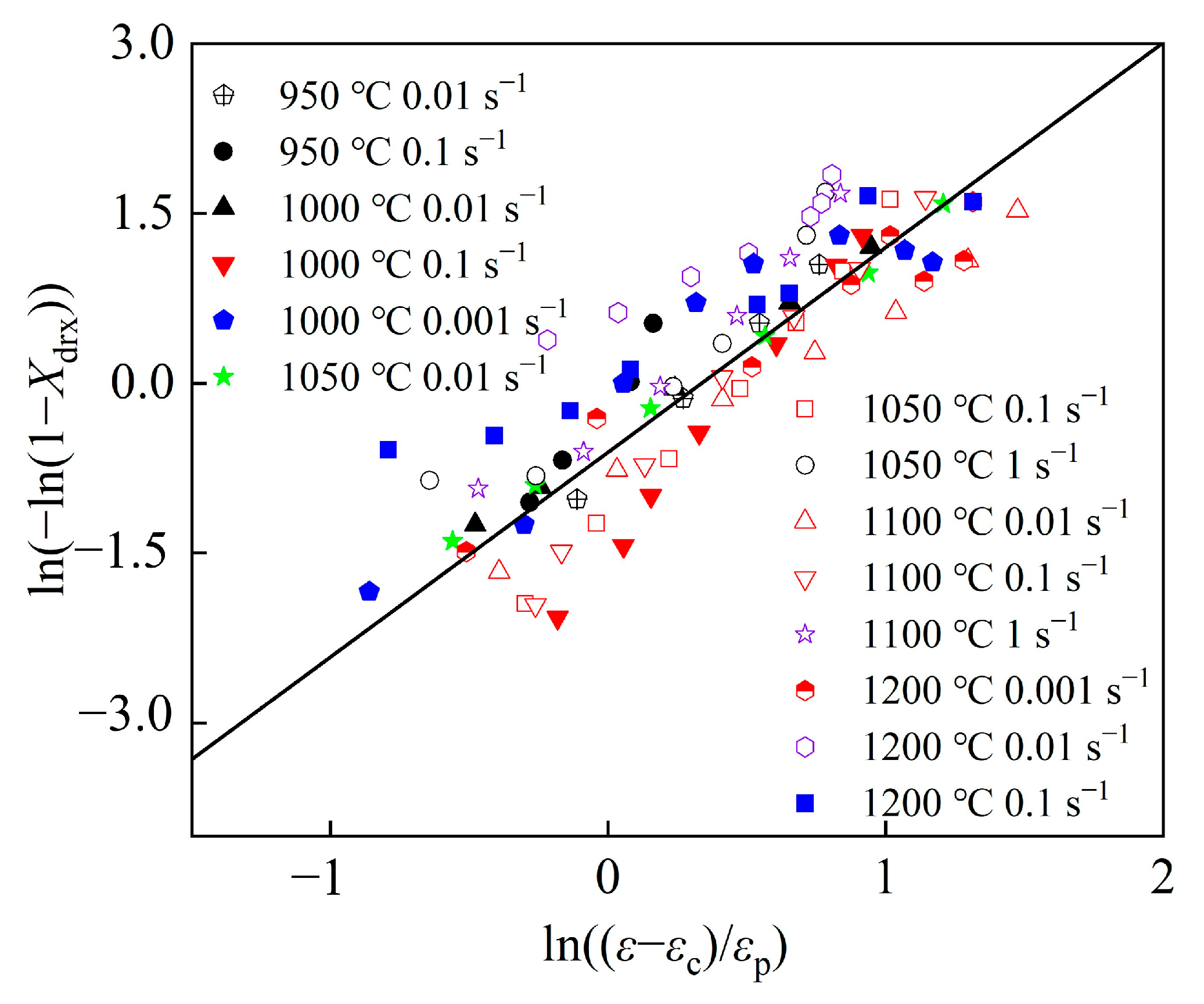
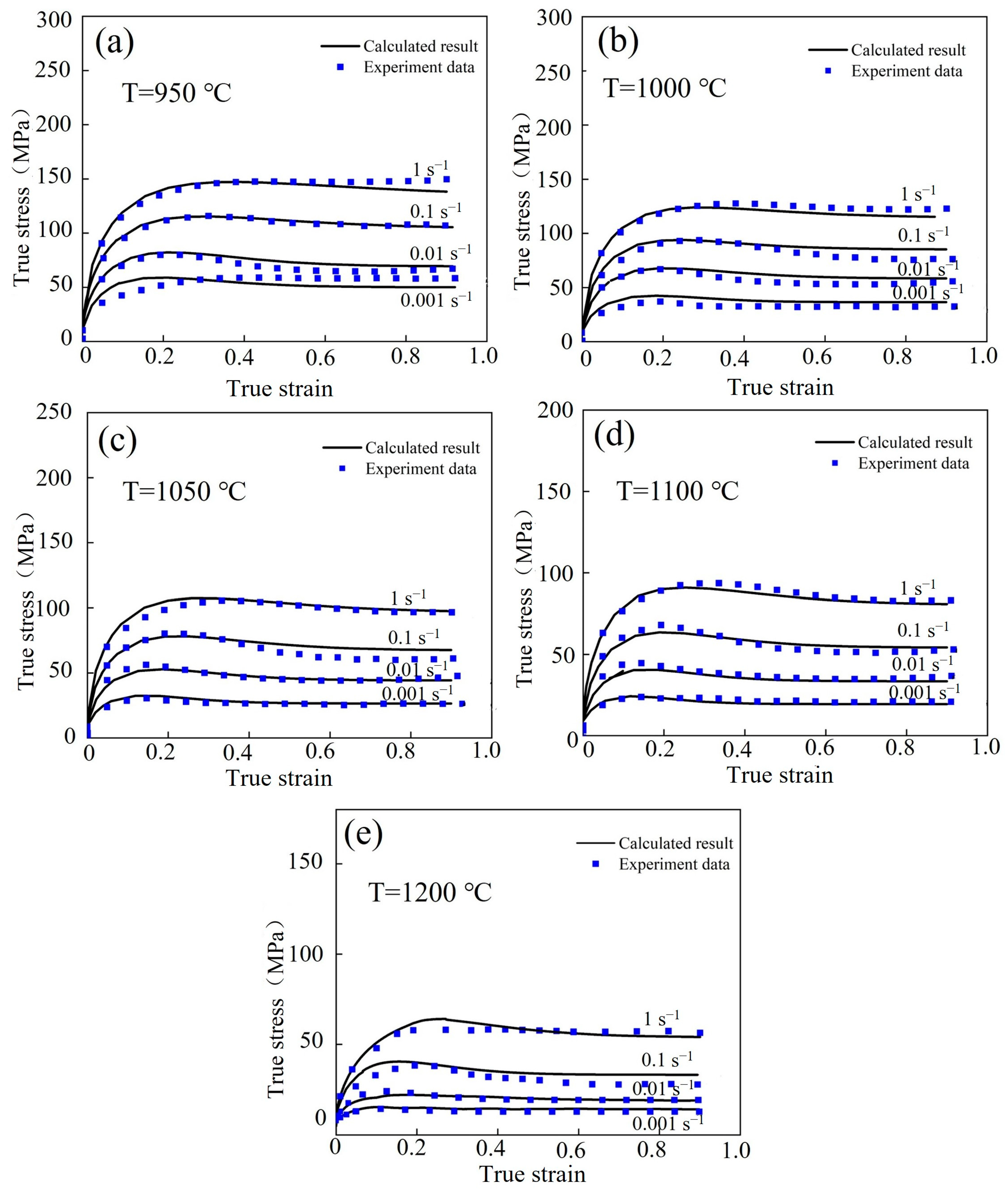
3.3. Construction of the Laasraoui Segmented and DRX Models
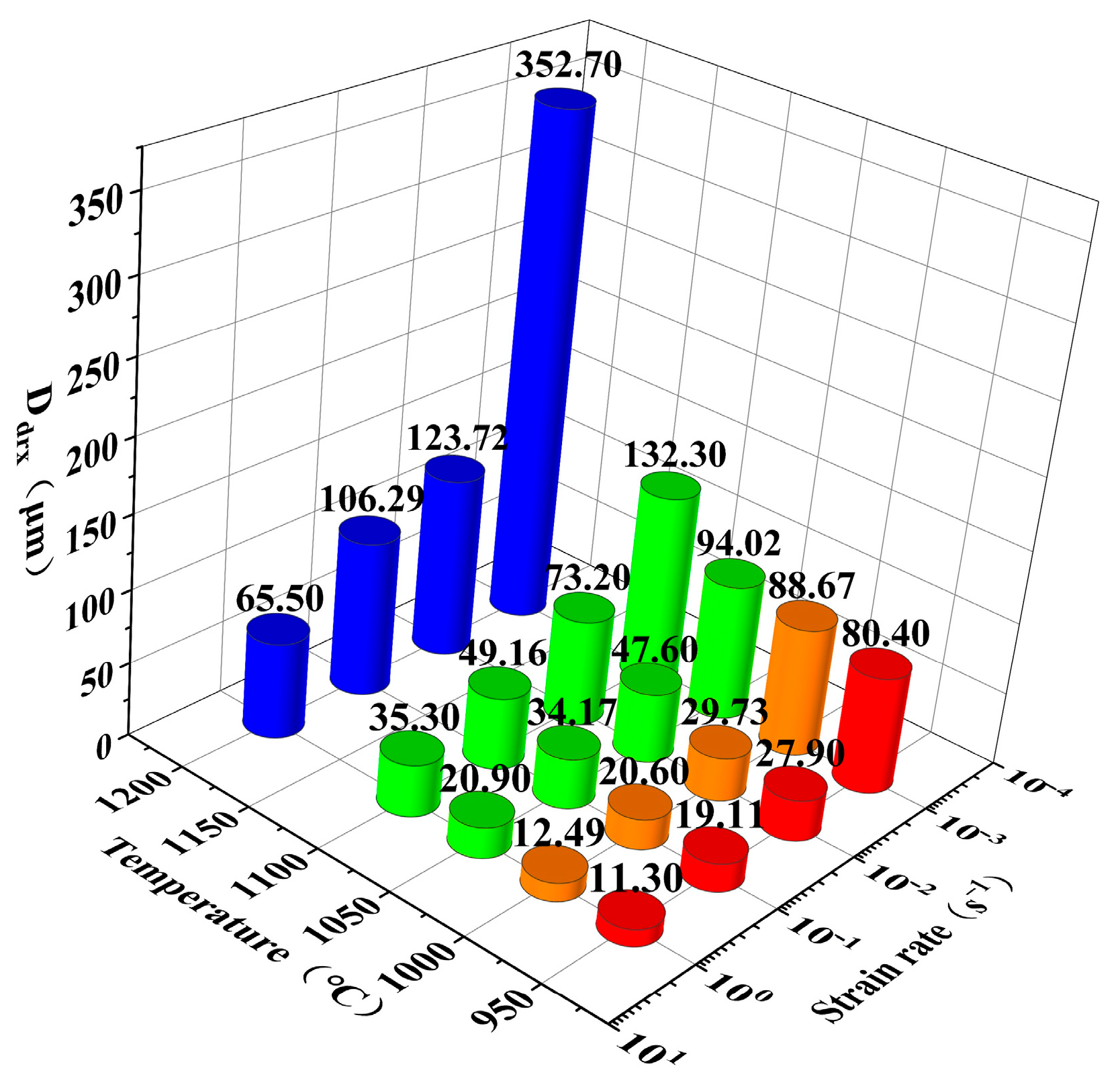
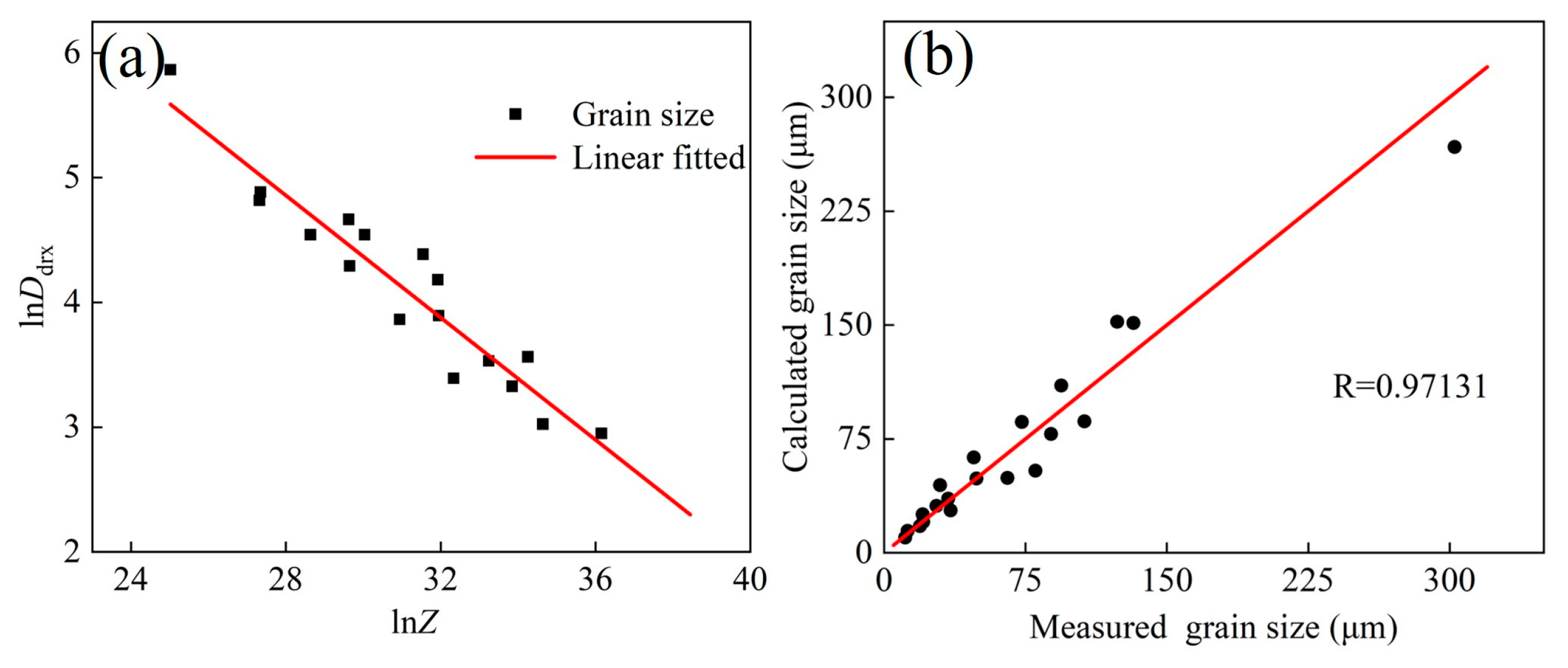
3.4. Grain Size Prediction Model
3.5. Construction of the HPMs
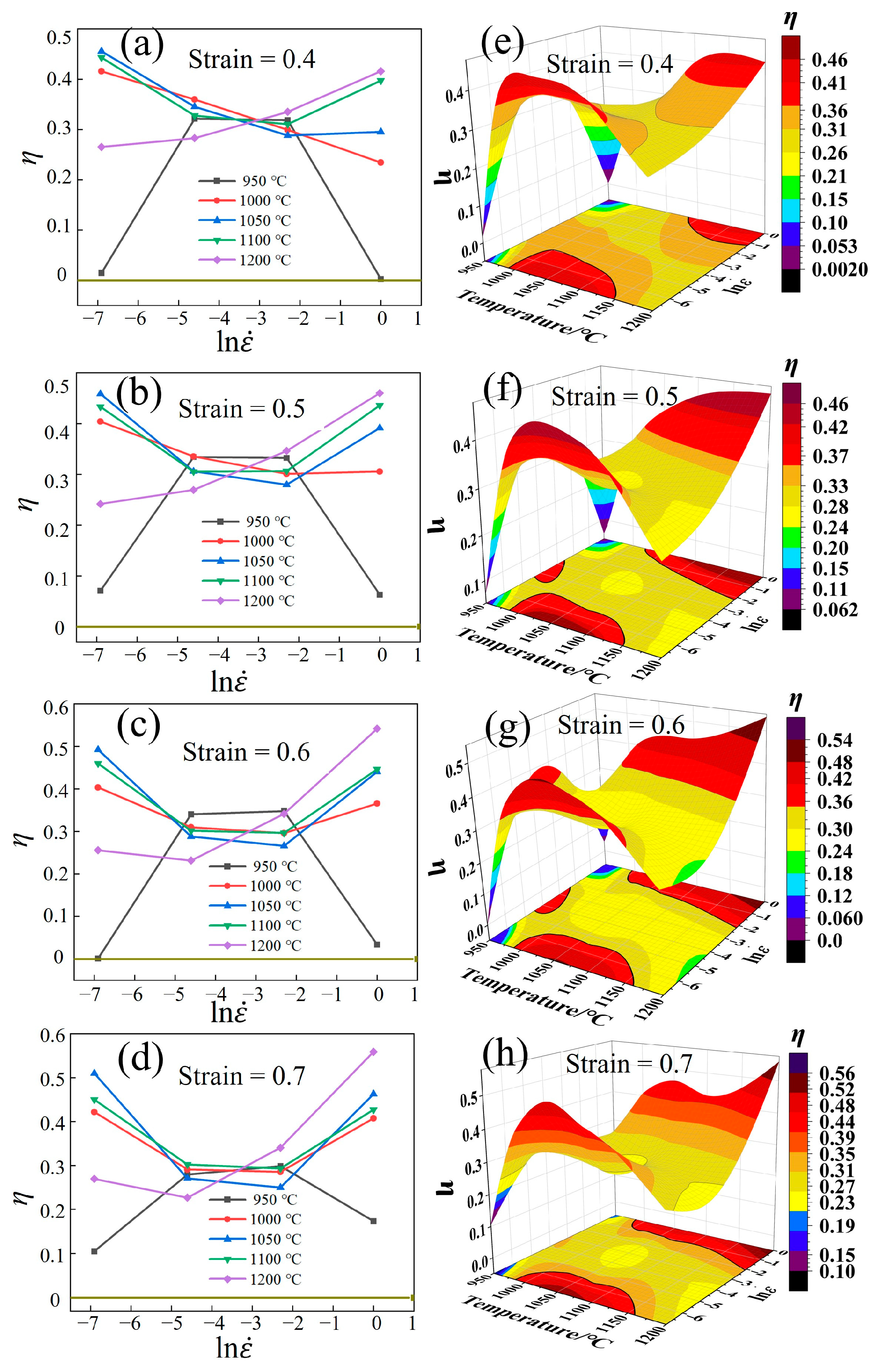
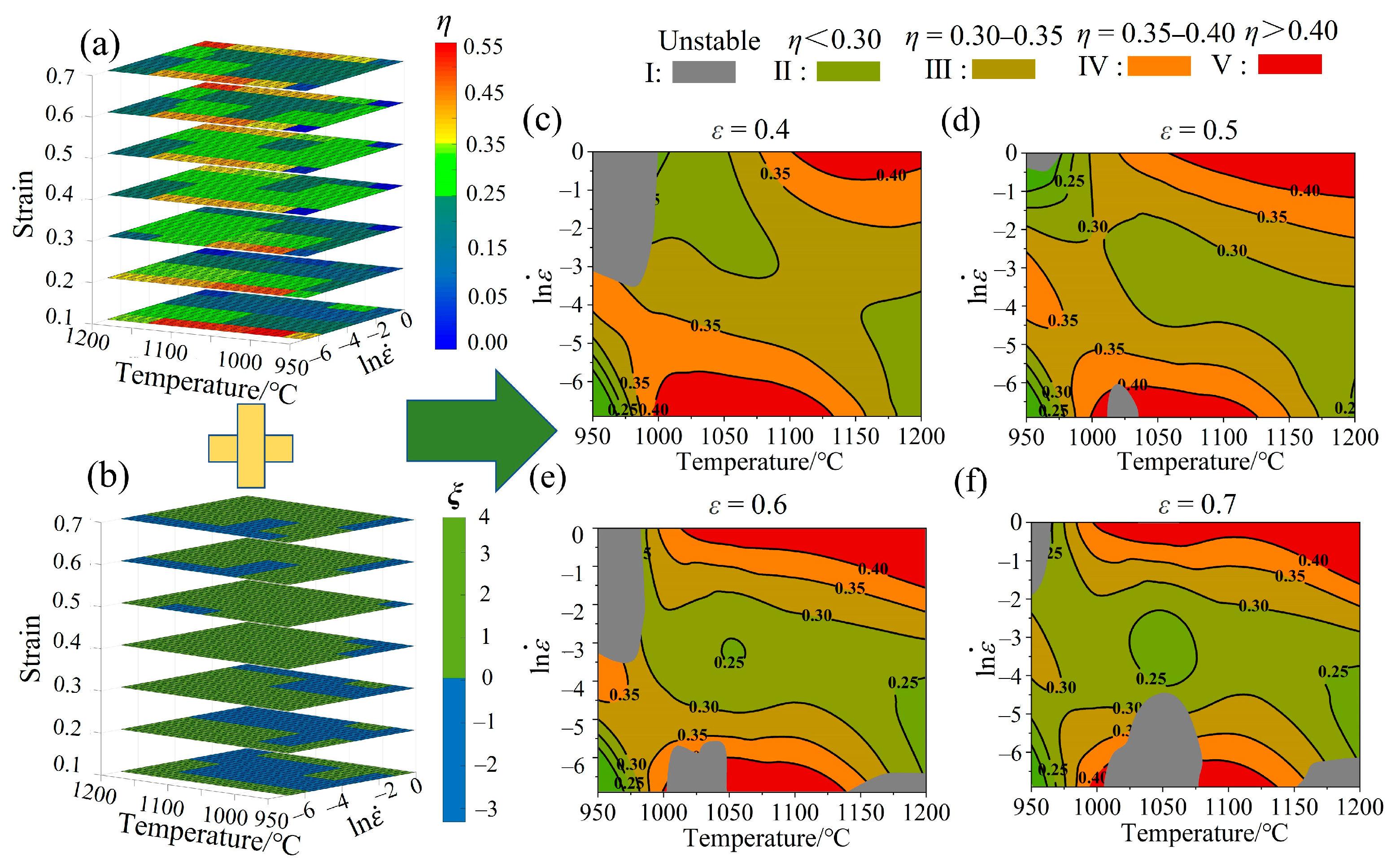
3.5.1. Power Dissipation Efficiency Maps
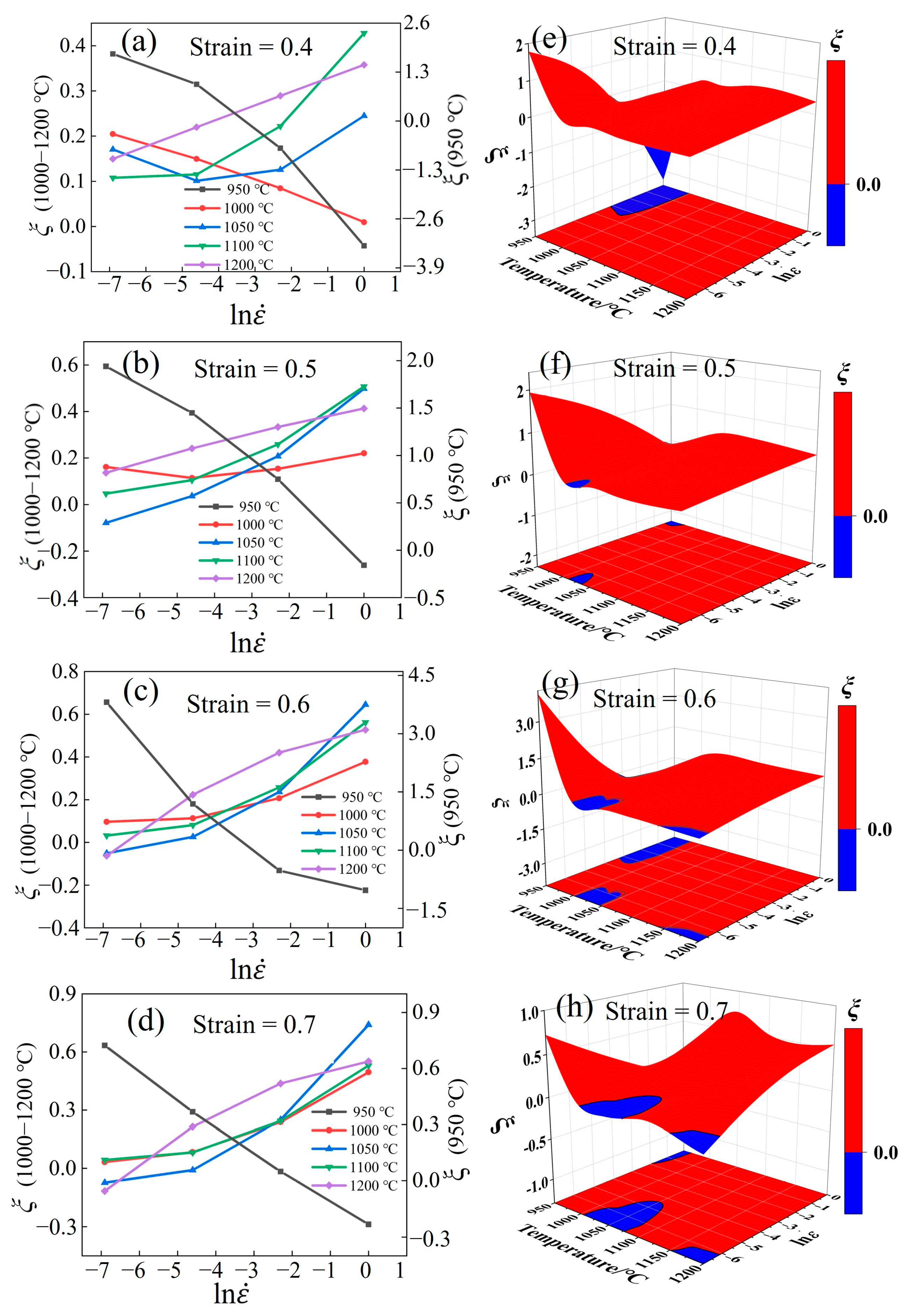
3.5.2. Instability Maps
3.5.3. Analysis of HPMs
3.6. Analysis and Discussion
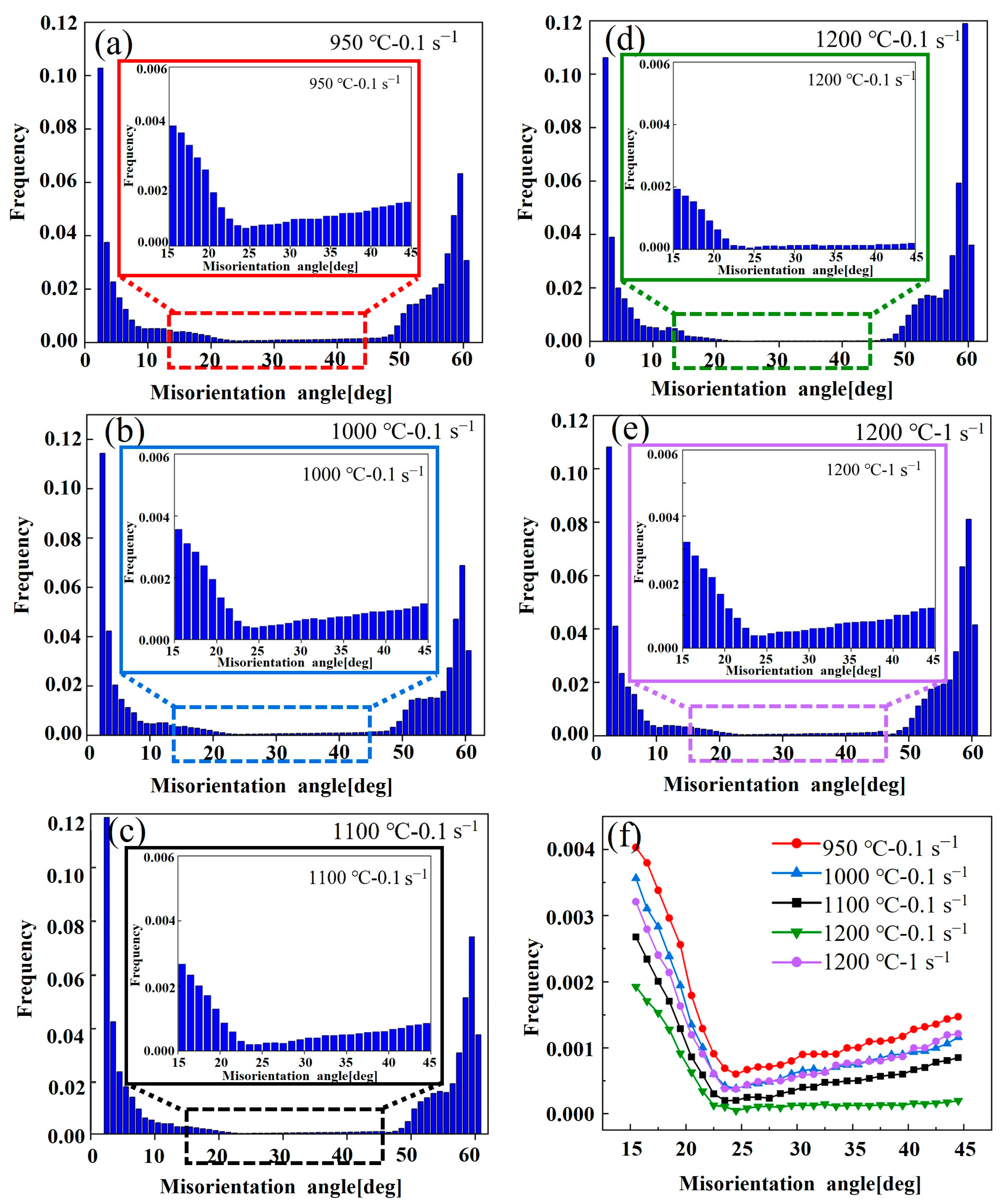
3.6.1. Effect of Hot Deformation on High-Temperature Microstructure
3.6.2. Effect of Hot Deformation Behavior on Quenched Structure
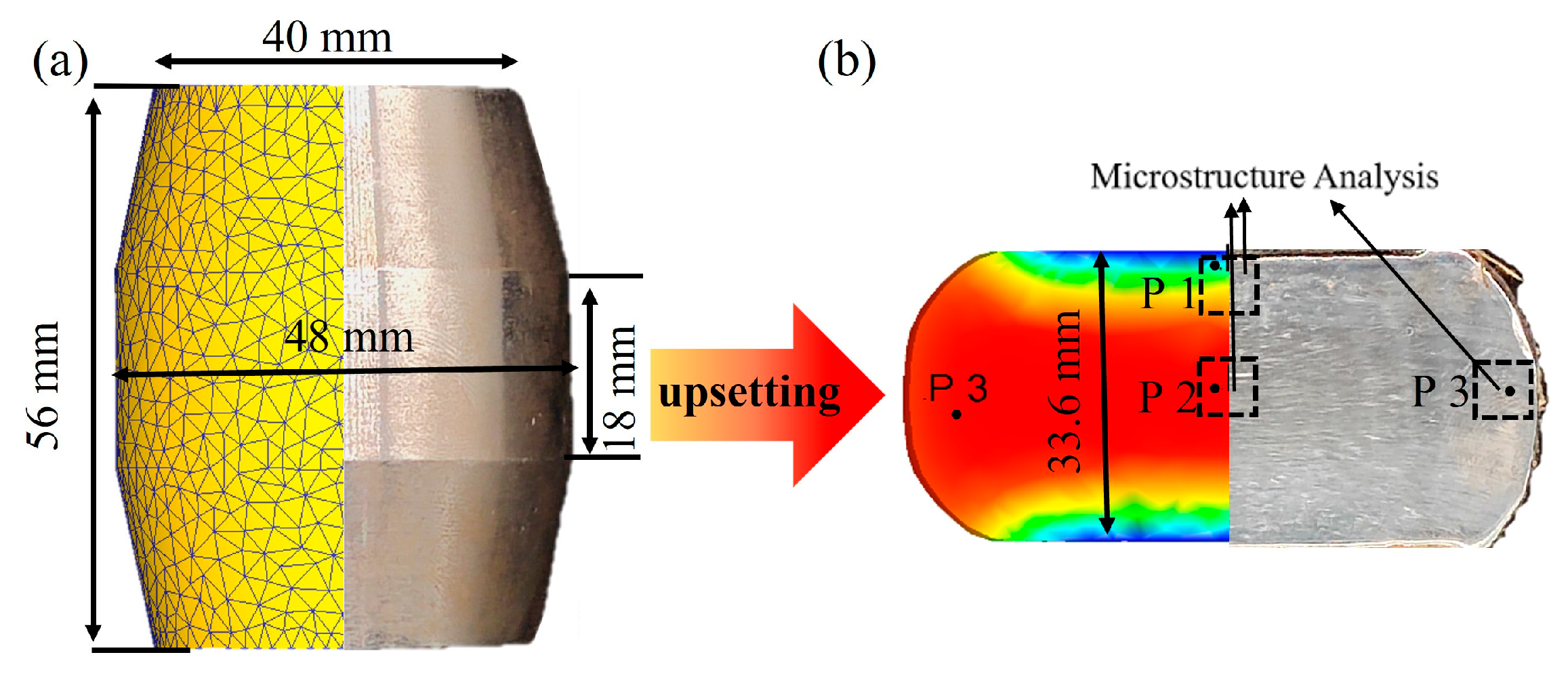
4. Upsetting Experiment of Imitation Hammer Shaped Parts
4.1. Simulation Model
4.2. Numerical Simulation
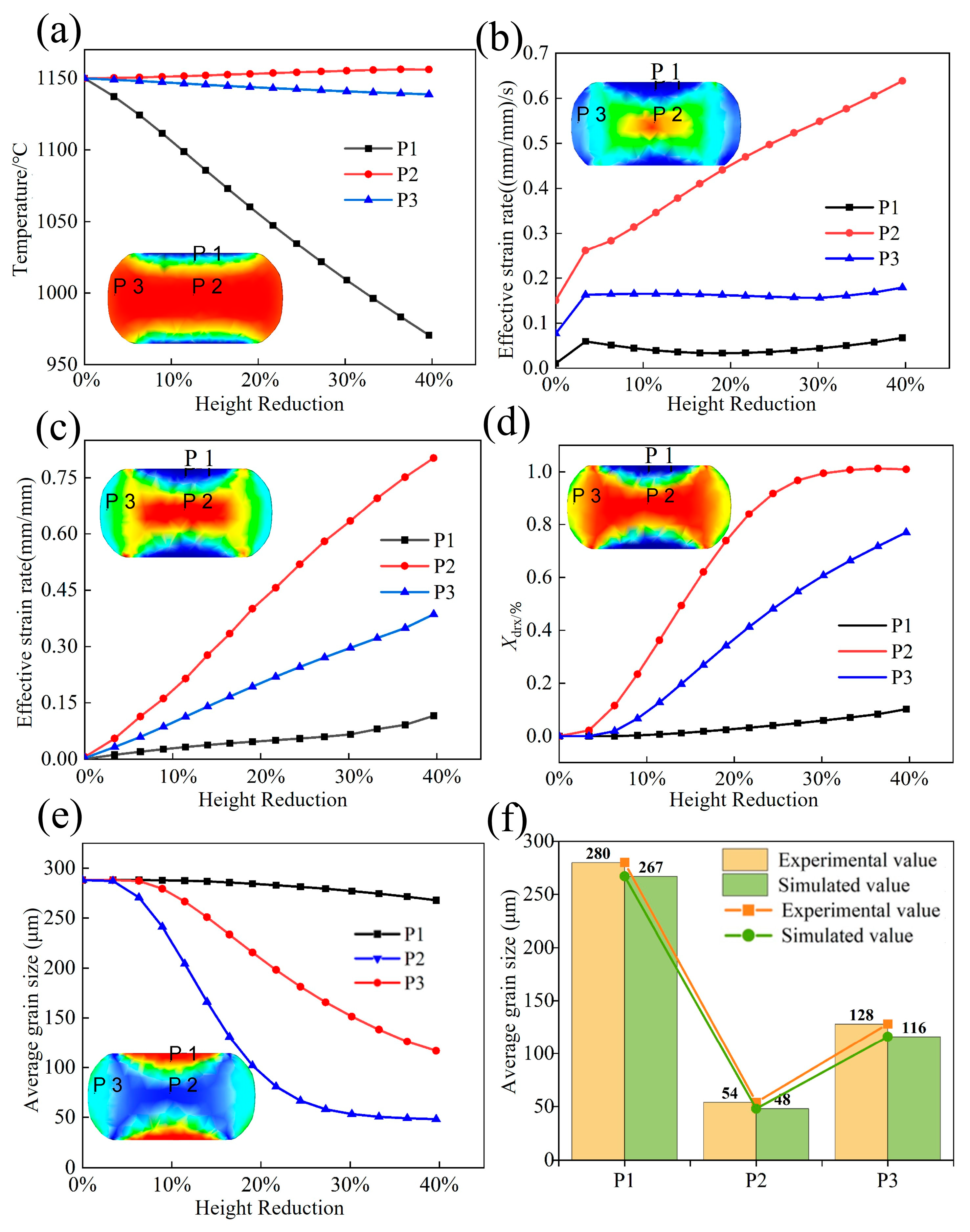
4.3. Result Analysis
5. Conclusions
- (1)
- As the deformation temperature decreased or the strain rate increased, the grain size and Xdrx of the Fe-Cr-Mo-Mn steel gradually decreased, while the flow stress gradually increased. Highly precise Laasraoui segmented and Arrhenius models were established, and the correlation coefficient R of each was as high at 0.99784 and 0.99679. Moreover, DRX and average grain size models were developed.
- (2)
- The substructure introduced by the austenite deformation could inhibit the formation of multi-stage martensite. With the increase in temperature or strain rate, the structure of martensite evolved from single-stage to multistage with order transformation. In the optimum processing region, the mixture microstructure composed by complete DRX and multistage martensitic enhance the hot deformation capability of the material.
- (3)
- The optimal processing parameters for the Fe-Cr-Mo-Mn steel were determined: a temperature range of 1050–1200 °C and a strain rate range of 0.369–1 s−1. The secondary development Laasraoui segmented model and the microstructure evolution model were embedded into the Deform-3D subroutine to verify the result of the upsetting experiment. The accuracy of the models was demonstrated, providing a robust theoretical foundation for the hot forging processes of the Fe-Cr-Mo-Mn steel.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Areitioaurtena, M.; Segurajauregi, U.; Fisk, M.; Cabello, M.J.; Ukar, E. Numerical and experimental investigation of residual stresses during the induction hardening of 42CrMo4 steel. Eur. J. Mech. A-Solid. 2022, 96, 104766. [Google Scholar] [CrossRef]
- Chen, M.S.; Yuan, W.Q.; Lin, Y.C.; Li, H.B.; Zou, Z.H. Modeling and Simulation of Dynamic Recrystallization Behavior for 42CrMo Steel by an Extended Cellular Automaton Method. Vacuum 2017, 146, 142–151. [Google Scholar] [CrossRef]
- Quan, G.; Zhao, L.; Chen, T.; Wang, Y.; Mao, Y.; Lv, W.; Zhou, J. Identification for the Optimal Working Parameters of As-Extruded 42CrMo High-Strength Steel from a Large Range of Strain. Strain Rate and Temperature. Mater. Sci. Eng. A 2012, 538, 364–373. [Google Scholar] [CrossRef]
- Guo, L.; Wang, F.; Zhen, P.; Li, X.; Zhan, M. A Novel Unified Model Predicting Flow Stress and Grain Size Evolutions during Hot Working of Non-Uniform as-Cast 42CrMo Billets. Chin. J. Aeronaut. 2019, 32, 531–545. [Google Scholar] [CrossRef]
- Deng, Z.; Wen, T.; You, J.; Du, K.; Sun, L. Manufacturing of Ultra-Large Plate Forgings by Unfolding and Flattening of Thick Cylinders. J. Cent. South Univ. 2020, 27, 2227–2238. [Google Scholar] [CrossRef]
- Brunner, C.; Deac, G.; Braun, S.; Zöphel, C. The Future Need for Flexibility and the Impact of Fluctuating Renewable Power Generation. Renew. Energy 2020, 149, 1314–1324. [Google Scholar] [CrossRef]
- Ogidi, O.O.; Khan, A.; Dehnavifard, H. Deployment of onshore wind turbine generator topologies: Opportunities and challenges. Int. Trans. Electr. Energy Syst. 2020, 30, 12308. [Google Scholar] [CrossRef]
- Feng, K.; Huang, X.; Wang, R.; Xue, W.; Fu, Y.; Li, Z. The Research on Recrystallization Behaviors and Mechanism of a Medium-Density Ni-Based Alloy. Metals 2022, 12, 137. [Google Scholar] [CrossRef]
- Dolzhenko, P.; Tikhonova, M.; Kaibyshev, R.; Belyakov, A. Dynamically Recrystallized Microstructures, Textures, and Tensile Properties of a Hot Worked High-Mn Steel. Metals 2019, 9, 30. [Google Scholar] [CrossRef]
- Sasaki, S.; Katsumura, T.; Ota, H. Effect of Thermal History on Hot Workability of Fe–Cr Multiphase Steel during Hot Working. Mater. Trans. 2021, 62, 177–184. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, Q.; Wei, Z.; Lin, B.; Jing, Y.; Shi, Y.; Misra, R.D.K.; Li, J. Hot Deformation Behaviors of AZ91 Magnesium Alloy: Constitutive Equation, ANN-Based Prediction, Processing Map and Microstructure Evolution. J. Alloys Compd. 2022, 908, 164580. [Google Scholar]
- Yu, J.; Li, Z.; Qian, C.; Huang, S.; Xiao, H. Investigation of Deformation Behavior, Microstructure Evolution, and Hot Processing Map of a New near-α Ti Alloy. J. Mater. Res. Technol. 2023, 23, 2275–2287. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, R.; Li, D.; Peng, Y.; Zhou, G.; Jia, Z.; Ma, W. Investigation on deformation behaviors and dynamic recrystallization mechanism of spray formed Al–Zn–Mg–Cu alloy under hot compression. J. Mater. Res. Technol. 2024, 28, 4401–4416. [Google Scholar] [CrossRef]
- Li, J.; Wu, X.; Cao, L.; Liao, B.; Wang, Y.; Liu, Q. Hot Deformation and Dynamic Recrystallization in Al-Mg-Si Alloy. Mater. Charact. 2021, 173, 110976. [Google Scholar] [CrossRef]
- Yi, H.; Ding, J.; Ni, C.; Dai, J.; Tang, Y.; Chen, X.; Song, K.; Xia, X. Hot Compression Deformation Behavior and Processing Maps of Al–0.5Mg–0.4Si–0.1Cu Alloy. J. Mater. Res. Technol. 2022, 19, 4890–4904. [Google Scholar] [CrossRef]
- Zhang, J.B.; Wu, C.J.; Peng, Y.Y.; Xia, X.C.; Li, J.G.; Ding, J.; Liu, C.; Chen, X.G.; Dong, J.; Liu, Y.C. Hot compression deformation behavior and processing maps of ATI 718Plus superalloy. J. Alloys Compd. 2020, 835, 155195. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, Y.; Xie, Q.; Li, D.; Gao, N. Mechanical Properties and Dynamic Constitutive Model of 42CrMo Steel. Mater. Des. 2017, 119, 171–179. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhao, S.D.; Fan, S.Q.; Zhong, B. Plastic Properties and Constitutive Equations of 42CrMo Steel during Warm Forming Process. Mater. Sci. Technol. 2014, 30, 645–652. [Google Scholar] [CrossRef]
- Quan, G.; Liang, J.; Lv, W.; Wu, D.; Liu, Y.; Luo, G.; Zhou, J. A Characterization for the Constitutive Relationships of 42CrMo High Strength Steel by Artificial Neural Network and Its Application in Isothermal Deformation. Mat. Res. 2014, 17, 1102–1114. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chen, M.-S.; Zhang, J. Modeling of Flow Stress of 42CrMo Steel under Hot Compression. Mater. Sci. Eng. A 2009, 499, 88–92. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, Y.; Byon, S.M. Study on Constitutive Relation of AISI 4140 Steel Subject to Large Strain at Elevated Temperatures. J. Mater. Process. Technol. 2003, 140, 84–89. [Google Scholar] [CrossRef]
- Qi, M.; Wu, H.; Dong, Y.; Du, L. On Hot Deformation Behavior and Workability Characteristic of 42CrMo4 Steel Based on Microstructure and Processing Map. J. Iron Steel Res. Int. 2023, 30, 537–547. [Google Scholar] [CrossRef]
- Ji, H.; Duan, H.; Li, Y.; Li, W.; Huang, X.; Pei, W.; Lu, Y. Optimization the Working Parameters of As-Forged 42CrMo Steel by Constitutive Equation-Dynamic Recrystallization Equation and Processing Maps. J. Mater. Res. Technol. 2020, 9, 7210–7224. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Zhang, H.; Ruan, J.; Huang, H.; Zhou, X.; Meng, F.; Zhang, S.; Jiang, L. Hot Deformation Behavior and New Grain Size Model of Hot Extruded FGH4096 Superalloy during Hot Compression. J. Alloys Compd. 2023, 938, 168574. [Google Scholar] [CrossRef]
- Zhou, P.W.; Song, Y.R.; Jiang, H.W.; Wu, Y.C.; Zong, Y.Y. Hot Deformation Behavior and Processing Maps of BG801 Bearing Steel. J. Mater. Res. Technol. 2022, 18, 3725–3738. [Google Scholar] [CrossRef]
- Lan, L.; Zhang, Y.; Fu, Y.; Guo, Y.; Shi, Q. Effect of Strain Inhomogeneity on Flow Behavior, Dynamic Recrystallization and Substructure Evolution of a 904 L Super Austenitic Stainless Steel. Mater. Today Commun. 2023, 37, 107140. [Google Scholar] [CrossRef]
- Lan, L.; Zhou, W.; Misra, R.D.K. Effect of Hot Deformation Parameters on Flow Stress and Microstructure in a Low Carbon Microalloyed Steel. Mater. Sci. Eng. A 2019, 756, 18–26. [Google Scholar] [CrossRef]
- Beladi, H.; Cizek, P.; Hodgson, P.D. On the Characteristics of Substructure Development through Dynamic Recrystallization. Acta Mater. 2010, 58, 3531–3541. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, J.; Su, R.; Zhang, H.; Chen, H.; Bai, L.; Wang, C. Hot Deformation Behaviour of 40CrNi Steel and Evaluation of Different Processing Map Construction Methods. J. Mater. Res. Technol. 2020, 9, 2856–2869. [Google Scholar] [CrossRef]
- Lu, Y.; Xie, H.; Wang, J.; Li, Z.; Jia, F.; Wu, H.; Han, J.; Jiang, Z. Influence of Hot Compressive Parameters on Flow Behaviour and Microstructure Evolution in a Commercial Medium Carbon Micro-Alloyed Spring Steel. J. Manuf. Process. 2020, 58, 1171–1181. [Google Scholar] [CrossRef]
- Morito, S.; Yoshida, H.; Maki, T.; Huang, X. Effect of Block Size on the Strength of Lath Martensite in Low Carbon Steels. Mater. Sci. Eng. A 2006, 438–440, 237–240. [Google Scholar] [CrossRef]
- Prawoto, Y.; Jasmawati, N.; Sumeru, K. Effect of Prior Austenite Grain Size on the Morphology and Mechanical Properties of Martensite in Medium Carbon Steel. J. Mater. Sci. Technol. 2012, 28, 461–466. [Google Scholar] [CrossRef]
- Wang, Q.; He, Z.; Du, Z.; Wang, Q.; Dang, X.; Qi, Z.; Yang, C. Softening Mechanisms and Microstructure Evolution of 42CrMo Steel during Hot Compressive Deformation. J. Mater. Res. Technol. 2023, 23, 5152–5163. [Google Scholar] [CrossRef]
- Chen, X.-M.; Lin, Y.C.; Wen, D.-X.; Zhang, J.-L.; He, M. Dynamic Recrystallization Behavior of a Typical Nickel-Based Superalloy during Hot Deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Chen, M.-S.; Li, K.-K.; Lin, Y.-C.; Yuan, W.-Q. An Improved Kinetics Model to Describe Dynamic Recrystallization Behavior under Inconstant Deformation Conditions. J. Mater. Res. 2016, 31, 2994–3003. [Google Scholar] [CrossRef]
- Dini, G.; Ueji, R.; Najafizadeh, A.; Monir-Vaghefi, S.M. Flow Stress Analysis of TWIP Steel via the XRD Measurement of Dislocation Density. Mater. Sci. Eng. A 2010, 527, 2759–2763. [Google Scholar] [CrossRef]
- Luo, R.; Chen, L.; Zhang, Y.; Cao, Y.; Peng, C.T.; Yang, Y.; Liu, T.; Zheng, Q.; Cheng, X. Characteristic and mechanism of dynamic recrystallization in a newly developed Fe-Cr-Ni-Al-Nb superalloy during hot deformation. J. Alloys Compd. 2021, 865, 158601. [Google Scholar] [CrossRef]
- Liu, A.; Wang, L.; Cheng, X.; Ning, Z.; Pan, L. Study on hot deformation behavior of as-cast 22%W high-density steel. J. Mater. Res. Technol. 2022, 17, 2355–2368. [Google Scholar] [CrossRef]
- Wang, S.; Luo, J.R.; Hou, L.G.; Zhang, J.S.; Zhuang, L.Z. Physically Based Constitutive Analysis and Microstructural Evolution of AA7050 Aluminum Alloy during Hot Compression. Mater. Des. 2016, 107, 277–289. [Google Scholar] [CrossRef]
- Medina, S.F.; Hernandez, C.A. General Expression of the Zener-Hollomon Parameter as a Function of the Chemical Composition of Low Alloy and Microalloyed Steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Sellars, C.M.; Whiteman, J.A. Recrystallization and Grain Growth in Hot Rolling. Mater. Sci. 1979, 13, 187–194. [Google Scholar] [CrossRef]
- McQueen, H.J. Development of Dynamic Recrystallization Theory. Mater. Sci. Eng. A 2004, 387–389, 203–208. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, Y.; Zhou, J.; Liu, Y.; Tang, S. Constitutive Modeling for Dynamic Recrystallization Kinetics of Mg-4Zn-2Al-2Sn Alloy. Trans. Nonferrous Met. Soc. China 2018, 28, 340–347. [Google Scholar] [CrossRef]
- Hor, A.; Morel, F.; Lebrun, J.-L.; Germain, G. An Experimental Investigation of the Behaviour of Steels over Large Temperature and Strain Rate Ranges. Int. J. Mech. Sci. 2013, 67, 108–122. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.; Chen, S. Recrystallization of 30Cr2Ni4MoV Ultra-Super-Critical Rotor Steel during Hot Deformation. Part I: Dynamic Recrystallization. Mater. Sci. Eng. A 2011, 528, 5073–5080. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, Z.; Yu, W.; Wang, G.; Zhou, J.; Cai, Q. Deformation Behavior and Constitutive Equation of 42CrMo Steel at High Temperature. Metals 2021, 11, 1614. [Google Scholar] [CrossRef]
- Ma, K.; Liu, Z.Y.; Bi, S.; Zhang, X.X.; Xiao, B.L.; Ma, Z.Y. Microstructure Evolution and Hot Deformation Behavior of Carbon Nanotube Reinforced 2009Al Composite with Bimodal Grain Structure. J. Mater. Sci. Technol. 2021, 70, 73–82. [Google Scholar] [CrossRef]
- Li, N.; Zhao, C.; Jiang, Z.; Zhang, H. Flow Behavior and Processing Maps of High-Strength Low-Alloy Steel during Hot Compression. Mater. Charact. 2019, 153, 224–233. [Google Scholar] [CrossRef]
- Ghosh, A.; Elasheri, A.; Parson, N.; Chen, X.G. Hot deformation behavior and processing maps for an Al-Mg-Si-Zr-Mn alloy. J. Alloys. Metall. Syst. 2024, 100077, 2949–9178. [Google Scholar] [CrossRef]
- Ning, M.; Chen, X.; Lin, Y.Y.; Hu, H.; Zhou, X.; Zhang, J.; Lu, X.; Wu, Y.; Chen, J.Q. Shen. Revealing the hot deformation behavior of AZ42 Mg alloy by using 3D hot processing map based on a novel NGO-ANN model. J. Mater. Res. Technol. 2023, 27, 2292–2310. [Google Scholar] [CrossRef]
- Tang, J.; Yi, Y.; He, H.; Huang, S.; Zhang, J.; Dong, F. Hot deformation behavior and microstructural evolution of the Al-Cu-Li alloy: A study with processing map. J. Alloys Compd. 2023, 934, 167755. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.; Li, C.; Xia, X.; Wu, J.; Li, H. Effect of Initial Microstructure on the Hot Deformation Behavior of a Ni3Al-Based Alloy. Intermetallics 2019, 113, 106584. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Anaele, J.U.; Kareem, S.A.; Deformability, H. Microstructural Evolution and Processing Map Assessment of High Entropy Alloys: A Systematic Review. J. Mater. Res. Technol. 2023, 26, 1754–1784. [Google Scholar] [CrossRef]
- Chen, X.M.; Ning, M.T.; Hu, H.W.; Lin, Y.C.; Zhou, X.J.; Zhang, J.; Lu, X.Z.; Chen, J.; Liu, Y.X. Characterization of hot deformation behavior and optimization of hot workability for GH4698 superalloy. Mater. Charact. 2023, 201, 112916. [Google Scholar] [CrossRef]
- Hu, D.; Wang, L.; Wang, N.; Chen, M.; Wang, H. Hot Tensile Deformation Behaviors of TA32 Titanium Alloy Based on Back-Propagation Neural Networks and Three-Dimensional Thermal Processing Maps. J. Mater. Res. Technol. 2022, 18, 4786–4795. [Google Scholar] [CrossRef]
- Li, C.; Huang, L.; Zhao, M.; Guo, S.; Li, J. Hot Deformation Behavior and Mechanism of a New Metastable β Titanium Alloy Ti-6Cr-5Mo-5V-4Al in Single Phase Region. Mater. Sci. Eng. A 2021, 814, 141231. [Google Scholar] [CrossRef]
- Chen, M.S.; Lin, Y.C.; Ma, X.S. The Kinetics of Dynamic Recrystallization of 42CrMo Steel. Mater. Sci. Eng. A 2012, 556, 260–266. [Google Scholar] [CrossRef]
- Flower, H.M.; Lindley, T.C. Electron Backscattering Diffraction Study of Acicular Ferrite, Bainite, and Martensite Steel Microstructures. Mater. Sci. Technol. 2000, 16, 26–40. [Google Scholar]
- Li, C.; Huang, L.; Zhao, M.; Guo, S.; Li, J. Study on microstructure evolution and deformation mechanism of Ti-6554 based on power dissipation efficiency at supertransus temperatures. J. Alloys Compd. 2022, 924, 166481. [Google Scholar] [CrossRef]
- Xu, K.; Luo, J.; Li, C.; Shen, Y.; Li, C.; Ma, X.; Li, M. Mechanisms of stress-induced martensitic transformation and transformation-induced plasticity in NiTi shape memory alloy related to superelastic stability. Scripta Mater. 2022, 217, 114775. [Google Scholar] [CrossRef]
- Feng, R.; Lu, S.; Li, X.; Zhou, X. Numerical Simulation of Unstable Deformation and Dynamic Recrystallization Behavior of BT25 Tita-Nium Alloy During Hot Forging. Rare Met. Mater. Eng. 2021, 50, 3149–3157. [Google Scholar]

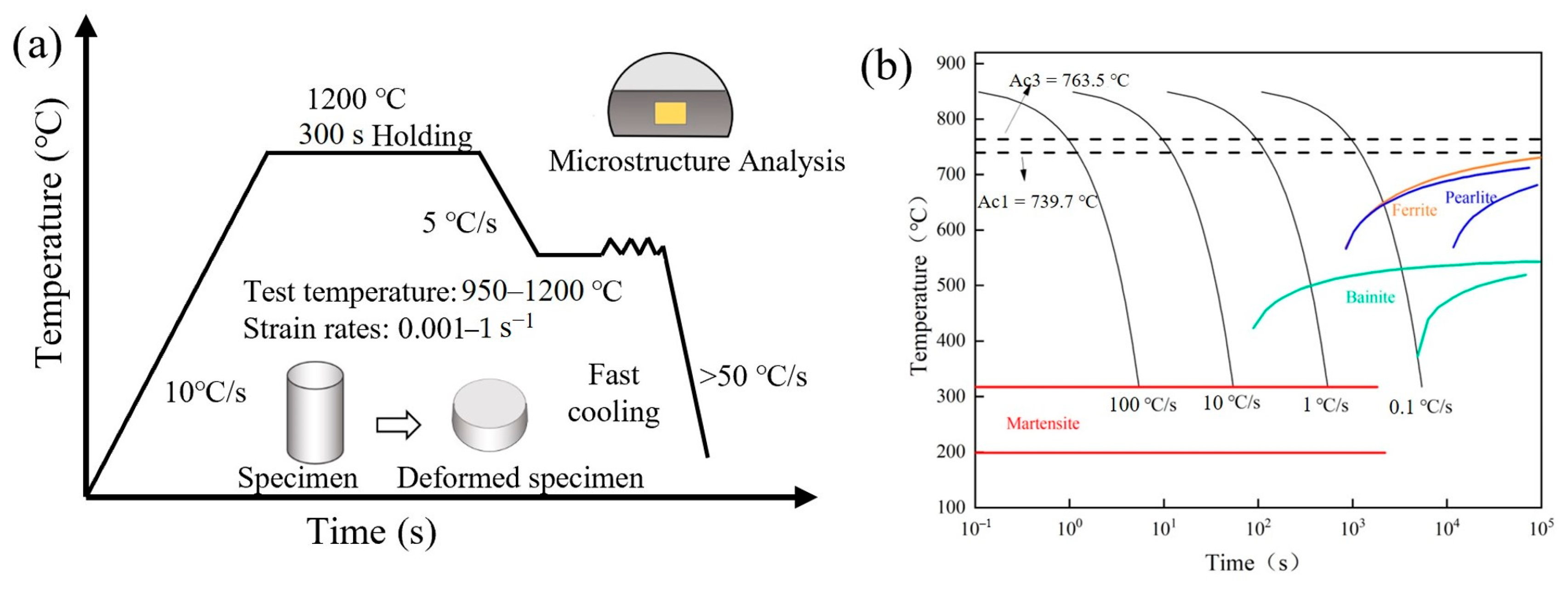

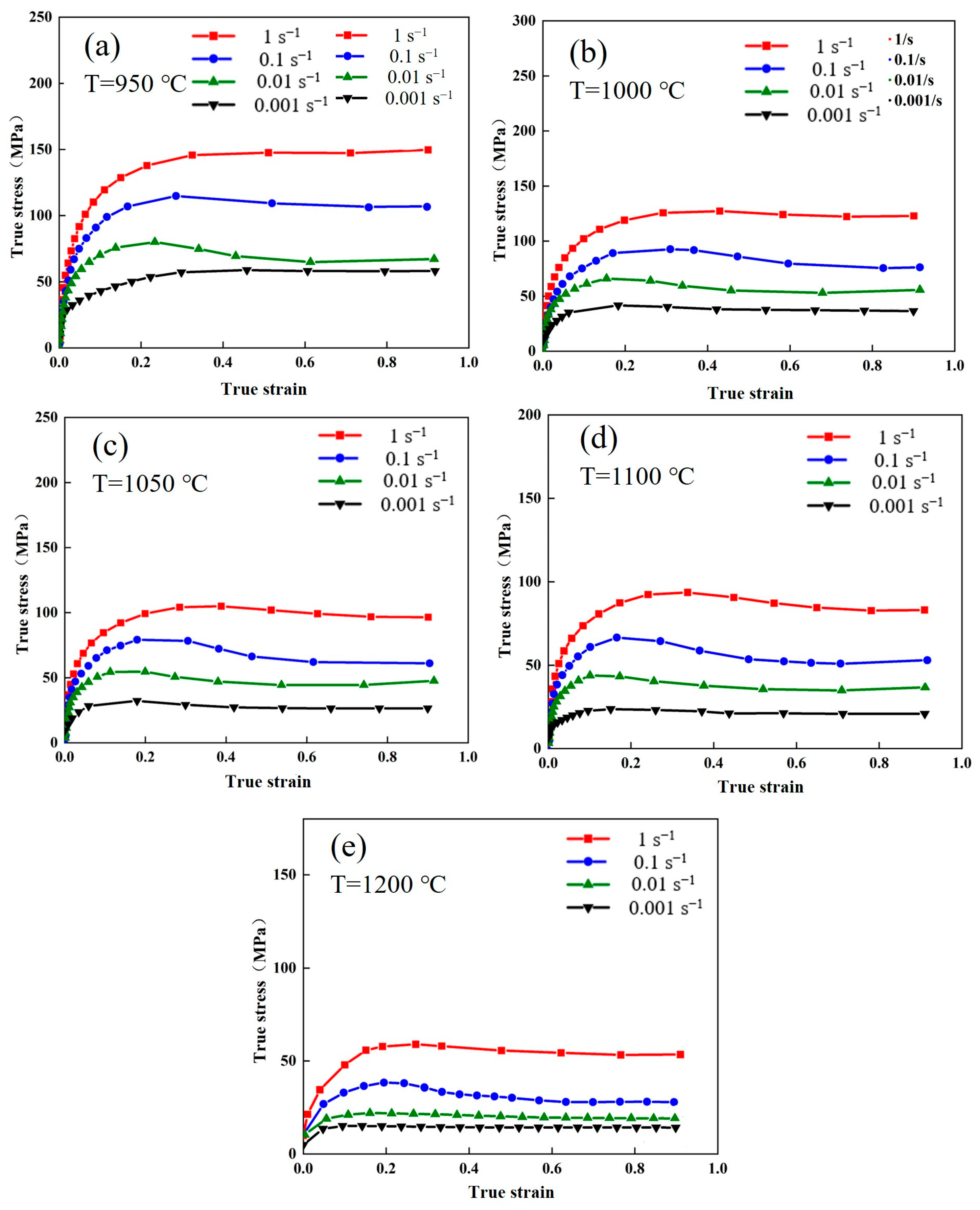


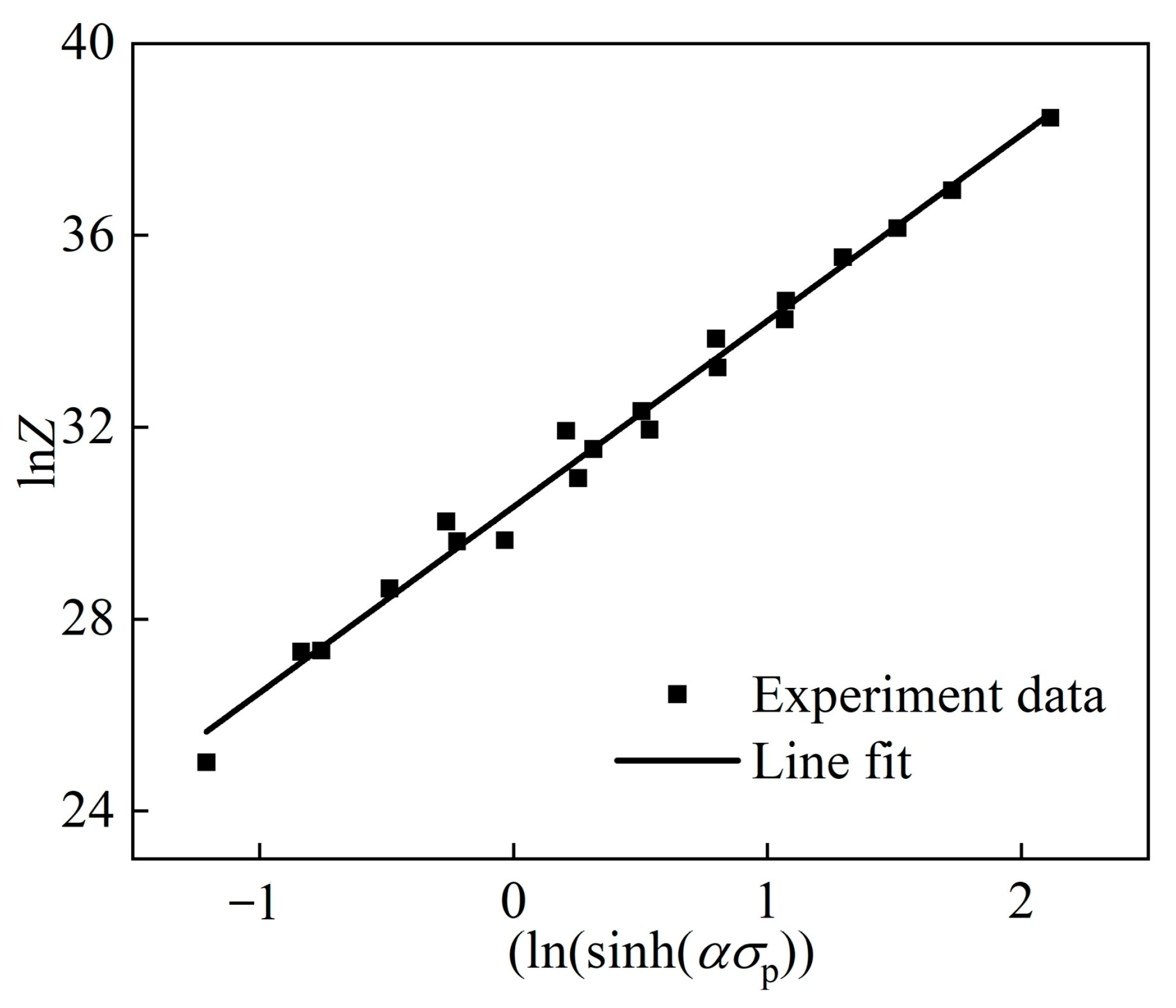
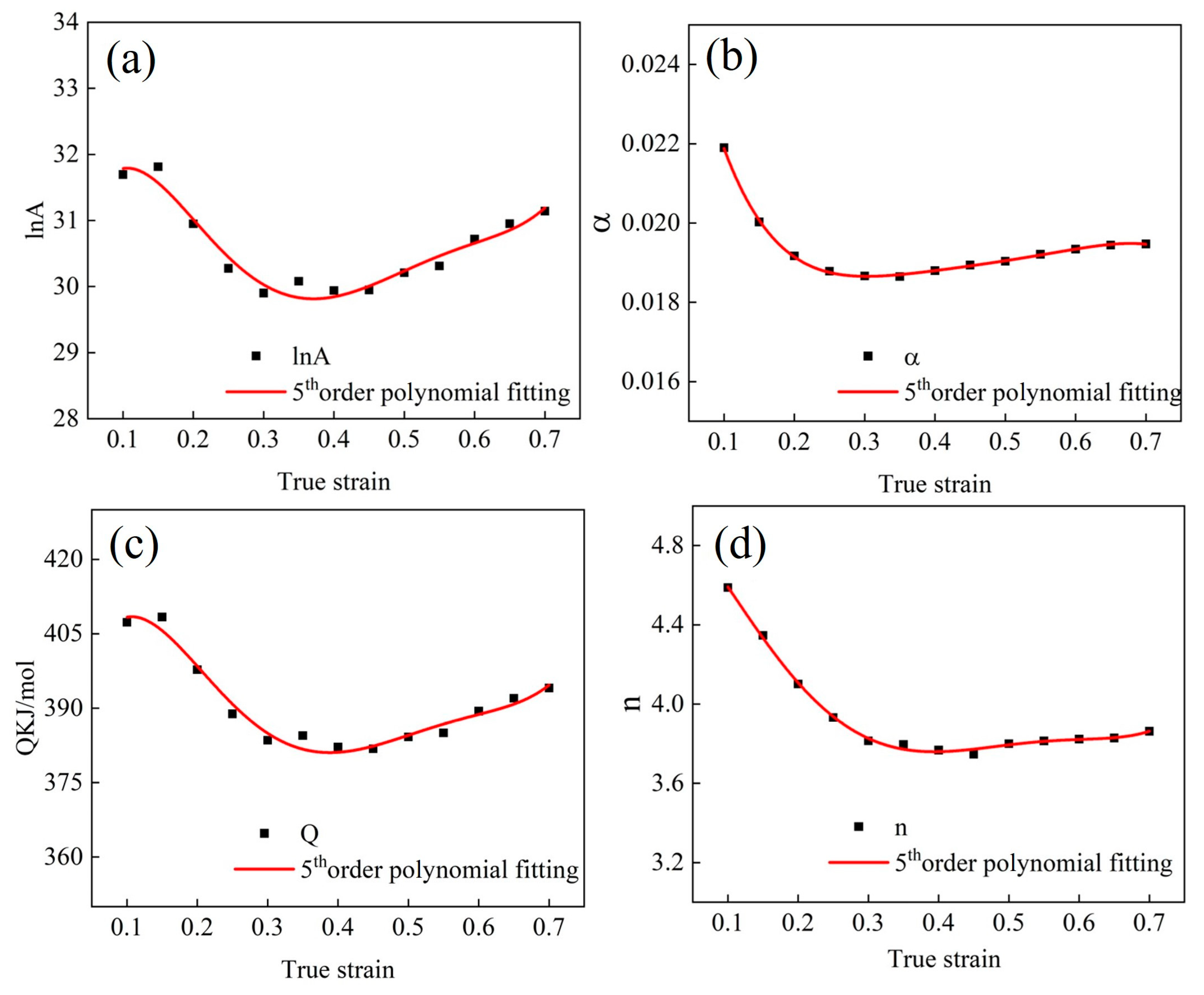








| C | Si | Mn | P | S | Cr | Mo | Cu | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.41 | 0.26 | 0.69 | 0.0063 | 0.0091 | 1.11 | 0.20 | 0.03 | Bal. |
| Deformation Temperature (°C) | Strain Rate (s−1) | |||
|---|---|---|---|---|
| 0.001 | 0.01 | 0.1 | 1 | |
| 950 °C | 1.0321 | 0.9691 | 1.0698 | 1.0232 |
| 1000 °C | 1.0926 | 1.0497 | 0.9841 | 1.0677 |
| 1050 °C | 1.0527 | 1.0423 | 1.0598 | 1.0698 |
| 1100 °C | 0.9941 | 1.0432 | 1.0872 | 1.0921 |
| 1200 °C | 1.0863 | 1.0818 | 1.0734 | 1.0310 |
| Strain | α | n | Q/(kJ/mol) | lnA |
|---|---|---|---|---|
| 0.10 | 0.021899869 | 4.587893 | 407.311 | 31.69569 |
| 0.15 | 0.020026631 | 4.346701 | 408.382 | 31.81251 |
| 0.20 | 0.019169447 | 4.101312 | 397.747 | 30.94919 |
| 0.25 | 0.018783997 | 3.932011 | 388.867 | 30.27511 |
| 0.30 | 0.018665743 | 3.814459 | 383.540 | 29.90283 |
| 0.35 | 0.018649029 | 3.795894 | 384.477 | 30.07963 |
| 0.40 | 0.018797260 | 3.767556 | 382.181 | 29.94070 |
| 0.45 | 0.018938808 | 3.747479 | 381.805 | 29.94879 |
| 0.50 | 0.019037187 | 3.800027 | 384.209 | 30.20930 |
| 0.55 | 0.019212378 | 3.814247 | 385.030 | 30.31099 |
| 0.60 | 0.019341395 | 3.823353 | 389.404 | 30.71907 |
| 0.65 | 0.019442589 | 3.828529 | 392.002 | 30.95220 |
| 0.70 | 0.019472766 | 3.862982 | 394.066 | 31.14102 |
| α | n | Q | lnA | ||||
|---|---|---|---|---|---|---|---|
| X0 | 0.03018 | N0 | 5.01577 | Q0 | 373,753 | Y0 | 29.10331 |
| X1 | −0.12723 | N1 | −2.17646 | Q1 | 795,498.55 | Y1 | 62.23573 |
| X2 | 0.54696 | N2 | −32.96995 | Q2 | −5,997,871.49 | Y2 | −474.19401 |
| X3 | −1.15679 | N3 | 143.72186 | Q3 | 17,025,652.65 | Y3 | 1363.84008 |
| X4 | 1.2227 | N4 | −210.73112 | Q4 | −21,094,491.99 | Y4 | −1703.96763 |
| X5 | −0.51441 | N5 | 106.06187 | Q5 | 9,686,499.7 | Y5 | 786.60111 |
| Temperature/°C | /MPa | /MPa | /MPa | /MPa | |||
|---|---|---|---|---|---|---|---|
| 950 | 0.001 | 42.37 | 58.93 | 73.56 | 58.2 | 0.091 | 0.221 |
| 0.01 | 65.69 | 80.81 | 88.29 | 64.62 | 0.076 | 0.204 | |
| 0.1 | 85.44 | 116.49 | 122.95 | 110.45 | 0.073 | 0.320 | |
| 1 | 115.47 | 147.73 | 155.97 | 147.23 | 0.098 | 0.441 | |
| 1000 | 0.001 | 27.82 | 37.13 | 42.82 | 32.40 | 0.058 | 0.189 |
| 0.01 | 54.61 | 67.16 | 80.85 | 53.03 | 0.066 | 0.201 | |
| 0.1 | 70.42 | 94.26 | 98.24 | 75.78 | 0.073 | 0.278 | |
| 1 | 101.39 | 127.56 | 140.58 | 122.15 | 0.096 | 0.369 | |
| 1050 | 0.001 | 23.89 | 30.49 | 38.07 | 26.30 | 0.051 | 0.136 |
| 0.01 | 47.87 | 56.32 | 67.14 | 44.12 | 0.064 | 0.151 | |
| 0.1 | 62.91 | 81.13 | 88.97 | 60.87 | 0.070 | 0.212 | |
| 1 | 79.47 | 107.52 | 113.77 | 102.70 | 0.075 | 0.352 | |
| 1100 | 0.001 | 18.88 | 23.82 | 28.68 | 20.95 | 0.049 | 0.131 |
| 0.01 | 39.43 | 45.05 | 48.99 | 34.75 | 0.065 | 0.133 | |
| 0.1 | 54.50 | 68.58 | 72.75 | 50.81 | 0.069 | 0.205 | |
| 1 | 69.29 | 94.06 | 103.77 | 82.62 | 0.069 | 0.329 | |
| 1200 | 0.001 | 13.62 | 15.45 | 17.67 | 14.32 | 0.048 | 0.112 |
| 0.01 | 19.23 | 22.10 | 30.42 | 19.10 | 0.059 | 0.159 | |
| 0.1 | 29.73 | 38.52 | 54.94 | 28.12 | 0.065 | 0.215 | |
| 1 | 40.66 | 54.39 | 62.39 | 54.15 | 0.097 | 0.316 |
| User Variables | USRE (1) | USRE (2) | USRE (3) | USRE (4) | USRE (5) | USRE (6) | USRE (7) |
|---|---|---|---|---|---|---|---|
| Implication | -Equivalent | Z | Xdrx | Ddrx |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, C.; Sun, Z.; Shen, D.; Guo, N.; Liu, Z.; Cheng, L.; Liu, Y.; Tang, B. Determining the Hot Workability and Microstructural Evolution of an Fe-Cr-Mo-Mn Steel Using 3D Processing Maps. Materials 2024, 17, 2715. https://doi.org/10.3390/ma17112715
Dou C, Sun Z, Shen D, Guo N, Liu Z, Cheng L, Liu Y, Tang B. Determining the Hot Workability and Microstructural Evolution of an Fe-Cr-Mo-Mn Steel Using 3D Processing Maps. Materials. 2024; 17(11):2715. https://doi.org/10.3390/ma17112715
Chicago/Turabian StyleDou, Cunchao, Zhendong Sun, Depeng Shen, Ning Guo, Zhe Liu, Lin Cheng, Yongchao Liu, and Bingtao Tang. 2024. "Determining the Hot Workability and Microstructural Evolution of an Fe-Cr-Mo-Mn Steel Using 3D Processing Maps" Materials 17, no. 11: 2715. https://doi.org/10.3390/ma17112715
APA StyleDou, C., Sun, Z., Shen, D., Guo, N., Liu, Z., Cheng, L., Liu, Y., & Tang, B. (2024). Determining the Hot Workability and Microstructural Evolution of an Fe-Cr-Mo-Mn Steel Using 3D Processing Maps. Materials, 17(11), 2715. https://doi.org/10.3390/ma17112715






