Research on the Asymmetric Phenomenon of Voltage Polarity Based on Dielectric Wetting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
2.1.1. Preparation of Hydrophobic Dielectric Layer
2.1.2. Experimental Reagent Configuration
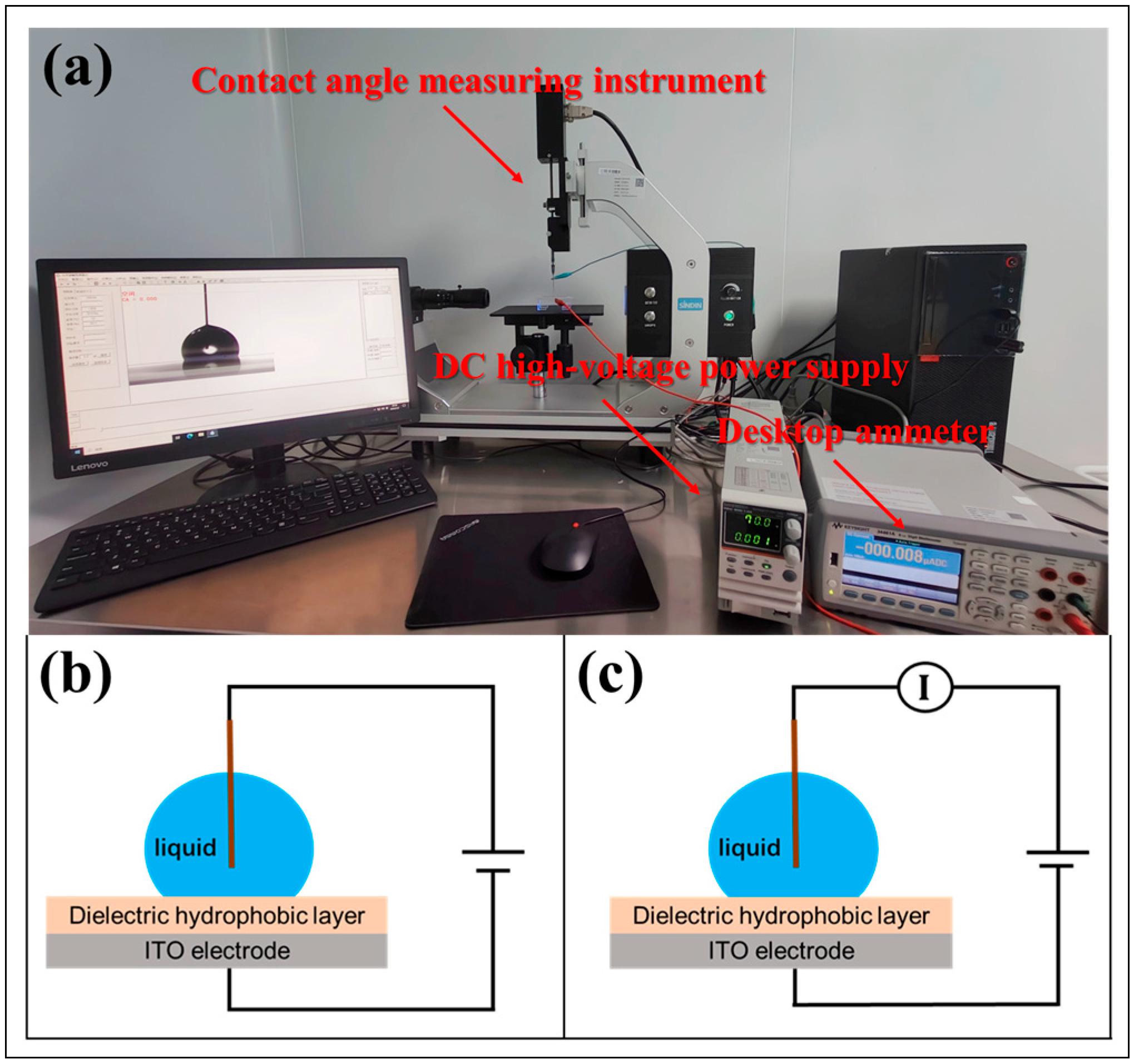
2.2. Experimental Methods
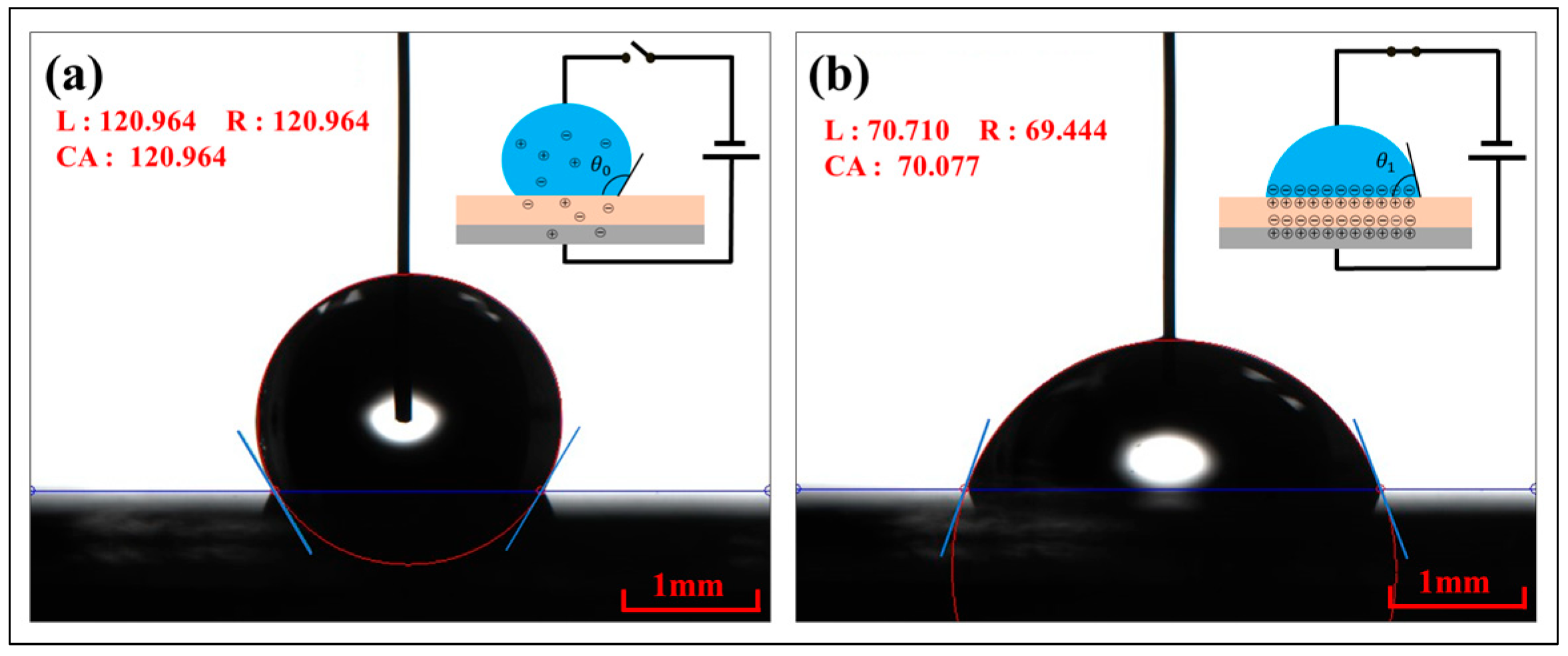
2.2.1. Contact Angle Measurement
2.2.2. Leakage Current Measurement
3. Results
3.1. Structure of the Hydrophobic Layer
3.2. Contact Angle
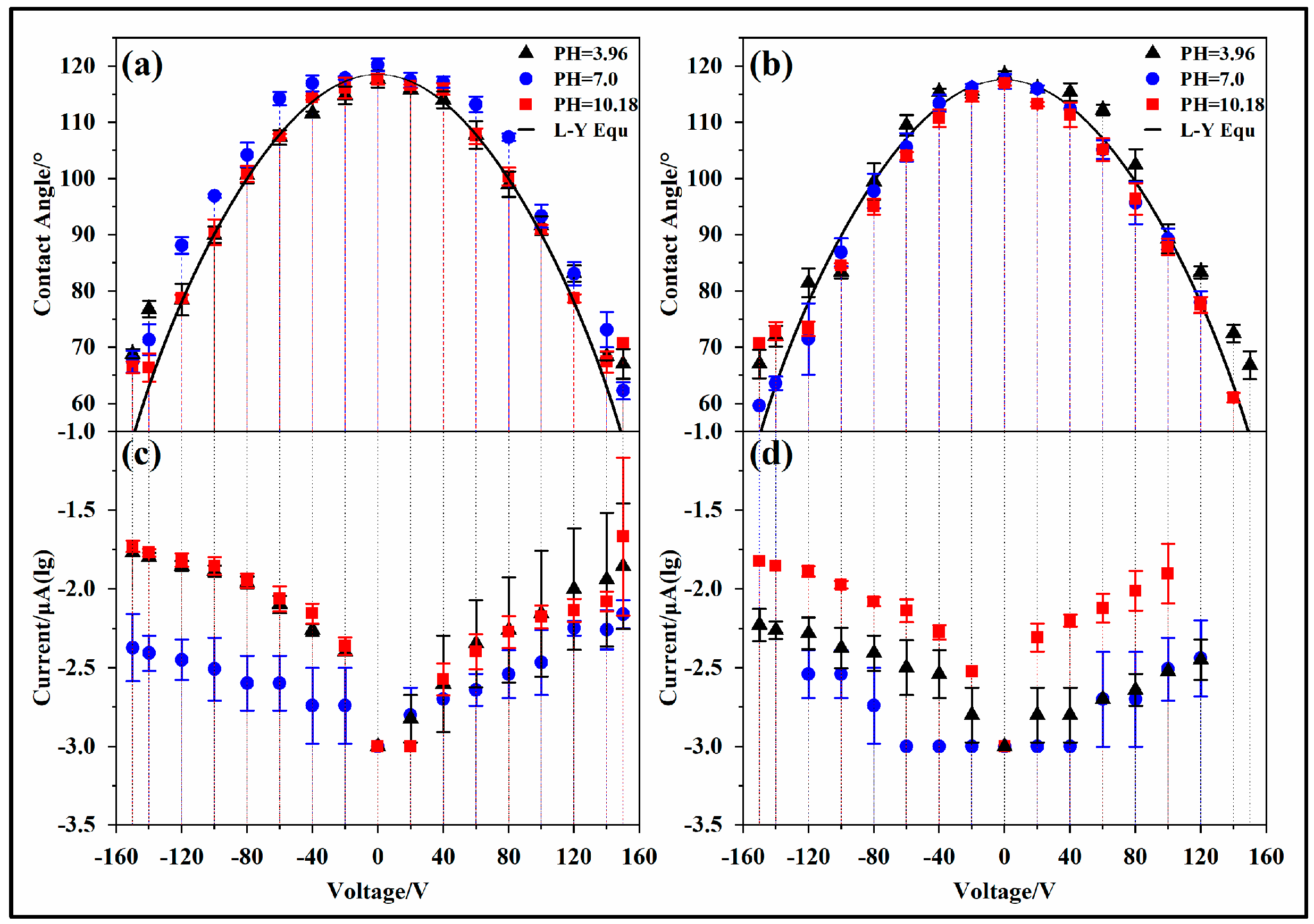
3.2.1. Thick Hydrophobic Dielectric Layer
3.2.2. Thin Hydrophobic Dielectric Layer
- Contact angle deviation
- 2.
- Contact angle asymmetry
- 3.
- Effect of pH
- 4.
- Effect of hydrophobic materials
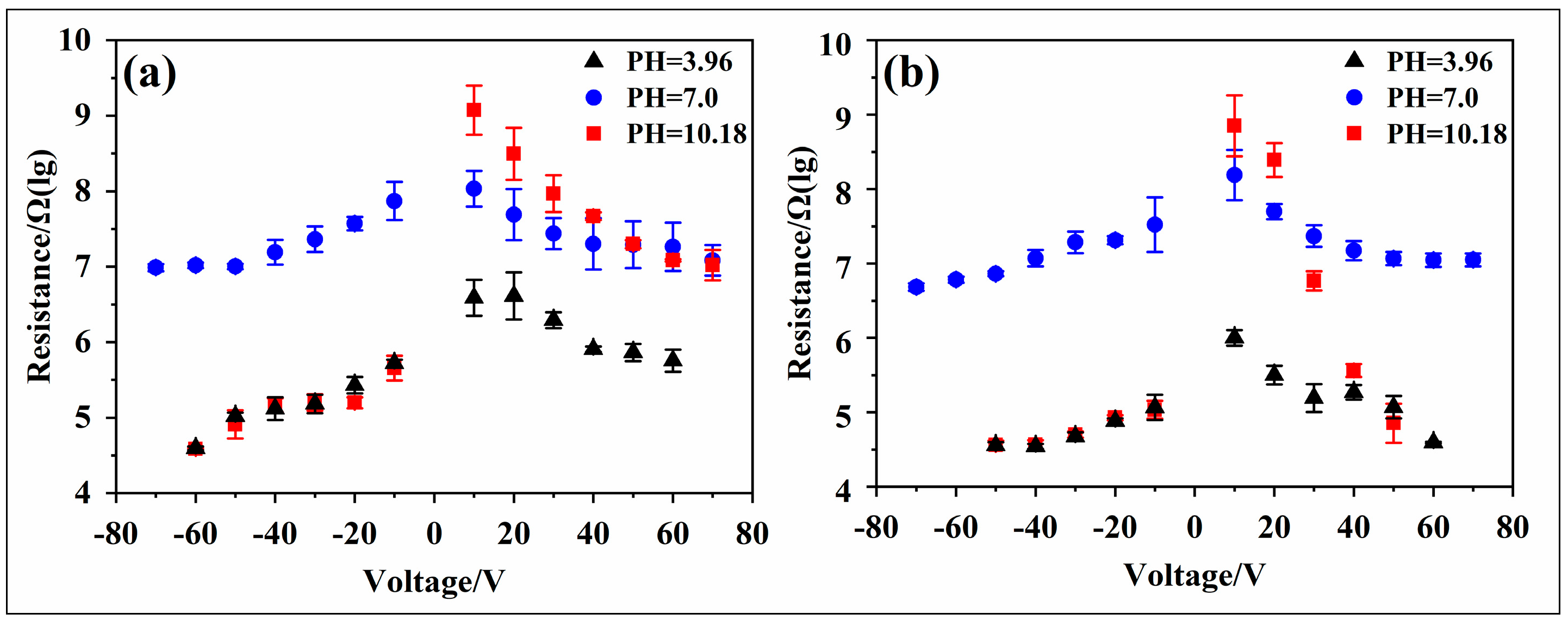
3.3. Leakage Current
4. Discussion
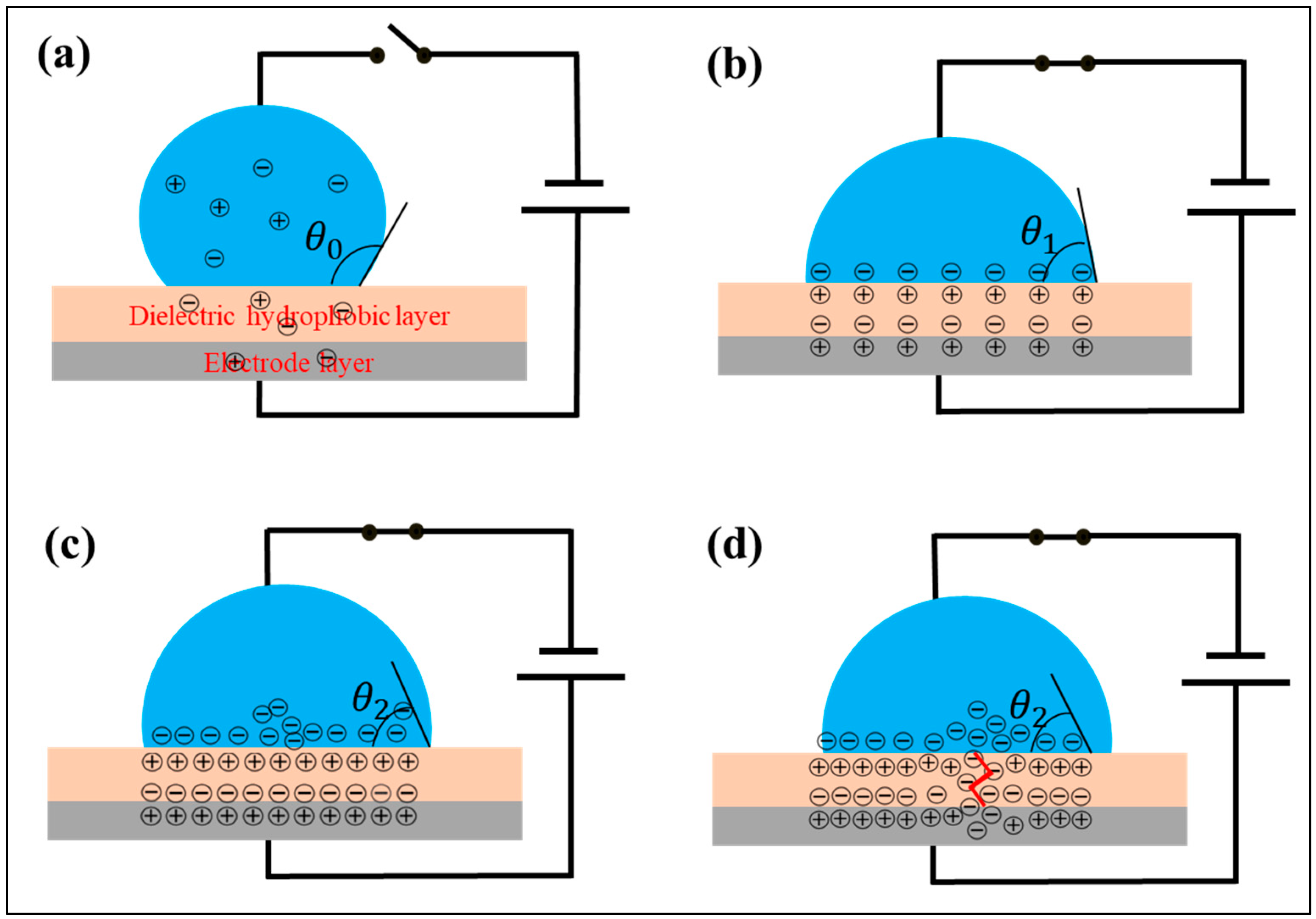
4.1. Dynamics of Droplets in the Electric Field
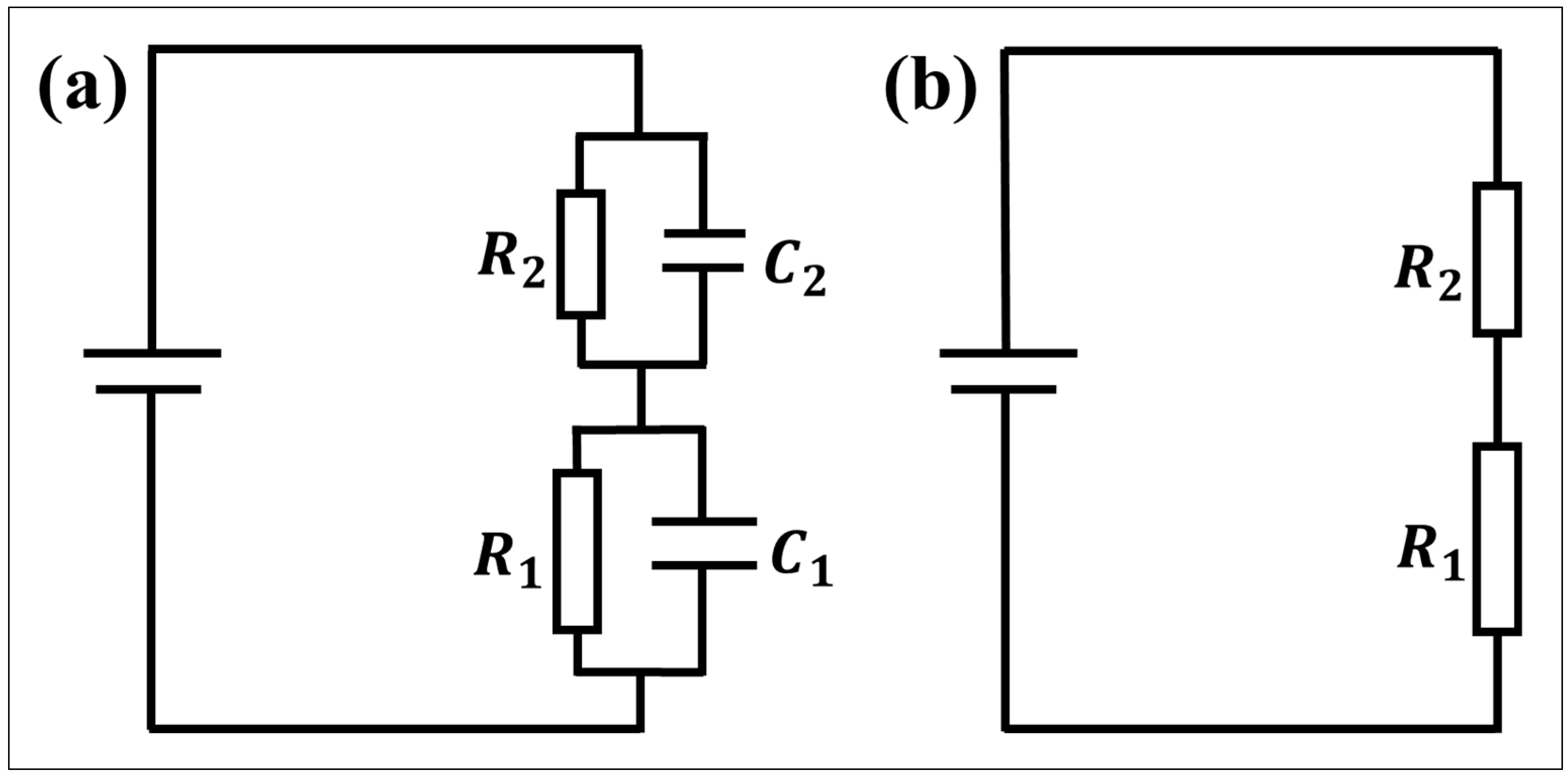
4.2. Equivalent Circuit of the Thick Hydrophobic Layer
4.3. Equivalent Circuit of the Thin Hydrophobic Layer
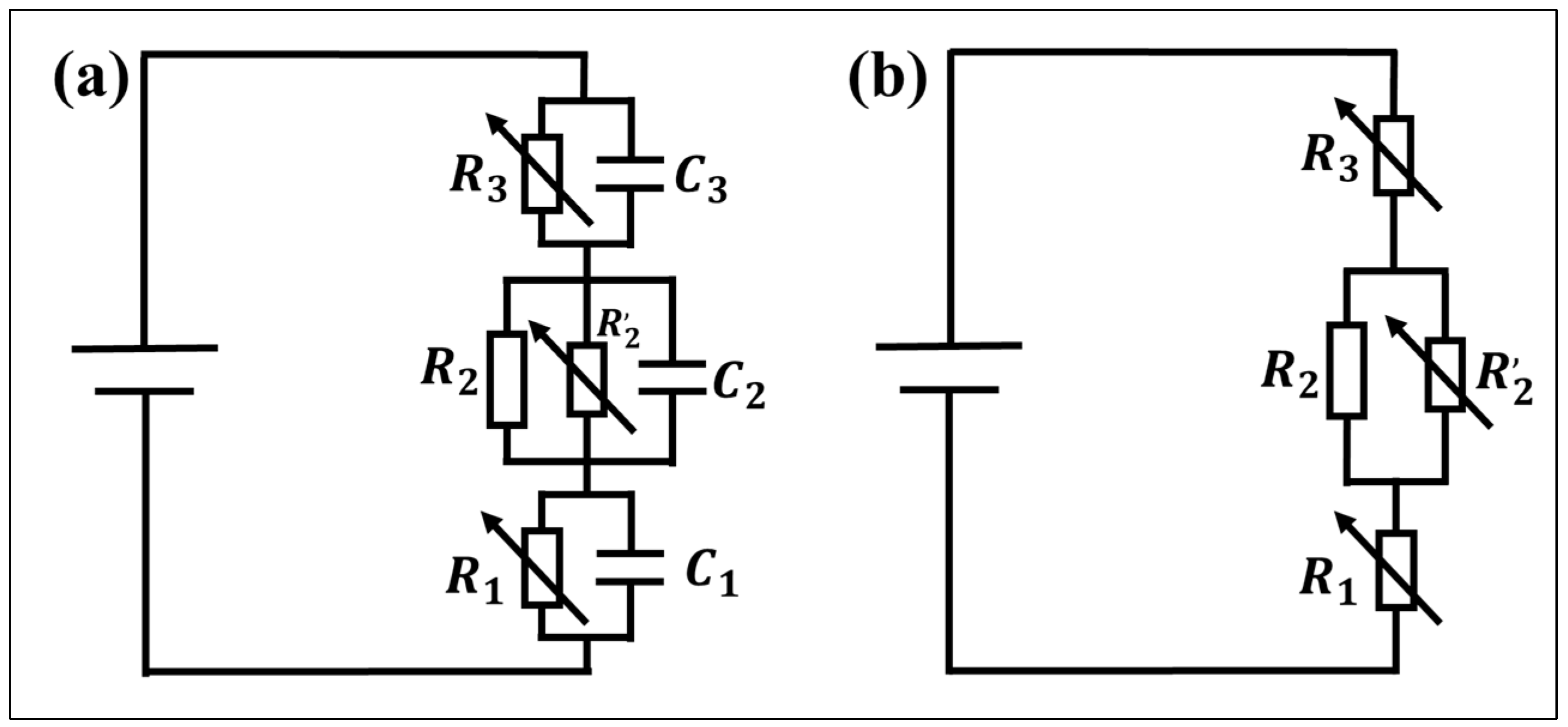
4.3.1. Contact Angle Deviation
4.3.2. Contact Angle Asymmetry
4.3.3. Effect of pH
4.3.4. Effect of Hydrophobic Materials
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Kim, C.C. Current Commercialization Status of Electrowetting-On-Dielectric (Ewod) Digital Microfluidics. Lab Chip 2020, 20, 1705–1712. [Google Scholar] [CrossRef]
- Drelich, J.W. Contact Angles: From Past Mistakes to New Developments through Liquid-Solid Adhesion Measurements. Adv. Colloid. Interface. Sci. 2019, 267, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Khademi, M.; Barz, D.P.J. Structure of the Electrical Double Layer Revisited: Electrode Capacitance in Aqueous Solutions. Langmuir 2020, 36, 4250–4260. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Szymczyk, K.; Krawczyk, J.; Jańczuk, B. Some Remarks on the Solid Surface Tension Determination from Contact Angle Measurements. Appl. Surf. Sci. 2017, 405, 88–101. [Google Scholar] [CrossRef]
- Dixon, C.; Lamanna, J.; Wheeler, A.R. Direct Loading of Blood for Plasma Separation and Diagnostic Assays on a Digital Microfluidic Device. Lab Chip 2020, 2, 1845–1855. [Google Scholar] [CrossRef]
- Hu, S.; Jie, Y.; Jin, K.; Zhang, Y.; Guo, T.; Huang, Q.; Mei, Q.; Ma, F.; Ma, H. All-in-One Digital Microfluidics System for Molecular Diagnosis with Loop-Mediated Isothermal Amplification. Biosensors 2022, 12, 324. [Google Scholar] [CrossRef]
- Jin, K.; Hu, C.; Hu, S.; Hu, C.; Li, J.; Ma, H. “One-to-Three” Droplet Generation in Digital Microfluidics for Parallel Chemiluminescence Immunoassays. Lab Chip 2021, 21, 2892–2900. [Google Scholar] [CrossRef]
- Li, D.; Liu, X.; Chai, Y.; Shan, J.; Xie, Y.; Liang, Y.; Huang, S.; Zheng, W.; Li, Z. Point-of-Care Blood Coagulation Assay Enabled by Printed Circuit Board-Based Digital Microfluidics. Lab Chip 2022, 22, 79–716. [Google Scholar] [CrossRef] [PubMed]
- Sista, R.; Hua, Z.; Thwar, P.; Sudarsan, A.; Srinivasan, V.; Eckhardt, A.; Pollack, M.; Pamula, V. Development of a Digital Microfluidic Platform for Point of Care Testing. Lab Chip 2008, 8, 2091–2104. [Google Scholar] [CrossRef]
- Hendriks, B.H.W.; Kuiper, S.; Van As, M.A.J.; Renders, C.A.; Tukker, T.W. Electrowetting-Based Variable-Focus Lens for Miniature Systems. Opt. Rev. 2005, 12, 255–259. [Google Scholar] [CrossRef]
- Kedzierski, J.; Berry, S. Engineering the Electrocapillary Behavior of Electrolyte Droplets on Thin Fluoropolymer Films. Langmuir 2006, 22, 5690–5696. [Google Scholar] [CrossRef] [PubMed]
- Hayes, R.A.; Feenstra, B.J. Video-Speed Electronic Paper Based on Electrowetting. Nature 2003, 425, 383–385. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, B.; Yang, G.; Guo, Y.; Liu, L.; Henzen, A. Progress in Advanced Properties of Electrowetting Displays. Micromachines 2021, 12, 206. [Google Scholar] [CrossRef] [PubMed]
- Carraro, G.; Passaglia, S.; Paolini, G.; Bracco, G.; Savio, L.; Luciano, G.; Vattuone, L.; Masini, R.; Smerieri, M. Rewod-Based Vibrational Energy Harvesting Exploiting Saline-Solutions Loaded Paam Hydrogels on Micro-Structured Aluminium Oxides Electrodes. Appl. Surf. Sci. 2023, 611, 155522. [Google Scholar] [CrossRef]
- Krupenkin, T.; Taylor, J.A. Reverse Electrowetting as a New Approach to High-Power Energy Harvesting. Nat. Commun. 2011, 2, 448. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Gao, S.; Xu, W.; Wang, Z. Nanogenerators with Superwetting Surfaces for Harvesting Water/Liquid Energy. Adv. Funct. Mater. 2020, 30, 1908252. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J. Electrowetting: From Basics to Applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Fromille, S.; Phillips, J. Super Dielectric Materials. Materials 2014, 7, 8197–8212. [Google Scholar] [CrossRef]
- Markodimitrakis, I.E.; Sema, D.G.; Chamakos, N.T.; Papadopoulos, P.; Papathanasiou, A.G. Impact of Substrate Elasticity On Contact Angle Saturation in Electrowetting. Soft Matter 2021, 17, 4335–4341. [Google Scholar] [CrossRef]
- Guo, Y.; Deng, Y.; Xu, B.; Henzen, A.; Hayes, R.; Tang, B.; Zhou, G. Asymmetrical Electrowetting on Dielectrics Induced by Charge Transfer through an Oil/Water Interface. Langmuir 2018, 34, 11943–11951. [Google Scholar] [CrossRef]
- He, X.; Qiang, W.; Du, C.; Shao, Q.; Zhang, X.; Deng, Y. Modification of Lubricant Infused Porous Surface for Low-Voltage Reversible Electrowetting. J. Mater. Chem. A Mater. Energy Sustain. 2017, 5, 19159–19167. [Google Scholar] [CrossRef]
- Arscott, S. Electrowetting and Semiconductors. Rsc. Adv. 2014, 4, 29223. [Google Scholar] [CrossRef]
- Vallet, M.; Vallade, M.; Berge, B. Limiting Phenomena for the Spreading of Water on Polymer Films by Electrowetting. Eur. Phys. J. B 1999, 11, 583–591. [Google Scholar] [CrossRef]
- Shapiro, B.; Moon, H.; Garrell, R.L.; Kim, C.C. Equilibrium Behavior of Sessile Drops Under Surface Tension, Applied External Fields, and Material Variations. J. Appl. Phys. 2003, 93, 5794–5811. [Google Scholar] [CrossRef]
- Verheijen, H.J.J.; Prins, M.W.J. Reversible Electrowetting and Trapping of Charge: Model and Experiments. Langmuir 1999, 15, 6616–6620. [Google Scholar] [CrossRef]
- Quinn, A.; Sedev, R.; Ralston, J. Contact Angle Saturation in Electrowetting. J. Phys. Chem. B 2005, 109, 6268–6275. [Google Scholar] [CrossRef] [PubMed]
- Seyrat, E.; Hayes, R.A. Amorphous Fluoropolymers as Insulators for Reversible Low-Voltage Electrowetting. J. Appl. Phys. 2001, 90, 1383–1386. [Google Scholar] [CrossRef]
- Moon, H.; Cho, S.K.; Garrell, R.L.; Kim, C.C. Low Voltage Electrowetting-On-Dielectric. J. Appl. Phys. 2002, 92, 4080–4087. [Google Scholar] [CrossRef]
- Khodayari, M.; Crane, N.B.; Volinsky, A.A. Electrochemical Explanation for Asymmetric Electrowetting Response. Thin Solid Films 2013, 548, 632–635. [Google Scholar] [CrossRef]
- Banpurkar, A.G.; Sawane, Y.; Wadhai, S.M.; Murade, C.U.; Siretanu, I.; van den Ende, D.; Mugele, F. Spontaneous Electrification of Fluoropolymer-Water Interfaces Probed by Electrowetting. Faraday Discuss. 2017, 199, 29–47. [Google Scholar] [CrossRef]
- Wu, H.; Dey, R.; Siretanu, I.; van den Ende, D.; Shui, L.; Zhou, G.; Mugele, F. Electrically Controlled Localized Charge Trapping at Amorphous Fluoropolymer–Electrolyte Interfaces. Small 2020, 16, e1905726. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Xu, J.; Yang, B.; Yang, F. Asymmetric Electrodes for Droplet Directional Actuation by a Square Wave on an Open Surface. Results Phys. 2023, 48, 106401. [Google Scholar] [CrossRef]
- Susrisweta, B.; Veselý, L.; Štůsek, R.; Hauptmann, A.; Loerting, T.; Heger, D. Investigating Freezing-Induced Acidity Changes in Citrate Buffers. Int. J. Pharm. 2023, 643, 123211. [Google Scholar] [CrossRef] [PubMed]
- Duong, T.T.; Piret, J.M.; Balcarcel, R.R. A Semi-Empirical Mathematical Model to Specify the Ph of Bicarbonate-Buffered Cell Culture Dielectric Formulations. Can. J. Chem. Eng. 2021, 99, 2570–2583. [Google Scholar] [CrossRef]
- Guo, S.; Lu, C.; Wang, K.; Wang, J.; Zhang, Z.; Liu, H.; Jing, Y.; Zhang, Q. Effect of Citrate Buffer on Hydrogen Production by Photosynthetic Bacteria. Bioresour. Technol. 2022, 347, 126636. [Google Scholar] [CrossRef]
- Kosikowsky, F.V.; Dahlberg, A.C. Effectiveness of the Carbonate-Bicarbonate Buffer in Maintaining the Optimum Ph Range. The Carbonate-Bicarbonate Buffer Substrate Used in this Portion of. J. Dairy Sci. 1949, 32, 760–763. [Google Scholar] [CrossRef]
- Montes Ruiz-Cabello, F.J.; Bermúdez-Romero, S.; Ibáñez-Ibáñez, P.F.; Cabrerizo-Vílchez, M.A.; Rodríguez-Valverde, M.A. Freezing Delay of Sessile Drops: Probing the Impact of Contact Angle, Surface Roughness and Thermal Conductivity. Appl. Surf. Sci. 2021, 537, 147964. [Google Scholar] [CrossRef]
- Kim, T.; Yi, J. Application of Hydrophobic Coating to Reduce Leakage Current through Surface Energy Control of High Voltage Insulator. Appl. Surf. Sci. 2022, 578, 151820. [Google Scholar] [CrossRef]
- Mibus, M.; Hu, X.; Knospe, C.; Reed, M.L.; Zangari, G. Failure Modes During Low-Voltage Electrowetting. Acs Appl. Mater. Interfaces 2016, 8, 15767–15777. [Google Scholar] [CrossRef]
- Papathanasiou, A.G.; Papaioannou, A.T.; Boudouvis, A.G. Illuminating the Connection Between Contact Angle Saturation and Dielectric Breakdown in Electrowetting through Leakage Current Measurements. J. Appl. Phys. 2008, 103, 034901. [Google Scholar] [CrossRef]
- Thomas, D.; Audry, M.; Thibaut, R.; Kleimann, P.; Chassagneux, F.; Maillard, M.; Brioude, A. Charge Injection in Dielectric Films During Electrowetting Actuation Under Direct Current Voltage. Thin Solid Films 2015, 590, 224–229. [Google Scholar] [CrossRef]
- Weiqiang Wang, Y.S. Leakage Current Study for Dielectric Breakdown in Electrowetting Systems. Adv. Eng. Res. 2016, 90, 227–230. [Google Scholar]
- Senthilkumar, M.; Mathiyarasu, J.; Joseph, J.; Phani, K.L.N.; Yegnaraman, V. Electrochemical Instability of Indium Tin Oxide (Ito) Glass in Acidic Ph Range During Cathodic Polarization. Mater. Chem. Phys. 2008, 108, 403–407. [Google Scholar] [CrossRef]
- Matveeva, E. Electrochemistry of the Indium-Tin Oxide Electrode in 1 M Naoh Electrolyte. J. Electrochem. Soc. 2005, 152, H138. [Google Scholar] [CrossRef]
- van der Helm, M.W.; Henry, O.Y.F.; Bein, A.; Hamkins-Indik, T.; Cronce, M.J.; Leineweber, W.D.; Odijk, M.; van der Meer, A.D.; Eijkel, J.C.T.; Ingber, D.E.; et al. Non-Invasive Sensing of Transepithelial Barrier Function and Tissue Differentiation in Organs-On-Chips Using Impedance Spectroscopy. Lab Chip 2019, 19, 452–463. [Google Scholar] [CrossRef]


| Reagent | CA-SCB | SC-SBB | ||
|---|---|---|---|---|
| Citric Acid | Sodium Citrate | Sodium Carbonate | Sodium Bicarbonate | |
| Ratio | 3.8 | 16.2 | 6 | 4 |
| Conc (mol/L) | 0.1 | 0.1 | 0.1 | 0.1 |
| Target pH value | 4.0 | 10.0 | ||
| EWOD Models | Hydrophobic Layers | Droplets | ||||
|---|---|---|---|---|---|---|
| Type | δ (nm) | ρ (Ω m) | Type | pH | σ (S/m) | |
| ITKAD | AF1601 | 2489 ± 35 | 3.3 × 1011 ± 1010 | CA-SCB | 3.96 ± 0.12 | 1.03 ± 0.05 |
| UP water | 7.00 ± 0.32 | 8 × 10−5 ± 10−6 | ||||
| SC-SBB | 10.18 ± 0.14 | 0.52 ± 0.03 | ||||
| ITNAD | AF1601 | 344 ± 2 | 1.9 × 1012 ± 5 × 1010 | CA-SCB | 3.96 ± 0.12 | 1.03 ± 0.05 |
| UP water | 7.00 ± 0.32 | 8 × 10−5 ± 10−6 | ||||
| SC-SBB | 10.18 ± 0.14 | 0.52 ± 0.03 | ||||
| ITK6D | 6%T6 | 2501 ± 176 | 2.9 × 1011 ± 9 × 109 | CA-SCB | 3.96 ± 0.12 | 1.03 ± 0.05 |
| UP water | 7.00 ± 0.32 | 8 × 10−5 ± 10−6 | ||||
| SC-SBB | 10.18 ± 0.14 | 0.52 ± 0.03 | ||||
| ITN6D | 6%T6 | 343 ± 12 | 2.0 × 1012 ± 0 | CA-SCB | 3.96 ± 0.12 | 1.03 ± 0.05 |
| UP water | 7.00 ± 0.32 | 8 × 10−5 ± 10−6 | ||||
| SC-SBB | 10.18 ± 0.14 | 0.52 ± 0.03 | ||||
| Reagent Type | Voltage (V) | Measured Value–Theoretical Value (°) | ||||
|---|---|---|---|---|---|---|
| −70~−60 V | −50~−40 V | −30~30 V | 40~50 V | 60~70 V | ||
| CA-SCB | ITNAD | >42 | ~10 | ~3 | ~6 | >34 |
| ITN6D | >54 | ~19 | ~2 | ~5 | >35 | |
| UP water | ITNAD | >34 | ~10 | ~3 | ~10 | >26 |
| ITN6D | >33 | ~6 | ~3 | ~4 | >28 | |
| SC-SBB | ITNAD | >37 | ~8 | ~3 | ~5 | >32 |
| ITN6D | >53 | ~19 | ~2 | ~3 | >35 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Jin, H.; Zhao, M.; Xu, F.; Jiang, Z. Research on the Asymmetric Phenomenon of Voltage Polarity Based on Dielectric Wetting. Materials 2024, 17, 2717. https://doi.org/10.3390/ma17112717
Ye Y, Jin H, Zhao M, Xu F, Jiang Z. Research on the Asymmetric Phenomenon of Voltage Polarity Based on Dielectric Wetting. Materials. 2024; 17(11):2717. https://doi.org/10.3390/ma17112717
Chicago/Turabian StyleYe, Yuxing, Hui Jin, Meng Zhao, Fengying Xu, and Zhuo Jiang. 2024. "Research on the Asymmetric Phenomenon of Voltage Polarity Based on Dielectric Wetting" Materials 17, no. 11: 2717. https://doi.org/10.3390/ma17112717
APA StyleYe, Y., Jin, H., Zhao, M., Xu, F., & Jiang, Z. (2024). Research on the Asymmetric Phenomenon of Voltage Polarity Based on Dielectric Wetting. Materials, 17(11), 2717. https://doi.org/10.3390/ma17112717






