The Effect of Cesium Incorporation on the Vibrational and Elastic Properties of Methylammonium Lead Chloride Perovskite Single Crystals
Abstract
:1. Introduction
2. Experimental Section
2.1. Precursors
2.2. Single-Crystal Synthesis
2.3. Characterization Techniques
3. Results and Discussions
3.1. Structure of the Grown Mixed Crystals
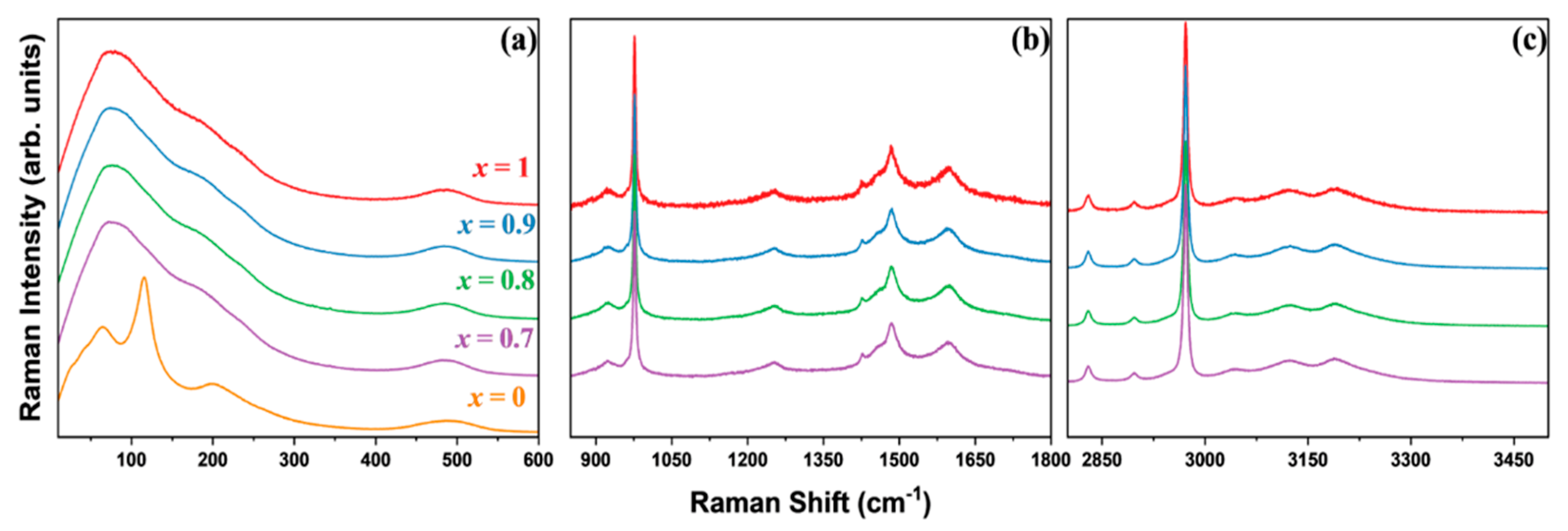
3.2. Vibrational Properties Probed Using Raman Spectroscopy
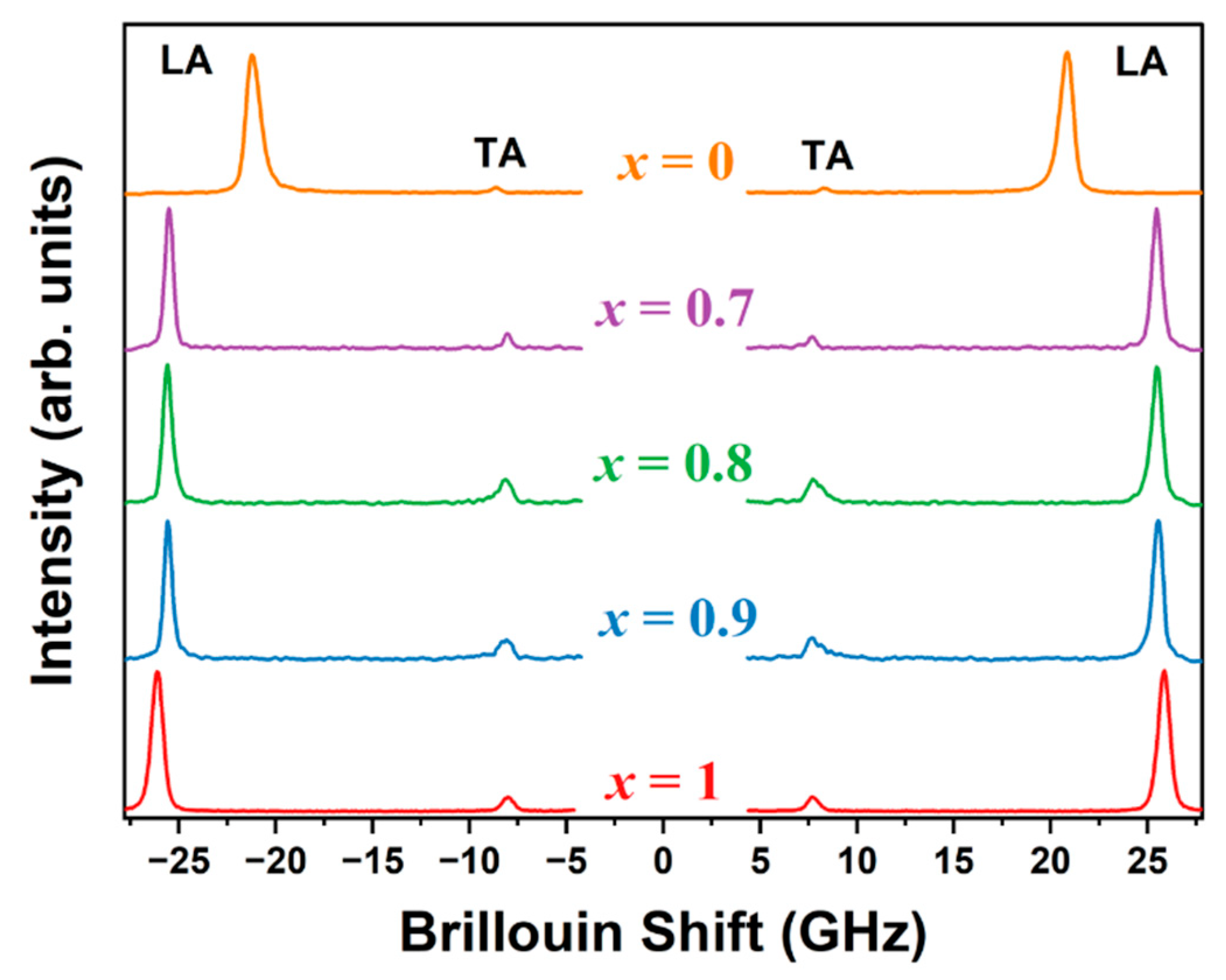
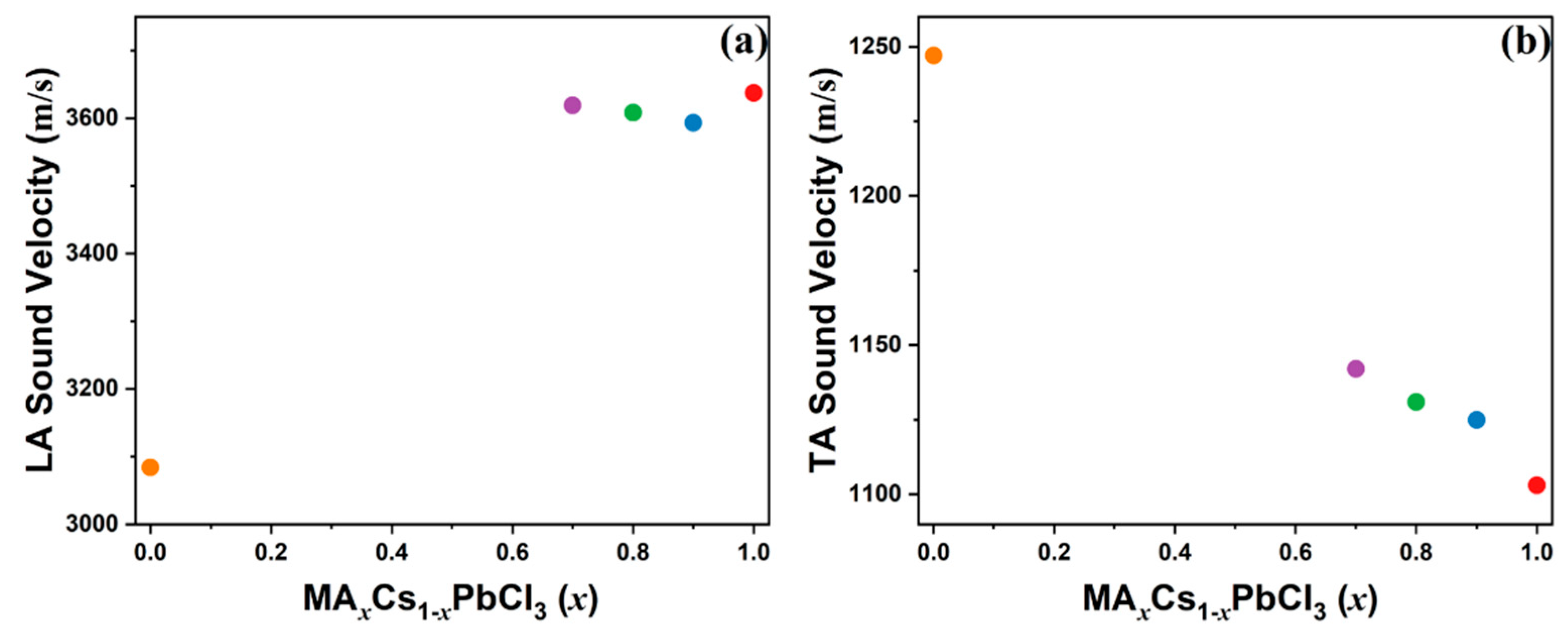
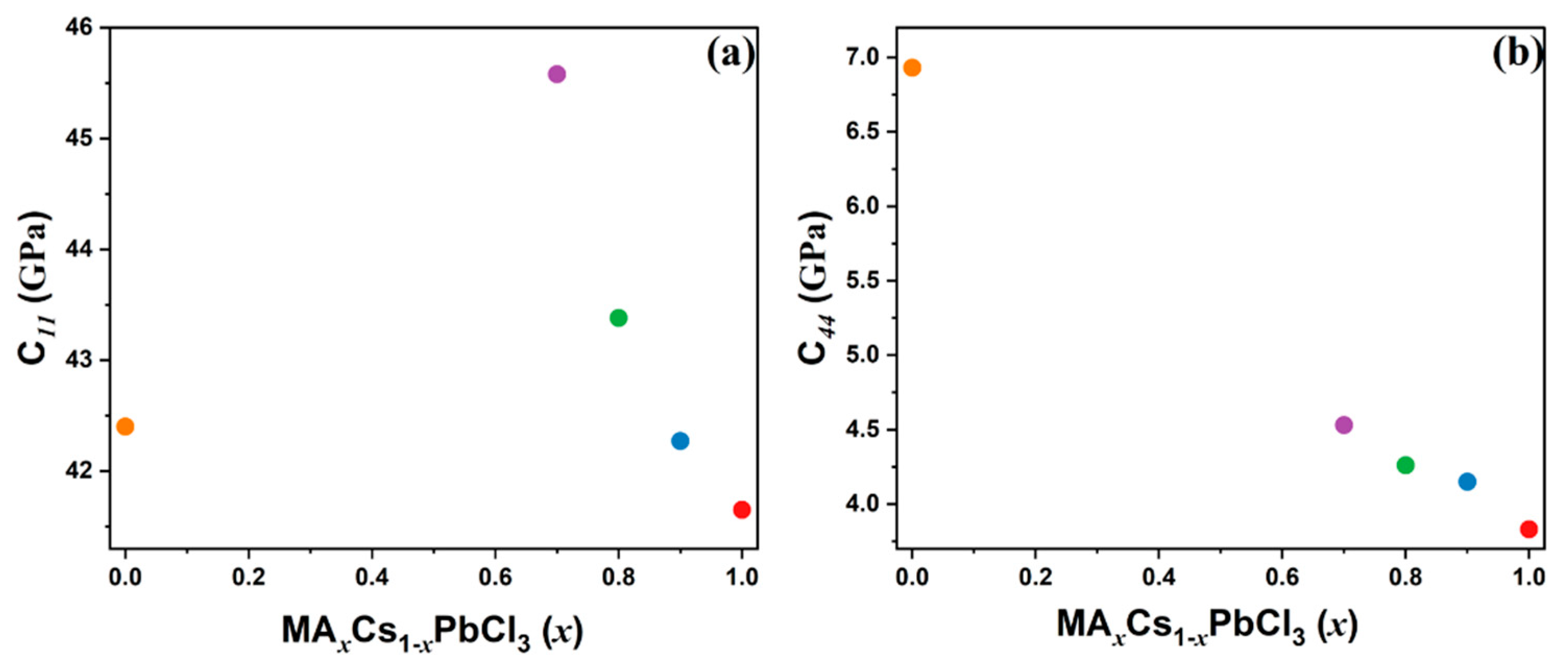
3.3. Elastic Properties Probed Using Brillouin Spectroscopy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Zhu, K. Organic-Inorganic Hybrid Lead Halide Perovskites for Optoelectronic and Electronic Applications. Chem. Soc. Rev. 2016, 45, 655–689. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Adinolfi, V.; Comin, R.; Yuan, M.; Alarousu, E.; Buin, A.; Chen, Y.; Hoogland, S.; Rothenberger, A.; Katsiev, K.; et al. Low Trap-State Density and Long Carrier Diffusion in Organolead Trihalide Perovskite Single Crystals. Science 2015, 347, 519–522. [Google Scholar] [CrossRef] [PubMed]
- De Wolf, S.; Holovsky, J.; Moon, S.J.; Löper, P.; Niesen, B.; Ledinsky, M.; Haug, F.J.; Yum, J.H.; Ballif, C. Organometallic Halide Perovskites: Sharp Optical Absorption Edge and Its Relation to Photovoltaic Performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef] [PubMed]
- Dou, L.; Yang, Y.M.; You, J.; Hong, Z.; Chang, W.H.; Li, G.; Yang, Y. Solution-Processed Hybrid Perovskite Photodetectors with High Detectivity. Nat. Commun. 2014, 5, 5404. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Liu, K.; Yang, J.; Chen, X.; Xie, X.; Li, B.; Zhang, Z.; Liu, L.; Shan, C.; Shen, D. High-Performance Planar-Type Ultraviolet Photodetector Based on High-Quality CH3NH3PbCl3 Perovskite Single Crystals. ACS Appl. Mater. Interfaces 2019, 11, 34144–34150. [Google Scholar] [CrossRef] [PubMed]
- Burschka, J.; Pellet, N.; Moon, S.J.; Humphry-Baker, R.; Gao, P.; Nazeeruddin, M.K.; Grätzel, M. Sequential Deposition as a Route to High-Performance Perovskite-Sensitized Solar Cells. Nature 2013, 499, 316–319. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient Hybrid Solar Cells Based on Meso-Superstructured Halide Perovskites. Science 2012, 338, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.J.; Seo, G.; Chua, M.R.; Park, T.G.; Lu, Y.; Rotermund, F.; Kim, Y.K.; Moon, C.S.; Jeon, N.J.; Correa-Baena, J.P.; et al. Efficient Perovskite Solar Cells via Improved Carrier Management. Nature 2021, 590, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Min, H.; Lee, D.Y.; Kim, J.; Kim, G.; Lee, K.S.; Kim, J.; Paik, M.J.; Kim, Y.K.; Kim, K.S.; Kim, M.G.; et al. Perovskite Solar Cells with Atomically Coherent Interlayers on SnO2 Electrodes. Nature 2021, 598, 444–450. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, S.; Kakekhani, A.; Park, J.; Park, J.; Lee, Y.H.; Xu, H.; Nagane, S.; Wexler, R.B.; Kim, D.H.; et al. Comprehensive Defect Suppression in Perovskite Nanocrystals for High-Efficiency Light-Emitting Diodes. Nat. Photonics 2021, 15, 148–155. [Google Scholar] [CrossRef]
- Zia, W.; Malekshahi Byranvand, M.; Rudolph, T.; Rai, M.; Kot, M.; Das, C.; Kedia, M.; Zohdi, M.; Zuo, W.; Yeddu, V.; et al. MAPbCl3 Light Absorber for Highest Voltage Perovskite Solar Cells. ACS Energy Lett. 2024, 9, 1017–1024. [Google Scholar] [CrossRef]
- Snaith, H.J. Perovskites: The Emergence of a New Era for Low-Cost, High-Efficiency Solar Cells. J. Phys. Chem. Lett. 2013, 4, 3623–3630. [Google Scholar] [CrossRef]
- Grätzel, M. The Light and Shade of Perovskite Solar Cells. Nat. Mater. 2014, 13, 838–842. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Misra, R.K.; Aharon, S.; Li, B.; Mogilyansky, D.; Visoly-Fisher, I.; Etgar, L.; Katz, E.A. Temperature- and Component-Dependent Degradation of Perovskite Photovoltaic Materials under Concentrated Sunlight. J. Phys. Chem. Lett. 2015, 6, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Conings, B.; Drijkoningen, J.; Gauquelin, N.; Babayigit, A.; D’Haen, J.; D’Olieslaeger, L.; Ethirajan, A.; Verbeeck, J.; Manca, J.; Mosconi, E.; et al. Intrinsic Thermal Instability of Methylammonium Lead Trihalide Perovskite. Adv. Energy Mater. 2015, 5, 1500477. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of P-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Eperon, G.E.; Stranks, S.D.; Menelaou, C.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. Formamidinium Lead Trihalide: A Broadly Tunable Perovskite for Efficient Planar Heterojunction Solar Cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Kanatzidis, M.G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef]
- Lee, J.W.; Seol, D.J.; Cho, A.N.; Park, N.G. High-Efficiency Perovskite Solar Cells Based on the Black Polymorph of HC(NH2)2PbI3. Adv. Mater. 2014, 26, 4991–4998. [Google Scholar] [CrossRef]
- Jeon, N.J.; Noh, J.H.; Yang, W.S.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S. Il Compositional Engineering of Perovskite Materials for High-Performance Solar Cells. Nature 2015, 517, 476–480. [Google Scholar] [CrossRef]
- Møller, C.K. Crystal Structure and Photoconductivity of Cæsium Plumbohalides. Nature 1958, 182, 1436. [Google Scholar] [CrossRef]
- Tsai, H.; Nie, W.; Blancon, J.C.; Stoumpos, C.C.; Asadpour, R.; Harutyunyan, B.; Neukirch, A.J.; Verduzco, R.; Crochet, J.J.; Tretiak, S.; et al. High-Efficiency Two-Dimensional Ruddlesden-Popper Perovskite Solar Cells. Nature 2016, 536, 312–317. [Google Scholar] [CrossRef]
- Cao, D.H.; Stoumpos, C.C.; Farha, O.K.; Hupp, J.T.; Kanatzidis, M.G. 2D Homologous Perovskites as Light-Absorbing Materials for Solar Cell Applications. J. Am. Chem. Soc. 2015, 137, 7843–7850. [Google Scholar] [CrossRef] [PubMed]
- Pellet, N.; Gao, P.; Gregori, G.; Yang, T.Y.; Nazeeruddin, M.K.; Maier, J.; Grätzel, M. Mixed-Organic-Cation Perovskite Photovoltaics for Enhanced Solar-Light Harvesting. Angew. Chem.-Int. Ed. 2014, 53, 3151–3157. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X.; Jiang, Q.; Wang, P.; Yin, Z.; Zhang, X.; Tan, H.; Yang, Y.M.; Wei, M.; Sutherland, B.R.; et al. Ultra-Bright and Highly Efficient Inorganic Based Perovskite Light-Emitting Diodes. Nat. Commun. 2017, 8, 15640. [Google Scholar] [CrossRef]
- Noh, J.H.; Im, S.H.; Heo, J.H.; Mandal, T.N.; Seok, S. Il Chemical Management for Colorful, Efficient, and Stable Inorganic-Organic Hybrid Nanostructured Solar Cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- Correa Baena, J.P.; Steier, L.; Tress, W.; Saliba, M.; Neutzner, S.; Matsui, T.; Giordano, F.; Jacobsson, T.J.; Srimath Kandada, A.R.; Zakeeruddin, S.M.; et al. Highly Efficient Planar Perovskite Solar Cells through Band Alignment Engineering. Energy Environ. Sci. 2015, 8, 2928–2934. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J.; Kim, H.B.; Kim, S.; Walker, B.; Kim, G.H.; Kim, J.Y. Cesium-Doped Methylammonium Lead Iodide Perovskite Light Absorber for Hybrid Solar Cells. Nano Energy 2014, 7, 80–85. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, D.H.; Kim, H.S.; Seo, S.W.; Cho, S.M.; Park, N.G. Formamidinium and Cesium Hybridization for Photo- and Moisture-Stable Perovskite Solar Cell. Adv. Energy Mater. 2015, 5, 1501310. [Google Scholar] [CrossRef]
- Yi, C.; Luo, J.; Meloni, S.; Boziki, A.; Ashari-Astani, N.; Grätzel, C.; Zakeeruddin, S.M.; Röthlisberger, U.; Grätzel, M. Entropic Stabilization of Mixed A-Cation ABX3 Metal Halide Perovskites for High Performance Perovskite Solar Cells. Energy Environ. Sci. 2016, 9, 656–662. [Google Scholar] [CrossRef]
- McMeekin, D.P.; Sadoughi, G.; Rehman, W.; Eperon, G.E.; Saliba, M.; Hörantner, M.T.; Haghighirad, A.; Sakai, N.; Korte, L.; Rech, B.; et al. A Mixed-Cation Lead Mixed-Halide Perovskite Absorber for Tandem Solar Cells. Science 2016, 351, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Saliba, M.; Matsui, T.; Seo, J.Y.; Domanski, K.; Correa-Baena, J.P.; Nazeeruddin, M.K.; Zakeeruddin, S.M.; Tress, W.; Abate, A.; Hagfeldt, A.; et al. Cesium-Containing Triple Cation Perovskite Solar Cells: Improved Stability, Reproducibility and High Efficiency. Energy Environ. Sci. 2016, 9, 1989–1997. [Google Scholar] [CrossRef] [PubMed]
- Ibaceta-Jaña, J.; Muydinov, R.; Rosado, P.; Mirhosseini, H.; Chugh, M.; Nazarenko, O.; Dirin, D.N.; Heinrich, D.; Wagner, M.R.; Kühne, T.D.; et al. Vibrational Dynamics in Lead Halide Hybrid Perovskites Investigated by Raman Spectroscopy. Phys. Chem. Chem. Phys. 2020, 22, 5604–5614. [Google Scholar] [CrossRef] [PubMed]
- Svane, K.L.; Forse, A.C.; Grey, C.P.; Kieslich, G.; Cheetham, A.K.; Walsh, A.; Butler, K.T. How Strong Is the Hydrogen Bond in Hybrid Perovskites? J. Phys. Chem. Lett. 2017, 8, 6154–6159. [Google Scholar] [CrossRef] [PubMed]
- Yin, T.; Fang, Y.; Fan, X.; Zhang, B.; Kuo, J.L.; White, T.J.; Chow, G.M.; Yan, J.; Shen, Z.X. Hydrogen-Bonding Evolution during the Polymorphic Transformations in CH3NH3PbBr3: Experiment and Theory. Chem. Mater. 2017, 29, 5974–5981. [Google Scholar] [CrossRef]
- Dintakurti, S.S.H.; Walker, D.; Bird, T.A.; Fang, Y.; White, T.; Hanna, J.V. A Powder XRD, Solid State NMR and Calorimetric Study of the Phase Evolution in Mechanochemically Synthesized Dual Cation (Csx(CH3NH3)1−x)PbX3 Lead Halide Perovskite Systems. Phys. Chem. Chem. Phys. 2022, 24, 18004–18021. [Google Scholar] [CrossRef] [PubMed]
- Ko, U.H.; Ri, J.H.; Jang, J.H.; Ri, C.H.; Jong, U.G.; Yu, C.J. First-Principles Study on the Elastic, Electronic and Optical Properties of All-Inorganic Halide Perovskite Solid Solutions of CsPb(Br1−xClx)3 within the Virtual Crystal Approximation. RSC Adv. 2022, 12, 9755–9762. [Google Scholar] [CrossRef] [PubMed]
- Amat, A.; Mosconi, E.; Ronca, E.; Quarti, C.; Umari, P.; Nazeeruddin, M.K.; Grätzel, M.; De Angelis, F. Cation-Induced Band-Gap Tuning in Organohalide Perovskites: Interplay of Spin-Orbit Coupling and Octahedra Tilting. Nano Lett. 2014, 14, 3608–3616. [Google Scholar] [CrossRef]
- Calistru, D.M.; Mihut, L.; Lefrant, S.; Baltog, I. Identification of the Symmetry of Phonon Modes in CsPbCl3 in Phase IV by Raman and Resonance-Raman Scattering. J. Appl. Phys. 1997, 82, 5391–5395. [Google Scholar] [CrossRef]
- Maalej, A.; Abid, Y.; Kallel, A.; Daoud, A.; Lautié, A.; Romain, F. Phase Transitions and Crystal Dynamics in the Cubic Perovskite-CH3NH3PbCl3. Solid State Commun. 1997, 103, 279–284. [Google Scholar] [CrossRef]
- Niemann, R.G.; Kontos, A.G.; Palles, D.; Kamitsos, E.I.; Kaltzoglou, A.; Brivio, F.; Falaras, P.; Cameron, P.J. Halogen Effects on Ordering and Bonding of CH3NH3+ in CH3NH3PbX3 (X = Cl, Br, I) Hybrid Perovskites: A Vibrational Spectroscopic Study. J. Phys. Chem. C 2016, 120, 2509–2519. [Google Scholar] [CrossRef]
- Liao, M.; Shan, B.; Li, M. In Situ Raman Spectroscopic Studies of Thermal Stability of All-Inorganic Cesium Lead Halide (CsPbX3, X = Cl, Br, I) Perovskite Nanocrystals. J. Phys. Chem. Lett. 2019, 10, 1217–1225. [Google Scholar] [CrossRef] [PubMed]
- Théorêt, A.; Sandorfy, C. The Infrared Spectra of Solid Methylammonium Halides-II. Spectrochim. Acta A 1967, 23, 519–542. [Google Scholar] [CrossRef]
- Carabatos-Nédelec, C.; Oussaïd, M.; Nitsch, K. Raman Scattering Investigation of Cesium Plumbochloride, CsPbCl3, Phase Transitions. J. Raman Spectrosc. 2003, 34, 388–393. [Google Scholar] [CrossRef]
- Glaser, T.; Müller, C.; Sendner, M.; Krekeler, C.; Semonin, O.E.; Hull, T.D.; Yaffe, O.; Owen, J.S.; Kowalsky, W.; Pucci, A.; et al. Infrared Spectroscopic Study of Vibrational Modes in Methylammonium Lead Halide Perovskites. J. Phys. Chem. Lett. 2015, 6, 2913–2918. [Google Scholar] [CrossRef] [PubMed]
- Leguy, A.M.A.; Goñi, A.R.; Frost, J.M.; Skelton, J.; Brivio, F.; Rodríguez-Martínez, X.; Weber, O.J.; Pallipurath, A.; Alonso, M.I.; Campoy-Quiles, M.; et al. Dynamic Disorder, Phonon Lifetimes, and the Assignment of Modes to the Vibrational Spectra of Methylammonium Lead Halide Perovskites. Phys. Chem. Chem. Phys. 2016, 18, 27051–27066. [Google Scholar] [CrossRef]
- Yesudhas, S.; Burns, R.; Lavina, B.; Tkachev, S.N.; Sun, J.; Ullrich, C.A.; Guha, S. Coupling of Organic Cation and Inorganic Lattice in Methylammonium Lead Halide Perovskites: Insights into a Pressure-Induced Isostructural Phase Transition. Phys. Rev. Mater. 2020, 4, 105403. [Google Scholar] [CrossRef]
- Yaffe, O.; Guo, Y.; Tan, L.Z.; Egger, D.A.; Hull, T.; Stoumpos, C.C.; Zheng, F.; Heinz, T.F.; Kronik, L.; Kanatzidis, M.G.; et al. Local Polar Fluctuations in Lead Halide Perovskite Crystals. Phys. Rev. Lett. 2017, 118, 136001. [Google Scholar] [CrossRef] [PubMed]
- Onoda-Yamamuro, N.; Matsuo, T.; Suga, H. Calorimetric and IR Spectroscopic Studies of Phase Transitions in Methylammonium Trihalogenoplumbates (II). J. Phys. Chem. Solids 1990, 51, 1383–1395. [Google Scholar] [CrossRef]
- Ding, J.; Du, S.; Zhou, T.; Yuan, Y.; Cheng, X.; Jing, L.; Yao, Q.; Zhang, J.; He, Q.; Cui, H.; et al. Cesium Decreases Defect Density and Enhances Optoelectronic Properties of Mixed MA1−XCs XPbBr3 Single Crystal. J. Phys. Chem. C 2019, 123, 14969–14975. [Google Scholar] [CrossRef]
- Premkumar, S.; Kundu, K.; Umapathy, S. Impact of Cesium in Methylammonium Lead Bromide Perovskites: Insights into the Microstructures, Stability and Photophysical Properties. Nanoscale 2019, 11, 10292–10305. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zha, G.; Deng, C.; An, Y.; Mao, R.; Liu, Y.; Lu, Y.; Chen, Z. Refractive Index Dispersion of Organic–Inorganic Hybrid Halide Perovskite CH3NH3PbX3 (X = Cl, Br, I) Single Crystals. Cryst. Res. Technol. 2019, 54, 1407–1416. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, L.; Liu, X.; Liu, Z.; Gu, H.; Bo, S.; Liao, G. Optimizing the Design of the Vapor-Deposited CsPbCl3-Based Optoelectronic Devices via Simulations and Experiments. Adv. Funct. Mater. 2024, 34, 2310945. [Google Scholar] [CrossRef]

| Concentration | Cubic Phase | Orthorhombic Phase |
|---|---|---|
| x = 0.9 | 132 nm | 116 nm |
| x = 0.8 | 124 nm | 105 nm |
| x = 0.7 | 100 nm | 91 nm |
| x = 1 (cm−1) | x = 0.9 (cm−1) | x = 0.8 (cm−1) | x = 0.7 (cm−1) | x = 0 (cm−1) | Mode Assignment |
|---|---|---|---|---|---|
| 23 | PbCl6 vibrations [40] | ||||
| 36 | 36 | 36 | 36 | 41 | PbCl6 vibrations [40,41] |
| 63 | 62 | 62 | 63 | 64 | PbCl6 vibrations [40,41] |
| 90 | 89 | 89 | 90 | δs (Cl-Pb-Cl) [42] | |
| 109 | PbCl6 vibrations [40,43] | ||||
| 116 | PbCl6 vibrations [40,43] | ||||
| 122 | 122 | 122 | 123 | δas (Cl-Pb-Cl) [42] | |
| 182 | 182 | 182 | 182 | νas (Pb–Cl) [42] | |
| 203 | First-order phonon mode [40] | ||||
| 239 | 235 | 235 | 234 | R+ of the MA cation [41] | |
| 484 | 485 | 485 | 485 | τ (MA) [41,44] | |
| 488 | Second-order phonon mode [40,45] | ||||
| 922 | 921 | 921 | 921 | ρ (MA) [41,44] | |
| 977 | 977 | 977 | 977 | ν (C–N) [44] | |
| 1253 | 1253 | 1252 | 1253 | ρ (MA) [46] | |
| 1427 | 1427 | 1427 | 1427 | δs (CH3) [44] | |
| 1455 | 1455 | 1455 | 1456 | δas (CH3) [44] | |
| 1485 | 1485 | 1485 | 1485 | δs (NH3) [46] | |
| 1598 | 1597 | 1598 | 1597 | δas (NH3) [46] | |
| 2830 | 2830 | 2830 | 2830 | νas (C–H) [47] | |
| 2897 | 2897 | 2897 | 2897 | νs (C–H) [47] | |
| 2947 | 2946 | 2947 | 2947 | Symmetric CH3 stretch [46] | |
| 2972 | 2972 | 2972 | 2972 | νs (C–H) [47] | |
| 3042 | 3043 | 3043 | 3042 | νas (N–H) [47] | |
| 3120 | 3120 | 3120 | 3120 | νs (N–H) [47] | |
| 3189 | 3189 | 3190 | 3190 | νs (N–H) [47] |
| Raman Mode | x = 1 | x = 0.9 | x = 0.8 | x = 0.7 |
|---|---|---|---|---|
| PbCl6 octahedral mode (~122 cm−1) | 72 fs | 68 fs | 66 fs | 68 fs |
| Torsional mode (~484 cm−1) | 72 fs | 71 fs | 72 fs | 71 fs |
| C–N stretching mode (~977 cm−1) | 1001 fs | 913 fs | 927 fs | 920 fs |
| Composition | VLA (m/s) | VTA (m/s) | C11 (GPa) | C44 (GPa) |
|---|---|---|---|---|
| x = 1 | 3637 | 1103 | 41.65 | 3.83 |
| x = 0.9 | 3593 | 1125 | 42.27 | 4.15 |
| x = 0.8 | 3608 | 1131 | 43.38 | 4.26 |
| x = 0.7 | 3619 | 1142 | 45.58 | 4.31 |
| x = 0 (a) | 3084 | 1247 | 42.40 | 6.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junaid, S.B.; Naqvi, F.H.; Ko, J.-H. The Effect of Cesium Incorporation on the Vibrational and Elastic Properties of Methylammonium Lead Chloride Perovskite Single Crystals. Materials 2024, 17, 2862. https://doi.org/10.3390/ma17122862
Junaid SB, Naqvi FH, Ko J-H. The Effect of Cesium Incorporation on the Vibrational and Elastic Properties of Methylammonium Lead Chloride Perovskite Single Crystals. Materials. 2024; 17(12):2862. https://doi.org/10.3390/ma17122862
Chicago/Turabian StyleJunaid, Syed Bilal, Furqanul Hassan Naqvi, and Jae-Hyeon Ko. 2024. "The Effect of Cesium Incorporation on the Vibrational and Elastic Properties of Methylammonium Lead Chloride Perovskite Single Crystals" Materials 17, no. 12: 2862. https://doi.org/10.3390/ma17122862






