Multiphase Reconstruction of Heterogeneous Materials Using Machine Learning and Quality of Connection Function
Abstract
1. Introduction
2. Materials and Methods
2.1. Initial Input
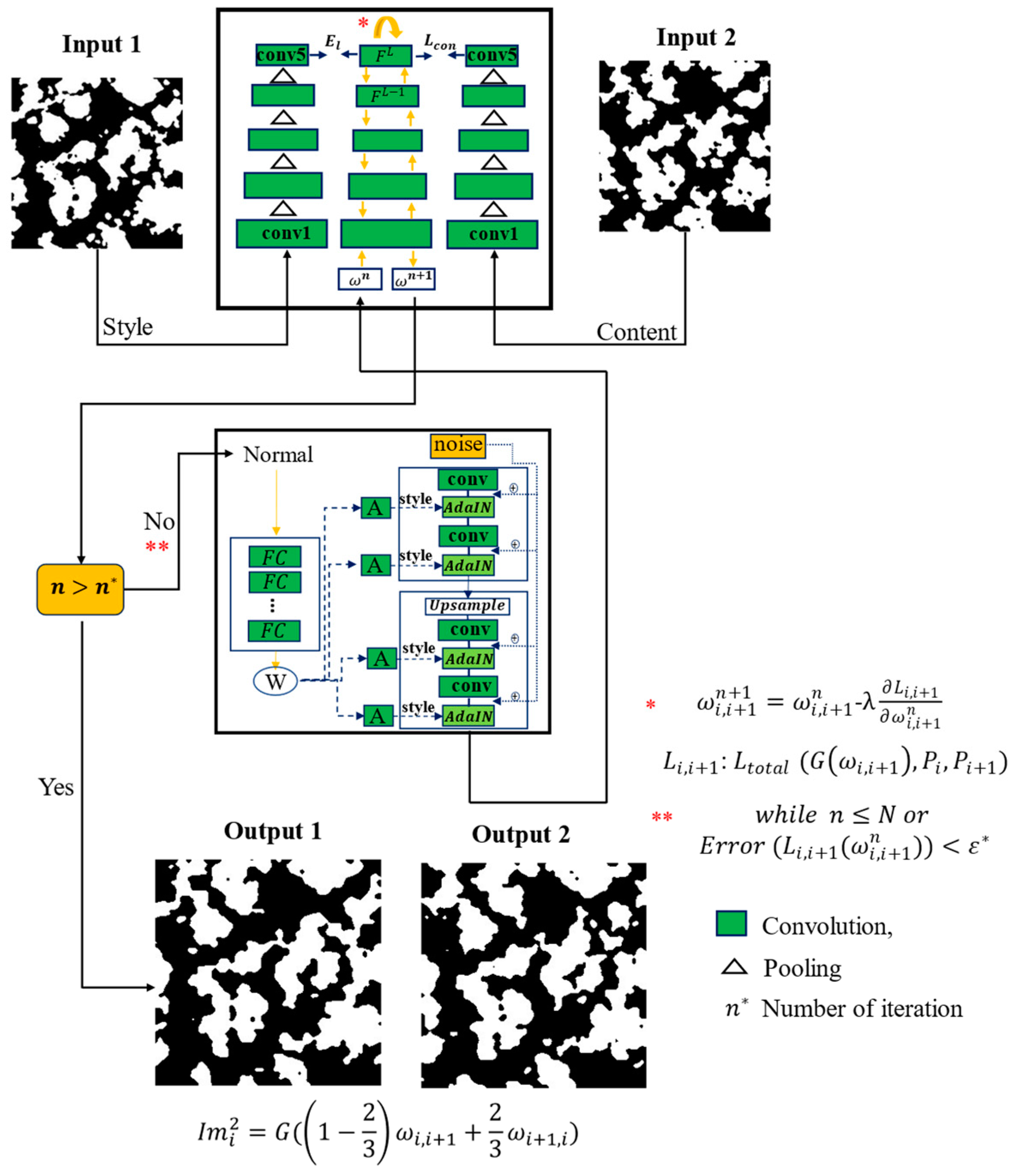
2.2. Representation of Optimized Transfer Learning Method for 3D Reconstruction of the Structure
3. Results and Discussion
4. Conclusions
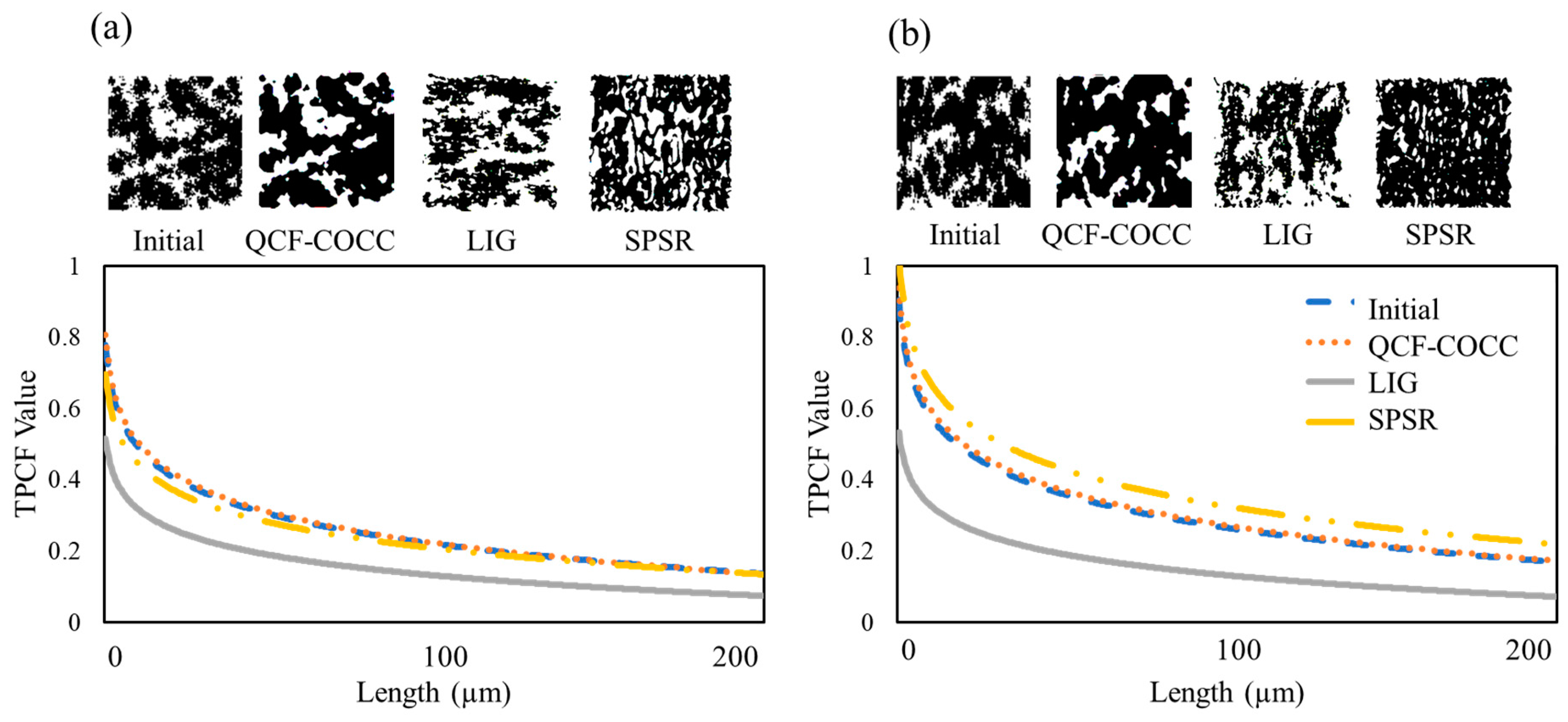
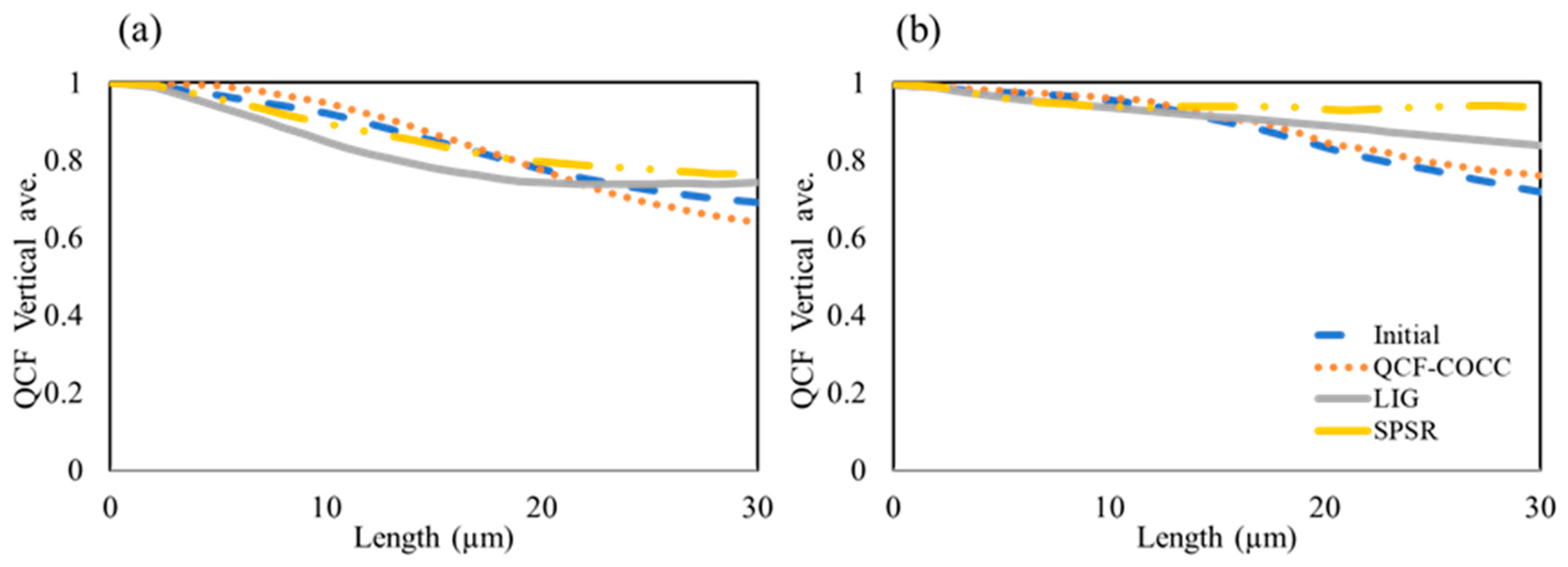
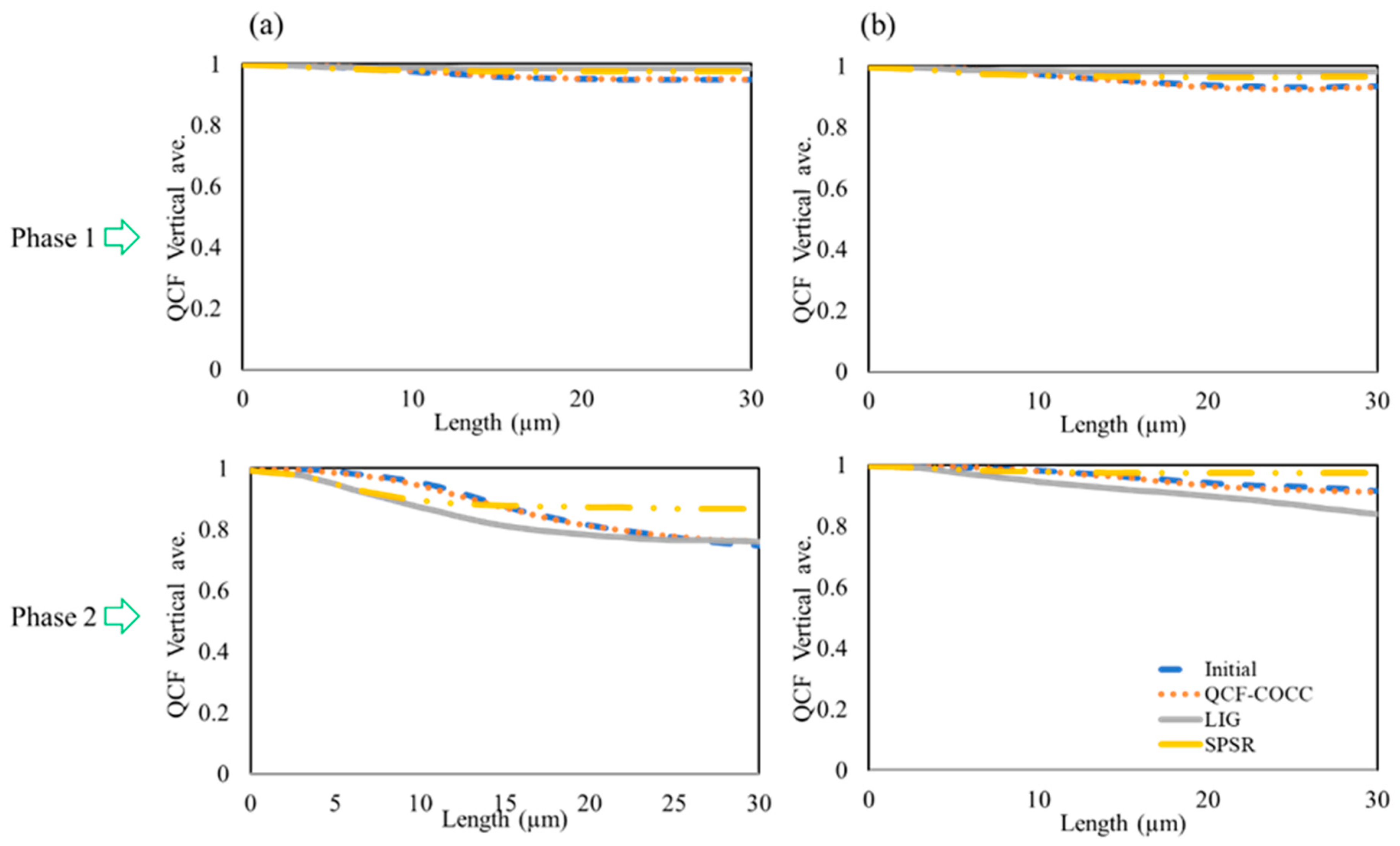
- It was demonstrated that the QCF-COCC model excels in reconstructing the 3D microstructure of both isotropic and anisotropic materials with two and three phases. This model notably outperforms other methods such as Screened Poisson Surface Reconstruction (SPSR) and Local Implicit Grid (LIG) representations, particularly in capturing detailed features within the microstructures’ inner regions.
- In terms of phase accuracy and detail, the QCF-COCC model accurately distinguishes and connects different phases in reconstructed 3D structures without any phase separation. This represents a significant advantage over other examined models, which frequently struggle with phase distinction and detailed reconstruction.
- Visual comparisons and statistical analyses confirm the superior performance of the QCF-COCC model. This model not only replicates the intricate geometries of various materials structures with greater accuracy but also maintains high fidelity to the original 2D images used as inputs.
- The QCF-COCC model significantly advances 3D microstructure reconstruction, showing consistent QCF trends across various materials. The model’s superior phase connectivity and structural fidelity, validated by close alignment of QCF and TPCF values of cut-sections of reconstructed microstructure with initial images, underscore its accuracy and reliability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sebdani, M.M.; Baniassadi, M.; Jamali, J.; Ahadiparast, M.; Abrinia, K.; Safdari, M. Designing an optimal 3D microstructure for three-phase solid oxide fuel cell anodes with maximal active triple phase boundary length (TPBL). Int. J. Hydrogen Energy 2015, 40, 15585–15596. [Google Scholar] [CrossRef]
- Brahme, A.; Alvi, M.; Saylor, D.; Fridy, J.; Rollett, A. 3D reconstruction of microstructure in a commercial purity aluminum. Scr. Mater. 2006, 55, 75–80. [Google Scholar] [CrossRef]
- Uchic, M.D.; Holzer, L.; Inkson, B.J.; Principe, E.L.; Munroe, P. Three-dimensional microstructural characterization using focused ion beam tomography. MRS Bull. 2007, 32, 408–416. [Google Scholar] [CrossRef]
- Echlin, M.P.; Burnett, T.L.; Polonsky, A.T.; Pollock, T.M.; Withers, P.J. Serial sectioning in the SEM for three dimensional materials science. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100817. [Google Scholar] [CrossRef]
- Li, X.; Duan, L.; Zhou, S.; Liu, X.; Yao, Z.; Yan, Z. Freeze-Casting of Alumina and Permeability Analysis Based on a 3D Microstructure Reconstructed Using Generative Adversarial Networks. Materials 2024, 17, 2432. [Google Scholar] [CrossRef]
- Mura, F.; Cognigni, F.; Ferroni, M.; Morandi, V.; Rossi, M. Advances in Focused Ion Beam Tomography for Three-Dimensional Characterization in Materials Science. Materials 2023, 16, 5808. [Google Scholar] [CrossRef] [PubMed]
- Seyed Mahmoud, S.M.A.; Faraji, G.; Baghani, M.; Hashemi, M.S.; Sheidaei, A.; Baniassadi, M. Design of Refractory Alloys for Desired Thermal Conductivity via AI-Assisted In-Silico Microstructure Realization. Materials 2023, 16, 1088. [Google Scholar] [CrossRef] [PubMed]
- Jing, H.; Dan, H.; Shan, H.; Liu, X. Investigation on Three-Dimensional Void Mesostructures and Geometries in Porous Asphalt Mixture Based on Computed Tomography (CT) Images and Avizo. Materials 2023, 16, 7426. [Google Scholar] [CrossRef] [PubMed]
- Groeber, M.A.; Haley, B.; Uchic, M.D.; Dimiduk, D.M.; Ghosh, S. 3D reconstruction and characterization of polycrystalline microstructures using a FIB–SEM system. Mater. Charact. 2006, 57, 259–273. [Google Scholar] [CrossRef]
- Xu, H.; Bae, C. Stochastic 3D microstructure reconstruction and mechanical modeling of anisotropic battery separators. J. Power Sources 2019, 430, 67–73. [Google Scholar] [CrossRef]
- Landis, E.N.; Keane, D.T. X-ray microtomography. Mater. Charact. 2010, 61, 1305–1316. [Google Scholar] [CrossRef]
- Brilakis, I.; Fathi, H.; Rashidi, A. Progressive 3D reconstruction of infrastructure with videogrammetry. Autom. Constr. 2011, 20, 884–895. [Google Scholar] [CrossRef]
- Politis, M.; Kikkinides, E.; Kainourgiakis, M.; Stubos, A. A hybrid process-based and stochastic reconstruction method of porous media. Microporous Mesoporous Mater. 2008, 110, 92–99. [Google Scholar] [CrossRef]
- Zhang, W.; Song, L.; Li, J. Efficient 3D reconstruction of random heterogeneous media via random process theory and stochastic reconstruction procedure. Comput. Methods Appl. Mech. Eng. 2019, 354, 1–15. [Google Scholar] [CrossRef]
- Wang, G.; Ye, J.C.; De Man, B. Deep learning for tomographic image reconstruction. Nat. Mach. Intell. 2020, 2, 737–748. [Google Scholar] [CrossRef]
- Reader, A.J.; Corda, G.; Mehranian, A.; da Costa-Luis, C.; Ellis, S.; Schnabel, J.A. Deep learning for PET image reconstruction. IEEE Trans. Radiat. Plasma Med. Sci. 2020, 5, 1–25. [Google Scholar] [CrossRef]
- Zhang, H.-M.; Dong, B. A review on deep learning in medical image reconstruction. J. Oper. Res. Soc. China 2020, 8, 311–340. [Google Scholar] [CrossRef]
- Yamada, H.; Liu, C.; Wu, S.; Koyama, Y.; Ju, S.; Shiomi, J.; Morikawa, J.; Yoshida, R. Predicting materials properties with little data using shotgun transfer learning. ACS Cent. Sci. 2019, 5, 1717–1730. [Google Scholar] [CrossRef]
- Zhang, Y.; An, M. Deep learning-and transfer learning-based super resolution reconstruction from single medical image. J. Healthc. Eng. 2017, 2017, 5859727. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Zhao, H.; Burkhart, C.; Brinson, L.C.; Chen, W. A transfer learning approach for microstructure reconstruction and structure-property predictions. Sci. Rep. 2018, 8, 13461. [Google Scholar] [CrossRef]
- Bostanabad, R. Reconstruction of 3D microstructures from 2D images via transfer learning. Comput. Aided Des. 2020, 128, 102906. [Google Scholar] [CrossRef]
- Xu, Y.; Weng, H.; Ju, X.; Ruan, H.; Chen, J.; Nan, C.; Guo, J.; Liang, L. A method for predicting mechanical properties of composite microstructure with reduced dataset based on transfer learning. Compos. Struct. 2021, 275, 114444. [Google Scholar] [CrossRef]
- Bagherian, A.; Famouri, S.; Baghani, M.; George, D.; Sheidaei, A.; Baniassadi, M. A new statistical descriptor for the physical characterization and 3D reconstruction of heterogeneous materials. Transp. Porous Media 2022, 142, 23–40. [Google Scholar] [CrossRef]
- Gerstner, T.; Pajarola, R. Topology preserving and controlled topology simplifying multiresolution isosurface extraction. In Proceedings of the Visualization 2000. VIS 2000 (Cat. No.00CH37145), Salt Lake City, UT, USA, 8–13 October 2000. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Jiang, C.; Sud, A.; Makadia, A.; Huang, J.; Nießner, M.; Funkhouser, T. Local implicit grid representations for 3d scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6001–6010. [Google Scholar]
- Baniassadi, M.; Garmestani, H.; Li, D.; Ahzi, S.; Khaleel, M.; Sun, X. Three-phase solid oxide fuel cell anode microstructure realization using two-point correlation functions. Acta Mater. 2011, 59, 30–43. [Google Scholar] [CrossRef]
- Kurita, T. Principal component analysis (PCA). In Computer Vision: A Reference Guide; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–4. [Google Scholar]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Safar, A.A.; Salih, D.M.; Murshid, A.M. Pattern recognition using the multi-layer perceptron (MLP) for medical disease: A survey. Int. J. Nonlinear Anal. Appl. 2023, 14, 1989–1998. [Google Scholar]
- Dȩbska, B. SCANNET: A spectroscopy database. Anal. Chim. Acta 1992, 265, 201–209. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamidpour, P.; Araee, A.; Baniassadi, M.; Garmestani, H. Multiphase Reconstruction of Heterogeneous Materials Using Machine Learning and Quality of Connection Function. Materials 2024, 17, 3049. https://doi.org/10.3390/ma17133049
Hamidpour P, Araee A, Baniassadi M, Garmestani H. Multiphase Reconstruction of Heterogeneous Materials Using Machine Learning and Quality of Connection Function. Materials. 2024; 17(13):3049. https://doi.org/10.3390/ma17133049
Chicago/Turabian StyleHamidpour, Pouria, Alireza Araee, Majid Baniassadi, and Hamid Garmestani. 2024. "Multiphase Reconstruction of Heterogeneous Materials Using Machine Learning and Quality of Connection Function" Materials 17, no. 13: 3049. https://doi.org/10.3390/ma17133049
APA StyleHamidpour, P., Araee, A., Baniassadi, M., & Garmestani, H. (2024). Multiphase Reconstruction of Heterogeneous Materials Using Machine Learning and Quality of Connection Function. Materials, 17(13), 3049. https://doi.org/10.3390/ma17133049







