Research on the Analysis of Residual Stress in Heat Treatment of Bellows Using ABAQUS
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Material Performance Parameters
2.2. Residual Stress Measurement Experiment
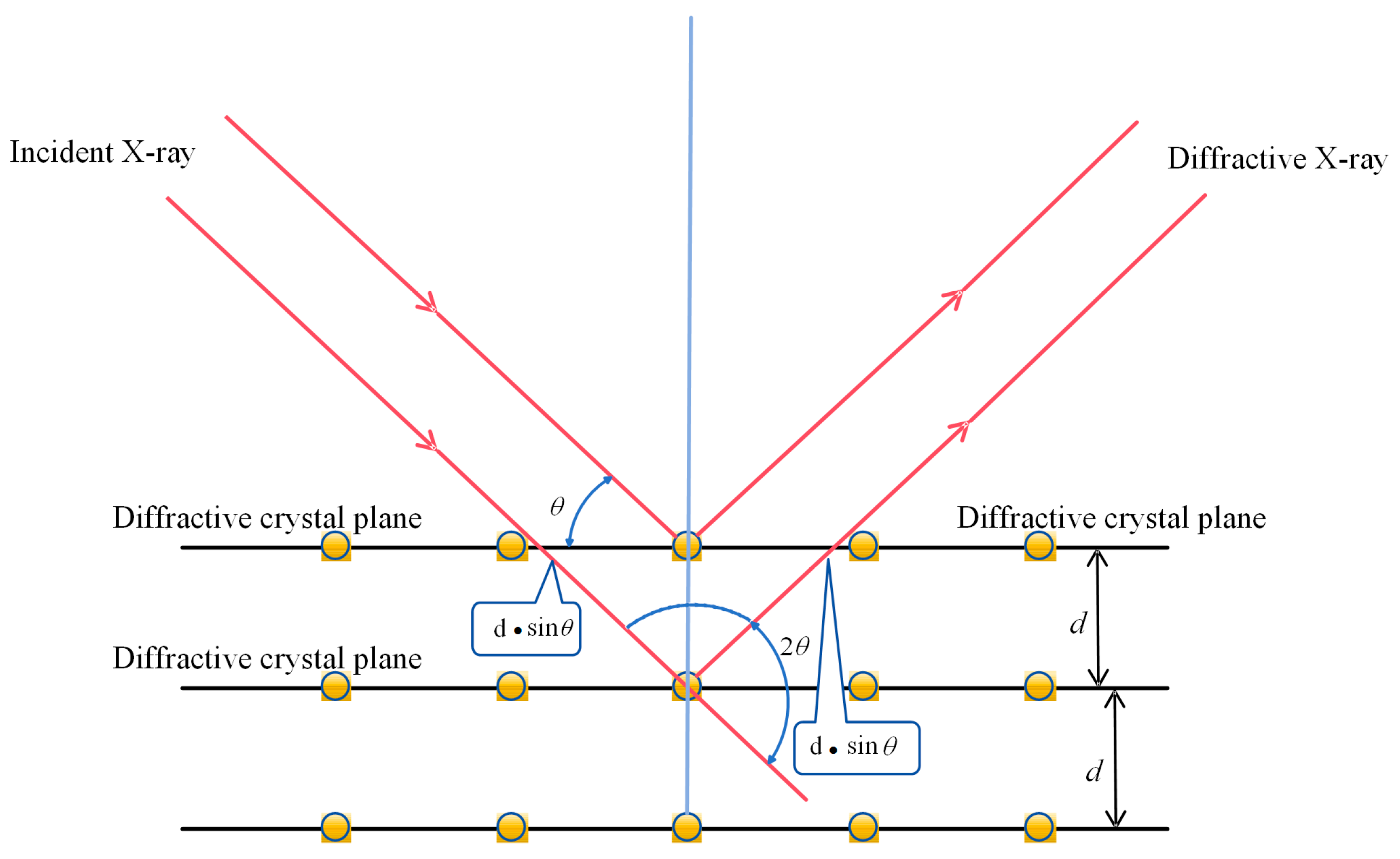
2.2.1. Measurement Principle
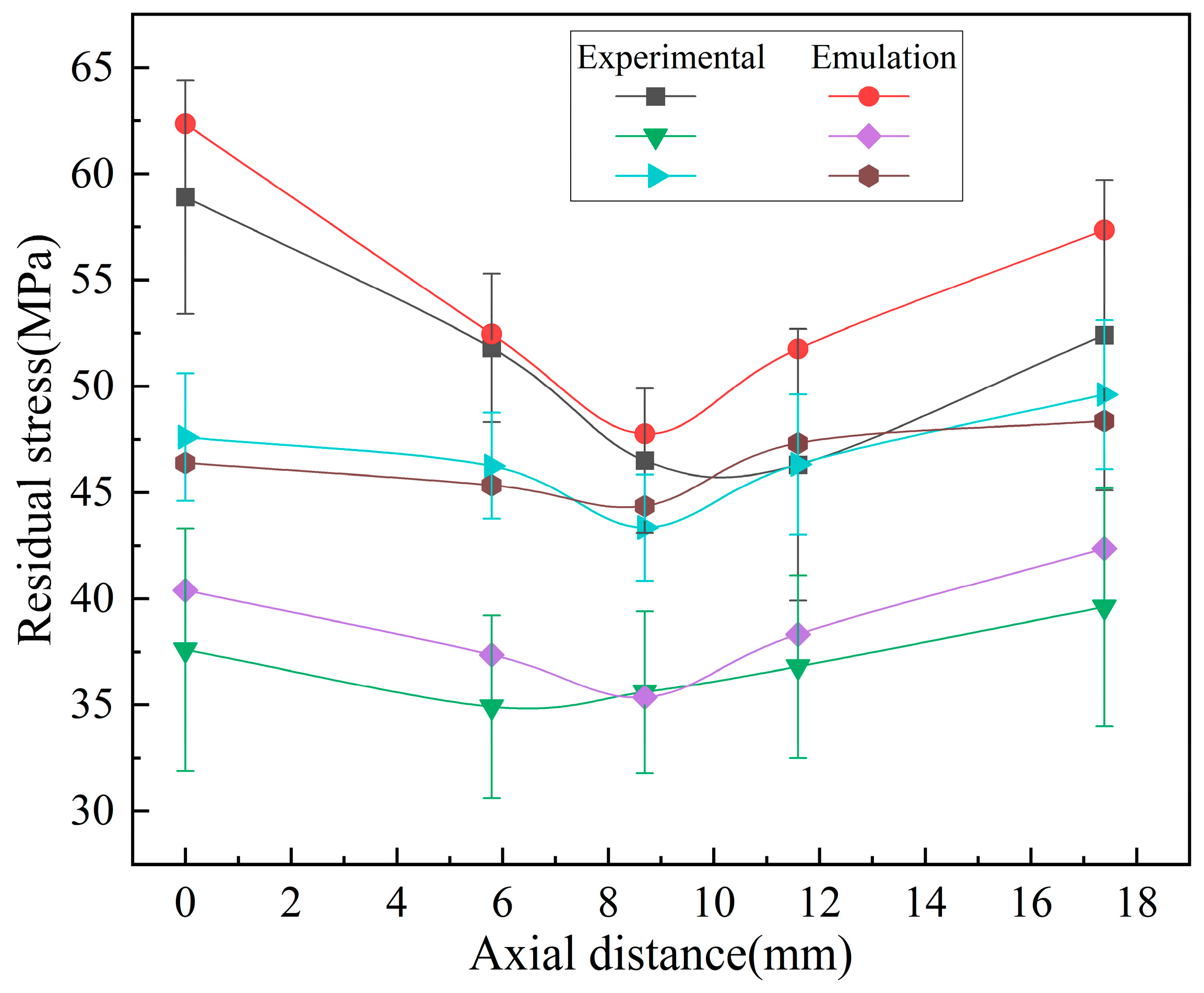
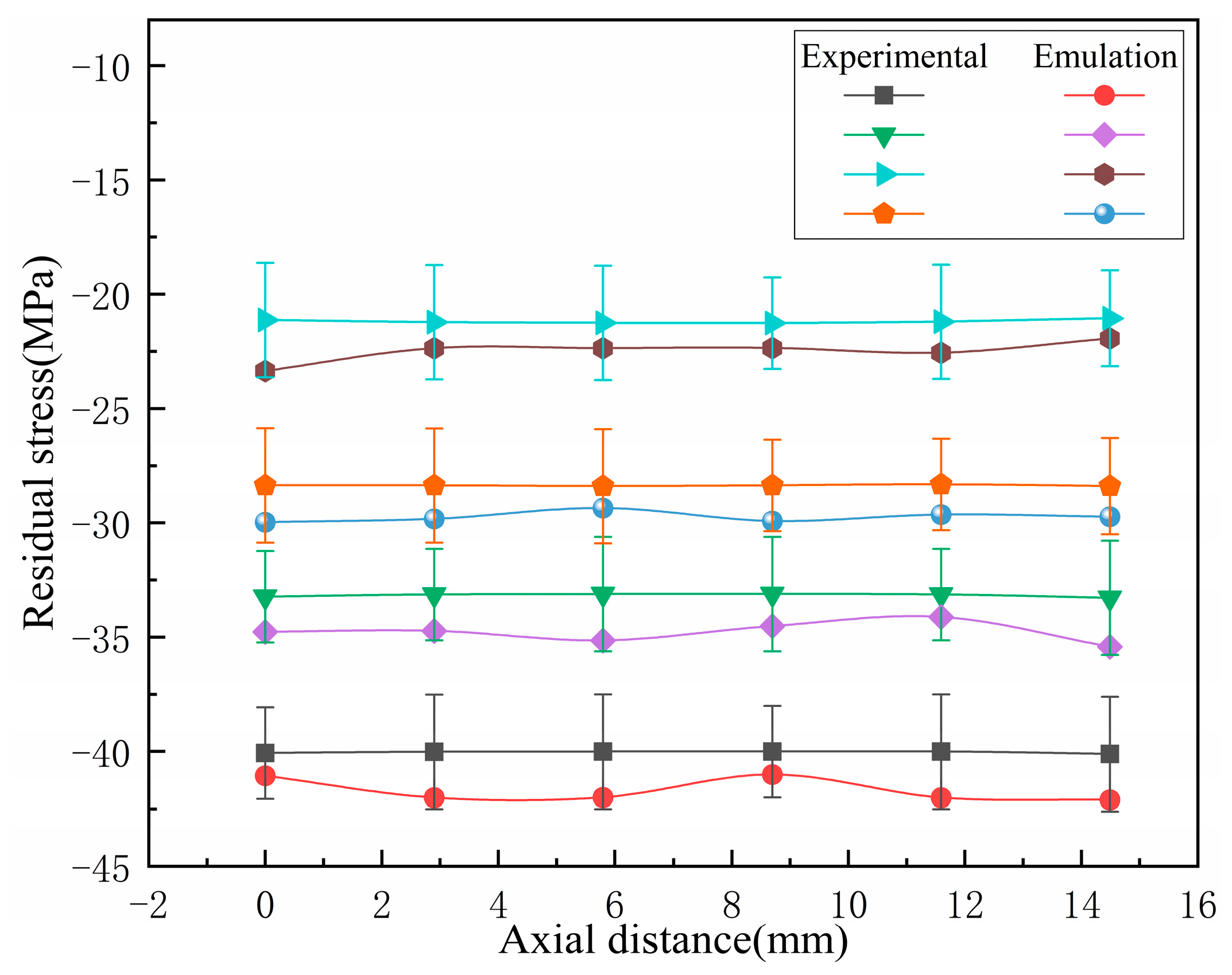
2.2.2. Residual Stress Measurement
2.3. Micro Organization and Macro Structure
2.4. Mechanism of Residual Stress Generation
3. Construction of Finite Element Model for Bellows
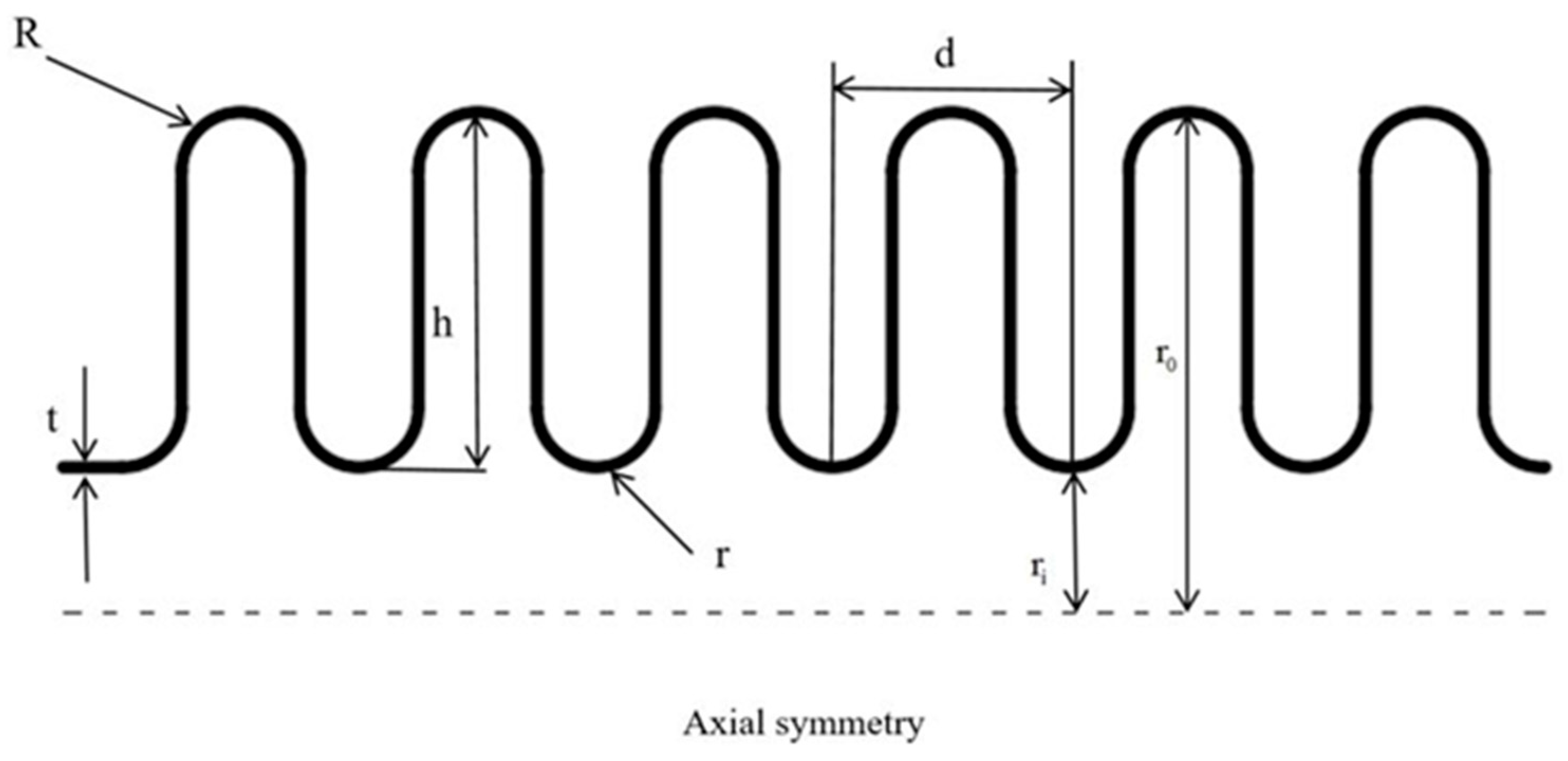
3.1. Geometric Model
3.2. Grid Division
3.3. Boundary Conditions
3.4. Theoretical Model
3.5. Simulation of Heat Treatment Conditions
4. Analysis of Numerical Simulation Results
4.1. Distribution of Residual Stress under Different Cooling Times
4.1.1. Evolution Law of Residual Stress Distribution
4.1.2. The Trend of Residual Stress Variation on the Wave Crest
4.1.3. The Trend of Residual Stress Variation on the Trough
4.2. The Influence of Different Cooling Times on the Deformation of Bellows
4.2.1. Deformation Evolution Law of Bellows
4.2.2. Axial Deformation Trend of Bellows
5. Conclusions
- (1)
- A residual stress analysis model for stainless-steel bellows during heat treatment was constructed using ABAQUS CAE 2022 software. The distribution trends of residual stress and deformation in the bellows during the heat treatment cooling stage and after heat treatment under different cooling time conditions were explored.
- (2)
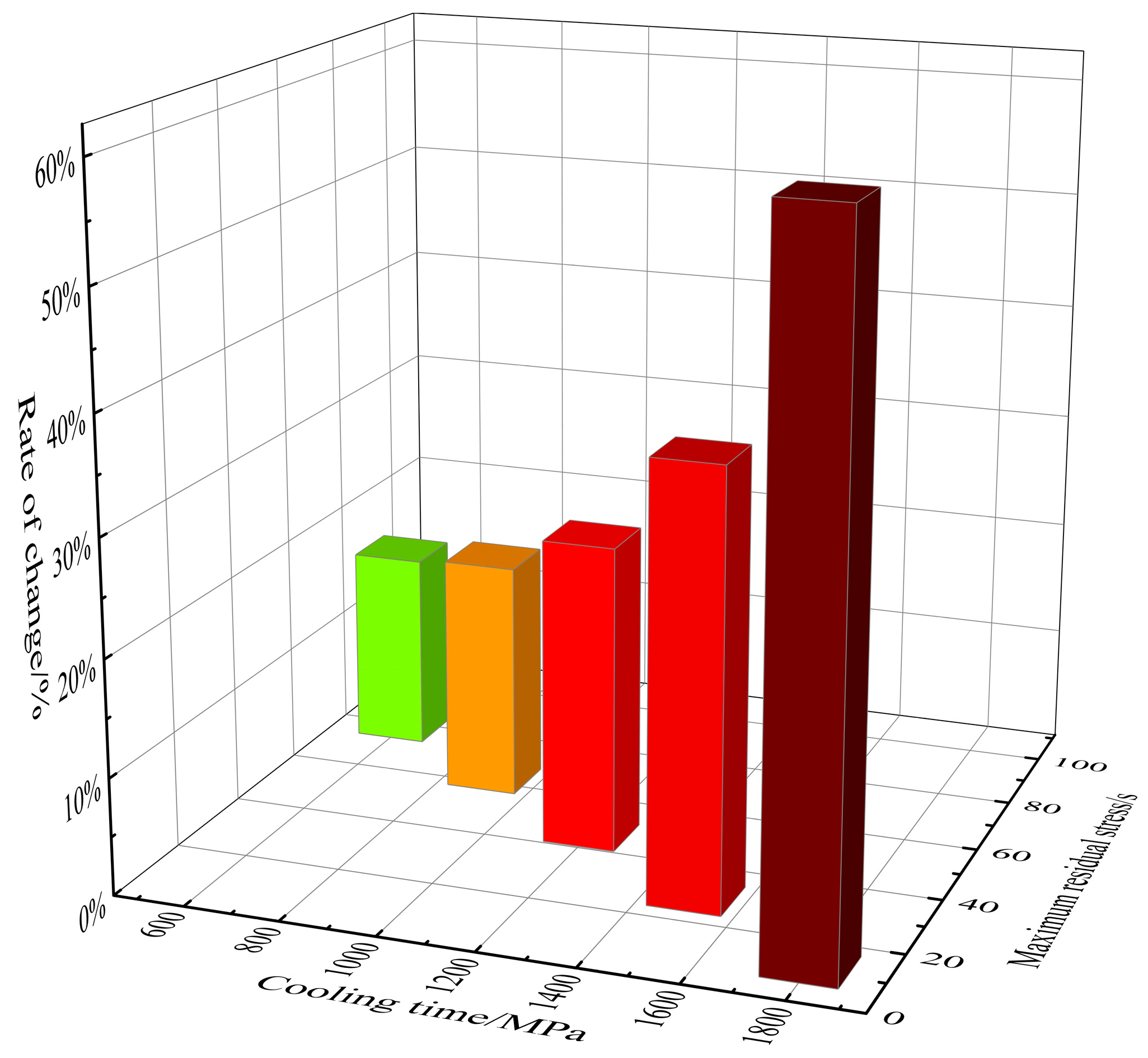
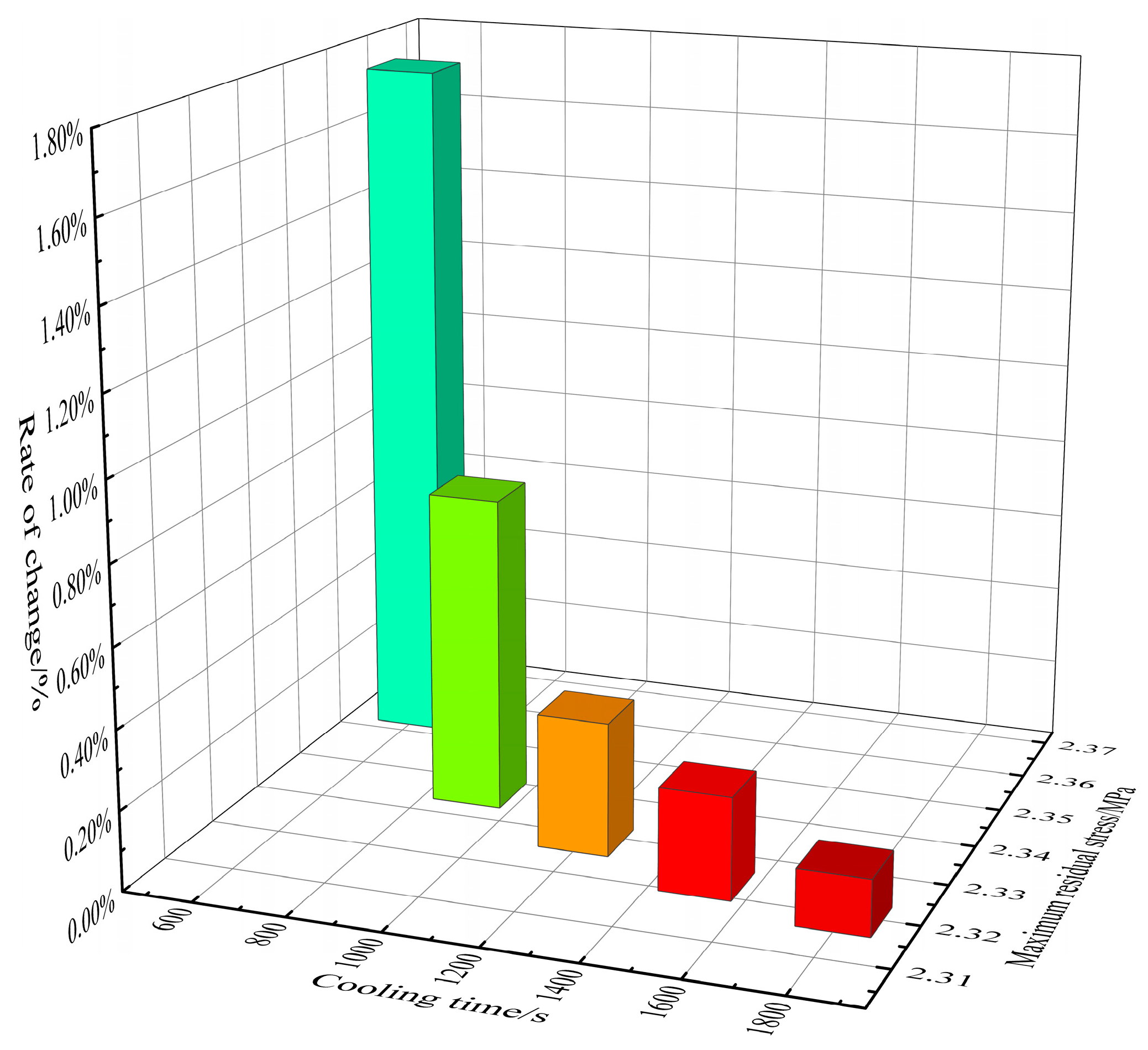
- Based on numerical simulation, it was found that the residual stress on the surface of the bellows under different cooling times decreases with the increased cooling time. The cooling time starts from 300 s, and the percentage of residual stress reduction for each additional 300 s is 17.00%, 20.36%, 26.27%, 37.14%, and 60.15%, respectively, showing an upward trend.
- (3)
- The analysis of the experimental and simulation results shows that the peak residual stress of the bellow in the middle position is significantly reduced after heat treatment, and the distribution trend of the residual stress in the valley is more uniform. This helps to reduce the risk of stress concentration and stress corrosion cracking, thereby improving the fatigue life of bellows.
- (4)
- The different cooling times of heat treatment have a certain impact on the deformation of bellows, but the impact is relatively small. As the cooling time increases, the formation decreases. Starting from 300 s, for every additional 300 s on the original basis, the deformation decreases by 1.748%, 0.794%, 0.338%, 0.258%, and 0.142%, respectively. The deformation at the peaks and valleys of the bellow is relatively evenly distributed along the axis direction, avoiding the structural instability caused by local stress concentration, making the bellow more resistant to external pressure and impact during use, thus extending its service life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.; Du, Y.; Han, J.; Li, F.; Chi, P. Experimental and numerical study of low-yield-point steel corrugated pipe dampers. Soil Dyn. Earthq. Eng. 2024, 180, 108615. [Google Scholar] [CrossRef]
- Min, N.H. Improving the noise reduction performance of gangway bellows by using multilayered structures. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 1077–1085. [Google Scholar]
- Zhao, Q.; Cao, Y.; Jiao, Z.; Zhen, Y.; Zu, Y. A dynamic fracture model of the pipeline with girth weld considering welding residual stresses. Fatigue Fract. Eng. Mater. Struct. 2023, 47, 261–274. [Google Scholar] [CrossRef]
- Liu, Q.; Qiang, B.; Xie, Y.; Xie, Q.; Zou, Y.; Yao, C.; Li, Y. PWHT influence on welding residual stress in 45 mm bridge steel butt-welded joint. J. Constr. Steel Res. 2024, 217, 108674. [Google Scholar] [CrossRef]
- Xiang, X.M.; Lu, G.; Li, Z.X.; Lv, Y. Finite element analysis and experimental study on a bellows joint. Eng. Struct. 2017, 151, 584–598. [Google Scholar] [CrossRef]
- Jiang, L.; He, Y.; Lin, Y.; Zhang, S.; Feng, Y.; Sun, M.; Guo, X. Influence of process parameters on thinning ratio and fittability of bellows hydroforming. Int. J. Adv. Manuf. Technol. 2020, 107, 3371–3387. [Google Scholar] [CrossRef]
- Wu, B.; Ming, H.; Li, R.; Meng, F.; Wang, J.; Han, E.H. The single effect of microstructure, residual strain and geometric structure on the stress corrosion cracking behavior of scratched alloy 690TT. Corros. Sci. 2024, 227, 111709. [Google Scholar] [CrossRef]
- Lu, W.L.; Sun, J.L.; Su, H.; Chen, L.J.; Zhou, Y.Z. Experimental research and numerical analysis of welding residual stress of butt welded joint of thick steel plate. Case Stud. Constr. Mater. 2023, 18, e1991. [Google Scholar] [CrossRef]
- Guo, H.; Huang, A.; Xiong, W.; Xing, S.; Wang, L.; Zhang, C.; Luo, J. Finite Element Simulation and Residual Stress Analysis of the Whole Process of Metal Bellows Forming. J. Mater. Eng. Perform. 2024, 33, 3758–3769. [Google Scholar] [CrossRef]
- Mai, C.; Hu, X.; Zhang, L.; Song, B.; Zheng, X. Influence of Interlayer Temperature and Welding Sequence on the Temperature Distribution and Welding Residual Stress of the Saddle-Shaped Joint of Weldolet-Header Butt Welding. Materials 2021, 14, 5980. [Google Scholar] [CrossRef]
- Rebelo Kornmeier, J.; Marques, M.J.; Gan, W.; Batista, A.C.; Paddea, S.; Loureiro, A. Quantification of Residual Stress Relief by Heat Treatments in Austenitic Cladded Layers. Materials 2022, 15, 1364. [Google Scholar] [CrossRef]
- Yu, J.H.; Jin, Q.Y.; Ha, K.; Lee, W. Influence of Several Heat Treatments on Residual Stress in Laser Powder Bed-Fused Maraging 18Ni-300 Steel. Appl. Sci. 2023, 13, 6572. [Google Scholar] [CrossRef]
- Ji, X.; Zhao, Z.; Sun, C.; Liu, X.; Wang, R.; Su, C. Study on Residual Stress Evolution Mechanism and Influencing Factors of 316L/Q235B Composite Plate during Solution Heat Treatment. Crystals 2023, 13, 436. [Google Scholar] [CrossRef]
- Fan, M.; Chen, C.; Xuan, H.; Qin, H.; Qu, M.; Shi, S.; Bi, Z.; Hong, W. Effect of Residual Stress Induced by Different Cooling Methods in Heat Treatment on the Fatigue Crack Propagation Behaviour of GH4169 Disc. Materials 2022, 15, 5228. [Google Scholar] [CrossRef]
- Lin, J.; Wang, X.; Lei, Y.; Ding, J.; Li, K.; Guo, F. Residual stress analysis and measurement in multi-layer bellows. J. Manuf. Process. 2021, 72, 179–194. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, R.; Chen, D.; Xie, Q.; Kang, J.; Yuan, G.; Wang, G. Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation. Metals 2022, 12, 1363. [Google Scholar] [CrossRef]
- Wu, G.; Luo, J.; Li, L.; Long, Y.; Zhang, S.; Wang, Y.; Zhang, Y.; Xie, S. Control of Welding Residual Stress in Large Storage Tank by Finite Element Method. Metals 2022, 12, 1502. [Google Scholar] [CrossRef]
- Mamane, A.I.; Giljean, S.; Pac, M.J.; L’hostis, G. Optimization of the measurement of residual stresses by the incremental hole drilling method. Part I: Numerical correction of experimental errors by a configurable numerical–experimental coupling. Compos. Struct. 2022, 294, 115703. [Google Scholar] [CrossRef]
- Garcia Ruano, S.A.; Delijaicov, S.; dos Santos Junior, A.A. Acoustoelasticity to measure residual stresses in plates of 5052 aluminum joined by FSW. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 82. [Google Scholar] [CrossRef]
- Luo, Q. A modified X-ray diffraction method to measure residual normal and shear stresses of machined surfaces. Int. J. Adv. Manuf. Technol. 2022, 119, 3595–3606. [Google Scholar] [CrossRef]
- Gangwar, K.; Ramulu, M. Residual Stress Measurement Using X-ray Diffraction in Friction Stir-Welded Dissimilar Titanium Alloys. Materials 2024, 17, 1482. [Google Scholar] [CrossRef]
- Park, S.C.; Kim, I.; Lee, K.A.; Seo, S.J.; Kim, D.K.; Lee, B. Microstructure and residual stress analysis as heat treatment of additive manufactured A356.2 alloy by powder bed fusion. Mater. Charact. 2024, 207, 113538. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, D.; Wang, L.; Davies, C.M.; Mirihanage, W.; Tong, M.; Harrison, N.M. X-ray diffraction measurements and computational prediction of residual stress mitigation scanning strategies in powder bed fusion additive manufacturing. Addit. Manuf. 2023, 61, 103275. [Google Scholar] [CrossRef]
- Liu, G.; Gong, Z.; Yang, Y.; Shi, J.; Liu, Y.; Dou, X.; Li, C. Electrochemical dissolution behavior of stainless steels with different metallographic phases and its effects on micro electrochemical machining performance. Electrochem. Commun. 2024, 160, 107677. [Google Scholar] [CrossRef]
- Zhong, B.; Dang, J.; Xue, S.; Wang, D.; Liu, Z.; An, Q.; Chen, M. Surface integrity of carbon steel under three heat treatment states subjected to orthogonal turning process. J. Manuf. Process. 2024, 119, 699–714. [Google Scholar] [CrossRef]
- Zhang, X.; Karagiozova, D.; Lu, G.; Durandet, Y.; Wang, S. Analytical and finite element analyses on axial tensile behaviour of origami bellows with polygonal cross-section. Thin-Walled Struct. 2023, 193, 111234. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Durandet, Y.; Palanisamy, S.; Lu, G. Energy absorption behavior of origami bellows under tension. Int. J. Mech. Sci. 2023, 246, 108143. [Google Scholar] [CrossRef]
- Dong, H.Y.; Cheng, X.W.; Wang, J.; Xiao, L.C.; Liu, M.P. Johnson-Cook (JC) constitutive equation for ZGMn18 high manganese steel. Metalurgija 2024, 63, 89–92. [Google Scholar]
- Wu, J.; Huang, J.; Li, Z.; Yang, H.; Ge, H.; Meng, X.; Zhao, Y. Influence of electrochemical descaling treatment in simulated cooling water on the corrosion behavior of stainless steel. J. Clean. Prod. 2024, 451, 142066. [Google Scholar] [CrossRef]
- Zhu, W.; Moumni, Z.; Zhu, J.; Zhang, Y.; You, Y.; Zhang, W. A multi-scale experimental investigation on fatigue crack propagation rate behavior of powder bed fusion-laser beam 316L stainless steel subjected to various heat treatments. Eng. Fract. Mech. 2024, 302, 110064. [Google Scholar] [CrossRef]







| Element | C | Si | Mn | P | S | Cr | Ni | Other |
|---|---|---|---|---|---|---|---|---|
| Content | 0.043 | 0.41 | 1.07 | 0.030 | 0.004 | 18.01 | 8.03 | 0.002 |
| Performance Parameter | Elastic Modulus/GPa | Poisson’s Ratio | Yield Strength/MPa | Tensile Strength/MPa | Elongation Rate/% | HV |
|---|---|---|---|---|---|---|
| Numerical value | 197 | 0.3 | 267 | 738 | 68.0 | 160 |
| External Diameter r0/mm | Internal Diameter ri/mm | Ridge Radius R/mm | Valley Radius r/mm | Wave Distance d/mm | Wall Thickness t/mm | Wave Number | Number of Plies |
|---|---|---|---|---|---|---|---|
| ∅14.9 | ∅10.8 | 0.8 | 0.65 | 2.9 | 0.16 | 7 | 1 |
| Constraint | End Face 1 | End Face 2 |
|---|---|---|
| Displacement (mm) | Z = 0 | Z = 0 |
| Rotation (rad) | XY = 0 | XY = 0 |
| Cooling Time/s | 300 | 600 | 900 | 1200 | 1500 | 1800 |
|---|---|---|---|---|---|---|
| Maximum residual stress/MPa | 94.43 | 78.38 | 62.42 | 46.02 | 28.93 | 11.53 |
| Cooling Time/s | 300 | 600 | 900 | 1200 | 1500 | 1800 |
|---|---|---|---|---|---|---|
| Maximum deformation/mm | 2.3973 | 2.3554 | 2.3367 | 2.3288 | 2.3228 | 2.3195 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Ling, C.; Zhao, X.; Wang, H.; Wang, T.; Tao, G.; Fu, Y.; Cheng, T. Research on the Analysis of Residual Stress in Heat Treatment of Bellows Using ABAQUS. Materials 2024, 17, 3263. https://doi.org/10.3390/ma17133263
Wang A, Ling C, Zhao X, Wang H, Wang T, Tao G, Fu Y, Cheng T. Research on the Analysis of Residual Stress in Heat Treatment of Bellows Using ABAQUS. Materials. 2024; 17(13):3263. https://doi.org/10.3390/ma17133263
Chicago/Turabian StyleWang, Anheng, Chuanwen Ling, Xiang Zhao, Hui Wang, Tao Wang, Guangming Tao, Yanchao Fu, and Tao Cheng. 2024. "Research on the Analysis of Residual Stress in Heat Treatment of Bellows Using ABAQUS" Materials 17, no. 13: 3263. https://doi.org/10.3390/ma17133263
APA StyleWang, A., Ling, C., Zhao, X., Wang, H., Wang, T., Tao, G., Fu, Y., & Cheng, T. (2024). Research on the Analysis of Residual Stress in Heat Treatment of Bellows Using ABAQUS. Materials, 17(13), 3263. https://doi.org/10.3390/ma17133263






