Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper—A Machine Learning Approach
Abstract
:1. Introduction
2. Methodology
2.1. The EVPSC Model
2.2. Machine Learning
3. Results
- 1.
- Very good or reasonable agreement of SS curves obtained using parameters optimized in both approaches—Figure 6a and Supplementary Figure S1;
- 2.
- Disagreement in the first cycle and reasonable agreement of SS curves obtained using parameters optimized in both approaches—Figure 6b and Supplementary Figure S2;
- 3.
- Reasonable agreement of SS curves obtained using parameters optimized in App 1 (lack of convergence for App 2 parameters)—Figure 6c and Supplementary Figure S3;
- 4.
- Reasonable agreement of SS curves obtained using parameters optimized in App 2 (lack of convergence for App 1 parameters)—Figure 6d and Supplementary Figure S4;
- 5.
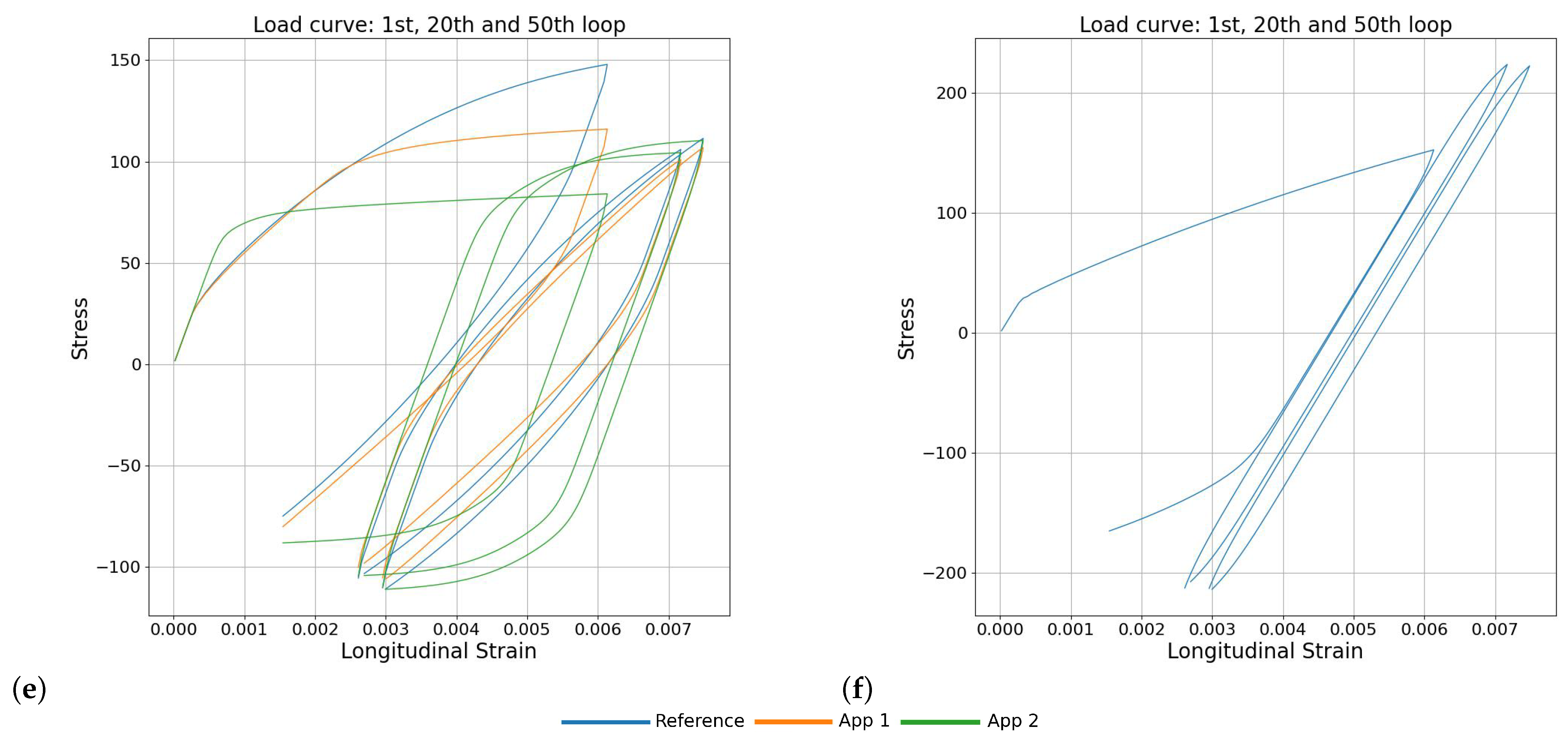
- Striking disagreement or lack of convergence—Figure 6e and Supplementary Figure S5;
- 6.
- Lack of convergence for the optimized parameters in both approaches—Figure 6f and Supplementary Figure S6.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Chen, X.; Park, C.; Fay, C.C.; Stupkiewicz, S.; Ke, C. Mechanical deformations of boron nitride nanotubes in crossed junctions. J. Appl. Phys. 2014, 115, 164305. [Google Scholar] [CrossRef]
- Kacprzak, G.; Zbiciak, A.; Józefiak, K.; Nowak, P.; Frydrych, M. One-Dimensional Computational Model of Gyttja Clay for Settlement Prediction. Sustainability 2023, 15, 1759. [Google Scholar] [CrossRef]
- Ganesan, S.; Yaghoobi, M.; Githens, A.; Chen, Z.; Daly, S.; Allison, J.E.; Sundararaghavan, V. The effects of heat treatment on the response of WE43 Mg alloy: Crystal plasticity finite element simulation and SEM-DIC experiment. Int. J. Plast. 2021, 137, 102917. [Google Scholar] [CrossRef]
- Guery, A.; Hild, F.; Latourte, F.; Roux, S. Identification of crystal plasticity parameters using DIC measurements and weighted FEMU. Mech. Mater. 2016, 100, 55–71. [Google Scholar] [CrossRef]
- Cruzado, A.; LLorca, J.; Segurado, J. Modeling cyclic deformation of inconel 718 superalloy by means of crystal plasticity and computational homogenization. Int. J. Solids Struct. 2017, 122, 148–161. [Google Scholar] [CrossRef]
- Kuhn, J.; Spitz, J.; Sonnweber-Ribic, P.; Schneider, M.; Böhlke, T. Identifying material parameters in crystal plasticity by Bayesian optimization. Optim. Eng. 2021, 23, 1489–1523. [Google Scholar] [CrossRef]
- Hu, L.; Jiang, S.Y.; Zhang, Y.Q.; Zhu, X.M.; Sun, D. Texture evolution and inhomogeneous deformation of polycrystalline Cu based on crystal plasticity finite element method and particle swarm optimization algorithm. J. Cent. South Univ. 2017, 24, 2747–2756. [Google Scholar] [CrossRef]
- Skippon, T.; Mareau, C.; Daymond, M.R. On the determination of single-crystal plasticity parameters by diffraction: Optimization of a polycrystalline plasticity model using a genetic algorithm. J. Appl. Crystallogr. 2012, 45, 627–643. [Google Scholar] [CrossRef]
- Acar, P.; Ramazani, A.; Sundararaghavan, V. Crystal plasticity modeling and experimental validation with an orientation distribution function for ti-7al alloy. Metals 2017, 7, 459. [Google Scholar] [CrossRef]
- Cauvin, L.; Raghavan, B.; Bouvier, S.; Wang, X.; Meraghni, F. Multi-scale investigation of highly anisotropic zinc alloys using crystal plasticity and inverse analysis. Mater. Sci. Eng. A 2018, 729, 106–118. [Google Scholar] [CrossRef]
- Kapoor, K.; Sangid, M.D. Initializing type-2 residual stresses in crystal plasticity finite element simulations utilizing high-energy diffraction microscopy data. Mater. Sci. Eng. A 2018, 729, 53–63. [Google Scholar] [CrossRef]
- Sedighiani, K.; Diehl, M.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D. An efficient and robust approach to determine material parameters of crystal plasticity constitutive laws from macro-scale stress–strain curves. Int. J. Plast. 2020, 134, 102779. [Google Scholar] [CrossRef]
- Frydrych, K.; Maj, M.; Urbański, L.; Kowalczyk-Gajewska, K. Twinning-induced anisotropy of mechanical response of AZ31B extruded rods. Mater. Sci. Eng. A 2020, 771, 138610. [Google Scholar] [CrossRef]
- Girard, G.; Frydrych, K.; Kowalczyk-Gajewska, K.; Martiny, M.; Mercier, S. Cyclic response of electrodeposited copper films. Experiments versus elastic-viscoplastic mean-field approach predictions. Mech. Mater. 2021, 153, 1–17. [Google Scholar] [CrossRef]
- Savage, D.J.; Feng, Z.; Knezevic, M. Identification of crystal plasticity model parameters by multi-objective optimization integrating microstructural evolution and mechanical data. Comput. Methods Appl. Mech. Eng. 2021, 379, 113747. [Google Scholar] [CrossRef]
- Frydrych, K.; Kowalczyk-Gajewska, K.; Libura, T.; Kowalewski, Z.; Maj, M. On the role of slip, twinning and detwinning in magnesium alloy AZ31b sheet. Mater. Sci. Eng. A 2021, 813, 141152. [Google Scholar] [CrossRef]
- Frydrych, K.; Jarzebska, A.; Virupakshi, S.; Kowalczyk-Gajewska, K.; Bieda, M.; Chulist, R.; Skorupska, M.; Schell, N.; Sztwiertnia, K. Texture-Based Optimization of Crystal Plasticity Parameters: Application to Zinc and Its Alloy. Metall. Mater. Trans. A 2021, 52, 3257–3273. [Google Scholar] [CrossRef]
- Frydrych, K. Texture evolution of magnesium alloy AZ31B subjected to severe plastic deformation. Eng. Trans. 2021, 69, 337–352. [Google Scholar]
- Frydrych, K.; Papanikolaou, S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals 2022, 12, 1341. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, B.; Hui, C.Y.; Zehnder, A.T. Determination of material parameters in constitutive models using adaptive neural network machine learning. J. Mech. Phys. Solids 2023, 177, 105324. [Google Scholar] [CrossRef]
- Schulte, R.; Karca, C.; Ostwald, R.; Menzel, A. Machine learning-assisted parameter identification for constitutive models based on concatenated loading path sequences. Eur. J. Mech.-A/Solids 2023, 98, 104854. [Google Scholar] [CrossRef]
- Pogorelko, V.; Mayer, A.; Fomin, E.; Fedorov, E. Examination of machine learning method for identification of material model parameters. Int. J. Mech. Sci. 2024, 265, 108912. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K.; Petryk, H. Sequential linearization method for viscous/elastic heterogeneous materials. Eur. J. Mech. Solids/A 2011, 30, 650–664. [Google Scholar] [CrossRef]
- Mercier, S.; Molinari, A. Homogenization of elastic-viscoplastic heterogeneous materials: Self-consistent and Mori-Tanaka schemes. Int. J. Plast. 2009, 25, 1024–1048. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K. Micromechanical Modelling of Metals and Alloys of High Specific Strength. IFTR Reports 1/2011. 2011, pp. 1–299. Available online: https://rcin.org.pl/Content/32190/PDF/WA727_9322_56416-1-2011_Micromechanical.pdf (accessed on 5 July 2024).
- Molinari, A.; Ahzi, S.; Kouddane, R. On the self-consistent modelling of elastic-plastic behavior of polycrystals. Mech. Mater. 1997, 26, 43–62. [Google Scholar] [CrossRef]
- Molinari, A. Averaging Models for heterogeneous viscoplastic and elastic viscoplastic materials. J. Eng. Mater. Technol. 2002, 124, 62–70. [Google Scholar] [CrossRef]
- Hennessey, C.; Castelluccio, G.M.; McDowell, D.L. Sensitivity of polycrystal plasticity to slip system kinematic hardening laws for Al 7075-T6. Mater. Sci. Eng. A 2017, 687, 241–248. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Yao, K.; Zweig, G.; Hwang, M.Y.; Shi, Y.; Yu, D. Recurrent neural networks for language understanding. In Proceedings of the Interspeech 2013, Lyon, France, 25–29 August 2013; pp. 2524–2528. [Google Scholar]
- Shewalkar, A.; Nyavanandi, D.; Ludwig, S.A. Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU. J. Artif. Intell. Soft Comput. Res. 2019, 9, 235–245. [Google Scholar] [CrossRef]
- El-Danaf, E.; Kalidindi, S.R.; Doherty, R.D. Influence of deformation path on the strain hardening behavior and microstructure evolution in low SFE fcc metals. Int. J. Plast. 2001, 17, 1245–1265. [Google Scholar] [CrossRef]
- Peeters, B.; Seefeldt, M.; Teodosiu, C.; Kalidindi, S.; Van Houtte, P.; Aernoudt, E. Work-hardening/softening behaviour of b.c.c. polycrystals during changing strain paths: I. An integrated model based on substructure and texture evolution, and its prediction of the stress-strain behaviour of an IF steel during two-stage strain paths. Acta Mater. 2001, 49, 1607–1619. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tomè, C.N. Modeling transients in the mechanical response of copper due to strain path changes. Int. J. Plast. 2007, 23, 640–664. [Google Scholar] [CrossRef]
- Petryk, H.; Stupkiewicz, S. Modelling of microstructure evolution on complex paths of large plastic deformation. Int. J. Mat. Res. 2014, 103, 271–277. [Google Scholar] [CrossRef]
- Frydrych, K.; Kowalczyk-Gajewska, K.; Stupkiewicz, S. Modelling of microstructure evolution in hcp polycrystals on non-proportional strain paths. In Proceedings of the 39th Solid Mechanics Conference, Zakopane, Poland, 1–5 September 2014. [Google Scholar]
- Kowalczyk-Gajewska, K.; Stupkiewicz, S.; Frydrych, K.; Petryk, H. Modelling of Texture Evolution and Grain Refinement on Complex SPD Paths. IOP Conf. Ser. Mater. Sci. Eng. 2014, 63, 012040. [Google Scholar] [CrossRef]
- Hama, T.; Nagao, H.; Kobuki, A.; Fujimoto, H.; Takuda, H. Work-hardening and twinning behaviors in a commercially pure titanium sheet under various loading paths. Mater. Sci. Eng. A 2015, 620, 390–398. [Google Scholar] [CrossRef]
- Kowalczyk-Gajewska, K.; Sztwiertnia, K.; Kawałko, J.; Wierzbanowski, K.; Wronski, K. Frydrych, K.; Stupkiewicz, S.; Petryk, H. Texture evolution in titanium on complex deformation paths: Experiment and modelling. Mater. Sci. Eng. A 2015, 637, 251–263. [Google Scholar] [CrossRef]
- Heidenreich, J.N.; Mohr, D. Recurrent neural network plasticity models: Unveiling their common core through multi-task learning. Comput. Methods Appl. Mech. Eng. 2024, 426, 116991. [Google Scholar] [CrossRef]
- Wu, L.; Kilingar, N.G.; Noels, L.; Nguyen, V.D. A recurrent neural network-accelerated multi-scale model for elasto-plastic heterogeneous materials subjected to random cyclic and non-proportional loading paths. Comput. Methods Appl. Mech. Eng. 2020, 369, 113234. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- PyTorch Contributors. PyTorch LSTM Description. Available online: https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html#torch.nn.LSTM (accessed on 6 November 2023).
- Ley, A.; Bormann, H.; Casper, M. Intercomparing LSTM and RNN to a conceptual hydrological model for a low-land river with a focus on the flow duration curve. Water 2023, 15, 505. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Salmenjoki, H.; Alava, M.; Laurson, L. Machine learning plastic deformation of crystals. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, S.; Lengiewicz, J.; Bordas, S.P. Probabilistic deep learning for real-time large deformation simulations. Comput. Methods Appl. Mech. Eng. 2022, 398, 115307. [Google Scholar] [CrossRef]
- Yuan, M.; Paradiso, S.; Meredig, B.; Niezgoda, S. Machine learning–based reduce order crystal plasticity modeling for ICME applications. Integr. Mater. Manuf. Innov. 2018, 7, 214–230. [Google Scholar] [CrossRef]
- Ali, U.; Muhammad, W.; Brahme, A.; Skiba, O.; Inal, K. Application of artificial neural networks in micromechanics for polycrystalline metals. Int. J. Plast. 2019, 120, 205–219. [Google Scholar] [CrossRef]
- Miyazawa, Y.; Briffod, F.; Shiraiwa, T.; Enoki, M. Prediction of cyclic stress–strain property of steels by crystal plasticity simulations and machine learning. Materials 2019, 12, 3668. [Google Scholar] [CrossRef]
- Pandey, A.; Pokharel, R. Machine learning based surrogate modeling approach for mapping crystal deformation in three dimensions. Scr. Mater. 2021, 193, 1–5. [Google Scholar] [CrossRef]
- Ibragimova, O.; Brahme, A.; Muhammad, W.; Levesque, J.; Inal, K. A new ANN based crystal plasticity model for FCC materials and its application to non-monotonic strain paths. Int. J. Plast. 2021, 144, 103059. [Google Scholar] [CrossRef]
- Li, Q.J.; Cinbiz, M.N.; Zhang, Y.; He, Q.; Beausoleil II, G.; Li, J. Robust deep learning framework for constitutive relations modeling. Acta Mater. 2023, 254, 118959. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. One for all: Universal material model based on minimal state-space neural networks. Sci. Adv. 2021, 7, eabf3658. [Google Scholar] [CrossRef] [PubMed]
- Rutecka, A.; Kowalewski, Z.; Pietrzak, K.; Dietrich, L.; Makowska, K.; Woźniak, J.; Kostecki, M.; Bochniak, W.; Olszyna, A. Damage development of Al/SiC metal matrix composite under fatigue, creep and monotonic loading conditions. Procedia Eng. 2011, 10, 1420–1425. [Google Scholar] [CrossRef]

| Min | 10.0 | 10.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Max | 80.0 | 120.0 | 5.0 | 120.0 | 1.0 | 1000.0 | 10.0 |
| Category 1 | |||||||
| Reference | 1.00 | 6.50 | 4.17 | 4.00 | 1.00 | 5.00 | 3.33 |
| App 1 | 2.91 | 9.00 | 4.09 | 1.09 | 1.00 | 4.55 | 2.73 |
| App 2 | 1.64 | 8.00 | 1.36 | 2.18 | 1.00 | 4.55 | 2.73 |
| Category 2 | |||||||
| Reference | 1.00 | 8.33 | 8.33 | 1.20 | 3.33 | 1.00 | 0.00 |
| App 1 | 6.73 | 1.00 | 5.00 | 1.09 | 9.09 | 5.45 | 9.09 |
| App 2 | 6.73 | 1.20 | 4.55 | 1.09 | 9.09 | 8.18 | 3.64 |
| Category 3 | |||||||
| Reference | 1.00 | 1.00 | 1.67 | 1.20 | 3.33 | 8.33 | 8.33 |
| App 1 | 1.00 | 1.00 | 5.00 | 2.18 | 2.73 | 8.18 | 7.27 |
| App 2 | 1.64 | 1.00 | 5.00 | 2.18 | 2.73 | 7.27 | 3.64 |
| Category 4 | |||||||
| Reference | 1.00 | 2.83 | 5.00 | 8.00 | 1.00 | 5.00 | 3.33 |
| App 1 | 4.18 | 2.00 | 1.82 | 2.18 | 1.00 | 4.55 | 2.73 |
| App 2 | 2.91 | 1.20 | 1.36 | 0.00 | 1.00 | 4.55 | 2.73 |
| Category 5 | |||||||
| Reference | 1.00 | 1.00 | 5.00 | 1.20 | 3.33 | 6.67 | 0.00 |
| App 1 | 1.00 | 1.00 | 5.00 | 2.18 | 2.73 | 9.09 | 8.18 |
| App 2 | 22.73 | 30.00 | 5.00 | 32.73 | 0.00 | 0.00 | 0.00 |
| Category 6 | |||||||
| Reference | 10.00 | 83.33 | 1.67 | 60.00 | 0.00 | 1000.00 | 0.00 |
| App 1 | 35.45 | 90.00 | 2.73 | 43.64 | 0.00 | 1000.00 | 4.55 |
| App 2 | 22.73 | 90.00 | 0.91 | 54.55 | 0.00 | 727.27 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frydrych, K.; Tomczak, M.; Papanikolaou, S. Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper—A Machine Learning Approach. Materials 2024, 17, 3397. https://doi.org/10.3390/ma17143397
Frydrych K, Tomczak M, Papanikolaou S. Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper—A Machine Learning Approach. Materials. 2024; 17(14):3397. https://doi.org/10.3390/ma17143397
Chicago/Turabian StyleFrydrych, Karol, Maciej Tomczak, and Stefanos Papanikolaou. 2024. "Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper—A Machine Learning Approach" Materials 17, no. 14: 3397. https://doi.org/10.3390/ma17143397
APA StyleFrydrych, K., Tomczak, M., & Papanikolaou, S. (2024). Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper—A Machine Learning Approach. Materials, 17(14), 3397. https://doi.org/10.3390/ma17143397







