Design and Control of the Natural Frequency of Brake Discs in the Aspect of the Gray Cast Iron Production Process
Abstract
1. Introduction
2. Research Material and Research Methodology
3. Research Results and Discussion
3.1. Mechanical Properties Testing
3.2. Results of the Microstructural Tests
- -
- The graphite distribution was uniform—type A (70–75%) and interdendritic types D and E (19–26%);
- -
- The size of the graphite precipitates corresponded to the size patterns from number 3 to number 5. The largest share, over 90%, consisted of graphite precipitates corresponding to the length patterns 4 and 5 (from 60 to 250 μm);
- -
- The graphite precipitates had a straight flake shape and corresponded to pattern I.
3.3. Testing the Elastic Properties of Cast Iron Using the Ultrasonic Method
3.4. Simulations and Experimental Tests of the Natural Frequency of Brake Discs
3.5. Development of a Production Material Database
3.6. Predicting the Natural Frequency when Implementing a New Brake Disc
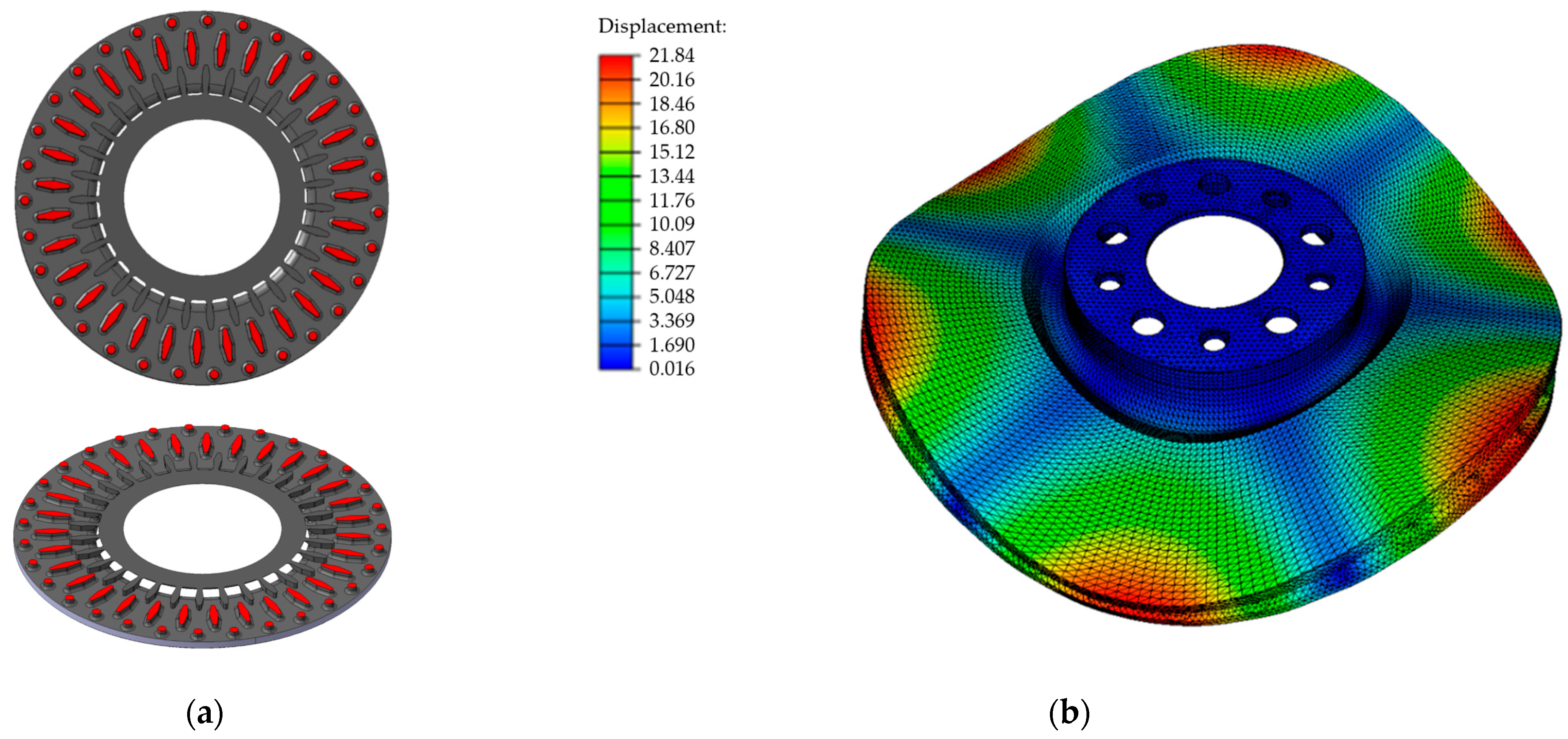
3.6.1. Design and Simulation Work
3.6.2. Experimental Verification of the Modal Simulation Results
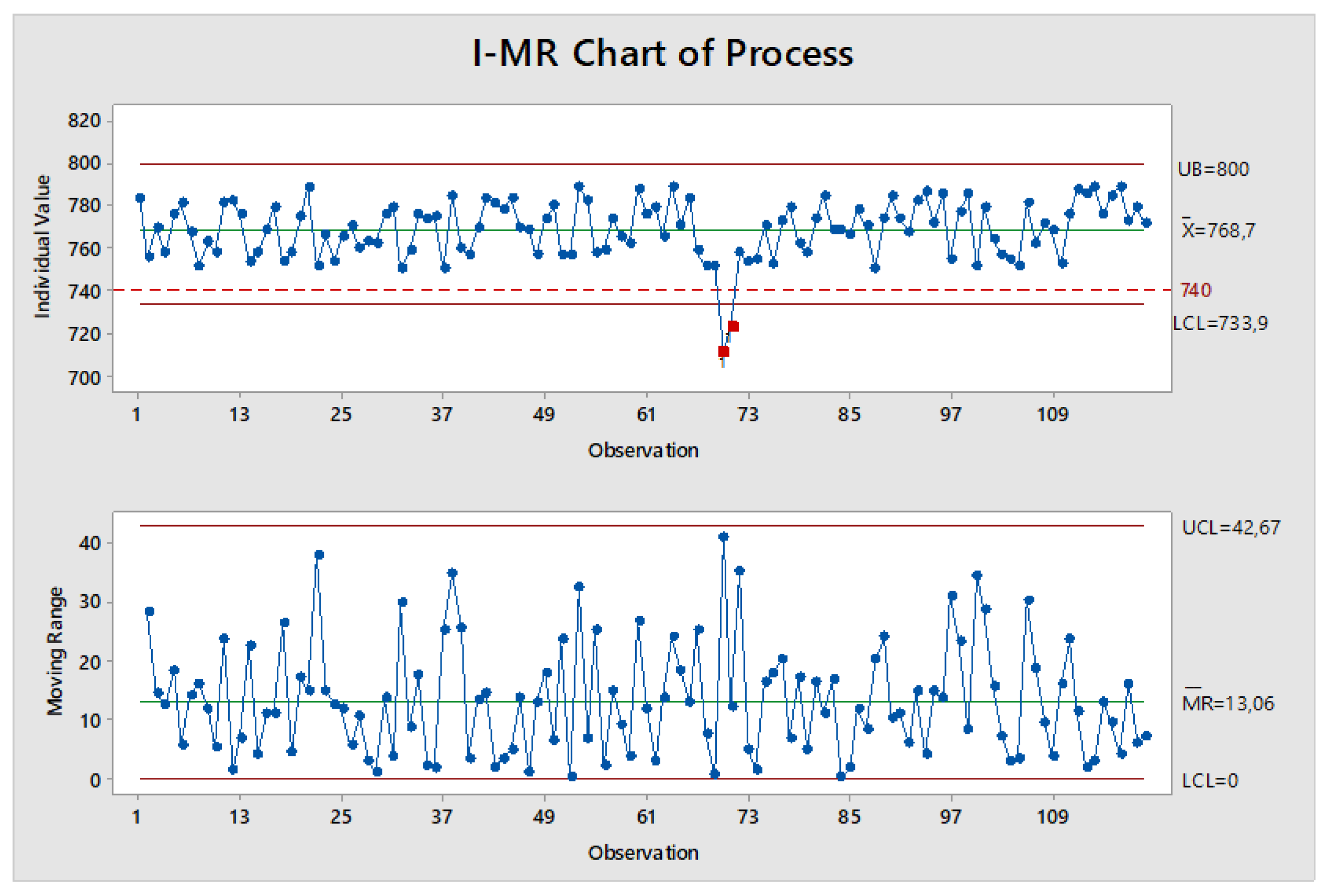
3.7. Production Control of the Implemented Brake Disc
4. Summary and Concluding Statements
Final Statements
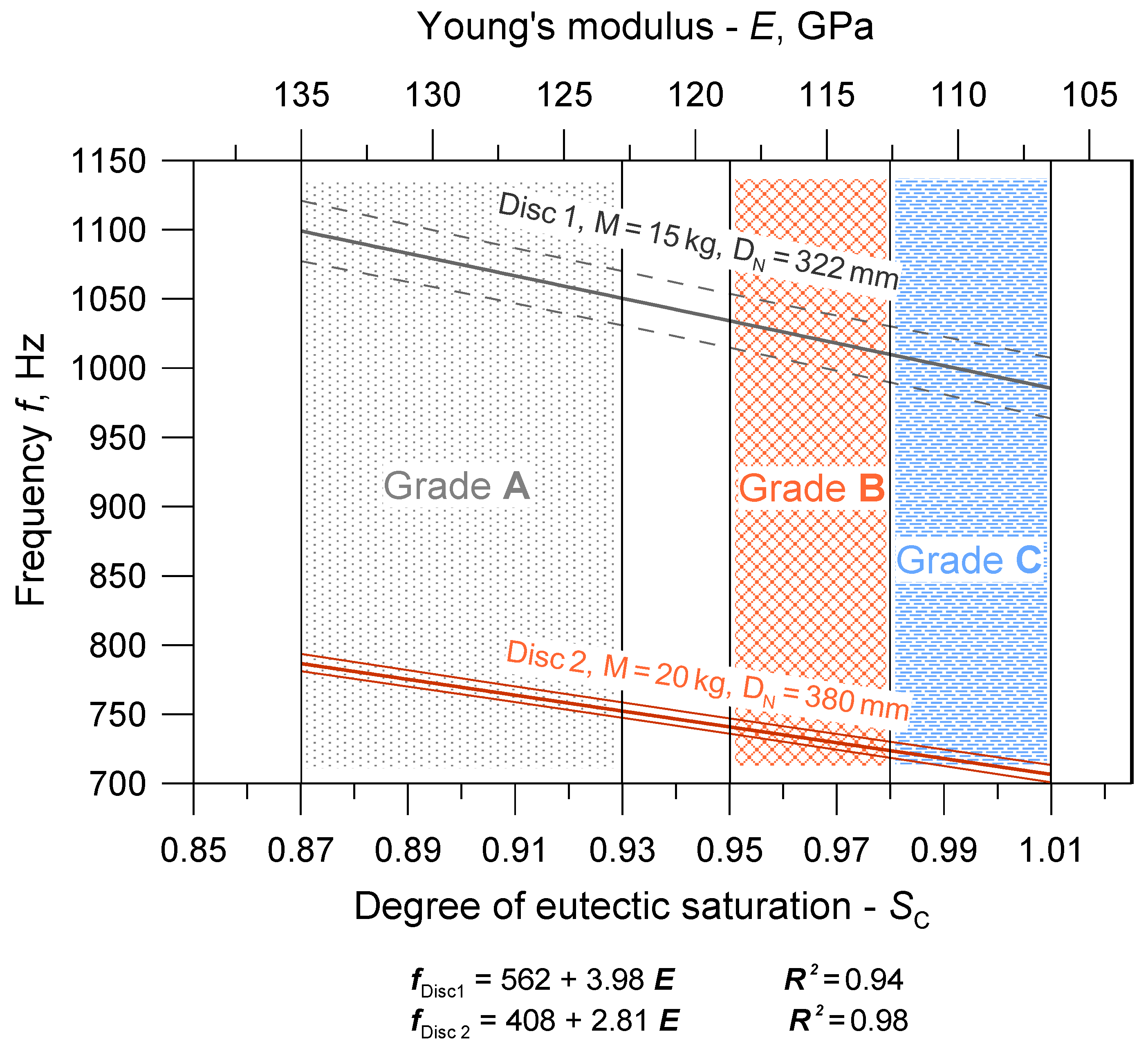
- An increase in the degree of saturation of eutectic cast iron from 0.87 to 1.01 resulted in a 21% reduction in Young’s modulus and a 10–11% reduction in the first natural vibration frequency of the brake discs.
- During the production cycle, even slight changes in the chemical composition of cast iron may affect the frequency stability of the discs. The high sensitivity of the first natural frequency to changes in the SC coefficient requires the use of high-quality input materials and strict process control at the stages of melting and modification of cast iron.
- The numerical prediction of the first natural frequency and the range of its changes are determined by the accuracy of the measurement of the elastic properties of cast iron. The ultrasonic method based on measuring the propagation speed of longitudinal and transverse waves allows for a quick and accurate determination of Young’s modulus and Poisson number of brake discs.
- For the analyzed brake disc geometries and cast iron grades (SC from 0.88 to 1.01), the relationships between the first natural frequency and Young’s modulus describe linear functions with direction coefficients ranging from 2.8 to 4.0 Hz/GPa
- Carrying out design and simulation work using the production material database is an effective method for optimizing the design of brake discs. The error of the numerical simulations of the first natural vibration frequency was on average below 1%.
- Control tests performed using I-MR cards confirmed both the effectiveness of the design and prediction of natural vibrations of brake discs, as well as the stability of the gray cast iron production and disc casting processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pevec, M.; Potrc, I.; Bombek, G. Prediction of cooling factors of a vehicle brake disc and its influence on results of thermal numerical simulation. Int. J. Automot. Technol. 2012, 13, 725–733. [Google Scholar] [CrossRef]
- Vadiraj, A.; Balachandran, G.; Kamaraj, M.; Gopalakrishna, B.; Venkateshwara Rao, D. Wear behavior of alloyed hypereutectic gray cast iron. Tribol. Int. 2010, 43, 647–653. [Google Scholar] [CrossRef]
- Mackin, T.J.; Noe, S.C.; Ball, K.J.; Bedell, B.C.; Bim-Merle, D.P.; Bingaman, M.C.; Bingaman, D.M.; Bomleny, G.J.; Chemlir, D.B.; Clayton, H.A.; et al. Thermal cracking in disc brakes. Eng. Fail. Anal. 2002, 9, 63–76. [Google Scholar] [CrossRef]
- Pevec, M.; Oder, G.; Potrc, I.; Sraml, M. Elevated temperature low cycle fatigue of grey cast iron used for automotive brake discs. Eng. Fail. Anal. 2014, 42, 221–230. [Google Scholar] [CrossRef]
- Kchaou, M.; Sellami, A.; Elleuch, R.; Singh, H. Friction characteristics of a brake friction material under different braking conditions. Mater. Des. 2013, 52, 533–540. [Google Scholar] [CrossRef]
- Kumar, N.; Bharti, A.; Goyal, H.S.; Kant Patel, K. The evolution of brake friction materials: A review. Mater. Phys. Mech. 2021, 47, 796–815. [Google Scholar]
- Borawski, A. Conventional and unconventional materials used in the production of brake pads—Review. Sci. Eng. Compos. Mater. 2020, 27, 374–396. [Google Scholar] [CrossRef]
- Szymański, P.; Czarnecka-Komorowska, D.; Gawdzińska, K.; Trubas, A.; Kostecka, E. A review of composite materials used in brake disc pad manufacturing process. Compos. Theory Pract. 2020, 20, 60–66. [Google Scholar]
- Aranke, O.; Algenaid, W.; Awe, S.; Joshi, S. Coatings for Automotive Gray Cast Iron Brake Discs: A Review. Coatings 2019, 9, 552. [Google Scholar] [CrossRef]
- Federici, M.; Menapace, C.; Moscatelli, A.; Gialanella, S.; Straffelini, G. Pin-on-disc study of a friction material dry sliding against HVOF coated discs at room temperature and 300 degrees C. Tribol. Int. 2017, 115, 89–99. [Google Scholar] [CrossRef]
- Menapace, C.; Mancini, A.; Federici, M.; Straffelini, G.; Gialanella, S. Characterization of airborne wear debris produced by brake pads pressed against HVOF-coated discs. Friction 2019, 8, 421–432. [Google Scholar] [CrossRef]
- Krawczyk, J. Microstructure and tribological properties of mottled cast iron with different chemical composition. Arch. Mat. Sci. Eng. 2011, 51, 5–15. [Google Scholar]
- Jakubus, A.; Soiński, M.S. Thermal shock resistance of cast iron with various shapes of graphite precipitates. Arch. Foundry Eng. 2018, 18, 121–124. [Google Scholar] [CrossRef]
- Casati, R.; Faccin, R.; Vedani, M. Microstructural evolution and thermal fatigue resistance of grey cast iron. Fatigue Fract. Eng. Mat. Struct. 2018, 41, 99–110. [Google Scholar] [CrossRef]
- Mróz, M.; Orłowicz, A.W.; Tupaj, M.; Burek, M.; Radoń, M.; Kawiński, M. The Effect of Structure on Thermal Power of Cast-iron Heat Exchangers. Arch. Foundry Eng. 2020, 20, 27–30. [Google Scholar] [CrossRef]
- Podrzucki, C. Żeliwo. Struktura, Właściwości, Zastosowanie. (Cast Iron. Structure, Properties, Application); ZG STOP: Kraków, Poland, 1991. (In Polish) [Google Scholar]
- Elliott, R. Cast Iron Technology; Butterworths: London, Boston, UK, 1988. [Google Scholar]
- Rundman, K.B. Cast Irons. In Encyclopedia of Materials: Science and Technology; Elsevier: Oxford, UK, 2001; pp. 1003–1010. [Google Scholar]
- Masoud, I.M.; Al-Jarrah, J.A.; Abu Mansour, T. Manufacturing of Gray Cast Iron Automotive Disc Brake. Indian J. Appl. Res. 2014, 4, 129–131. [Google Scholar] [CrossRef]
- Djafri, M.; Bouchetara, M.; Busch, C.; Weber, S. Effects of humidity and corrosion on the tribological behaviour of the brake disc materials. Wear 2014, 321, 8–15. [Google Scholar] [CrossRef]
- Xu, W.; Ferry, M.; Wang, Y. Influence of alloying elements on as-cast microstructure and strength of gray iron. Mater. Sci. Eng. A 2005, 33, 326–333. [Google Scholar] [CrossRef]
- Tsujikawa, M.; Nagamine, K.; Ikenaga, A.; Hino, M. Influence of graphite morphology on dry sliding wear of flake graphite cast irons. Int. J. Cast Met. Res. 2008, 21, 76–80. [Google Scholar] [CrossRef]
- Polak, A.; Grzybek, J. The mechanism of changes in the surface layer of grey cast iron automotive brake disc. Mater. Res. 2005, 8, 475–479. [Google Scholar] [CrossRef]
- Maluf, O.; Angeloni, M.; Milan, M.T.; Spinelli, D.; Filho, W.W.B. Development of materials for automotive disc brakes. Pesqui. Technol Minerva 2004, 2, 149–158. [Google Scholar]
- Tonolini, P.; Montesano, L.; Pola, A.; Bontempi, G.; Gelfi, M. Wear Behavior of Nb Alloyed Gray Cast Iron for Automotive Brake Disc Application. Metals 2023, 13, 365. [Google Scholar] [CrossRef]
- Konopka, Z.; Łągiewka, M.; Zyska, A. Influence of Cast Iron Modification on Free Vibration Frequency of Casting. Arch. Foundry Eng. 2020, 20, 23–26. [Google Scholar] [CrossRef]
- PN-EN ISO 945-1; Microstructure of Cast Irons. Part 1: Graphite Classification by Bisual Analysis. PKN: Warsaw, Poland, 2019.
- Liles, G.D. Analysis of Disc Brake Squeal Using Finite Element Methods; SAE: Warrendale, PA, USA, 1989. [Google Scholar]
- Liu, P.; Zheng, H.; Cai, C.; Wang, Y.Y.; Lu, C.; Ang, K.H.; Liu, G.R. Analysis of disc brake squeal using the complex eigenvalue method. Appl Acoust. 2007, 68, 603–615. [Google Scholar] [CrossRef]
- Kung, S.W.; Dunlap, K.B.; Ballinger, R.S. Complex Eigenvalue Analysis for Reducing Low Frequency Brake Squeal; SAE: Warrendale, PA, USA, 2000. [Google Scholar]
- Belhocine, A.; Ghazaly, N.M. Effects of Young’s Modulus on Disc Brake Squeal using Finite Element Analysis. Int. J. Acoust. Vib. 2016, 21, 292–300. [Google Scholar] [CrossRef]
- Sinou, J.J. Transient non-linear dynamic analysis of automotive disc brake squeal—On the need to consider both stability and non-linear analysis. Mech. Res. Commun. 2010, 37, 96–105. [Google Scholar] [CrossRef]
- Nouby, M.; Sujatha, C.; Srinivasan, K. Modelling of Automotive Disc Brake Squeal and Its Reduction Using Rotor Design Modification. Int. J. Veh Noise Vib. 2011, 7, 129–148. [Google Scholar] [CrossRef]
- Genuit, K. The Future of NVH Research—A Challenge by New Powertrains; SAE: Warrendale, PA, USA, 2010. [Google Scholar]
- PN-EN ISO 6506-1; Metallic Materials — Brinell Hardness Test Part 1: Test Method. PKN: Warsaw, Poland, 2014.
- PN-EN 12668-1; Non-Destructive testing—Characterization and Verification of Ultrasonic Testing Equipment - Part 1: Instruments. PKN: Warsaw, Poland, 2010.
- PN-EN 12668-2; Non-Destructive Testing - Characterization and Verification of Ultrasonic Examination Equipment - Part 2: Probes. PKN: Warsaw, Poland, 2010.
- BN-75/4051-10; Odlewnicze Stopy Aluminium i Miedzi. Badania Technologiczne. Pomiar Stopnia Zagazowania. Instytut Odlewnictwa: Krakow, Polska, 1975. (In Polish)
- PN-75/H-04661; Gray, Spheroidal Graphite and Malleable Cast Iron. Metallographic examination. Evaluation of microstructure. PKN: Warsaw, Poland, 1975.
- Wojciechowski, A.; Sobczak, J. Kompozytowe Tarcze Hamulcowe Pojazdów Drogowych (Composite brake discs for road vehicles); ITS: Warszawa, Poland, 2001. (In Polish) [Google Scholar]
- Wehr, J. Measurements of the Velocity and Attenuation of Ultrasonic Waves; PWN: Warszawa, Poland, 1972. (In Polish) [Google Scholar]
- PN-ISO 8258; Shewhart Control Charts. PKN: Warsaw, Poland, 1996.








| Disc Code | Outer Diameter [mm] | Inner Diameter [mm] | Thickness [mm] | Mass [kg] | |
|---|---|---|---|---|---|
 | Disc 1 | 322 | 191 | 32 | 15 |
| Disc 2 | 380 | 221 | 34 | 19.9 |
| Cast Iron Grade | Type of Chemical Composition | Chemical Composition, wt.% | Degree of Eutectic Saturation SC | Carbon Equivalent (CE) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Cu | Cr | Mo | Ni | Sn | ||||
| A | MIN | 3.25 | 1.70 | 0.50 | 0.00 | 0.05 | 0.10 | 0.13 | 0.00 | 0.00 | 0.00 | 0.87 | 3.78 |
| OPT | 3.35 | 1.75 | 0.60 | - | 0.08 | 0.15 | 0.15 | - | - | - | 0.90 | 3.90 | |
| MAX | 3.40 | 1.80 | 0.70 | 0.10 | 0.10 | 0.25 | 0.20 | 0.20 | 0.20 | 0.09 | 0.93 | 3.99 | |
| B | MIN | 3.67 | 1.40 | 0.55 | 0.00 | 0.00 | 0.30 | 0.25 | 0.00 | 0.00 | 0.00 | 0.95 | 4.07 |
| OPT | 3.70 | 1.45 | 0.60 | - | 0.08 | 0.32 | 0.25 | - | - | - | 0.97 | 4.12 | |
| MAX | 3.72 | 1.50 | 0.70 | 0.10 | 0.15 | 0.35 | 0.35 | 0.15 | 0.10 | 0.09 | 0.98 | 4.16 | |
| C | MIN | 3.70 | 1.60 | 0.50 | 0.00 | 0.00 | 0.15 | 0.13 | 0.00 | 0.00 | 0.00 | 0.98 | 4.18 |
| OPT | 3.73 | 1.65 | 0.55 | - | 0.08 | 0.20 | 0.15 | - | - | - | 1.00 | 4.25 | |
| MAX | 3.75 | 1.70 | 0.75 | 0.08 | 0.10 | 0.25 | 0.25 | 0.10 | 0.10 | 0.09 | 1.01 | 4.29 | |
| Cast Iron Grade | Disc Code | Graphite | Metal Matrix | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Shape | Distribution, % | Length, % | Perlite, % | Ferrite, % | Cementite, % | ||||||
| A | B | D–E | 5 | 4 | 3 | ||||||
| A | Disc 1 | I | 71 | 4 | 25 | 59 | 36 | 5 | 93 | 6 | <1 |
| Disc 2 | I | 75 | 4 | 21 | 63 | 31 | 6 | 95 | 4 | <1 | |
| B | Disc 1 | I | 72 | 4 | 24 | 63 | 32 | 5 | 94 | 5 | <1 |
| Disc 2 | I | 75 | 4 | 21 | 65 | 29 | 6 | 95 | 4 | <1 | |
| C | Disc 1 | I | 72 | 4 | 24 | 70 | 24 | 6 | 93 | 6 | <1 |
| Disc 2 | I | 76 | 3 | 21 | 74 | 22 | 4 | 95 | 4 | <1 | |
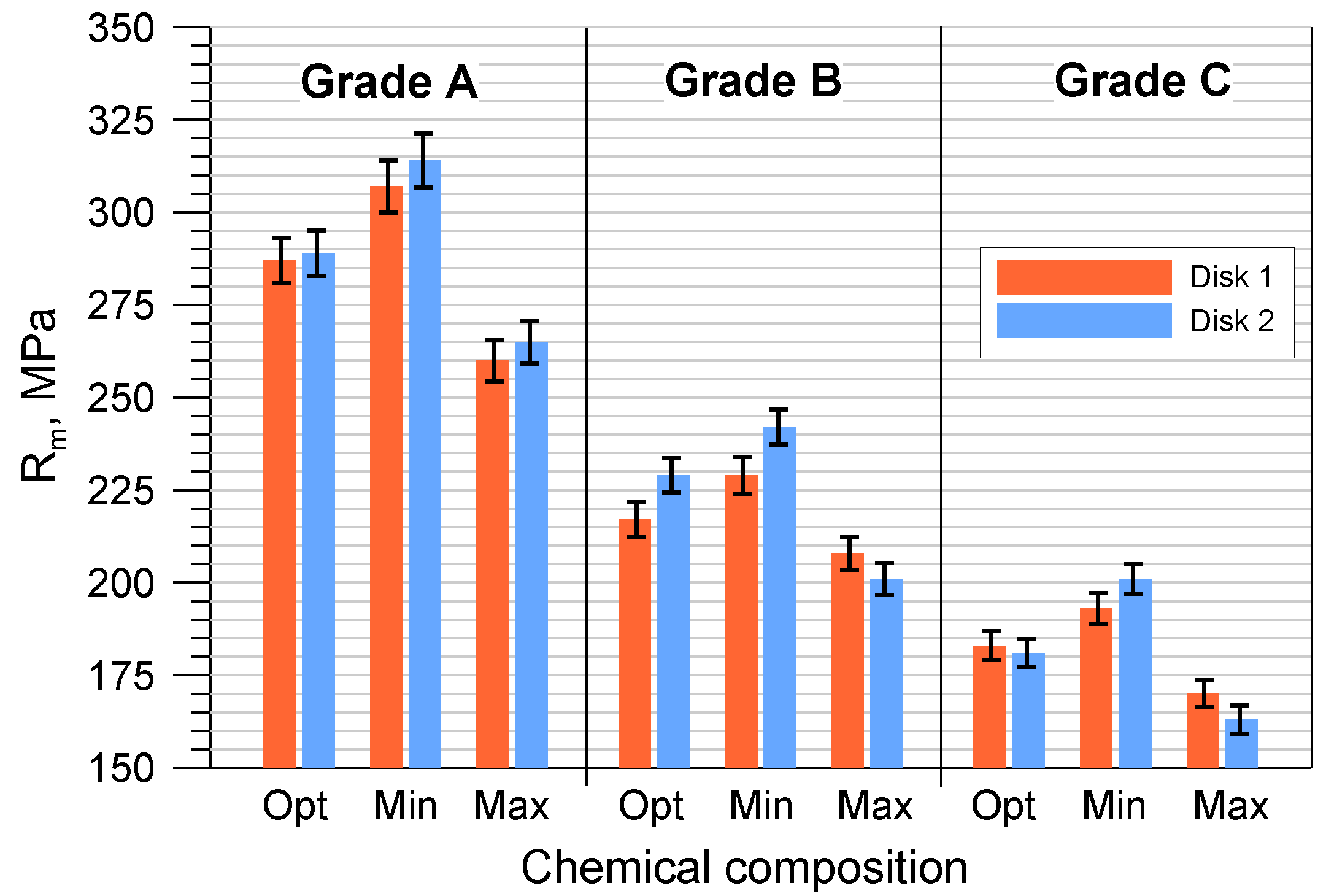
| Cast Iron Grade | Chemical Composition | Disc Code | Average Speed (mm/µs) | E (GPa) | E According to Chemical Composition (GPa) | Standard Deviation σ(E) | Poisson’s Number | Density, g/cm3 | |
|---|---|---|---|---|---|---|---|---|---|
| VL | VS | ||||||||
| A | MIN | Disc 1 | 4.87 | 2.71 | 135 | 135 | 3.15 | 0.26 | 7.192 |
| Disc 2 | 4.84 | 2.72 | 135 | ||||||
| OPT | Disc 1 | 4.77 | 2.67 | 131 | 131.5 | 0.26 | 7.188 | ||
| Disc 2 | 4.78 | 2.69 | 132 | ||||||
| MAX | Disc 1 | 4.71 | 2.64 | 128 | 128 | 0.26 | 7.181 | ||
| Disc 2 | 4.69 | 2.65 | 128 | ||||||
| B | MIN | Disc 1 | 4.51 | 2.59 | 120 | 121 | 2.34 | 0.26 | 7.148 |
| Disc 2 | 4.54 | 2.61 | 122 | ||||||
| OPT | Disc 1 | 4.55 | 2.59 | 121 | 120.5 | 0.27 | 7.143 | ||
| Disc 2 | 4.52 | 2.58 | 120 | ||||||
| MAX | Disc 1 | 4.52 | 2.53 | 117 | 116.5 | 0.26 | 7.319 | ||
| Disc 2 | 4.47 | 2.54 | 116 | ||||||
| C | MIN | Disc 1 | 4.47 | 2.54 | 116 | 116 | 4.32 | 0.27 | 7.117 |
| Disc 2 | 4.50 | 2.54 | 116 | ||||||
| OPT | Disc 1 | 4.43 | 2.51 | 113 | 112.5 | 0.27 | 7.113 | ||
| Disc 2 | 4.39 | 2.50 | 112 | ||||||
| MAX | Disc 1 | 4.30 | 2.44 | 107 | 106.5 | 0.26 | 7.111 | ||
| Disc 2 | 4.29 | 2.43 | 106 | ||||||
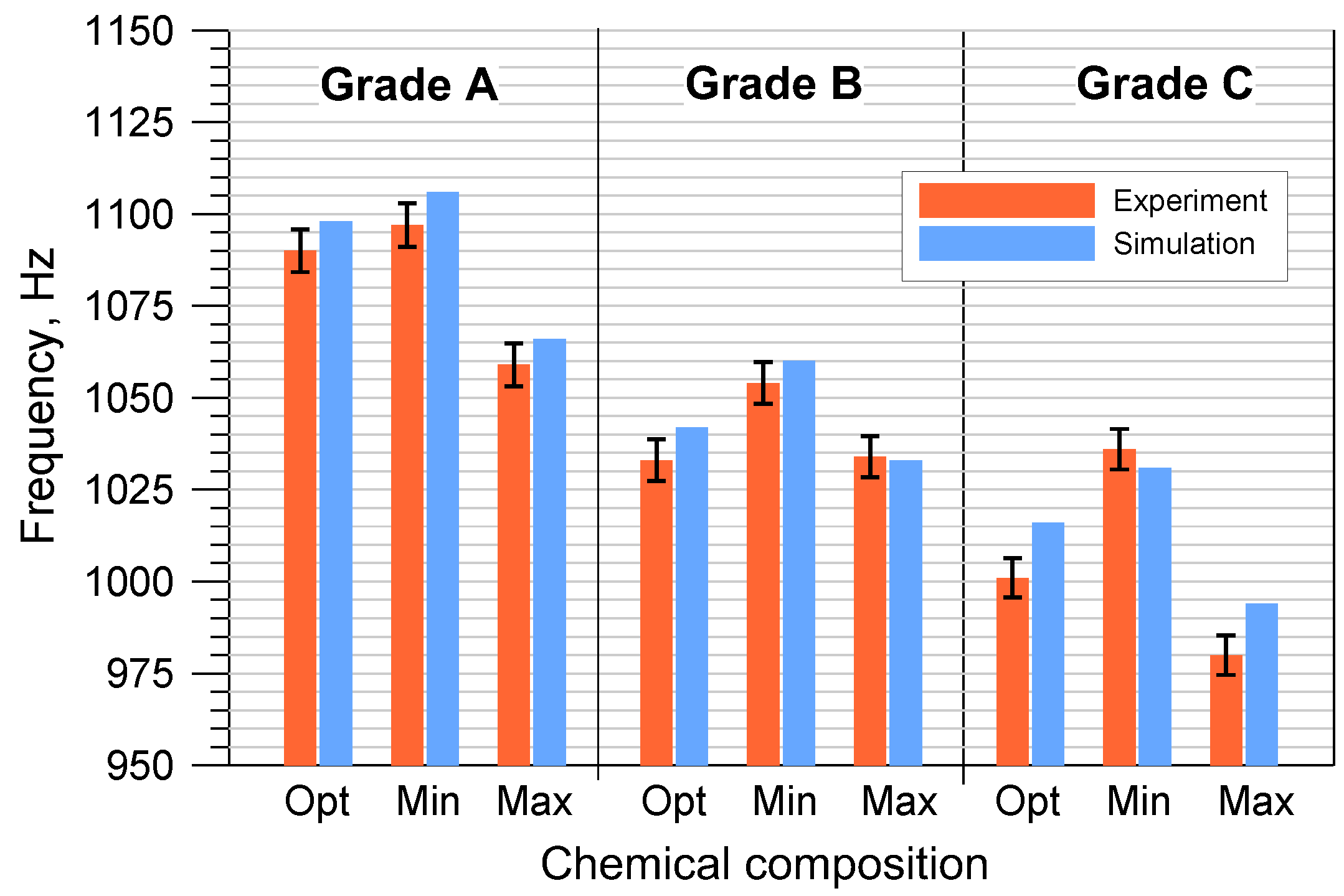
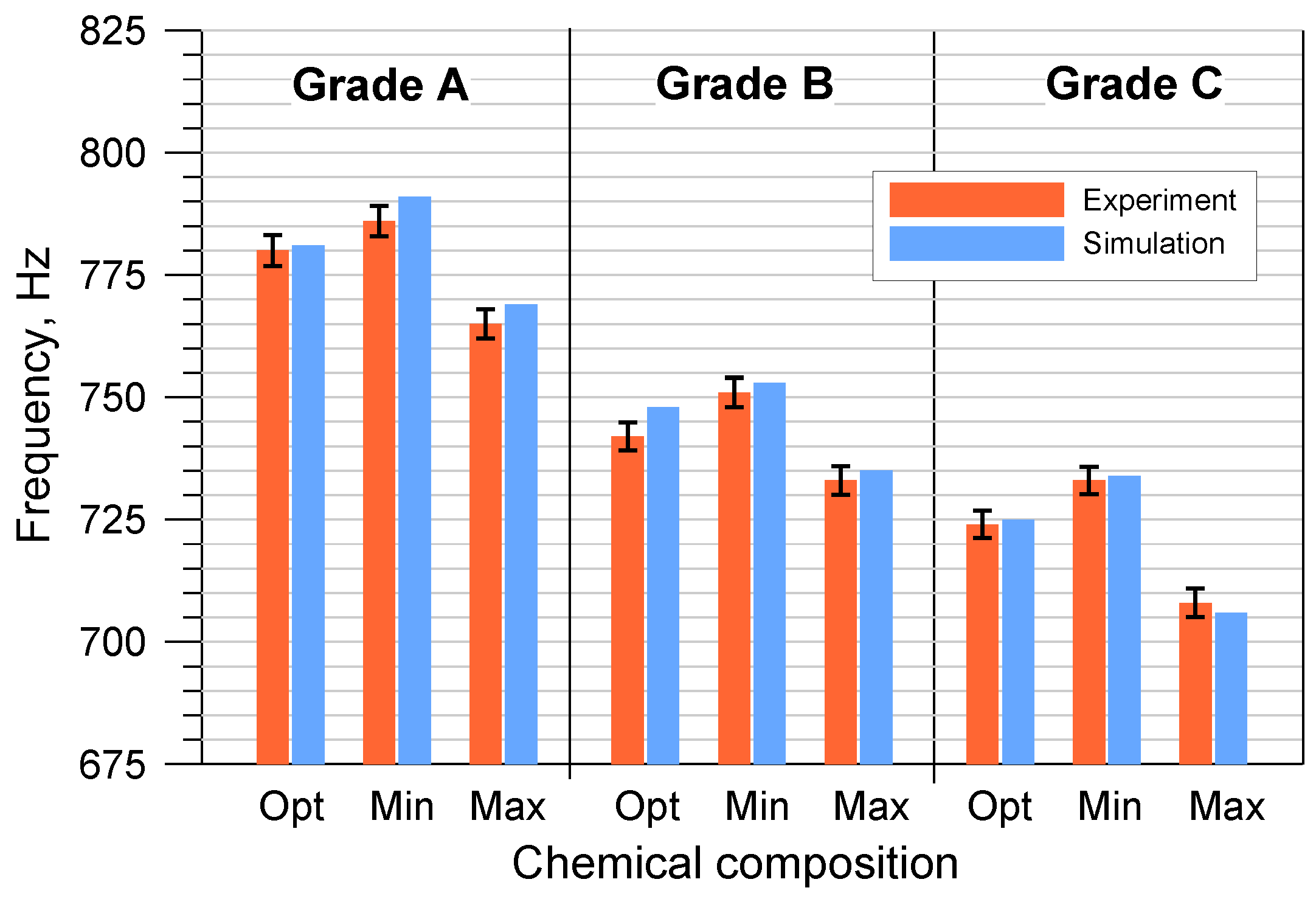
| Cast Iron Grade | Chemical Composition | Disc Code | First Natural Frequency, Hz | Calculation Error, % | ||
|---|---|---|---|---|---|---|
| Experiment | Simulation | |||||
| Average Value | Standard Deviation | |||||
| A | OPT | Disc 1 | 1090 | 8.1 | 1098 | 0.73 |
| Disc 2 | 780 | 5.2 | 781 | 0.13 | ||
| MIN | Disc 1 | 1097 | 8.3 | 1106 | 0.82 | |
| Disc 2 | 786 | 5.2 | 791 | 0.64 | ||
| MAX | Disc 1 | 1059 | 8.0 | 1066 | 0.66 | |
| Disc 2 | 765 | 5.1 | 769 | 0.52 | ||
| B | OPT | Disc 1 | 1033 | 8.0 | 1042 | 0.87 |
| Disc 2 | 742 | 5.1 | 748 | 0.27 | ||
| MIN | Disc 1 | 1054 | 8.0 | 1060 | 0.57 | |
| Disc 2 | 751 | 5.0 | 753 | 0.27 | ||
| MAX | Disc 1 | 1034 | 7.8 | 1033 | 0.10 | |
| Disc 2 | 733 | 5.0 | 735 | 0.81 | ||
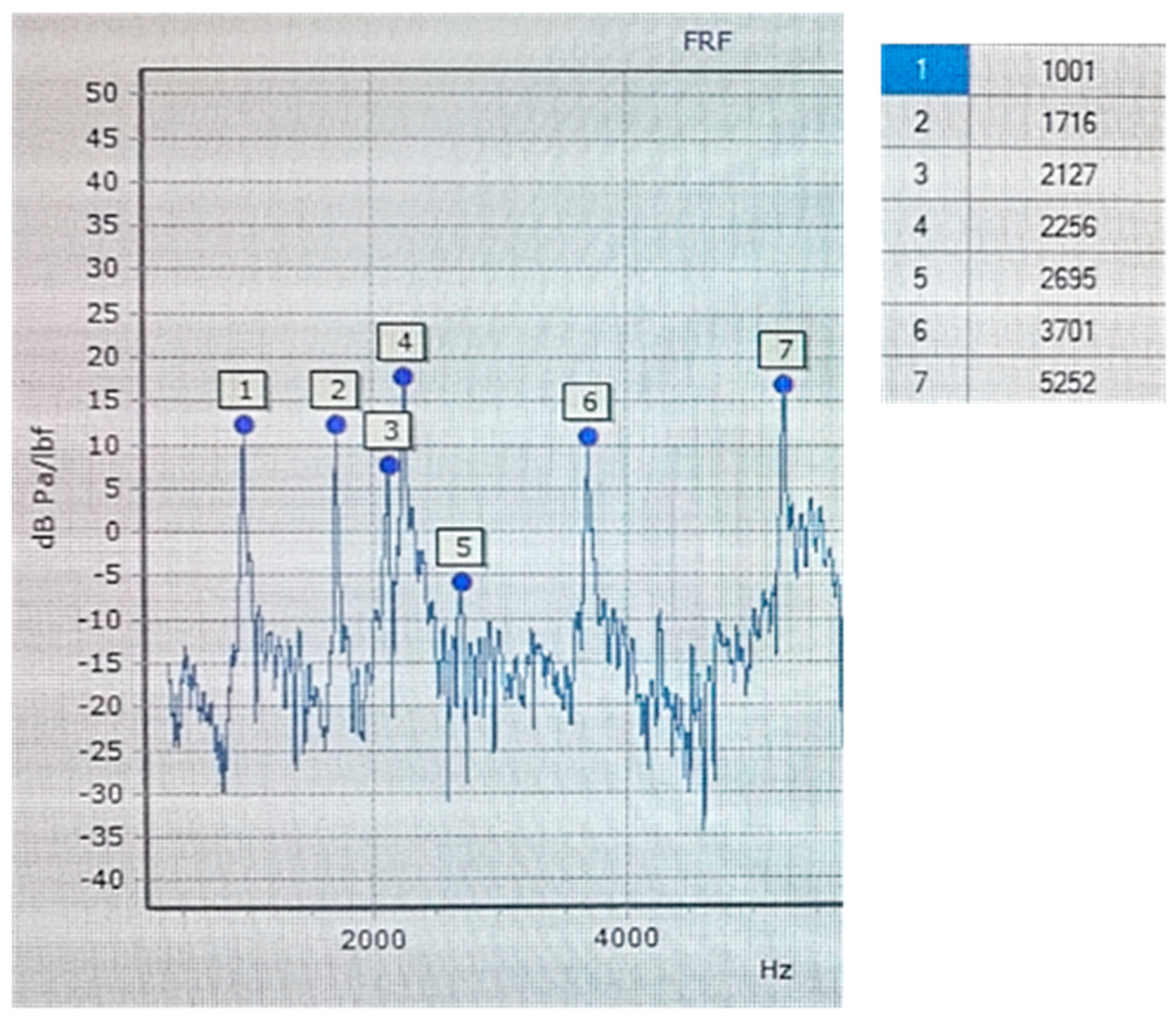
| C | OPT | Disc 1 | 1001 | 7.5 | 1016 | 1.50 |
| Disc 2 | 724 | 4.8 | 725 | 0.14 | ||
| MIN | Disc 1 | 1036 | 7.6 | 1031 | 0.48 | |
| Disc 2 | 733 | 4.7 | 734 | 0.14 | ||
| MAX | Disc 1 | 980 | 7.5 | 994 | 1.43 | |
| Disc 2 | 708 | 4.6 | 706 | 0.28 | ||
| Average calculation error | 0.63 | |||||
| Mode No | Natural Frequency, Hz | Difference, % | |
|---|---|---|---|
| Disc before Blade Modification | Disc after Blade Modification | ||
| Mod I (0;2) | 706 | 770 | 8.3 |
| Mod II (0;3) | 1676 | 1851 | 9.5 |
| Mod III (0;4) | 2751 | 3066 | 10.3 |
| Parameter | Predicted Value | Actual Value | Error, % | |
|---|---|---|---|---|
| Average Value | Standard Deviation | |||
| Natural frequency, Hz | 770 | 765 | 5.1 | 0.65 |
| Young’s modulus, GPa | 119 | 118.5 | 0.8 | 0.42 |
| Tensile strength, MPa | 222.4 | 218 | 7.7 | 2.01 |
| Hardness, HB | 202.9 | 204 | 6.1 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zyska, A.; Bieroński, M.; Naplocha, K.; Popielarski, P. Design and Control of the Natural Frequency of Brake Discs in the Aspect of the Gray Cast Iron Production Process. Materials 2024, 17, 3490. https://doi.org/10.3390/ma17143490
Zyska A, Bieroński M, Naplocha K, Popielarski P. Design and Control of the Natural Frequency of Brake Discs in the Aspect of the Gray Cast Iron Production Process. Materials. 2024; 17(14):3490. https://doi.org/10.3390/ma17143490
Chicago/Turabian StyleZyska, Andrzej, Mariusz Bieroński, Krzysztof Naplocha, and Paweł Popielarski. 2024. "Design and Control of the Natural Frequency of Brake Discs in the Aspect of the Gray Cast Iron Production Process" Materials 17, no. 14: 3490. https://doi.org/10.3390/ma17143490
APA StyleZyska, A., Bieroński, M., Naplocha, K., & Popielarski, P. (2024). Design and Control of the Natural Frequency of Brake Discs in the Aspect of the Gray Cast Iron Production Process. Materials, 17(14), 3490. https://doi.org/10.3390/ma17143490






