Thomson/Joule Power Compensation and the Measurement of the Thomson Coefficient
Abstract
1. Introduction
2. Theory
2.1. Energy Balance in the Observable Formulation
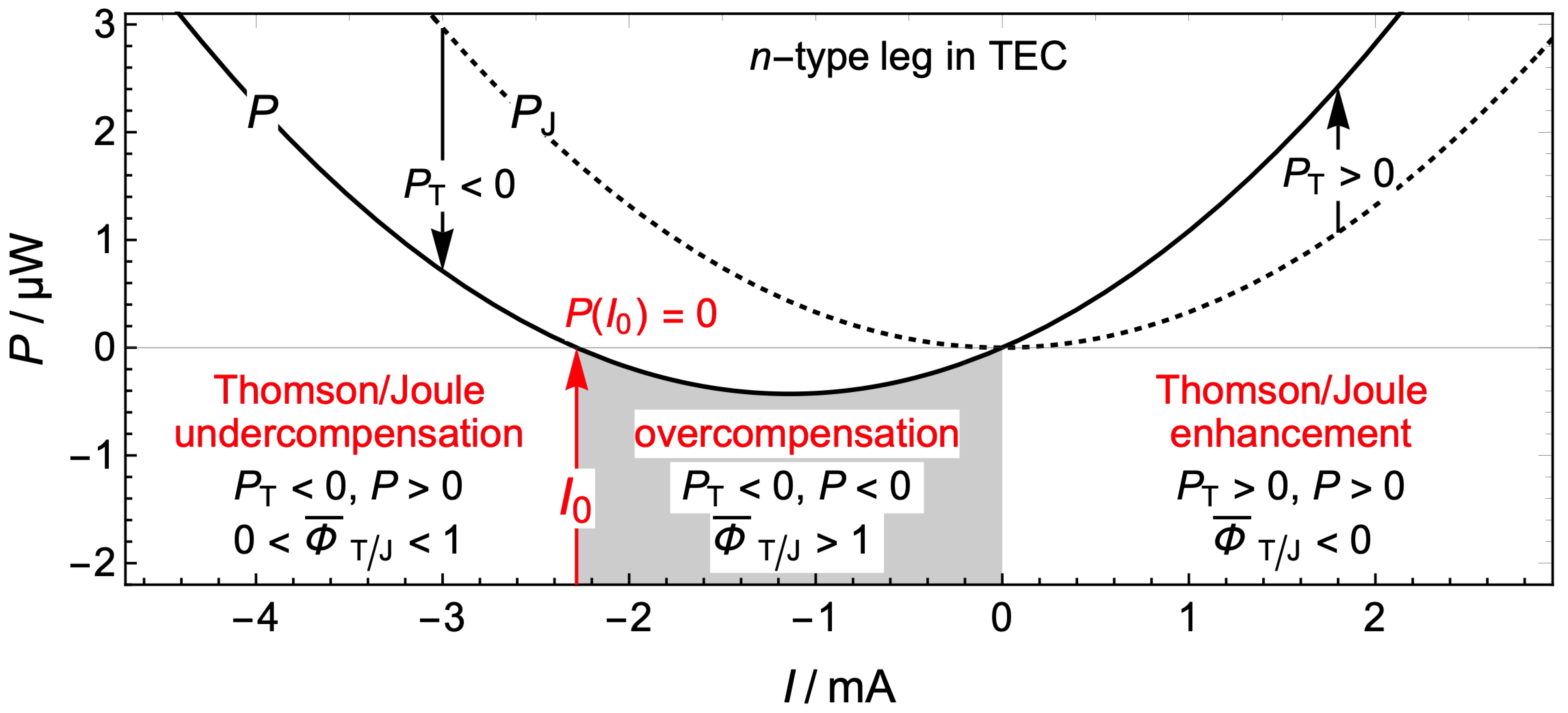
2.2. Thomson/Joule Power Compensation in a Thermoelectric Element
2.3. Measurements of the Thomson Coefficient Based on the Constant Transport Coefficients Model
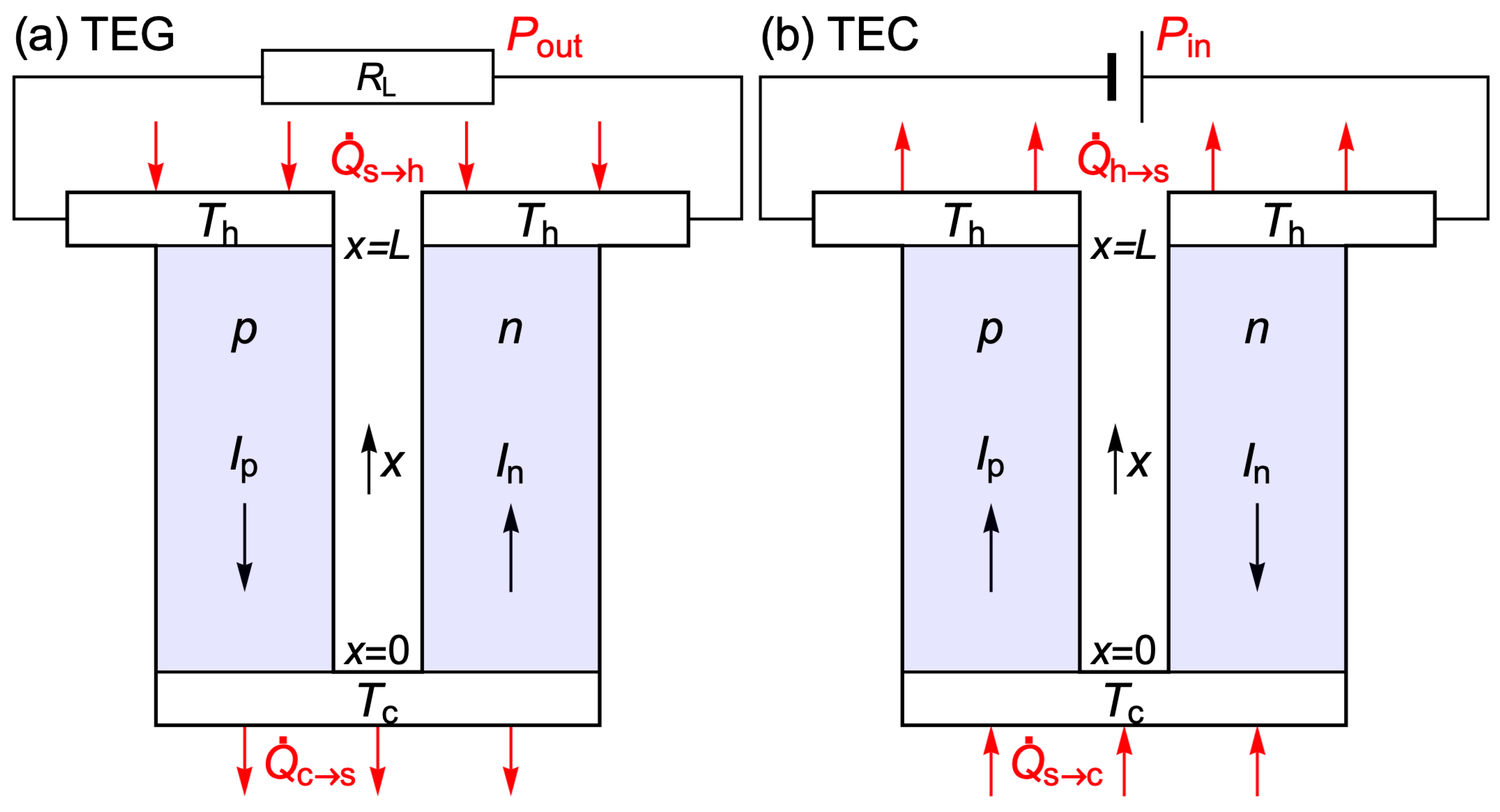
2.4. Energy Balances and Thomson/Joule Compensation in TEGs and TECs
3. Results
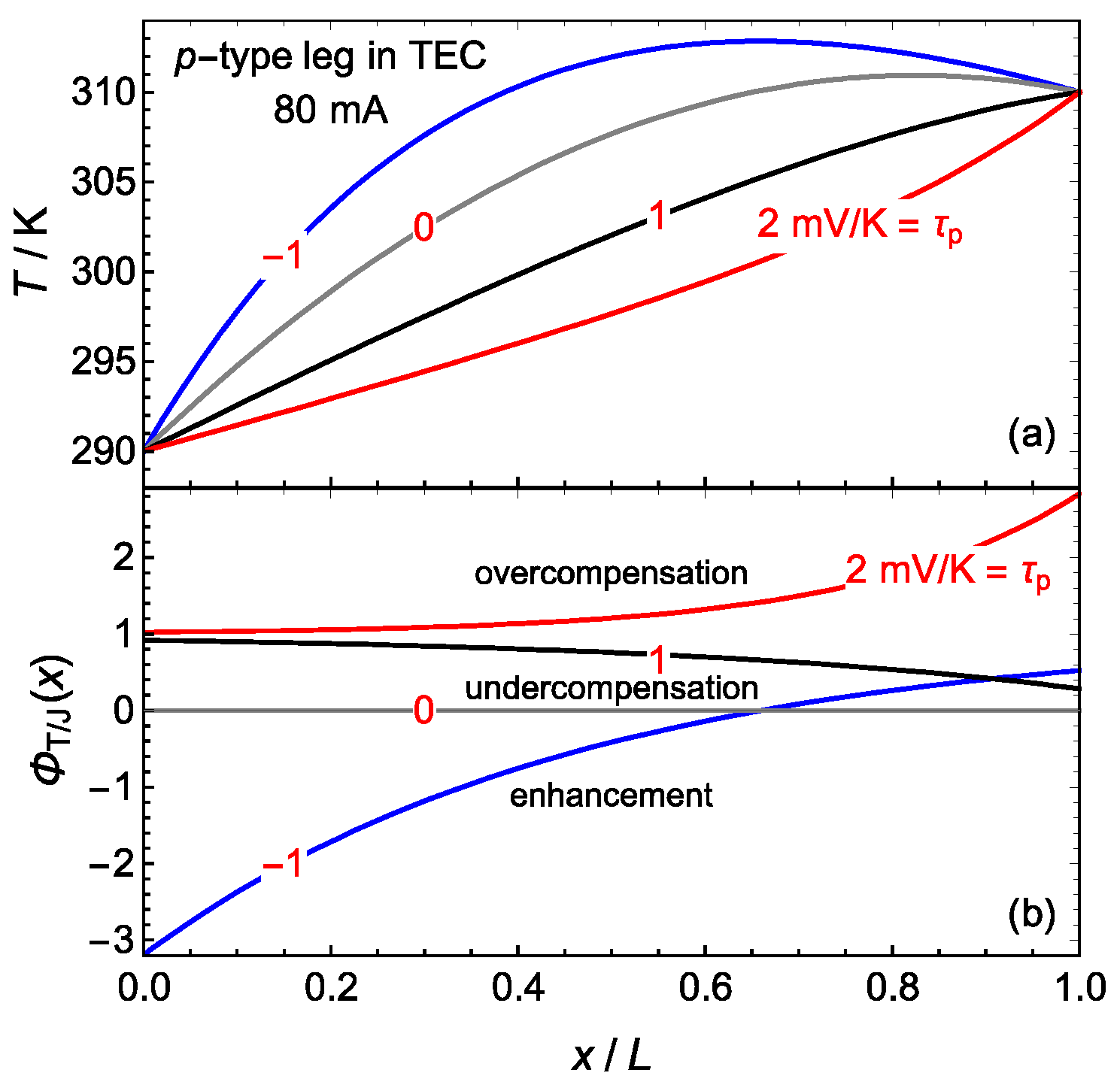
3.1. Thomson Effect in a TEC Using the Constant Transport Coefficients Model
3.2. The Effect of the Thomson Coefficient on the Thomson/Joule Compensation
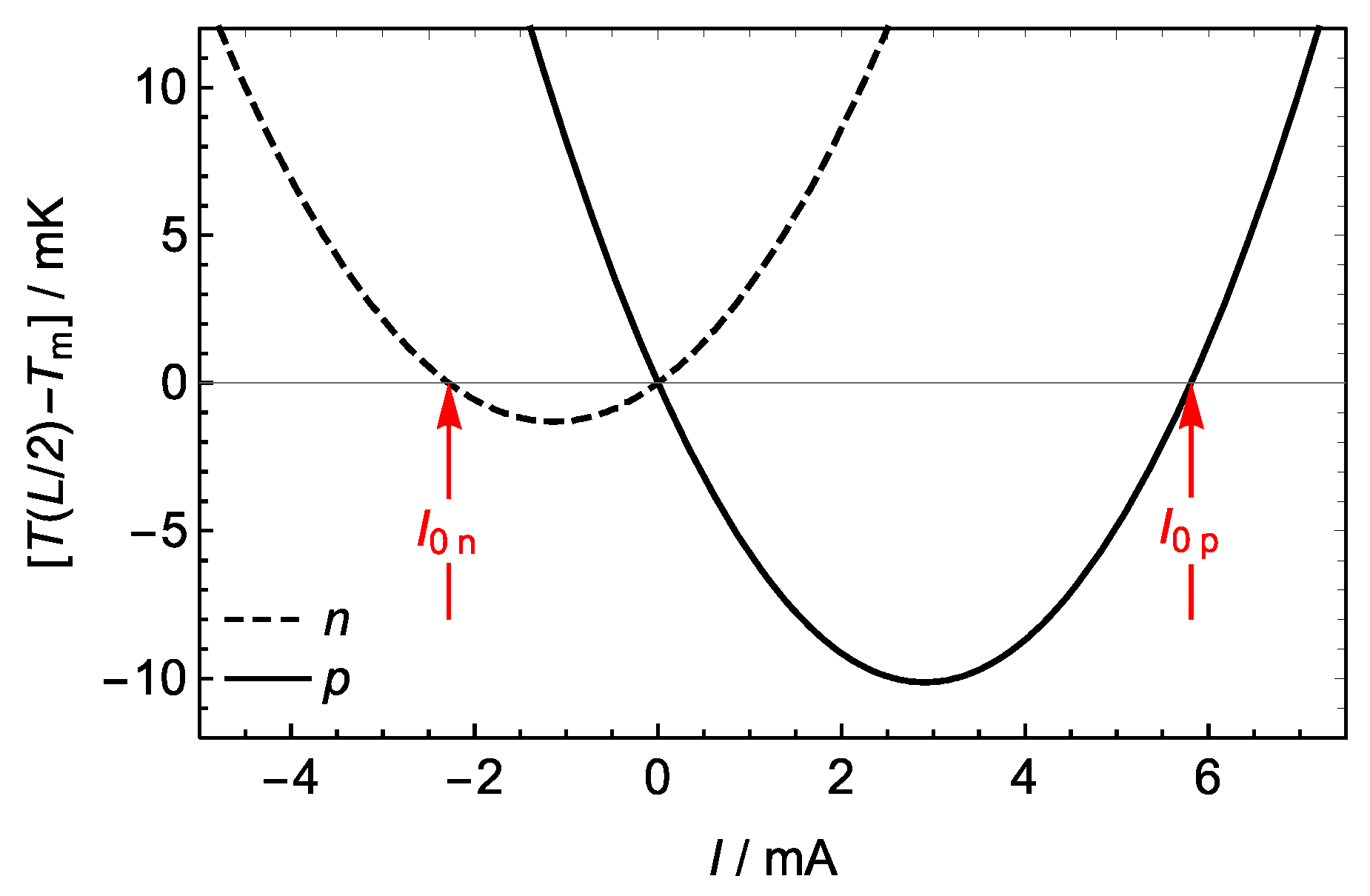
3.3. The Thomson/Joule Compensation Enables the Measurement of the Thomson Coefficient
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. On the Concept of “Heat Source”
Appendix B. Compensation in a Closed Circuit with No External Power Source
References
- Rowe, D.M.; Bhandari, C.M. Modern Thermoelectrics; Holt, Rinehart and Winston: London, UK, 1983. [Google Scholar]
- Rowe, D.M. (Ed.) Thermoelectrics Handbook: Macro to Nano; CRC/Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Rowe, D.M. (Ed.) Thermoelectrics and Its Energy Harvesting. Modules, Systems, and Applications in Thermoelectrics; CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Fan, W.; Shen, Z.; Zhang, Q.; Liu, F.; Fu, C.; Zhu, T.; Zhao, X. High-power-density wearable thermoelectric generators for human body heat harvesting. ACS Appl. Mater. Interfaces 2022, 14, 21224–21231. [Google Scholar] [CrossRef] [PubMed]
- Ishibe, T.; Tomeda, A.; Komatsubara, Y.; Kitaura, R.; Uenuma, M.; Uraoka, Y.; Yamashita, Y.; Nakamura, Y. Carrier and phonon transport control by domain engineering for high-performance transparent thin film thermoelectric generator. Appl. Phys. Lett. 2021, 118, 151601. [Google Scholar] [CrossRef]
- Garrido, J.; Manzanares, J.A. Heat and work fluxes in thermoelectric coolers. Therm. Sci. Eng. Prog. 2021, 22, 100817. [Google Scholar] [CrossRef]
- Modak, R.; Murata, M.; Hou, D.; Miura, A.; Iguchi, R.; Xu, B.; Guo, R.; Shiomi, J.; Sakuraba, Y.; Uchida, K. Phase-transition-induced giant Thomson effect for thermoelectric cooling. Appl. Phys. Rev. 2022, 9, 011414. [Google Scholar] [CrossRef]
- Qing, S.; Yuan, H.; Chen, C.; Tang, S.; Wen, X.; Zhong, J.; Gou, X. Characteristics and single/multi-objective optimization of thermoelectric generator by comprehensively considering inner-connection-and-contact effects and side-surface heat loss. Energy Convers. Manag. 2022, 251, 115003. [Google Scholar] [CrossRef]
- Maduabuchi, C.; Lamba, R.; Ozoegwu, C.; Njoku, H.O.; Eke, M.; Gurevich, Y.G.; Ejiogu, E.C. Thomson effect and nonlinear performance of thermoelectric generator. Heat Mass Transf. 2022, 58, 967–980. [Google Scholar] [CrossRef]
- He, H.; Liu, W.; Wu, Y.; Rong, M.; Zhao, P.; Tang, X. An approximate and efficient characterization method for temperature-dependent parameters of thermoelectric modules. Energy Convers. Manag. 2019, 180, 584–597. [Google Scholar] [CrossRef]
- Fallah Kohan, H.R.; Eslami, M.; Jafarpur, K. A hybrid analytical-computational method for three dimensional modeling of thermoelectric generators. Int. J. Energy Res. 2021, 45, 2680–2693. [Google Scholar] [CrossRef]
- Xin, J.; Xu, G.; Guo, T.; Nan, B. Optimization design and performance study of wearable thermoelectric device using phase change material as heat sink. Materials 2024, 17, 3266. [Google Scholar] [CrossRef]
- Lan, Y.; Lu, J.; Li, Y.; Wang, S. Effects of temperature-dependent thermal properties and the side leg heat dissipation on the performance of the thermoelectric generator. Energy 2022, 243, 123035. [Google Scholar] [CrossRef]
- Luo, D.; Wang, R.; Yu, W.; Zhou, W. Parametric study of a thermoelectric module used for both power generation and cooling. Renew. Energy 2020, 154, 542–552. [Google Scholar] [CrossRef]
- Zhang, M.; Tian, Y.; Xie, H.; Wu, Z.; Wang, Y. Influence of Thomson effect on the thermoelectric generator. Int. J. Heat Mass Transf. 2019, 137, 1183–1190. [Google Scholar] [CrossRef]
- Chengjian, J.; Xing, Z.; Dui, G.; Wang, Y.; Zhang, L. Modeling of annular thermoelectric generator considering temperature dependent material properties and side surface heat convection. J. Appl. Phys. 2023, 133, 125102. [Google Scholar] [CrossRef]
- Chen, L.; Lorenzini, G. Heating load, COP and exergetic efficiency optimizations for TEG-TEH combined thermoelectric device with Thomson effect and external heat transfer. Energy 2023, 270, 126824. [Google Scholar] [CrossRef]
- Bakan, G.; Gokirmak, A.; Silva, H. Suppression of thermoelectric Thomson effect in silicon microwires under large electrical bias and implications for phase-change memory devices. J. Appl. Phys. 2014, 116, 234507. [Google Scholar] [CrossRef]
- Qiu, C.; Shi, W. Comprehensive modeling for optimized design of a thermoelectric cooler with non-constant cross-section: Theoretical considerations. Appl. Thermal. Eng. 2020, 176, 115384. [Google Scholar] [CrossRef]
- Ponnusamy, P.; de Boor, J.; Müller, E. Discrepancy between constant properties model and temperature-dependent material properties for performance estimation of thermoelectric generators. Entropy 2020, 22, 1128. [Google Scholar] [CrossRef]
- Ruiz-Ortega, P.E.; Olivares-Robles, M.A.; Enciso-Montes de Oca, O.Y. Supercooling in a new two-stage thermoelectric cooler design with phase change material and Thomson effect. Energy Convers. Manag. 2021, 243, 114355. [Google Scholar] [CrossRef]
- Wielgosz, S.E.; Clifford, C.E.; Yu, K.; Barry, M.M. Fully–coupled thermal–electric modeling of thermoelectric generators. Energy 2023, 266, 126324. [Google Scholar] [CrossRef]
- Gong, T.R.; Gao, L.; Wu, Y.J.; Tan, H.S.; Qin, F.; Xin, X.; Shen, L.M.; Li, J.T.; Ming, T.Z. A model to evaluate the device-level performance of thermoelectric cooler with Thomson effect considered. J. Therm. Sci. 2022, 31, 712–726. [Google Scholar] [CrossRef]
- Sun, D.; Shen, L.; Chen, H.; Jiang, B.; Jie, D.; Liu, H.; Yao, Y.; Tang, J. Modeling and analysis of the influence of Thomson effect on microthermoelectric coolers considering interfacial and size effects. Energy 2020, 196, 117116. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y.; Chen, Z. Energy and exergy analysis of an integrated photovoltaic module and two-stage thermoelectric generator system. Appl. Therm. Eng. 2022, 212, 118605. [Google Scholar] [CrossRef]
- Cui, Y.J.; Wang, K.F.; Wang, B.L.; Li, J.E.; Zhou, J.Y. A comprehensive analysis of delamination and thermoelectric performance of thermoelectric pn-junctions with temperature-dependent material properties. Compos. Struct. 2019, 229, 111484. [Google Scholar] [CrossRef]
- Shi, P.; Qin, W.; Xie, J. Thermoelectric conversion efficiency of a two-dimensional thermoelectric plate of finite-size with a center crack. Acta Mech. 2022, 233, 4785–4803. [Google Scholar] [CrossRef]
- Lafaurie-Ponce, L.G.; Chejne, F.; Ramírez-Aristeguieta, L.M.; Gómez, C.A. A study of the non-linear Thomson effect produced by changing the current in a thermoelectric cooler. J. Non-Equilib. Thermodyn. 2022, 47, 339–354. [Google Scholar] [CrossRef]
- Chiva, T.; Iguchi, R.; Komine, T.; Hasegawa, Y.; Uchida, K. Temperature profile of the Thomson-effect-induced heat release/absorption in junctionless single conductors. Jpn. J. Appl. Phys. 2023, 62, 037001. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Akbari, O. A model for material metrics in thermoelectric Thomson coolers. Entropy 2023, 25, 1540. [Google Scholar] [CrossRef]
- Maxwell, G.M.; Lloyd, J.N.; Keller Jr., D. V. Measurement of the Thomson heat in metallic systems. Rev. Sci. Instrum. 1967, 38, 1084–1089. [Google Scholar] [CrossRef]
- Roberts, R.B. The absolute scale of thermoelectricity II. Philos. Mag. B 1981, 43, 1125–1135. [Google Scholar] [CrossRef]
- Fijiki, H.; Amagai, Y.; Okawa, K.; Harumoto, T. Development on measurement method of Thomson coefficient of thin film. Measurement 2021, 185, 110010. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S.; Khanna, R.; Seifert, W. Improved thermoelectric cooling based on the Thomson effect. Phys. Rev. B 2012, 86, 045202. [Google Scholar] [CrossRef]
- Lee, H. The Thomson effect and the ideal equation on thermoelectric coolers. Energy 2013, 56, 61–69. [Google Scholar] [CrossRef]
- Garrido, J.; Casanovas, A.; Manzanares, J.A. Thomson power in the model constant transport coefficients for thermoelectric elements. J. Electron. Mater. 2019, 48, 5821–5826. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Jokinen, M.; Cervera, J. On the different formalisms for the transport equations of thermoelectricity: A review. J. Non-Equilib. Thermodyn. 2015, 40, 211–227. [Google Scholar] [CrossRef]
- Garrido, J. Peltier’s and Thomson’s coefficients of thermoelectric phenomena in the observable formulation. J. Phys. Condens. Matter 2009, 21, 155802. [Google Scholar] [CrossRef]
- Apertet, Y.; Goupil, C. On the fundamental aspect of the first Kelvin’s relation in thermoelectricity. Int. J. Therm. Sci. 2016, 104, 225–227. [Google Scholar] [CrossRef][Green Version]
- Logvinov, G.N.; Velázquez, J.E.; Lashkevych, I.M.; Gurevich, Y.G. Heating and cooling in semiconductor structures by an electric current. Appl. Phys. Lett. 2006, 89, 092118. [Google Scholar] [CrossRef]
- Titov, O.Y.; Gurevich, Y.G. Temperature gradient and transport of heat and charge in a semiconductor structure. Low Temp. Phys. 2021, 47, 550–554. [Google Scholar] [CrossRef]
- Wang, X.D.; Huang, Y.X.; Cheng, C.H.; Lin, D.T.W.; Kang, C.H. A three-dimensional numerical modeling of thermoelectric device with consideration of coupling of temperature field and electric potential field. Energy 2012, 47, 488–497. [Google Scholar] [CrossRef]
- Yamashita, O.; Sugihara, S. High-performance bismuth-telluride compounds with highly stable thermoelectric figure of merit. J. Mater. Sci. 2005, 40, 6439–6444. [Google Scholar] [CrossRef]
- Meng, J.H.; Wang, X.D.; Zhang, X.X. Transient modeling and dynamic characteristics of thermoelectric cooler. Appl. Energy 2013, 108, 340–348. [Google Scholar] [CrossRef]
- Liu, W.D.; Yin, L.C.; Li, L.; Yang, Q.; Wang, D.Z.; Li, M.; Shi, X.L.; Liu, Q.; Bai, Y.; Gentle, I.; et al. Grain boundary re-crystallization and sub-nano regions leading to high plateau figure of merit for Bi2Te3 nanoflakes. Energy Environ. Sci. 2023, 16, 5123–5135. [Google Scholar] [CrossRef]
- Yang, J.; Mou, C.; Han, J.; Ge, Y.; Zhu, W.; Liang, W. Investigation on performance of a new thermoelectric cooler with hot and cold side separation for suppressing Fourier effect. Energy Convers. Manag. 2023, 298, 117760. [Google Scholar] [CrossRef]
- Kostic, M.M. Entropy generation results of convenience but without purposeful analysis and due comprehension. Entropy 2016, 18, 28. [Google Scholar] [CrossRef]
- Gadomski, A. Dissipative, entropy production systems across condensed matter and interdisciplinary classical vs. quantum physics. Entropy 2022, 24, 1094. [Google Scholar] [CrossRef]
- Bakker, F.L.; Slachter, A.; Adam, J.P.; van Wees, B.J. Interplay of Peltier and Seebeck effects in nanoscale nonlocal spin valves. Phys. Rev. Lett. 2010, 105, 136601. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrido, J.; Manzanares, J.A. Thomson/Joule Power Compensation and the Measurement of the Thomson Coefficient. Materials 2024, 17, 4640. https://doi.org/10.3390/ma17184640
Garrido J, Manzanares JA. Thomson/Joule Power Compensation and the Measurement of the Thomson Coefficient. Materials. 2024; 17(18):4640. https://doi.org/10.3390/ma17184640
Chicago/Turabian StyleGarrido, Javier, and José A. Manzanares. 2024. "Thomson/Joule Power Compensation and the Measurement of the Thomson Coefficient" Materials 17, no. 18: 4640. https://doi.org/10.3390/ma17184640
APA StyleGarrido, J., & Manzanares, J. A. (2024). Thomson/Joule Power Compensation and the Measurement of the Thomson Coefficient. Materials, 17(18), 4640. https://doi.org/10.3390/ma17184640






