A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances
Abstract
1. Introduction
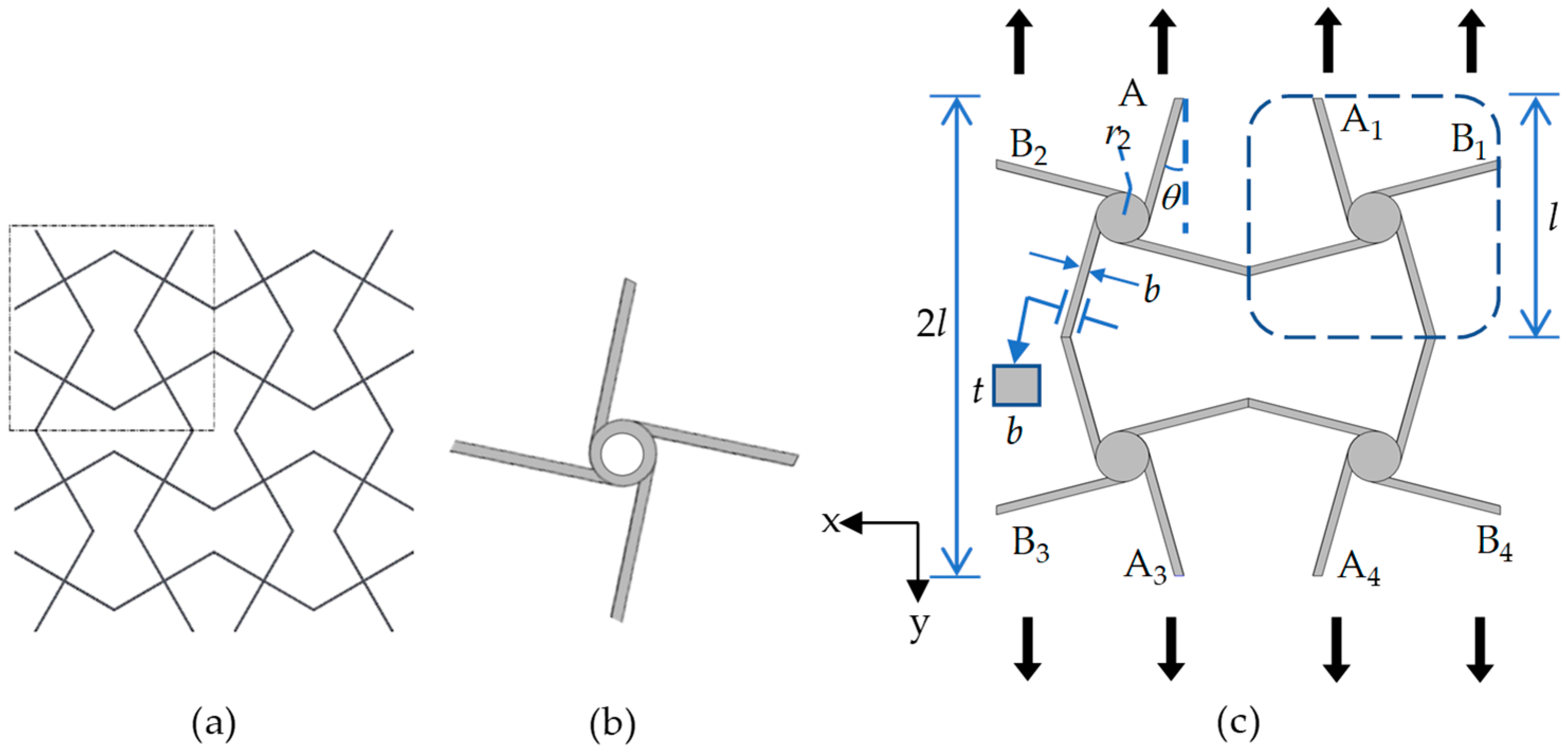
2. Cross Tetrachiral Honeycomb Metamaterials
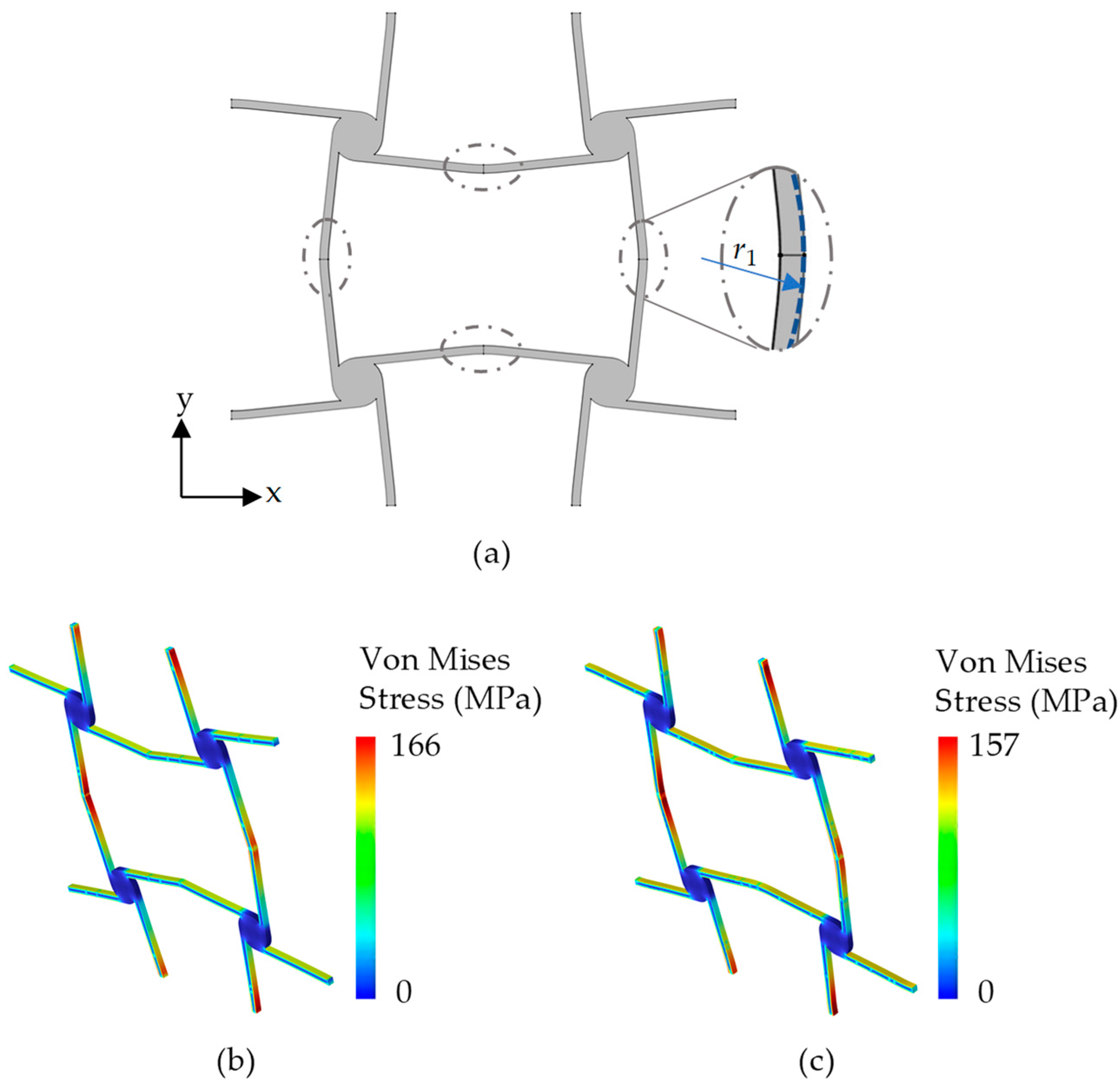
2.1. Model
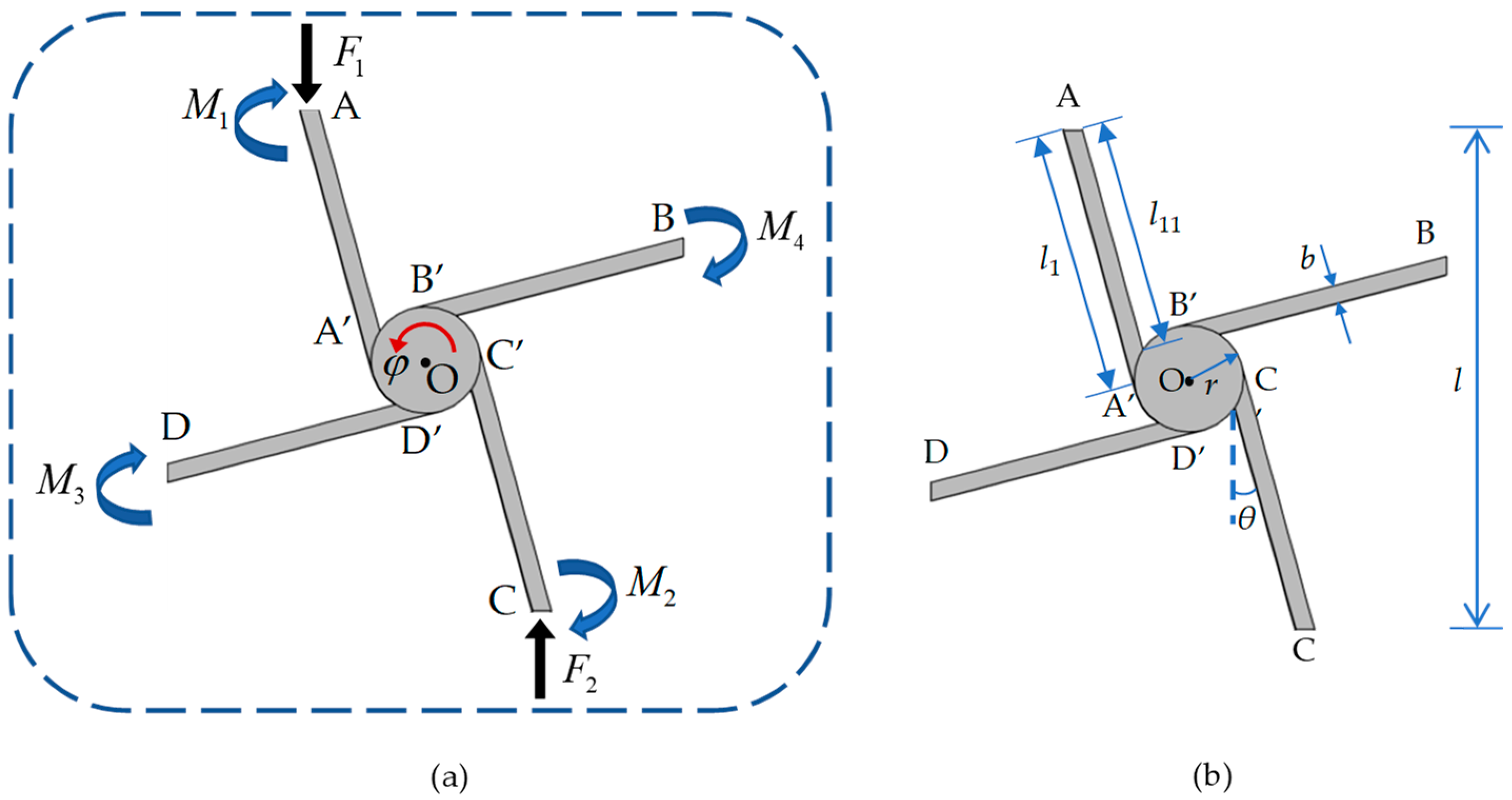
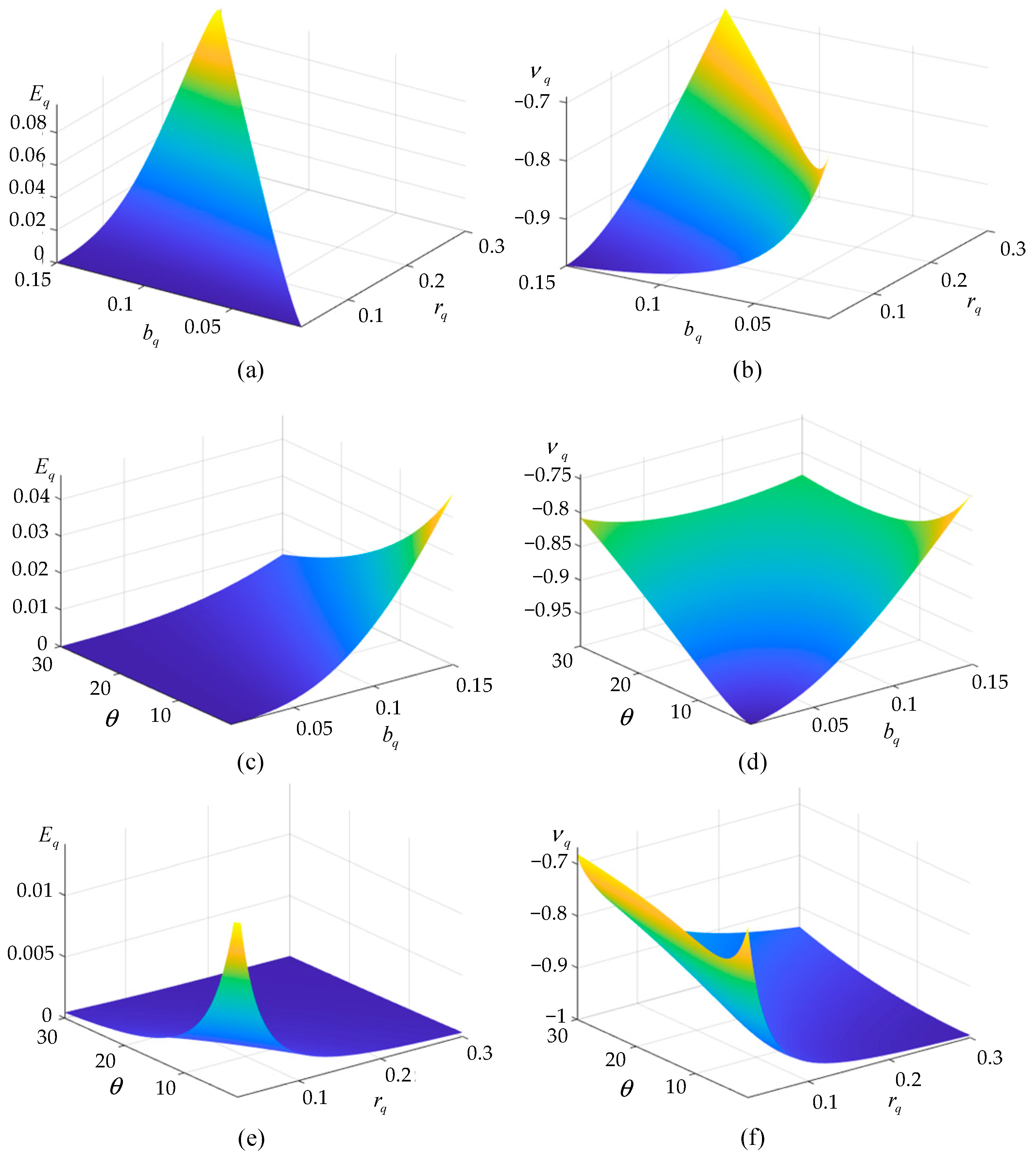
2.2. Effective Elastic Parameters
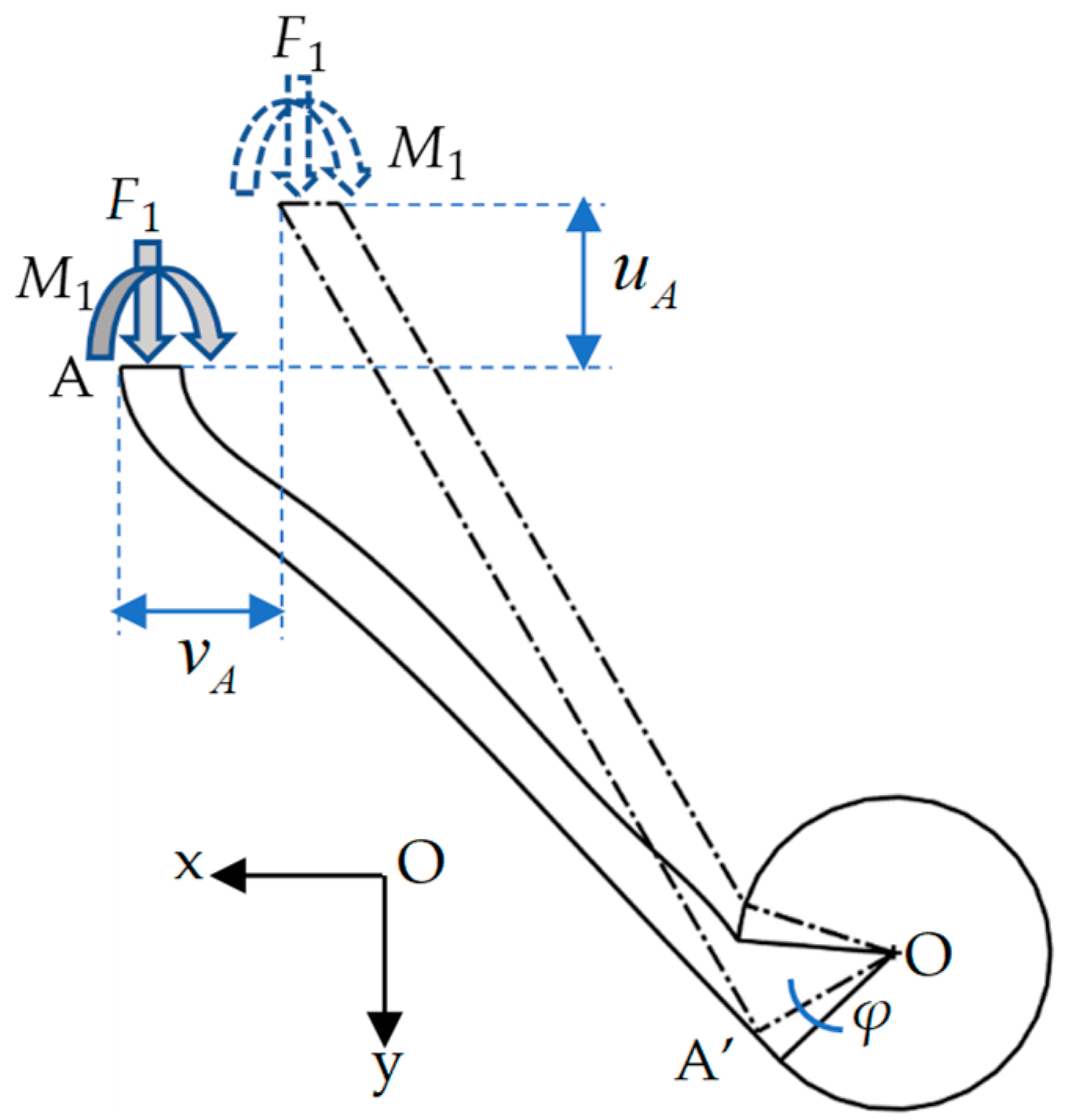
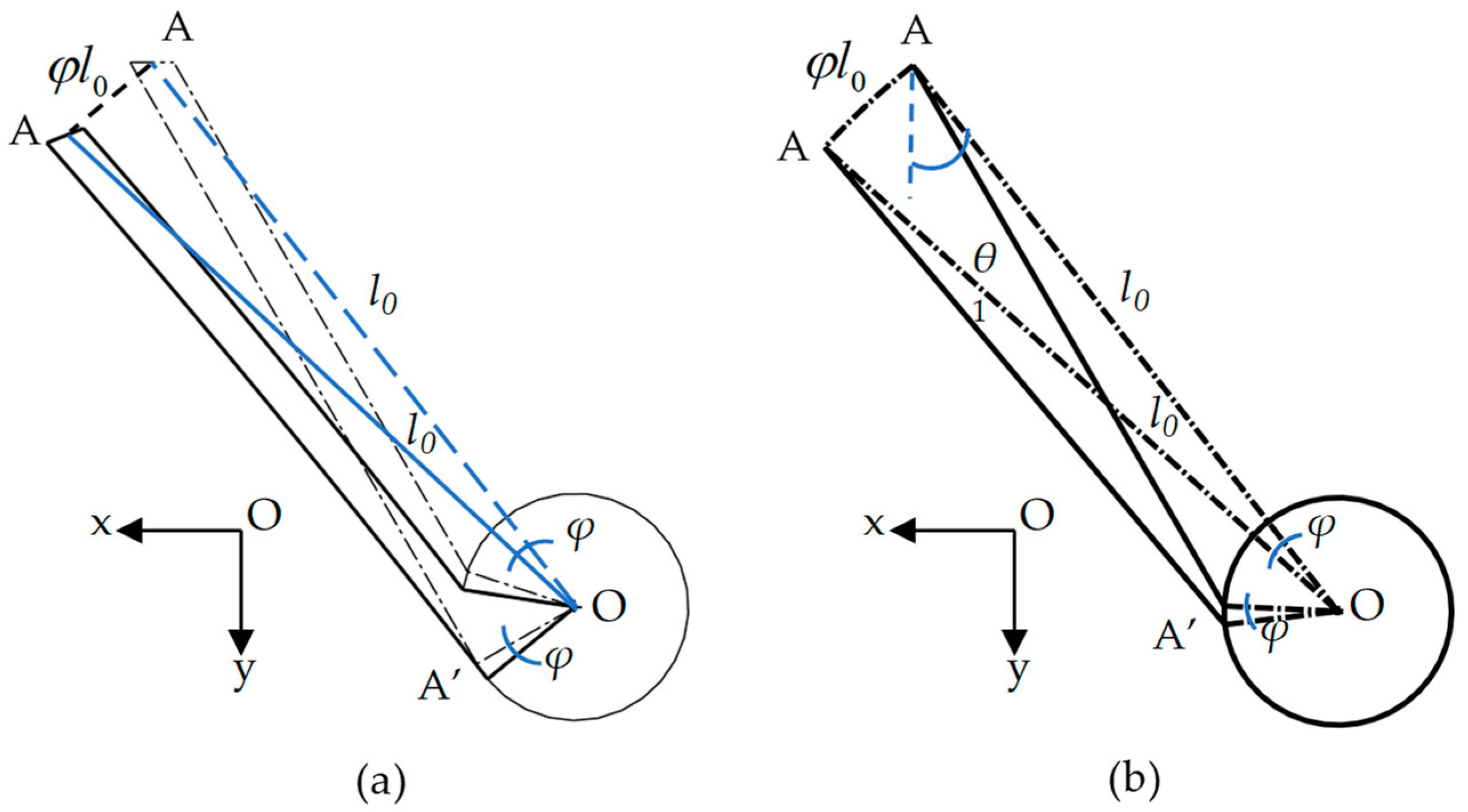
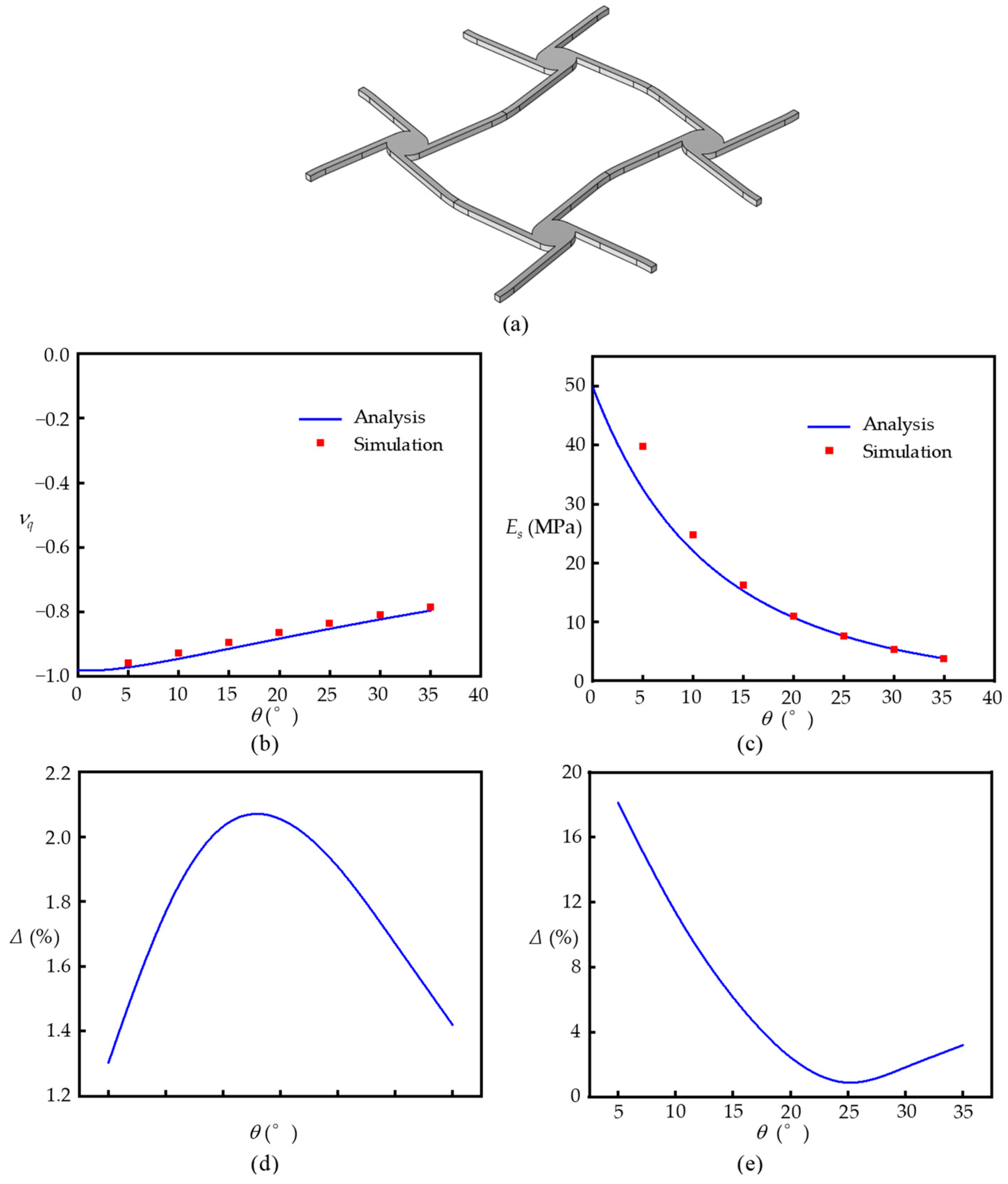
3. Static Performance
4. Dynamic Performance
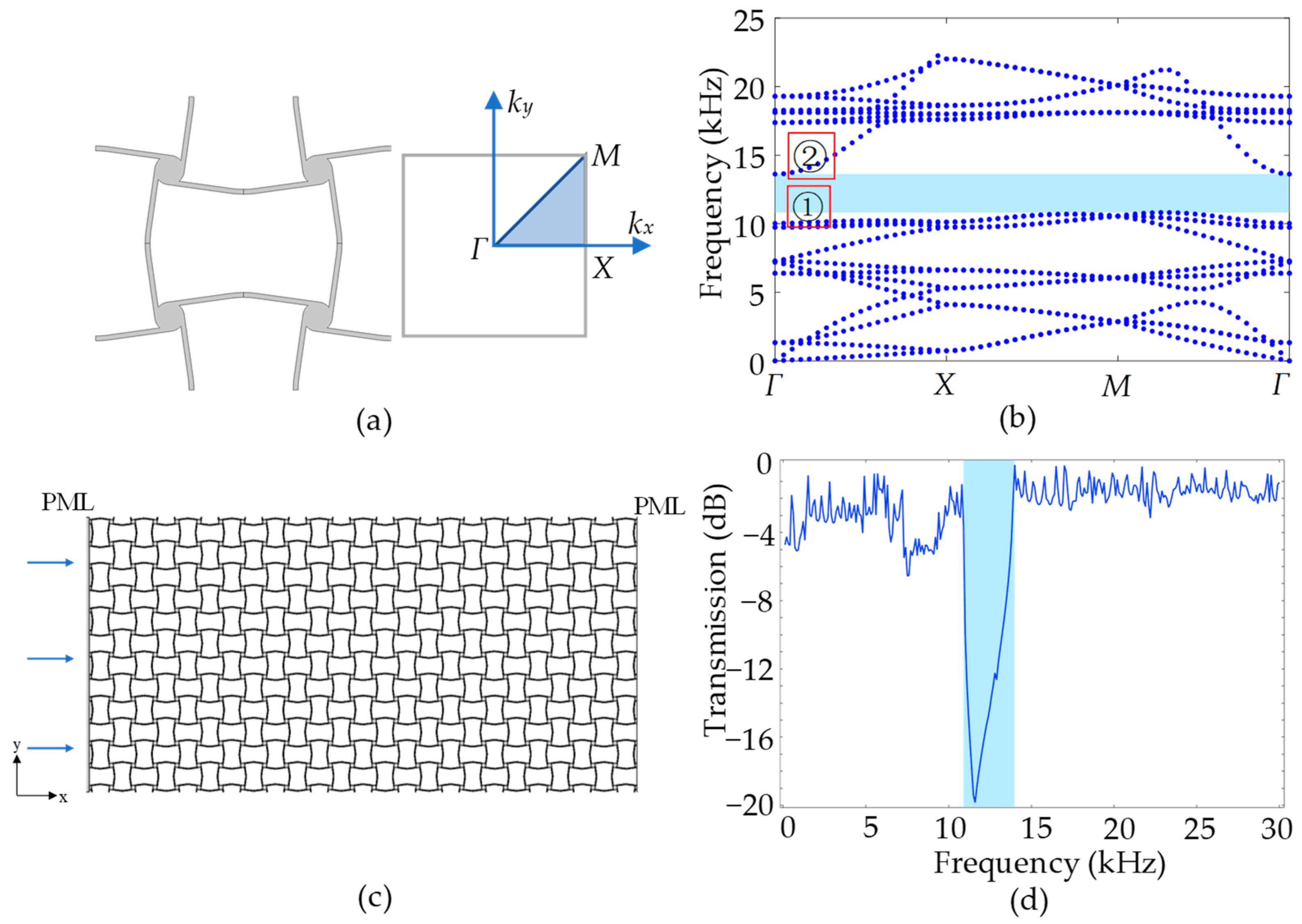
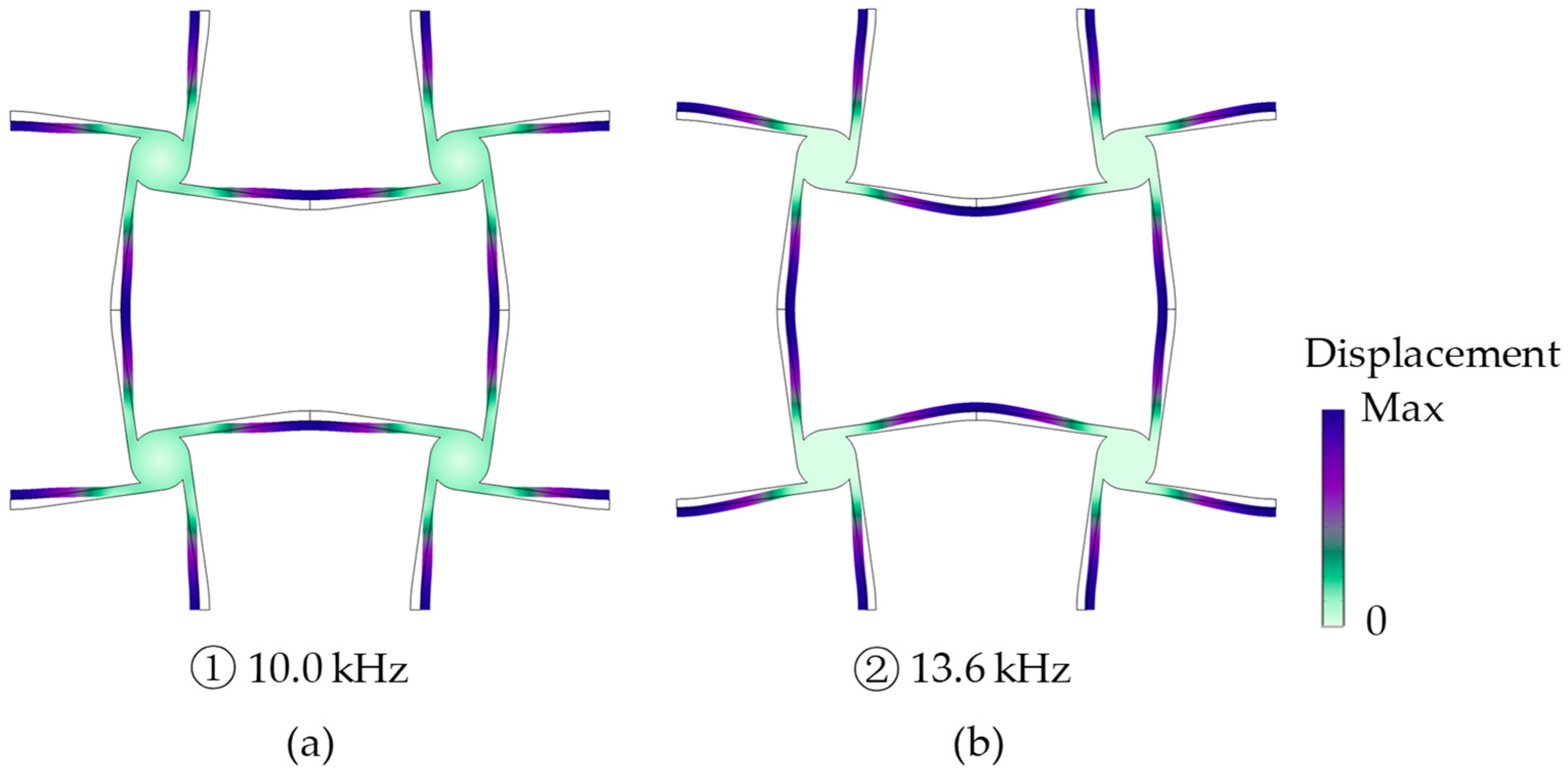
4.1. Band Structures
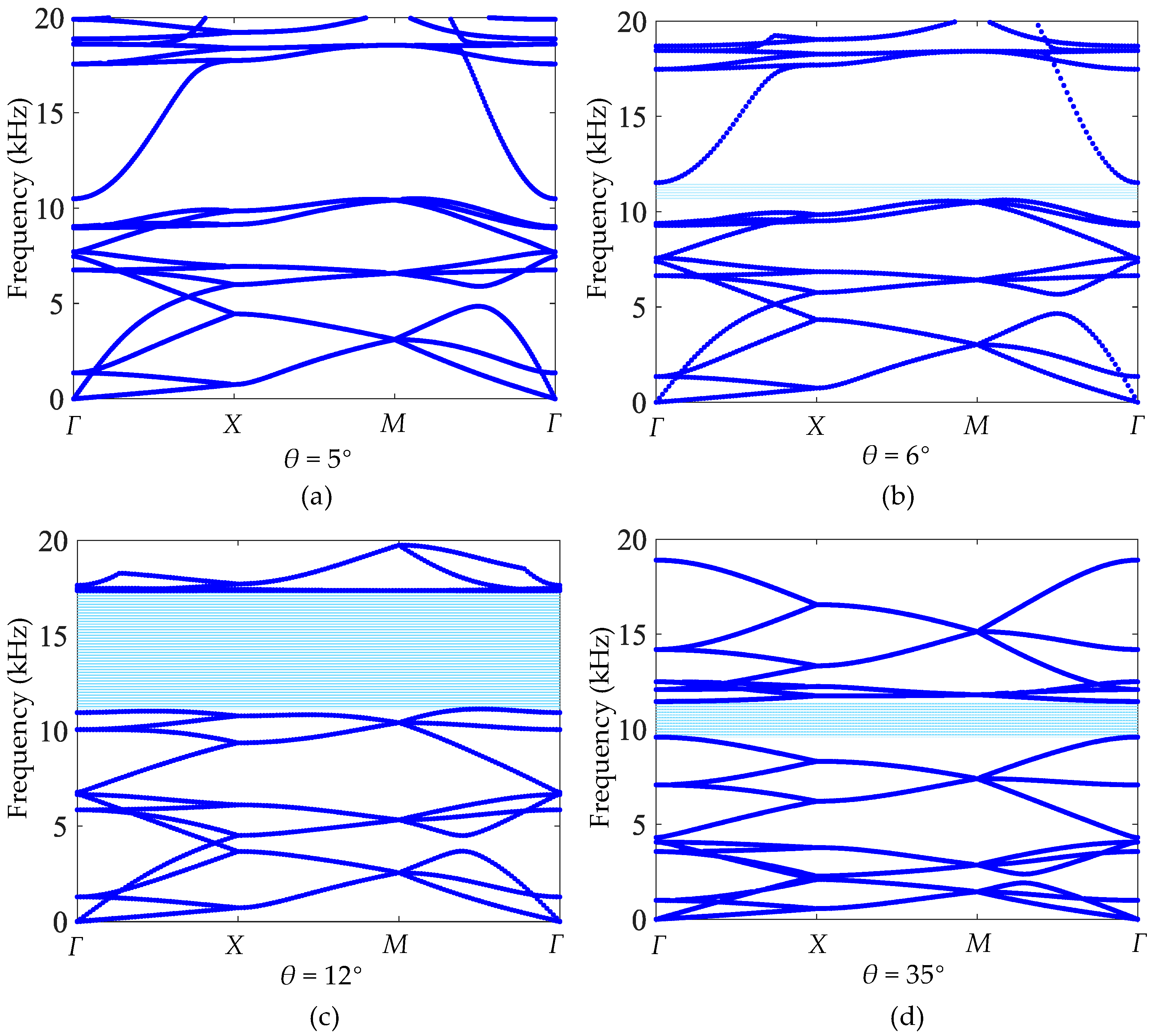
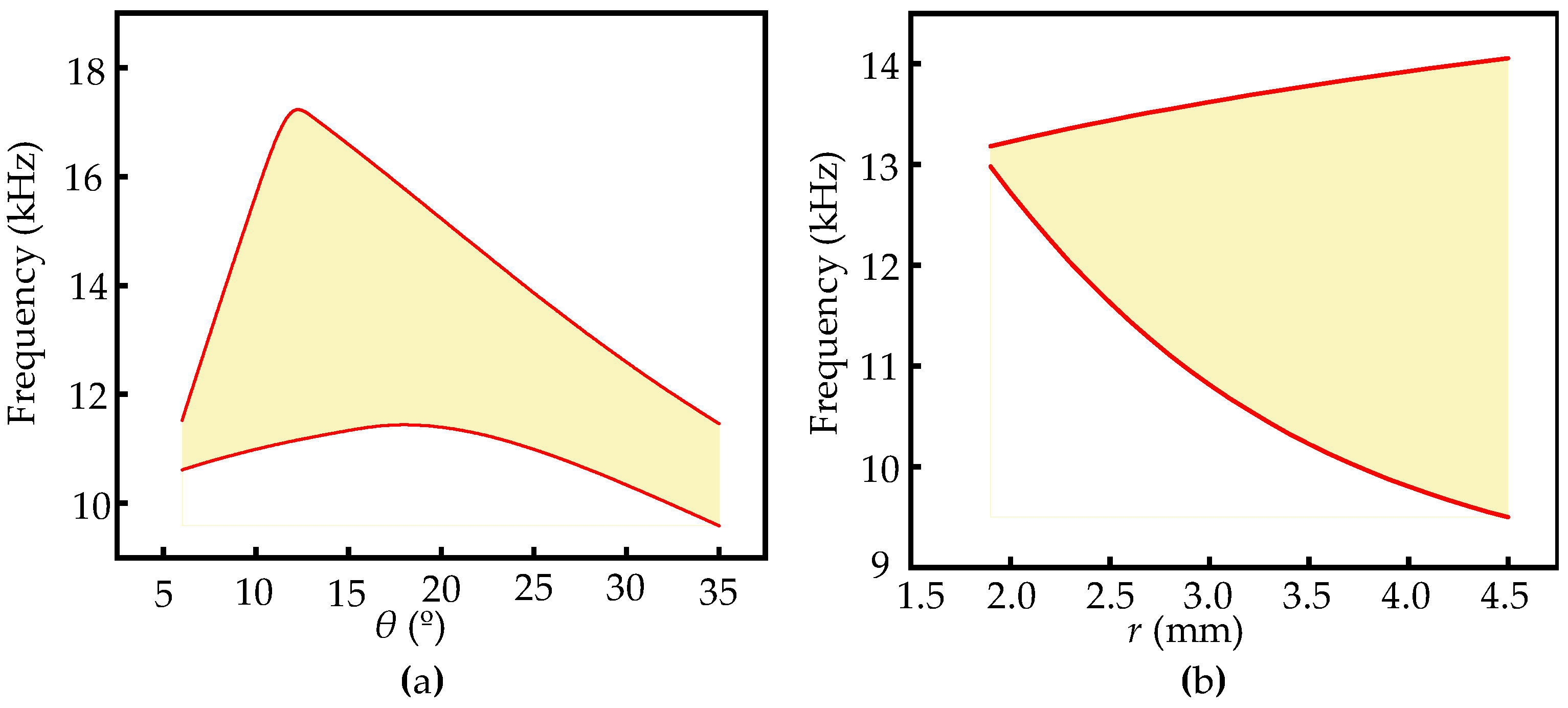
4.2. Bandgap Influenced by Geometric Parameters
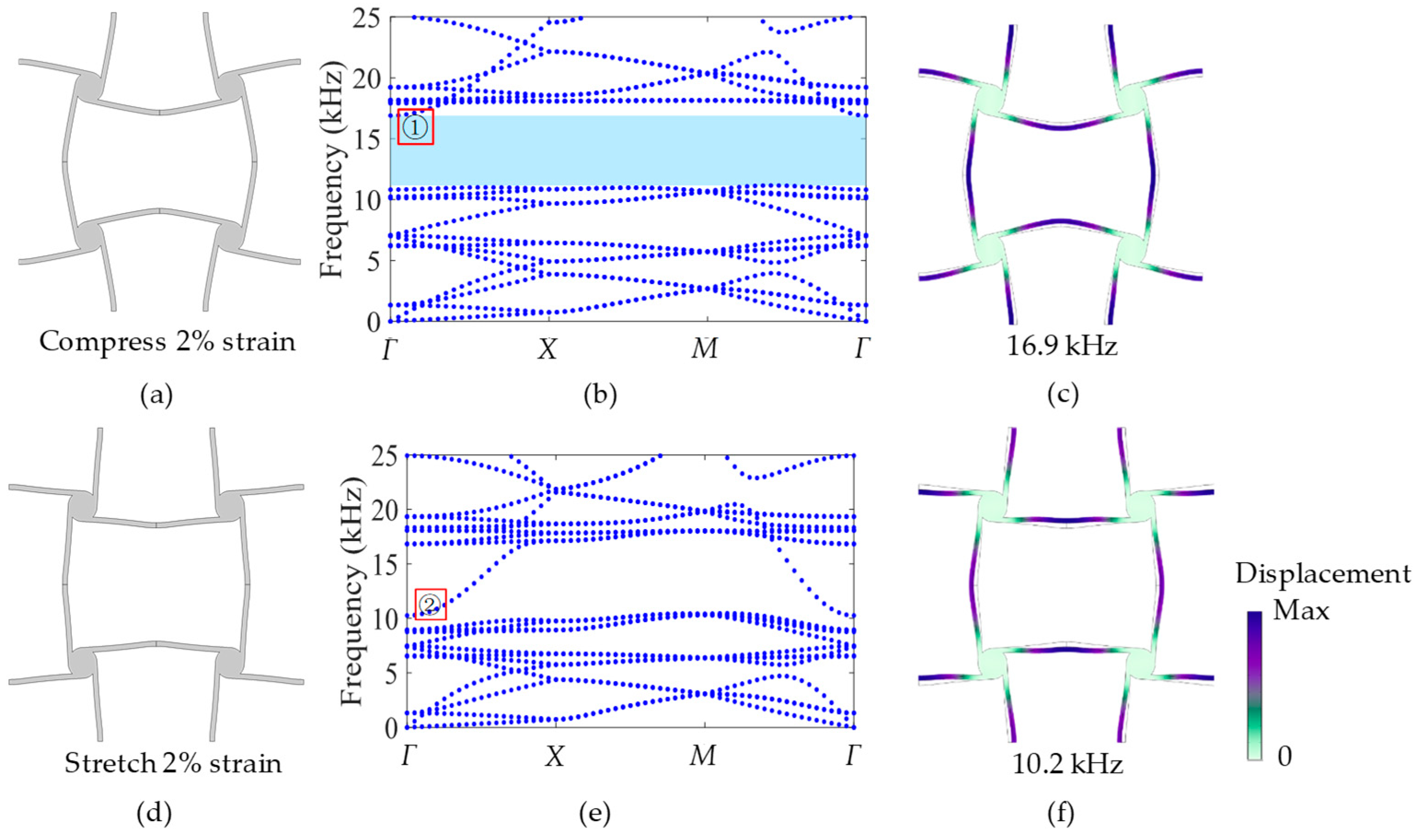
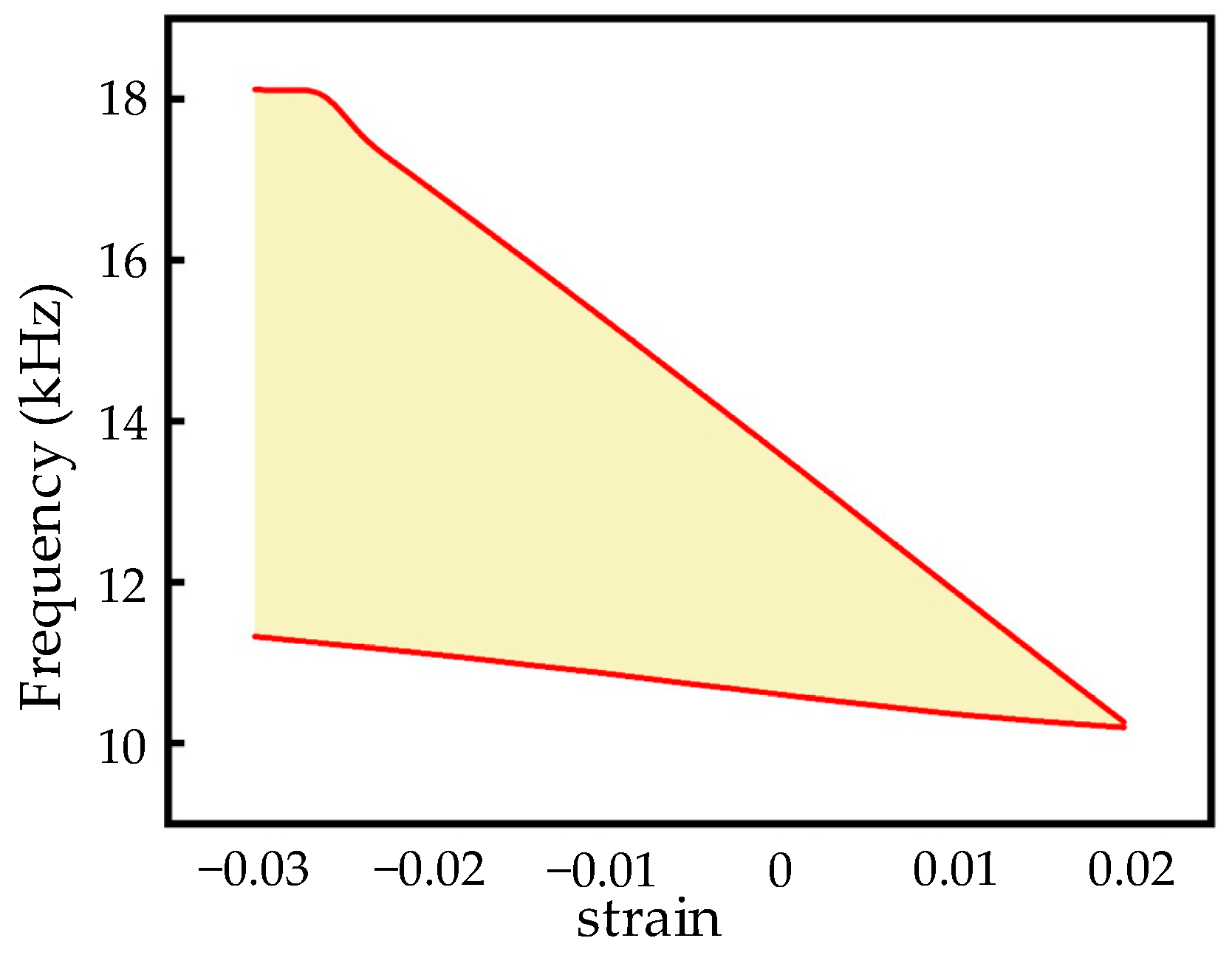
4.3. Bandgap Changed by External Load
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Jia, Z.; Wang, L. Hierarchical honeycomb lattice metamaterials with improved thermal resistance and mechanical properties. Compos. Struct. 2016, 152, 395–402. [Google Scholar] [CrossRef]
- Walser, R.M. Electromagnetic metamaterials. In Complex Mediums II: Beyond Linear Isotropic Dielectrics, Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 29 July–3 August 2001; SPIE: Bellingham, WA, USA, 2001; Volume 4467, pp. 1–15. [Google Scholar]
- Lincoln, R.L.; Scarpa, F.; Ting, V.P.; Trask, R.S. Multifunctional composites: A metamaterial perspective. Multifunct. Mater. 2019, 2, 043001. [Google Scholar] [CrossRef]
- Airoldi, A.; Bettini, P.; Panichelli, P.; Oktem, M.F.; Sala, G. Chiral topologies for composite morphing structures—Part I: Development of a chiral rib for deformable airfoils. Phys. Status Solidi B 2015, 252, 1435–1445. [Google Scholar] [CrossRef]
- Jung, J.; Kim, H.-G.; Goo, S.; Chang, K.-J.; Wang, S. Realisation of a locally resonant metamaterial on the automobile panel structure to reduce noise radiation. Mech. Syst. Signal Process. 2019, 122, 206–231. [Google Scholar] [CrossRef]
- Akbari, M.; Shahbazzadeh, M.J.; La Spada, L.; Khajehzadeh, A. The graphene field effect transistor modeling based on an optimized ambipolar virtual source model for DNA detection. Appl. Sci. 2021, 11, 8114. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, F.; Yang, K.; Chen, Y. A novel omnidirectional self-locked energy absorption system inspired by windmill. J. Appl. Mech.-Trans. Asme 2020, 87, 085001. [Google Scholar] [CrossRef]
- Coulais, C.; Teomy, E.; de Reus, K.; Shokef, Y.; van Hecke, M. Combinatorial design of textured mechanical metamaterials. Nature 2016, 535, 529–532. [Google Scholar] [CrossRef]
- Fu, K.; Zhao, Z.; Jin, L. Programmable granular metamaterials for reusable energy absorption. Adv. Funct. Mater. 2019, 29, 1901258. [Google Scholar] [CrossRef]
- Pan, F.; Li, Y.; Li, Z.; Yang, J.; Liu, B.; Chen, Y. 3D pixel mechanical metamaterials. Adv. Mater. 2019, 31, 1900548. [Google Scholar] [CrossRef]
- Wenxuan, T.; Zhonglei, M.; Tiejun, C. Theory, experiment and applications of metamaterials. Sci. China-Phys. Mech. Astron. 2015, 58, 127001. [Google Scholar]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Qu, J.; Gerber, A.; Mayer, F.; Kadic, M.; Wegener, M. Experiments on metamaterials with negative effective static compressibility. Phys. Rev. X 2017, 7, 041060. [Google Scholar] [CrossRef]
- Evans, J.S.O. Negative thermal expansion materials. J. Chem. Soc.-Dalton Trans. 1999, 19, 3317–3326. [Google Scholar] [CrossRef]
- Lipton, J.I.; MacCurdy, R.; Manchester, Z.; Chin, L.; Cellucci, D.; Rus, D. Handedness in shearing auxetics creates rigid and compliant structures. Science 2018, 360, 632–635. [Google Scholar] [CrossRef]
- Zhua, R.; Liub, X.N.; Hub, G.K.; Sunc, C.T.; Huang, G.L. A chiral elastic metamaterial beam for broadband vibration suppression. J. Sound Vib. 2014, 333, 2759–2773. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Auxetic cellular materials—A Review. Stroj. Vestn. J. Mech. Eng. 2016, 62, 485–493. [Google Scholar] [CrossRef]
- Lakes, R. Deformation mechanisms in negative poisson ratio materials—Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.-S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi B-Basic Solid State Phys. 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic constants of 3-, 4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef]
- Yang, S.; Qi, C.; Wang, D.; Gao, R.; Hu, H.; Shu, J. A comparative study of ballistic resistance of sandwich panels with aluminum foam and auxetic honeycomb cores. Adv. Mech. Eng. 2013, 5, 589216. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative poissons ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- May, P.R.A.; Fuster, J.M.; Haber, J. Woodpecker drilling behavior—endorsement of the rotational theory of impact brain injury. Arch. Neurol. 1979, 36, 370–373. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Wang, H.; Wang, C.; Cheng, S.; Zhao, Q.; Sun, Y.; Gao, H.; Ren, F. Properties and tunability of band gaps in innovative reentrant and star-shaped hybrid honeycomb metamaterials. Results Phys. 2021, 24, 104024. [Google Scholar] [CrossRef]
- Chen, L.; Guo, Y.; Yi, H. Optimization study of bandgaps properties for two-dimensional chiral phononic crystals base on lightweight design. Phys. Lett. A 2021, 388, 127054. [Google Scholar] [CrossRef]
- Liu, X.N.; Hu, G.K.; Sun, C.T.; Huang, G.L. Wave propagation characterization and design of two-dimensional elastic chiral metacomposite. J. Sound Vib. 2011, 330, 2536–2553. [Google Scholar] [CrossRef]
- Sun, P.; Guo, H.; Jin, F.; Zhang, Z.; Liu, N.; Yuan, T.; Ma, L.; Wang, Y. Mechanics and extreme low-frequency band gaps of auxetic hexachiral acoustic metamaterial with internal resonant unit. Appl. Acoust. 2022, 200, 109046. [Google Scholar] [CrossRef]
- Alomarah, A.; Masood, S.H.; Sbarski, I.; Faisal, B.; Gao, Z.; Ruan, D. Compressive properties of 3D printed auxetic structures: Experimental and numerical studies. Virtual Phys. Prototyp. 2020, 15, 1–21. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Lepidi, M.; Gnecco, G.; Vadalà, F.; Gambarotta, L. Optimal design of the band structure for beam lattice metamaterials. Front. Mater. 2019, 6, 2. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gnecco, G.; Lepidi, M.; Gambarotta, L. Computational design of innovative mechanical metafilters via adaptive surrogate-based optimization. Comput. Methods Appl. Mech. Eng. 2021, 375, 113623. [Google Scholar] [CrossRef]
- Grima, J.N.; Cassar, R.N.; Gatt, R. On the effect of hydrostatic pressure on the auxetic character of NAT-type silicates. J. Non-Cryst. Solids 2009, 355, 1307–1312. [Google Scholar] [CrossRef]
- Smith, C.W.; Grima, J.N.; Evans, K.E. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Q.; Li, X.; Yang, Z. Elastic properties of two novel auxetic 3D cellular structures. Int. J. Solids Struct. 2017, 124, 46–56. [Google Scholar] [CrossRef]


| E (GPa) | υ | ρ (kg/m3) | t (m) | b (m) | l (m) | r (m) | A (m2) | I (m4) |
|---|---|---|---|---|---|---|---|---|
| 70 | 0.33 | 2700 | 0.001 | 0.001 | 0.06 | 0.003 | 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Shao, S.; Wang, W.; Xia, R.; Negahban, M.; Li, Z. A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances. Materials 2024, 17, 4652. https://doi.org/10.3390/ma17184652
Liu F, Shao S, Wang W, Xia R, Negahban M, Li Z. A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances. Materials. 2024; 17(18):4652. https://doi.org/10.3390/ma17184652
Chicago/Turabian StyleLiu, Fengming, Shixuan Shao, Weihan Wang, Rongyu Xia, Mehrdad Negahban, and Zheng Li. 2024. "A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances" Materials 17, no. 18: 4652. https://doi.org/10.3390/ma17184652
APA StyleLiu, F., Shao, S., Wang, W., Xia, R., Negahban, M., & Li, Z. (2024). A Novel Cross Tetrachiral Honeycomb Metamaterial with Designable Static and Dynamic Performances. Materials, 17(18), 4652. https://doi.org/10.3390/ma17184652






