Tool Wear Prediction in Machining of Aluminum Matrix Composites with the Use of Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Processing Conditions
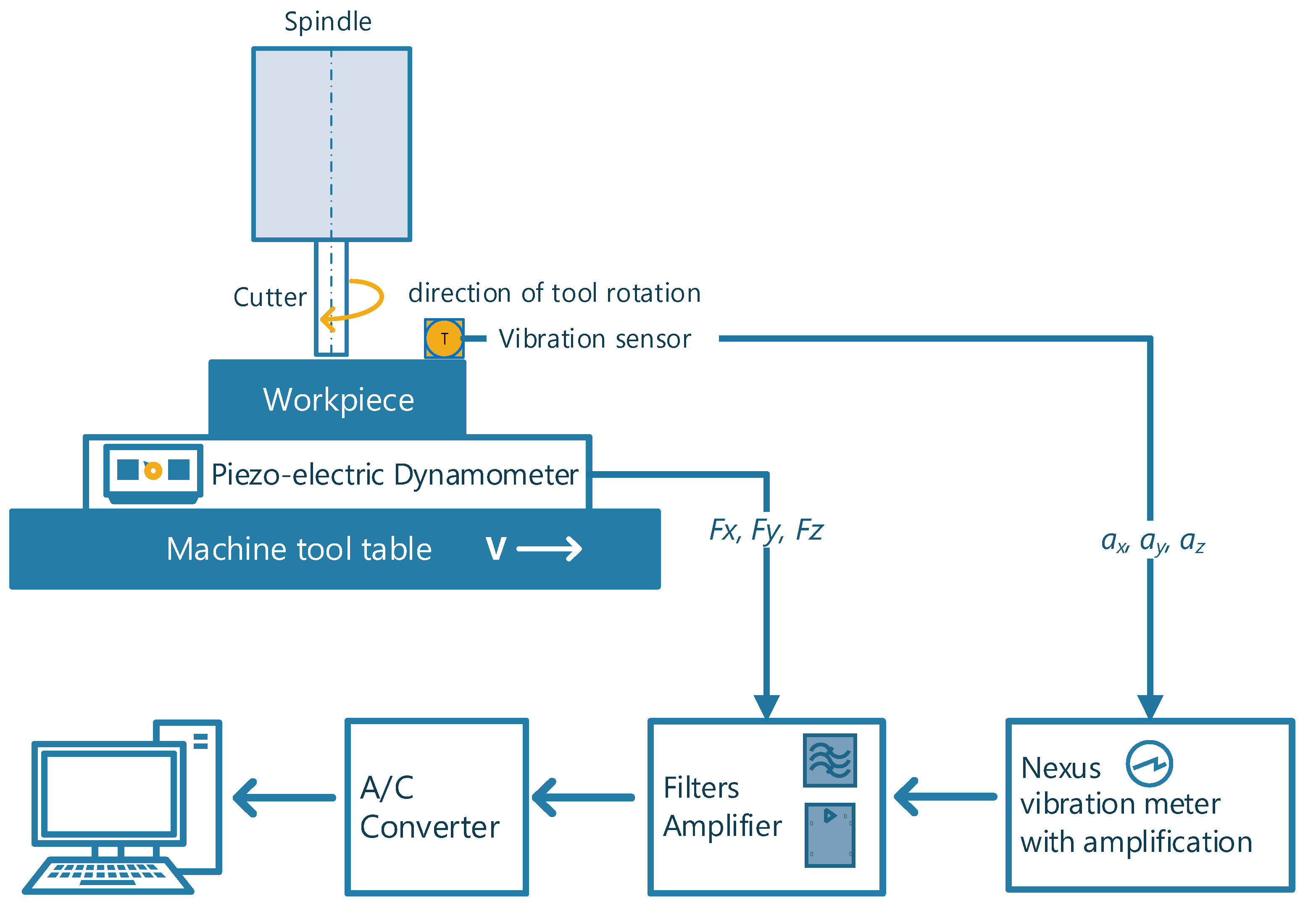
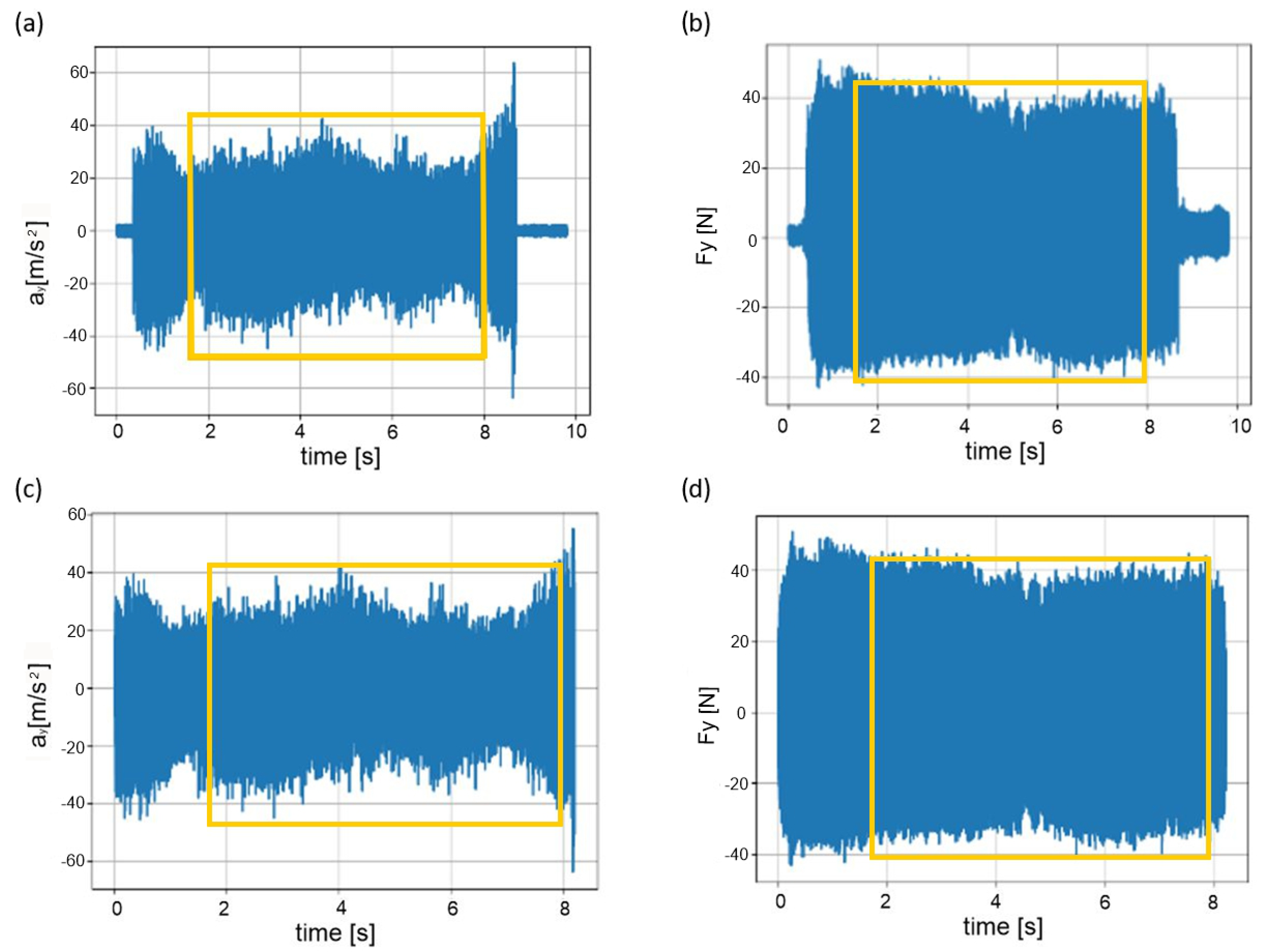
2.2. Measurement of Cutting Force and Vibration Acceleration
2.3. Creation of Signal Measures
2.4. Creating Data for the Training Set and the Test Set
- Training set (75% of the records);
- Test set (25% of the records); records were assigned to the subsets in a random manner (non-return draw).
2.5. Diagnostic Models
- (a)
- One-dimensional.
- Simple regression (SR).
- (b)
- Multidimensional.
- Multiple linear regression (MLR);
- Elastic net regression (ENR);
- Classification and regression trees (CART);
- Random forest (RF);
- Nearest neighbor algorithm (NNA);
- Multilayer perceptron (MLP).
2.6. Quality Measures of the Diagnostic Models
- (a)
- With regard to the predictive models:
- Root Mean Square Error (RMSE);
- Standard Deviation of RMSE (σ_RMSE);
- Coefficient of Determination (R2).
- (b)
- with regard to the classification models the measure listed below in the so-called confusion matrix (Table 3).
- True Positives (TP): when the actual value is Positive class and prediction is also Positive.
- True Negatives (TN): when the actual value is Negative class and prediction is also Negative.
- False Positives (FP): when the actual is Negative, but the prediction is Positive. Also known as the Type I error.
- False Negatives (FN): when the actual is Positive, but the prediction is Negative. Also known as the Type II error.
- Accuracy: A measure of how often the classifier makes the correct prediction. It is the ratio between the number of correct predictions and the total number of predictions:Accuracy = (TP + TN)/(TP + TN + FN + FP)
- Precision: A measure of correctness that is achieved in true prediction. It determines how many predictions are actually positive out of all the total positive predicted:Precision = TP/(TP + FP)
- Sensitivity: A measure of actual observations which are predicted correctly, i.e., how many observations of positive classes are actually predicted as positive. It is defined as the ratio of the total number of correctly classified positive classes divide by the total number of positive classes:Sensitivity = TP/(TP + FN)
- F1: A number between 0 and 1 and the harmonic mean of precision and sensitivity:F1 = 2 · TP/(2TP + FN + FP)
3. Results
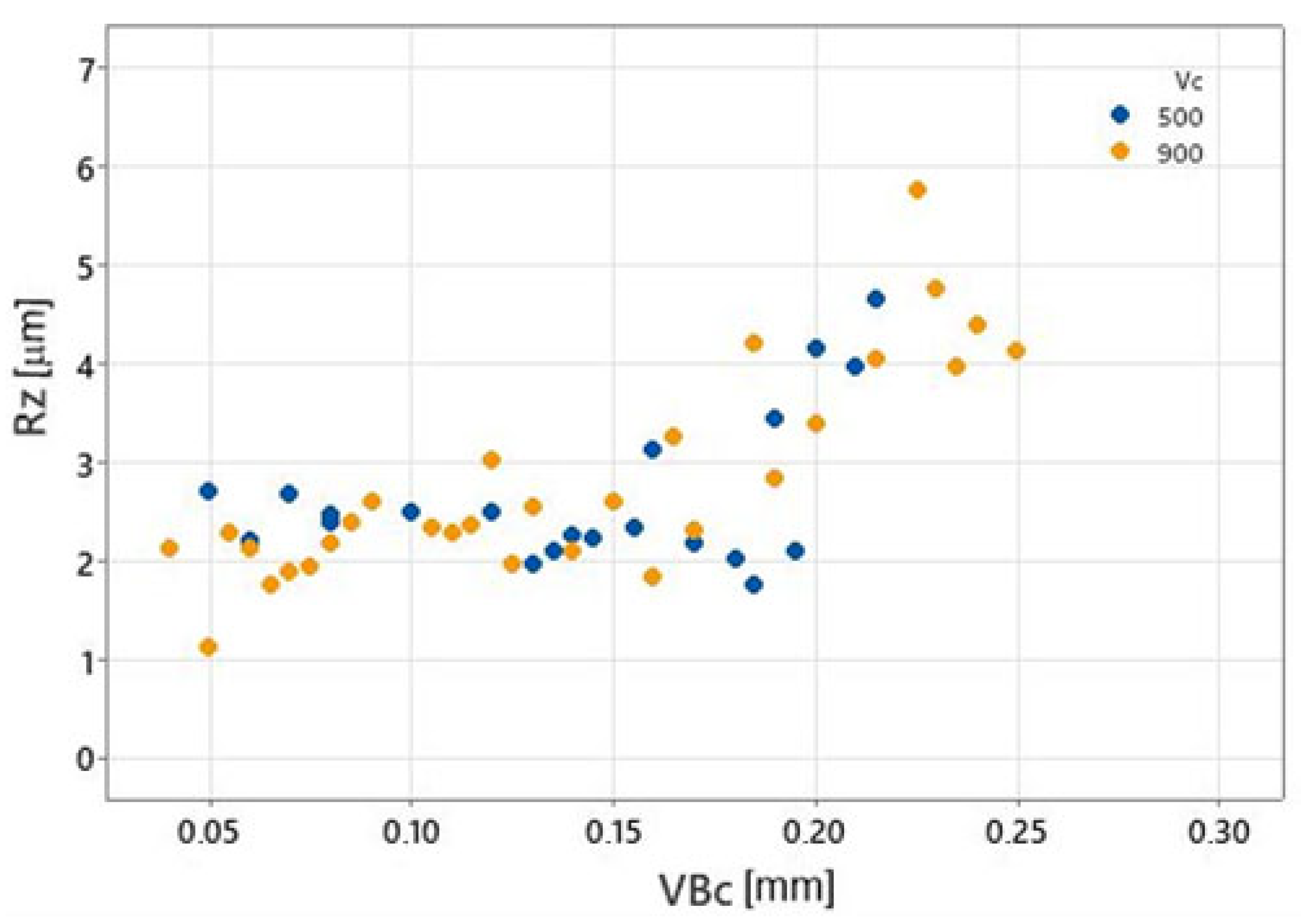
3.1. Tool Wear
3.2. Predictive Diagnostic Models
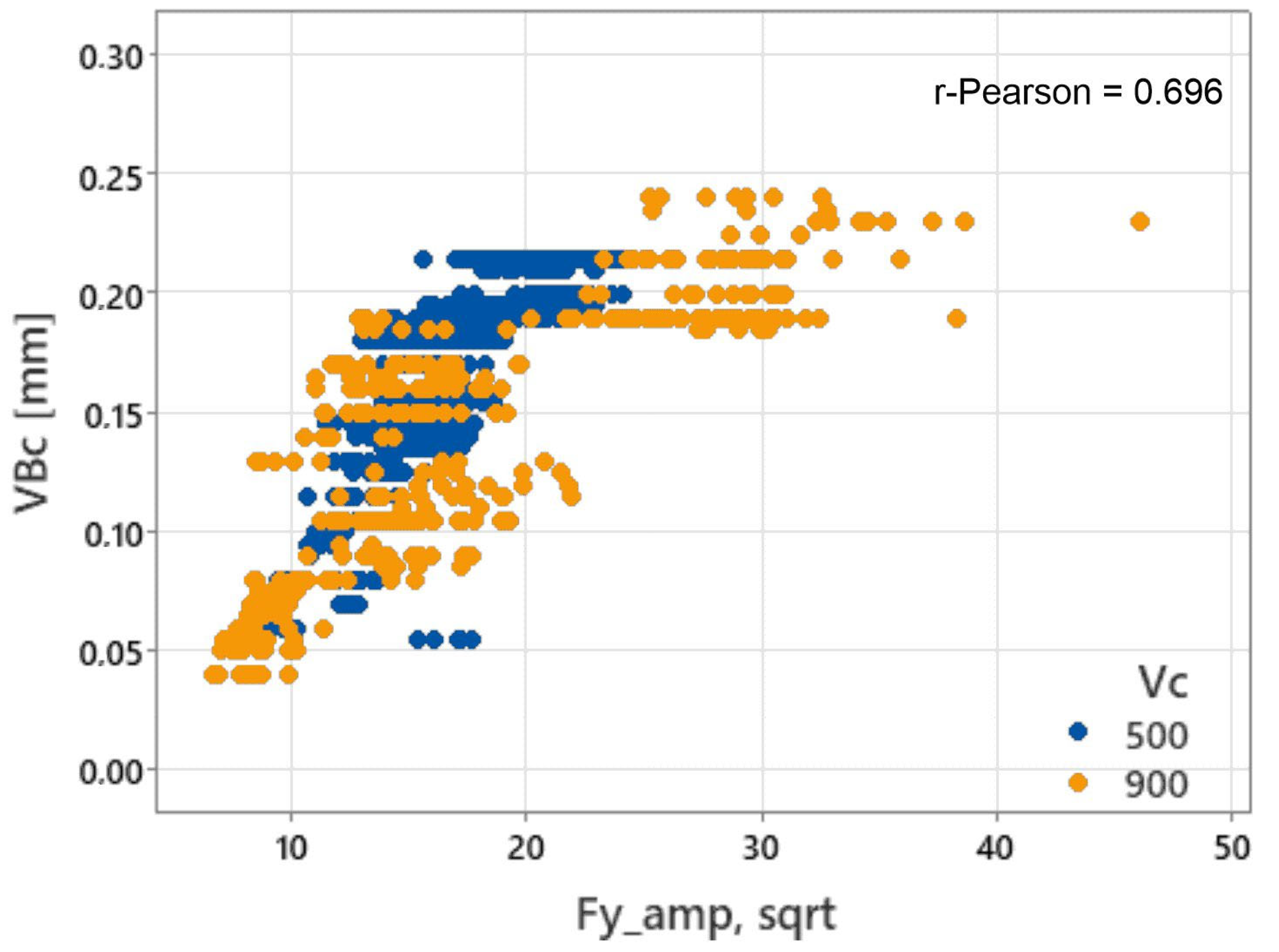
3.2.1. One-Dimensional
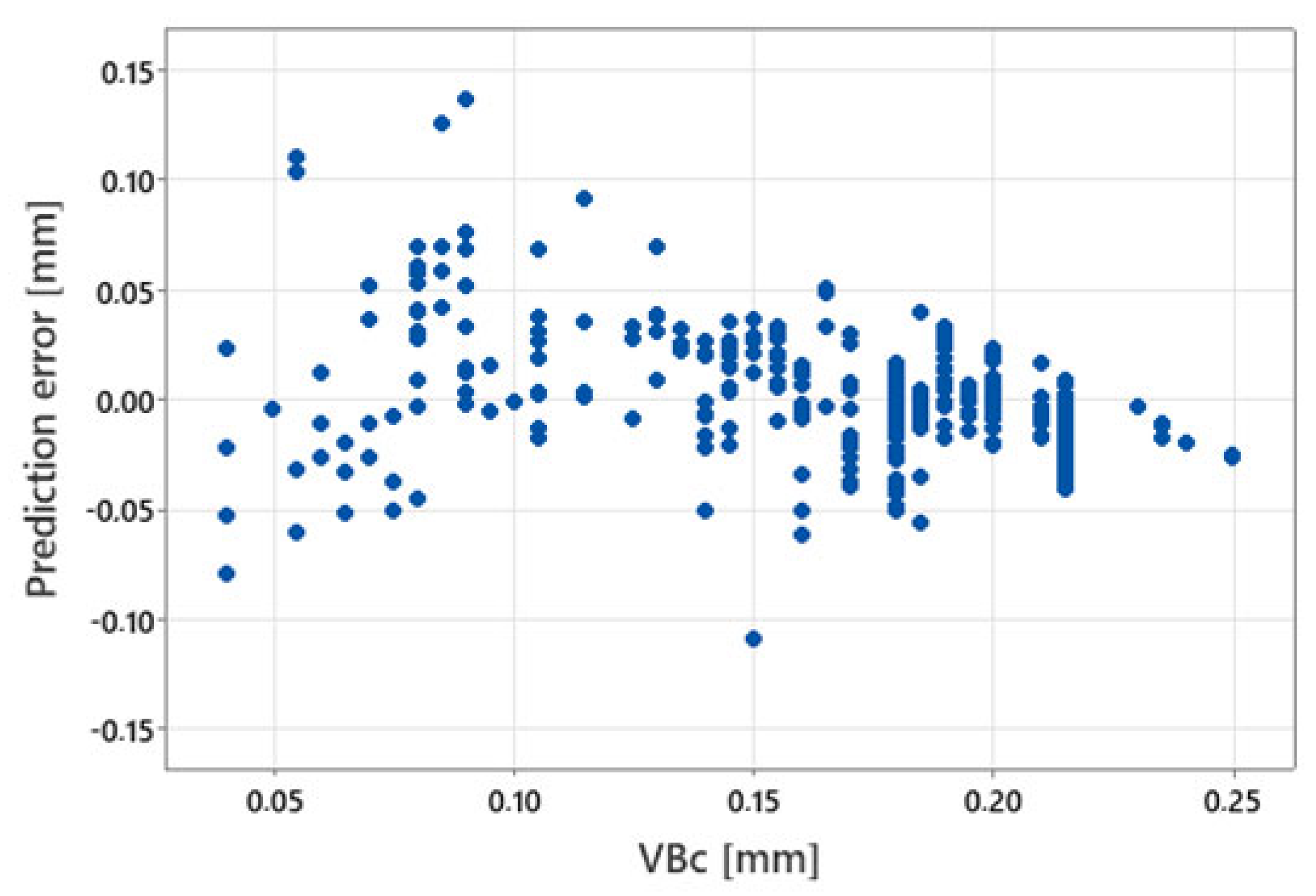
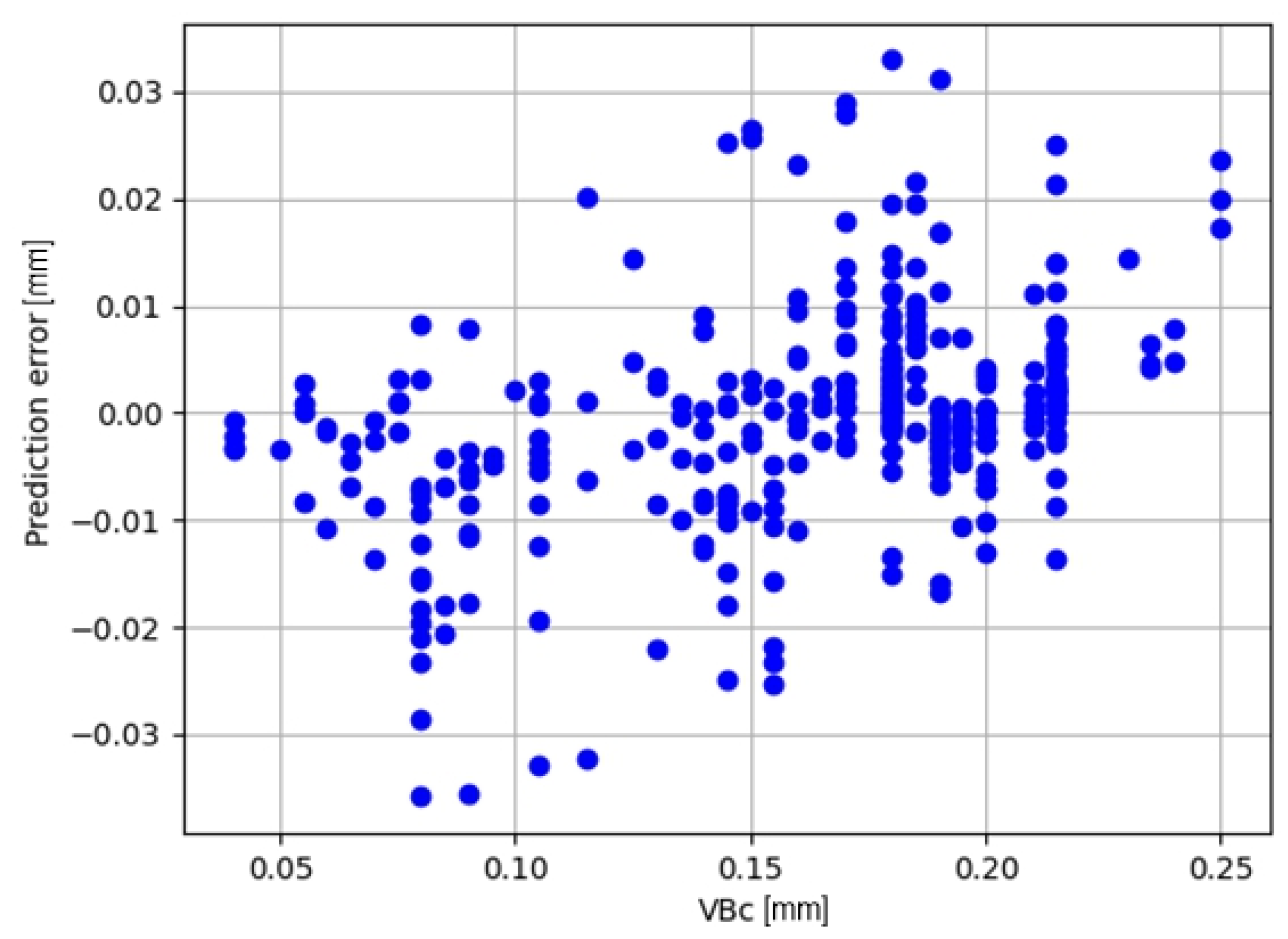
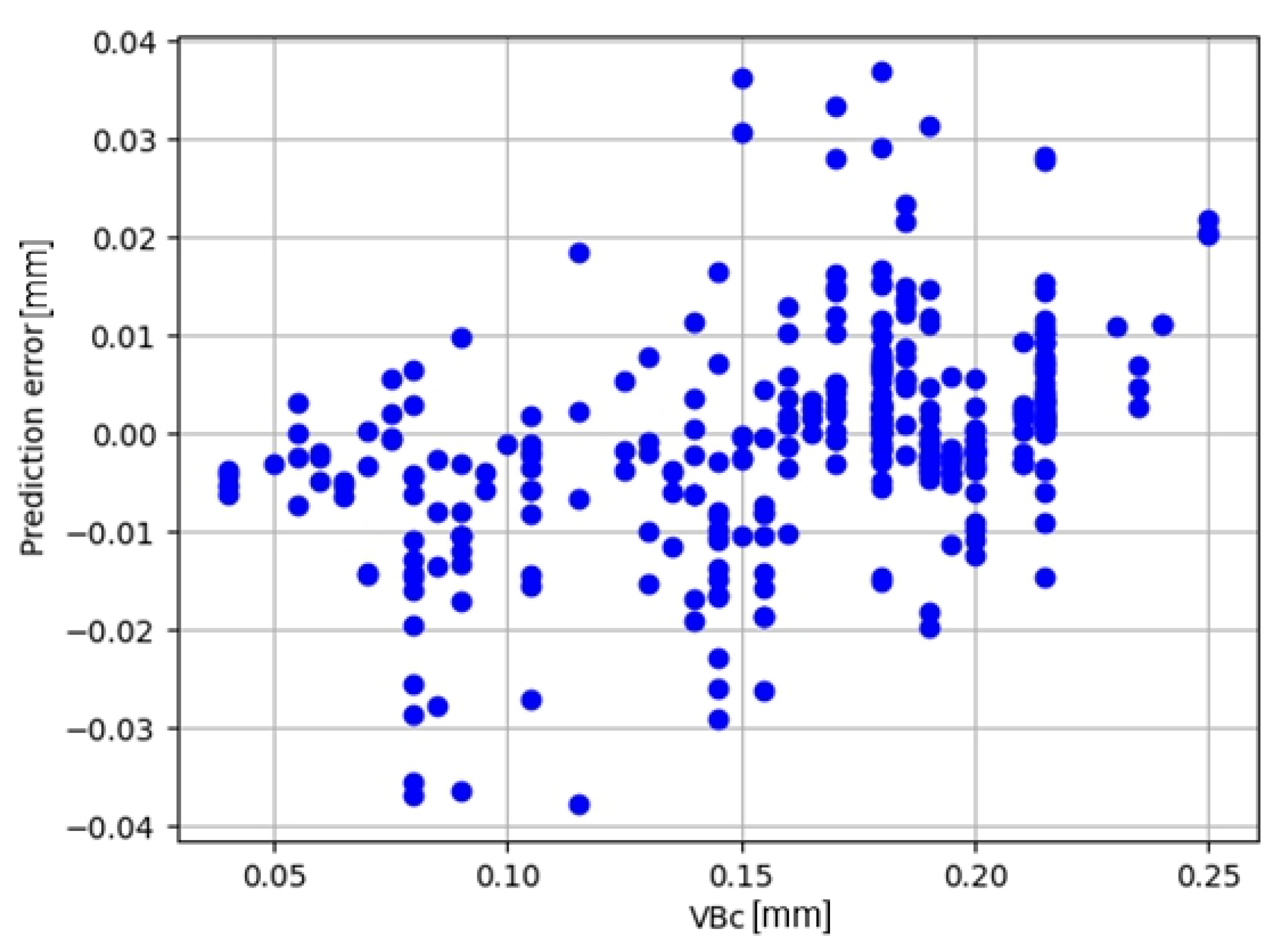
3.2.2. Multidimensional
- For the ENR, the proportion of two sets regularizations and the multiplicative factor of the corresponding expressions in the penalty function.
- In regression using the CART, the maximum tree depth.
- For the RF, the maximum number of MSi considered at a given split, the number of trees in the forest and the inclusion or not of bootstrap samples [33].
- (a)
- Full set of signal measures;
- (b)
- Reduced set of signal measures.
- (a)
- Full set of signal measures
- (b)
- Reduced set of signal measures
3.3. Classification Models Derived from Prediction Models
- (a)
- Simple regression (SR).
- (b)
- Random forest (RF) with the full set of signal measures.
- (c)
- Random forest (RF) with the selected set of signal measures.
3.4. Classification Models Constructed Directly from Raw Data
- (a)
- Full set of signal measures;
- (b)
- Reduced set of signal measures.
4. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tomadi, S.H.; Ghani, J.; Haron, C.; Hassan, M.A.; Daud, R. Ffect of Cutting Parameters on Surface Roughness in End Milling of AlSi/AlN Metal Matrix Composite. Procedia Eng. 2017, 184, 58–59. [Google Scholar] [CrossRef]
- Matuszak, J. Tool Wear Measurement After Milling of Aluminum Alloy Using Combined Roughness and Contour Device. Appl. Comput. Sci. 2015, 11, 51–57. [Google Scholar]
- Wang, P.; Gao, R. Stochastic Tool Wear Prediction for Sustainable Manufacturing. Procedia CIRP 2016, 48, 236–241. [Google Scholar] [CrossRef]
- Palanisamy, P.; Rajendran, I.; Shanmugasundaram, S. Prediction of Tool Wear Using Regression and ANN Models in End-Milling Operation. Int. J. Adv. Manuf. Technol. 2008, 37, 29–41. [Google Scholar] [CrossRef]
- Hosseinkhani, K.; Ng, E.-G. Unique Methodology for Tool Life Prediction in Machining. J. Manuf. Mater. Process. 2020, 4, 16. [Google Scholar] [CrossRef]
- Li, B. A Review of Tool Wear Estimation Using Theoretical Analysis and Numerical Simulation Technologies. Int. J. Refract. Met. Hard Mater. 2012, 35, 143–151. [Google Scholar] [CrossRef]
- Hamrol, A. Process Diagnostic as a Means of Improving the Efficiency of Quality Control. Prod. Plan. Control 2000, 11, 797–805. [Google Scholar] [CrossRef]
- Leo, G.; Liguori, C.; Pietrosanto, A.; Sommella, P. A Vision System for the Online Quality Monitoring of Industrial Manufacturing. Opt. Lasers Eng. 2016, 89, 162–168. [Google Scholar] [CrossRef]
- Filippov, A.; Rubtsov, V.; Tarasov, S. Acoustic Emission Study of Surface Deterioration in Tribocontacting. Appl. Acoust. 2017, 117, 106–112. [Google Scholar] [CrossRef]
- Mikołajczyk, T.; Nowicki, K.; Kłodowski, A.; Pimenov, D.Y. Neural Network Approach for Automatic Image Analysis of Cutting Edge Wear. Mech. Syst. Signal Process. 2017, 88, 100–110. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y.; Xie, Q.; Zhang, Y. Force Based Tool Wear Monitoring System for Milling Process Based on Relevance Vector Machine. Adv. Eng. Softw. 2014, 71, 46–51. [Google Scholar] [CrossRef]
- Zheng, G.; Xu, R.; Cheng, X.; Zhao, G.; Li, L.; Zhao, J. Effect of Cutting Parameters on Wear Behavior of Coated Tool and Surface Roughness in High-Speed Turning of 300 M. Meas. J. Int. Meas. Confed. 2018, 125, 99–108. [Google Scholar] [CrossRef]
- Navarro-Devia, J.H.; Chen, Y.; Dao, D.V.; Li, H. Chatter Detection in Milling Processes—A Review on Signal Processing and Condition Classification. Int. J. Adv. Manuf. Technol. 2023, 125, 3943–3980. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Gupta, M.K.; da Silva, L.R.R.; Kiran, M.; Khanna, N.; Krolczyk, G.M. Application of Measurement Systems in Tool Condition Monitoring of Milling: A Review of Measurement Science Approach. Measurement 2022, 199, 111503. [Google Scholar] [CrossRef]
- Ratava, J.; Lohtander, M.; Varis, J. Tool Condition Monitoring in Interrupted Cutting with Acceleration Sensors. Robot. Comput. Integr. Manuf. 2016, 47, 70–75. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.; Choudhury, I.; Yusoff, N.; Dawal, S. Application of Acoustic Emission Sensor to Investigate the Frequency of Tool Wear and Plastic Deformation in Tool Condition Monitoring. Measurement 2016, 92, 208–217. [Google Scholar] [CrossRef]
- Tabaszewski, M.; Twardowski, P.; Wiciak-Pikuła, M.; Znojkiewicz, N.; Felusiak-Czyryca, A.; Czyżycki, J. Machine Learning Approaches for Monitoring of Tool Wear during Grey Cast-Iron Turning. Materials 2022, 15, 4359. [Google Scholar] [CrossRef]
- Rogalewicz, M.; Piłacińska, M.; Kujawińska, A. Selection of Data Mining Method for Multidimensional Evaluation of the Manufacturing Process State. Manag. Prod. Eng. Rev. 2012, 3, 27–35. [Google Scholar]
- Jauregui, J.; Rodriguez, J.; Thenozhi, S.; Szalay, T.; Jacsó, Á.; Takacs, M. Frequency and Time-Frequency Analysis of Cutting Force and Vibration Signals for Tool Condition Monitoring. IEEE Access 2018, 6, 6400–6410. [Google Scholar] [CrossRef]
- Chuo, Y.S.; Lee, J.W.; Mun, C.H.; Noh, I.W.; Rezvani, S.; Kim, D.C.; Lee, J.; Lee, S.W.; Park, S.S. Artificial Intelligence Enabled Smart Machining and Machine Tools. J. Mech. Sci. Technol. 2022, 36, 1–23. [Google Scholar] [CrossRef]
- Osowski, S. Metody i Narzędzia Eksploracji Danych; BTC: Legionowo, Poland, 2013; ISBN 9788360233924. (In Polish) [Google Scholar]
- Zhao, X.; Ye, B. Singular Value Decomposition Packet and Its Application to Extraction of Weak Fault Feature. Mech. Syst. Signal Process. 2016, 70, 73–86. [Google Scholar] [CrossRef]
- Niquini, F.G.F.; Branches, A.M.B.; Costa, J.F.C.L.; Moreira, G.d.C.; Schneider, C.L.; Araújo, F.C.D.; Capponi, L.N. Recursive Feature Elimination and Neural Networks Applied to the Forecast of Mass and Metallurgical Recoveries in A Brazilian Phosphate Mine. Minerals 2023, 13, 748. [Google Scholar] [CrossRef]
- Stuart, W.; Graeme, L.H.; Stuart, J.H. Statistical Primer: Multivariable Regression Considerations and Pitfalls. Eur. J. Cardio-Thoracic Surg. 2019, 55, 179–185. [Google Scholar] [CrossRef]
- Smith, G. Step Away from Stepwise. J. Big Data 2018, 5, 32. [Google Scholar] [CrossRef]
- Krzyśko, M.; Wołyński, W.; Górecki, T.; Skorzybut, M. Systemy Uczące Się. Rozpoznawanie Wzorców, Analiza Skupień i Redukcja Wymiarowości; Wydawnictwo Naukowo-Techniczne: Warsaw, Poland, 2009; ISBN 978-83-204-3459-0. (In Polish) [Google Scholar]
- Jessel, T.; Byrne, C.; Eaton, M.; Merrifield, B.; Harris, S.; Pullin, R. Tool Condition Monitoring of Diamond-Coated Burrs with Acoustic Emission Utilising Machine Learning Methods. Int. J. Adv. Manuf. Technol. 2023, 130, 1107–1124. [Google Scholar] [CrossRef]
- Iu, Y.; Wang, F.; Lv, J.; Wang, X. A Novel Method for Tool Identification and Wear Condition Assessment Based on Multi-Sensor Data. Appl. Sci. 2020, 10, 2746. [Google Scholar] [CrossRef]
- Cempel, C. Vibroacoustic Condition Monitoring; Ellis Horwood Ltd.: Chichester, UK, 1991. [Google Scholar]
- Wu, D.; Jennings, C.; Terpenny, J.; Gao, R.X.; Soundar, K. A Comparative Study on Machine Learning Algorithms for Smart Manufacturing: Tool Wear Prediction Using Random Forests. J. Manuf. Sci. Eng. 2017, 139, 071018. [Google Scholar] [CrossRef]
- Abdualgalil, B.; Abraham, S. Applications of machine learning algorithms and performance comparison: A review. In Proceedings of the 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE), Vellore, India, 24–25 February 2020. [Google Scholar]
- Geron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019; ISBN 978-14-920-3259-5. [Google Scholar]
- Rawal, S.P. Metal-Matrix Composites for Space Applications. JOM 2001, 53, 14–17. [Google Scholar] [CrossRef]
- Ashwath, P.; Xavior, M.A. Processing methods and property evaluation of Al2O3 and SiC reinforced metal matrix composites based on aluminium 2xxx alloys. J. Mater. Res. 2016, 31, 1201–1219. [Google Scholar] [CrossRef]
- Ramnath, B.V.; Elanchezhian, C.; Annamalai, R.; Aravind, S.; Sri Ananda Atreya, T.; Vignesh, V.; Subramanian, C. Aluminum Metal Matrix Composites—A Review. Rev. Adv. Mater. Sci. 2014, 38, 55–60. [Google Scholar]
- Fraś, E.; Kolbus, A.; Janas, A. Selected Mechanical Properties of in Situ Al-TiC Composites Compared with Ex Situ Duralcan-SiC Composites. Composites 2002, 2, 176–179. [Google Scholar]
- Sklearn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.RFECV.html (accessed on 6 May 2024).
- Wiciak, M.; Twardowski, P.; Wojciechowski, S. Comparison of Various Tool Wear Prediction Methods during End Milling of Metal Matrix Composite. Arch. Mech. Technol. Mater. 2018, 38, 1–7. [Google Scholar] [CrossRef]
- Gururaja, S.; Ramulu, M.; Pedersen, W. Machining of MMCs: A Review. Mach. Sci. Technol. 2013, 17, 41–73. [Google Scholar] [CrossRef]
- Cempel, C. Fundamentals of Vibroacoustical Condition Monitoring. In Handbook of Condition Monitoring; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Zhang, Y.; Zhu, K.; Duan, X.; Li, S. Tool wear estimation and life prognostics in milling: Model extension and generalization. Mech. Syst. Signal Process. 2021, 155, 107617. [Google Scholar] [CrossRef]
- Fazlija, B.; Harder, P. Using Financial News Sentiment for Stock Price Direction Prediction. Mathematics 2022, 10, 2156. [Google Scholar] [CrossRef]
- Krishnakumar, P.; Rameshkumar, K.; Ramachandran, K.I. Tool Wear condition prediction using vibration signals in high speed machining (HSM) of titanium (Ti-6Al-4V) alloy. Procedia Comput. Sci. 2015, 50, 270–275. [Google Scholar] [CrossRef]
- Bagri, S.; Manwar, A.; Varghese, A.; Mujumdar, S.; Joshi, S.S. Tool wear and remaining useful life prediction in micro-milling along complex tool paths using neural networks. J. Manuf. Process. 2021, 71, 679–698. [Google Scholar] [CrossRef]



| Tool Parameters | Value | |
|---|---|---|
| end mill cutter diameter D1 [mm] | 10 | |
| number of cutting edges z | 2 | |
| Machining parameters | 1st set | 2nd set |
| spindle speed n [rpm] | 15,923 | 28,662 |
| cutting speed vc [m/min] | 500 | 900 |
| cutting feed rate vf [mm/min] | 1115 | 2006 |
| feed per tooth fz [mm/edge] | 0.035 | 0.035 |
| axial cutting depth ap [mm] | 5 | 5 |
| radial depth of cut ae [mm] | 0.1 | 0.1 |
| Symbol | Description | Frequency Band | |
|---|---|---|---|
| 1 | ax_rms_(1000.0, 2500.0) | Rms value of vibration acceleration | 1.0–2.5 kHz |
| 2 | ax_rms_(7000.0, 8000.0) | Rms value of vibration acceleration | 7.0–8.0 kHz |
| 3 | ax_mean_peak | Average peak value of vibration accelerations | Full |
| 4 | ax_CF | Crest factor of the vibration acceleration signal | |
| 5 | ax_FF | Form factor of the vibration acceleration signal | |
| 6 | ax_f.Ricea | Rice frequency | |
| 7 | ay_rms_(1500.0, 2500.0) | Rms value of vibration acceleration | 1.5–2.5 kHz |
| 8 | ay_rms_(3000.0, 3500.0) | Rms value of vibration acceleration | 3.0–3.5 kHz |
| 9 | ay_rms_(7500.0, 8000.0) | Rms value of vibration acceleration | 7.5–8.0 kHz |
| 10 | ay_rms_(11,000.0, 11,500.0) | Rms value of vibration acceleration | 11.0–11.5 kHz |
| 11 | ay_mean_peak | Average peak value of vibration accelerations | Full |
| 12 | ay_avg | Average value of the vibration acceleration signal | |
| 13 | ay_CF | Crest factor of the vibration acceleration signal | |
| 14 | ay_FF | Form factor of the vibration acceleration signal | |
| 15 | ay_IF | Impulse factor for vibration acceleration | |
| 16 | ay_kurt | Vibration acceleration kurtosis | |
| 17 | az_mean_peak | Average peak value of vibration accelerations | Full |
| 18 | az_avg | Average value of the vibration acceleration signal | |
| 19 | az_CF | Crest factor of the vibration acceleration signal | |
| 20 | az_FF | Form factor of the vibration acceleration signal | |
| 21 | az_IF | Impulse factor for vibration acceleration | |
| 22 | az_kurt, | Vibration acceleration kurtosis | |
| 23 | az_f.Ricea | Rice frequency | |
| 24 | Fy_rms | Effective value of the dynamic component of the force | Full |
| 25 | Fy_mean_peak | Average peak force | |
| 26 | Fy_avg | Average value of the force signal | |
| 27 | Fy_amp_sqrt | The root amplitude of the force signal | |
| 28 | Fy_CF | Crest factor of the force signal | |
| 29 | Fy_FF | Form factor of the force signal | |
| 30 | Fz_rms | Effective value of the dynamic component of the force | Full |
| 31 | Fz_mean_peak | Average peak force | |
| 32 | Fz_avg | Average value of the force signal | |
| 33 | Fz_CF | Crest factor of the force signal | |
| 34 | Fz_FF | Form factor of the force signal | |
| 35 | vc | Cutting speed | - |
| Predicted Class Positive (P) | Predicted Class Negative (N) | |
|---|---|---|
| Real class: Positive + | True Positive (TP) | False Negative (FN) |
| Real class: Negative − | False Positive (FP) | True Negative (TN) |
| Measure MS | RMSE | σ_RMSE | R2 |
|---|---|---|---|
| Fy_avg | 0.063780 | 0.0270937 | 0.522 |
| Fy_rms | 0.067685 | 0.0263348 | 0.695 |
| Fy_mean peak | 0.069352 | 0.0302427 | 0.549 |
| Fy_amp, sqrt | 0.0490801 | 0.0270609 | 0.696 |
| Model | RMSE | σ-RMSE | R2 |
|---|---|---|---|
| SR | 0.0221 | 0.0020 | 0.7543 |
| ENR | 0.0241 | 0.0028 | 0.7037 |
| CART | 0.0179 | 0.0015 | 0.8605 |
| RF | 0.0117 | 0.0009 | 0.9573 |
| Forecast Class VBc ≥ 0.2 mm | Forecast Class VBc < 0.2 mm | |
|---|---|---|
| Actual class VBc ≥ 0.2 mm | 72 (TP) | 23 (FN) |
| Actual class VBc < 0.2 mm | 26 (FP) | 243 (TN) |
| Accuracy | 0.865 | |
| Precision | 0.735 | |
| Sensitivity | 0.758 | |
| F1 | 0.746 | |
| Forecast Class VBc ≥ 0.2 mm | Forecast Class VBc < 0.2 mm | |
|---|---|---|
| Actual class VBc ≥ 0.2 mm | 83 (TP) | 12 (FN) |
| Actual class VBc < 0.2 mm | 3 (FP) | 266 (TN) |
| Accuracy | 0.959 | |
| Precision | 0.965 | |
| Sensitivity | 0.874 | |
| F1 | 0.917 | |
| Forecast Class VBc ≥ 0.2 mm | Forecast Class VBc < 0.2 mm | |
|---|---|---|
| Actual class VBc ≥ 0.2 mm | 88 (TP) | 7 (FN) |
| Actual class VBc < 0.2 mm | 3 (FP) | 266 (TN) |
| Accuracy | 0.973 | |
| Precision | 0.967 | |
| Sensitivity | 0.926 | |
| F1 | 0.946 | |
| Accuracy | ||
|---|---|---|
| Model | Full setof SMi | Reduced set of SMi |
| CART | 0.881 | 0.881 |
| RF | 0.969 | 0.966 |
| NNA | 0.743 | 0.726 |
| MLP | 0.988 | 0.960 |
| Forecast Class VBc ≥ 0.2 mm | Forecast Class VBc < 0.2 mm | |
|---|---|---|
| Actual class VBc ≥ 0.2 mm | 88 (TP) | 7 (FN) |
| Actual class VBc < 0.2 mm | 3 (FP) | 266 (TN) |
| Accuracy | 0.973 | |
| Precision | 0.967 | |
| Sensitivity | 0.926 | |
| F1 | 0.946 | |
| Forecast Class VBc ≥ 0.2 mm | Forecast Class VBc < 0.2 mm | |
|---|---|---|
| Actual class VBc ≥ 0.2 mm | 89 (TP) | 6 (FN) |
| Actual class VBc < 0.2 mm | 4 (FP) | 265 (TN) |
| Accuracy | 0.973 | |
| Precision | 0.957 | |
| Sensitivity | 0.937 | |
| F1 | 0.947 | |
| Predictive Models | RMSE | σ_RMSE | R2 | |
| (1) One-dimensional (for Fy_amp, sqrt) | 0.0491 | 0.0271 | 0.696 | |
| (2) Multidimensional: | ||||
| • RF (full number of SMi) | 0.0117 | 0.0009 | 0.9573 | |
| • RF (reduced number of SMi) | 0.0380 | 0.0009 | 0.949 | |
| Classification models | Accuracy | Precision | Sensitivity | F1 |
| (1) From regression models: | ||||
| • SR | 0.865 | 0.735 | 0.758 | 0.746 |
| • RF (full number of SMi) | 0.959 | 0.965 | 0.874 | 0.917 |
| • RF (reduced number of SMi) | 0.973 | 0.967 | 0.926 | 0.946 |
| (2) From raw data—full number of SMi: | ||||
| • MLP | 0.973 | 0.967 | 0.926 | 0.946 |
| (3) From raw data—reduced number of SMi: | ||||
| • RF | 0.973 | 0.957 | 0.937 | 0.947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamrol, A.; Tabaszewski, M.; Kujawińska, A.; Czyżycki, J. Tool Wear Prediction in Machining of Aluminum Matrix Composites with the Use of Machine Learning Models. Materials 2024, 17, 5783. https://doi.org/10.3390/ma17235783
Hamrol A, Tabaszewski M, Kujawińska A, Czyżycki J. Tool Wear Prediction in Machining of Aluminum Matrix Composites with the Use of Machine Learning Models. Materials. 2024; 17(23):5783. https://doi.org/10.3390/ma17235783
Chicago/Turabian StyleHamrol, Adam, Maciej Tabaszewski, Agnieszka Kujawińska, and Jakub Czyżycki. 2024. "Tool Wear Prediction in Machining of Aluminum Matrix Composites with the Use of Machine Learning Models" Materials 17, no. 23: 5783. https://doi.org/10.3390/ma17235783
APA StyleHamrol, A., Tabaszewski, M., Kujawińska, A., & Czyżycki, J. (2024). Tool Wear Prediction in Machining of Aluminum Matrix Composites with the Use of Machine Learning Models. Materials, 17(23), 5783. https://doi.org/10.3390/ma17235783







