Multi-Physics Modeling of Melting-Solidification Characteristics in Laser Powder Bed Fusion Process of 316L Stainless Steel
Abstract
:1. Introduction
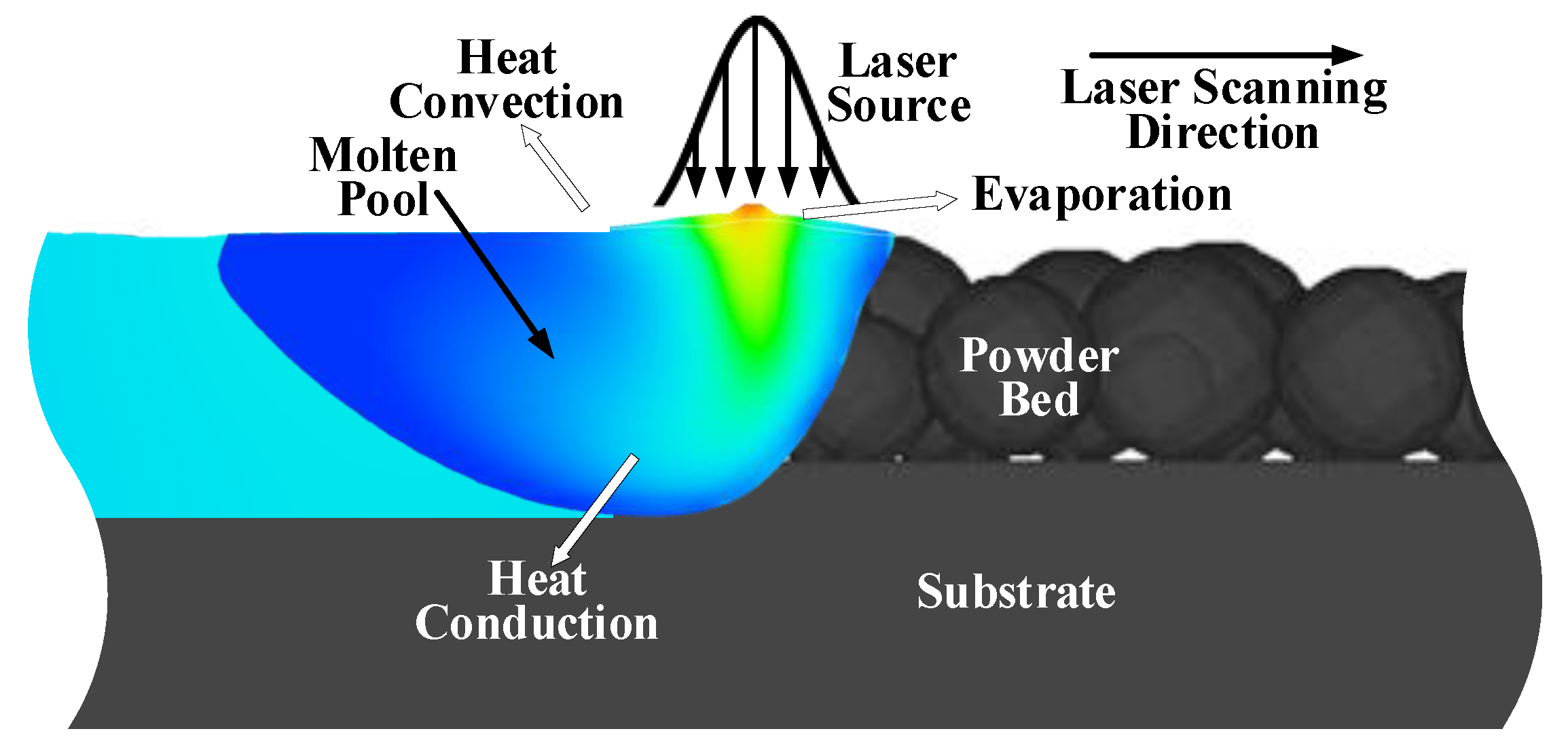
2. Computational Models
- The fluid in the molten pool is assumed to be Newtonian and laminar flow;
- The mushy zone is assumed to be isotropic during the solid–liquid phase change process;
- The distribution of powder particles is assumed to be fixed in space;
- The effect of the surrounding argon’s flow on the molten pool is neglected;
- The influence of ambient gas on laser energy absorption is neglected.
2.1. Governing Equations
2.2. Initial and Boundary Conditions
2.3. Simulation Cases and Computation
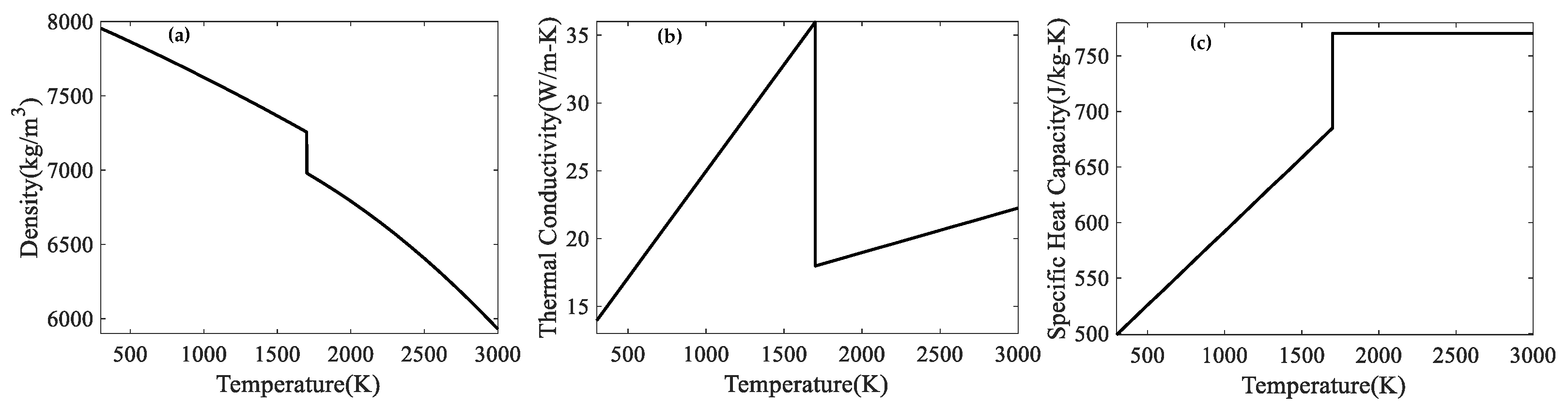
| Material Property | Value |
|---|---|
| Surface tension coefficient | 1.76 N/m [37] |
| Change rate of surface tension | −4.002 × 10−4 N/m/K [37] |
| Density | see Figure 2a |
| Thermal conductivity | see Figure 2b |
| Specific heat capacity | see Figure 2c |
| Solidus temperature | 1658 K [38] |
| Liquidus temperature | 1723 K [38] |
| Evaporation temperature | 3086 K [38] |
| Latent heat of fusion | 2.8 × 105 J/kg [10] |
| Latent heat of evaporation | 7.45 × 106 J/kg [38] |
| Molar mass | 5.58 × 10−2 kg/mol [38] |
| Dynamic viscosity | 5.6 × 10−3 Pa·s [39] |
| Surface radiation coefficient | 0.4 [39] |
| Absorption coefficient | 0.55 (solid), 0.3 (liquid) [10] |
3. Results and Discussion
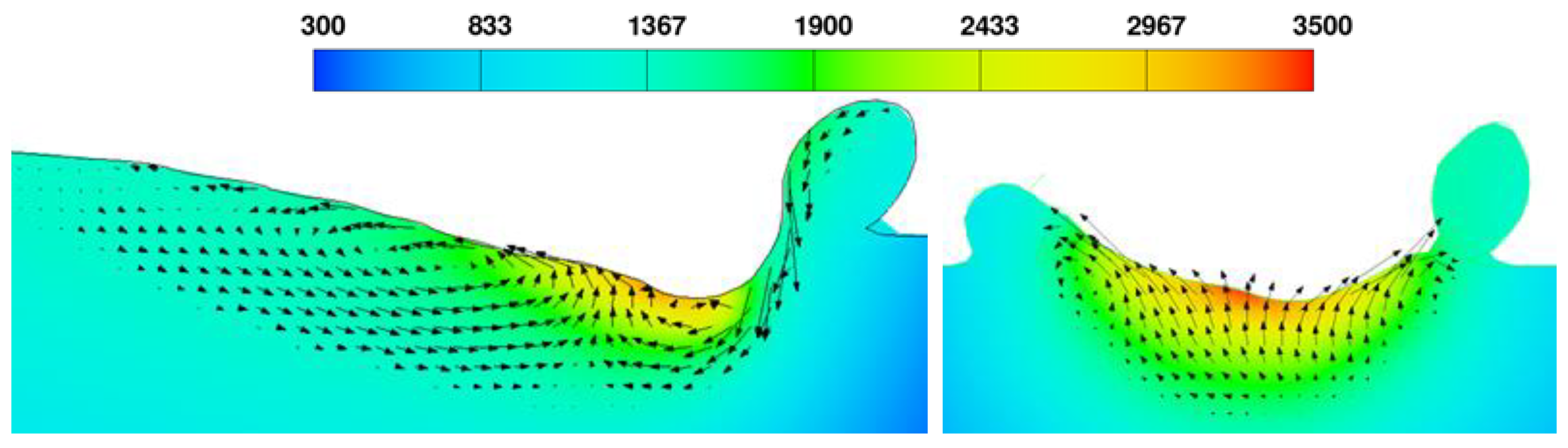
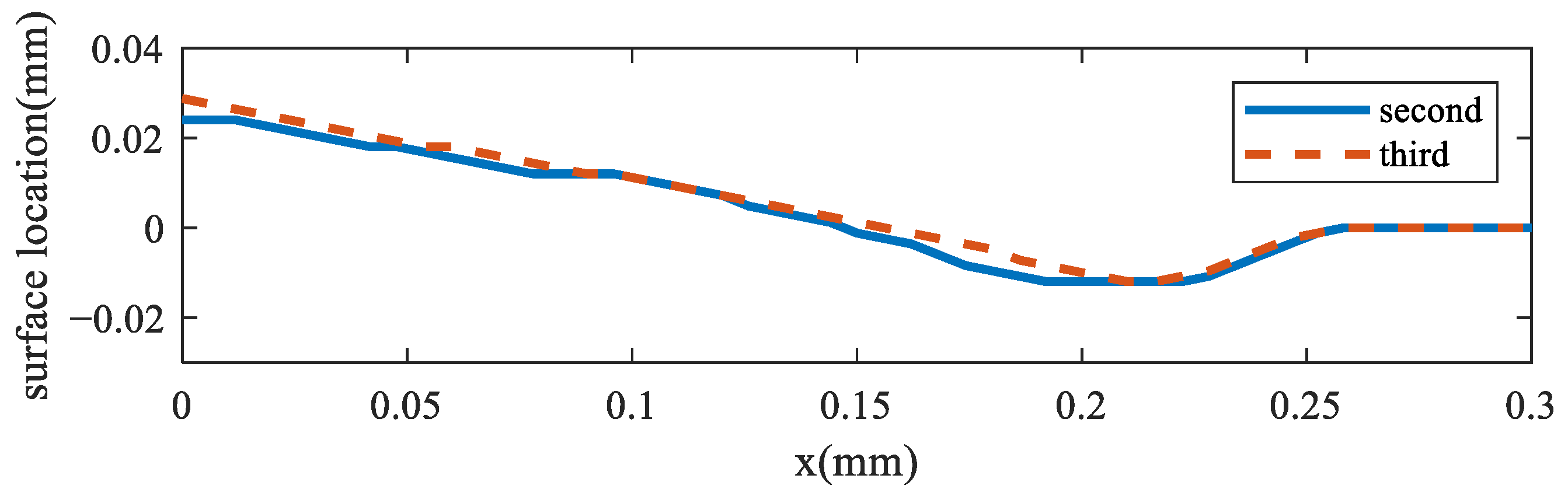
3.1. Molten Pool Morphology Analysis
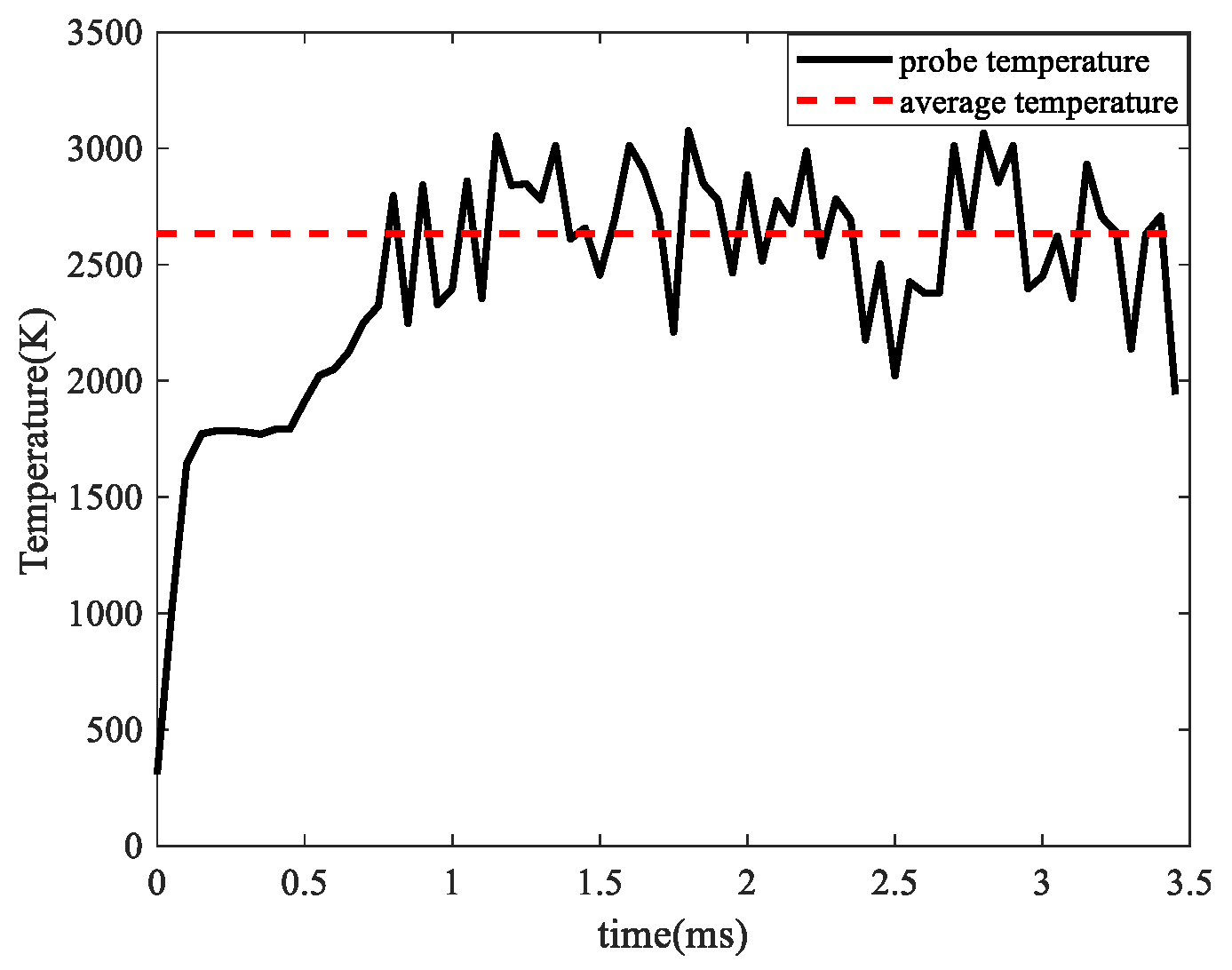
3.2. Temperature Distribution Analysis
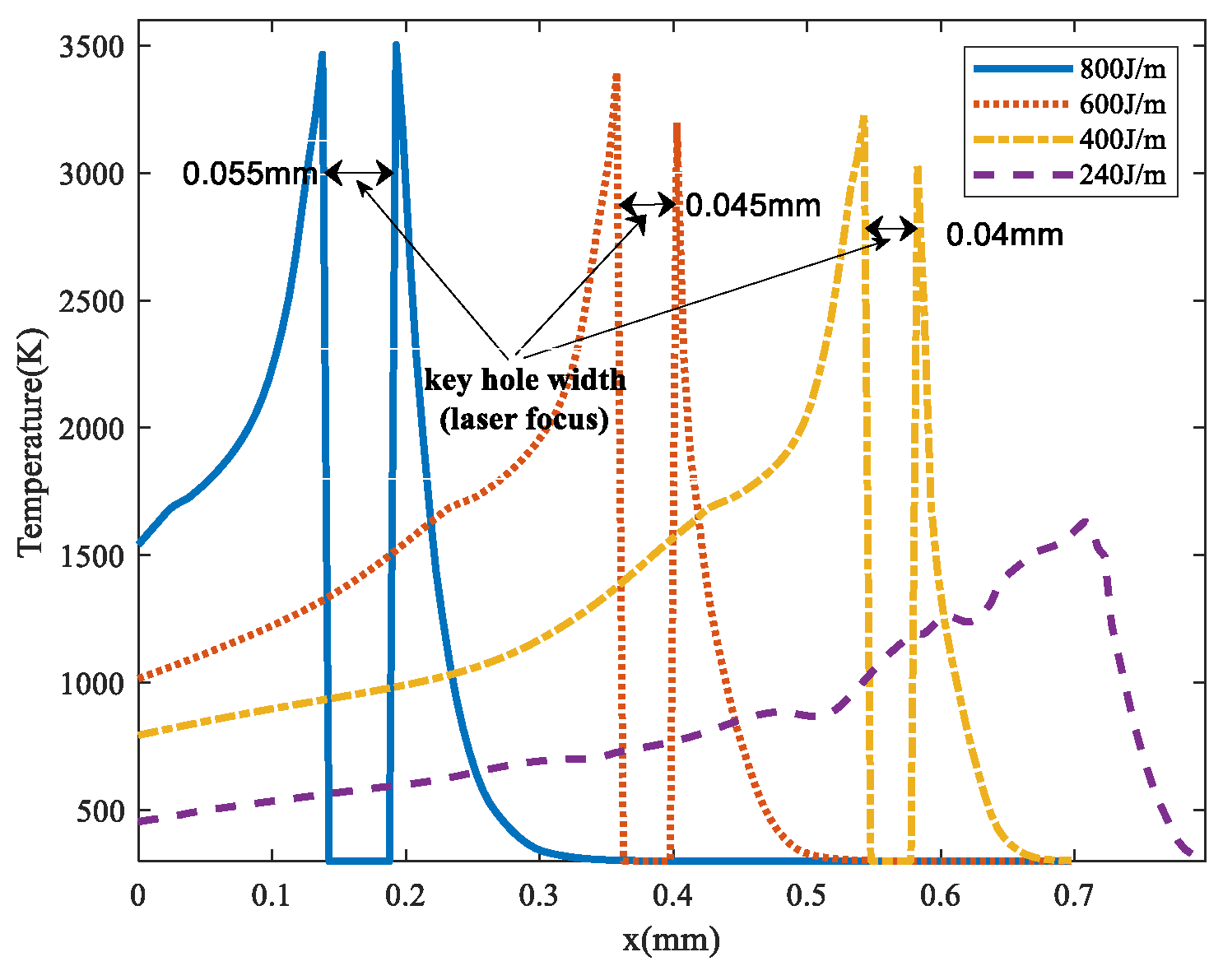
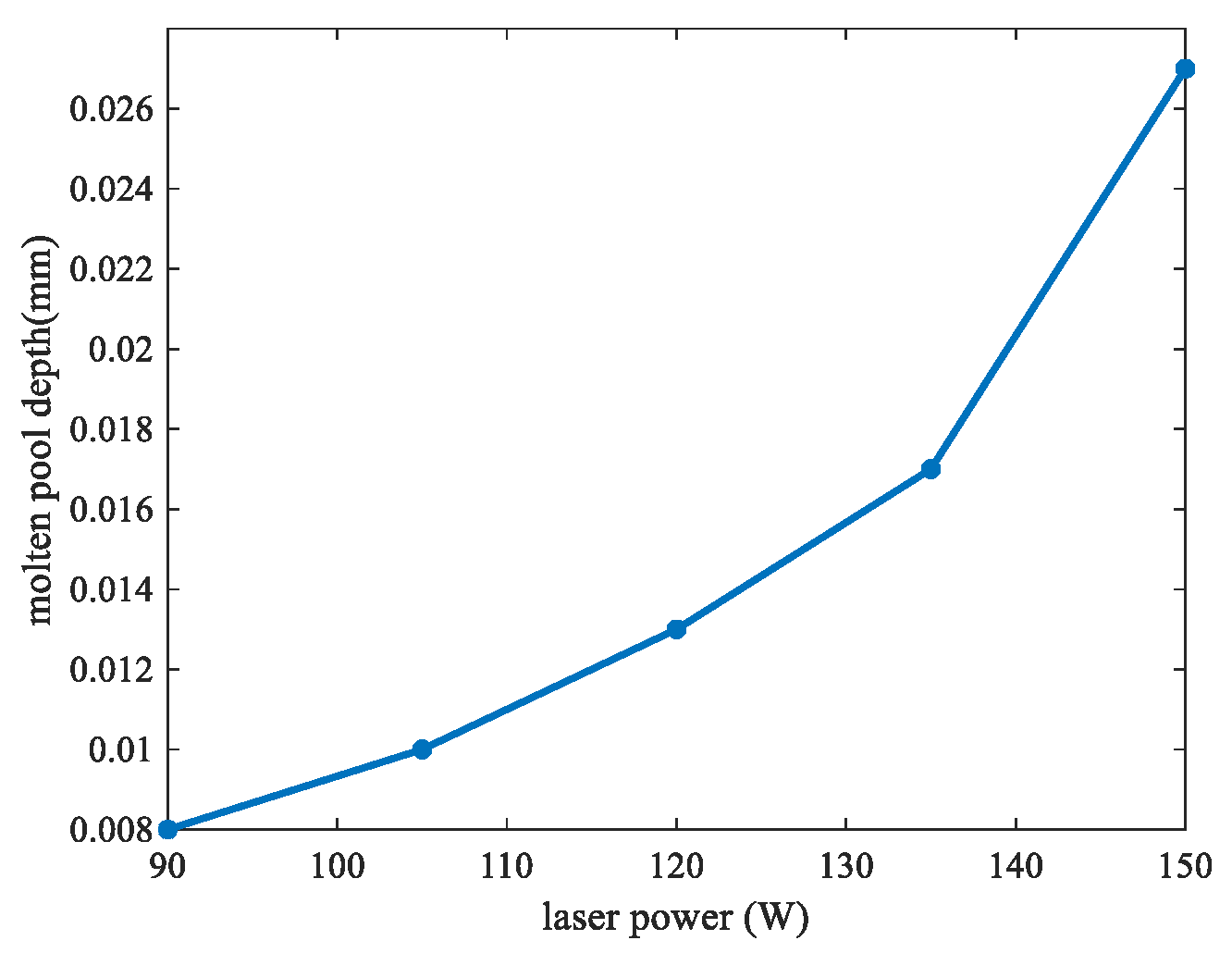
3.3. Keyhole Depth Analysis
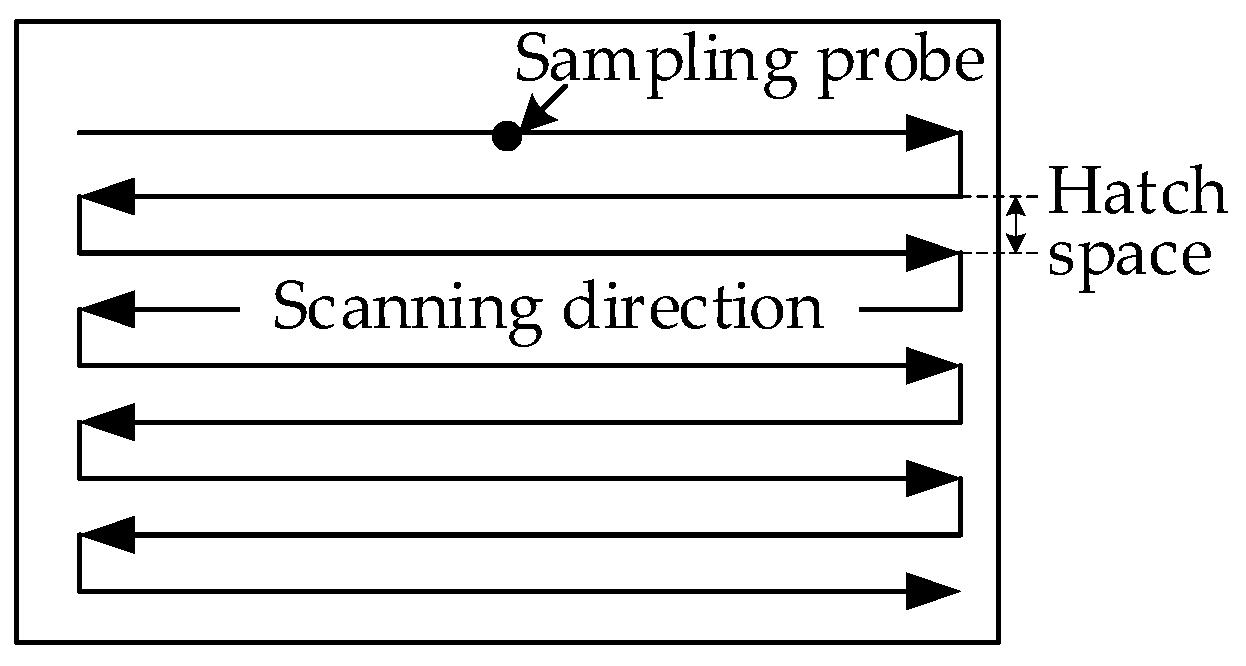
3.4. Hatch Space Analysis
3.5. Analysis of Powder Bed Distribution Effects
4. Conclusions
- The convection flow in the molten pool can effectively widen the molten pool width and promote strong bonding between adjacent scan tracks. Therefore, the hatch space can be enlarged by increasing the laser power or decreasing the scanning speed to enhance the convection flow behavior.
- When the LED decreases to 240 J/m, the keyhole depth becomes too small to fuse the previously processed layer with the currently processed one, potentially leading to degradation in part densification. To ensure better densification of the final parts, it is suggested that the LED be set to over 400 J/m when the layer thickness is 45 μm.
- The keyhole depth can be enlarged more effectively by further increasing the energy input after the keyhole is formed, such as by increasing the laser power or decreasing the scanning speed.
- If the hatch space is too large or the powder bed is sparsely distributed, internal void defects may form, significantly affecting workpiece quality. To prevent these defects, it is suggested that the hatch space be narrower than the single-track width.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milton, G.; Briane, M.; Harutyunyan, D. On the possible effective elasticity tensors of 2-dimensional and 3-dimensional printed materials. Math. Mech. Complex Syst. 2017, 5, 41–94. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar]
- Gao, B.W.; Zhao, H.J.; Peng, L.Q.; Sun, Z.X. A Review of Research Progress in Selective Laser Melting (SLM). Micromachines 2023, 14, 57. [Google Scholar] [CrossRef]
- Sefene, E.M. State-of-the-art of selective laser melting process: A comprehensive review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- Ciallella, A.; Giorgio, I.; Barchiesi, E.; Alaimo, G.; Cattenone, A.; Smaniotto, B.; Vintache, A.; D’Annibale, F.; dell’Isola, F.; Hild, F.; et al. A 3D pantographic metamaterial behaving as a mechanical shield: Experimental and numerical evidence. Mater. Des. 2024, 237, 112554. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Z.; Tse, Y.; Huang, C.; Zhang, W. Optimization of processing parameters and establishment of a relationship between microstructure and mechanical properties of SLM titanium alloy. Opt. Laser Technol. 2019, 112, 159–167. [Google Scholar] [CrossRef]
- Lo, Y.-L.; Liu, B.-Y.; Tran, H.-C. Optimized hatch space selection in double-scanning track selective laser melting process. Int. J. Adv. Manuf. Technol. 2019, 105, 2989–3006. [Google Scholar] [CrossRef]
- Chowdhury, S.; Yadaiah, N.; Prakash, C.; Ramakrishna, S.; Dixit, S.; Gulta, L.R.; Buddhi, D. Laser powder bed fusion: A state-of-the-art review of the technology, materials, properties & defects, and numerical modelling. J. Mater. Res. Technol.-JmrT 2022, 20, 2109–2172. [Google Scholar]
- Chen, J.; Wei, H.; Bao, K.; Zhang, X.; Cao, Y.; Peng, Y.; Kong, J.; Wang, K. Dynamic mechanical properties of 316L stainless steel fabricated by an additive manufacturing process. J. Mater. Res. Technol. 2021, 11, 170–179. [Google Scholar] [CrossRef]
- Ansari, P.; Rehman, A.U.; Pitir, F.; Veziroglu, S.; Mishra, Y.K.; Aktas, O.C.; Salamci, M.U. Selective Laser Melting of 316L Austenitic Stainless Steel: Detailed Process Understanding Using Multiphysics Simulation and Experimentation. Metals 2021, 11, 1076. [Google Scholar] [CrossRef]
- Wang, D.; Wu, S.; Yang, Y.; Dou, W.; Deng, S.; Wang, Z.; Li, S. The Effect of a Scanning Strategy on the Residual Stress of 316L Steel Parts Fabricated by Selective Laser Melting (SLM). Materials 2018, 11, 1821. [Google Scholar] [CrossRef]
- Miranda, G.; Faria, S.; Bartolomeu, F.; Pinto, E.; Madeira, S.; Mateus, A.; Carreira, P.; Alves, N.; Silva, F.S.; Carvalho, O. Predictive models for physical and mechanical properties of 316L stainless steel produced by selective laser melting. Mater. Sci. Eng. A 2016, 657, 43–56. [Google Scholar] [CrossRef]
- Ponticelli, G.S.; Venettacci, S.; Giannini, O.; Guarino, S.; Horn, M. Fuzzy process optimization of laser powder bed fusion of 316L stainless steel. Prog. Addit. Manuf. 2022, 8, 437–458. [Google Scholar] [CrossRef]
- Theeda, S.; Jagdale, S.H.; Ravichander, B.B.; Kumar, G. Optimization of Process Parameters in Laser Powder Bed Fusion of SS 316L Parts Using Artificial Neural Networks. Metals 2023, 13, 842. [Google Scholar] [CrossRef]
- Qiu, C.; Kindi, M.A.; Aladawi, A.S.; Hatmi, I.A. A comprehensive study on microstructure and tensile behaviour of a selectively laser melted stainless steel. Sci. Rep. 2018, 8, 7785. [Google Scholar] [CrossRef]
- Iqbal, N.; Jimenez-Melero, E.; Ankalkhope, U.; Lawrence, J. Microstructure and Mechanical Properties of 316L Stainless Steel Fabricated Using Selective Laser Melting. MRS Adv. 2019, 4, 2431–2439. [Google Scholar] [CrossRef]
- Kaynak, Y.; Kitay, O. The effect of post-processing operations on surface characteristics of 316L stainless steel produced by selective laser melting. Addit. Manuf. 2019, 26, 84–93. [Google Scholar] [CrossRef]
- Soylemez, E.; Koç, E.; Coşkun, M. Thermo-mechanical simulations of selective laser melting for AlSi10Mg alloy to predict the part-scale deformations. Prog. Addit. Manuf. 2019, 4, 465–478. [Google Scholar] [CrossRef]
- Greco, S.; Gutzeit, K.; Hotz, H.; Kirsch, B.; Aurich, J.C. Selective laser melting (SLM) of AISI 316L—Impact of laser power, layer thickness, and hatch spacing on roughness, density, and microhardness at constant input energy density. Int. J. Adv. Manuf. Technol. 2020, 108, 1551–1562. [Google Scholar] [CrossRef]
- Röttger, A.; Boes, J.; Theisen, W.; Thiele, M.; Esen, C.; Edelmann, A.; Hellmann, R. Microstructure and mechanical properties of 316L austenitic stainless steel processed by different SLM devices. Int. J. Adv. Manuf. Technol. 2020, 108, 769–783. [Google Scholar] [CrossRef]
- Suryawanshi, J.; Prashanth, K.G.; Ramamurty, U. Mechanical behavior of selective laser melted 316L stainless steel. Mater. Sci. Eng. A 2017, 696, 113–121. [Google Scholar] [CrossRef]
- Şener, B.; Çavuşoğlu, O.; Yuce, C. Effects of process parameters on surface quality and mechanical performance of 316L stainless steel produced by selective laser melting. Optik 2023, 287, 171050. [Google Scholar] [CrossRef]
- Waqar, S.; Guo, K.; Sun, J. FEM analysis of thermal and residual stress profile in selective laser melting of 316L stainless steel. J. Manuf. Process. 2021, 66, 81–100. [Google Scholar] [CrossRef]
- Trejos-Taborda, J.; Reyes-Osorio, L.; Garza, C.; del Carmen Zambrano-Robledo, P.; Lopez-Botello, O. Finite element modeling of melt pool dynamics in laser powder bed fusion of 316L stainless steel. Int. J. Adv. Manuf. Technol. 2022, 120, 3947–3961. [Google Scholar] [CrossRef]
- Luo, Z.; Zhao, Y. Efficient thermal finite element modeling of selective laser melting of Inconel 718. Comput. Mech. 2019, 65, 763–787. [Google Scholar] [CrossRef]
- Mayer, T.; Brandle, G.; Schonenberger, A.; Eberlein, R. Simulation and validation of residual deformations in additive manufacturing of metal parts. Heliyon 2020, 6, e03987. [Google Scholar] [CrossRef] [PubMed]
- Pagac, M.; Hajnys, J.; Halama, R.; Aldabash, T.; Mesicek, J.; Jancar, L.; Jansa, J. Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L. Appl. Sci. 2021, 11, 1656. [Google Scholar] [CrossRef]
- Kumar, A.; Shukla, M. Numerical Modeling of Selective Laser Melting: Influence of Process Parameters on the Melt Pool Geometry. J. Mater. Eng. Perform. 2022, 32, 7998–8013. [Google Scholar] [CrossRef]
- Ahmed, N.; Barsoum, I.; Haidemenopoulos, G.; Al-Rub, R.K.A. Process parameter selection and optimization of laser powder bed fusion for 316L stainless steel: A review. J. Manuf. Process. 2022, 75, 415–434. [Google Scholar] [CrossRef]
- Gan, Z.; Yu, G.; He, X.; Li, S. Numerical simulation of thermal behavior and multicomponent mass transfer in direct laser deposition of Co-base alloy on steel. Int. J. Heat Mass Transf. 2017, 104, 28–38. [Google Scholar] [CrossRef]
- Rasch, M.; Roider, C.; Kohl, S.; Strauß, J.; Maurer, N.; Nagulin, K.Y.; Schmidt, M. Shaped laser beam profiles for heat conduction welding of aluminium-copper alloys. Opt. Lasers Eng. 2019, 115, 179–189. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, J.; Yan, Y.; Yang, J.; Uher, C.; Tang, X. Finite element analysis of temperature and stress fields during the selective laser melting process of thermoelectric SnTe. J. Mater. Process. Technol. 2018, 261, 74–85. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. (1980–2015) 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Shi, R.; Khairallah, S.A.; Roehling, T.T.; Heo, T.W.; McKeown, J.T.; Matthews, M.J. Microstructural control in metal laser powder bed fusion additive manufacturing using laser beam shaping strategy. Acta Mater. 2020, 184, 284–305. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, L.; Wang, C.; Ding, X.; Liu, J. Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting. Materials 2020, 14, 75. [Google Scholar] [CrossRef]
- Cho, M.H.; Lim, Y.C.; Farson, D.F. Simulation of weld pool dynamics in the stationary pulsed gas metal arc welding process and final weld shape. Weld. J. 2006, 85, 271–283. [Google Scholar]
- Cao, L. Workpiece-scale numerical simulations of SLM molten pool dynamic behavior of 316L stainless steel. Comput. Math. Appl. 2021, 96, 209–228. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Sattari, M.; Bremer, S.J.L.; Luckabauer, M.; Römer, G.-w.R.B.E.; Richardson, I.M.; Kleijn, C.R.; Hermans, M.J.M. The influence of laser characteristics on internal flow behaviour in laser melting of metallic substrates. Mater. Des. 2022, 214, 110385. [Google Scholar] [CrossRef]
- Chang, C.-S.; Wu, K.-T.; Han, C.-F.; Tsai, T.-W.; Liu, S.-H.; Lin, J.-F. Establishment of the Model Widely Valid for the Melting and Vaporization Zones in Selective Laser Melting Printings Via Experimental Verifications. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 9, 143–162. [Google Scholar] [CrossRef]
- Kim, C.S. Thermophysical Properties of Stainless Steels; Argonne National Lab.: Lemont, IL, USA, 1975. [Google Scholar] [CrossRef]
- Fürstenau, J.-P.; Wessels, H.; Weißenfels, C.; Wriggers, P. Generating virtual process maps of SLM using powder-scale SPH simulations. Comput. Part. Mech. 2019, 7, 655–677. [Google Scholar] [CrossRef]
- Le, T.-N.; Lo, Y.-L. Effects of sulfur concentration and Marangoni convection on melt-pool formation in transition mode of selective laser melting process. Mater. Des. 2019, 179, 107866. [Google Scholar] [CrossRef]
- Mao, S.; Zhang, D.Z.; Ren, Z.; Fu, G.; Ma, X. Effects of process parameters on interfacial characterization and mechanical properties of 316L/CuCrZr functionally graded material by selective laser melting. J. Alloys Compd. 2022, 899, 163256. [Google Scholar] [CrossRef]
- Wei, K.; Wang, Z.; Zeng, X. Influence of element vaporization on formability, composition, microstructure, and mechanical performance of the selective laser melted Mg–Zn–Zr components. Mater. Lett. 2015, 156, 187–190. [Google Scholar] [CrossRef]
- Shrestha, S.; Starr, T.; Chou, K. A Study of Keyhole Porosity in Selective Laser Melting: Single-Track Scanning with Micro-CT Analysis. J. Manuf. Sci. Eng. 2019, 141, 071004. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, Z.; Chen, P. Effect of selective laser melting process parameters on microstructure and mechanical properties of 316L stainless steel helical micro-diameter spring. Int. J. Adv. Manuf. Technol. 2019, 104, 2117–2131. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, X.; Pan, Z.; Gao, M.; Han, L.; Choi, J.-P.; Zhang, H. Multi-Physics Modeling of Melting-Solidification Characteristics in Laser Powder Bed Fusion Process of 316L Stainless Steel. Materials 2024, 17, 946. https://doi.org/10.3390/ma17040946
Shan X, Pan Z, Gao M, Han L, Choi J-P, Zhang H. Multi-Physics Modeling of Melting-Solidification Characteristics in Laser Powder Bed Fusion Process of 316L Stainless Steel. Materials. 2024; 17(4):946. https://doi.org/10.3390/ma17040946
Chicago/Turabian StyleShan, Xiuyang, Zhenggao Pan, Mengdi Gao, Lu Han, Joon-Phil Choi, and Haining Zhang. 2024. "Multi-Physics Modeling of Melting-Solidification Characteristics in Laser Powder Bed Fusion Process of 316L Stainless Steel" Materials 17, no. 4: 946. https://doi.org/10.3390/ma17040946
APA StyleShan, X., Pan, Z., Gao, M., Han, L., Choi, J.-P., & Zhang, H. (2024). Multi-Physics Modeling of Melting-Solidification Characteristics in Laser Powder Bed Fusion Process of 316L Stainless Steel. Materials, 17(4), 946. https://doi.org/10.3390/ma17040946







