Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise
Abstract
:1. Introduction
2. Materials and Methods
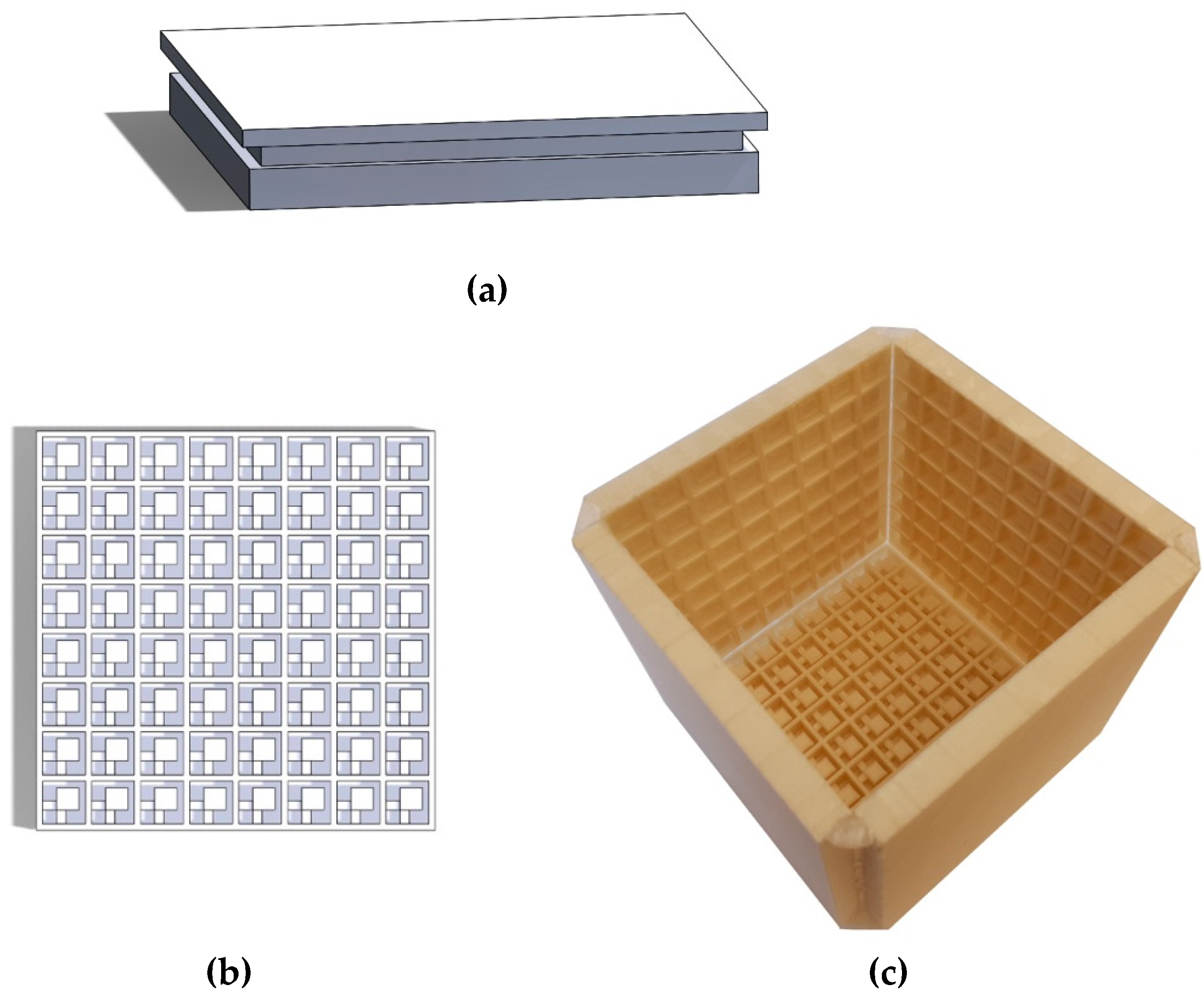
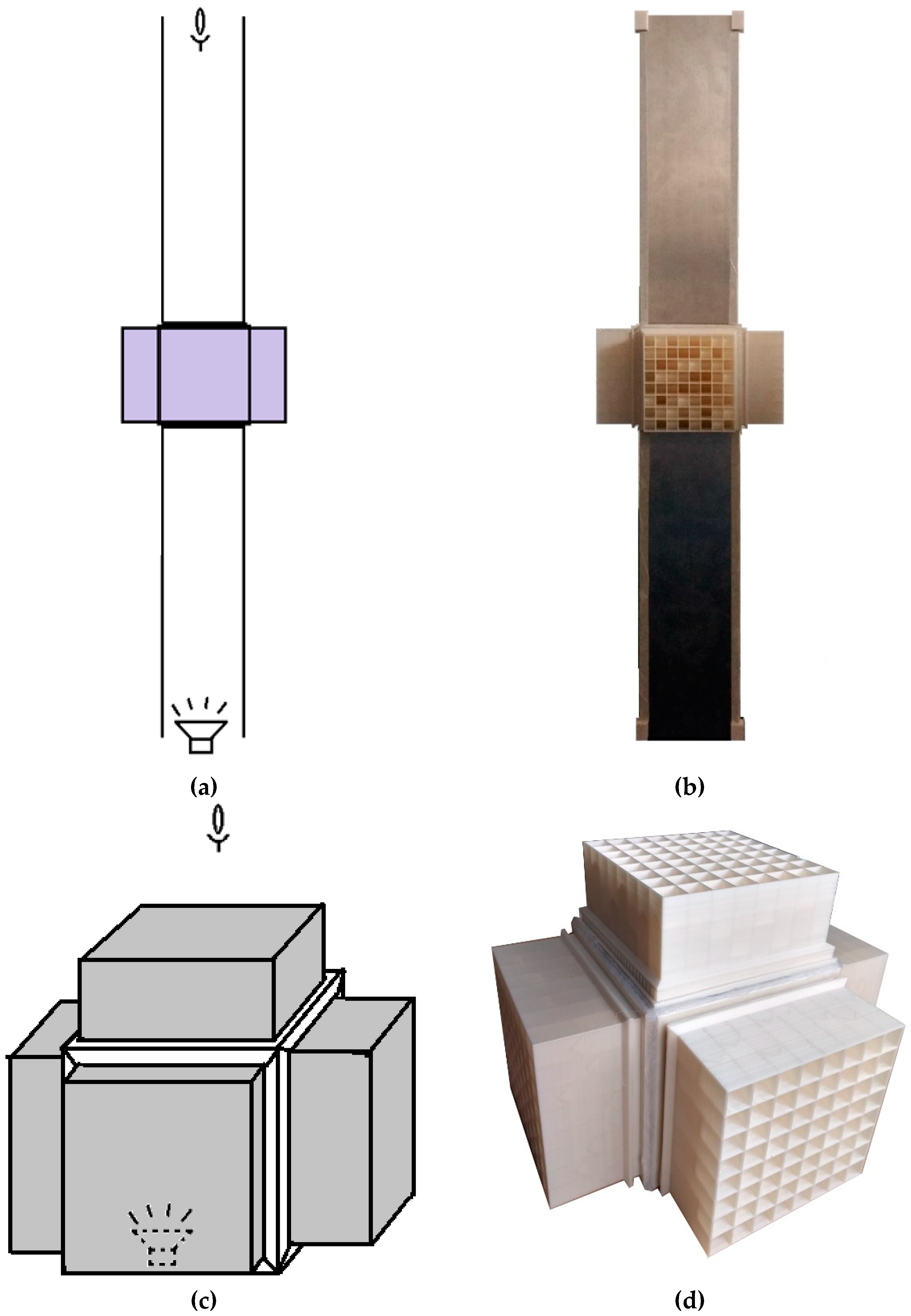
2.1. Metamaterial Wall Design and Fabrication
2.1.1. Passive Metamaterial
2.1.2. Reference Models
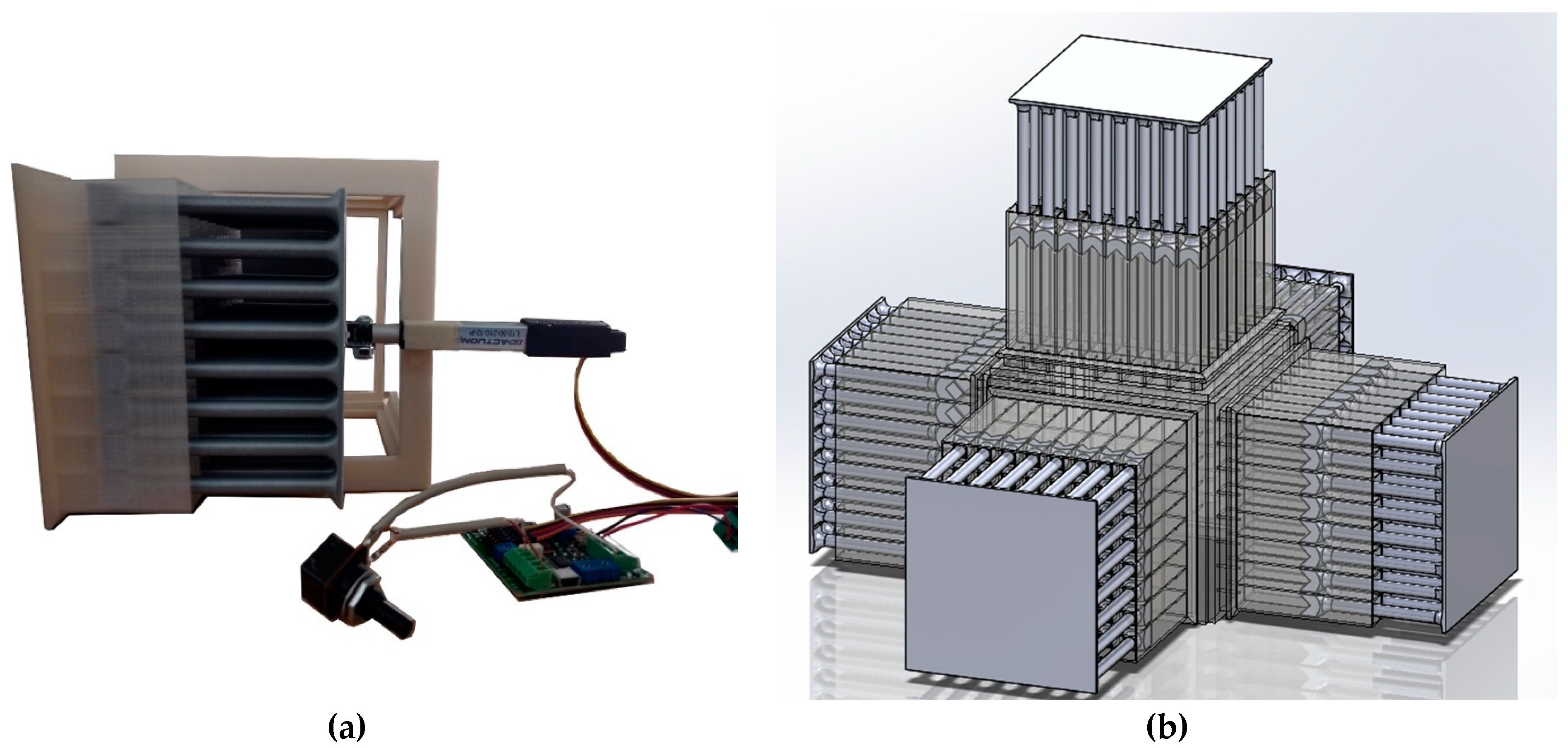
2.1.3. Electric-Actuated Active Metamaterial
2.2. Experimental Set-Up
Electric Linear Actuation Setup
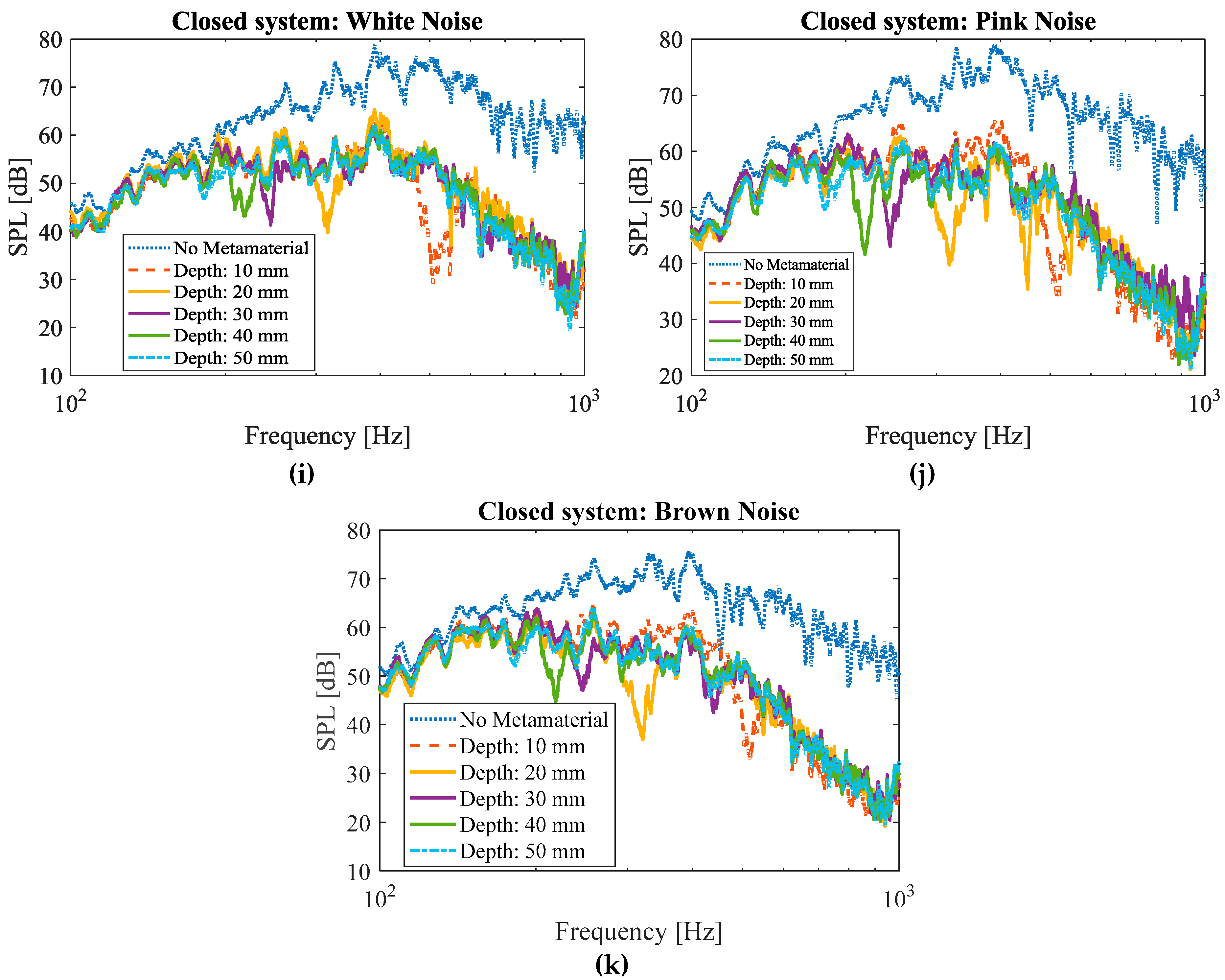
2.3. Noise Types and Measurement Techniques
- White noise: white noise has a uniform power distribution in any band of a given frequency bandwidth, if the bandwidth is plotted in Hz.
- Pink noise: In homogeny with white noise, the pink noise has a uniform power distribution if the bandwidth is plotted on a logarithmic scale. Consequently, if the frequency spectrum is plotted linearly, the sound amplitude concentrates more on the lower end of the frequency spectrum.
- Brown noise: In brown noise, the power amplitude decreases with a proportion of 1/f2 with respect to frequency. In other words, in brown noise sample, the power amplitude decreases by 6 dB per octave.
- A frequency sweep of 10,000→20 Hz to provide a wide range of separated frequency noises while measuring loudness in real-time
3. Results and Discussions
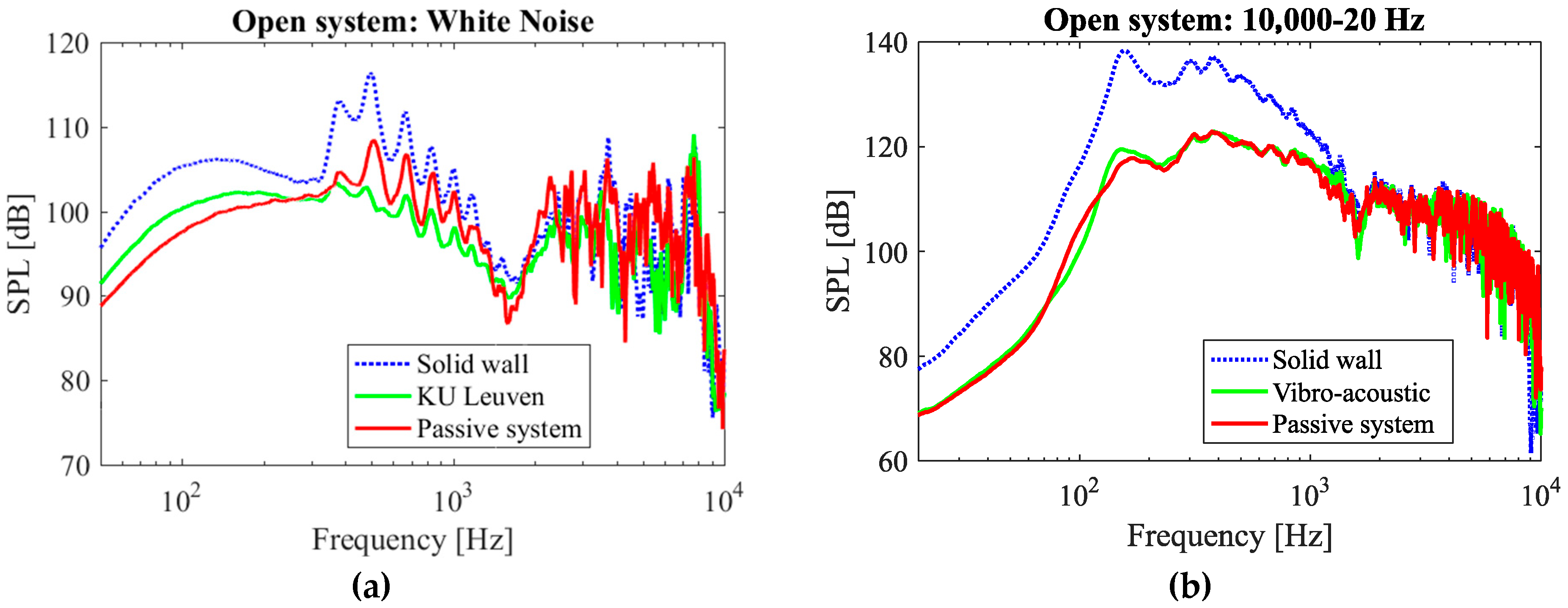
3.1. Passive Metamaterial
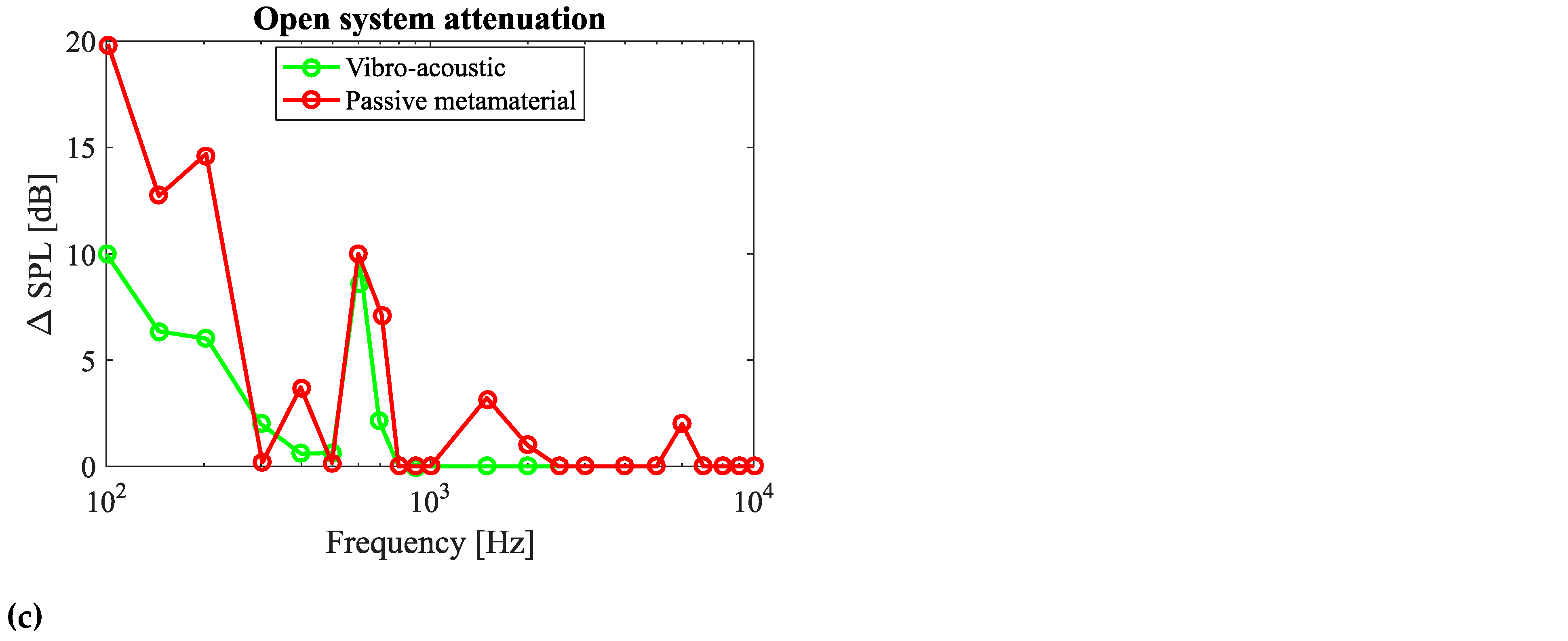
3.1.1. Open System
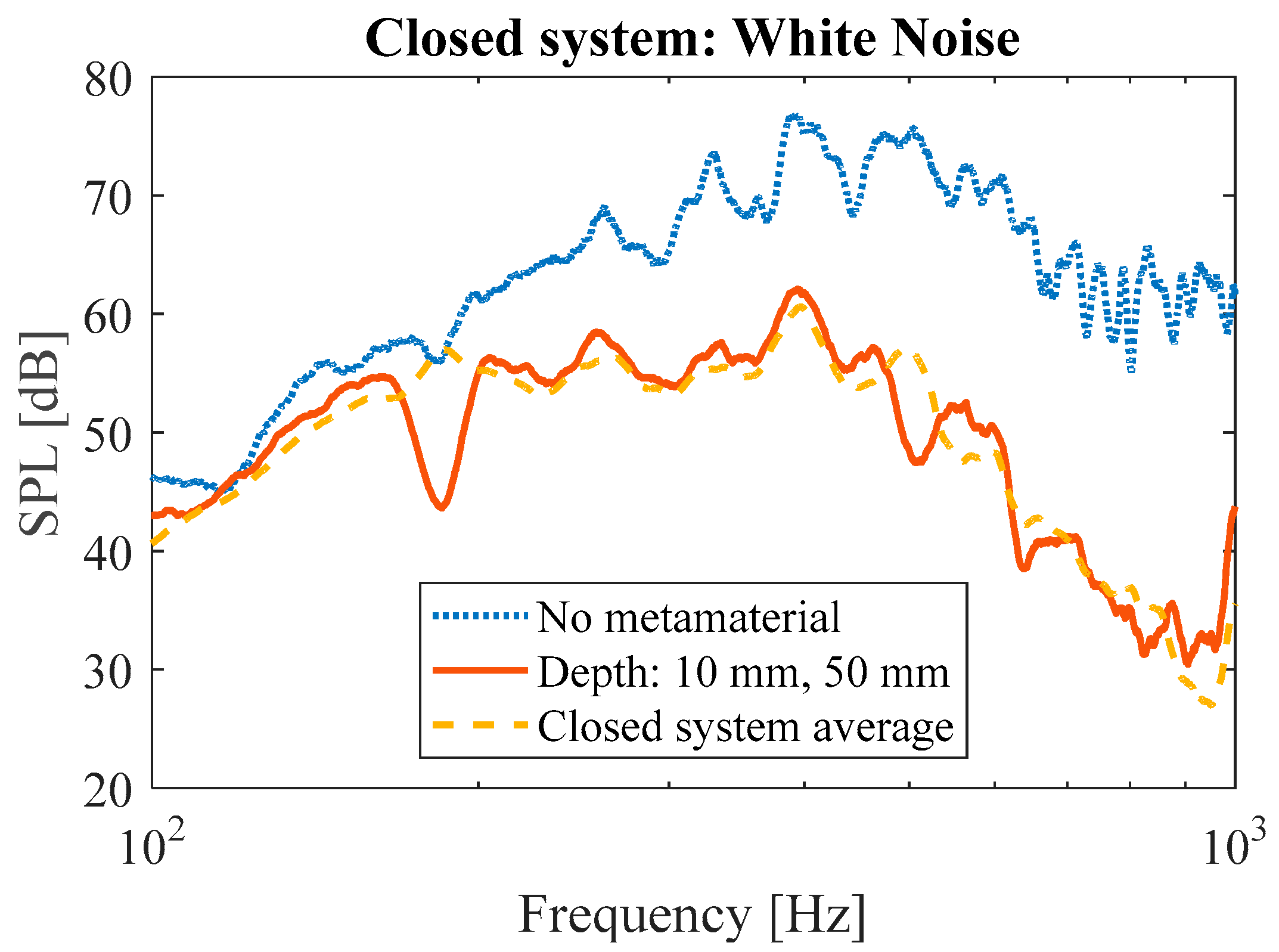
3.1.2. Closed System
3.2. Electric-Actuated Active Metamaterial
3.2.1. Open System
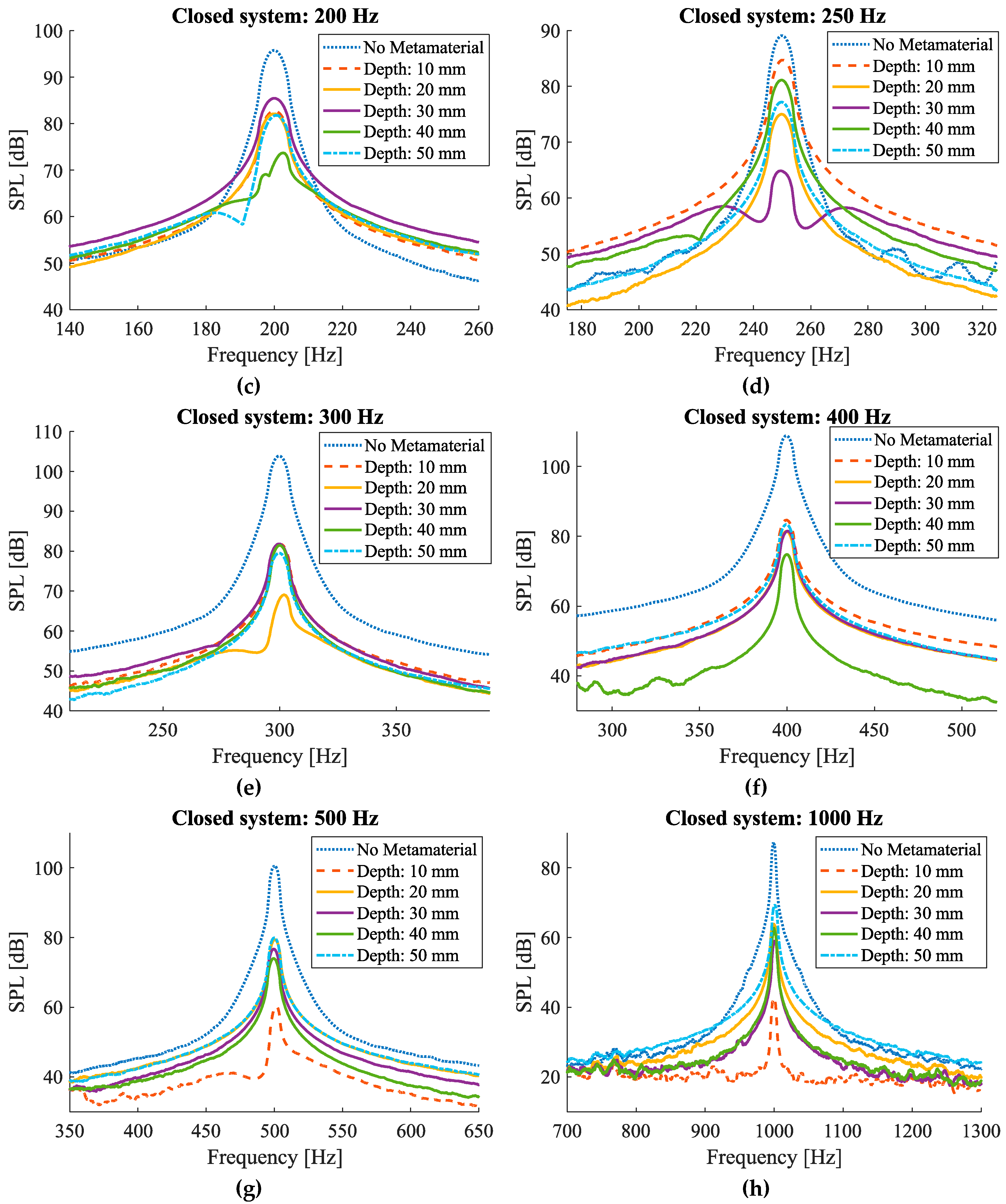
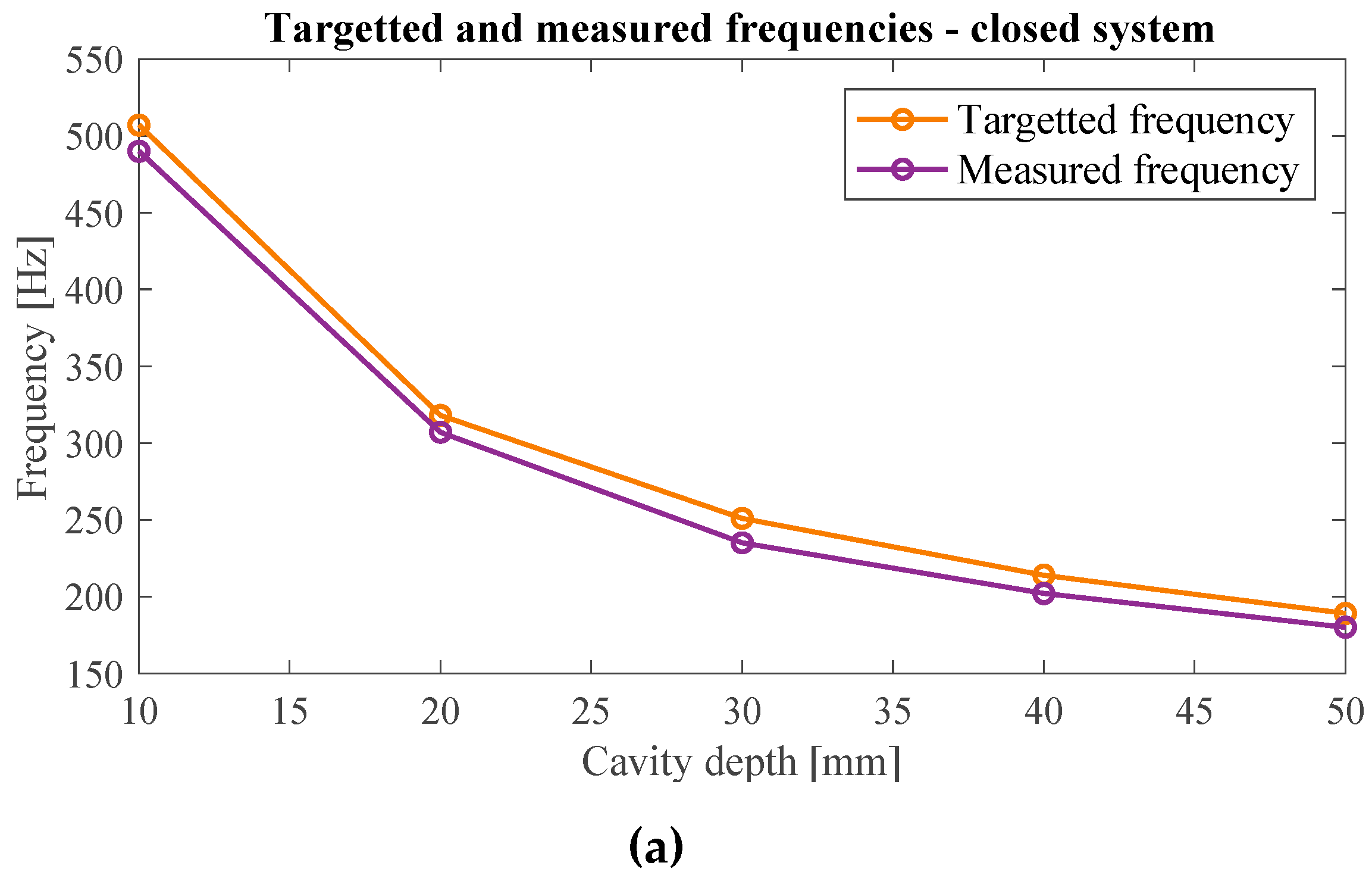
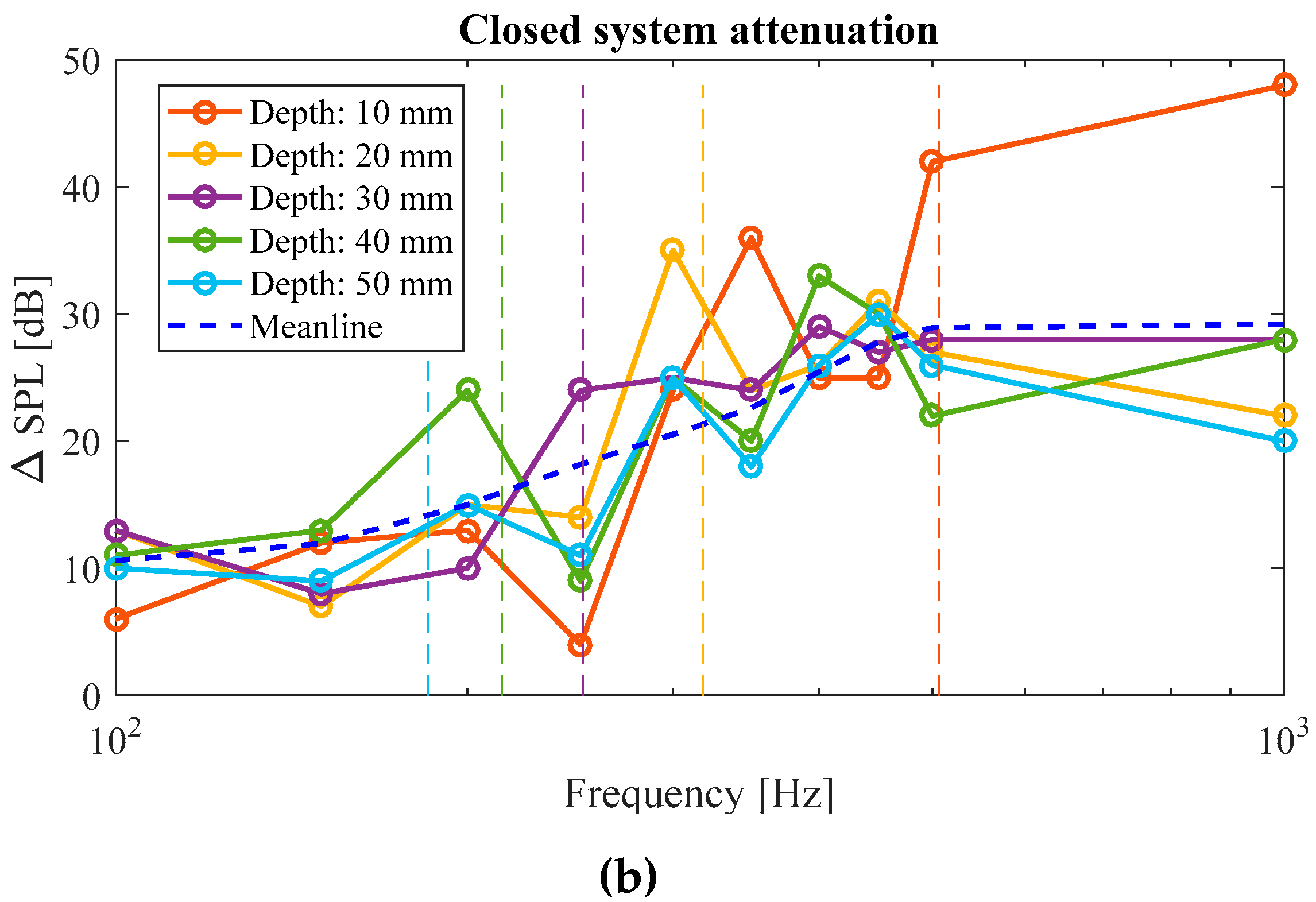
3.2.2. Closed System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations
| A | Cross-section area of neck |
| AM | Additive manufacturing |
| c | Speed of sound |
| f | Resonant frequency |
| FDM | Fused Deposition Modelling |
| L | Length of neck |
| PLA | Polylactic acid |
| SPL | Sound pressure level |
| V | Volume of cavity |
Appendix A
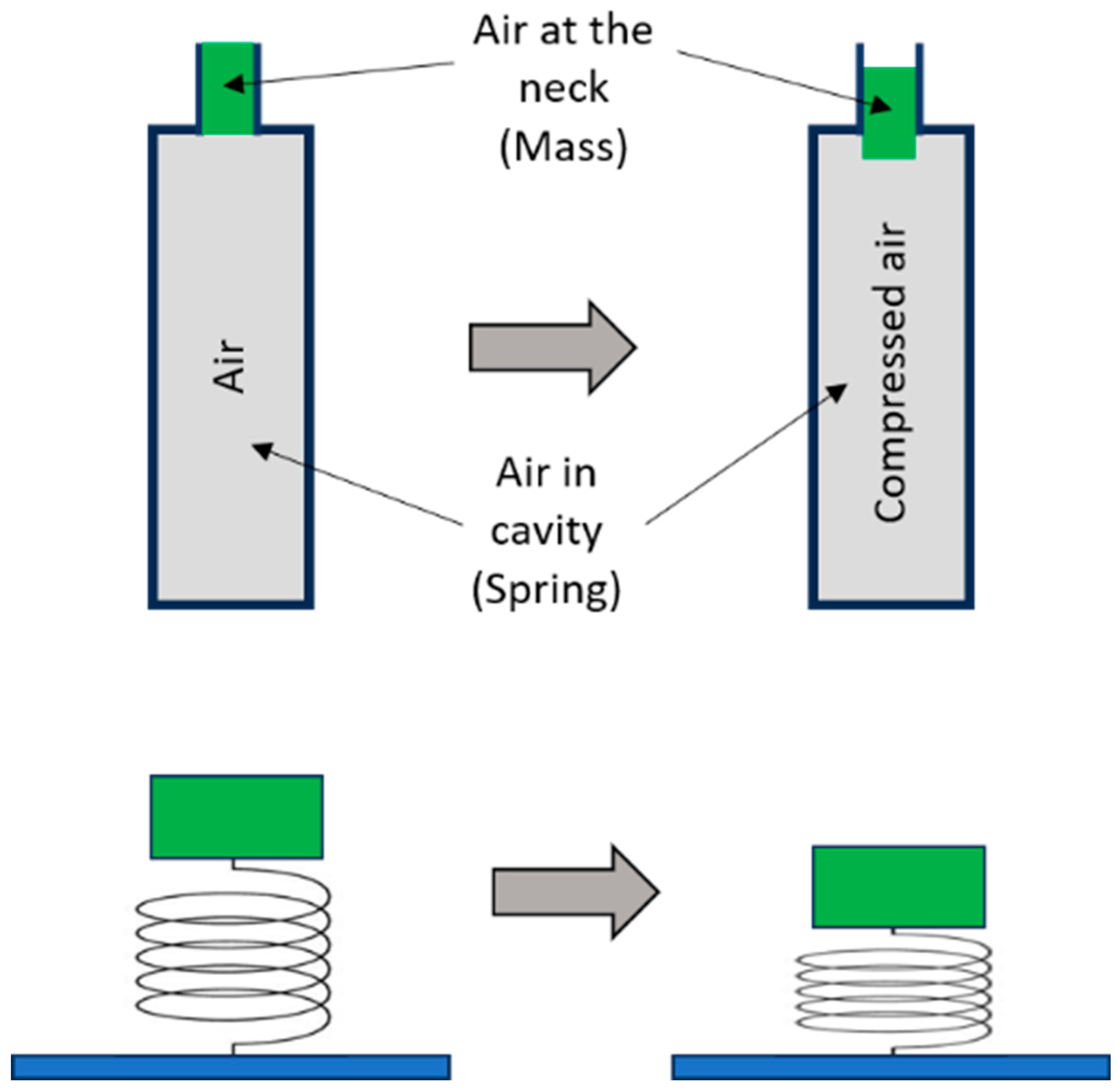
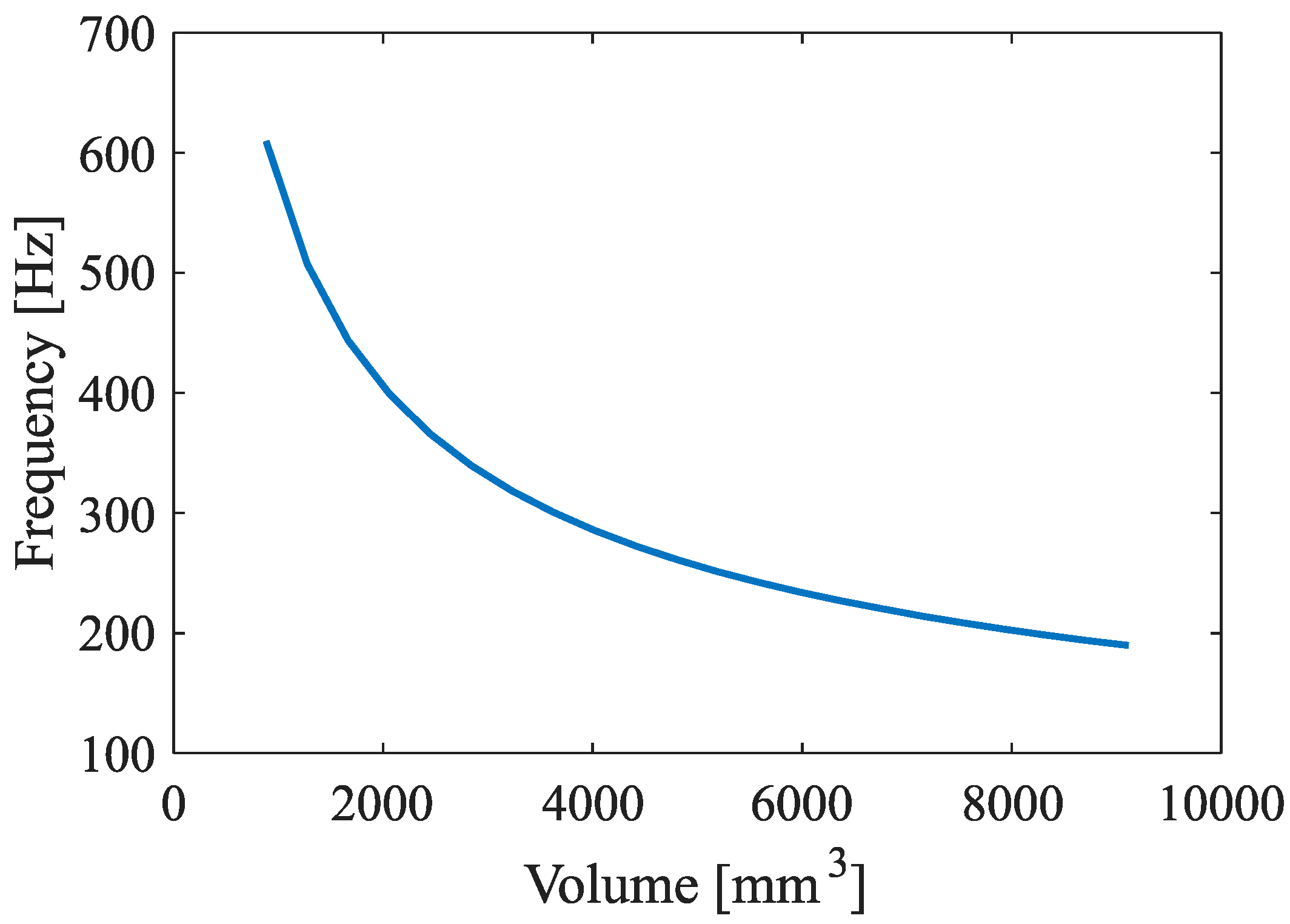
Appendix A.1. More Information on the Vibroacoustic Mechanical Metamaterial
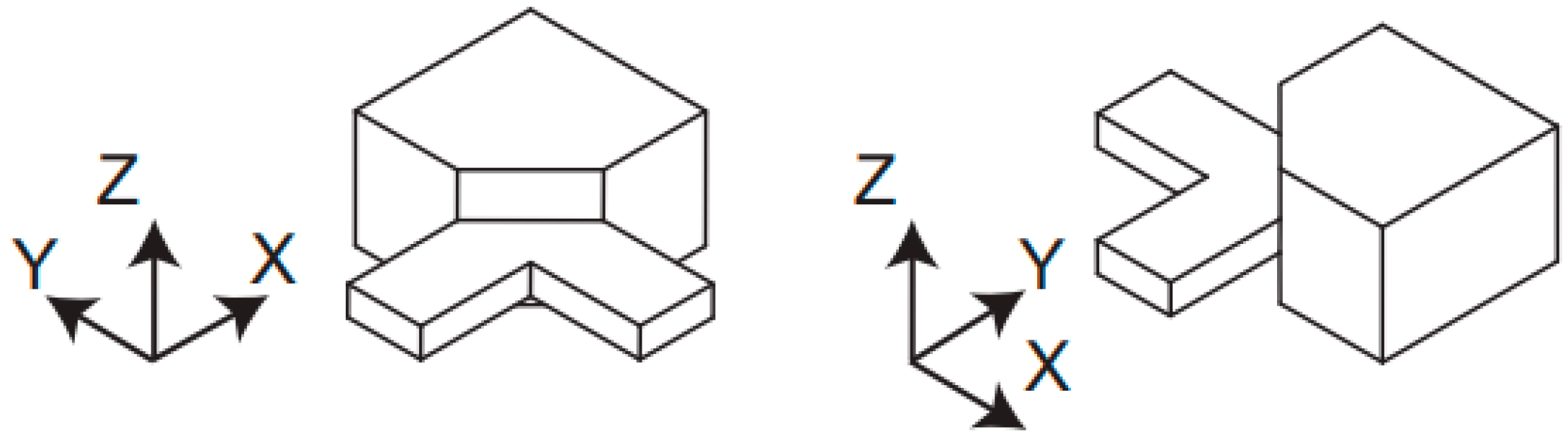
Appendix A.2. Survey on State-of-the-Art Work on Active Actuation
| Type of Volume Change (Neck/Cell) | Decrease in Noise (dB) | Range of Frequency (Hz) | Actuation Type | Range of Changing Parameter | Type (Self-Tuning, Active, Adjustable) | Reference |
|---|---|---|---|---|---|---|
| Length of cavity | Up to 50 dB | 100–1000 | Electronic-actuated | 10–50 mm | Active | This study |
| Cell Volume change | 100% | 80–170 | Pneumatic | NA | Adjustable | [53] |
| Neck diameter | 4.2 dB | 75–115 | Rotary-actuated aperture | 9–58 mm | Adjustable | [54] |
| Volume | 29 dB | 65–150 | Rotary-actuated walls | 1491 cm3–14,093 cm3 | Self-tuning | [55] |
| Cavity Length | 20 dB | 35–46 (Max Attenuation) | Hydraulic | 43–243 mm | Active | [56] |
| Internal Pressure | - | 50–500 (Max–160) | Electromagnetic diaphragm/piezoelectric | NA | Active | [57] |
| Cavity length | 18 dB | 0–400 (max-226) | - | 60–90 mm | Adjustable | [58] |
| Neck length | - | 3–75 | Hydraulic | 39–60 cm | Adjustable | [59] |
| Length of cavity | 30 dB | 80–140 | Pneumatic | 560–940 cm3 1.8–17 cm | Adjustable | [60] |
| Area of neck | 25 dB | 100–3000 | Rotary | - | Self-tuning | [61] |
| Length of cavity | - | 100–350 | Pneumatic | 5–12 cm | Adjustable | [67] |
References
- Roudbarian, N.; Jebellat, E.; Famouri, S.; Baniasadi, M.; Hedayati, R.; Baghani, M. Shape-memory polymer metamaterials based on triply periodic minimal surfaces. Eur. J. Mech. A/Solids 2022, 96, 104676. [Google Scholar] [CrossRef]
- Ghavidelnia, N.; Salami, S.J.; Hedayati, R. Analytical relationships for yield stress of five mechanical meta-biomaterials. Mech. Based Des. Struct. Mach. 2020, 50, 3452–3474. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Heyman, E. Wave propagation in media having negative permittivity and permeability. Phys. Rev. E 2001, 64, 056625. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Smith, D.R. Electric-field-coupled resonators for negative permittivity metamaterials. Appl. Phys. Lett. 2006, 88, 041109. [Google Scholar] [CrossRef]
- Ishikawa, A.; Tanaka, T.; Kawata, S. Negative Magnetic Permeability in the Visible Light Region. Phys. Rev. Lett. 2005, 95, 237401. [Google Scholar] [CrossRef]
- Mirzaali, M.J.; Hedayati, R.; Vena, P.; Vergani, L.; Strano, M.; Zadpoor, A.A. Rational design of soft mechanical metamaterials: Independent tailoring of elastic properties with randomness. Appl. Phys. Lett. 2017, 111, 051903. [Google Scholar] [CrossRef]
- Hedayati, R.; Güven, A.; van der Zwaag, S. 3D gradient auxetic soft mechanical metamaterials fabricated by additive manufacturing. Appl. Phys. Lett. 2021, 118, 141904. [Google Scholar] [CrossRef]
- Hedayati, R.; Roudbarian, N.; Tahmasiyan, S.; Bodaghi, M. Gradient origami metamaterials for programming out-of-plane curvatures. Adv. Eng. Mater. 2023, 25, 2201838. [Google Scholar] [CrossRef]
- Tao, Z.; Ren, X.; Zhao, A.G.; Sun, L.; Zhang, Y.; Jiang, W.; Han, D.; Zhang, X.Y.; Xie, Y.M. A novel auxetic acoustic metamaterial plate with tunable bandgap. Int. J. Mech. Sci. 2022, 226, 107414. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef]
- Boardman, A. Pioneers in metamaterials: John Pendry and Victor Veselago. J. Opt. 2010, 13, 020401. [Google Scholar] [CrossRef]
- Monticone, F.; Alù, A. Metamaterial, plasmonic and nanophotonic devices. Rep. Prog. Phys. 2017, 80, 036401. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Srivastava, Y.K.; Manjappa, M.; Singh, R. Sensing with toroidal metamaterial. Appl. Phys. Lett. 2017, 110, 121108. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Metamaterials acoustic barrier. Appl. Acoust. 2021, 181, 108172. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled Membranes with Doubly Negative Mass Density and Bulk Modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Langfeldt, F.; Kemsies, H.; Gleine, W.; von Estorff, O. Perforated membrane-type acoustic metamaterials. Phys. Lett. A 2017, 381, 1457–1462. [Google Scholar] [CrossRef]
- Ma, F.; Wu, J.H. Plate-Type Acoustic Metamaterials. In Proceedings of the 21st International Conference on Composite Materials, Xi’an, China, 20–25 August 2017. [Google Scholar]
- Assouar, M.B.; Senesi, M.; Oudich, M.; Ruzzene, M.; Hou, Z. Broadband plate-type acoustic metamaterial for low-frequency sound attenuation. Appl. Phys. Lett. 2012, 101, 173505. [Google Scholar] [CrossRef]
- Liang, Z.; Li, J. Extreme Acoustic Metamaterial by Coiling Up Space. Phys. Rev. Lett. 2012, 108, 114301. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Tao, X.; Zhu, X.-F.; Zou, X.-Y.; Cheng, J.-C. Acoustic focusing by coiling up space. Appl. Phys. Lett. 2012, 101, 233508. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Holt, R.G.; Anderson, S.; Zhang, X. Horn-like space-coiling metamaterials toward simultaneous phase and amplitude modulation. Nat. Commun. 2018, 9, 1349. [Google Scholar] [CrossRef] [PubMed]
- Krushynska, A.O.; Bosia, F.; Pugno, N.M. Labyrinthine Acoustic Metamaterials with Space-Coiling Channels for Low-Frequency Sound Control. Acta Acust. United Acust. 2018, 104, 200–210. [Google Scholar] [CrossRef]
- Liang, Z.; Feng, T.; Lok, S.; Liu, F.; Ng, K.B.; Chan, C.H.; Wang, J.; Han, S.; Lee, S.; Li, J. Space-coiling metamaterials with double negativity and conical dispersion. Sci. Rep. 2013, 3, 1614. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, R.; Bodaghi, M. Acoustic Metamaterials and Acoustic Foams: Recent Advances. Appl. Sci. 2022, 12, 3096. [Google Scholar] [CrossRef]
- Iannace, G.; Bevilacqua, A.; Amadasi, G.; Trematerra, A. Experimental methods to evaluate the effective acoustic performance of screen made in metamaterials. In Proceedings of the SAPEM2023—Symposium on the Acoustics of Poro-Elastic Materias, Sorrento, Italy, 7–10 November 2023. [Google Scholar]
- Chen, X.; Xu, X.; Ai, S.; Chen, H.; Pei, Y.; Zhou, X. Active acoustic metamaterials with tunable effective mass density by gradient magnetic fields. Appl. Phys. Lett. 2014, 105, 071913. [Google Scholar] [CrossRef]
- Popa, B.-I.; Shinde, D.; Konneker, A.; Cummer, S.A. Active acoustic metamaterials reconfigurable in real time. Phys. Rev. B 2015, 91, 220303. [Google Scholar] [CrossRef]
- Xiao, S.; Ma, G.; Li, Y.; Yang, Z.; Sheng, P. Active control of membrane-type acoustic metamaterial by electric field. Appl. Phys. Lett. 2015, 106, 091904. [Google Scholar] [CrossRef]
- Xu, H.; Kong, D. A thin-film acoustic metamaterial absorber with tunable sound absorption characteristics. J. Acoust. Soc. Am. 2023, 153, 3493–3500. [Google Scholar] [CrossRef]
- Casadei, F.; Delpero, T.; Bergamini, A.; Ermanni, P.; Ruzzene, M. Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials. J. Appl. Phys. 2012, 112, 064902. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, D.; Xu, K.; Dong, L.; Chen, X. Topological phononic crystal plates with locally resonant elastic wave systems. Appl. Acoust. 2021, 177, 107931. [Google Scholar] [CrossRef]
- Bacigalupo, A.; De Bellis, M.L.; Misseroni, D. Design of tunable acoustic metamaterials with periodic piezoelectric microstructure. Extrem. Mech. Lett. 2020, 40, 100977. [Google Scholar] [CrossRef]
- Ning, S.; Chu, D.; Jiang, H.; Yang, F.; Liu, Z.; Zhuang, Z. The role of material and geometric nonlinearities and damping effects in designing mechanically tunable acoustic metamaterials. Int. J. Mech. Sci. 2021, 197, 106299. [Google Scholar] [CrossRef]
- Celli, P.; Gonella, S. Tunable directivity in metamaterials with reconfigurable cell symmetry. Appl. Phys. Lett. 2015, 106, 091905. [Google Scholar] [CrossRef]
- Ding, C.-L.; Zhao, X.-P. Multi-band and broadband acoustic metamaterial with resonant structures. J. Phys. D Appl. Phys. 2011, 44, 215402. [Google Scholar] [CrossRef]
- Cheer, J.; Daley, S.; McCormick, C. Feedforward control of sound transmission using an active acoustic metamaterial. Smart Mater. Struct. 2017, 26, 025032. [Google Scholar] [CrossRef]
- Reynolds, M.; Daley, S. An active viscoelastic metamaterial for isolation applications. Smart Mater. Struct. 2014, 23, 045030. [Google Scholar] [CrossRef]
- Hedayati, R.; Lakshmanan, S. Pneumatically-Actuated Acoustic Metamaterials Based on Helmholtz Resonators. Materials 2020, 13, 1456. [Google Scholar] [CrossRef]
- Hedayati, R.; Casalino, D.; Ragni, D.; van der Zwaag, S.; Avallone, F. Acoustic Liner. NL Patent NL2021916B1, 2020. [Google Scholar]
- Baz, A. The structure of an active acoustic metamaterial with tunable effective density. New J. Phys. 2009, 11, 123010. [Google Scholar] [CrossRef]
- Hedayati, R.; Carpio, A.R.; Luesutthiviboon, S.; Ragni, D.; Avallone, F.; Casalino, D.; van der Zwaag, S. Role of Polymeric Coating on Metallic Foams to Control the Aeroacoustic Noise Reduction of Airfoils with Permeable Trailing Edges. Materials 2019, 12, 1087. [Google Scholar] [CrossRef]
- Hedayati, R.; Ghavidelnia, N.; Sadighi, M.; Bodaghi, M. Improving the Accuracy of Analytical Relationships for Mechanical Properties of Permeable Metamaterials. Appl. Sci. 2021, 11, 1332. [Google Scholar] [CrossRef]
- Wen, G.; Zhang, S.; Wang, H.; Wang, Z.-P.; He, J.; Chen, Z.; Liu, J.; Xie, Y.M. Origami-based acoustic metamaterial for tunable and broadband sound attenuation. Int. J. Mech. Sci. 2023, 239, 107872. [Google Scholar] [CrossRef]
- Kwon, B.-J.; Jung, J.-Y.; Lee, D.; Park, K.-C.; Oh, I.-K. Tunable acoustic waveguide based on vibro-acoustic metamaterials with shunted piezoelectric unit cells. Smart Mater. Struct. 2015, 24, 105018. [Google Scholar] [CrossRef]
- De Melo Filho, N.; Claeys, C.; Deckers, E.; Desmet, W. Realisation of a thermoformed vibro-acoustic metamaterial for increased STL in acoustic resonance driven environments. Appl. Acoust. 2019, 156, 78–82. [Google Scholar] [CrossRef]
- Wolfe, J. Helmholtz Resonance; School of Physics at UNSW: Sydney, Australia, 2000; Available online: http://www.phys.unsw.edu.au/jw/Helmholtz.html (accessed on 20 January 2013).
- Wu, D.; Zhang, N.; Mak, C.M.; Cai, C. Noise Attenuation Performance of a Helmholtz Resonator Array Consist of Several Periodic Parts. Sensors 2017, 17, 1029. [Google Scholar] [CrossRef]
- Zhao, D.; A’Barrow, C.; Morgans, A.S.; Carrotte, J. Acoustic Damping of a Helmholtz Resonator with an Oscillating Volume. AIAA J. 2009, 47, 1672–1679. [Google Scholar] [CrossRef]
- Anwar, A. Low Frequency Finite Element Modeling of Passive Noise Attenuation in Ear Defenders. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 2005. [Google Scholar]
- Sacarcelik, O. Acoustic Devices for the Active & Passive Control of Sound in a Payload Compartment. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2004. [Google Scholar]
- Birdsong, C.; Radcliffe, C.J. An Electronically Tunable Resonator for Noise Control. SAE Trans. 2001, 110, 2097–2103. [Google Scholar]
- Estève, S.J.; Johnson, M.E. Adaptive Helmholtz resonators and passive vibration absorbers for cylinder interior noise control. J. Sound Vib. 2005, 288, 1105–1130. [Google Scholar] [CrossRef]
- de Bedout, J.; Franchek, M.; Bernhard, R.; Mongeau, L. Adaptive-Passive Noise Control with Self-Tuning Helmholtz Resonators. J. Sound Vib. 1997, 202, 109–123. [Google Scholar] [CrossRef]
- Kela, L. Adaptive Helmholtz resonator in a hydraulic system. World Acad. Sci. Eng. Technol. 2010, 44, 1002–1009. [Google Scholar]
- Yuan, J. Active Helmholtz Resonator with Positive Real Impedance. J. Vib. Acoust. 2006, 129, 94–100. [Google Scholar] [CrossRef]
- Singh, S.; Howard, C.; Hansen, C. Tuning a semi-active Helmholtz resonator. In Proceedings of the 6th International Symposium on Active Noise and Vibration Control (ACTIVE 2006), Adelaide, Australia, 18–20 September 2006. [Google Scholar]
- Kela, L. Resonant frequency of an adjustable Helmholtz resonator in a hydraulic system. Arch. Appl. Mech. 2009, 79, 1115–1125. [Google Scholar] [CrossRef]
- Matsuhisa, H.; Ren, B.; Sato, S. Semiactive control of duct noise by a volume-variable resonator. JSME Int. J. Ser. 3 Vib. Control Eng. Eng. Ind. 1992, 35, 223–228. [Google Scholar] [CrossRef]
- Nagaya, K.; Hano, Y.; Suda, A. Silencer consisting of two-stage Helmholtz resonator with auto-tuning control. J. Acoust. Soc. Am. 2001, 110, 289–295. [Google Scholar] [CrossRef]
- Akl, W.; Baz, A. Analysis and experimental demonstration of an active acoustic metamaterial cell. J. Appl. Phys. 2012, 111, 044505. [Google Scholar] [CrossRef]
- Sharp, B.H.; Gurovich, Y.A.; Albee, W.W. Status of Low-Frequency Aircraft Noise Research and Mitigation; Wyle Report WR.; Wyle Acoustics Group: Arlington, VA, USA, 2001; pp. 1–21. [Google Scholar]
- Dawson, H. Practical Aspects of the Low Frequency Noise Problem. J. Low Freq. Noise Vib. Act. Control 1982, 1, 28–44. [Google Scholar] [CrossRef]
- Claeys, C.; Deckers, E.; Pluymers, B.; Desmet, W. A lightweight vibro-acoustic metamaterial demonstrator: Numerical and experimental investigation. Mech. Syst. Signal Process. 2016, 70–71, 853–880. [Google Scholar] [CrossRef]
- Hazir, A.G.; Casalino, D. Effect of Temperature Variations on the Acoustic Properties of Engine Liners. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Prydz, R.A.; Wirt, L.S.; Kuntz, H.L.; Pope, L.D. Transmission loss of a multilayer panel with internal tuned Helmholtz resonators. J. Acoust. Soc. Am. 1990, 87, 1597–1602. [Google Scholar] [CrossRef]



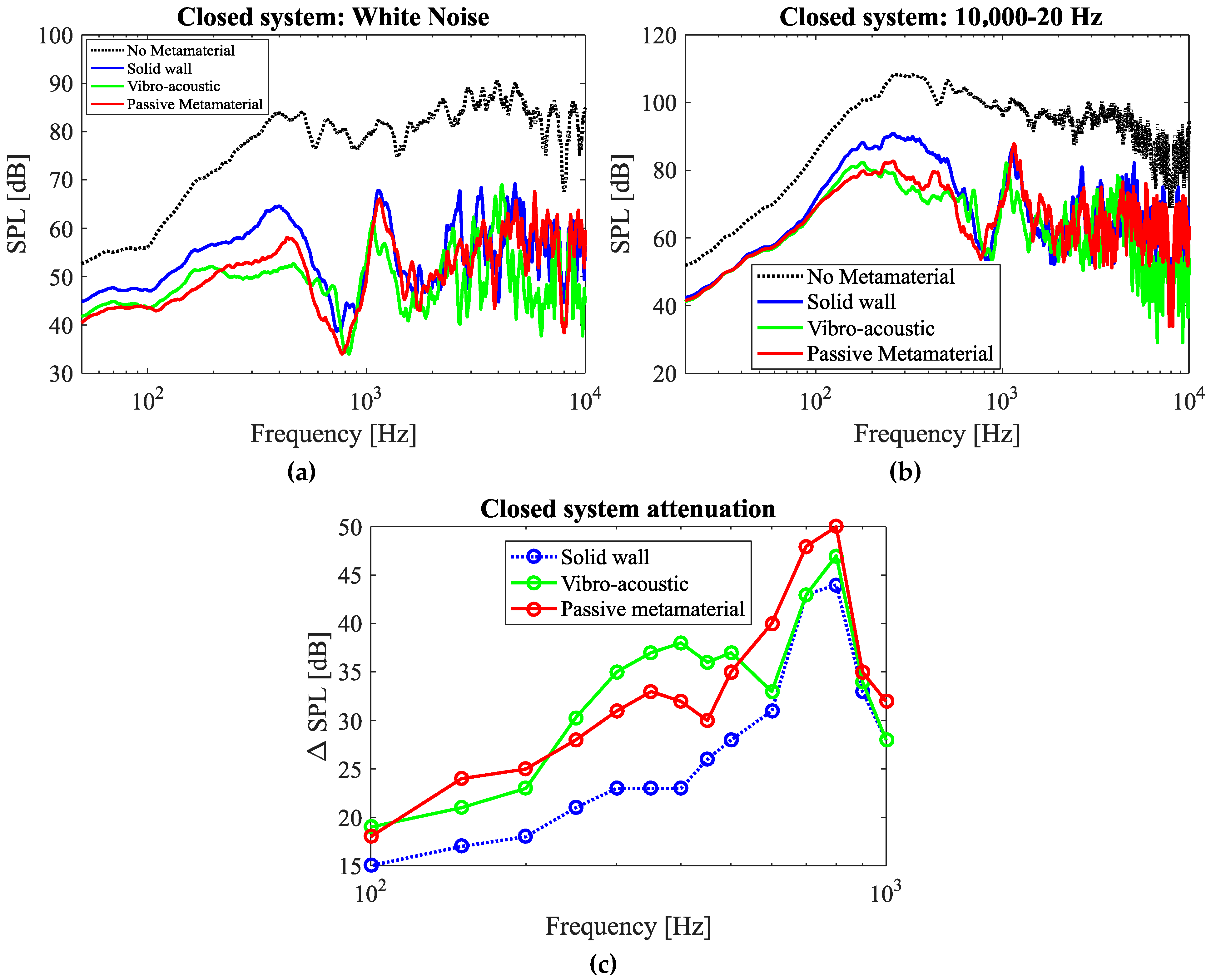
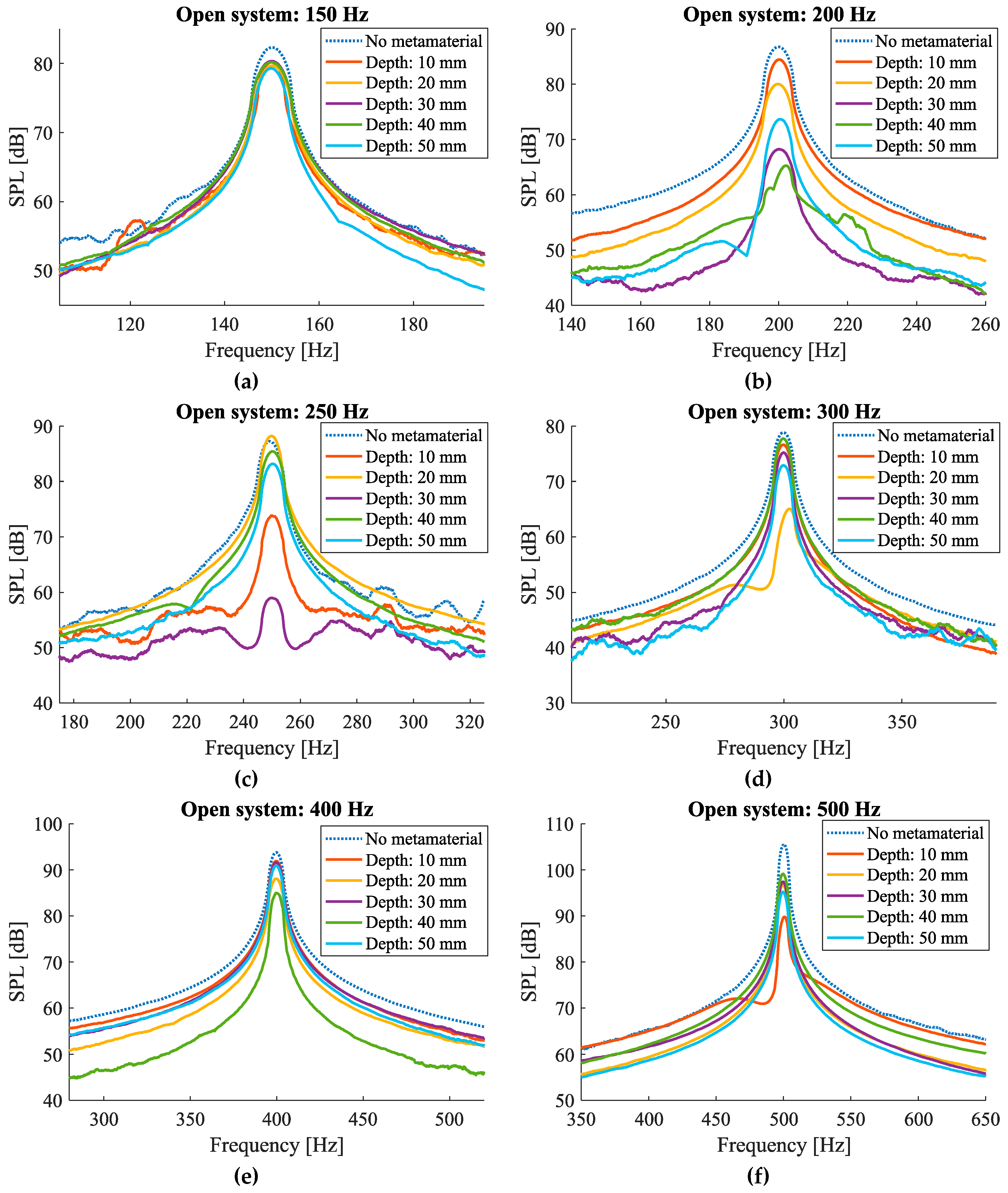
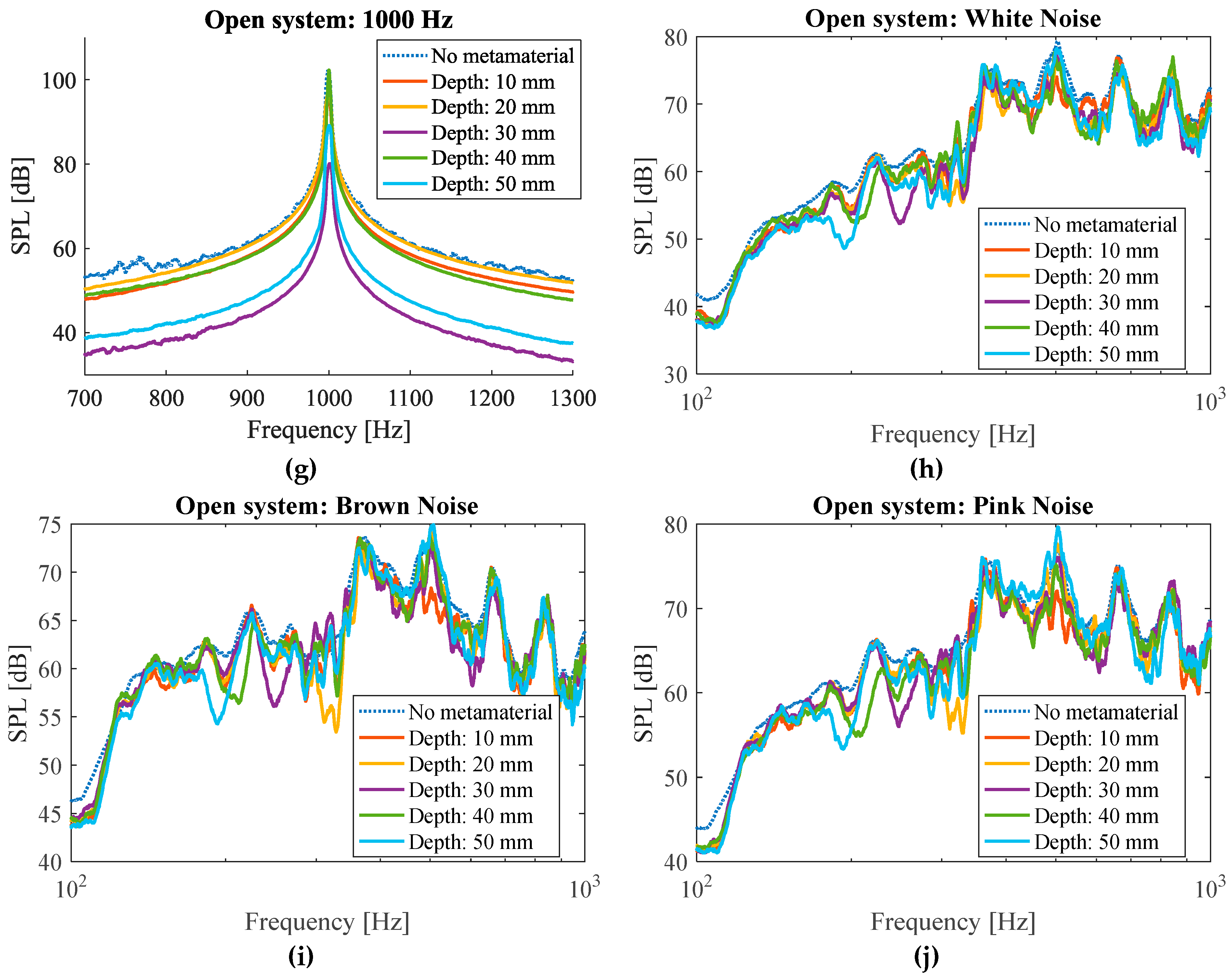
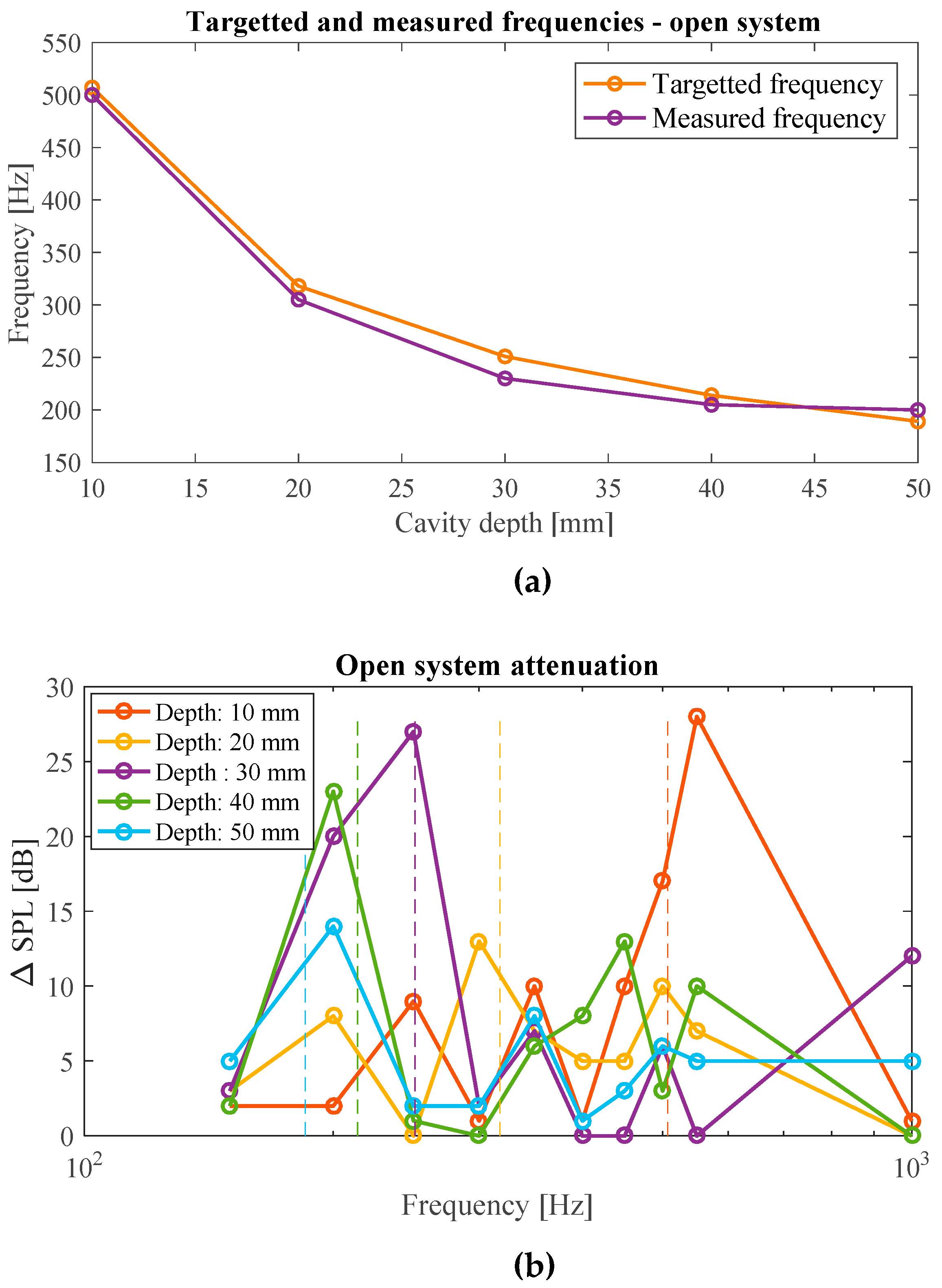

| Parameter | Dimensions |
|---|---|
| Diameter of the neck | 1.2 mm |
| Length of the neck | 14 mm |
| Cross-section of the cavity | 14 × 14 mm2 |
| Lengths of the cavities | 8–42 mm |
| Area of the metamaterial wall | 135 × 135 mm2 |
| Depth of the metamaterial wall | 61 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hedayati, R.; Lakshmanan, S.P. Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise. Materials 2024, 17, 962. https://doi.org/10.3390/ma17040962
Hedayati R, Lakshmanan SP. Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise. Materials. 2024; 17(4):962. https://doi.org/10.3390/ma17040962
Chicago/Turabian StyleHedayati, Reza, and Sandhya P. Lakshmanan. 2024. "Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise" Materials 17, no. 4: 962. https://doi.org/10.3390/ma17040962
APA StyleHedayati, R., & Lakshmanan, S. P. (2024). Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise. Materials, 17(4), 962. https://doi.org/10.3390/ma17040962






