Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites
Abstract
1. Introduction
1.1. SMA-Integrated Composites
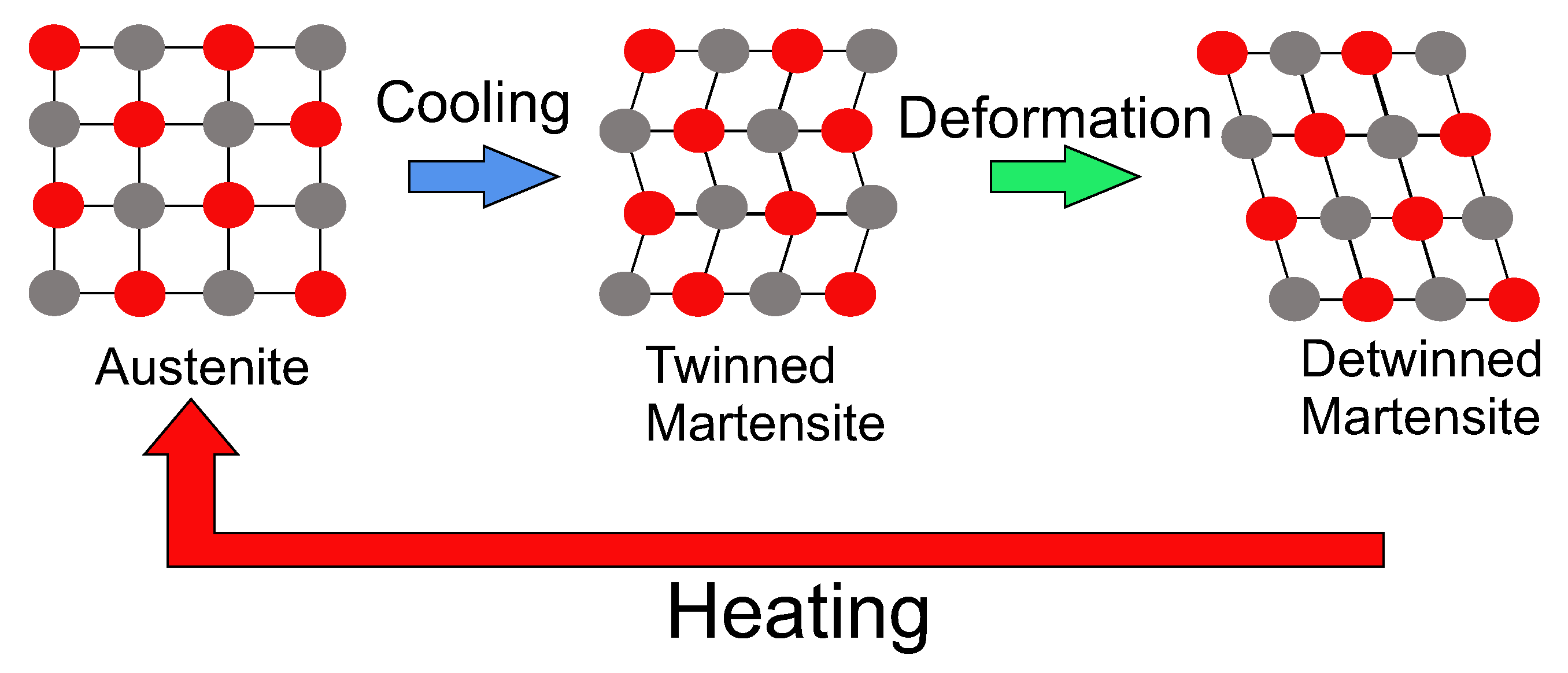
1.2. SMA Material Models
1.3. Objectives
2. Materials and Methods
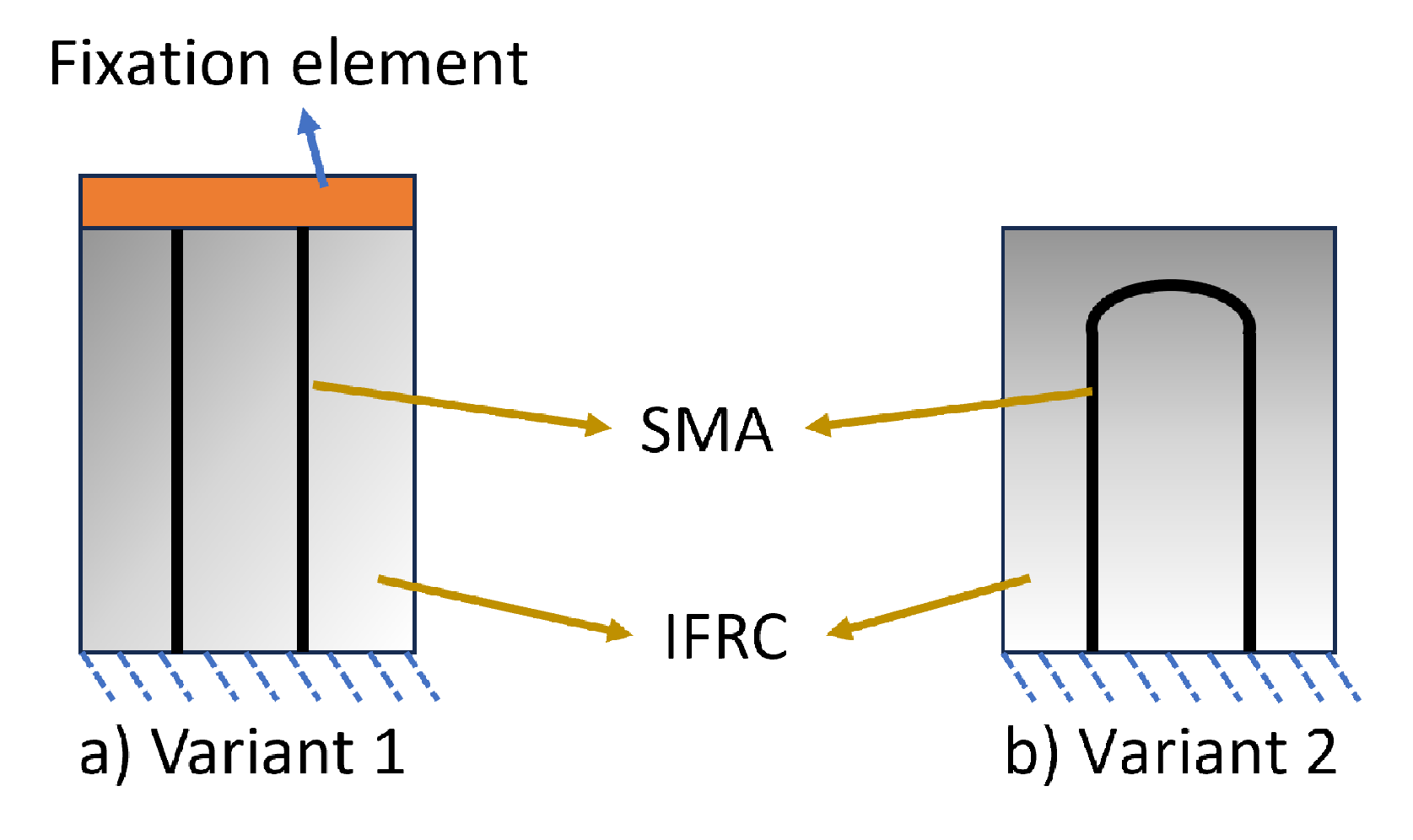
2.1. Materials
2.2. Souza and Auricchio Model
2.3. Woodworth and Kaliske Model
2.4. Material Models for Elastomer and Fibres
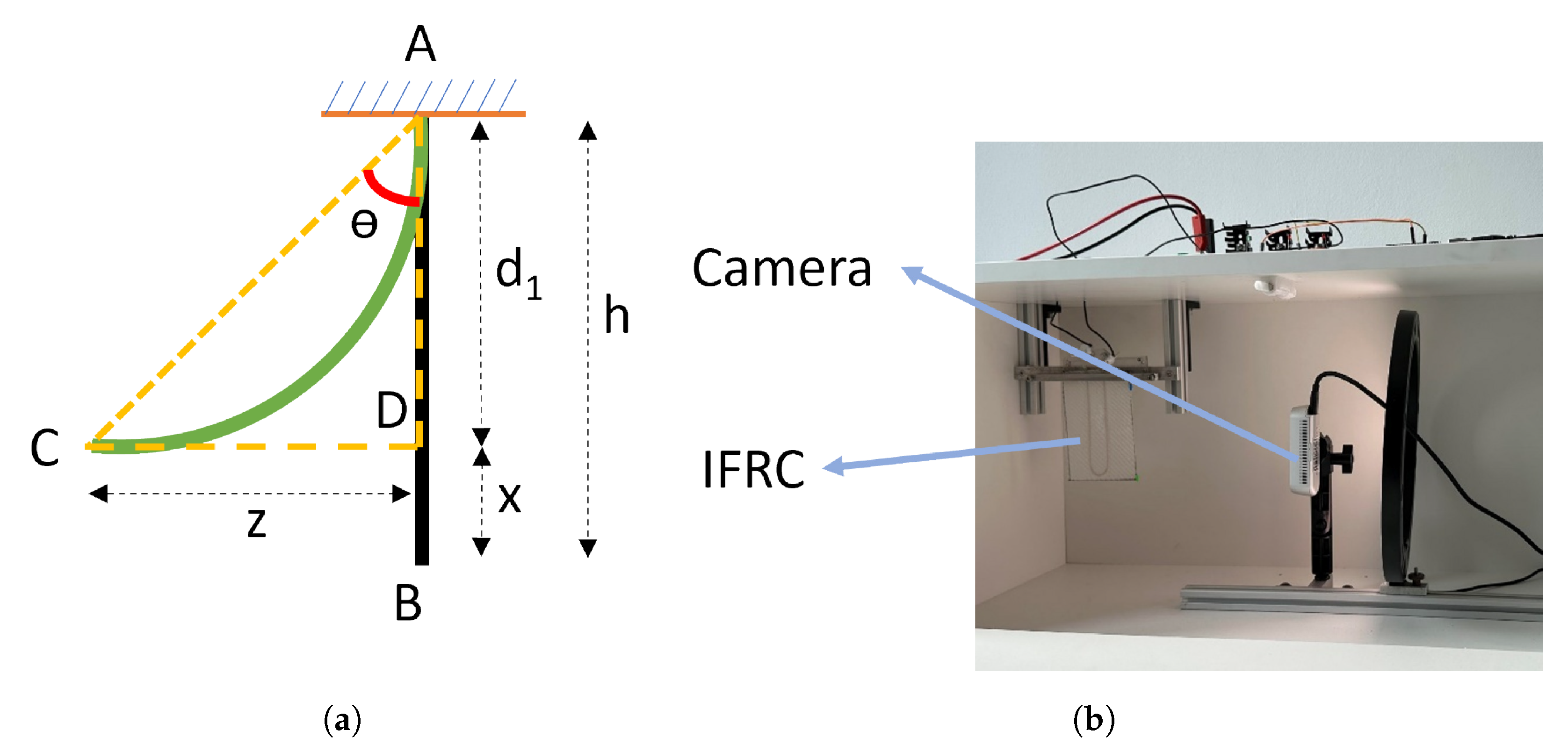
2.5. Modelling Approach
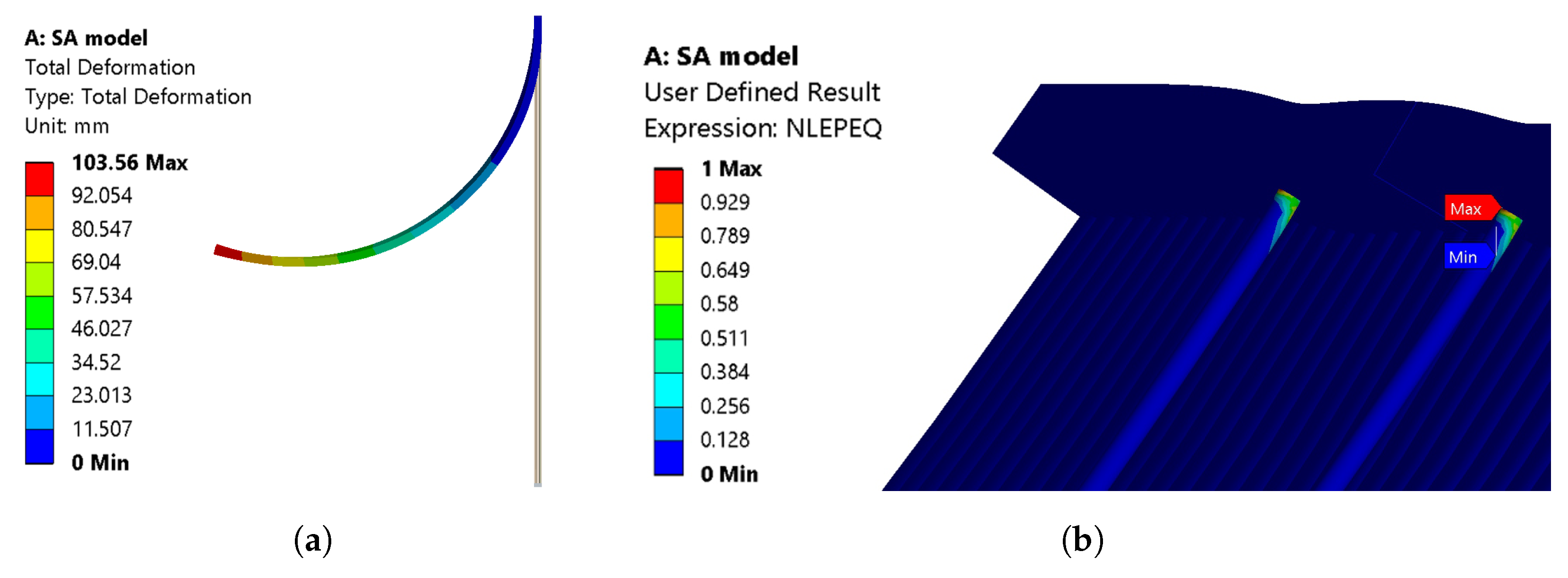
2.5.1. Souza and Auricchio Model
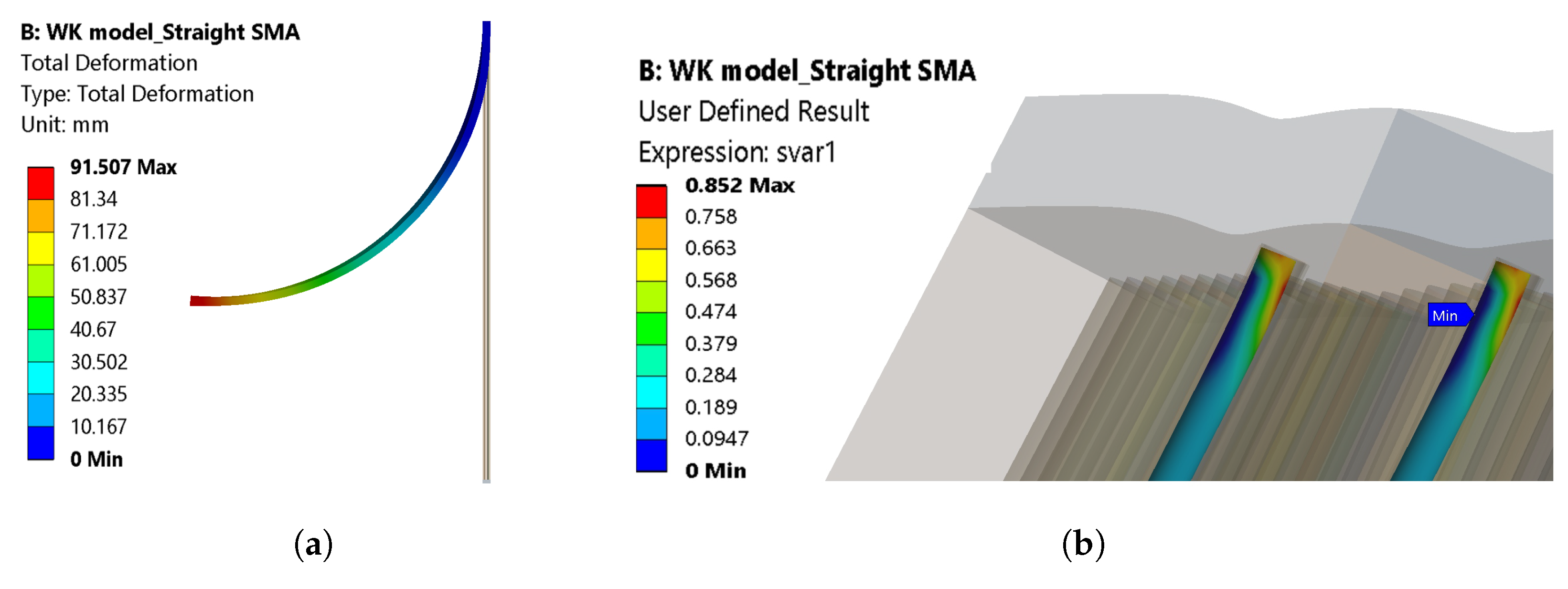
2.5.2. Woodworth and Kaliske Model
- A polytetrafluoroethylene (PTFE) tube with an inner diameter of 0.4 mm and an outer diameter of 0.5 mm was used in the simulation in place of the braided yarns. This assumption is made because the sole purpose of the braid around the SMA is to have indirect contact between the SMA and the elastomer. It is assumed that the effects of braiding and the braiding yarns are negligible.
- Since the targeted deformation bends, the modelling of weft yarns is neglected as they have much less influence during bending deformations [41].
- Cooling and cyclic effects are not considered in order to reduce the computational effort.
- Symmetry boundary condition in the simulation model was considered for both the variants.
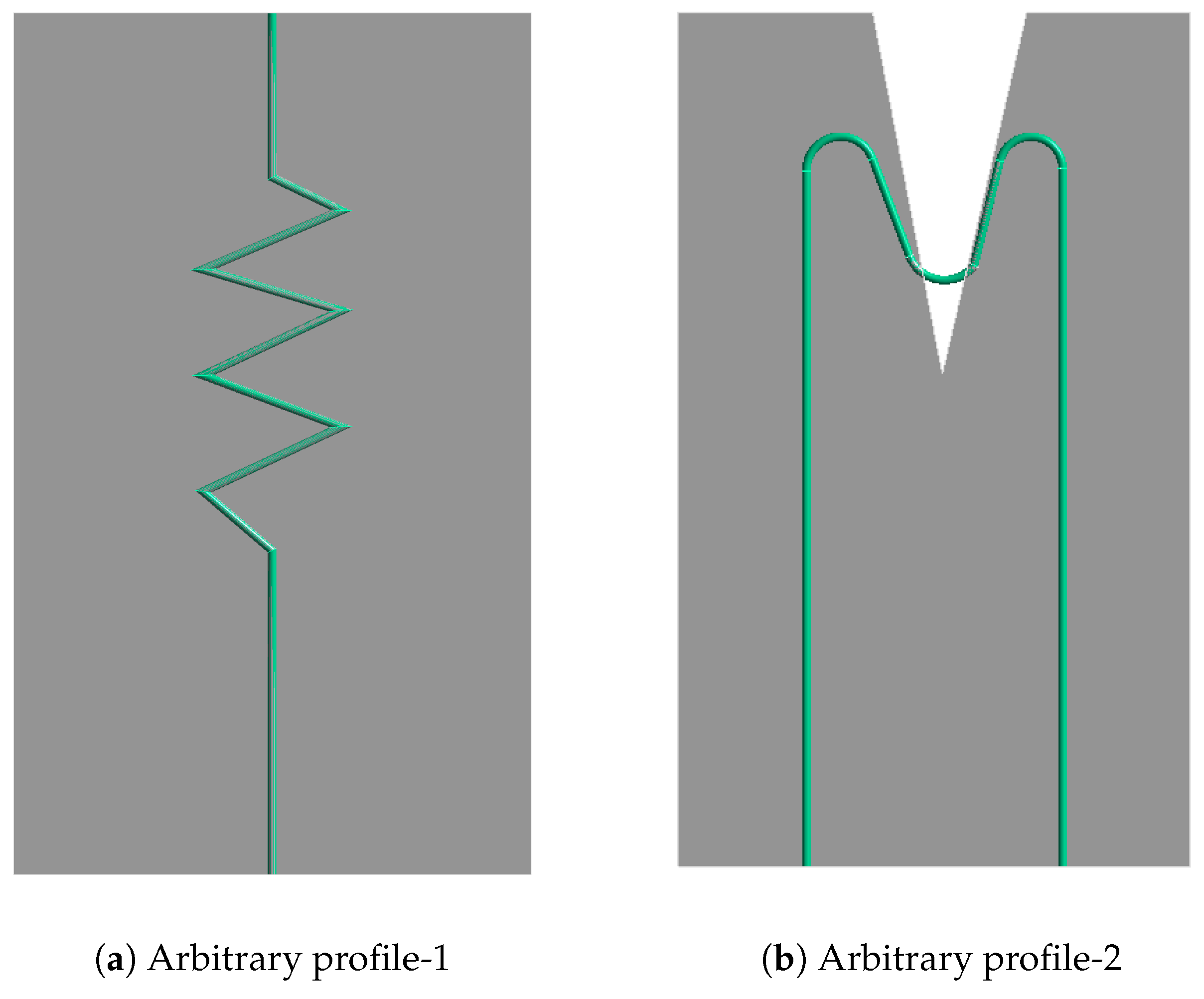
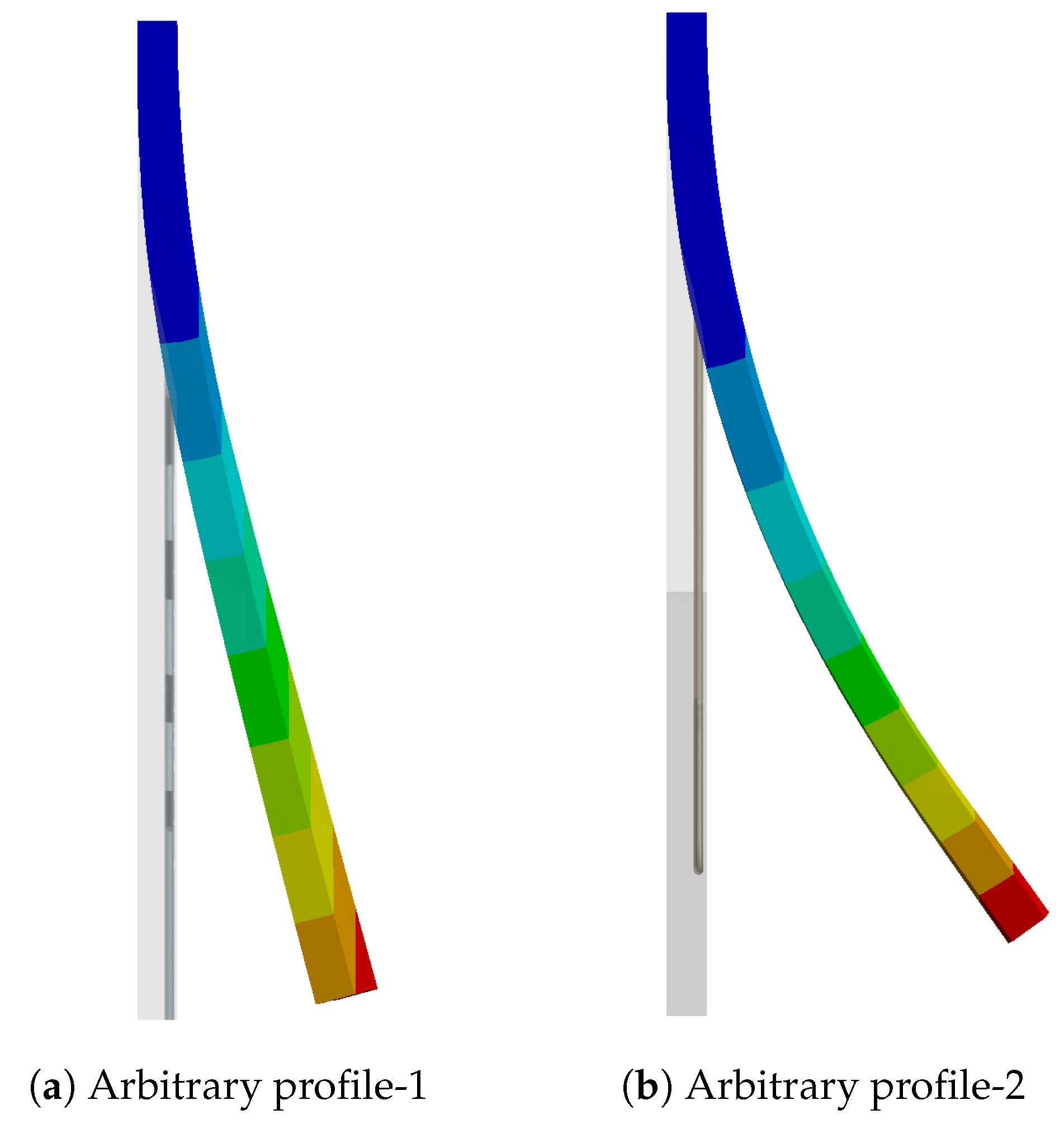
- The “U” bend for the SA model was neglected, as it is not feasible to pre-strain the SMA wire, and although the WK model offers an initial pre-stretch, straight SMA wires were still modelled to validate the WK model approach against that of the SA model.
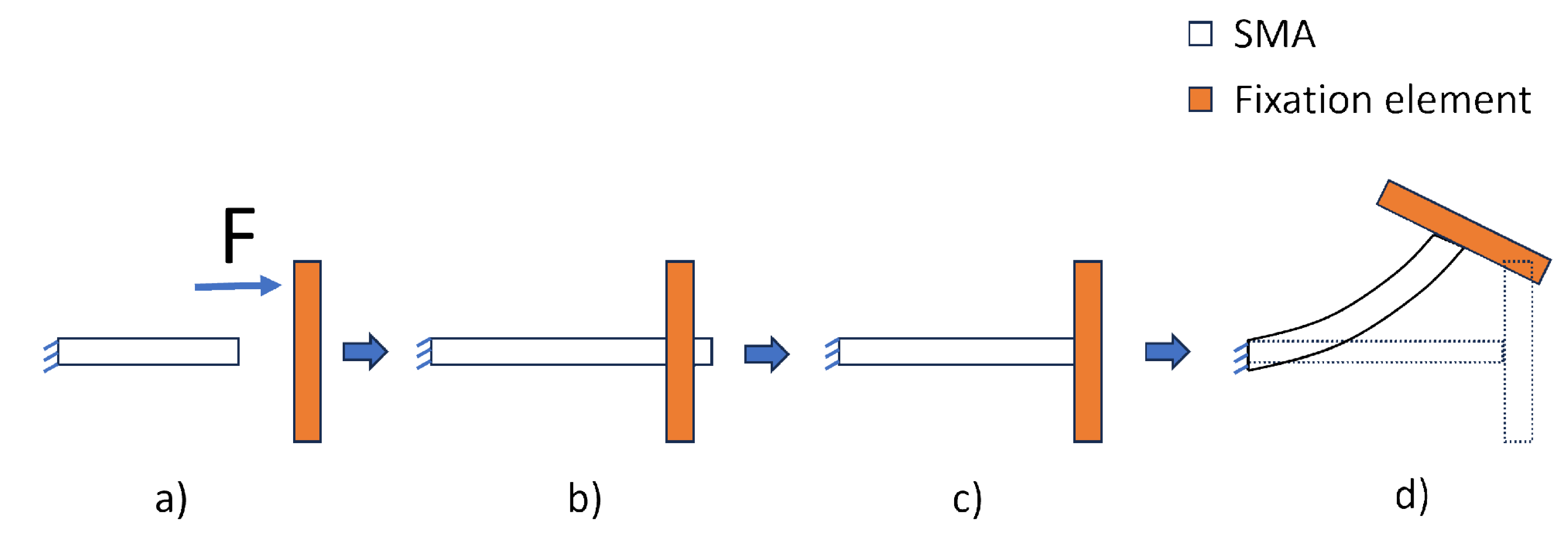
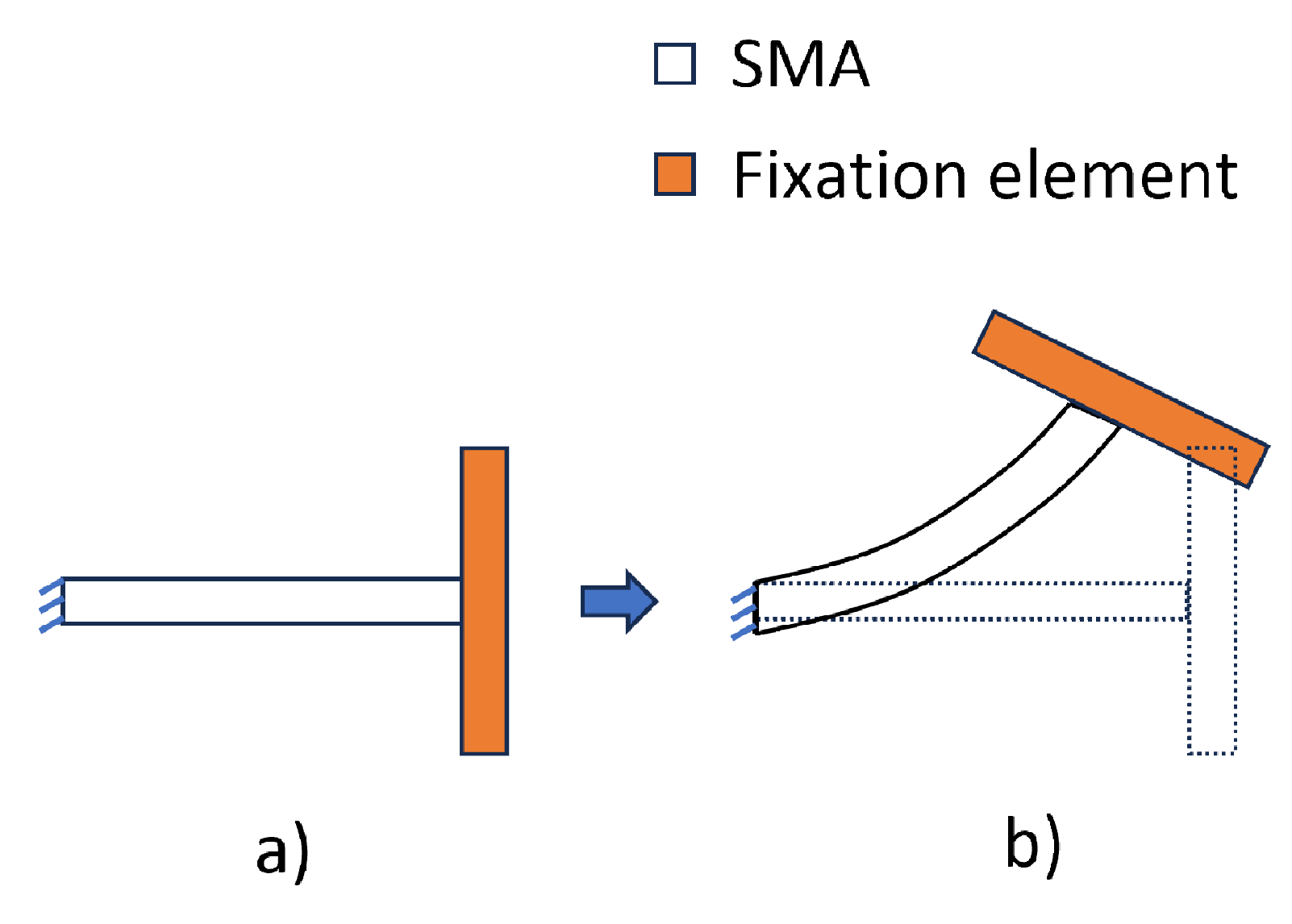
- The free end of the straight SMAs was bonded with a fixation element (polyethylene body), as shown in Figure 7a.
2.6. Experimental Approach—SMA Activation
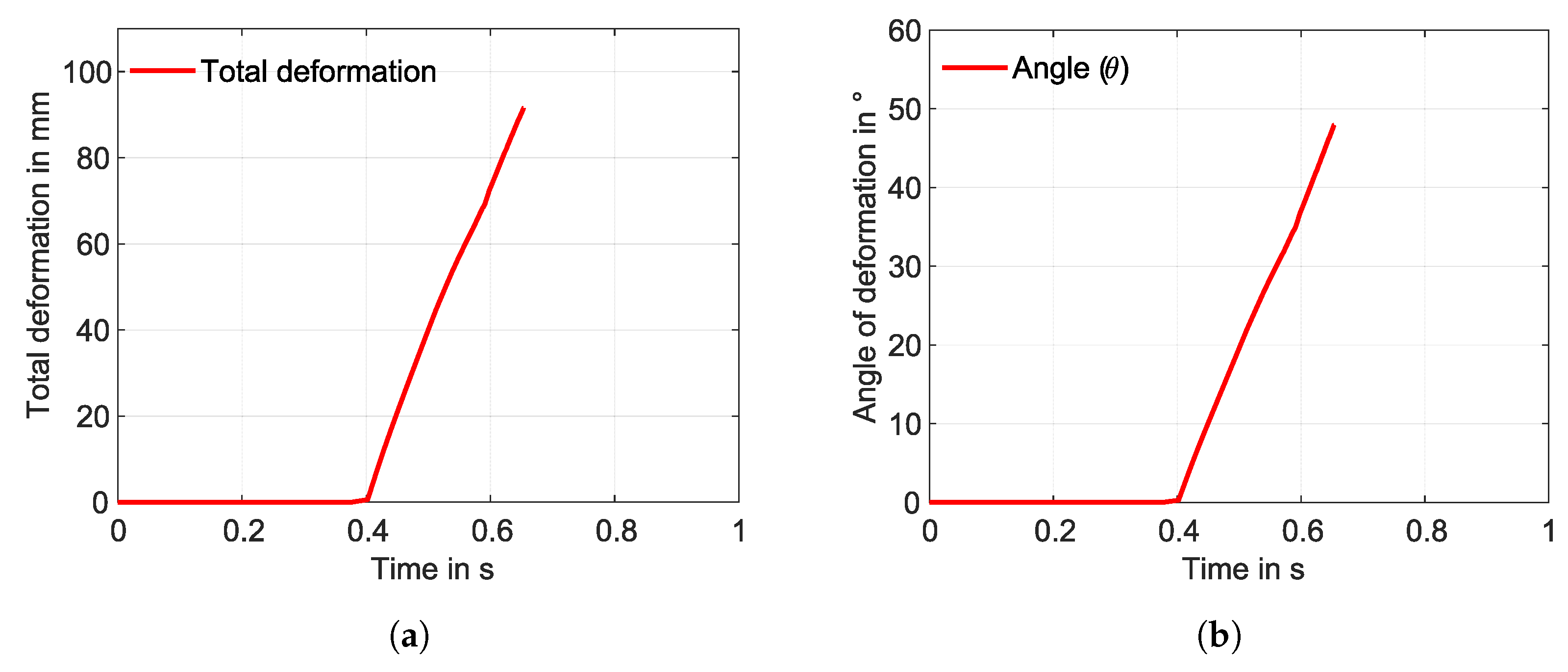
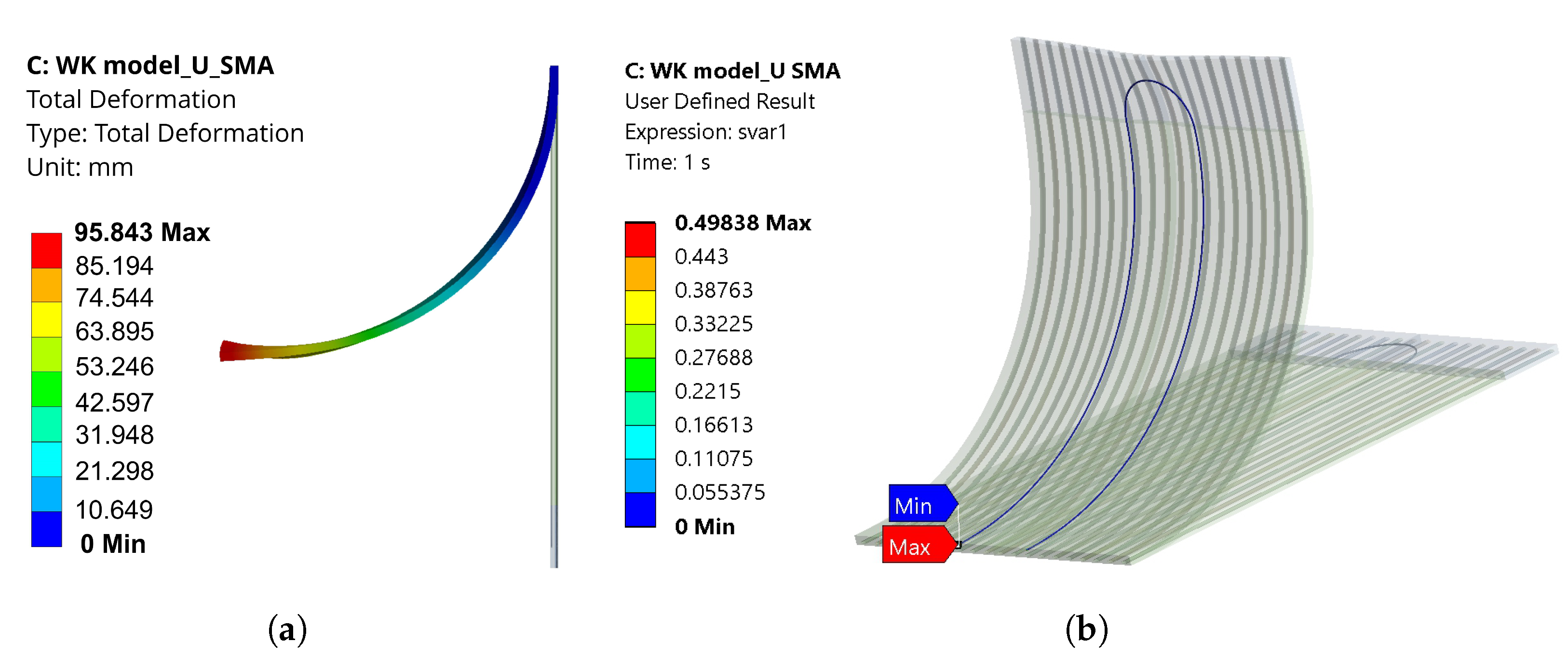
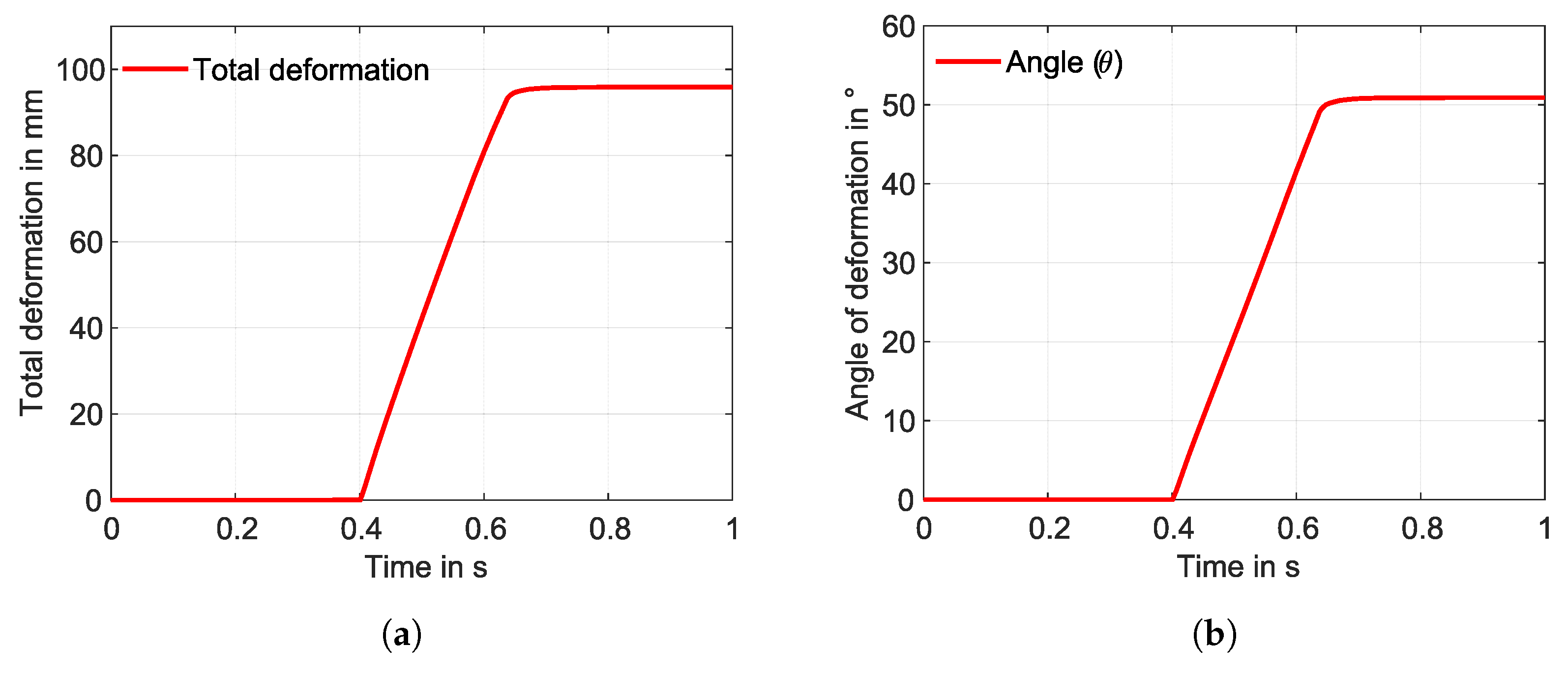
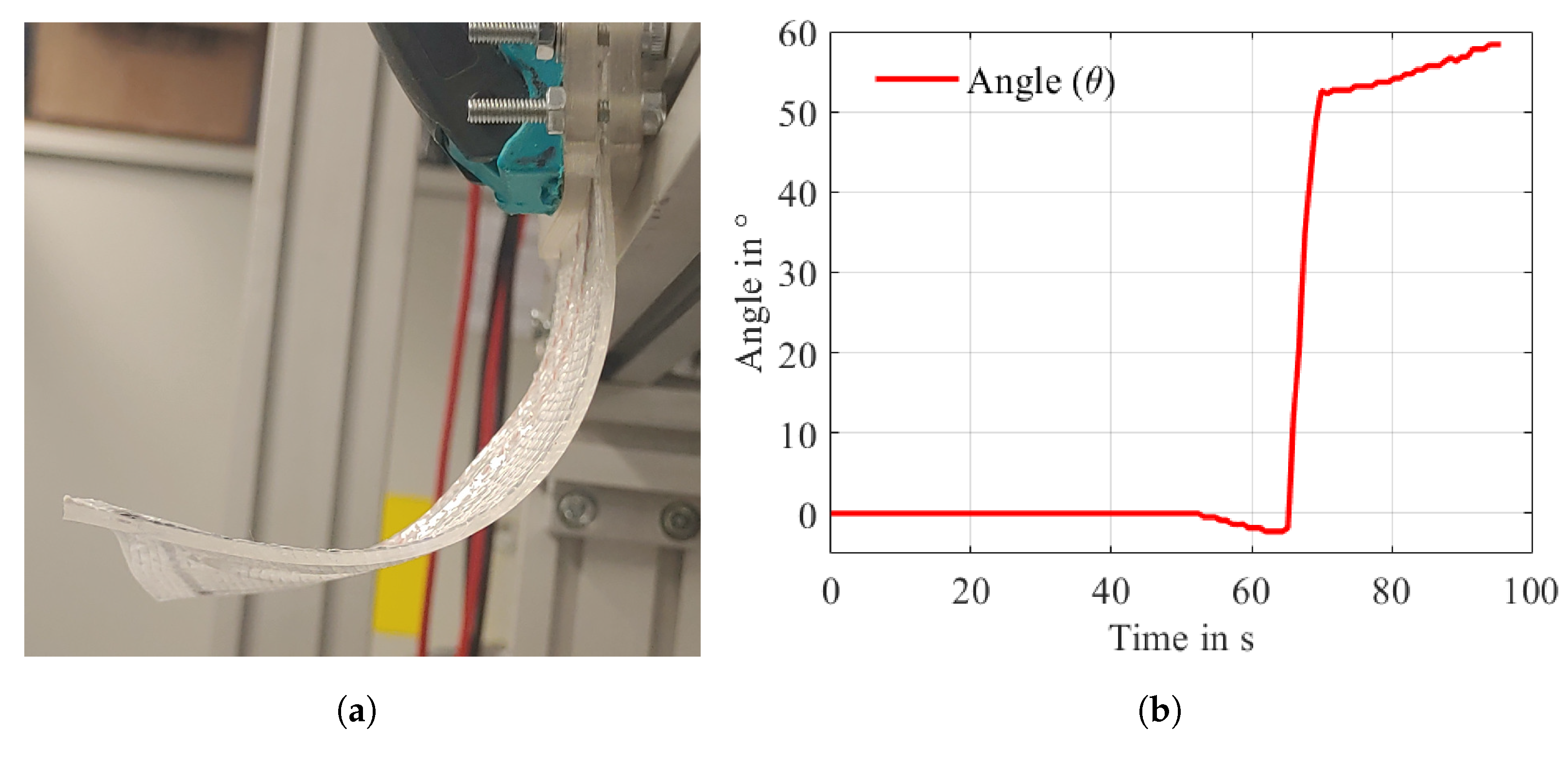
3. Results
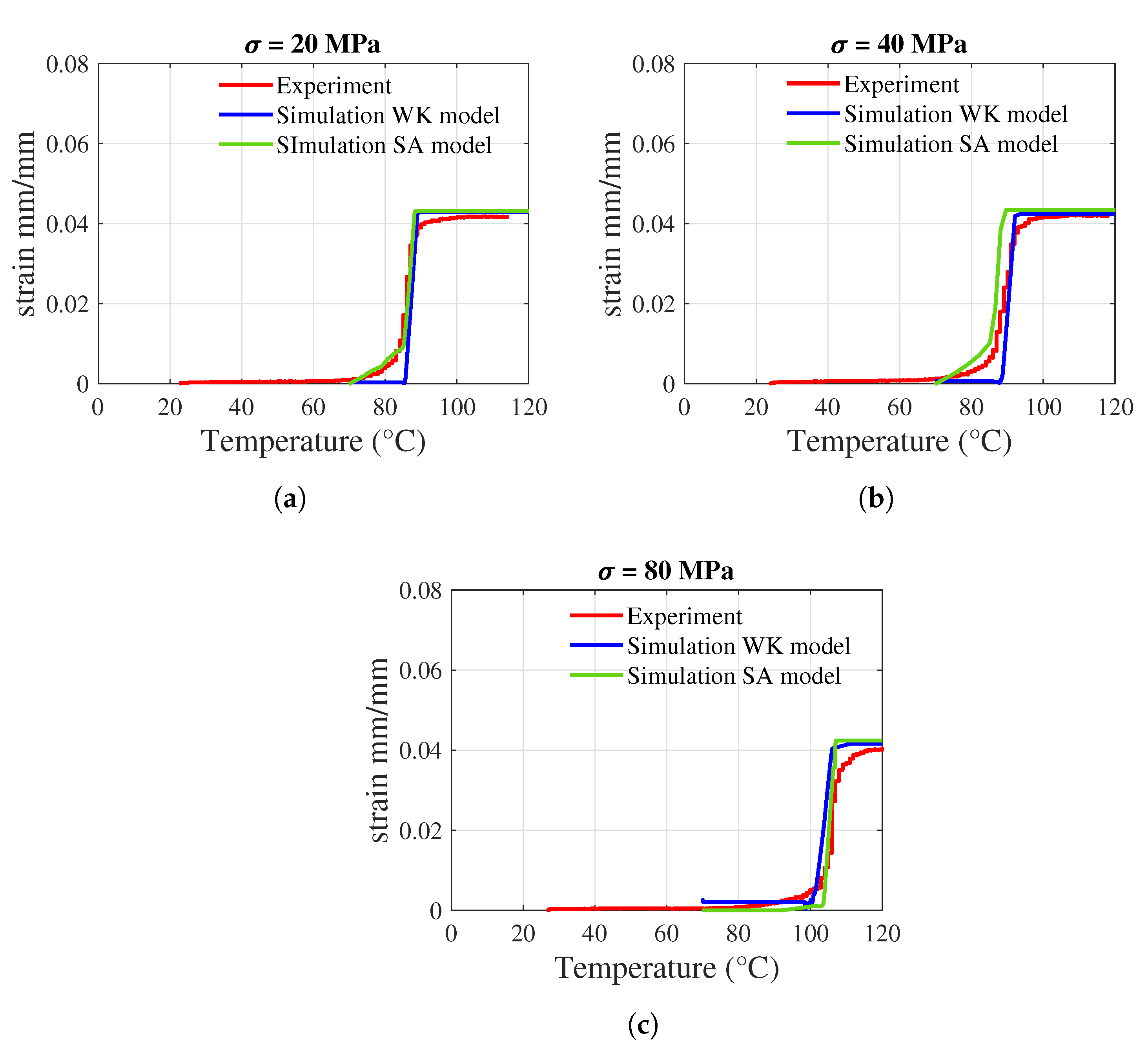
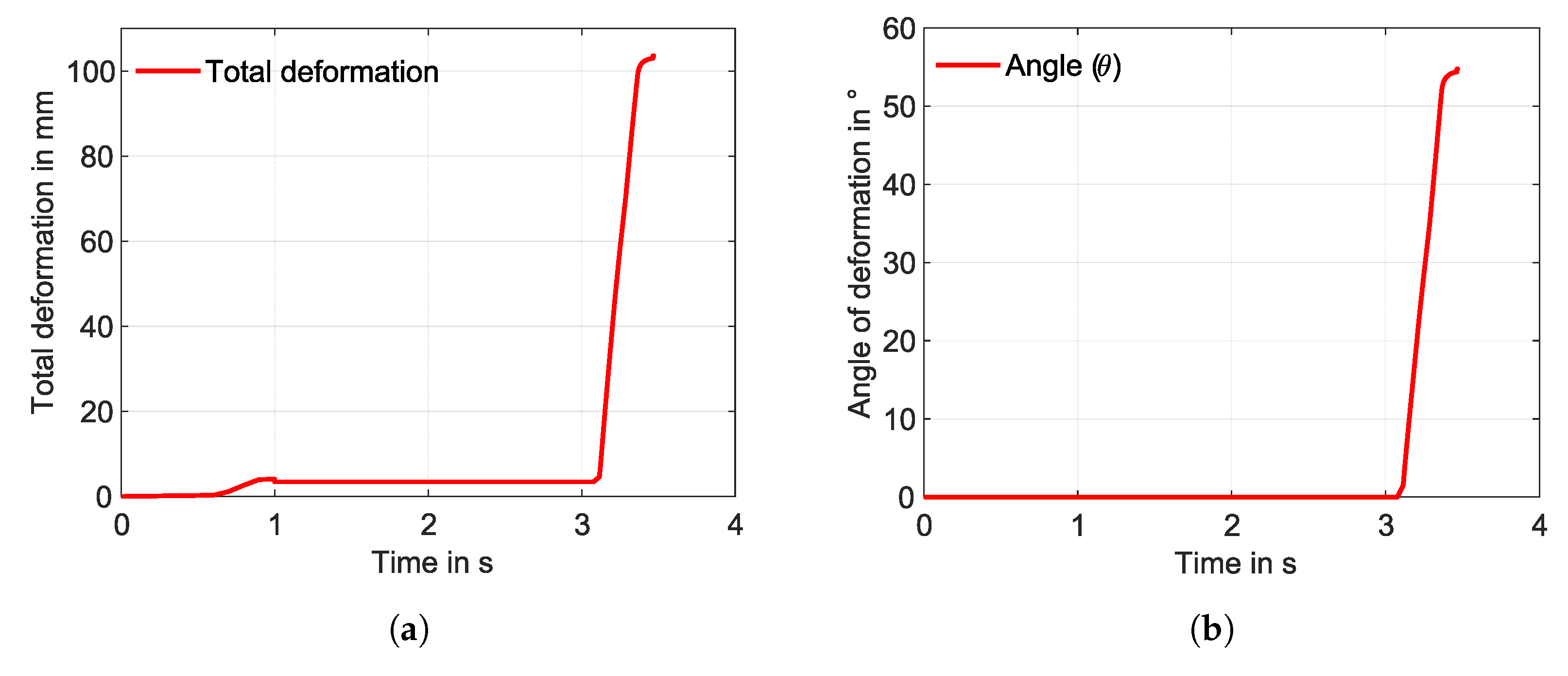
3.1. Simulation
3.2. Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FF | Functional Fatigue |
| GF | Glass Fibres |
| IFRC | Interactive Fibre Rubber Composites |
| MOSFET | Metal-Oxide-Semiconductor Field-Effect Transistor |
| Ni-Ti | Nickel-Titanium Alloy |
| OWSME | One-Way Shape Memory Effect |
| PDMS | Polydimethylsiloxane |
| PTFE | Polytetrafluoroethylene |
| PWM | Pulse Width Modulation |
| SMA | Shape Memory Alloy |
| SA | Souza and Auricchio |
| SME | Shape Memory Effect |
| TWSME | Two-Way Shape Memory Effect |
| TRIP | Transformation Induced Plasticity |
| TFP | Tailored Fibre Placement |
| UPFR | Uni-axial Pre-Strain Free Recovery |
| VARI | Vacuum Assisted Resin Infusion |
| WK | Woodworth and Kaliske |
References
- Hartl, D.J.; Lagoudas, D.C. Aerospace applications of shape memory alloys. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 535–552. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Cianchetti, M. Fundamentals on the Use of Shape Memory Alloys in Soft Robotics. In Interdisciplinary Mechatronics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 10; pp. 227–254. [Google Scholar]
- Petrini, L.; Migliavacca, F. Biomedical Applications of Shape Memory Alloys. J. Metall. 2011, 2011, 15. [Google Scholar] [CrossRef]
- Kumar, S.; Peruvazhuthi, S.; Gopalakrishnan, S. A half a decade timeline of shape memory alloys in modeling and applications. ISSS J. Micro Smart Syst. 2020, 9, 1–32. [Google Scholar] [CrossRef]
- Van Humbeeck, J. Shape Memory Alloys: A Material and a Technology. Adv. Eng. Mater. 2001, 3, 837–850. [Google Scholar] [CrossRef]
- Lagoudas, D. Shape Memory Alloys: Modeling and Engineering Applications; Springer Ebook Collection/Chemistry and Materials Science 2005–2008; Springer: Greer, SC, USA, 2008. [Google Scholar]
- Chaudhari, R.; Vora, J.J.; Parikh, D. A review on applications of nitinol shape memory alloy. In Recent Advances in Mechanical Infrastructure; Springer: Singapore, 2021; pp. 123–132. [Google Scholar]
- Alipour, S.; Taromian, F.; Ghomi, E.R.; Zare, M.; Singh, S.; Ramakrishna, S. Nitinol: From historical milestones to functional properties and biomedical applications. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2022, 236, 1595–1612. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E. Shape Memory Alloys for Aerospace, Recent Developments, and New Applications: A Short Review. Materials 2020, 13, 1856. [Google Scholar] [CrossRef] [PubMed]
- Budholiya, S.; Bhat, A.; Raj, S.A.; Hameed Sultan, M.T.; Md Shah, A.U.; A. Basri, A. State of the Art Review about Bio-Inspired Design and Applications: An Aerospace Perspective. Appl. Sci. 2021, 11, 5054. [Google Scholar] [CrossRef]
- Kim, H.I.; Han, M.W.; Song, S.H.; Ahn, S.H. Soft morphing hand driven by SMA tendon wire. Compos. Part B Eng. 2016, 105, 138–148. [Google Scholar] [CrossRef]
- Liu, C.; Liao, W. A Snake Robot Using Shape Memory Alloys. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shenyang, China, 22–26 August 2004; pp. 601–605. [Google Scholar]
- Sugiyama, Y.; Hirai, S. Crawling and Jumping by a Deformable Robot. Int. J. Robot. Res. 2006, 25, 603–620. [Google Scholar] [CrossRef]
- Hao, L.H.; Park, S.H.; Park, J.O. Shape Memory Alloy based Flower Robot. In Proceedings of the 39th International Symposium on Robotics, Seoul, Republic of Korea, 15–17 October 2008; p. 7. [Google Scholar]
- Wang, Z.; Hang, G.; Li, J.; Wang, Y.; Xiao, K. A micro-robot fish with embedded SMA wire actuated flexible biomimetic fin. Sens. Actuators A Phys. 2008, 144, 354–360. [Google Scholar] [CrossRef]
- Chen, X.; Shigemune, H.; Sawada, H. An Untethered Bionic Robotic Fish Using SMA Actuators. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; pp. 1768–1773. [Google Scholar]
- Coral, W.; Rossi, C.; Curet, O.M.; Castro, D. Design and assessment of a flexible fish robot actuated by shape memory alloys. Bioinspiration Biomimetics 2018, 13, 056009. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Wagner, R.; Liu, S.; He, Q.; Li, T.; Pan, W.; Feng, Y.; Feng, H.; Meng, Q.; Zou, X.; et al. Locomotion of an untethered, worm-inspired soft robot driven by a shape-memory alloy skeleton. Sci. Rep. 2022, 12, 12392. [Google Scholar] [CrossRef] [PubMed]
- Maeno, T.; Hino, T. Miniature five-fingered robot hand driven by shape memory alloy actuators. In Proceedings of the IASTED International Conference on Robotics and Applications, Honolulu, HI, USA, 14–16 August 2006; pp. 174–179. [Google Scholar]
- Lee, J.H.; Chung, Y.; Rodrigue, H. Long Shape Memory Alloy Tendon-based Soft Robotic Actuators and Implementation as a Soft Gripper. Sci. Rep. 2019, 9, 11251. [Google Scholar] [CrossRef] [PubMed]
- Frémond, M.; Rocca, E. A model for shape memory alloys with the possibility of voids. Discret. Contin. Dyn. Syst. 2009, 27, 1633–1659. [Google Scholar] [CrossRef]
- Colli, P.; Frémond, M.; Rocca, E.; Shirakawa, K. Attractors for a Three-Dimensional ThermoMechanical Model of Shape Memory Alloys. Chin. Ann. Math. Ser. B 2006, 27, 683–700. [Google Scholar] [CrossRef]
- Falk, F.; Konopka, P. Three-dimensional Landau theory describing the martensitic phase transformation of shape-memory alloys. J. Phys. Condens. Matter 1990, 2, 61. [Google Scholar] [CrossRef]
- Colli, P.; Sprekels, J. Positivity of temperature in the general Frémond model for shape memory alloys. Contin. Mech. Thermodyn. 1993, 5, 255–264. [Google Scholar] [CrossRef]
- Brinson, L. One-Dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-Constant Material Functions and Redefined Martensite Internal Variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Dunić, V.; Busarac, N.; Slavković, V.; Slavković, R. Thermo-mechanical numerical analysis of stent unit cell. In Proceedings of the 2015 IEEE 15th International Conference on Bioinformatics and Bioengineering (BIBE), Belgrade, Serbia, 2–4 November 2015; pp. 1–5. [Google Scholar]
- Gédouin, P.A.; Pino, L.; Bourgeot, J.M.; Delaleau, E.; Chirani, S.A.; Calloch, S. Thermo-mechanical modelling of spring-based SMA actuators. In Proceedings of the 2016 11th France-Japan & 9th Europe-Asia Congress on Mechatronics (MECATRONICS)/17th International Conference on Research and Education in Mechatronics (REM), Compiegne, France, 15–17 June 2016; pp. 373–378. [Google Scholar]
- Sedlák, P.; Frost, M.; Benešová, B.; Ben Zineb, T.; Šittner, P. Thermomechanical model for NiTi-based shape memory alloys including R-phase and material anisotropy under multi-axial loadings. Int. J. Plast. 2012, 39, 132–151. [Google Scholar] [CrossRef]
- Choudhry, S.; Yoon, J.W. A General Thermo-Mechanical Shape Memory Alloy Model: Formulation and Applications. AIP Conf. Proc. 2004, 712, 1589–1594. [Google Scholar]
- Auricchio, F.; Petrini, L. Improvements and algorithmical considerations on a recent three-dimensional model describing stress-induced solid phase transformations. Int. J. Numer. Methods Eng. 2002, 55, 1255–1284. [Google Scholar] [CrossRef]
- Souza, A.C.; Mamiya, E.N.; Zouain, N. Three-dimensional model for solids undergoing stress-induced phase transformations. Eur. J. Mech.-A/Solids 1998, 17, 789–806. [Google Scholar] [CrossRef]
- Grandi, D.; Stefanelli, U. The Souza-Auricchio model for shape-memory alloys. Discret. Contin. Dyn. Syst.-Ser. S 2014, 8, 723–747. [Google Scholar] [CrossRef]
- Woodworth, L.A.; Kaliske, M. A temperature dependent constitutive model for functional fatigue in shape memory alloys. Mech. Mater. 2022, 165, 104126. [Google Scholar] [CrossRef]
- Woodworth, L.A.; Lohse, F.; Kopelmann, K.; Cherif, C.; Kaliske, M. Development of a constitutive model considering functional fatigue and pre-stretch in shape memory alloy wires. Int. J. Solids Struct. 2022, 234–235, 111242. [Google Scholar] [CrossRef]
- Mizzi, L.; Spaggiari, A.; Dragoni, E. Design of shape memory alloy sandwich actuators: An analytical and numerical modelling approach. Smart Mater. Struct. 2020, 29, 085027. [Google Scholar] [CrossRef]
- Song, J.J.; Chen, Q.; Naguib, H.E. Constitutive modeling and experimental validation of the thermo-mechanical response of a shape memory composite containing shape memory alloy fibers and shape memory polymer matrix. J. Intell. Mater. Syst. Struct. 2016, 27, 625–641. [Google Scholar] [CrossRef]
- Wang, X. Shape memory alloy volume fraction of pre-stretched shape memory alloy wire-reinforced composites for structural damage repair. Smart Mater. Struct. 2002, 11, 590. [Google Scholar] [CrossRef]
- Cherif, C. Textile Materials for Lightweight Constructions; Technol Methods Mater Proper; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kyosev, Y. Braiding Technology for Textiles: Principles, Design and Processes; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Lohse, F.; Kopelmann, K.; Grellmann, H.; Ashir, M.; Gereke, T.; Häntzsche, E.; Sennewald, C.; Cherif, C. Experimental and Numerical Analysis of the Deformation Behavior of Adaptive Fiber-Rubber Composites with Integrated Shape Memory Alloys. Materials 2022, 15, 582. [Google Scholar] [CrossRef] [PubMed]
- Mersch, J.; Bruns, M.; Nocke, A.; Cherif, C.; Gerlach, G. High-Displacement, Fiber-Reinforced Shape Memory Alloy Soft Actuator with Integrated Sensors and Its Equivalent Network Model. Adv. Intell. Syst. 2021, 3, 2000221. [Google Scholar] [CrossRef]
- Simon, J.; Hamila, N.; Binetruy, C.; Comas-Cardona, S.; Masseteau, B. Design and numerical modelling strategy to form Tailored Fibre Placement preforms: Application to the tetrahedral part with orthotropic final configuration. Compos. Part A Appl. Sci. Manuf. 2022, 158, 106952. [Google Scholar] [CrossRef]
- Annadata, A.; Endesfelder, A.; Koenigsdorff, M.; Mersch, J.; Gereke, T.; Zimmermann, M.; Cherif, C. Evaluation of Bend-Twist Coupling in Shape Memory Alloy Integrated Fiber Rubber Composites. In Proceedings of the 9th ECCOMAS Thematic Conference on the Mechanical Response of Composites (COMPOSITES 2023), Trapani, Italy, 12–14 September 2023. [Google Scholar]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Lohse, F.; Annadata, A.R.; Häntzsche, E.; Gereke, T.; Trümper, W.; Cherif, C. Hinged Adaptive Fiber-Rubber Composites Driven by Shape Memory Alloys—Development and Simulation. Materials 2022, 15, 3830. [Google Scholar] [CrossRef] [PubMed]
- Stachiv, I.; Alarcon, E.; Lamac, M. Shape Memory Alloys and Polymers for MEMS/NEMS Applications: Review on Recent Findings and Challenges in Design, Preparation, and Characterization. Metals 2021, 11, 28. [Google Scholar] [CrossRef]
- Coda, A.; Cadelli, A.; Manjeri, M.; Sczerzenie, F. Uniaxial Pre-strain and Free Recovery (UPFR) as a Flexible Technique for Nitinol Characterization. Shape Mem. Superelasticity 2015, 2, 86–94. [Google Scholar]



| Model Parameter | Units | Value |
|---|---|---|
| Pa | 770,623.97 | |
| Pa | −386,308.55 | |
| Pa | 196,852.40 | |
| 0 | ||
| 0 | ||
| 0 |
| Model Parameter | Units | Value |
|---|---|---|
| elastic modulus in x | GPa | 5 |
| elastic modulus in y | GPa | |
| elastic modulus in z | GPa | |
| Poisson’s ratio (xy) | - | 0.22 |
| Poisson’s ratio (yz) | - | 0.22 |
| Poisson’s ratio (xz) | - | 0.22 |
| shear modulus (xy) | GPa | 0.04 |
| shear modulus (yz) | GPa | 0.02 |
| shear modulus (xz) | GPa | 0.04 |
| Model Parameter | Units | Value at Room Temperature |
|---|---|---|
| austenite modulus | MPa | 25,000 |
| Poisson’s ratio | - | |
| hardening parameter | MPa | 610 |
| reference temperature | °C | 70 |
| elastic limit | MPa | 52 |
| temperature scaling parameter | MPa/°C | 7 |
| maximum transformation strain | % | 0.0355 |
| martensite modulus | MPa | 20,000 |
| load dependency parameter | - | 0 |
| Model Parameter | Units | Value at Room Temperature |
|---|---|---|
| shear modulus of austenite | MPa | |
| bulk modulus | MPa | 20,833 |
| hardening parameter | MPa | 610 |
| reference temperature | °C | 70 |
| elastic limit | MPa | 52 |
| temperature scaling parameter | MPa/°C | 7 |
| maximum transformation strain | % | |
| shear modulus of martensite | MPa | |
| initial martensite volume fraction | - | |
| direction of pre-stretch (x, y, z) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annadata, A.R.; Acevedo-Velazquez, A.I.; Woodworth, L.A.; Gereke, T.; Kaliske, M.; Röbenack, K.; Cherif, C. Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites. Materials 2024, 17, 1163. https://doi.org/10.3390/ma17051163
Annadata AR, Acevedo-Velazquez AI, Woodworth LA, Gereke T, Kaliske M, Röbenack K, Cherif C. Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites. Materials. 2024; 17(5):1163. https://doi.org/10.3390/ma17051163
Chicago/Turabian StyleAnnadata, Achyuth Ram, Aline Iobana Acevedo-Velazquez, Lucas A. Woodworth, Thomas Gereke, Michael Kaliske, Klaus Röbenack, and Chokri Cherif. 2024. "Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites" Materials 17, no. 5: 1163. https://doi.org/10.3390/ma17051163
APA StyleAnnadata, A. R., Acevedo-Velazquez, A. I., Woodworth, L. A., Gereke, T., Kaliske, M., Röbenack, K., & Cherif, C. (2024). Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites. Materials, 17(5), 1163. https://doi.org/10.3390/ma17051163








