Analysis of the Dielectric Properties of Alkali-Free Aluminoborosilicate Glasses by Considering the Contributions of Electronic and Ionic Polarizabilities in the GHz Frequency Range
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of Alkali-Free Aluminoborosilicate Glasses
2.2. Characterization of Alkali-Free Aluminoborosilicate Glasses
3. Results
3.1. Physical Properties
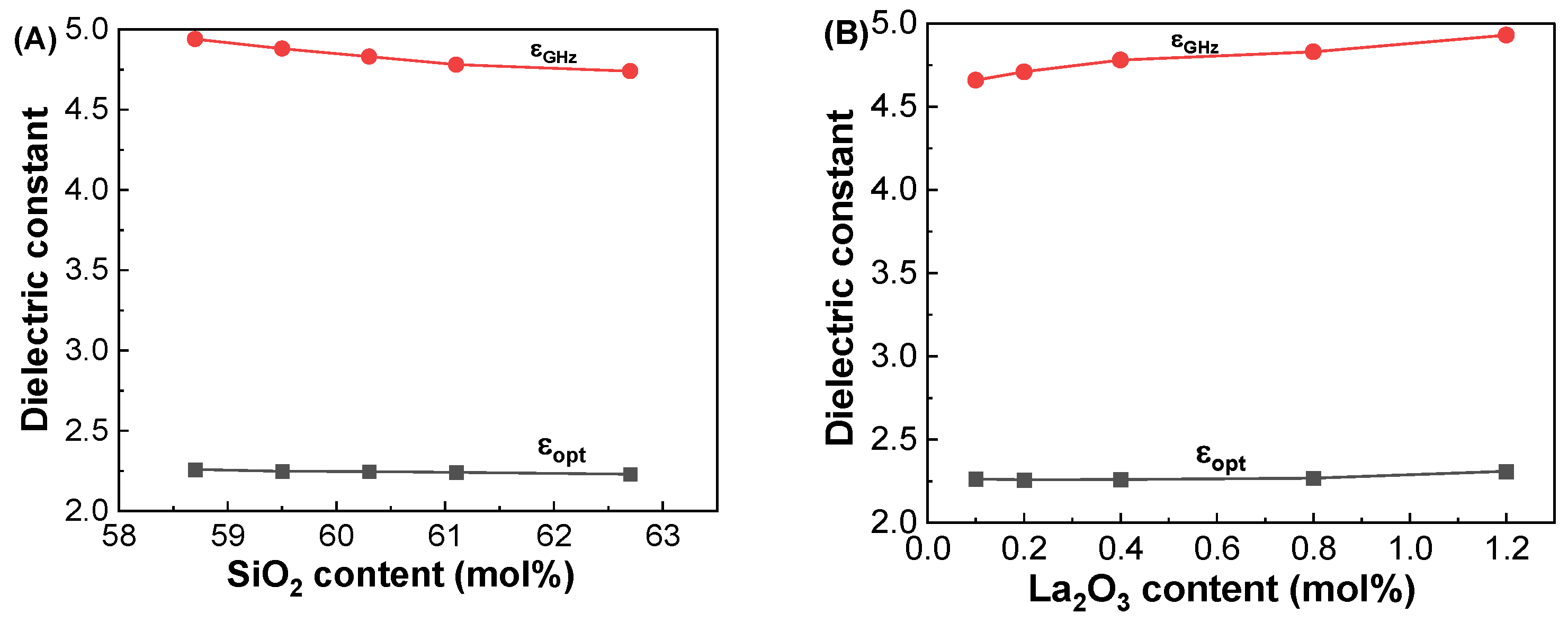
3.2. Dielectric and Polarizability Properties at GHz Frequencies
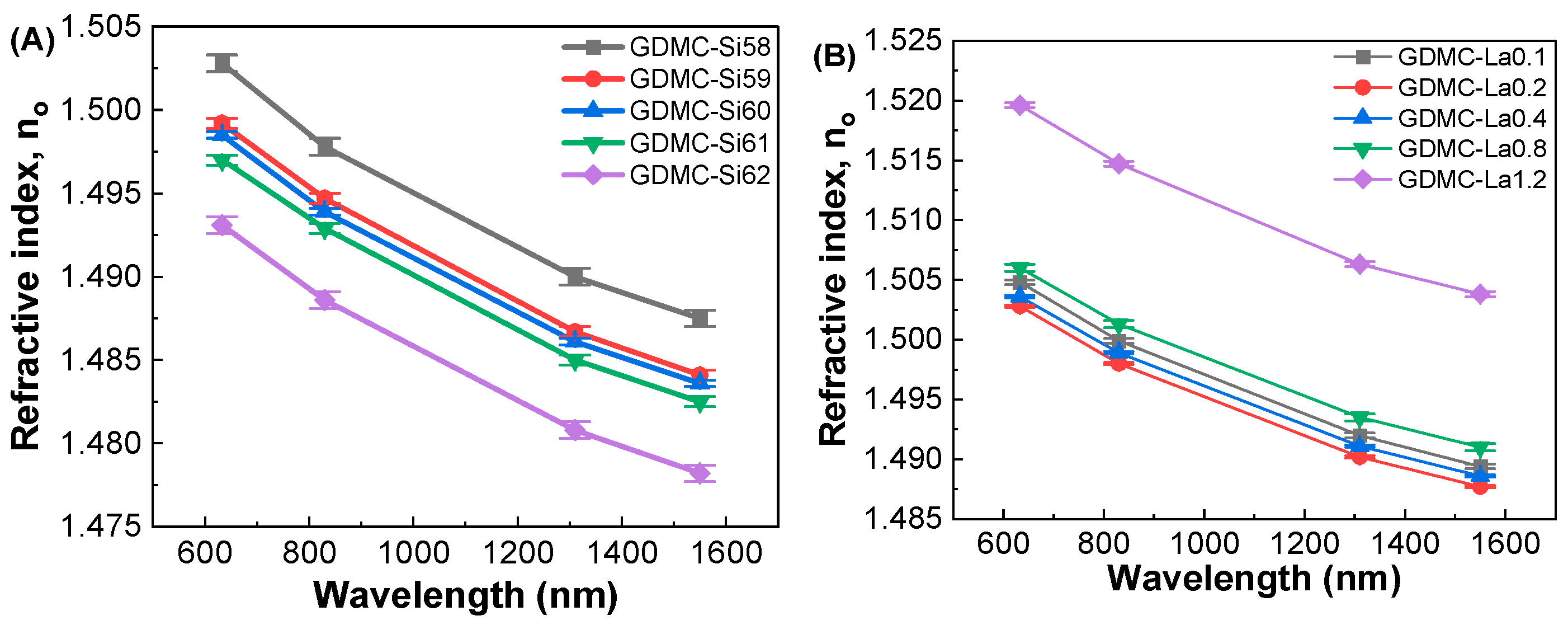
3.3. Dielectric and Polarizability Properties at Optical Frequencies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Pan, J.; Hu, H.; Zhu, H. Recent advances in new materials for 6G communications. Adv. Electron. Mater. 2022, 8, 2100978. [Google Scholar] [CrossRef]
- Orloff, N.D.; Ubic, R.; Lanagan, M. Special topic on materials and devices for 5G electronics. Appl. Phys. Lett. 2022, 120, 060402. [Google Scholar] [CrossRef]
- Rodriguez-Cano, R.; Perini, S.E.; Foley, B.M.; Lanagan, M. Broadband characterization of silicate materials for potential 5G/6G Applications. IEEE Trans. Instrum. Meas. 2023, 72, 6003008. [Google Scholar] [CrossRef]
- Rodriguez-Cano, R.; Lanagan, M.; Perini, S.; Li, X.; Gopalan, V. Broadband dielectric characterization of glasses and other silicates up to the THz frequencies. In Proceedings of the IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Portland, OR, USA, 23−28 July 2023. [Google Scholar]
- Rodriguez-Cano, R.; Perini, S.; Lanagan, M.T. Dielectric characterization of materials at 5G mm-wave frequencies. In Proceedings of the IEEE 18th edition of the European Conference on Antennas and Propagation (EuCAP), Glasgow, Scotland, 17–22 March 2024. [Google Scholar]
- Lanagan, M.T.; Brown, T.; Perini, S.; Yang, Q.X. High frequency dielectric materials for medicine and telecommunications. Jpn. J. Appl. Phys. 2021, 60, SF0801. [Google Scholar] [CrossRef]
- Cai, L.; Wu, J.; Lamberson, L.; Streltsova, E.; Daly, C.; Zakharian, A.; Borrelli, N.F. Glass for 5G applications. Appl. Phys. Lett. 2021, 119, 082901. [Google Scholar] [CrossRef]
- Kamutzki, F.; Schneider, S.; Barowski, J.; Gurlo, A.; Hanaor, D.A.H. Silicate dielectric ceramics for millimeter wave applications. J. Eur. Ceram. Soc. 2021, 41, 3879–3894. [Google Scholar] [CrossRef]
- Gerace, K.S.; Lanagan, M.T.; Mauro, J.C. Dielectric polarizability of SiO2 in niobiosilicate glasses. J. Am. Ceram. Soc. 2023, 106, 4546–4553. [Google Scholar] [CrossRef]
- Kanehara, K.; Urata, S.; Yasuhara, S.; Tsurumi, T.; Hoshina, T. Dielectric property and polarization mechanism of sodium silicate glass in GHz–THz range. Jpn. J. Appl. Phys. 2022, 61, SN1001. [Google Scholar] [CrossRef]
- Kanehara, K.; Urata, S.; Yasuhara, S.; Tsurumi, T.; Hoshina, T. Dielectric response and polarization mechanism of alkali silicate glasses in gigahertz to terahertz frequency range. J. Am. Ceram. Soc. 2023, 106, 5341–5350. [Google Scholar] [CrossRef]
- Nieves, C.A.; Lanagan, M.T. Exploring the dielectric polarization and ionic conduction mechanisms in sodium-containing silicate and borosilicate glasses. J. Non-Cryst. Solids. 2023, 617, 122505. [Google Scholar] [CrossRef]
- Shannon, R.D. Dielectric polarizabilities of ions in oxides and fluorides. J. Appl. Phys. 1993, 73, 348. [Google Scholar] [CrossRef]
- Lanagan, M.T.; Cai, L.; Lamberson, L.A.; Wu, J.; Streltsova, E.; Smith, N.J. Dielectric polarizability of alkali and alkaline-earth modified silicate glasses at microwave frequency. Appl. Phys. Lett. 2020, 116, 222902. [Google Scholar] [CrossRef]
- Wada, O.; Ramachari, D.; Yang, C.-S.; Uchino, T.; Pan, C.-L. High refractive index properties of oxyfluorosilicate glasses and a unified dielectric model of silicate oxide glasses in the sub-terahertz frequency region. Opt. Mater. Express 2020, 10, 607–621. [Google Scholar] [CrossRef]
- Naftaly, M.; Miles, R.E. Terahertz time-domain spectroscopy of silicate glasses and the relationship to material properties. J. Appl. Phys. 2007, 102, 043517. [Google Scholar] [CrossRef]
- Duffy, J.A.; Ingram, M.D. An interpretation of glass chemistry in terms of the optical basicity concept. J. Non-Cryst. Solids 1976, 21, 373. [Google Scholar] [CrossRef]
- Duffy, J.A.; Ingram, M.D. Establishment of an optical scale for Lewis basicity in inorganic oxyacids, molten salts, and glasses. J. Am. Chem. Soc. 1971, 93, 6448–6454. [Google Scholar] [CrossRef]
- Duffy, J.A. The electronic polarizability of oxygen in glass and the effect of composition. J. Non-Cryst. Solids 2002, 297, 275–284. [Google Scholar] [CrossRef]
- Dimitrov, V.; Sakka, S. Electronic oxide polarizability and optical basicity of simple oxides. I. J. Appl. Phys. 1996, 79, 1736. [Google Scholar] [CrossRef]
- Dimitrov, V.; Komatsu, T. An interpretation of optical properties of oxides and oxide glasses in terms of the electronic ion polarizability and average single bond strength. J. Univ. Chem. Technol. Metall. 2010, 45, 219–250. [Google Scholar]
- Komatsu, T.; Dimitrov, V.; Tasheva, T.; Honma, T. Electronic polarizability in silicate glasses by comparison of experimental and theoretical optical basicities. Int. J. Appl. Glass Sci. 2021, 12, 424–442. [Google Scholar] [CrossRef]
- Komatsu, T.; Dimitrov, V. Features of electronic polarizability and approach to unique properties in tellurite glasses. Int. J. Appl. Glass Sci. 2020, 11, 253–271. [Google Scholar] [CrossRef]
- Komatsu, T.; Dimitrov, V.; Tasheva, T.; Honma, T. A review: A new insight for electronic polarizability and chemical bond strength in Bi2O3-based glasses. J. Non-Cryst. Solids 2020, 550, 120365. [Google Scholar] [CrossRef]
- Li, H.; Richards, C.; Watson, J. High-Performance Glass Fiber Development for Composite Applications. Int. J. Appl. Glass Sci. 2014, 5, 65–81. [Google Scholar] [CrossRef]
- Ellison, A.; Cornejo, I.A. Glass substrates for liquid crystal displays. Int. J. Appl. Glass Sci. 2010, 1, 87–103. [Google Scholar] [CrossRef]
- Kato, Y.; Yamazaki, H.; Watanabe, T.; Saito, K.; Ikushima, A.J. Early Stage of Phase Separation in Aluminoborosilicate Glass for Liquid Crystal Display Substrate. J. Am. Ceram. Soc. 2005, 88, 473–477. [Google Scholar] [CrossRef]
- Cui, J.; Cao, X.; Shi, L.; Zhong, Z.; Wang, P.; Ma, L. The effect of substitution of Al2O3 and B2O3 for SiO2 on the properties of cover glass for liquid crystal display: Structure, thermal, visco-elastic, and physical properties. Int. J. Appl. Glass Sci. 2021, 12, 443–456. [Google Scholar] [CrossRef]
- Grema, L.U.; Hand, R.J. Structural and thermophysical behaviour of barium zinc aluminoborosilicate glasses for potential application in SOFCs. J. Non-Cryst. Solids 2021, 572, 121082. [Google Scholar] [CrossRef]
- Junfeng, K.; Junzhu, C.; Sheng, L.; Ya, Q.; Yansheng, H.; Khater, G.A.; Yunlong, Y. Structure, dielectric property and viscosity of alkali-free boroaluminosilicate glasses with the substitution of Al2O3 for SiO2. J. Non-Cryst. Solids 2020, 537, 120022. [Google Scholar] [CrossRef]
- Zhang, L.; Qua, Y.; Wan, X.; Zhao, J.; Zhao, J.; Yue, Y.; Kang, J. Influence of rare earth oxides on structure, dielectric properties and viscosity of alkali-free aluminoborosilicate glasses. J. Non-Cryst. Solids 2020, 532, 119886. [Google Scholar] [CrossRef]
- Liu, J.; Luo, Z.; Lin, C.; Han, L.; Gui, H.; Song, J.; Liu, T.; Lu, A. Influence of Y2O3 substitution for B2O3 on the structure and properties of alkali-free B2O3-Al2O3-SiO2 glasses containing alkaline-earth metal oxides. Phys. B Condens. Matter 2019, 553, 47–52. [Google Scholar] [CrossRef]
- Basics of Measuring the Dielectric Properties of Materials. Available online: https://www.keysight.com/us/en/assets/7018-01284/application-notes/5989-2589.pdf (accessed on 8 January 2024).
- Ray, N.H. Composition-property relationships in inorganic oxide glasses. J. Non-Cryst. Solids 1974, 15, 423–434. [Google Scholar] [CrossRef]
- Li, S.; Lu, Y.; Qu, Y.; Kang, J.; Yue, Y.; Liang, X. Dielectric and thermal properties of aluminoborosilicate glasses doped with mixed rare-earth oxides. J. Non-Cryst. Solids 2021, 556, 120550. [Google Scholar] [CrossRef]
- Darwish, H.; Gomaa, M.M. Effect of compositional changes on the structure and properties of alkali aluminoborosilicate glasses. J. Mater. Sci. Mater. Electron. 2006, 17, 35–42. [Google Scholar] [CrossRef]
- Wu, J.; Stebbins, J.F. Effects of cation field strength on the structure of aluminoborosilicate glasses: High-resolution 11B, 27Al and 23Na MAS NMR. J. Non-Cryst. Solids 2020, 355, 556–562. [Google Scholar] [CrossRef]
- Tuheen, M.I.; Du, J. Effect of modifier cation field strength on the structure of magnesium oxide containing aluminoborosilicate glasses. Int. J. Appl. Glass Sci. 2022, 13, 554–567. [Google Scholar] [CrossRef]
- Iftekhar, S.; Grins, J.; Edén, M. Composition–property relationships of the La2O3–Al2O3–SiO2 glass system. J. Non-Cryst. Solids 2010, 356, 1043–1048. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, H.; Qu, Y.; Lu, H.; Huang, S.; Yue, Y. Influence of La2O3 and Ce2O3 additions on structure and properties of aluminoborosilicate glasses. J. Mater. Sci Mater. Electron. 2017, 28, 2716–2722. [Google Scholar] [CrossRef]
- Grammes, T.; Limbach, R.; Bruns, S.; van Wüllen, L.; de Ligny, D.; Kamitsos, E.I.; Durst, K.; Wondraczek, L.; Brauer, D.S. Tailoring the Mechanical Properties of Metaluminous Aluminosilicate Glasses by Phosphate Incorporation. Front. Mater. 2020, 7, 115. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Optical Absorption, Electronic Processes in Non-Crystalline Materials, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 1979; pp. 287–292. [Google Scholar]




| Glass Label | Glass Composition (mol%) | |||||
|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | B2O3 | CaO | MgO | La2O3 | |
| GDMC-Si58 | 58.7 | 10.90 | 19.7 | 5.5 | 5.20 | 0 |
| GDMC-Si59 | 59.5 | 10.20 | 19.6 | 5.5 | 5.20 | 0 |
| GDMC-Si60 | 60.3 | 9.50 | 19.5 | 5.5 | 5.20 | 0 |
| GDMC-Si61 | 61.1 | 8.80 | 19.4 | 5.5 | 5.20 | 0 |
| GDMC-Si62 | 62.7 | 7.40 | 19.2 | 5.5 | 5.20 | 0 |
| GDMC-La0.1 | 59.5 | 10.13 | 19.6 | 5.5 | 5.17 | 0.1 |
| GDMC-La0.2 | 59.5 | 10.07 | 19.6 | 5.5 | 5.13 | 0.2 |
| GDMC-La0.4 | 59.5 | 9.93 | 19.6 | 5.5 | 5.07 | 0.4 |
| GDMC-La0.8 | 59.5 | 9.67 | 19.6 | 5.5 | 4.93 | 0.8 |
| GDMC-La1.2 | 59.5 | 9.40 | 19.6 | 5.5 | 4.80 | 1.2 |
| Glass Label | Physical Property | |||
|---|---|---|---|---|
| (g/cm3) | Vm (cm3/mol) | ox (mol/cm3) | Vox (cm3/mol) | |
| GDMC-Si58 | 2.366 ± 0.003 | 27.589 ± 0.006 | 0.0797 ± 0.0001 | 12.546 ± 0.002 |
| GDMC-Si59 | 2.346 ± 0.003 | 27.695 ± 0.006 | 0.0791 ± 0.0001 | 12.640 ± 0.002 |
| GDMC-Si60 | 2.334 ± 0.003 | 27.708 ± 0.006 | 0.0788 ± 0.0001 | 12.693 ± 0.002 |
| GDMC-Si61 | 2.325 ± 0.003 | 27.685 ± 0.006 | 0.0786 ± 0.0001 | 12.729 ± 0.002 |
| GDMC-Si62 | 2.311 ± 0.003 | 27.591 ± 0.006 | 0.0782 ± 0.0001 | 12.779 ± 0.002 |
| GDMC-La0.1 | 2.369 ± 0.003 | 27.529 ± 0.009 | 0.0796 ± 0.0001 | 12.561 ± 0.001 |
| GDMC-La0.2 | 2.375 ± 0.003 | 27.564 ± 0.009 | 0.0795 ± 0.0001 | 12.572 ± 0.001 |
| GDMC-La0.4 | 2.389 ± 0.003 | 27.605 ± 0.009 | 0.0794 ± 0.0001 | 12.584 ± 0.001 |
| GDMC-La0.8 | 2.417 ± 0.003 | 27.691 ± 0.009 | 0.0793 ± 0.0001 | 12.608 ± 0.001 |
| GDMC-La1.2 | 2.449 ± 0.003 | 27.728 ± 0.009 | 0.0793 ± 0.0001 | 12.609 ± 0.001 |
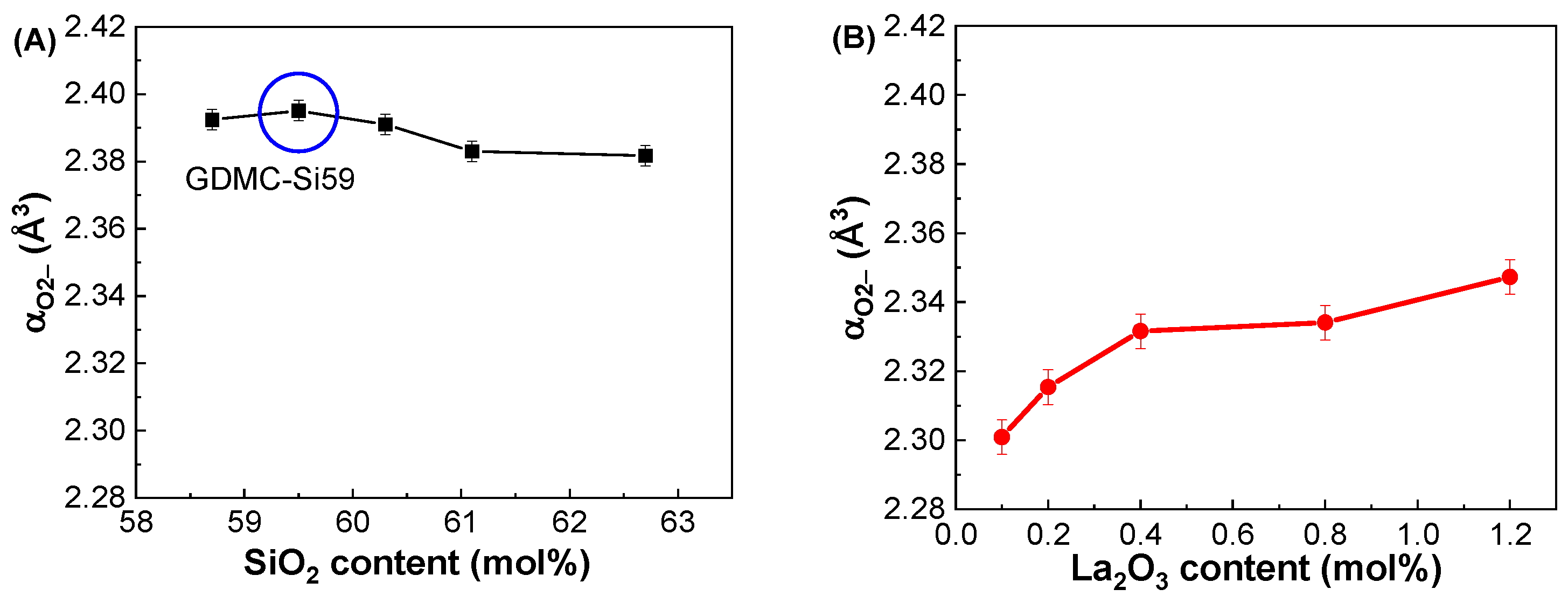
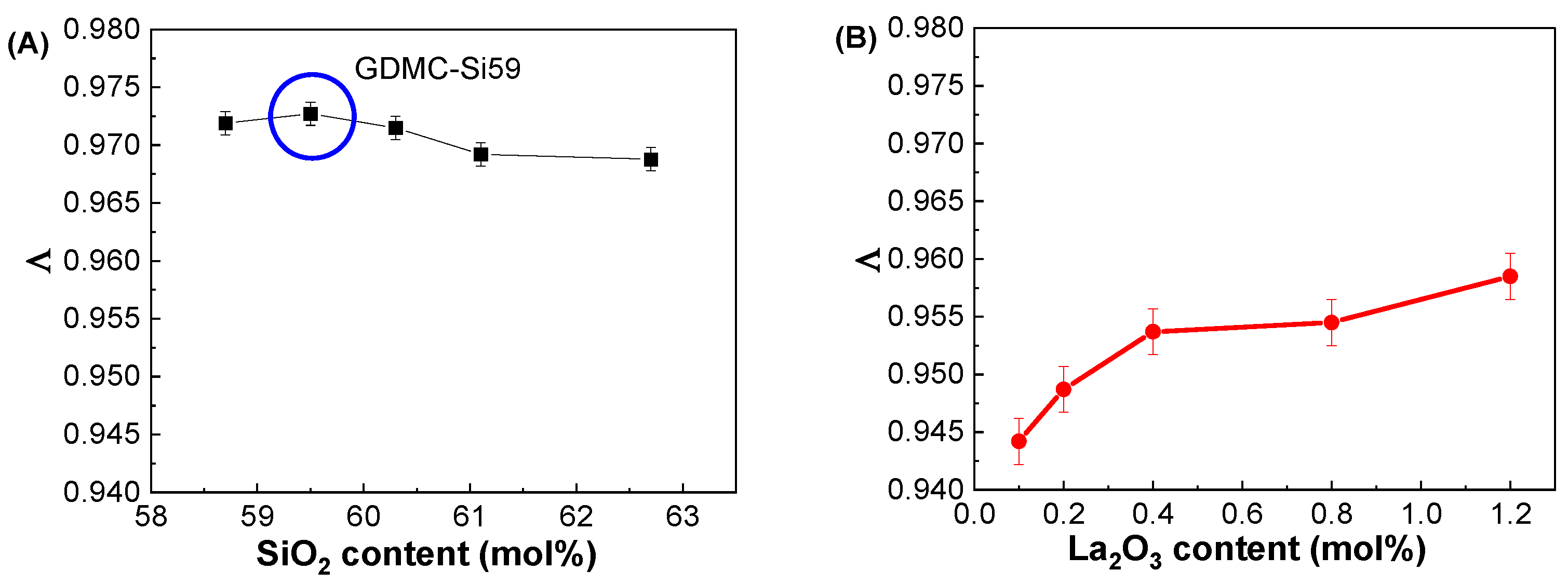
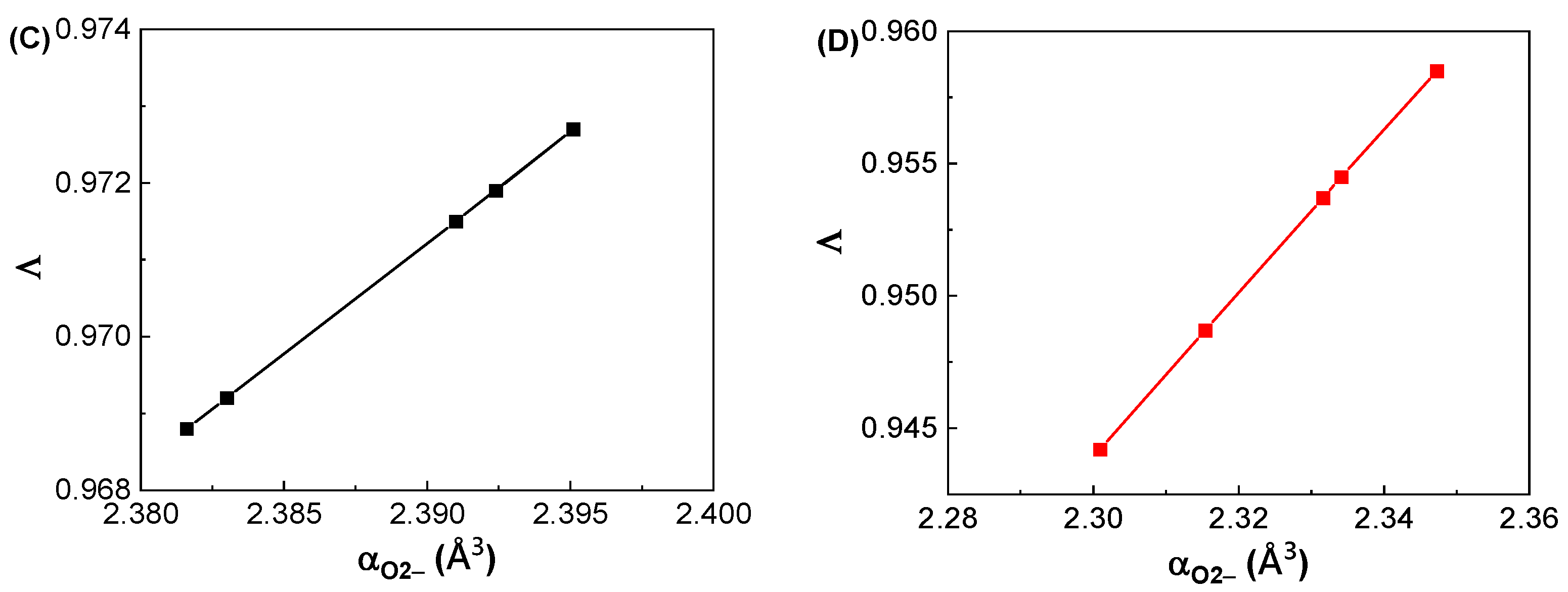
| Glass Label | εGHz at 1 GHz | αD (Å3) | αO2− (Å3) | Λ |
|---|---|---|---|---|
| GDMC-Si58 | 4.94 ± 0.02 | 6.21 ± 0.01 | 2.392 ± 0.003 | 0.972 ± 0.001 |
| GDMC-Si59 | 4.88 ± 0.02 | 6.19 ± 0.01 | 2.395 ± 0.003 | 0.973 ± 0.001 |
| GDMC-Si60 | 4.83 ± 0.02 | 6.16 ± 0.01 | 2.391 ± 0.003 | 0.972 ± 0.001 |
| GDMC-Si61 | 4.78 ± 0.02 | 6.12 ± 0.01 | 2.383 ± 0.003 | 0.969 ± 0.001 |
| GDMC-Si62 | 4.74 ± 0.02 | 6.07 ± 0.01 | 2.382 ± 0.003 | 0.969 ± 0.001 |
| GDMC-La0.1 | 4.66 ± 0.02 | 5.99 ± 0.01 | 2.301 ± 0.005 | 0.944 ± 0.002 |
| GDMC-La0.2 | 4.71 ± 0.02 | 6.04 ± 0.01 | 2.315 ± 0.005 | 0.949 ± 0.002 |
| GDMC-La0.4 | 4.78 ± 0.02 | 6.10 ± 0.01 | 2.332 ± 0.005 | 0.954 ± 0.002 |
| GDMC-La0.8 | 4.83 ± 0.02 | 6.15 ± 0.01 | 2.334 ± 0.005 | 0.955 ± 0.002 |
| GDMC-La1.2 | 4.93 ± 0.02 | 6.23 ± 0.01 | 2.347 ± 0.005 | 0.959 ± 0.002 |
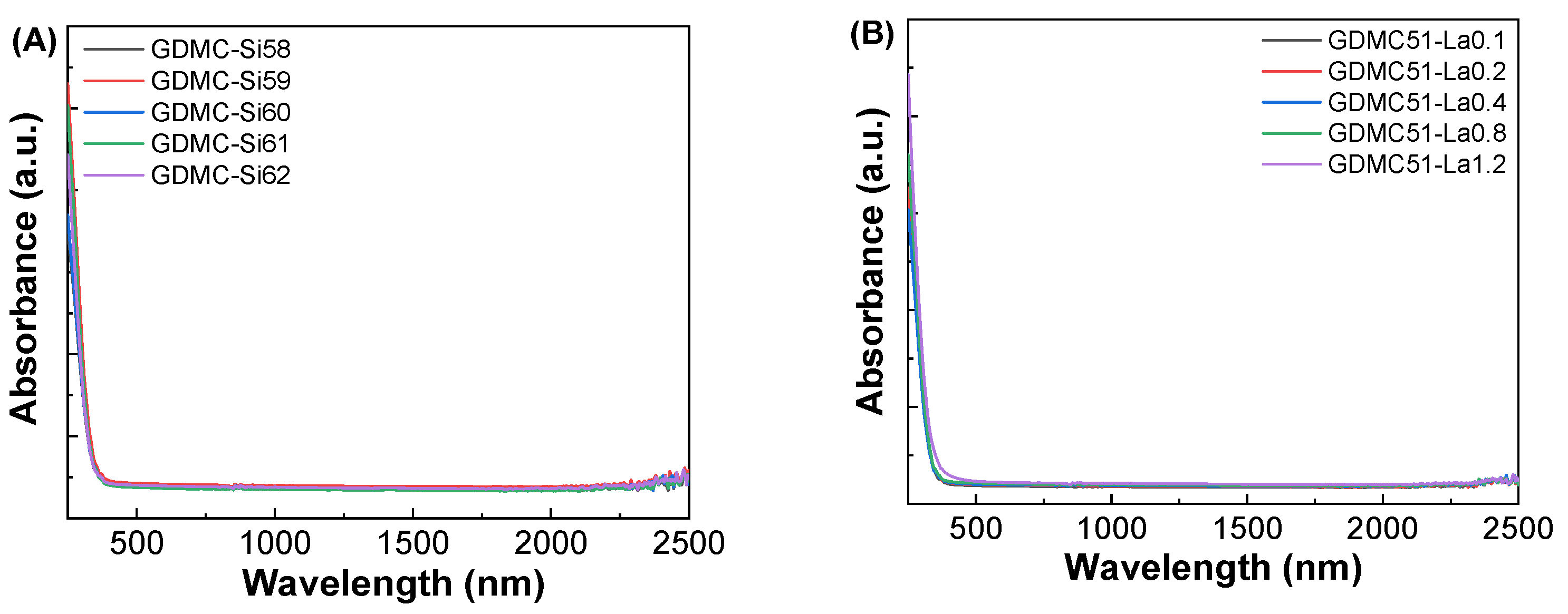
| Glass Label | Refractive Index, no | εopt | αe (Å3) | αi (Å3) | |||
|---|---|---|---|---|---|---|---|
| 633 nm | 830 nm | 1310 nm | 1550 nm | ||||
| GDMC-Si58 | 1.5028 ± 0.0005 | 1.4978 ± 0.0005 | 1.4900 ± 0.0005 | 1.4875 ± 0.0005 | 2.258 ± 0.001 | 3.230 ± 0.001 | 2.980 ± 0.001 |
| GDMC-Si59 | 1.4992 ± 0.0003 | 1.4947 ± 0.0003 | 1.4867 ± 0.0003 | 1.4841 ± 0.0003 | 2.248 ± 0.001 | 3.223 ± 0.001 | 2.967 ± 0.001 |
| GDMC-Si60 | 1.4985 ± 0.0002 | 1.4939 ± 0.0002 | 1.4861 ± 0.0002 | 1.4836 ± 0.0002 | 2.246 ± 0.001 | 3.221 ± 0.001 | 2.939 ± 0.001 |
| GDMC-Si61 | 1.4970 ± 0.0003 | 1.4929 ± 0.0003 | 1.485 ± 0.0003 | 1.4825 ± 0.0003 | 2.241 ± 0.001 | 3.210 ± 0.001 | 2.910 ± 0.001 |
| GDMC-Si62 | 1.4931 ± 0.0005 | 1.4886 ± 0.0005 | 1.4808 ± 0.0005 | 1.4782 ± 0.0005 | 2.229 ± 0.001 | 3.178 ± 0.001 | 2.892 ± 0.001 |
| GDMC-La0.1 | 1.5048 ± 0.0002 | 1.4999 ± 0.0002 | 1.492 ± 0.0002 | 1.4894 ± 0.0002 | 2.264 ± 0.002 | 3.234 ± 0.002 | 2.756 ± 0.002 |
| GDMC-La0.2 | 1.5028 ± 0.0001 | 1.498 ± 0.0001 | 1.4902 ± 0.0001 | 1.4877 ± 0.0001 | 2.258 ± 0.002 | 3.227 ± 0.002 | 2.813 ± 0.002 |
| GDMC-La0.4 | 1.5036 ± 0.0001 | 1.4989 ± 0.0001 | 1.4911 ± 0.0001 | 1.4886 ± 0.0001 | 2.261 ± 0.002 | 3.236 ± 0.002 | 2.863 ± 0.002 |
| GDMC-La0.8 | 1.5060 ± 0.0003 | 1.5013 ± 0.0003 | 1.4935 ± 0.0003 | 1.491 ± 0.0003 | 2.268 ± 0.002 | 3.260 ± 0.002 | 2.890 ± 0.002 |
| GDMC-La1.2 | 1.5196 ± 0.0002 | 1.5147 ± 0.0002 | 1.5063 ± 0.0002 | 1.5038 ± 0.0002 | 2.309 ± 0.002 | 3.338 ± 0.002 | 2.892 ± 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadathala, L.; Park, Y.-O.; Oh, M.-K.; Han, W.-T.; Kim, B.H. Analysis of the Dielectric Properties of Alkali-Free Aluminoborosilicate Glasses by Considering the Contributions of Electronic and Ionic Polarizabilities in the GHz Frequency Range. Materials 2024, 17, 1404. https://doi.org/10.3390/ma17061404
Kadathala L, Park Y-O, Oh M-K, Han W-T, Kim BH. Analysis of the Dielectric Properties of Alkali-Free Aluminoborosilicate Glasses by Considering the Contributions of Electronic and Ionic Polarizabilities in the GHz Frequency Range. Materials. 2024; 17(6):1404. https://doi.org/10.3390/ma17061404
Chicago/Turabian StyleKadathala, Linganna, Young-Ouk Park, Myoung-Kyu Oh, Won-Taek Han, and Bok Hyeon Kim. 2024. "Analysis of the Dielectric Properties of Alkali-Free Aluminoborosilicate Glasses by Considering the Contributions of Electronic and Ionic Polarizabilities in the GHz Frequency Range" Materials 17, no. 6: 1404. https://doi.org/10.3390/ma17061404
APA StyleKadathala, L., Park, Y.-O., Oh, M.-K., Han, W.-T., & Kim, B. H. (2024). Analysis of the Dielectric Properties of Alkali-Free Aluminoborosilicate Glasses by Considering the Contributions of Electronic and Ionic Polarizabilities in the GHz Frequency Range. Materials, 17(6), 1404. https://doi.org/10.3390/ma17061404






