Electromechanical Deformations and Bifurcations in Soft Dielectrics: A Review
Abstract
1. Introduction
2. Basic Formulations
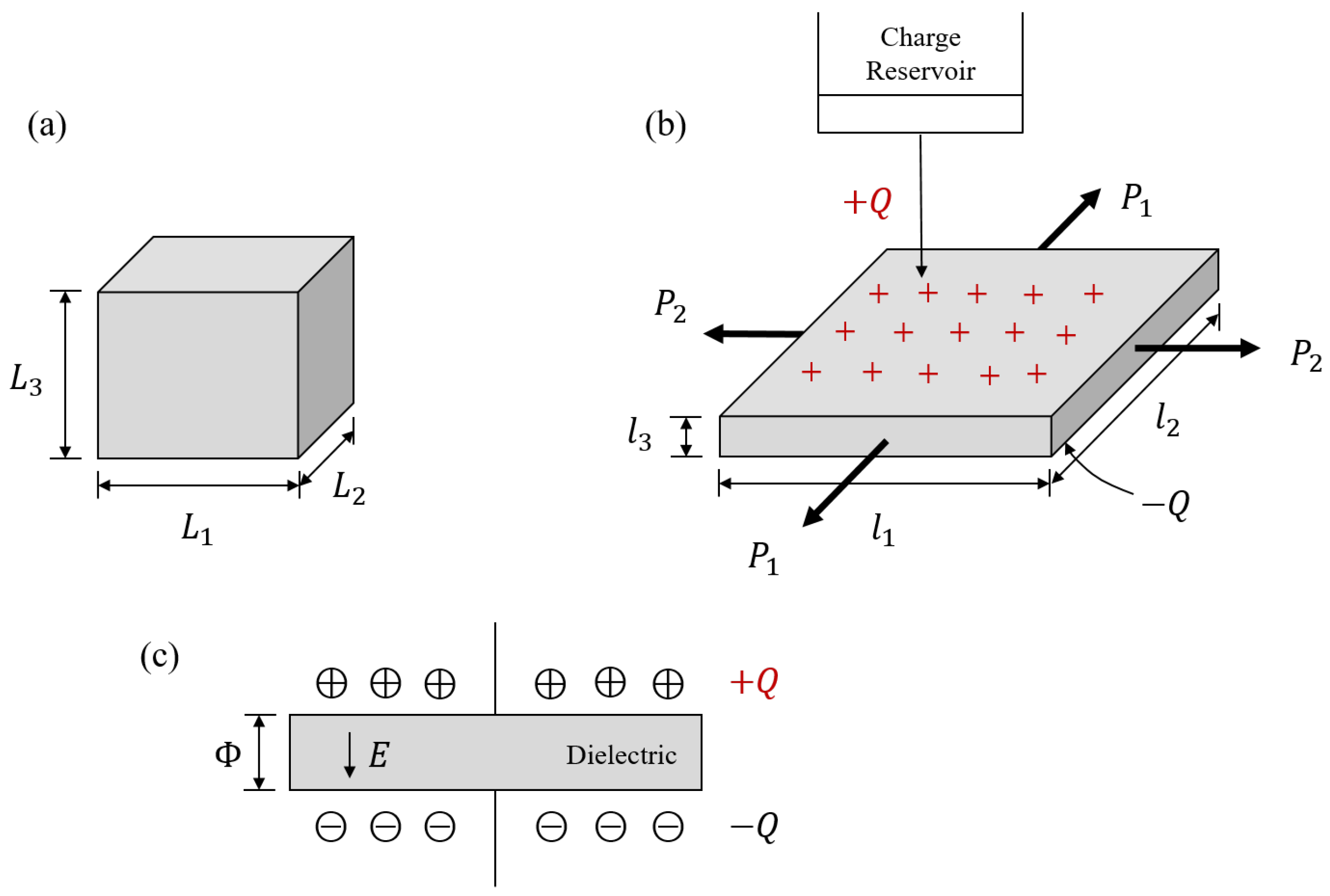
2.1. Finite Electroelasticity
2.2. Incremental Field Theory
3. Nonlinear Deformations in DE Structures
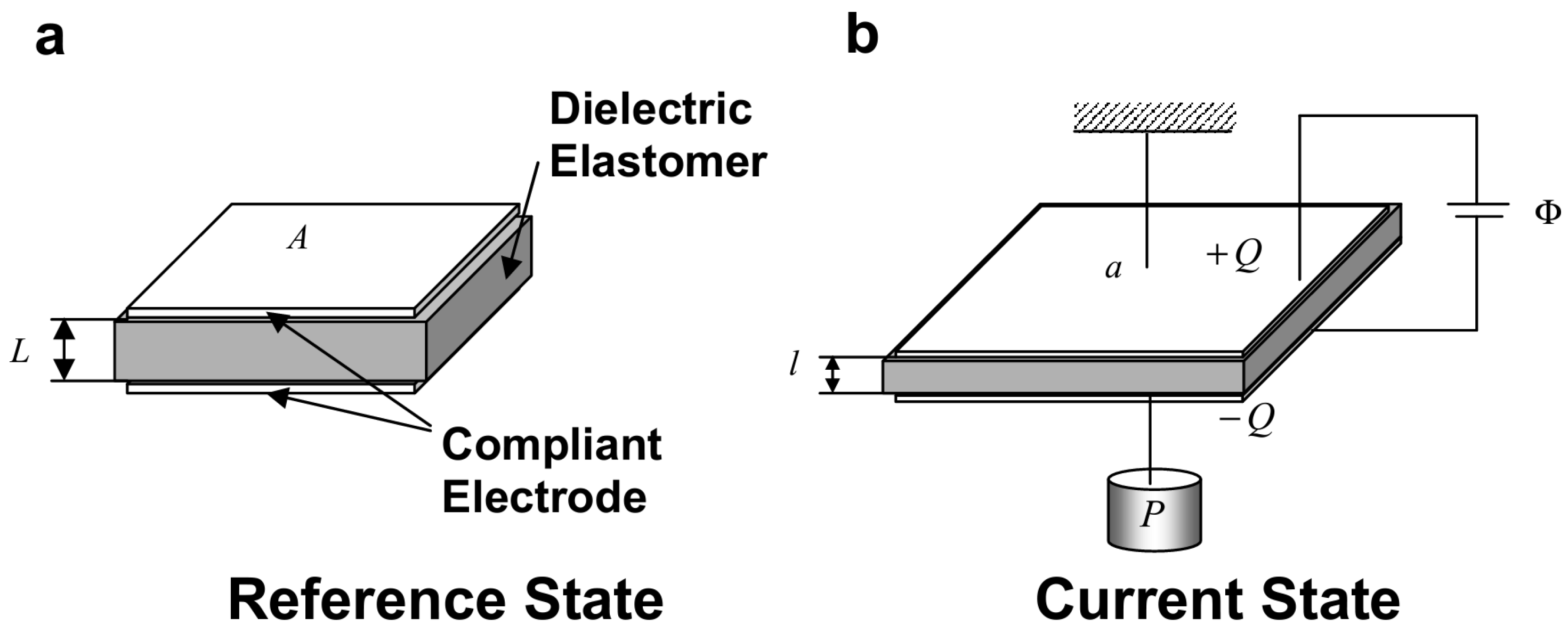
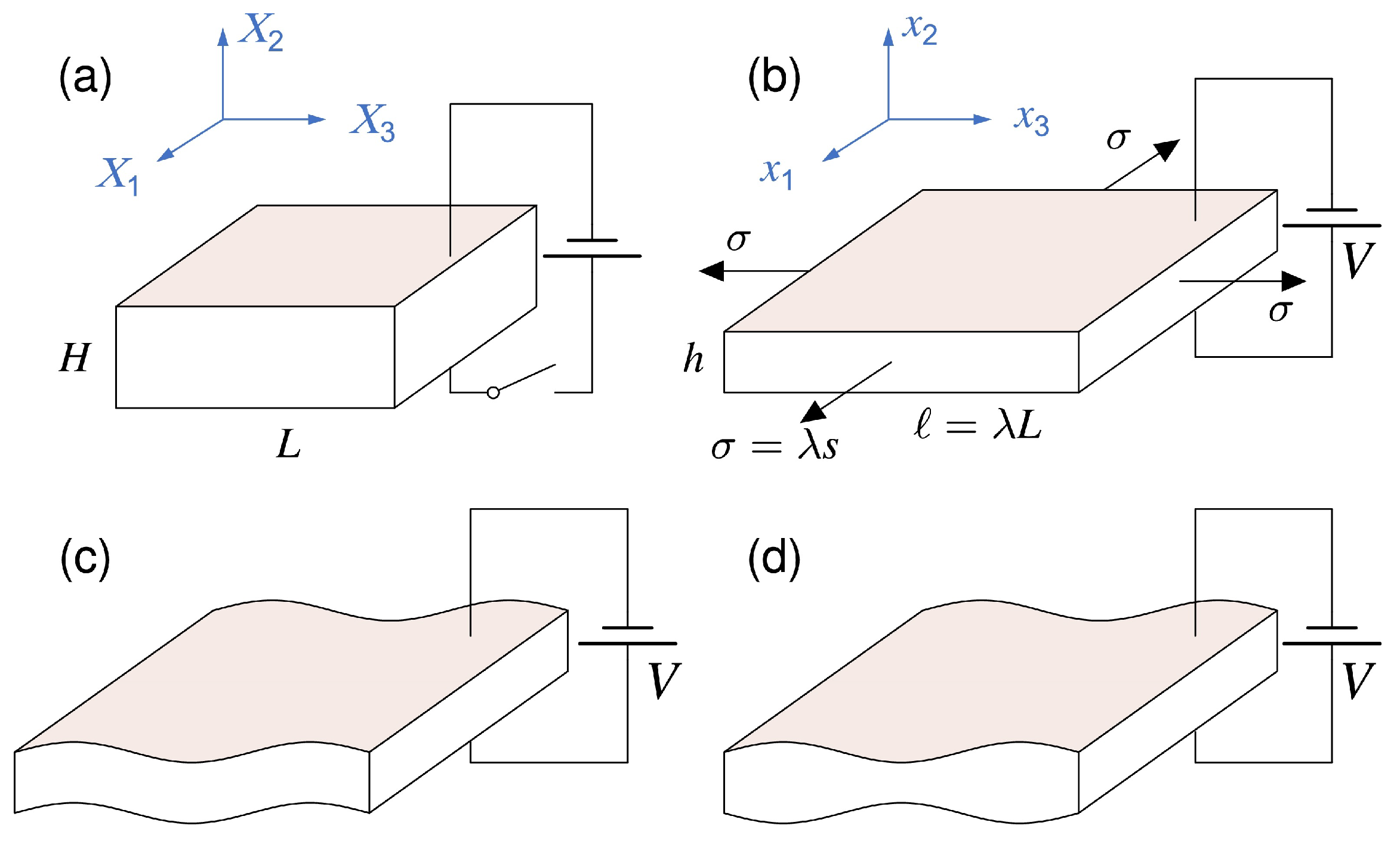
3.1. Plate
3.1.1. Voltage Control
3.1.2. Charge Control
3.2. Membrane
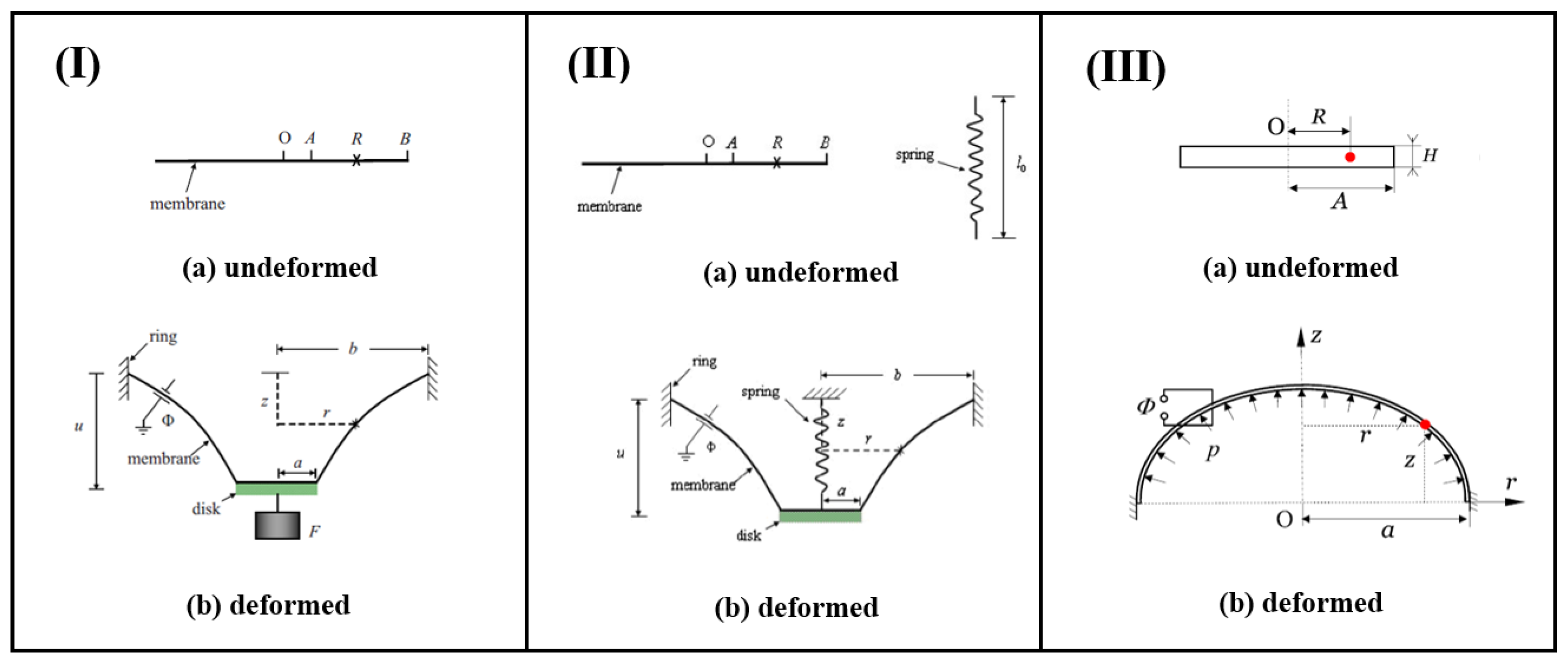
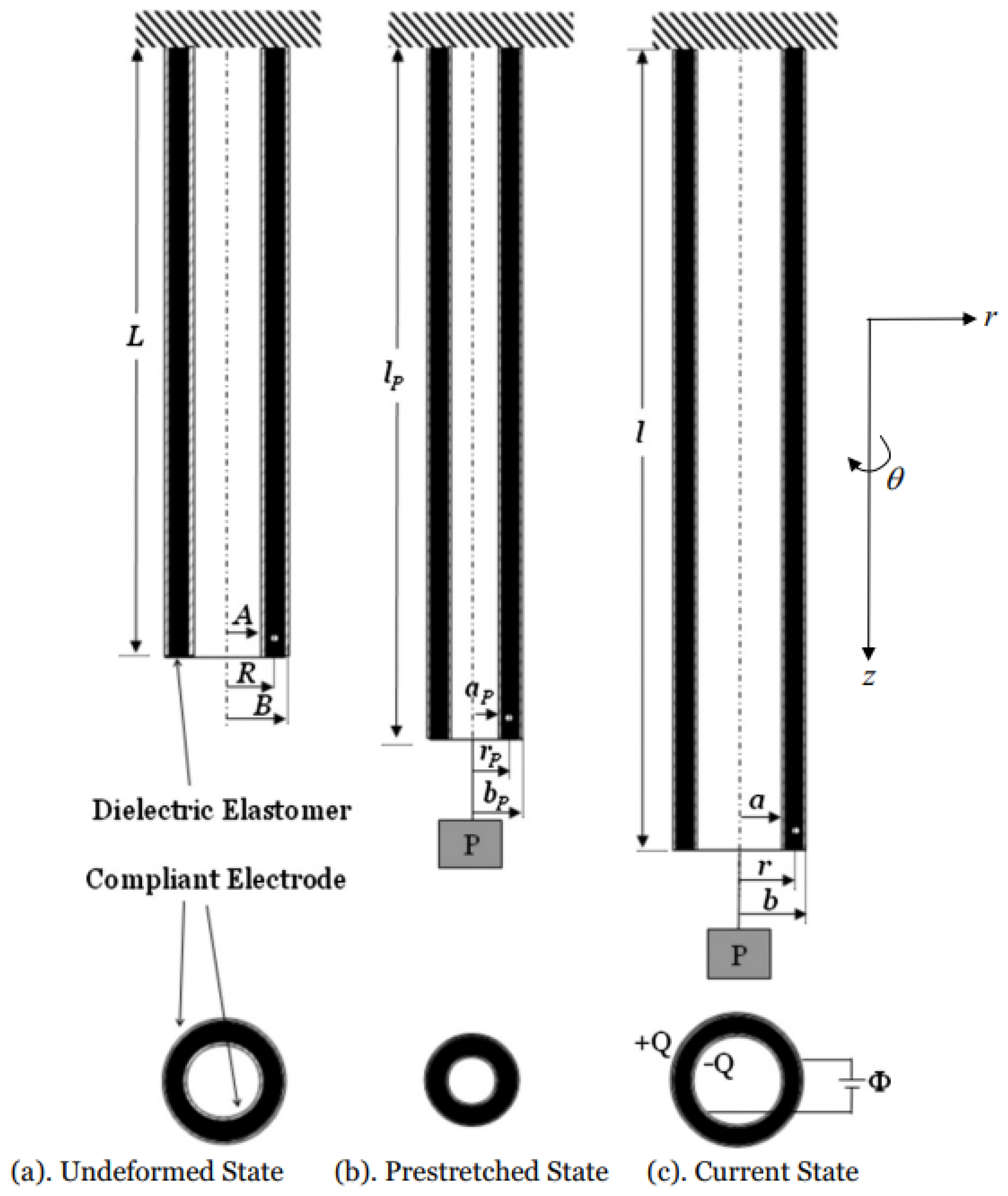
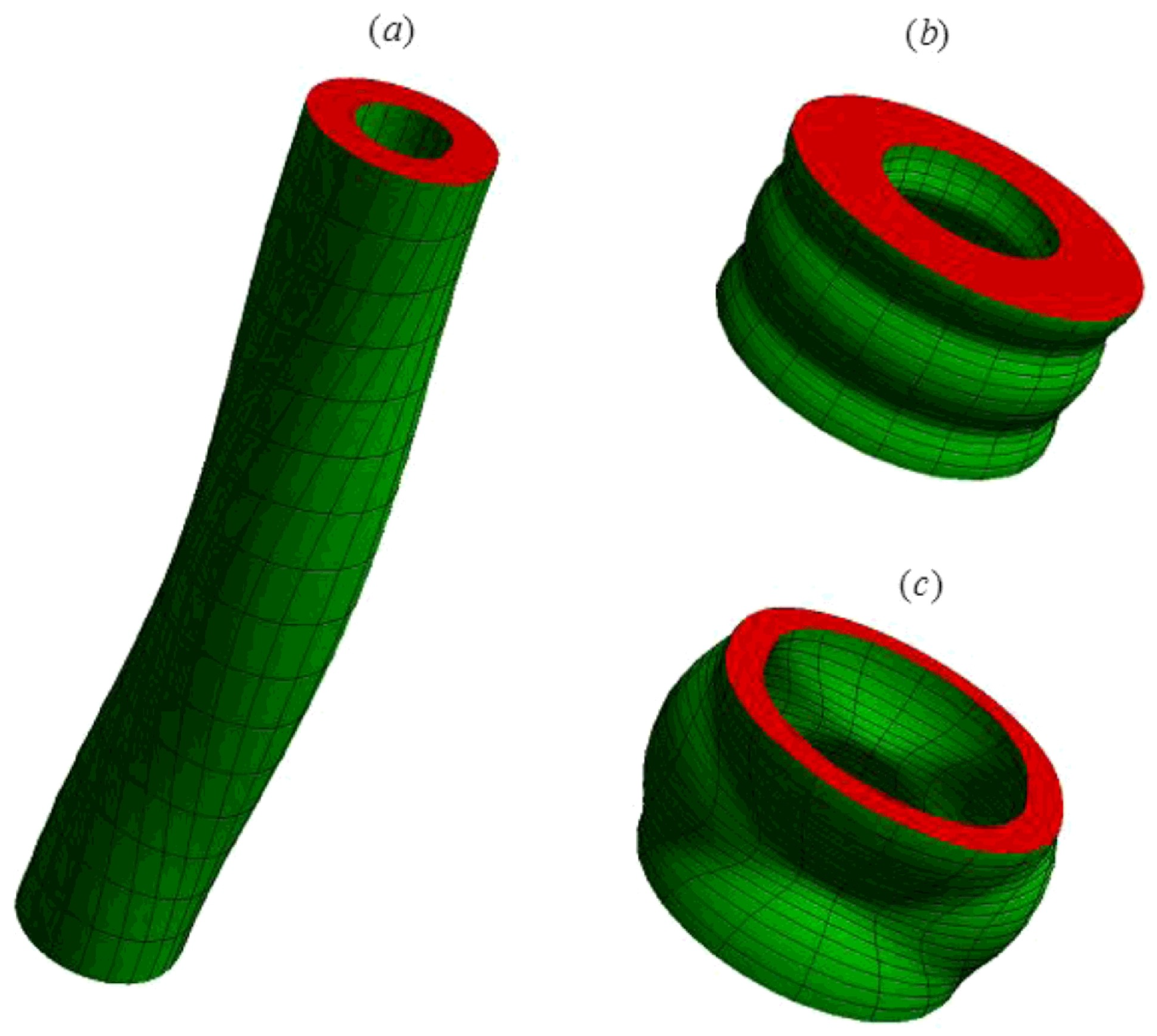
3.3. Solid and Hollow Tubes
3.3.1. Inflation and Extension
3.3.2. Torsion
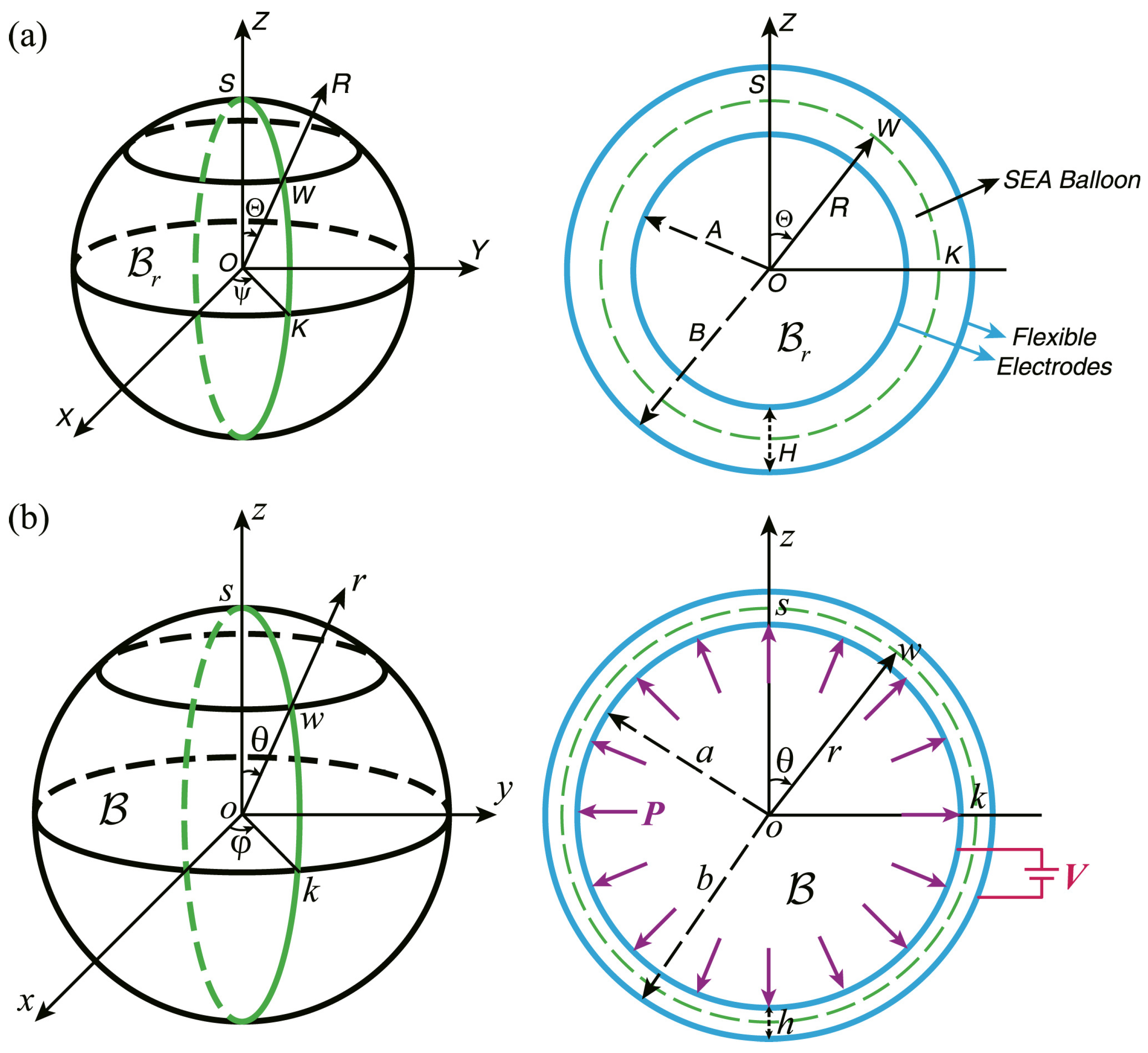
3.4. Spherical Balloons
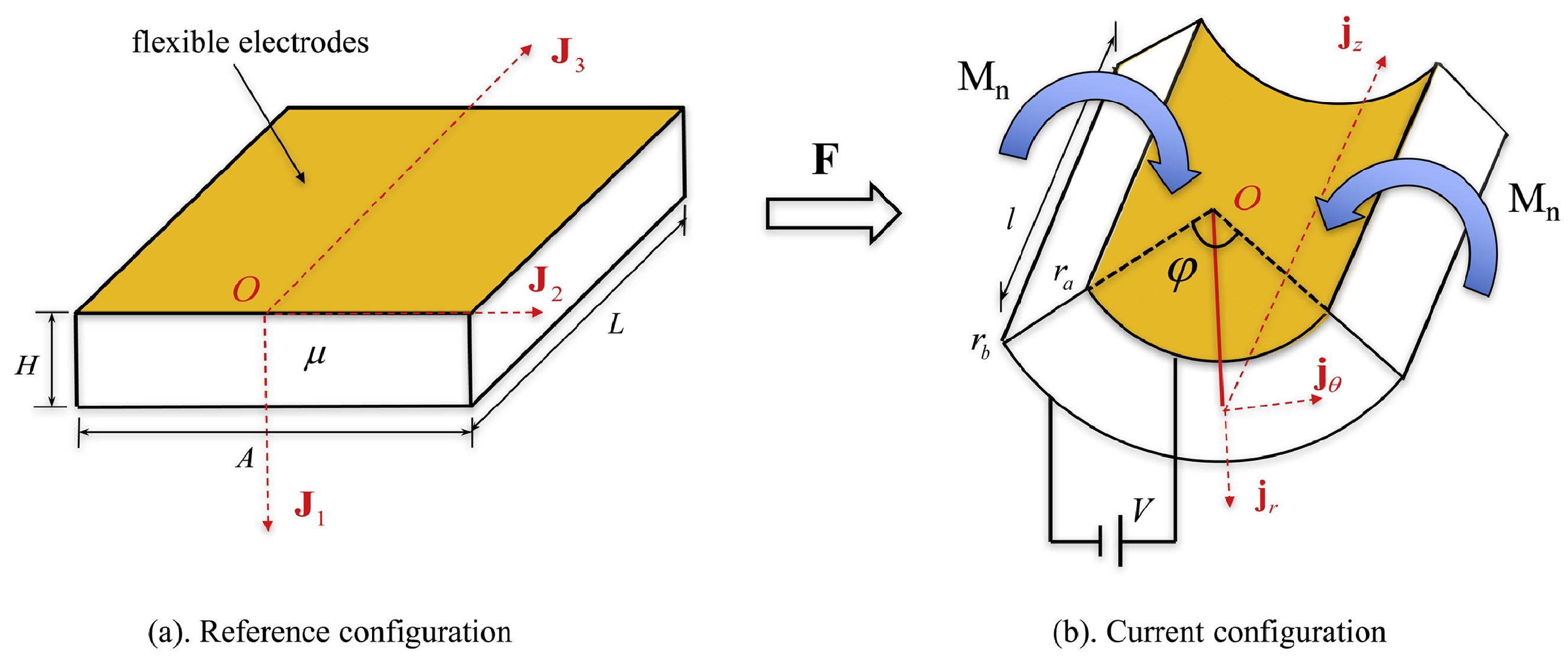
3.5. Finite Bending
4. Bifurcations in DE Structures
4.1. Half-Space
4.2. Membrane
4.3. Plate
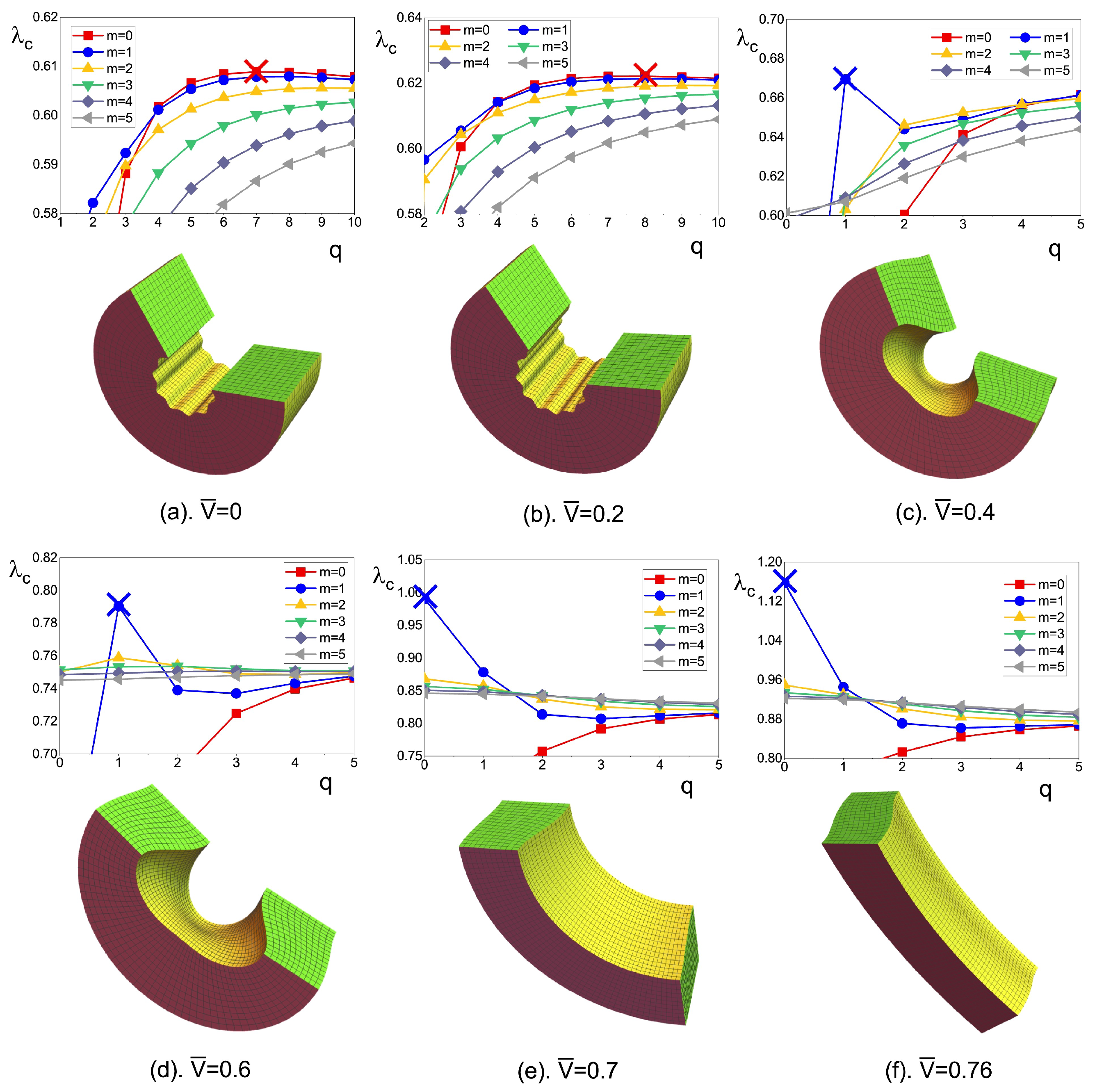
4.4. Solid and Hollow Tubes
4.5. Spherical Balloon
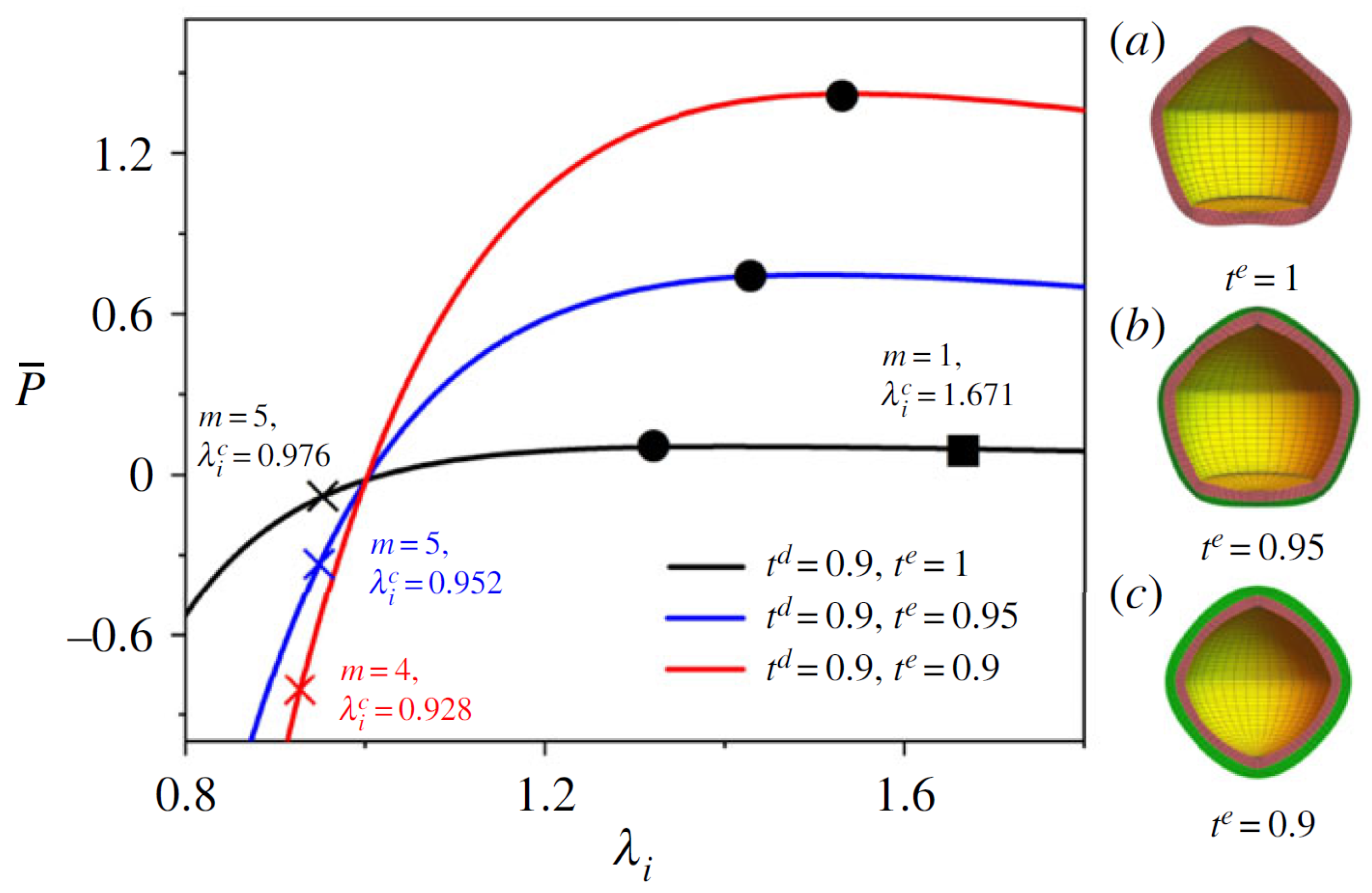
4.6. Bending Bifurcations
5. Conclusions and Outlooks
5.1. Conclusions
5.2. Outlooks
Funding
Conflicts of Interest
References
- Pron, A.; Gawrys, P.; Zagorska, M.; Djurado, D.; Demadrille, R. Electroactive materials for organic electronics: Preparation strategies, structural aspects and characterization techniques. Chem. Soc. Rev. 2010, 39, 2577–2632. [Google Scholar] [CrossRef]
- Biggs, J.; Danielmeier, K.; Hitzbleck, J.; Krause, J.; Kridl, T.; Nowak, S.; Orselli, E.; Quan, X.; Schapeler, D.; Sutherland, W.; et al. Electroactive polymers: Developments of and perspectives for dielectric elastomers. Angew. Chem. Int. Ed. 2013, 52, 9409–9421. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Vijaya, M.S. Piezoelectric Materials and Devices: Applications in Engineering and Medical Sciences; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Curie, J.; Curie, P. Development, via compression, of electric polarization in hemihedral crystals with inclined faces. Bull. Soc. Minerol. Fr. 1880, 3, 90–93. [Google Scholar]
- Ding, H.; Chen, W.Q. Three Dimensional Problems of Piezoelasticity; Nova Science Publishers: Hauppauge, NY, USA, 2001. [Google Scholar]
- Yang, J. An Introduction to the Theory of Piezoelectricity; Springer: New York, NY, USA, 2005; Volume 9, pp. 31–58. [Google Scholar]
- Freiman, S.W.; White, G.S. Intelligent ceramic materials: Issues of brittle fracture. J. Intell. Mater. Syst. Struct. 1995, 6, 49–54. [Google Scholar] [CrossRef]
- Hu, D.; Yao, M.; Fan, Y.; Ma, C.; Fan, M.; Liu, M. Strategies to achieve high performance piezoelectric nanogenerators. Nano Energy 2019, 55, 288–304. [Google Scholar] [CrossRef]
- O’Halloran, A.; O’malley, F.; McHugh, P. A review on dielectric elastomer actuators, technology, applications, and challenges. J. Appl. Phys. 2008, 104, 071101. [Google Scholar] [CrossRef]
- Hajiesmaili, E.; Clarke, D.R. Dielectric elastomer actuators. J. Appl. Phys. 2021, 129, 151102. [Google Scholar] [CrossRef]
- Chen, D.; Pei, Q. Electronic muscles and skins: A review of soft sensors and actuators. Chem. Rev. 2017, 117, 11239–11268. [Google Scholar] [CrossRef]
- Elahinia, M.H. Shape Memory Alloy Actuators: Design, Fabrication, and Experimental Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Toupin, R.A. The elastic dielectric. J. Ration. Mech. Anal. 1956, 5, 849–915. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Joseph, J.; Heydt, R.; Pei, Q.; Chiba, S. High-field electrostriction of elastomeric polymer dielectrics for actuation. In Smart Structures and Materials 1999: Electroactive Polymer Actuators and Devices; SPIE: Bellingham, WA, USA, 1999; Volume 3669, pp. 149–161. [Google Scholar]
- Kovetz, A. Electromagnetic Theory; Oxford University Press: Oxford, UK, 2000; pp. 216–219. [Google Scholar]
- Dorfmann, L.; Ogden, R.W. Nonlinear Theory of Electroelastic and Magnetoelastic Interactions; Springer: New York, NY, USA, 2014; Volume 1. [Google Scholar]
- Suo, Z.; Zhao, X.; Greene, W.H. A nonlinear field theory of deformable dielectrics. J. Mech. Phys. Solids 2008, 56, 467–486. [Google Scholar] [CrossRef]
- Tian, L.; Tevet-Deree, L.; deBotton, G.; Bhattacharya, K. Dielectric elastomer composites. J. Mech. Phys. Solids 2012, 60, 181–198. [Google Scholar] [CrossRef]
- Goulbourne, N.; Mockensturm, E.; Frecker, M. A nonlinear model for dielectric elastomer membranes. J. Appl. Mech. 2005, 72, 899–906. [Google Scholar] [CrossRef]
- Kollosche, M.; Zhu, J.; Suo, Z.; Kofod, G. Complex interplay of nonlinear processes in dielectric elastomers. Phys. Rev. E 2012, 85, 051801. [Google Scholar] [CrossRef] [PubMed]
- Lefèvre, V.; Lopez-Pamies, O. Nonlinear electroelastic deformations of dielectric elastomer composites: I—Ideal elastic dielectrics. J. Mech. Phys. Solids 2017, 99, 409–437. [Google Scholar] [CrossRef]
- Cao, C.; Hill, T.L.; Conn, A.T. On the nonlinear dynamics of a circular dielectric elastomer oscillator. Smart Mater. Struct. 2019, 28, 075020. [Google Scholar] [CrossRef]
- Wang, F.; Lu, T.; Wang, T.J. Nonlinear vibration of dielectric elastomer incorporating strain stiffening. Int. J. Solids Struct. 2016, 87, 70–80. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, B.; Carrera, E.; Rudykh, S.; Chen, W.Q. Axisymmetric vibration of multilayered electroactive circular plates in contact with fluid. J. Sound Vib. 2024, 573, 118189. [Google Scholar] [CrossRef]
- Zhu, F.; Wu, B.; Destrade, M.; Wang, H.; Bao, R.; Chen, W.Q. Voltage-controlled non-axisymmetric vibrations of soft electro-active tubes with strain-stiffening effect. Int. J. Solids Struct. 2024, 290, 112671. [Google Scholar] [CrossRef]
- Zhu, F.; Wu, B.; Destrade, M.; Chen, W.Q. Electrostatically tunable axisymmetric vibrations of soft electro-active tubes. J. Sound Vib. 2020, 483, 115467. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. Electroelastic waves in a finitely deformed electroactive material. IMA J. Appl. Math. 2010, 75, 603–636. [Google Scholar] [CrossRef]
- Wu, B.; Su, Y.; Chen, W.Q.; Zhang, C. On guided circumferential waves in soft electroactive tubes under radially inhomogeneous biasing fields. J. Mech. Phys. Solids 2017, 99, 116–145. [Google Scholar] [CrossRef]
- Su, Y.P.; Wang, H.M.; Zhang, C.L.; Chen, W.Q. Propagation of non-axisymmetric waves in an infinite soft electroactive hollow cylinder under uniform biasing fields. Int. J. Solids Struct. 2016, 81, 262–273. [Google Scholar] [CrossRef]
- Wu, B.; Destrade, M.; Chen, W.Q. Nonlinear response and axisymmetric wave propagation in functionally graded soft electro-active tubes. Int. J. Mech. Sci. 2020, 187, 106006. [Google Scholar] [CrossRef]
- Bertoldi, K.; Gei, M. Instabilities in multilayered soft dielectrics. J. Mech. Phys. Solids 2011, 59, 18–42. [Google Scholar] [CrossRef]
- Rudykh, S.; Bhattacharya, K.; DeBotton, G. Multiscale instabilities in soft heterogeneous dielectric elastomers. Proc. R. Soc. Math. Phys. Eng. Sci. 2014, 470, 20130618. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Riccobelli, D.; Chen, Y.; Chen, W.Q.; Ciarletta, P. Tunable morphing of electroactive dielectric-elastomer balloons. Proc. R. Soc. A 2023, 479, 20230358. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, W.; Bao, R.; Chen, W.Q. Tuning elastic waves in soft phononic crystal cylinders via large deformation and electromechanical coupling. J. Appl. Mech. 2018, 85, 031004. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, B.; Destrade, M.; Chen, W.Q. Voltage-controlled topological interface states for bending waves in soft dielectric phononic crystal plates. Int. J. Solids Struct. 2022, 259, 112013. [Google Scholar] [CrossRef]
- Shmuel, G. Electrostatically tunable band gaps in finitely extensible dielectric elastomer fiber composites. Int. J. Solids Struct. 2013, 50, 680–686. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Y.; Hu, X.; Bao, R.; Wu, B.; Chen, W.Q. Vibrations and waves in soft dielectric elastomer structures. Int. J. Mech. Sci. 2023, 239, 107885. [Google Scholar] [CrossRef]
- Lu, T.; Ma, C.; Wang, T. Mechanics of dielectric elastomer structures: A review. Extrem. Mech. Lett. 2020, 38, 100752. [Google Scholar] [CrossRef]
- Zhu, F.B.; Zhang, C.L.; Qian, J.; Chen, W.Q. Mechanics of dielectric elastomers: Materials, structures, and devices. J. Zhejiang Univ. Sci. A 2016, 17, 1–21. [Google Scholar]
- Wu, B.; Zhang, C.; Zhang, C.; Chen, W.Q. Theory of electroelasticity accounting for biasing fields: Retrospect, comparison and perspective. Adv. Mech. 2016, 46, 201601. [Google Scholar]
- Suo, Z. Theory of dielectric elastomers. Acta Mech. Solida Sin. 2010, 23, 549–578. [Google Scholar] [CrossRef]
- Su, Y.; Broderick, H.C.; Chen, W.Q.; Destrade, M. Wrinkles in soft dielectric plates. J. Mech. Phys. Solids 2018, 119, 298–318. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, Z. Method to analyze electromechanical stability of dielectric elastomers. Appl. Phys. Lett. 2007, 91, 061921. [Google Scholar] [CrossRef]
- Dorfmann, L.; Ogden, R.W. Nonlinear response of an electroelastic spherical shell. Int. J. Eng. Sci. 2014, 85, 163–174. [Google Scholar] [CrossRef]
- Dorfmann, L.; Ogden, R.W. Instabilities of an electroelastic plate. Int. J. Eng. Sci. 2014, 77, 79–101. [Google Scholar] [CrossRef]
- Zhao, X.; Hong, W.; Suo, Z. Electromechanical hysteresis and coexistent states in dielectric elastomers. Phys. Rev. B 2007, 76, 134113. [Google Scholar] [CrossRef]
- Nicolau-Kuklińska, A.; Latko-Durałek, P.; Nakonieczna, P.; Dydek, K.; Boczkowska, A.; Grygorczuk, J. A new electroactive polymer based on carbon nanotubes and carbon grease as compliant electrodes for electroactive actuators. J. Intell. Mater. Syst. Struct. 2018, 29, 1520–1530. [Google Scholar] [CrossRef]
- Carpi, F.; Chiarelli, P.; Mazzoldi, A.; De Rossi, D. Electromechanical characterisation of dielectric elastomer planar actuators: Comparative evaluation of different electrode materials and different counterloads. Sens. Actuators A Phys. 2003, 107, 85–95. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, Z. Electrostriction in elastic dielectrics undergoing large deformation. J. Appl. Phys. 2008, 104, 123530. [Google Scholar] [CrossRef]
- Plante, J.S.; Dubowsky, S. Large-scale failure modes of dielectric elastomer actuators. Int. J. Solids Struct. 2006, 43, 7727–7751. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Leng, J.; Yu, K.; Sun, S. Electromechanical stability of dielectric elastomer. Appl. Phys. Lett. 2009, 94, 211901, Erratum on: Appl. Phys. Lett. 2009, 95, 211901. [Google Scholar]
- Norris, A.N. Comment on “Method to analyze electromechanical stability of dielectric elastomers”. Appl. Phys. Lett. 2008, 92, 026101. [Google Scholar] [CrossRef]
- Kofod, G.; Sommer-Larsen, P.; Kornbluh, R.; Pelrine, R. Actuation response of polyacrylate dielectric elastomers. J. Intell. Mater. Syst. Struct. 2003, 14, 787–793. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L.; Zhang, Z.; Shi, L.; Leng, J. Comment on “Method to analyze electromechanical stability of dielectric elastomers”. Appl. Phys. Lett. 2008, 93, 106101. [Google Scholar] [CrossRef]
- Díaz-Calleja, R.; Ri, E.; Sanchis, M.J. On electromechanical stability of dielectric elastomers. Appl. Phys. Lett. 2008, 93, 101902. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Q. Harnessing large deformation and instabilities of soft dielectrics: Theory, experiment, and application. Appl. Phys. Rev. 2014, 1, 021304. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Bharti, V.; Zhao, X. Giant electrostriction and relaxor ferroelectric behavior in electron-irradiated poly (vinylidene fluoride-trifluoroethylene) copolymer. Science 1998, 280, 2101–2104. [Google Scholar] [CrossRef]
- Zhenyi, M.; Scheinbeim, J.I.; Lee, J.W.; Newman, B.A. High field electrostrictive response of polymers. J. Polym. Sci. Part Polym. Phys. 1994, 32, 2721–2731. [Google Scholar] [CrossRef]
- Pelrine, R.E.; Kornbluh, R.D.; Joseph, J.P. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators A Phys. 1998, 64, 77–85. [Google Scholar] [CrossRef]
- Shankar, R.; Ghosh, T.K.; Spontak, R.J. Electroactive nanostructured polymers as tunable actuators. Adv. Mater. 2007, 19, 2218–2223. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, Z. Theory of dielectric elastomers capable of giant deformation of actuation. Phys. Rev. Lett. 2010, 104, 178302. [Google Scholar] [CrossRef]
- Su, Y.; Wu, B.; Chen, W.Q.; Lü, C. Optimizing parameters to achieve giant deformation of an incompressible dielectric elastomeric plate. Extrem. Mech. Lett. 2018, 22, 60–68. [Google Scholar] [CrossRef]
- Li, B.; Zhou, J.; Chen, H. Electromechanical stability in charge-controlled dielectric elastomer actuation. Appl. Phys. Lett. 2011, 99, 244101. [Google Scholar] [CrossRef]
- Lu, T.; Keplinger, C.; Arnold, N.; Bauer, S.; Suo, Z. Charge localization instability in a highly deformable dielectric elastomer. Appl. Phys. Lett. 2014, 104, 022905. [Google Scholar] [CrossRef]
- Keplinger, C.; Kaltenbrunner, M.; Arnold, N.; Bauer, S. R¨ontgen’s electrode-free elastomer actuators without electromechanical pull-in instability. Proc. Natl. Acad. Sci. USA 2010, 107, 4505–4510. [Google Scholar] [CrossRef]
- Su, Y.P.; Chen, W.Q.; Destrade, M. Tuning the pull-in instability of soft dielectric elastomers through loading protocols. Int. J. Non-Linear Mech. 2019, 113, 62–66. [Google Scholar] [CrossRef]
- Veselov, D.S.; Voronov, Y.A.; Vanyukhin, K.D. Researching of dielectric membrane films obtained by reactive magnetron sputtering. Phys. Procedia 2015, 72, 495–499. [Google Scholar] [CrossRef]
- Wu, X.; Chen, X.; Zhang, Q.M.; Tan, D.Q. Advanced dielectric polymers for energy storage. Energy Storage Mater. 2022, 44, 29–47. [Google Scholar] [CrossRef]
- Li, P.; Yu, J.; Jiang, S.; Fang, H.; Liu, K.; Hou, H. Dielectric, mechanical and thermal properties of all-organic PI/PSF composite films by in situ polymerization. e-Polymers 2020, 20, 226–232. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Liu, Y.; Li, L.; Liu, Y.; Wang, Q. Dielectric polymers for high-temperature capacitive energy storage. Chem. Soc. Rev. 2021, 50, 6369–6400. [Google Scholar] [CrossRef]
- Huang, L.; Liu, S.; Van Tassell, B.J.; Liu, X.; Byro, A.; Zhang, H.; Lel, E.S.; Akins, D.L.; Steingart, D.A.; Li, J.; et al. Structure and performance of dielectric films based on self-assembled nanocrystals with a high dielectric constant. Nanotechnology 2013, 24, 415602. [Google Scholar] [CrossRef]
- Li, C.; Shi, L.; Yang, W.; Zhou, Y.; Li, X.; Zhang, C.; Yang, Y. All polymer dielectric films for achieving high energy density film capacitors by blending poly (vinylidene fluoride-trifluoroethylene-chlorofluoroethylene) with aromatic polythiourea. Nanoscale Res. Lett. 2020, 15, 36. [Google Scholar] [CrossRef]
- Tews, A.M.; Pope, K.L.; Snyder, A.J. Pressure-volume characteristics of dielectric elastomer diaphragms. In Smart Structures and Materials 2003: Electroactive Polymer Actuators and Devices (EAPAD); SPIE: Bellingham, WA, USA, 2003; Volume 5051, pp. 159–169. [Google Scholar]
- He, T.; Zhao, X.; Suo, Z. Dielectric elastomer membranes undergoing inhomogeneous deformation. J. Appl. Phys. 2009, 106, 083522. [Google Scholar] [CrossRef]
- Wang, B.; Wang, Z.; He, T. Investigation on the viscoelastic behaviors of a circular dielectric elastomer membrane undergoing large deformation. AIP Adv. 2016, 6, 125127. [Google Scholar] [CrossRef]
- He, T.; Cui, L.; Chen, C.; Suo, Z. Nonlinear deformation analysis of a dielectric elastomer membrane—Spring system. Smart Mater. Struct. 2010, 19, 085017. [Google Scholar] [CrossRef]
- Wang, H.M. Viscoelastic analysis of a spring-connected dielectric elastomer actuator undergoing large inhomogeneous deformation. Int. J. Mech. Sci. 2018, 136, 17–23. [Google Scholar] [CrossRef]
- Wang, H.; Lei, M.; Cai, S. Viscoelastic deformation of a dielectric elastomer membrane subject to electromechanical loads. J. Appl. Phys. 2013, 113, 213508. [Google Scholar] [CrossRef]
- Stoyanov, H.; Kofod, G.; Gerhard, R. A co-axial dielectric elastomer actuator. Adv. Sci. Technol. 2009, 61, 81–84. [Google Scholar]
- Cameron, C.G.; Szabo, J.P.; Johnstone, S.; Massey, J.; Leidner, J. Linear actuation in coextruded dielectric elastomer tubes. Sens. Actuators A Phys. 2008, 147, 286–291. [Google Scholar] [CrossRef]
- Brown, N.M.; Lai, F.C. Electrohydrodynamic gas pump in a vertical tube. J. Electrost. 2009, 67, 709–714. [Google Scholar] [CrossRef]
- Wang, F.; Yuan, C.; Lu, T.; Wang, T.J. Anomalous bulging behaviors of a dielectric elastomer balloon under internal pressure and electric actuation. J. Mech. Phys. Solids 2017, 102, 1–16. [Google Scholar] [CrossRef]
- Zhu, J.; Stoyanov, H.; Kofod, G.; Suo, Z. Large deformation and electromechanical instability of a dielectric elastomer tube actuator. J. Appl. Phys. 2010, 108, 074113. [Google Scholar] [CrossRef]
- He, T.; Wang, Z. Electro-viscoelastic performance of a tubular dielectric elastomer actuator. Int. J. Mech. Mater. Des. 2019, 15, 199–212. [Google Scholar] [CrossRef]
- Hong, W. Modeling viscoelastic dielectrics. J. Mech. Phys. Solids 2011, 59, 637–650. [Google Scholar] [CrossRef]
- Su, Y.; Zhou, W.; Chen, W.Q.; Lü, C. On buckling of a soft incompressible electroactive hollow cylinder. Int. J. Solids Struct. 2016, 97, 400–416. [Google Scholar] [CrossRef]
- Bortot, E. Analysis of multilayer electro-active tubes under different constraints. J. Intell. Mater. Syst. Struct. 2019, 30, 45–62. [Google Scholar] [CrossRef]
- Su, Y. Voltage-controlled instability transitions and competitions in a finitely deformed dielectric elastomer tube. Int. J. Eng. Sci. 2020, 157, 103380. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Du, J.; Wu, H. Voltage-induced torsion of a fiber-reinforced tubular dielectric elastomer actuator. Compos. Sci. Technol. 2017, 140, 106–115. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Du, J.; Wu, H. Voltage-driven nonuniform axisymmetric torsion of a tubular dielectric elastomer actuator reinforced with one family of inextensible fibers. Eur. J. Mech.-A/Solids 2018, 71, 386–393. [Google Scholar] [CrossRef]
- Bazaev, K.; Cohen, N. Electrically-induced twist in geometrically incompatible dielectric elastomer tubes. Int. J. Solids Struct. 2022, 250, 111707. [Google Scholar] [CrossRef]
- Huang, J.; Shian, S.; Suo, Z.; Clarke, D.R. Maximizing the energy density of dielectric elastomer generators using equi-biaxial loading. Adv. Funct. Mater. 2013, 23, 5056–5061. [Google Scholar] [CrossRef]
- Lv, X.; Liu, L.; Liu, Y.; Leng, J. Dynamic performance of dielectric elastomer balloon incorporating stiffening and damping effect. Smart Mater. Struct. 2018, 27, 105036. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Foo, C.C.; Godaba, H.; Zhu, J.; Yap, C.H. The mechanism for large-volume fluid pumping via reversible snap-through of dielectric elastomer. J. Appl. Phys. 2017, 122, 084503. [Google Scholar] [CrossRef]
- Hosoya, N.; Masuda, H.; Maeda, S. Balloon dielectric elastomer actuator speaker. Appl. Acoust. 2019, 148, 238–245. [Google Scholar] [CrossRef]
- Heydt, R.P.; Kornbluh, R.; Eckerle, J.; Pelrine, R.; Carpi, F.; De Rossi, D.; Kornbluh, R.; Pelrine, R.; Sommer-Larsen, P. Dielectric elastomer loudspeakers. In Dielectric Elastomers as Electromechanical Transducers; Elsevier: Amsterdam, The Netherlands, 2008; pp. 313–320. [Google Scholar]
- Rudykh, S.; Bhattacharya, K.; Debotton, G. Snap-through actuation of thick-wall electroactive balloons. Int. J. Non-Linear Mech. 2012, 47, 206–209. [Google Scholar]
- Mao, R.; Wu, B.; Carrera, E.; Chen, W.Q. Electrostatically tunable small-amplitude free vibrations of pressurized electro-active spherical balloons. Int. J. Non-Linear Mech. 2019, 117, 103237. [Google Scholar] [CrossRef]
- Bortot, E. Analysis of multilayer electro-active spherical balloons. J. Mech. Phys. Solids 2017, 101, 250–267. [Google Scholar] [CrossRef]
- Su, Y.; Wu, B.; Chen, W.Q.; Destrade, M. Finite bending and pattern evolution of the associated instability for a dielectric elastomer slab. Int. J. Solids Struct. 2019, 158, 191–209. [Google Scholar] [CrossRef]
- Li, T.; Li, G.; Liang, Y.; Cheng, T.; Dai, J.; Yang, X.; Liu, B.; Zeng, Z.; Huang, Z.; Luo, Y.; et al. Fast-moving soft electronic fish. Sci. Adv. 2017, 3, e1602045. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chen, X.; Zhou, F.; Liang, Y.; Xiao, Y.; Cao, X.; Zhang, Z.; Zhang, M.; Wu, B.; Yin, S.; et al. Self-powered soft robot in the Mariana Trench. Nature 2021, 591, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.Y.; Keplinger, C.; Whitesides, G.M.; Suo, Z. Ionic skin. Adv. Mater. 2014, 26, 7608–7614. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Lou, J.; Du, J.; Wang, J. Finite bending of a dielectric elastomer actuator and pre-stretch effects. Int. J. Mech. Sci. 2017, 122, 120–128. [Google Scholar] [CrossRef]
- Su, Y.; Wu, B.; Chen, W.Q.; Destrade, M. Pattern evolution in bending dielectric-elastomeric bilayers. J. Mech. Phys. Solids 2020, 136, 103670. [Google Scholar] [CrossRef]
- Su, Y.; Ogden, R.W.; Destrade, M. Bending control and stability of functionally graded dielectric elastomers. Extrem. Mech. Lett. 2021, 43, 101162. [Google Scholar] [CrossRef]
- Fu, Y.; Xie, Y.; Dorfmann, L. A reduced model for electrodes-coated dielectric plates. Int. J. Non-Linear Mech. 2018, 106, 60–69. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. Nonlinear electroelastostatics: Incremental equations and stability. Int. J. Eng. Sci. 2010, 48, 1–14. [Google Scholar] [CrossRef]
- Mao, G.; Wu, L.; Liang, X.; Qu, S. Morphology of voltage-triggered ordered wrinkles of a dielectric elastomer sheet. J. Appl. Mech. 2017, 84, 111005. [Google Scholar] [CrossRef]
- Mao, G.; Wu, L.; Fu, Y.; Liu, J.; Qu, S. Voltage-controlled radial wrinkles of a trumpet-like dielectric elastomer structure. AIP Adv. 2018, 8, 035314. [Google Scholar] [CrossRef]
- Díaz-Calleja, R.; Llovera-Segovia, P.; Quijano-López, A. Complex bifurcation maps in electroelastic elastomeric plates. Int. J. Solids Struct. 2017, 113, 70–84. [Google Scholar] [CrossRef]
- Yang, S.; Zhao, X.; Sharma, P. Revisiting the instability and bifurcation behavior of soft dielectrics. J. Appl. Mech. 2017, 84, 031008. [Google Scholar] [CrossRef]
- Su, Y.; Chen, W.Q.; Dorfmann, L.; Destrade, M. The effect of an exterior electric field on the instability of dielectric plates. Proc. R. Soc. A 2020, 476, 20200267. [Google Scholar] [CrossRef] [PubMed]
- Dorfmann, L.; Ogden, R.W. Electroelastic plate instabilities based on the Stroh method in terms of the energy function Ω∗(F, DL). Mech. Res. Commun. 2019, 96, 67–74. [Google Scholar] [CrossRef]
- Broderick, H.C.; Righi, M.; Destrade, M.; Ogden, R.W. Stability analysis of charge-controlled soft dielectric plates. Int. J. Eng. Sci. 2020, 151, 103280. [Google Scholar] [CrossRef]
- Destrade, M.; Annaidh, A.N.; Coman, C.D. Bending instabilities of soft biological tissues. Int. J. Solids Struct. 2009, 46, 4322–4330. [Google Scholar] [CrossRef]
- Melnikov, A.; Dorfmann, L.; Ogden, R.W. Bifurcation of finitely deformed thick-walled electroelastic spherical shells subject to a radial electric field. Int. J. Non-Linear Mech. 2020, 121, 103429. [Google Scholar] [CrossRef]
- Bortot, E.; Shmuel, G. Prismatic bifurcations of soft dielectric tubes. Int. J. Eng. Sci. 2018, 124, 104–114. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, Y.; Su, Y. Bifurcation of a finitely deformed functionally graded dielectric elastomeric tube. Int. J. Non-Linear Mech. 2020, 127, 103593. [Google Scholar] [CrossRef]
- Fu, Y.B.; Xie, Y. Stability of pear-shaped configurations bifurcated from a pressurized spherical balloon. J. Mech. Phys. Solids 2014, 68, 33–44. [Google Scholar] [CrossRef]
- Xie, Y.X.; Liu, J.C.; Fu, Y.B. Bifurcation of a dielectric elastomer balloon under pressurized inflation and electric actuation. Int. J. Solids Struct. 2016, 78, 182–188. [Google Scholar] [CrossRef]
- Löwe, C.; Zhang, X.; Kovacs, G. Dielectric elastomers in actuator technology. Adv. Eng. Mater. 2005, 7, 361–367. [Google Scholar] [CrossRef]
- Mao, G.; Xiang, Y.; Huang, X.; Hong, W.; Lu, T.; Qu, S. Viscoelastic effect on the wrinkling of an inflated dielectric-elastomer balloon. J. Appl. Mech. 2018, 85, 071003. [Google Scholar] [CrossRef]
- Haughton, D.M.; Ogden, R. On the incremental equations in non-linear elasticity—II. Bifurcation of pressurized spherical shells. J. Mech. Phys. Solids 1978, 26, 111–138. [Google Scholar] [CrossRef]
- Bustamante, R. Transversely isotropic non-linear electro-active elastomers. Acta Mech. 2009, 206, 237–259. [Google Scholar] [CrossRef]


| Type | Maximum Strain (%) | Maximum Pressure (MPa) | Specific Elastic Energy Density (J/g) | Relative Speed (Full Cycle) |
|---|---|---|---|---|
| dielectric elastomer (acrylic with prestrain) | 380 | 7.2 | 3.4 | medium |
| dielectric elastomer (silicone with prestrain) | 63 | 3 | 0.75 | fast |
| dielectric eastomer (Silicone—nominal prestrain) | 32 | 1.36 | 0.22 | fast |
| dielectric elastomer (polyurethane—nominal prestrain) | 11 | 1.6 | 0.087 | fast |
| electrostrictor polymer (P(VDF-TrFE-CFE)) | 4.5 | 1.1 | fast | |
| electrostatic devices (integrated force array) | 50 | 0.03 | 0.0015 | fast |
| electromagnetic (voice coil) | 50 | 0.1 | 0.003 | fast |
| piezoelectric ceramic (PZT) | 0.2 | 110 | 0.013 | fast |
| piezoelectric single crystal (PZT-PT) | 1.7 | 131 | 0.13 | fast |
| piezoelectric polymer (PVDF) | 0.1 | 4.8 | 0.0013 | fast |
| relaxor ferroelectric polymer (PVDF-TrFE-CFE) | 7 | 21 | 0.73 | fast |
| shape memory alloy (TiNi) | >5 | >200 | >15 | slow |
| shape memory polymer (polyurethane) | 100 | 4 | 2 | slow |
| thermomechanical twisted polymer fiber (nylon-6,6 monofilament) | 35 | 16 | slow | |
| thermal (expansion—Al dT = 500 K) | 1 | 78 | 0.15 | slow |
| conducting polymer (PANI) | 0.85 | 100 | 0.32 | slow |
| IPMC | 3 | 30 | ||
| carbon naotubes (CNT paper) | 1 | 27 | 0.04 | slow-fast |
| magnetostrictive (terfenol-D) | 0.2 | 70 | 0.025 | fast |
| natural muscle (peaks in nature) | 100 | 0.8 | 0.04 | slow-fast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Shen, X.; Zhao, Z.; Wu, B.; Chen, W. Electromechanical Deformations and Bifurcations in Soft Dielectrics: A Review. Materials 2024, 17, 1499. https://doi.org/10.3390/ma17071499
Su Y, Shen X, Zhao Z, Wu B, Chen W. Electromechanical Deformations and Bifurcations in Soft Dielectrics: A Review. Materials. 2024; 17(7):1499. https://doi.org/10.3390/ma17071499
Chicago/Turabian StyleSu, Yipin, Xudong Shen, Zinan Zhao, Bin Wu, and Weiqiu Chen. 2024. "Electromechanical Deformations and Bifurcations in Soft Dielectrics: A Review" Materials 17, no. 7: 1499. https://doi.org/10.3390/ma17071499
APA StyleSu, Y., Shen, X., Zhao, Z., Wu, B., & Chen, W. (2024). Electromechanical Deformations and Bifurcations in Soft Dielectrics: A Review. Materials, 17(7), 1499. https://doi.org/10.3390/ma17071499








