Diffusivities and Atomic Mobilities in BCC Ti-Fe-Cr Alloys
Abstract
:1. Introduction
2. Experimental Procedure
3. Methodology
3.1. Extraction of Inter-Diffusion Coefficients
3.2. Extraction of Impurity Diffusion Coefficients
3.3. Atomic Mobility and Diffusion Coefficient
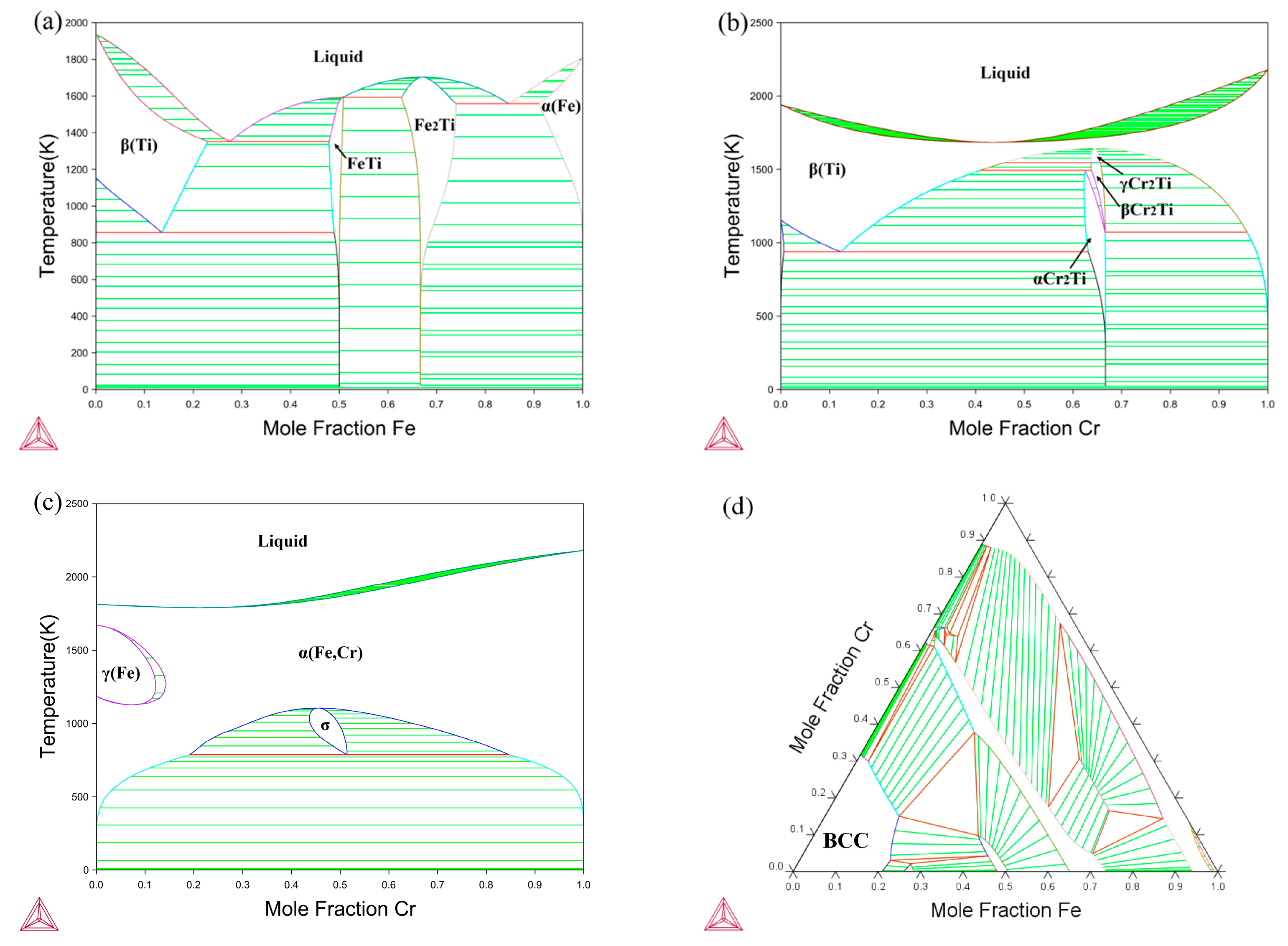
4. Results and Discussion
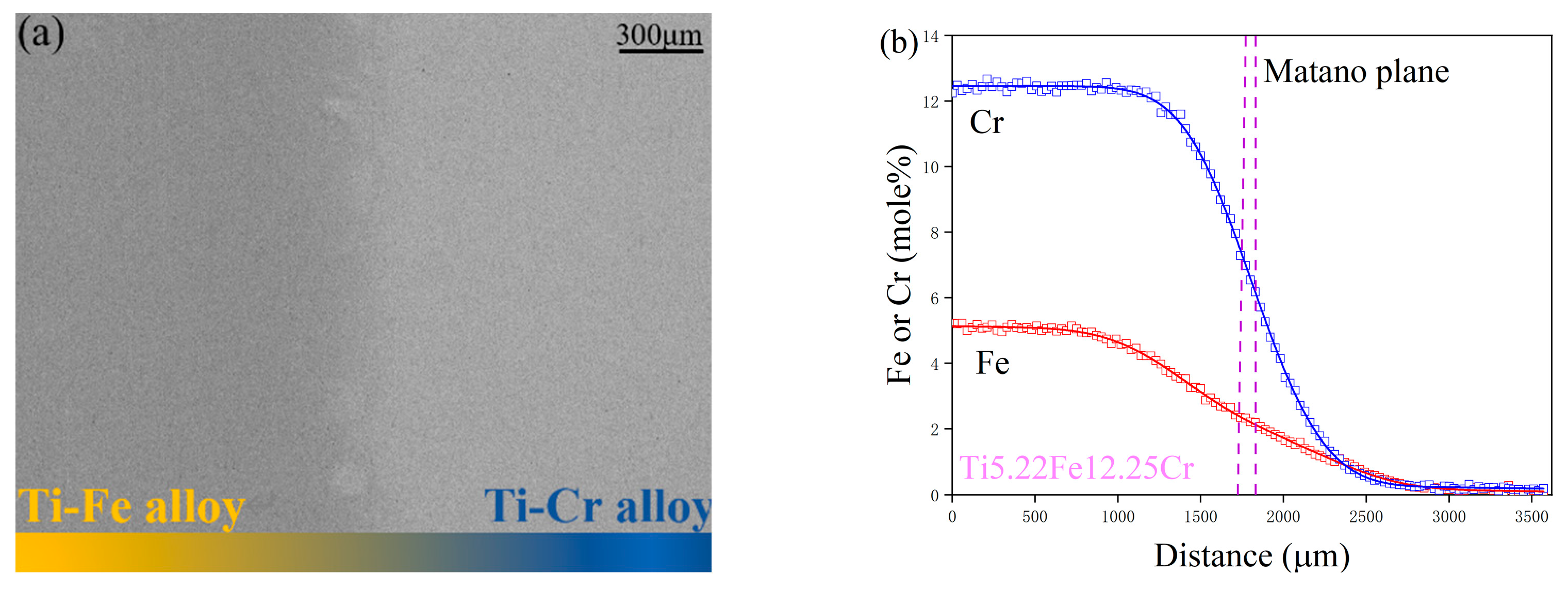
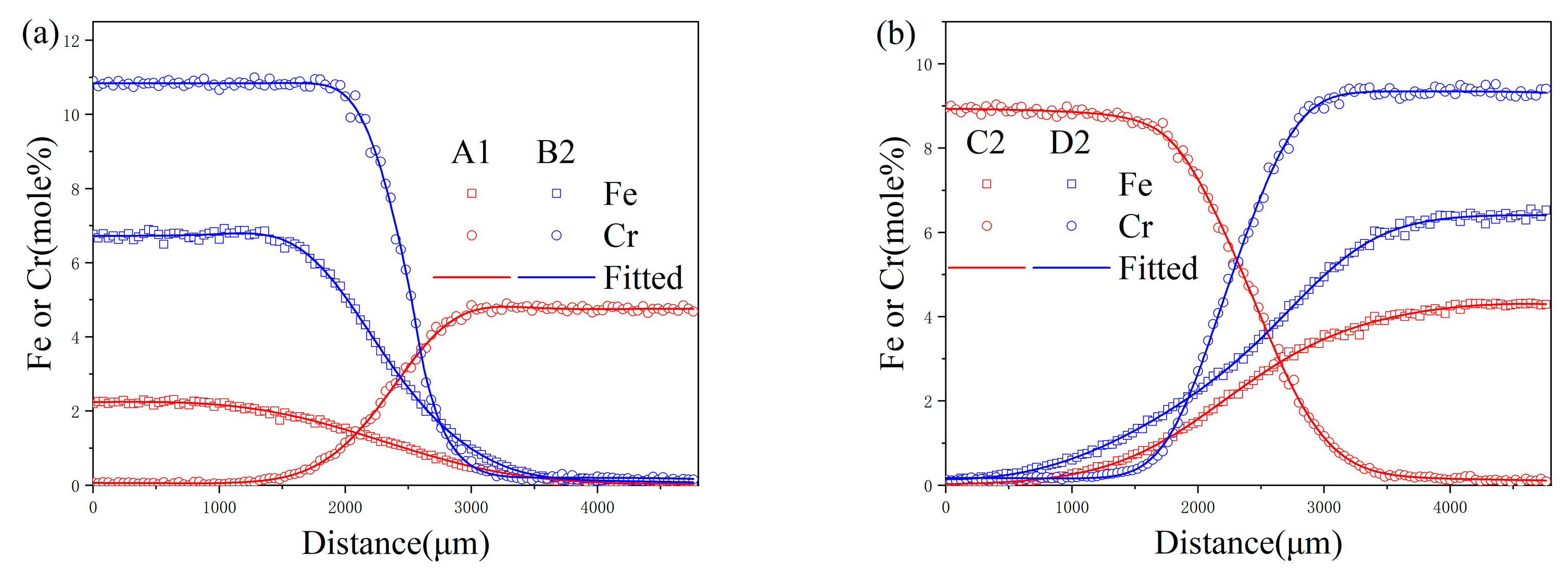
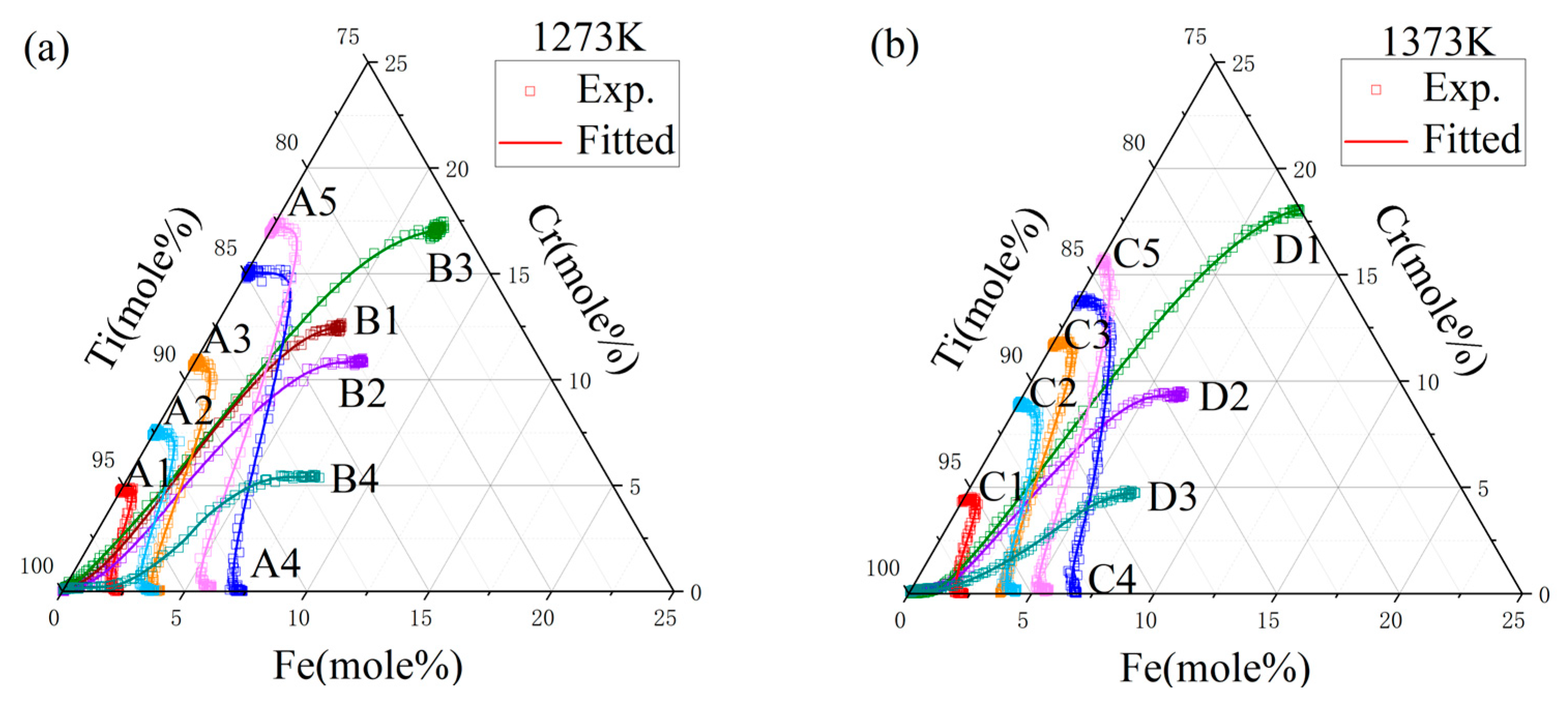
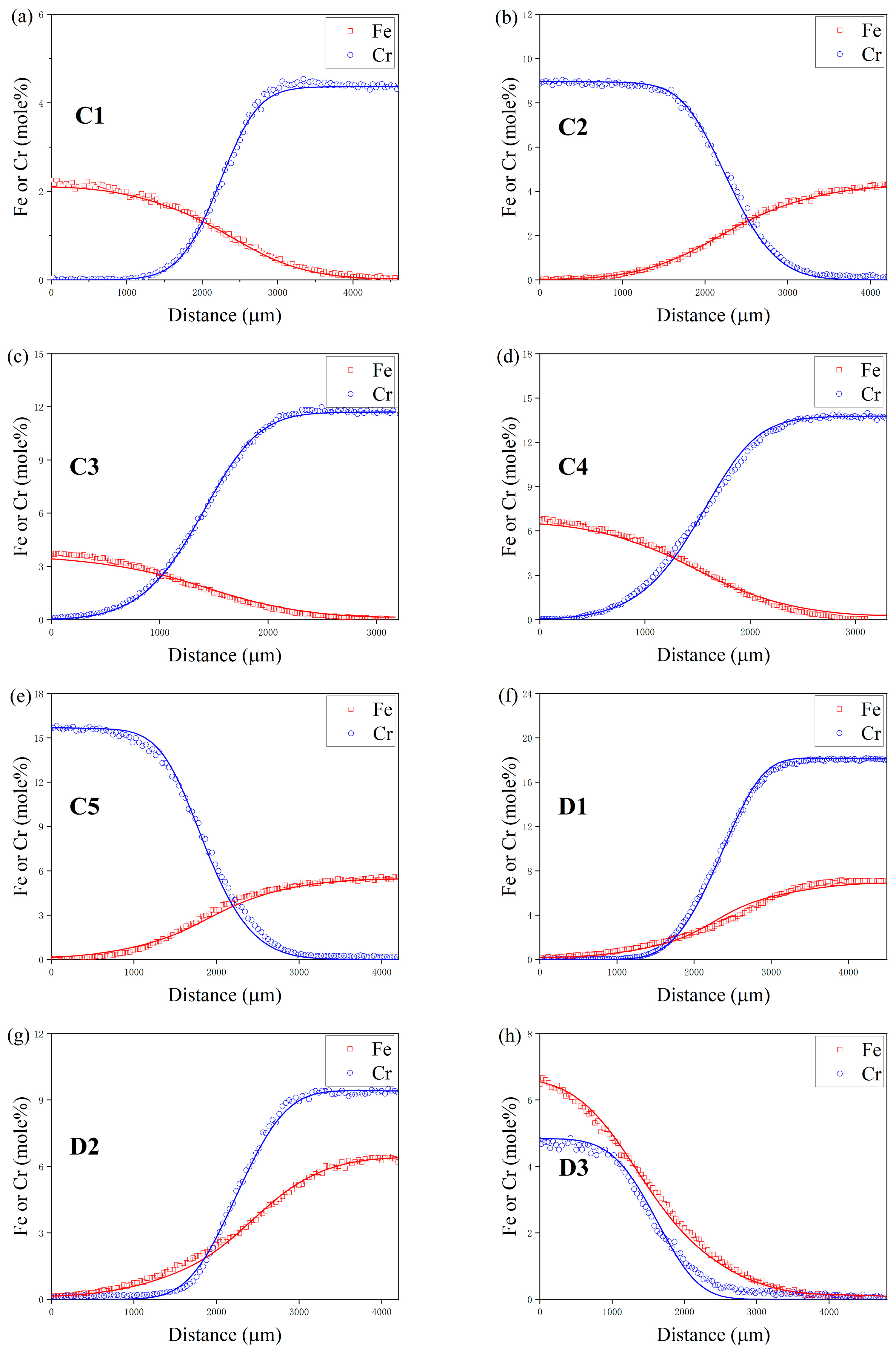
4.1. Composition–Distance Profiles and Diffusion Paths
4.2. Diffusion Coefficients
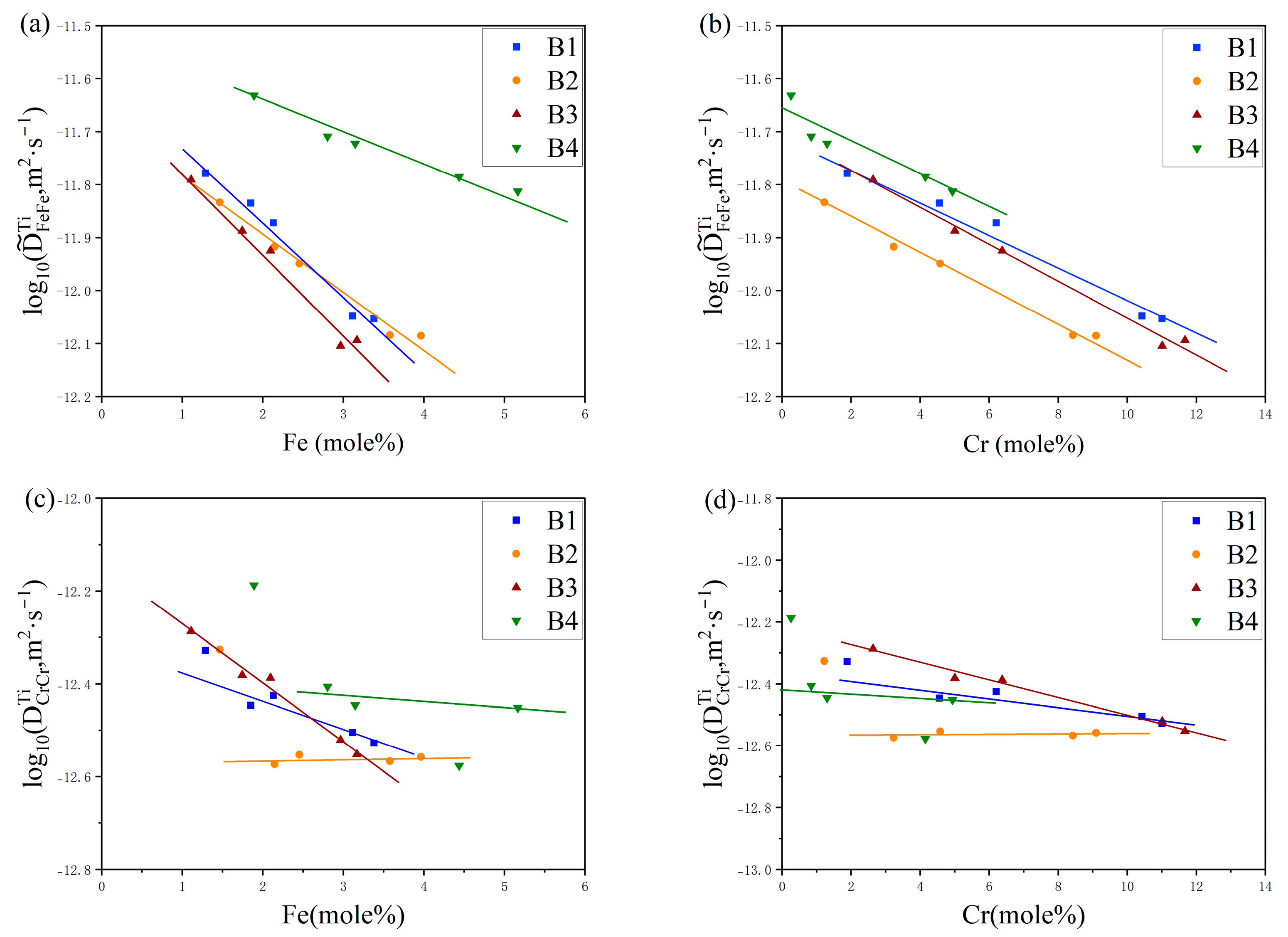
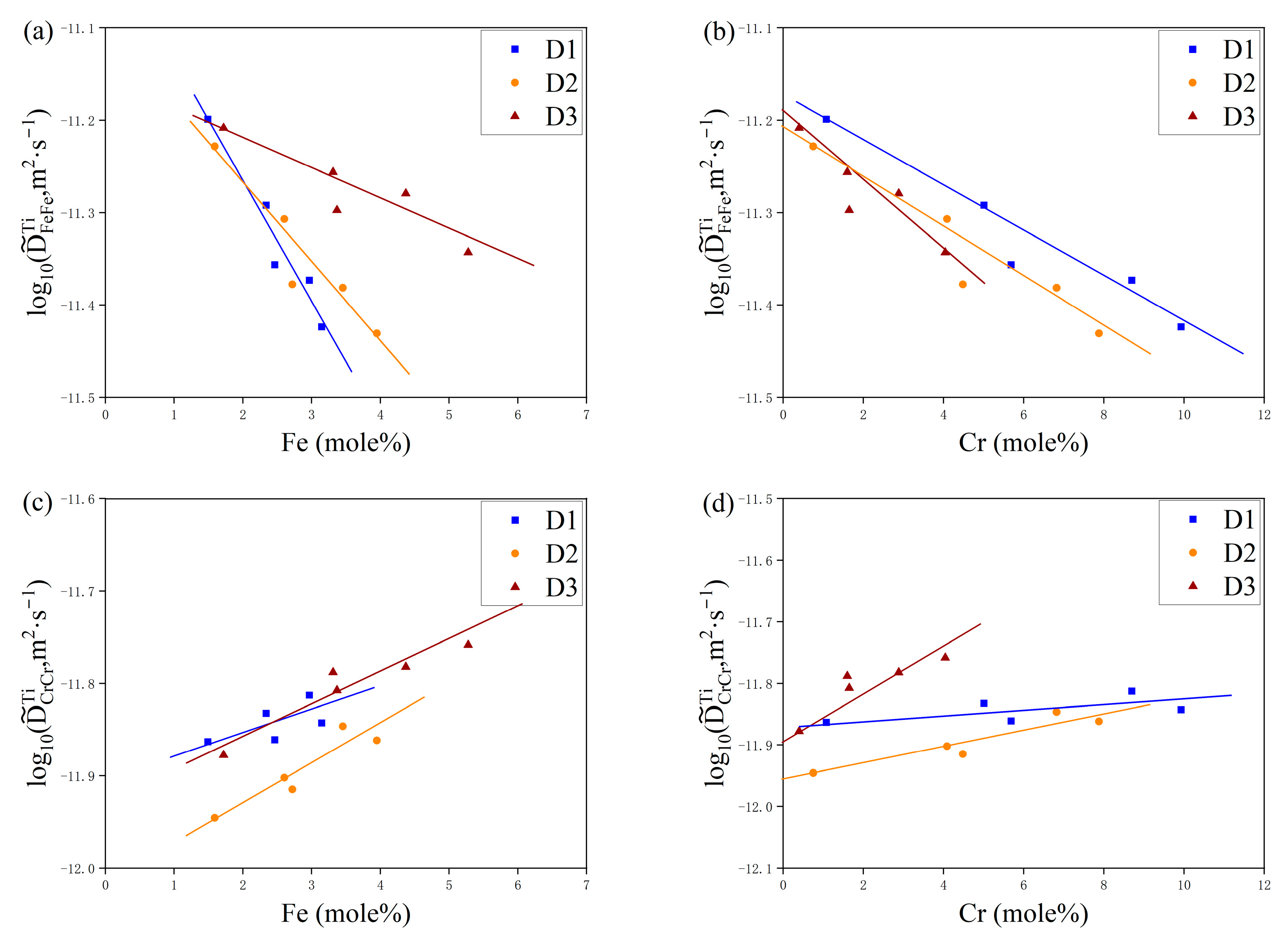
5. Atomic Mobility Optimization
6. Conclusions
- (1)
- Observations from the study elucidate that Fe manifests a higher diffusion velocity than Cr in the bcc Ti-Fe-Cr alloy when subjected to the same thermal conditions. The diffusion rates of both elements in the alloy are positively correlated with the temperature; as the temperature increases, the diffusion rate also increases.
- (2)
- At 1273 K and 1373 K, the main diffusion coefficient decreases with the increase in Fe and Cr elements. The main diffusion coefficient slowly decreases with the increase in Fe and Cr elements at 1273 K, but increases with the increase in Fe and Cr elements at 1373 K.
- (3)
- Using the atomic mobility parameters, the diffusion process of alloy in diffusion couple was simulated in DICTRA software. A comparative analysis of the simulation outcomes with the experimental data highlighted minor discrepancies, all of which fell within the bounds of acceptable error margins. This congruence attests to the reliability and accuracy of the atomic mobility parameters, validating the comprehensive approach employed in matching the experimental findings with the theoretical models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiu, C.; Fones, A.; Hamilton, H.G.C.; Adkins, N.J.E.; Attallah, M.M. A New Approach to Develop Palladium-Modified Ti-Based Alloys for Biomedical Applications. Mater. Des. 2016, 109, 98–111. [Google Scholar] [CrossRef]
- Banerjee, D.; Williams, J.C. Perspectives on Titanium Science and Technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Y.; Zhang, D. Multiscale Characterization of Erosion of TA2 Titanium Alloy Welded Joints. Front. Mater. 2022, 9, 910319. [Google Scholar] [CrossRef]
- Froes, F.H.; Imam, A. Titanium: A Historic and Current Perspective, Part II. AMP Tech. Artic. 2018, 176, 18–24. [Google Scholar] [CrossRef]
- Faga, M.G.; Priarone, P.C.; Robiglio, M.; Settineri, L.; Tebaldo, V. Technological and Sustainability Implications of Dry, near-Dry, and Wet Turning of Ti-6Al-4V Alloy. Int. J. Precis. Eng. Manuf.-Green Technol. 2017, 4, 129–139. [Google Scholar] [CrossRef]
- Uçak, N.; Aslantas, K.; Çiçek, A. Experimental Evaluation of Tool Wear and Surface Roughness under Different Conditions in High-Speed Turning of Ti6Al4V Alloy. J. Mater. Manuf. 2023, 2, 1–10. [Google Scholar] [CrossRef]
- Robertson, I.M.; Schaffer, G.B. Review of Densification of Titanium Based Powder Systems in Press and Sinter Processing. Powder Metall. 2010, 53, 146–162. [Google Scholar] [CrossRef]
- Yolton, C.F.; Froes, F.H.; Malone, R.F. Alloying Element Effects in Metastable Beta Titanium Alloys. Metall. Trans. A 1979, 10, 132–134. [Google Scholar] [CrossRef]
- Gunawarman, B.; Niinomi, M.; Akahori, T.; Souma, T.; Ikeda, M.; Toda, H. Mechanical Properties and Microstructures of Low Cost β Titanium Alloys for Healthcare Applications. Mater. Sci. Eng. C 2005, 25, 304–311. [Google Scholar] [CrossRef]
- Gunawarman; Niinomi, M.; Akahori, T.; Souma, T.; Ikeda, M.; Toda, H.; Terashima, K. Fatigue Characteristics of Low Cost β Titanium Alloys for Healthcare and Medical Applications. Mater. Trans. 2005, 46, 1570–1577. [Google Scholar] [CrossRef]
- Wang, J.; Qin, Z.; Xiong, F.; Wang, S.; Lu, X.; Li, C. Design and Preparation of Low-Cost A + β Titanium Alloy Based on Assessment of Ti-Al-Fe-Cr System. Mater. Sci. Eng. A 2018, 732, 63–69. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, L.; Tang, B. Binary Diffusion Behaviour in Ti–X (X = Al, Mo, V, Cr, Fe) Alloys. Int. J. Mater. Res. 2018, 109, 569–572. [Google Scholar] [CrossRef]
- Li, W.; Tang, B.; Cui, Y.-W.; Hu, R.; Chang, H.; Li, J.; Zhou, L. Assessment of Diffusion Mobility for the Bcc Phase of the Ti–Al–Cr System. Calphad 2011, 35, 384–390. [Google Scholar] [CrossRef]
- Takahashi, T.; Minamino, Y. Ternary Diffusion and Thermodynamic Interaction in the β Solid Solutions of Ti–Al–Fe Alloys at 1423 K. J. Alloys Compd. 2012, 545, 168–175. [Google Scholar] [CrossRef]
- Wu, D.; Hao, M.; Zhang, T.; Wang, Z.; Wang, J.; Rao, G.; Zhang, L.; Ding, C.; Zhou, K.; Liu, L.; et al. Heterostructures Enhance Simultaneously Strength and Ductility of a Commercial Titanium Alloy. Acta Mater. 2023, 257, 119182. [Google Scholar] [CrossRef]
- Słyk, E.; Skóra, T.; Kondrat, S. How Macromolecules Softness Affects Diffusion under Crowding. Soft Matter 2022, 18, 5366–5370. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, W.; Metzler, R.; Cherstvy, A.G. Anomalous Diffusion, Nonergodicity, Non-Gaussianity, and Aging of Fractional Brownian Motion with Nonlinear Clocks. Phys. Rev. E 2023, 108, 034113. [Google Scholar] [CrossRef]
- De Kee, D.; Liu, Q.; Hinestroza, J. Viscoelastic (Non-Fickian) Diffusion. Can. J. Chem. Eng. 2005, 83, 913–929. [Google Scholar] [CrossRef]
- Edwards, D.A. Non-Fickian Diffusion in Thin Polymer Films. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 981–997. [Google Scholar] [CrossRef]
- Klugkist, P.; Herzig, C. Tracer Diffusion of Titanium in α-Iron. Phys. Status Solidi A 1995, 148, 413–421. [Google Scholar] [CrossRef]
- Peart, R.F.; Tomlin, D.H. Diffusion of Solute Elements in Beta-Titanium. Acta Metall. 1962, 10, 123–134. [Google Scholar] [CrossRef]
- Taguchi, O.; Tiwari, G.P.; Iijima, Y. Growth Kinetics of β-Ti Solid Solution in Reaction Diffusion. Mater. Trans. 2003, 44, 83–88. [Google Scholar] [CrossRef]
- Mortlocks, A.J.; Tomlm, D.H. The Atomic Diffusion of Chromium in the Titanium-Chromium System. Philos. Mag. J. Theor. Exp. Appl. Phys. 1959, 4, 628–643. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Iijima, Y.; Hirano, K. Diffusion of Chromium and Palladium in β-Titanium. Mater. Trans. JIM 1991, 32, 451–456. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Du, Y. Investigations on Diffusion Behaviors in Ti–Rich Ti–Nb–Zr–Cr System: Experimental Measurement and CALPHAD Modeling. Calphad 2018, 62, 223–231. [Google Scholar] [CrossRef]
- Kučera, J.; Million, B.; Růžičková, J.; Foldyna, V.; Jakobová, A. Self-Diffusion of Iron in α-Phase of Iron and Fe-Cr Alloys. Acta Metall. 1974, 22, 135–140. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Sundman, B. Thermodynamic Properties of the Cr Fe System. Calphad 1987, 11, 83–92. [Google Scholar] [CrossRef]
- Chen, Q.; Ma, N.; Wu, K.; Wang, Y. Quantitative Phase Field Modeling of Diffusion-Controlled Precipitate Growth and Dissolution in Ti–Al–V. Scr. Mater. 2004, 50, 471–476. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q. CALPHAD-Type Modeling of Diffusion Kinetics in Multicomponent Alloys; Elsevier: Amsterdam, The Netherlands, 2017; pp. 321–362. [Google Scholar]
- Helander, T.; Ågren, J. Diffusion in the B2-b.c.c. Phase of the Al–Fe–Ni System—Application of a Phenomenological Model. Acta Mater. 1999, 47, 3291–3300. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, Computational Tools for Materials Science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Lukas, H.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method, 1st ed.; Cambridge University Press: New York, NY, USA, 2007; ISBN 978-0-521-86811-2. [Google Scholar]
- Borgenstam, A.; Höglund, L.; Ågren, J.; Engström, A. DICTRA, a Tool for Simulation of Diffusional Transformations in Alloys. J. Phase Equilibria 2000, 21, 269–280. [Google Scholar] [CrossRef]
- Thermo-Calc Software AB. Diffusion Module (DICTRA)—Thermo-Calc Software. Available online: https://www.thermocalc.com/products-services/software (accessed on 11 April 2024).
- Pandat Software: CALPHAD-Based Materials Design. Available online: https://computherm.com/software (accessed on 11 April 2024).
- Bai, W.; Nie, J.; Hu, S.; Wang, X.; Li, Z.; Yin, F.; Lin, J.; Zhang, L.; Liu, L. Diffusivities and Atomic Mobilities in Bcc Ti–Mo–Ta Alloys. Calphad 2022, 76, 102393. [Google Scholar] [CrossRef]
- Bai, W.; Tian, Y.; Xu, G.; Yang, Z.; Liu, L.; Masset, P.J.; Zhang, L. Diffusivities and Atomic Mobilities in Bcc Ti-Zr-Nb Alloys. Calphad 2019, 64, 160–174. [Google Scholar] [CrossRef]
- Bai, W.; Nie, J.; Hu, S.; Wang, X.; Yin, F.; Zhang, L.; Liu, L. Atomic Mobilities and Diffusivities in the Bcc Phase of Ti–Nb–Sn System. Calphad 2022, 79, 102478. [Google Scholar] [CrossRef]
- Liu, L.; Bai, W.; Zeng, L.; Xu, G.; Zhang, L. Development and Application of Thermodynamic and Kinetic Database for Titanium Alloys; Central South University Press: Changsha, China, 2021. [Google Scholar]
- Bo, H.; Wang, J.; Duarte, L.; Leinenbach, C.; Liu, L.; Liu, H.; Jin, Z. Thermodynamic Re-Assessment of Fe–Ti Binary System. Trans. Nonferrous Met. Soc. China 2012, 22, 2204–2211. [Google Scholar] [CrossRef]
- Ghosh, G. Thermodynamic and Kinetic Modeling of the Cr-Ti-V System. J. Phase Equilibria 2002, 23, 310–328. [Google Scholar] [CrossRef]
- Byeong-Joo, L. Revision of Thermodynamic Descriptions of the Fe-Cr & Fe-Ni Liquid Phases. Calphad 1993, 17, 251–268. [Google Scholar] [CrossRef]
- Wang, S.; Wang, K.; Chen, G.; Li, Z.; Qin, Z.; Lu, X.; Li, C. Thermodynamic Modeling of Ti-Fe-Cr Ternary System. Calphad 2017, 56, 160–168. [Google Scholar] [CrossRef]
- Kirkaldy, J. Diffusion in Multicomponant Metallic Systems. Can. J. Phys. 2011, 35, 435–440. [Google Scholar] [CrossRef]
- Kirkaldy, J.S. Diffusion in Multicomponent Metallic Systems: IV. A General Theorem for Construction of Multicomponent Solutions from Solutions of the Binary Diffusion Equation. Can. J. Phys. 1959, 37, 30–34. [Google Scholar] [CrossRef]
- Whittle, D.P.; Green, A. The Measurement of Diffusion Coefficients in Ternary Systems. Scr. Metall. 1974, 8, 883–884. [Google Scholar] [CrossRef]
- Hall, L.D. An Analytical Method of Calculating Variable Diffusion Coefficients. J. Chem. Phys. 1953, 21, 87–89. [Google Scholar] [CrossRef]
- Andersson, J.; Ågren, J. Models for Numerical Treatment of Multicomponent Diffusion in Simple Phases. J. Appl. Phys. 1992, 72, 1350–1355. [Google Scholar] [CrossRef]
- Jönsson, B. Assessment of the Mobility of Carbon in Fcc C-Cr-Fe-Ni Alloys. Int. J. Mater. Res. Former Z. Fuer Met. 1994, 85, 502–509. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Thermodynamics of Nonelectrolyte Solutions—x-y-t Relations in a Binary System. Ind. Eng. Chem. 1948, 40, 341–345. [Google Scholar] [CrossRef]
- Wang, C.; Xu, G.; Cui, Y. Mapping of Diffusion and Nanohardness Properties of Fcc Co-Al-V Alloys Using Ternary Diffusion Couples. Metall. Mater. Trans. A 2017, 48, 4286–4296. [Google Scholar] [CrossRef]
- Sha, W.; Malinov, S. Titanium Alloys: Modelling of Microstructure, Properties and Applications; Woodhead Publishing Limited: Sawston, UK, 2009. [Google Scholar]
- Chen, Y.; Li, J.; Tang, B.; Kou, H.; Segurado, J.; Cui, Y. Computational Study of Atomic Mobility for Bcc Phase in Ti–Al–Fe System. Calphad 2014, 46, 205–212. [Google Scholar] [CrossRef]
- Neumann, G.; Tuijn, C. Self-Diffusion and Impurity Diffusion in Pure Metals: Handbook of Experimental Data, 1st ed.; Pergamon Materials Series; Pergamon: Amsterdam, The Netherlands; Boston, MA, USA; London, UK, 2009; ISBN 978-1-85617-511-1. [Google Scholar]
- Zhang, Z.; Wang, J.; Liu, W.; Lu, X. Simulation of BCC Dissolution in Fe–Cr–Ni System by ICME. J. Iron Steel Res. Int. 2023, 30, 660–676. [Google Scholar] [CrossRef]

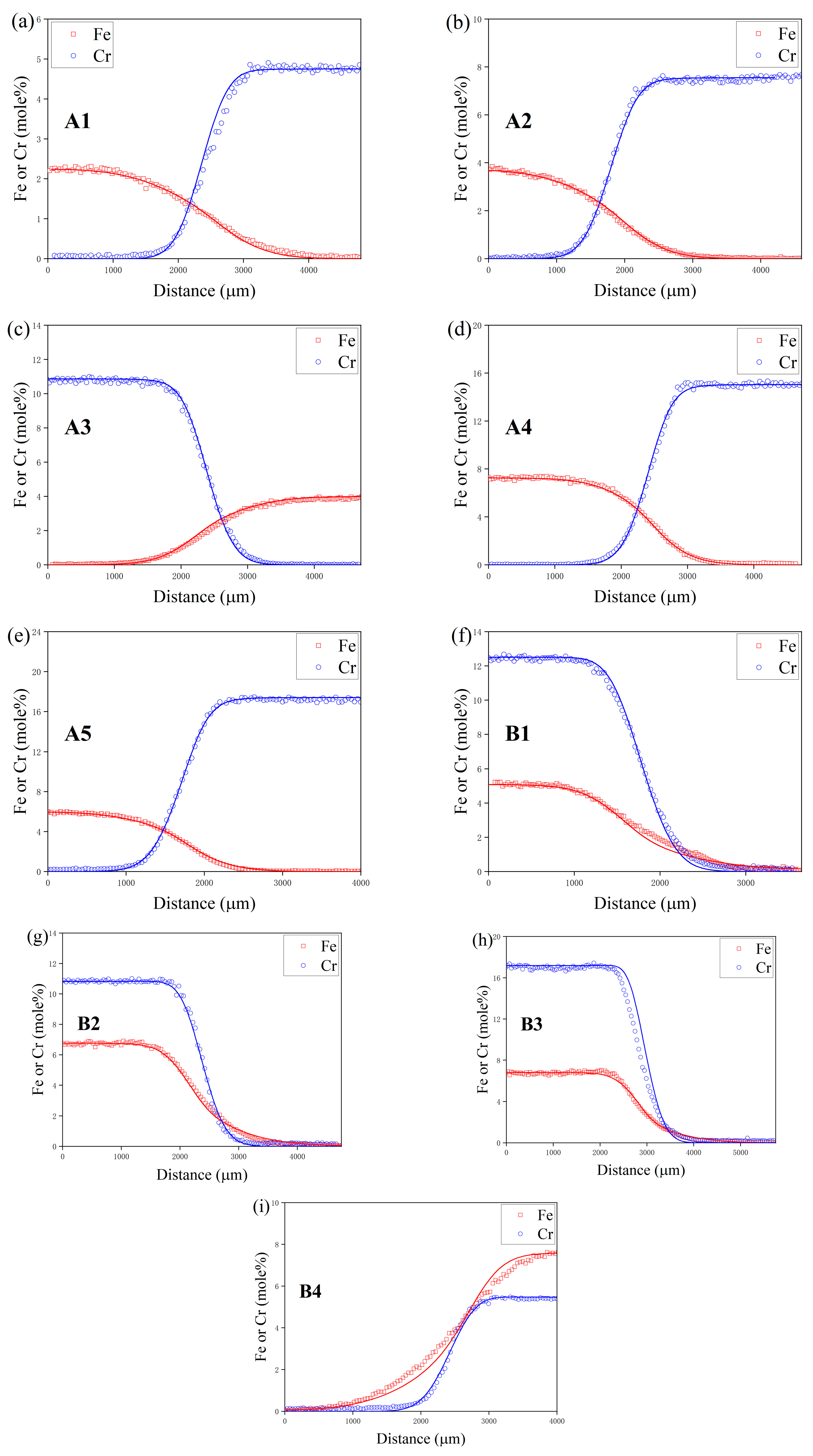

| Temperature (K) | Diffusion Couples | Composition (at.%) |
|---|---|---|
| 1273 | A1 | Ti-2.20Fe/Ti-4.69Cr |
| A2 | Ti-3.72Fe/Ti-7.55Cr | |
| A3 | Ti-4.00Fe/Ti-10.86Cr | |
| A4 | Ti-7.25Fe/Ti-15.04Cr | |
| A5 | Ti-6.00Fe/Ti-17.40Cr | |
| B1 | Pure Ti/Ti-5.22Fe-12.25Cr | |
| B2 | Pure Ti/Ti-6.77Fe-10.82Cr | |
| B3 | Pure Ti/Ti-6.81Fe-17.19Cr | |
| B4 | Pure Ti/Ti-7.59Fe-5.47Cr | |
| 1373 | C1 | Ti-2.15Fe/Ti-4.37Cr |
| C2 | Ti-4.29Fe/Ti-8.96Cr | |
| C3 | Ti-3.73Fe/Ti-11.73Cr | |
| C4 | Ti-6.81Fe/Ti-13.82Cr | |
| C5 | Ti-5.50Fe/Ti-15.70Cr | |
| D1 | Pure Ti/Ti-7.08Fe-18.06Cr | |
| D2 | Pure Ti/Ti-6.44Fe-9.41Cr | |
| D3 | Pure Ti/Ti-6.70Fe-4.83Cr |
| Diffusion Couple | Composition (at.%) | Interdiffusion Coefficients | ||||
|---|---|---|---|---|---|---|
| Fe | Cr | (×10−12 m2·s−1) | (×10−14 m2·s−1) | (×10−13 m2·s−1) | (×10−13 m2·s−1) | |
| A1-B1 | 1.29 | 1.88 | 1.67 ± 0.03 | −9.51 ± 0.35 | −2.39 ± 0.84 | 4.70 ± 0.13 |
| A1-B2 | 1.47 | 1.22 | 1.47 ± 0.06 | −16.19 ± 1.02 | −3.27 ± 1.27 | 4.72 ± 0.39 |
| A1-B3 | 1.11 | 2.63 | 1.62 ± 0.02 | −10.47 ± 0.45 | 1.73 ± 0.78 | 5.17 ± 0.09 |
| A1-B4 | 1.89 | 0.26 | 2.33 ± 0.01 | 39.91 ± 4.63 | 1.00 ± 0.26 | 6.50 ± 0.40 |
| A2-B1 | 1.85 | 4.55 | 1.46 ± 0.01 | 2.20 ± 0.02 | 1.13 ± 0.36 | 3.58 ± 0.08 |
| A2-B2 | 2.15 | 3.23 | 1.21 ± 0.04 | −3.48 ± 0.88 | −2.84 ± 0.14 | 2.67 ± 0.01 |
| A2-B3 | 1.74 | 5.00 | 1.30 ± 0.03 | −1.79 ± 0.69 | 3.21 ± 0.11 | 4.16 ± 0.01 |
| A2-B4 | 2.80 | 0.84 | 1.95 ± 0.04 | 23.87 ± 0.14 | −0.37 ± 0.88 | 3.93 ± 0.14 |
| A3-B1 | 2.13 | 6.20 | 1.34 ± 0.02 | 2.99 ± 0.02 | −0.31 ± 0.38 | 3.76 ± 0.02 |
| A3-B2 | 2.45 | 4.58 | 1.12 ± 0.07 | −1.83 ± 0.50 | −5.18 ± 0.64 | 2.80 ± 0.12 |
| A3-B3 | 2.09 | 6.38 | 1.19 ± 0.03 | −0.08 ± 0.62 | 1.33 ± 0.09 | 4.10 ± 0.02 |
| A3-B4 | 3.15 | 1.30 | 1.90 ± 0.03 | 16.91 ± 0.09 | −0.62 ± 0.89 | 3.58 ± 0.05 |
| A4-B1 | 3.38 | 11.00 | 0.89 ± 0.01 | 3.28 ± 0.22 | 1.26 ± 0.11 | 2.97 ± 0.11 |
| A4-B2 | 3.96 | 9.10 | 0.82 ± 0.09 | 0.31 ± 0.58 | −0.87 ± 0.18 | 2.77 ± 0.10 |
| A4-B3 | 3.17 | 11.67 | 0.81 ± 0.01 | 1.14 ± 0.06 | 1.52 ± 0.63 | 2.81 ± 0.06 |
| A4-B4 | 5.17 | 4.93 | 1.54 ± 0.07 | 19.79 ± 0.84 | −0.66 ± 0.47 | 3.54 ± 0.13 |
| A5-B1 | 3.11 | 10.24 | 0.90 ± 0.02 | 5.00 ± 0.09 | 1.22 ± 0.18 | 3.13 ± 0.04 |
| A5-B2 | 3.58 | 8.43 | 0.82 ± 0.04 | 1.83 ± 0.52 | −0.79 ± 0.13 | 2.71 ± 0.02 |
| A5-B3 | 2.96 | 11.01 | 0.79 ± 0.08 | 2.65 ± 0.19 | 1.10 ± 0.01 | 3.01 ± 0.05 |
| A5-B4 | 4.44 | 4.15 | 1.64 ± 0.05 | 15.00 ± 0.52 | −0.06 ± 0.62 | 2.65 ± 0.01 |
| Diffusion Couple | Composition (at.%) | Interdiffusion Coefficients | ||||
|---|---|---|---|---|---|---|
| Fe | Cr | (×10−12 m2·s−1) | (×10−13 m2·s−1) | (×10−13 m2·s−1) | (×10−12 m2·s−1) | |
| C1-D1 | 1.49 | 1.08 | 6.33 ± 0.02 | 2.70 ± 0.34 | −0.49 ± 0.06 | 1.37 ± 0.05 |
| C1-D2 | 1.59 | 0.75 | 5.91 ± 0.07 | 1.29 ± 0.53 | −6.63 ± 1.27 | 1.13 ± 0.06 |
| C1-D3 | 1.72 | 0.40 | 6.19 ± 0.04 | 2.55 ± 1.26 | 2.66 ± 0.97 | 1.33 ± 0.08 |
| C2-D1 | 2.34 | 5.01 | 5.10 ± 0.11 | 2.98 ± 0.28 | −2.92 ± 1.50 | 1.47 ± 0.02 |
| C2-D2 | 2.60 | 4.09 | 4.93 ± 0.03 | 2.03 ± 0.43 | −9.81 ± 0.03 | 1.25 ± 0.04 |
| C2-D3 | 3.31 | 1.60 | 5.54 ± 0.03 | 3.09 ± 0.28 | 3.53 ± 1.93 | 1.63 ± 0.09 |
| C3-D1 | 2.46 | 5.69 | 4.40 ± 0.06 | 3.87 ± 0.01 | 2.92 ± 0.50 | 1.38 ± 0.07 |
| C3-D2 | 2.72 | 4.48 | 4.19 ± 0.08 | 3.81 ± 0.31 | −7.57 ± 0.98 | 1.22 ± 0.06 |
| C3-D3 | 3.37 | 1.65 | 5.04 ± 0.08 | 7.80 ± 0.06 | 4.25 ± 2.21 | 1.56 ± 0.05 |
| C4-D1 | 3.15 | 9.93 | 3.77 ± 0.01 | 3.39 ± 0.35 | −0.84 ± 0.18 | 1.44 ± 0.03 |
| C4-D2 | 3.95 | 7.88 | 3.71 ± 0.07 | 2.41 ± 0.34 | −9.36 ± 0.20 | 1.37 ± 0.04 |
| C4-D3 | 5.28 | 4.04 | 4.54 ± 0.03 | 3.06 ± 0.59 | −1.75 ± 1.34 | 1.74 ± 0.06 |
| C5-D1 | 2.97 | 8.70 | 4.23 ± 0.01 | 3.02 ± 0.43 | −6.67 ± 0.05 | 1.54 ± 0.01 |
| C5-D2 | 3.45 | 6.82 | 4.16 ± 0.06 | 1.95 ± 0.23 | −11.45 ± 1.14 | 1.42 ± 0.02 |
| C5-D3 | 4.37 | 2.88 | 5.26 ± 0.01 | 1.77 ± 0.08 | −1.36 ± 1.91 | 1.65 ± 0.04 |
| Temperature (K) | Composition (at.%) | Impurity Diffusion Coefficients (×10−12 m2·s−1) | Composition (at.%) | Impurity Diffusion Coefficients (×10−12 m2·s−1) |
|---|---|---|---|---|
| 1273 | 1.750 ± 0.40 | 0.640 ± 0.46 | ||
| 1.256 ± 0.99 | 0.266 ± 0.13 | |||
| 1.002 ± 0.27 | 0.383 ± 0.21 | |||
| 0.560 ± 0.52 | 0.441 ± 0.23 | |||
| 0.521 ± 0.22 | 0.227 ± 0.51 | |||
| 1373 | 5.363 ± 0.15 | 1.323 ± 0.45 | ||
| 4.222 ± 0.87 | 1.458 ± 0.17 | |||
| 3.162 ± 0.37 | 1.013 ± 0.38 | |||
| 3.355 ± 0.44 | 1.844 ± 0.61 | |||
| 4.916 ± 0.25 | 1.678 ± 0.33 |
| Temperature (K) | Values | Diffusion Coefficients (m2·s−1) | |||
|---|---|---|---|---|---|
| 1273 | Minimum | 7.86 × 10−13 | 2.65 × 10−13 | 5.21 × 10−13 | 2.27 × 10−13 |
| Maximum | 2.33 × 10−12 | 6.50 × 10−13 | 1.75 × 10−12 | 6.40 × 10−13 | |
| Average | 1.34 × 10−12 | 3.66 × 10−13 | 1.02 × 10−12 | 3.91 × 10−13 | |
| 1373 | Minimum | 2.71 × 10−12 | 1.13 × 10−12 | 3.16 × 10−12 | 1.01 × 10−12 |
| Maximum | 6.33 × 10−12 | 1.74 × 10−12 | 5.36 × 10−12 | 1.84 × 10−12 | |
| Average | 4.89 × 10−12 | 1.43 × 10−12 | 4.20 × 10−12 | 1.46 × 10−12 | |
| Mobility | Parameters, J/mole | Reference |
|---|---|---|
| Mobilities of Ti | ||
| RTln(5.91 × 10−5exp(−23,700/RT) + 1.47 × 10−8 exp(−121,000/RT)) | [52] | |
| −293,200 + RTln(0.21) | [53] | |
| −401,358−35.5 × T | [41] | |
| −208,542.06 + 185.09 × T | [53] | |
| 221,687.185 | [13] | |
| Mobilities of Fe | ||
| RTln(7.8 × 10−7exp(−132,000/RT) + 2.7 × 10−4 exp(−230,300/RT)) | [53] | |
| −258,194 + RTln(6.6 × 10−4) | [54] | |
| −332,000 + RTln(4.7 × 10−5) | [54] | |
| −692,842.42 + 480.24 × T | [53] | |
| −1,903,266.41 + 1759.71 × T | This work | |
| −1,671,434.55 + 1590.81 × T | This work | |
| 256,342.886 | [55] | |
| −407,725.609 | [55] | |
| Mobilities of Cr | ||
| RTln(1.6 × 10−3exp(−276,284/RT) + 8.6 × 10−7 exp(−156,991/RT)) | [13] | |
| −266,300 + RTln(2.2 × 10−2) | [54] | |
| −441,974−16.94 × T | [41] | |
| 163,816.65 | [13] | |
| 832,547.16−935.52 × T | This work | |
| 2,693,787.95−2446.7 × T | This work | |
| 273,329.671 | [55] | |
| −19,802.888 | [55] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Nie, J.; Bai, W.; Hu, S.; Wang, X.; Zhang, L.; Liu, L. Diffusivities and Atomic Mobilities in BCC Ti-Fe-Cr Alloys. Materials 2024, 17, 1927. https://doi.org/10.3390/ma17081927
Huang Y, Nie J, Bai W, Hu S, Wang X, Zhang L, Liu L. Diffusivities and Atomic Mobilities in BCC Ti-Fe-Cr Alloys. Materials. 2024; 17(8):1927. https://doi.org/10.3390/ma17081927
Chicago/Turabian StyleHuang, Yi, Jingjing Nie, Weimin Bai, Songsong Hu, Xinming Wang, Ligang Zhang, and Libin Liu. 2024. "Diffusivities and Atomic Mobilities in BCC Ti-Fe-Cr Alloys" Materials 17, no. 8: 1927. https://doi.org/10.3390/ma17081927
APA StyleHuang, Y., Nie, J., Bai, W., Hu, S., Wang, X., Zhang, L., & Liu, L. (2024). Diffusivities and Atomic Mobilities in BCC Ti-Fe-Cr Alloys. Materials, 17(8), 1927. https://doi.org/10.3390/ma17081927









