First-Principles Study of the Heterostructure, ZnSb Bilayer/h-BN Monolayer for Thermoelectric Applications
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. ZnSb Bilayer
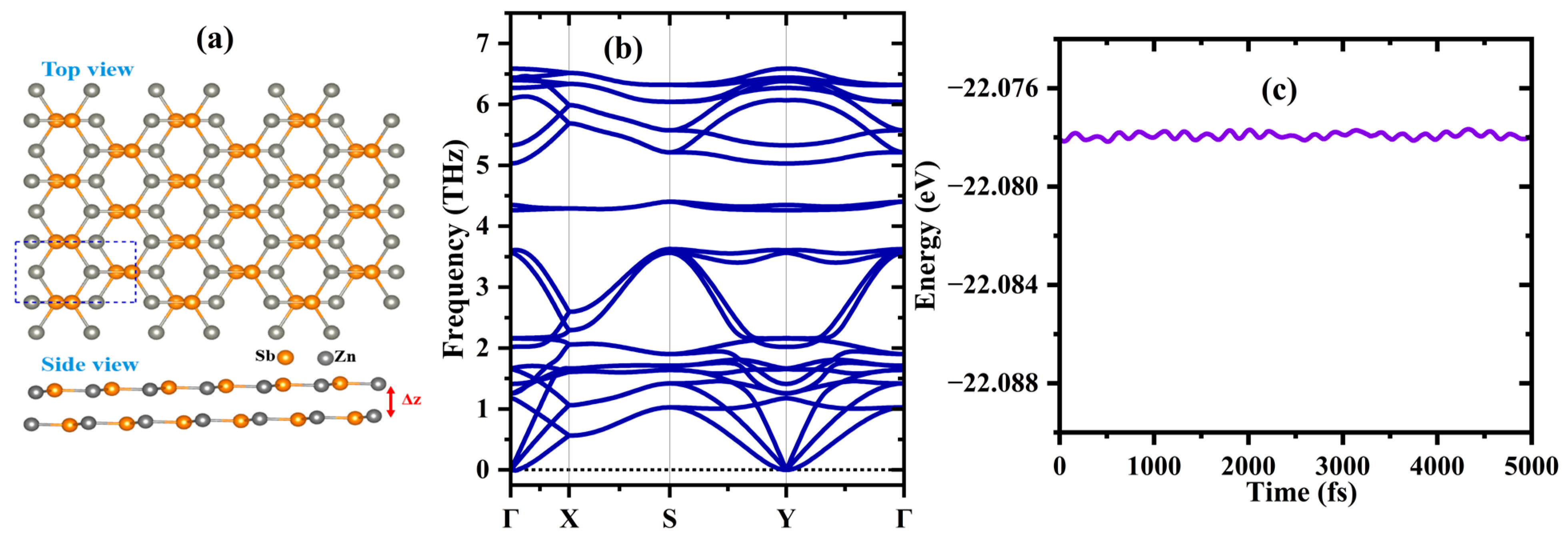
3.1.1. Structure and Stability
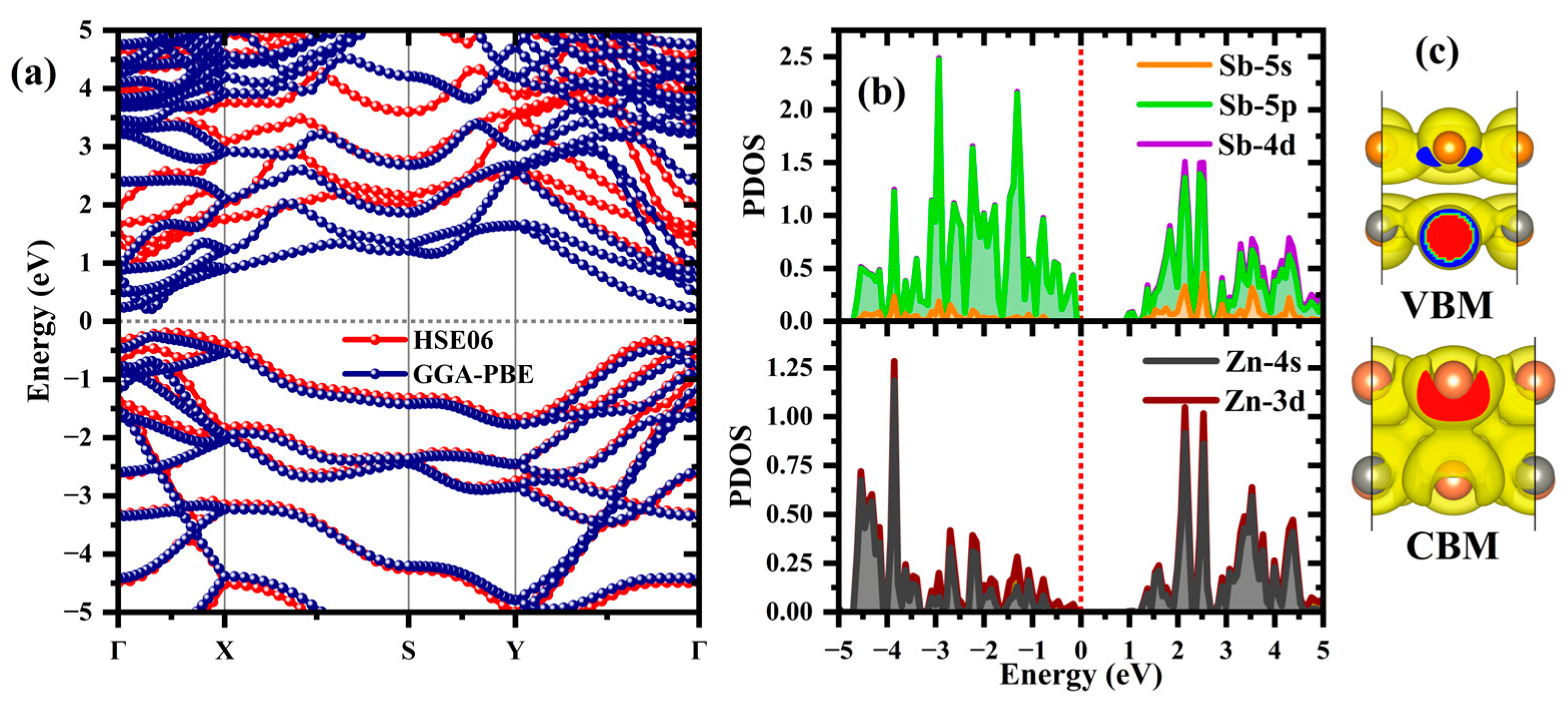
3.1.2. Electronic Properties
3.2. ZnSb Bilayer/h-BN Monolayer Heterostructure
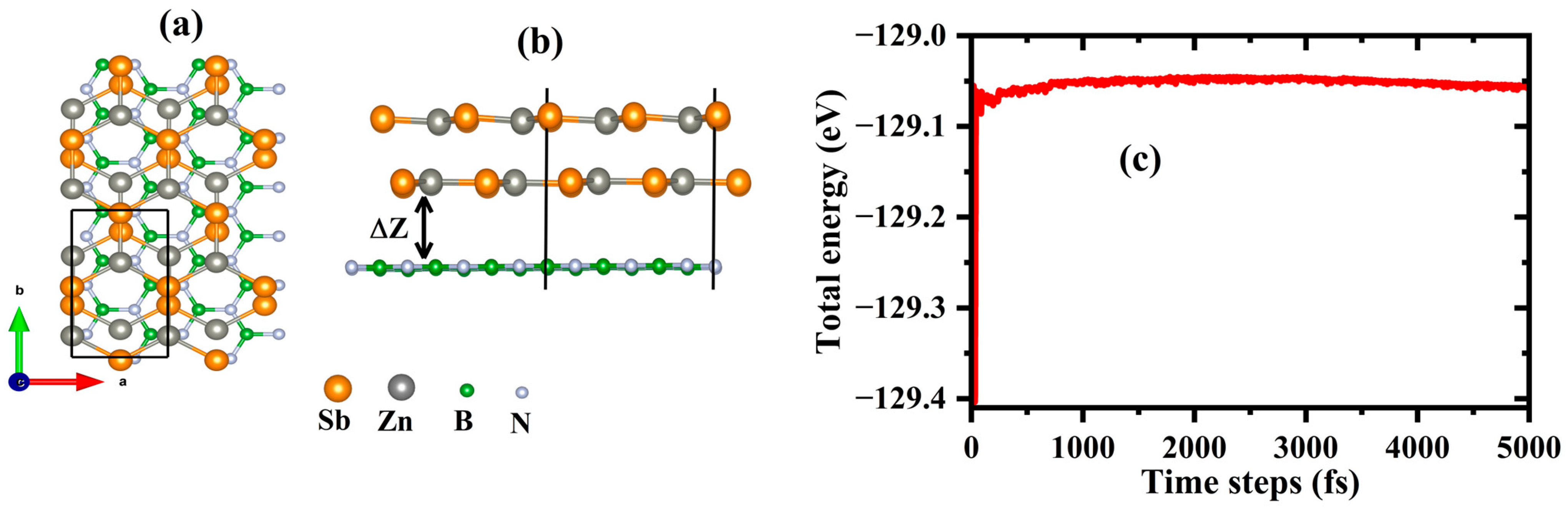
3.2.1. Structure and Stability
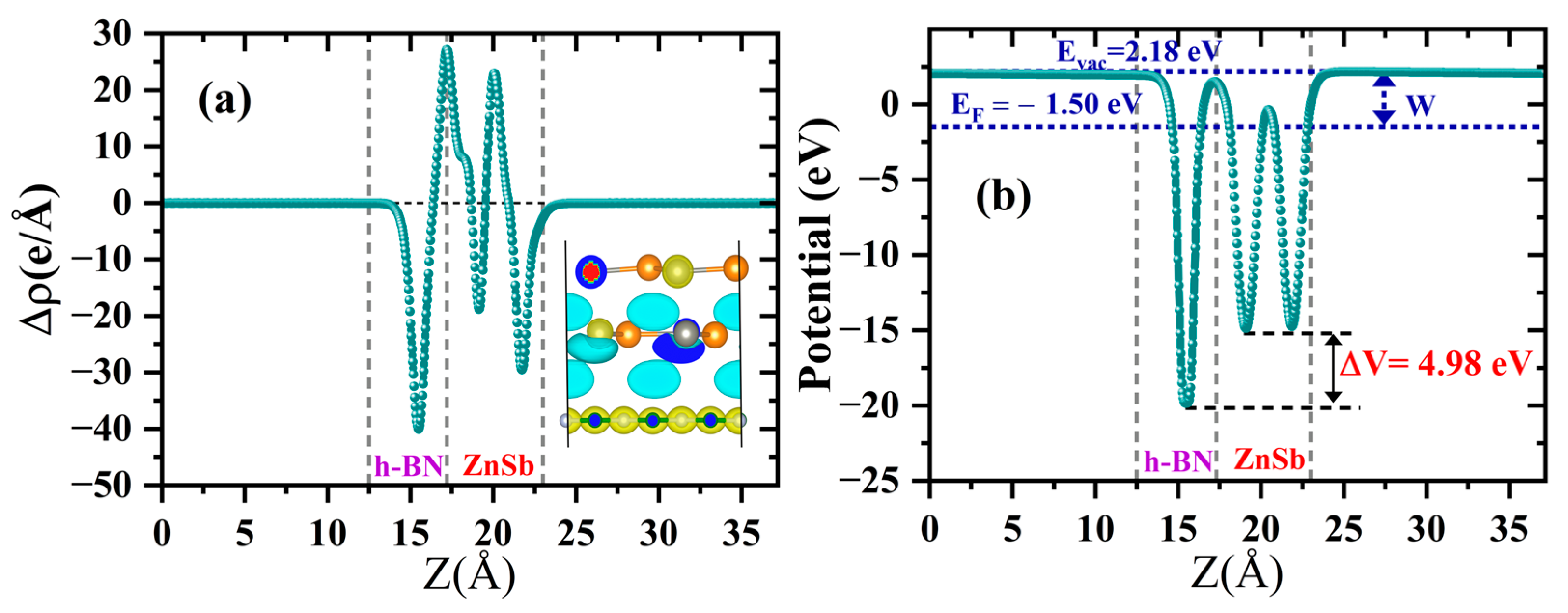
3.2.2. Electronic Properties
3.3. Transport Properties
3.4. Thermoelectric Performance
3.5. Mechanical Properties
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Late, D.J.; Huang, Y.-K.; Liu, B.; Acharya, J.; Shirodkar, S.N.; Luo, J.; Yan, A.; Charles, D.; Waghmare, U.V.; Dravid, V.P. Sensing behavior of atomically thin-layered MoS2 transistors. ACS Nano 2013, 7, 4879–4891. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.R.; Wang, R.; Zhang, H.; Wu, W. Emerging beyond-graphene elemental 2D materials for energy and catalysis applications. Chem. Soc. Rev. 2021, 50, 10983–11031. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, Y.; Yang, Z.; Yan, Y.; Sun, K. Synthesis of MoS2 and MoO2 for their applications in H2 generation and lithium ion batteries: A review. Sci. Technol. Adv. Mater. 2013, 14, 043501. [Google Scholar] [CrossRef] [PubMed]
- Kanahashi, K.; Pu, J.; Takenobu, T. 2D materials for large-area flexible thermoelectric devices. Adv. Energy Mater. 2020, 10, 1902842. [Google Scholar] [CrossRef]
- Sen, R.; Jatkar, K.; Johari, P. Modulation of electronic and transport properties of bilayer heterostructures: InSe/MoS2 and InSe/h-BN as the prototype. Phys. Rev. B 2020, 101, 235425. [Google Scholar] [CrossRef]
- Wang, B.; Kuang, A.; Luo, X.; Wang, G.; Yuan, H.; Chen, H. Bandgap engineering and charge separation in two-dimensional GaS-based van der Waals heterostructures for photocatalytic water splitting. Appl. Surf. Sci. 2018, 439, 374–379. [Google Scholar] [CrossRef]
- Amiri, P.; Taghizadeh, S.F. Ab-initio study of structural and electronic properties of WS2/h-BN van der Waals heterostructure. Surf. Sci. 2018, 672, 13–18. [Google Scholar]
- Li, D.; Li, R.; Zhou, D.; Zeng, F.; Yan, W.; Cai, S. The charge transfer feature and high photocatalytic activity of S-scheme TiO2/h-BN heterostructure from first-principles. Appl. Surf. Sci. 2022, 586, 152765. [Google Scholar] [CrossRef]
- Iqbal, M.W.; Iqbal, M.Z.; Khan, M.F.; Shehzad, M.A.; Seo, Y.; Park, J.H.; Hwang, C.; Eom, J. High-mobility and air-stable single-layer WS2 field-effect transistors sandwiched between chemical vapor deposition-grown hexagonal BN films. Sci. Rep. 2015, 5, 10699. [Google Scholar] [CrossRef]
- Böttger, P.M.; Pomrehn, G.S.; Snyder, G.J.; Finstad, T.G. Doping of p-type ZnSb: Single parabolic band model and impurity band conduction. Phys. Status Solidi 2011, 208, 2753–2759. [Google Scholar] [CrossRef]
- Eklöf, D.; Fischer, A.; Grins, J.; Scherer, W.; Häussermann, U. Transport properties of Ag-doped ZnSb. Z. Fur Anorg. Und Allg. Chem. 2021, 647, 34–40. [Google Scholar] [CrossRef]
- Ueda, T.; Okamura, C.; Noda, Y.; Hasezaki, K. Effect of Tellurium doping on the thermoelectric properties of ZnSb. Mater. Trans. 2009, 50, 2473–2475. [Google Scholar] [CrossRef]
- Yang, S.; Deng, T.; Qiu, P.; Xing, T.; Cheng, J.; Jin, Z.; Li, P.; Shi, X.; Chen, L. High-performance and stable (Ag, Cd)-containing ZnSb thermoelectric compounds. ACS Appl. Mater. Interfaces 2022, 14, 26662–26670. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Song, H.Y.; Wang, Z.; Lee, S.; Hwang, J.-Y.; Lee, S.Y.; Lee, J.; Kim, D.; Lee, K.H.; Kim, Y. Creation of two-dimensional layered Zintl phase by dimensional manipulation of crystal structure. Sci. Adv. 2019, 5, eaax0390. [Google Scholar] [CrossRef]
- Bafekry, A.; Shahrokhi, M.; Yagmurcukardes, M.; Gogova, D.; Ghergherehchi, M.; Akgenc, B.; Feghhi, S. Surface functionalization of the honeycomb structure of zinc antimonide (ZnSb) monolayer: A first-Principles study. Surf. Sci. 2021, 707, 121796. [Google Scholar] [CrossRef]
- Guan, Z.; Yang, W.; Wang, H.; Wang, H.; Li, J. Direct band gap and anisotropic transport of ZnSb monolayers tuned by hydrogenation and strain. RSC Adv. 2022, 12, 2693–2700. [Google Scholar] [CrossRef]
- Yang, W.; Guan, Z.; Wang, H.; Chen, Y.; Wang, H.; Li, J. Ultrahigh anisotropic carrier mobility in ZnSb monolayers functionalized with halogen atoms. RSC Adv. 2022, 12, 26994–27001. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, Y.; Li, S.; Zhang, X.; Liu, G. Two-dimensional antiferromagnetic type-II Weyl fermions in monolayer ZnSb and type-I Weyl fermions and topological insulator in bilayer ZnSb. Comput. Mater. Sci. 2024, 231, 112540. [Google Scholar] [CrossRef]
- Bafekry, A.; Yagmurcukardes, M.; Shahrokhi, M.; Ghergherehchi, M.; Kim, D.; Mortazavi, B. Electro-optical and mechanical properties of Zinc antimonide (ZnSb) monolayer and bilayer: A first-principles study. Appl. Surf. Sci. 2021, 540, 148289. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, B.; Guan, X.; Han, L.; Wu, L.; Guan, P.; Lu, P. Design and analysis of III-V two-dimensional van der Waals heterostructures for ultra-thin solar cells. Appl. Surf. Sci. 2022, 586, 152799. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Baroni, S.; De Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Eriksson, F.; Fransson, E.; Erhart, P. The hiphive package for the extraction of high-order force constants by machine learning. Adv. Theory Simul. 2019, 2, 1800184. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Richard, F.; Bader, R. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Björkman, T.; Gulans, A.; Krasheninnikov, A.V.; Nieminen, R.M. Van Der Waals Bonding in Layered Compounds from Advanced Density-Functional First-Principles Calculations. Phys. Rev. Lett. 2012, 108, 235502. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Jacobs, R.; Ma, T.; Chen, D.; Booske, J.; Morgan, D. Work function: Fundamentals, measurement, calculation, engineering, and applications. Phys. Rev. Appl. 2023, 19, 037001. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72. [Google Scholar] [CrossRef]
- Niedziółka, K.; Jund, P. Influence of the Exchange–Correlation Functional on the Electronic Properties of ZnSb As a Promising Thermoelectric Material. J. Electron. Mater. 2014, 44, 1540–1546. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Wang, V.; Tang, G.; Liu, Y.-C.; Wang, R.-T.; Mizuseki, H.; Kawazoe, Y.; Nara, J.; Geng, W.T. High-throughput computational screening of two-dimensional semiconductors. J. Phys. Chem. Lett. 2022, 13, 11581–11594. [Google Scholar] [CrossRef]
- Mohanta, M.K.; De Sarkar, A. Interfacial hybridization of Janus MoSSe and BX (X = P, As) monolayers for ultrathin excitonic solar cells, nanopiezotronics and low-power memory devices. Nanoscale 2020, 12, 22645–22657. [Google Scholar] [CrossRef]
- Pu, C.-Y.; Lv, L.-X.; Zhou, D.-W.; Yu, J.-H.; Tang, X. Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN: Theoretical Investigations. Commun. Theor. Phys. 2019, 71, 1363. [Google Scholar] [CrossRef]


| Direction | Structure | Carrier Type | (eV) | (N·m−1) | μ (cm2·V−1·s−1) | (fs) | |
|---|---|---|---|---|---|---|---|
| ZnSb bilayer | electron | 0.318 | −1.52 | 62.8 | 217.8 | 27.9 | |
| hole | 0.225 | −6.63 | 62.8 | 1004.7 | 181.7 | ||
| ZnSb/h-BN heterostructure | electron | 1.425 | −0.69 | 342.1 | 14,107.7 | 11,430.5 | |
| hole | 1.219 | −3.44 | 342.1 | 397.6 | 275.6 | ||
| ZnSb bilayer | electron | 0.353 | −7.59 | 68.5 | 297.8 | 192.3 | |
| hole | 0.481 | −4.24 | 68.5 | 703.0 | 59.7 | ||
| ZnSb/h-BN heterostructure | electron | 0.402 | −4.23 | 345.1 | 1350.0 | 308.6 | |
| Hole | 1.324 | −9.18 | 345.1 | 51.8 | 39.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darhi, Z.; El Farh, L.; Pandey, R. First-Principles Study of the Heterostructure, ZnSb Bilayer/h-BN Monolayer for Thermoelectric Applications. Materials 2025, 18, 294. https://doi.org/10.3390/ma18020294
Darhi Z, El Farh L, Pandey R. First-Principles Study of the Heterostructure, ZnSb Bilayer/h-BN Monolayer for Thermoelectric Applications. Materials. 2025; 18(2):294. https://doi.org/10.3390/ma18020294
Chicago/Turabian StyleDarhi, Zakariae, Larbi El Farh, and Ravindra Pandey. 2025. "First-Principles Study of the Heterostructure, ZnSb Bilayer/h-BN Monolayer for Thermoelectric Applications" Materials 18, no. 2: 294. https://doi.org/10.3390/ma18020294
APA StyleDarhi, Z., El Farh, L., & Pandey, R. (2025). First-Principles Study of the Heterostructure, ZnSb Bilayer/h-BN Monolayer for Thermoelectric Applications. Materials, 18(2), 294. https://doi.org/10.3390/ma18020294






