Experimental Study on Anti-Wrinkling Performance of TA1 Titanium Thin Sheet Assisted by Ultrasonic Vibration
Abstract
1. Introduction
2. Experimental Scheme
2.1. Experimental Materials and Specimen Preparation
2.1.1. Experimental Materials
2.1.2. Specimen Preparation
2.2. Experimental Apparatus and Methodology
2.3. Buckling Measurement
3. Results and Discussion
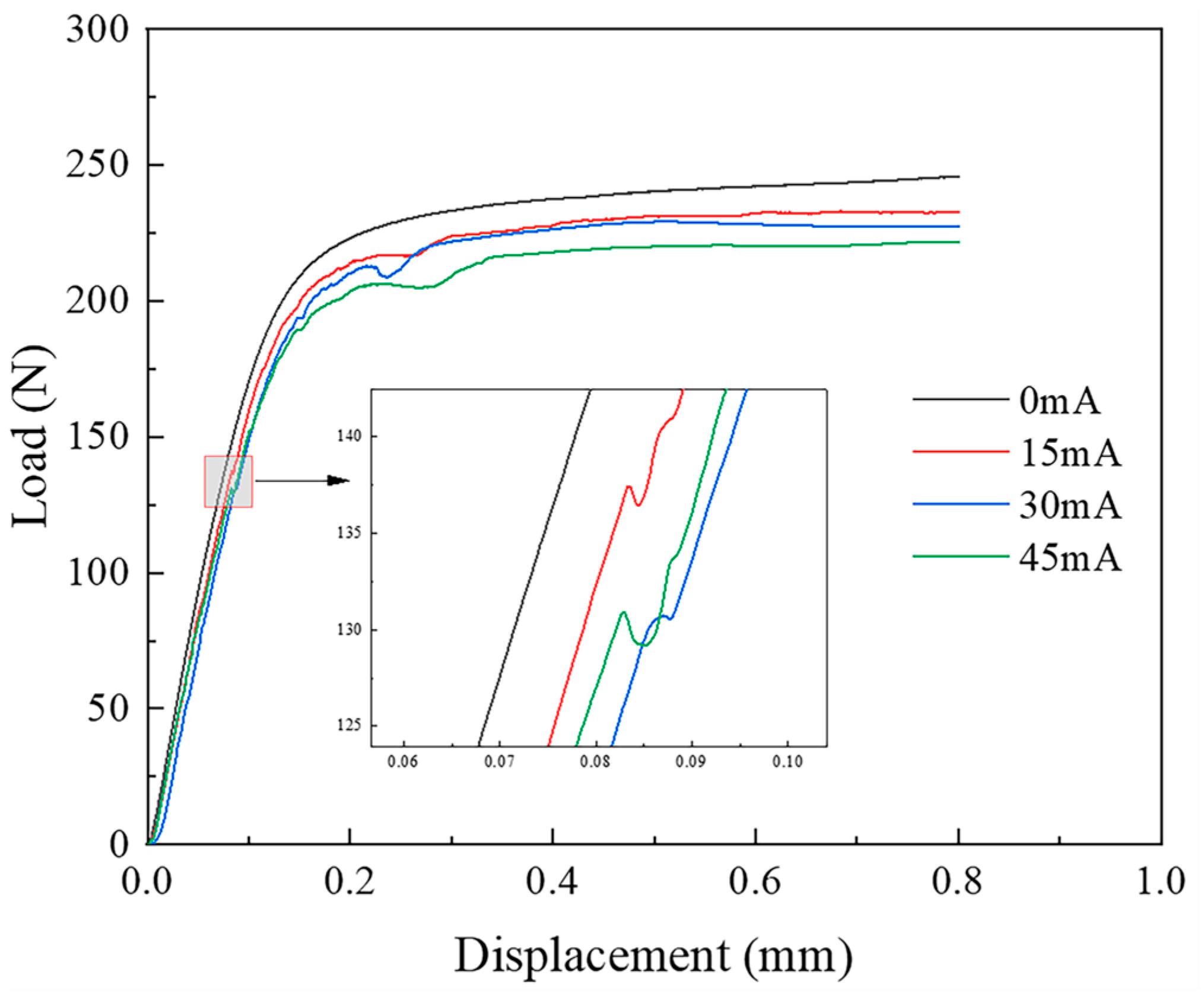
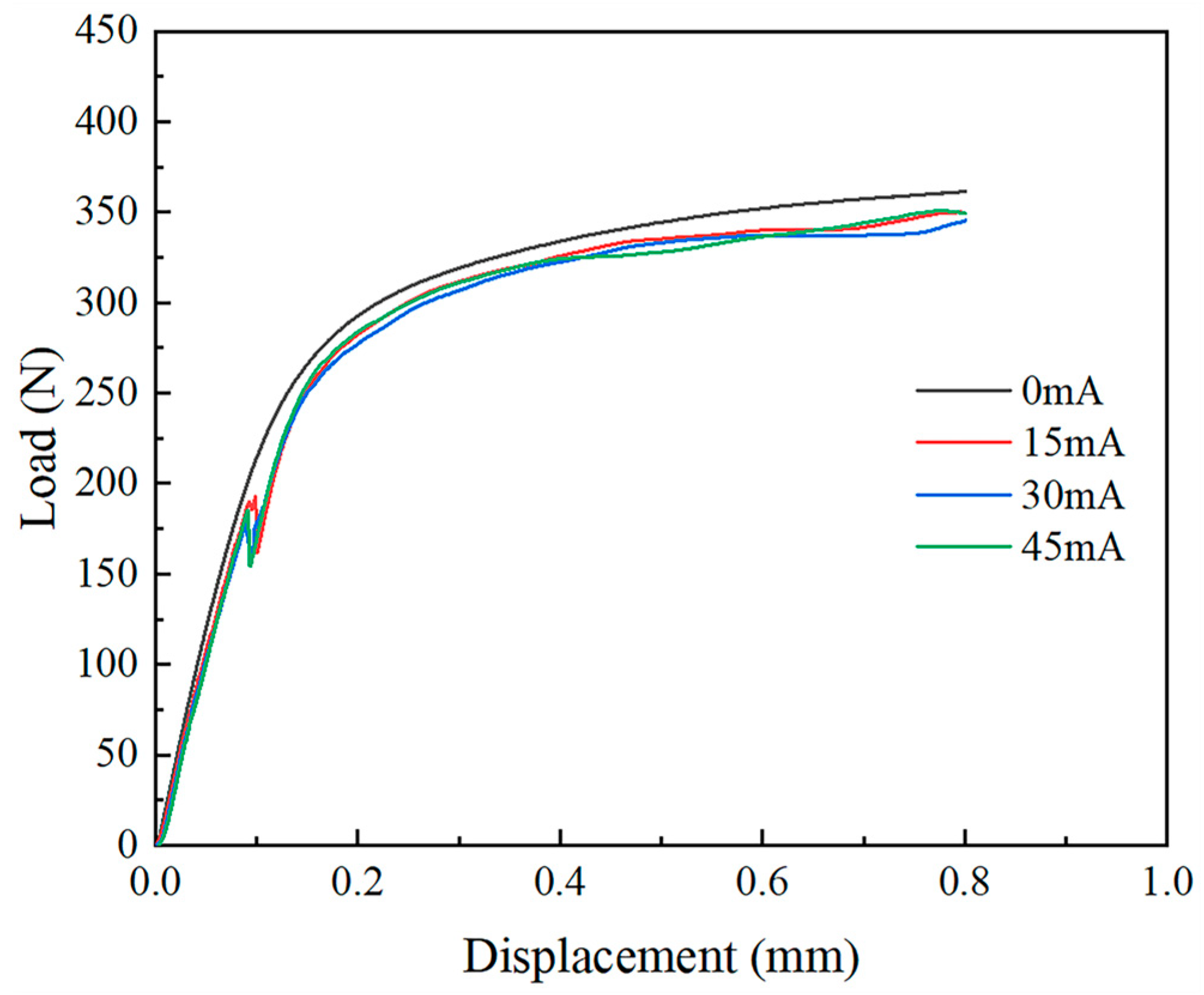
3.1. Load–Displacement Curves
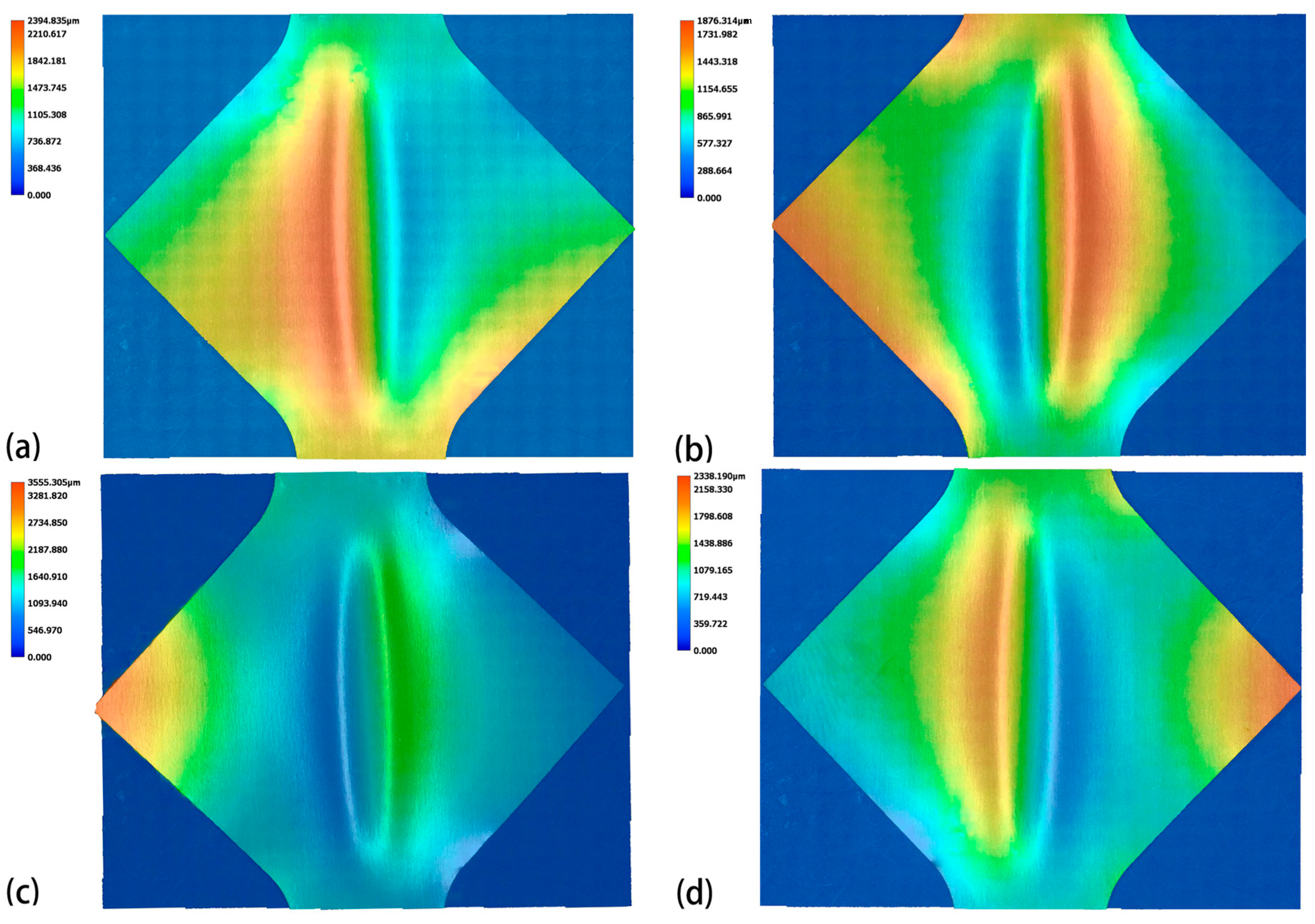
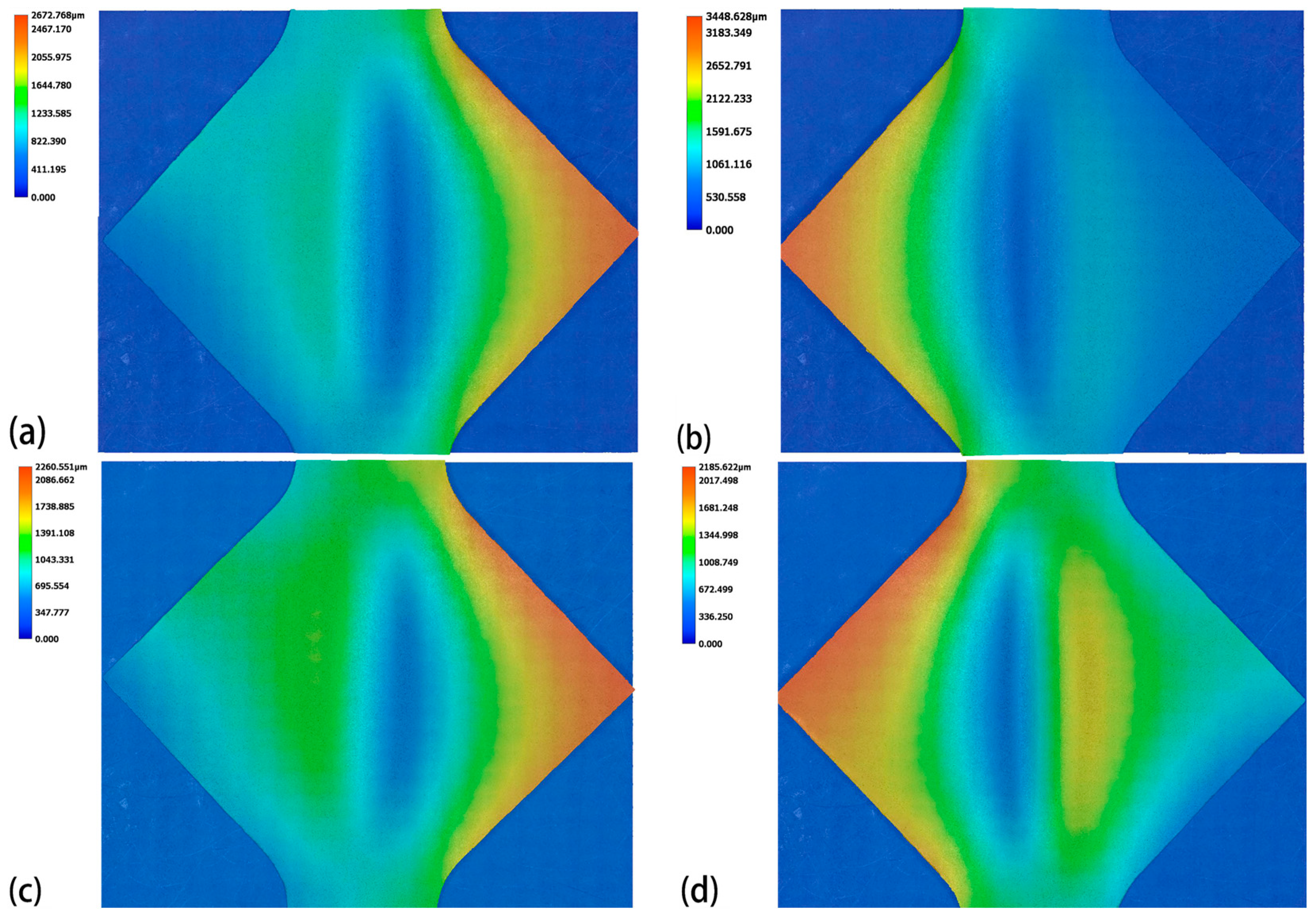
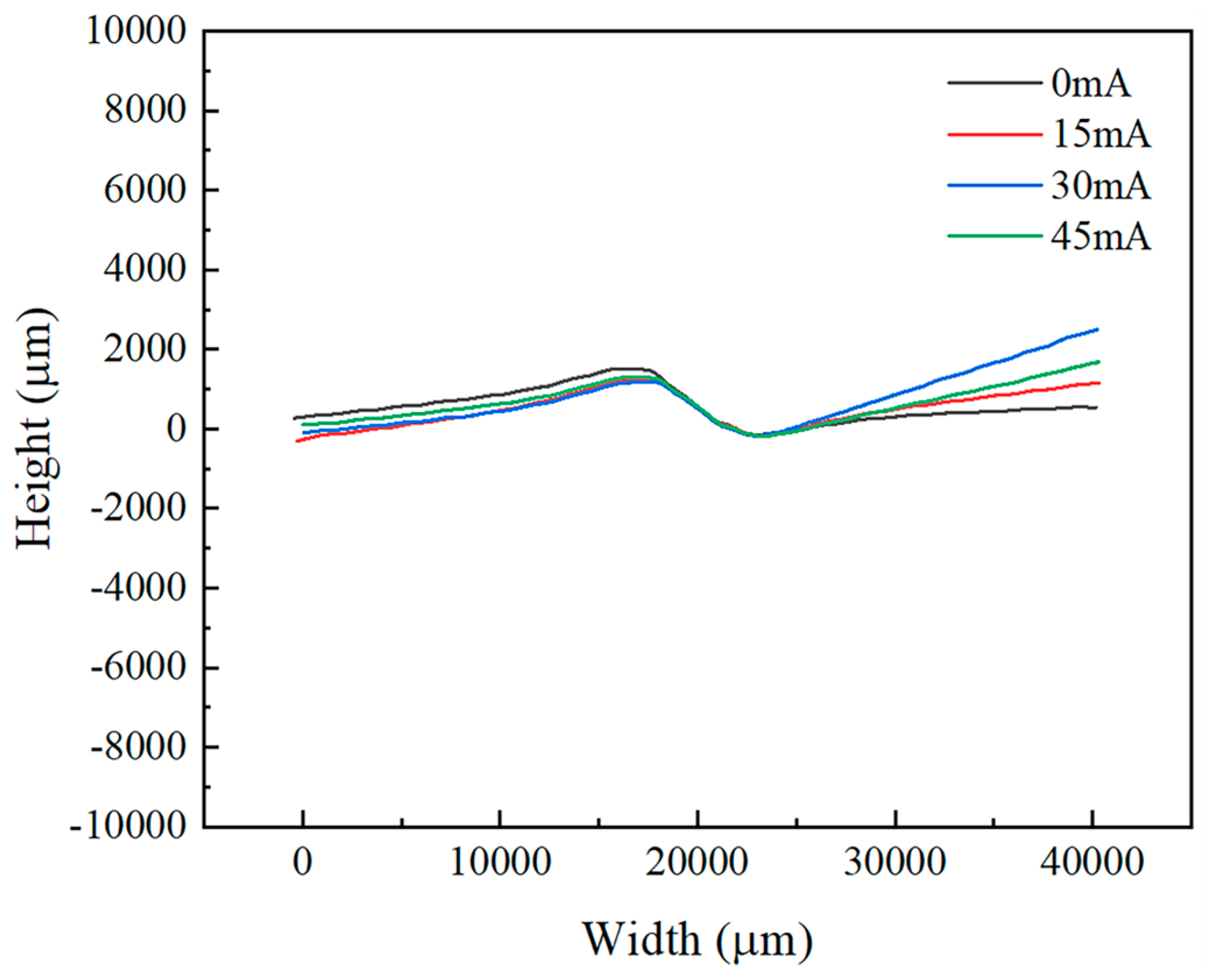
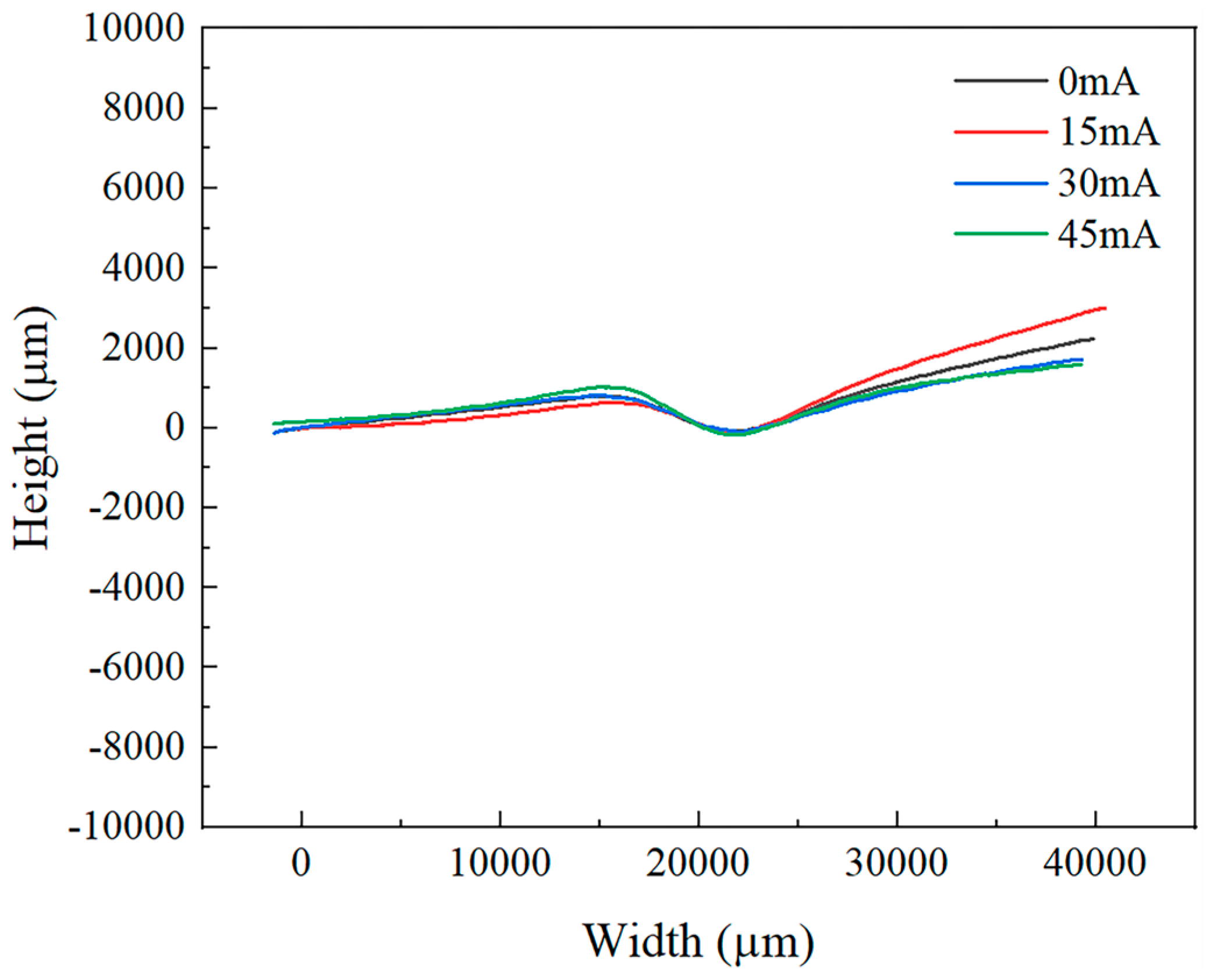
3.2. Wrinkle Morphology and Height
4. Conclusions
- Analysis of the load–displacement curves and wrinkle height maps for the 0.075 mm and 0.1 mm thick TA1 titanium sheets reveals that thinner sheets exhibit inferior anti-wrinkling performance and may experience localized secondary wrinkling.
- The ultrasonic-vibration energy field can induce branching buckling in the diagonal stretching test of square plates, allowing the onset of wrinkling in TA1 titanium sheets to be determined from the inflection points in the load–displacement curves.
- The ultrasonic-vibration energy field reduces both the yield and flow stresses of the material, facilitating wrinkle formation during the elastic deformation phase. As the amplitude increases, the stress reduction becomes more pronounced.
- At the same vibration frequency, the wrinkle height of the TA1 titanium sheets initially decreases and then increases as the amplitude increases. Specifically, the 0.075 mm thick sheet reaches its minimum wrinkle height at 15 mA, while the 0.1 mm thick sheet does so at 30 mA. Moderate ultrasonic amplitudes effectively suppress wrinkling, while excessively high amplitudes may exacerbate it.
- The ultrasonic-vibration energy field reduces the forming load of TA1 titanium sheets and, within an optimal amplitude range, enhances both the forming quality and anti-wrinkling performance. Therefore, the careful selection of ultrasonic amplitude and sheet thickness parameters can optimize ultrasonic-vibration-assisted stamping, thereby improving the forming quality and engineering applicability of bipolar plates for hydrogen fuel cells.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharaf, O.Z.; Orhan, M.F. An overview of fuel cell technology: Fundamentals and applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar]
- National Development and Reform Commission; National Energy Administration. Medium- and Long-Term Plan for the Development of the Hydrogen Energy Industry (2021–2035). 2022. Available online: https://climate-laws.org/document/medium-and-long-term-plan-for-the-development-of-the-hydrogen-energy-industry-2021-2035_37a6 (accessed on 21 March 2025).
- Hua, R.S.; Zhang, W.Q.; Cheng, L.D.; Wang, C.J. Review on Design and Forming Technology of Metallic Bipolar Plates for Fuel Cells. J. Netshape Form. Eng. 2022, 14, 25–33. [Google Scholar]
- Yang, Y.Y. Forming Technology for Large Sheet Metal, 1st ed.; National Defense Industry Press: Beijing, China, 1996; pp. 164–170. [Google Scholar]
- Li, H.; Yang, H.; Zhan, M.; Lin, Y.; Gu, R.J. A Review of the Research on Wrinkling in Thin-Walled Parts Plastic Forming Processes. Mech. Sci. Technol. 2004, 23, 837–842. [Google Scholar]
- Yoshida, K. Purpose and feature of Yoshida buckling test (YBT). J. Jpn. Soc. Technol. Plast. 1983, 24, 901–908. [Google Scholar]
- Szacinski, A.M.; Thomson, P.F. The effect of mechanical properties on the wrinkling behaviour of sheet materials in the yoshida test. J. Mech. Work. Technol. 1984, 10, 87–102. [Google Scholar] [CrossRef]
- Cao, J.; Wang, X.; Mills, F.J. Characterization of sheet buckling subjected to controlled boundary constraints. J. Manuf. Sci. Eng. 2002, 124, 493–501. [Google Scholar] [CrossRef]
- Cao, J.; Cheng, S.H.; Wang, H.P.; Wang, C.T. Buckling of sheet metals in contact with tool surfaces. CIRP Ann. 2007, 56, 253–256. [Google Scholar] [CrossRef]
- Du, B.; Xie, J.; Li, H.; Zhao, C.C.; Zhang, X.; Yuan, X.M. Determining factors affecting sheet metal plastic wrinkling in response to nonuniform tension using wrinkling limit diagrams. Thin-Walled Struct. 2020, 147, 106535. [Google Scholar] [CrossRef]
- Kim, J.B.; Yoon, J.W.; Yang, D.Y. Wrinkling initiation and growth in modified Yoshida buckling test: Finite element analysis and experimental comparison. Int. J. Mech. Sci. 2000, 42, 1683–1714. [Google Scholar] [CrossRef]
- Schleich, R.; Albiez, C.; Papaioanu, A. Investigation on simulation of buckling of aluminium sheet alloys. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Han, F.; Liewald, M. A new method to enhance the accuracy of the buckling test using modified Yoshida sample. Adv. Mater. Res. 2014, 1018, 199–206. [Google Scholar] [CrossRef]
- Peng, L.F.; Lai, X.M.; Liu, D.A.; Hu, P.; Ni, J. Flow channel shape optimum design for hydroformed metal bipolar plate in PEM fuel cell. J. Power Sources 2008, 178, 223–230. [Google Scholar] [CrossRef]
- Wang, C.J.; Guo, B.; Shan, D.B.; Zhang, M.M. Research Progress and Outlook of High-frequency/ultrasonic Vibration Assisted Microforming. J. Netshape Form. Eng. 2015, 7, 7–16. [Google Scholar]
- Langenecker, B. Effects of ultrasound on deformation characteristics of metals. IEEE Trans. Sonics Ultrason. 1966, 13, 1–8. [Google Scholar]
- Witthauer, A.T.; Kim, G.Y.; Faidley, L.E.; Zou, Q.Z.; Wang, Z. Effects of acoustic softening and hardening in high-frequency vibration-assisted punching of aluminum. Mater. Manuf. Process. 2014, 29, 1184–1189. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.J.; Han, H.B.; Shan, D.B.; Guo, B. Investigation on effect of ultrasonic vibration on micro-blanking process of copper foil. Int. J. Adv. Manuf. Technol. 2017, 93, 2243–2249. [Google Scholar]
- Kumar, V.C.; Hutchings, I.M. Reduction of the sliding friction of metals by the application of longitudinal or transverse ultrasonic vibration. Tribol. Int. 2004, 37, 833–840. [Google Scholar] [CrossRef]
- Huang, Y.M.; Wu, Y.S.; Huang, J.Y. The influence of ultrasonic vibration-assisted micro-deep drawing process. Int. J. Adv. Manuf. Technol. 2014, 71, 1455–1461. [Google Scholar] [CrossRef]
- Malekipour, E.; Sharifi, E.; Majd, N.S.; Heidary, H. Observation on the behavior of ultrasonic micro-hammer and its effects on the deep drawing process: Numerical simulation and experimental study. Ultrasonics 2022, 119, 106566. [Google Scholar]
- Xu, L.H.; Lei, Y.L.; Zhang, H.O.; Zhang, Z.C.; Sheng, Y.C.; Han, G.C. Research on the micro-extrusion process of copper T2 with different ultrasonic vibration modes. Metals 2019, 9, 1209. [Google Scholar] [CrossRef]
- Han, G.C.; Wan, W.Q.; Zhang, Z.C.; Xu, L.H.; Liu, F.C.; Zhang, H.O. Experimental investigation into effects of different ultrasonic vibration modes in micro-extrusion process. J. Manuf. Process. 2021, 67, 427–437. [Google Scholar]
- Liu, Y.W.; Yang, G.; Lian, J.S.; Liu, L.S. Moiré topography analysis of the buckling process of a square sheet-metal plate subjected to non-uniform tension. J. Mater. Process. Technol. 1992, 31, 327–333. [Google Scholar] [CrossRef]
- Hill, R. A general theory of uniqueness and stability in elastic-plastic solids. J. Mech. Phys. Solids 1958, 6, 236–249. [Google Scholar]
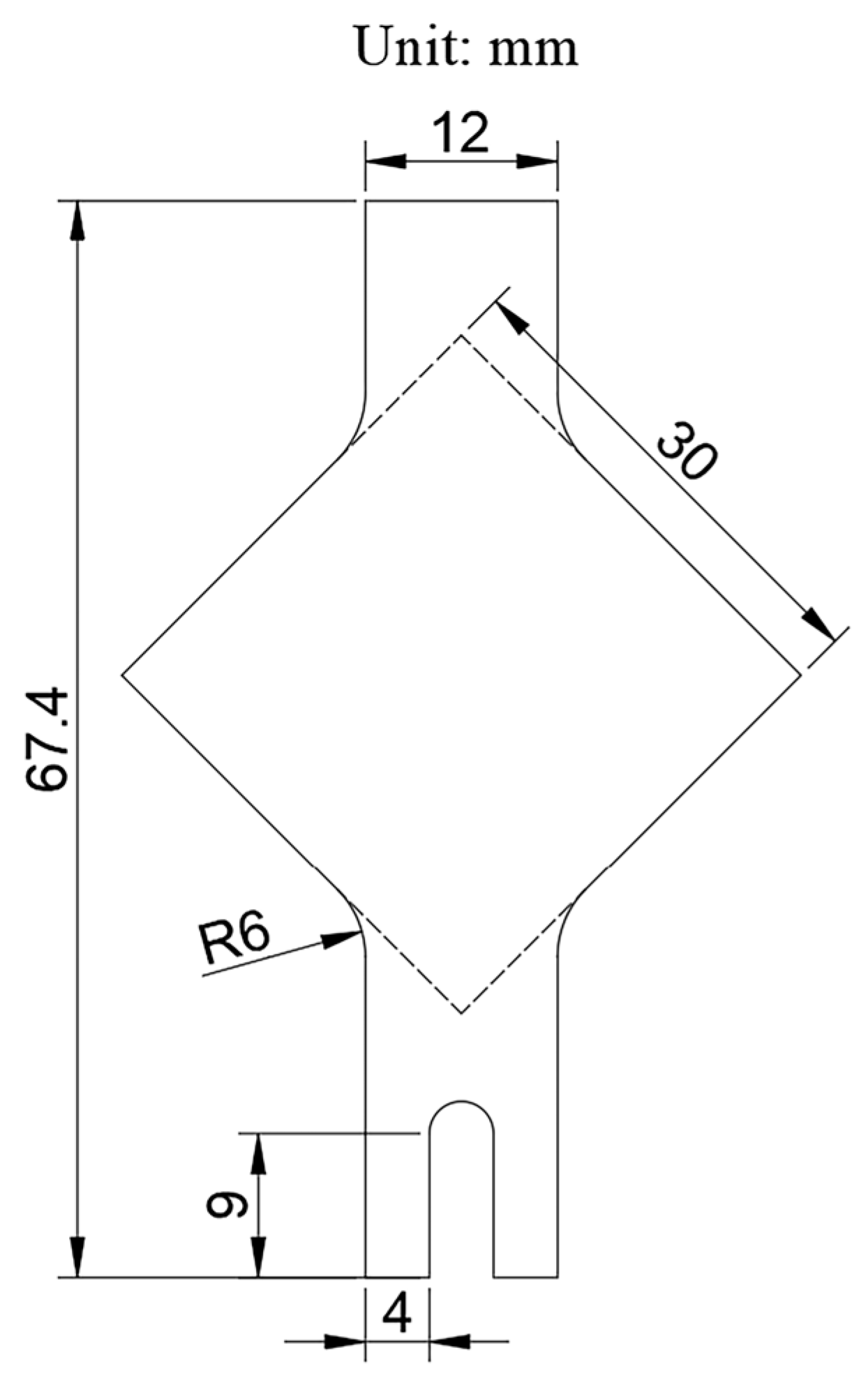
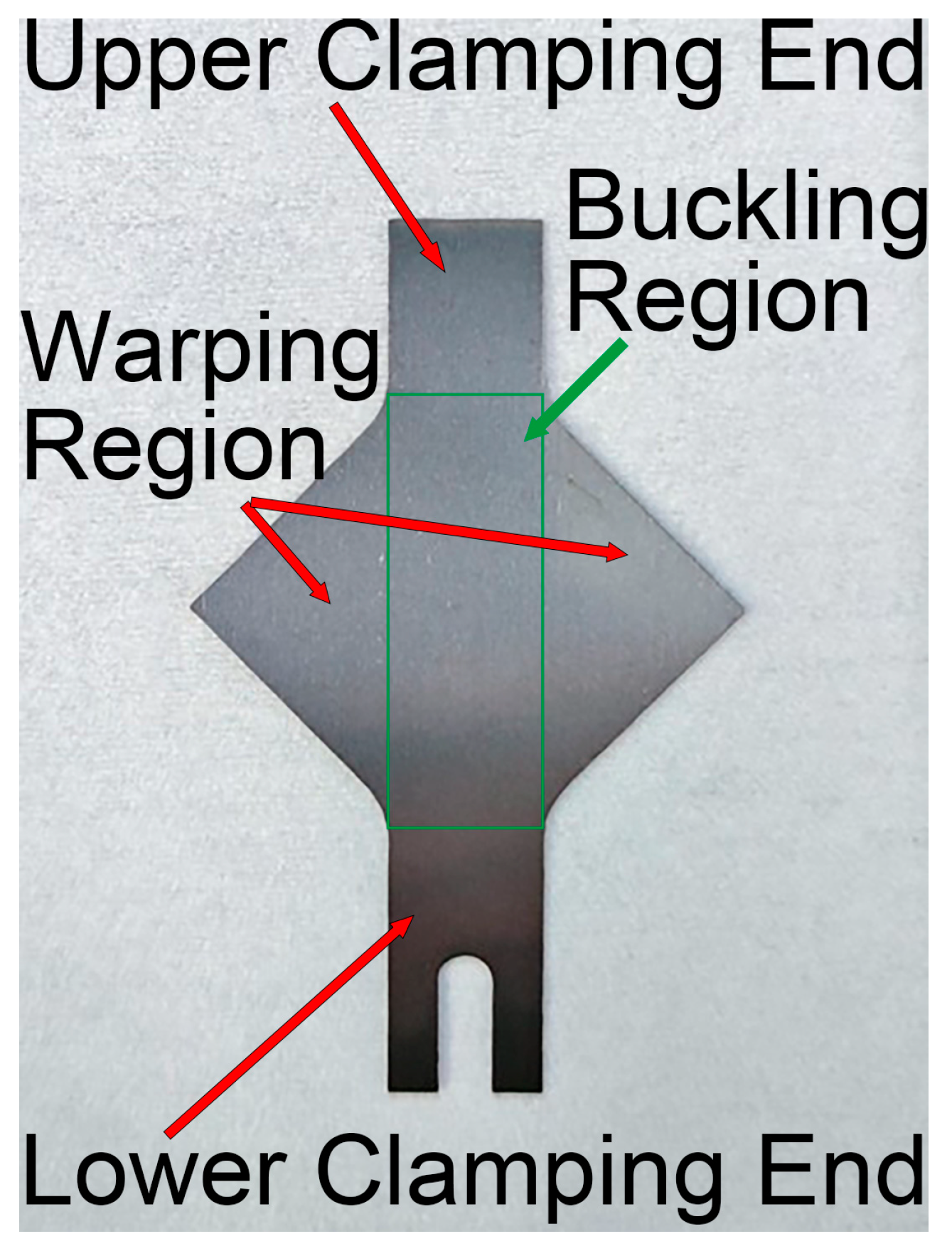



| Thickness (mm) | Elastic Modulus (Gpa) | Yield Strength (Mpa) | Tensile Strength (Mpa) | Elongation After Fracture (%) | Hardening Index n |
|---|---|---|---|---|---|
| 0.075 | 82.6 | 231.3 | 291.4 | 44 | 0.11 |
| 0.1 | 65.7 | 229.6 | 300.2 | 36 | 0.13 |
| Measurement Location | Measured Values (mm) | Mean Value (mm) | Variance (mm2) |
|---|---|---|---|
| Buckling Region | 0.074 0.073 0.074 0.075 0.072 | 0.0736 | 0.00000104 |
| Warping Region | 0.075 0.074 0.075 0.073 0.075 | 0.0744 | 0.00000064 |
| Measurement Location | Measured Values (mm) | Mean Value (mm) | Variance (mm2) |
|---|---|---|---|
| Buckling Region | 0.100 0.099 0.099 0.098 0.097 | 0.0986 | 0.00000104 |
| Warping Region | 0.098 0.098 0.099 0.098 0.099 | 0.0984 | 0.000000168 |
| Specimen Thickness (mm) | Measured Values (µm) | Mean Value (µm) | Variance (µm2) |
|---|---|---|---|
| 0.075 | 0.074 0.062 0.056 0.070 0.075 | 0.0674 | 0.00005374 |
| 0.1 | 0.051 0.042 0.055 0.057 0.052 | 0.0474 | 0.00008584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Wang, Y.; Wang, C.; He, H.; Chen, F.; Sun, L. Experimental Study on Anti-Wrinkling Performance of TA1 Titanium Thin Sheet Assisted by Ultrasonic Vibration. Materials 2025, 18, 1439. https://doi.org/10.3390/ma18071439
Ma J, Wang Y, Wang C, He H, Chen F, Sun L. Experimental Study on Anti-Wrinkling Performance of TA1 Titanium Thin Sheet Assisted by Ultrasonic Vibration. Materials. 2025; 18(7):1439. https://doi.org/10.3390/ma18071439
Chicago/Turabian StyleMa, Jiayi, Yucheng Wang, Chunju Wang, Haidong He, Feng Chen, and Lining Sun. 2025. "Experimental Study on Anti-Wrinkling Performance of TA1 Titanium Thin Sheet Assisted by Ultrasonic Vibration" Materials 18, no. 7: 1439. https://doi.org/10.3390/ma18071439
APA StyleMa, J., Wang, Y., Wang, C., He, H., Chen, F., & Sun, L. (2025). Experimental Study on Anti-Wrinkling Performance of TA1 Titanium Thin Sheet Assisted by Ultrasonic Vibration. Materials, 18(7), 1439. https://doi.org/10.3390/ma18071439









