Experimental and Numerical Characterization of Electrospun Piezoelectric Polyvinylidene Fluoride Nanocomposites Reinforced with Silver Nanoparticles
Abstract
:1. Introduction
2. Numerical and Analytical Modelling of Piezoelectric Composites
- The dilute approximation;
- The self-consistent method;
- The Mori–Tanaka mean field method;
- The differential scheme.
- 5.
- Analytical models:
- Micromechanics models based on averaging material properties through the constituent phases and with different types of connectivity, where 0-3 represents the random dispersion of elements within the composite that have isotropic properties; 1-3 represents structures with fibres where one observed phase can be connected through series (meaning constant properties within the composite) or parallel connections (where weights are calculated); and 3-3 connectivity represents the 3D distribution of elements, but, unlike the 0-3 type, it has a somewhat arranged orientation and alignment of the phases. However, these models cannot capture localized behaviour within small domains due to the averaged properties, such as commonly appearing fluctuations in properties (both mechanical and electrical) within the small domains in different phases and along their interfaces.
- Models based on Eshelby equations:
- i
- Dilute approximation models;
- ii
- Mori–Tanaka-based models;
- iii
- Extended Mori–Tanaka models, such as Mori–Tanaka–Eshelby models;
- iv
- Self-consistent models and their extended models;
- v
- Extended rule of mixture models.
- Models based on asymptotic homogenization (or periodic homogenization).
- 6.
- Numerical models or Finite Element (FE) models, which use representative volume elements (RVEs) throughout the 3D volumetric space of the composite for the calculation of composite properties and responses to external influences, where the definition of the size and shape of RVEs essentially determines the model validity. FEMs can capture localized behaviour to some degree, depending on the defined RVEs, with several established approaches, also related to the computational resources needed for calculations:
- Linear FE models (usually for elastic behaviour or small deformations);
- Nonlinear FE models (large deformations, elasto-plastic material or nonlinear contacts);
- The representative volume element method;
- The theory of periodic boundary conditions;
- Calculation methods for the effective coefficients;
- Optimization of piezoelectric behaviour with different possible methods, such as the Discrete Material Optimization (DMO) method.
3. Materials and Methods
3.1. Fabrication of PVDF Nanofibers with Incorporated AgNPs
3.2. SEM and EDS Analysis
3.3. FTIR Spectroscopy Analysis
3.4. Electromechanical Tests at Macro Scale
3.5. Finite Element Analysis (FEA)
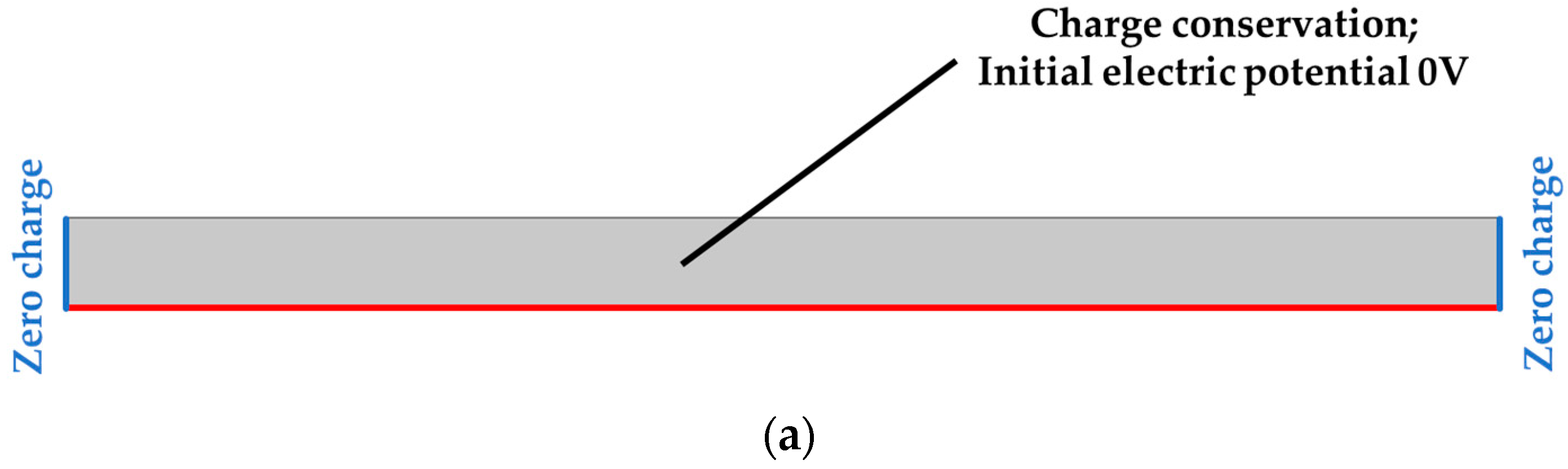
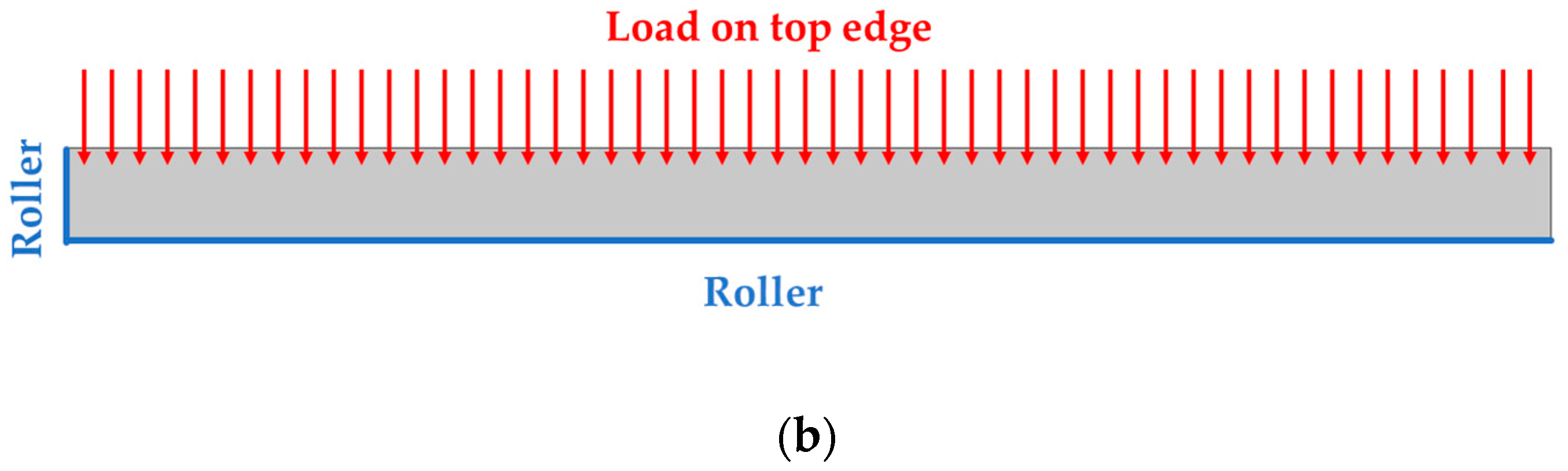
3.5.1. Piezoelectric Constitutive Relations
3.5.2. FE Model of PVDF/AgNPs Nanocomposite
4. Results and Discussion
4.1. SEM and EDS Results
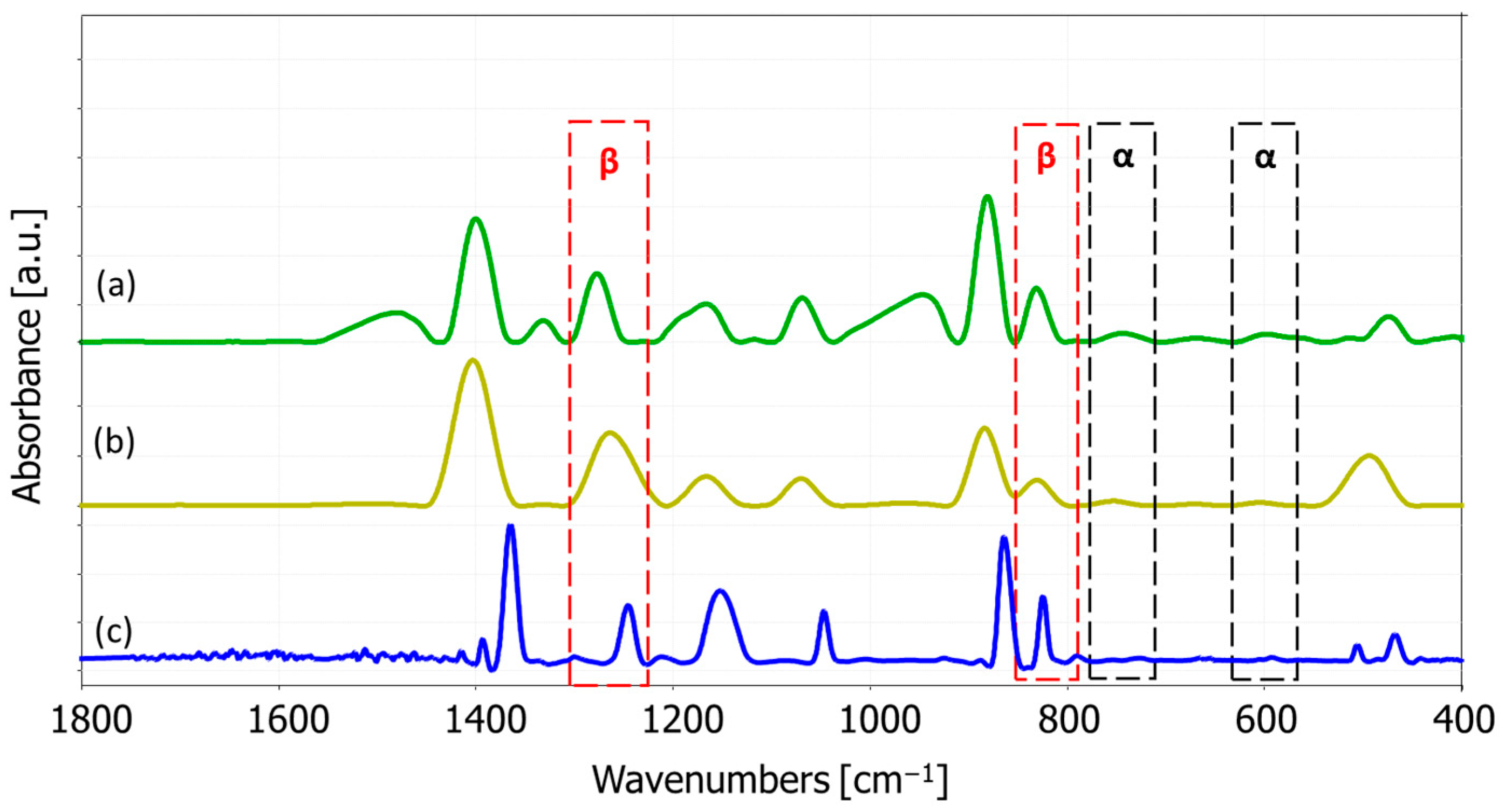
4.2. FTIR Spectroscopy Analysis Results
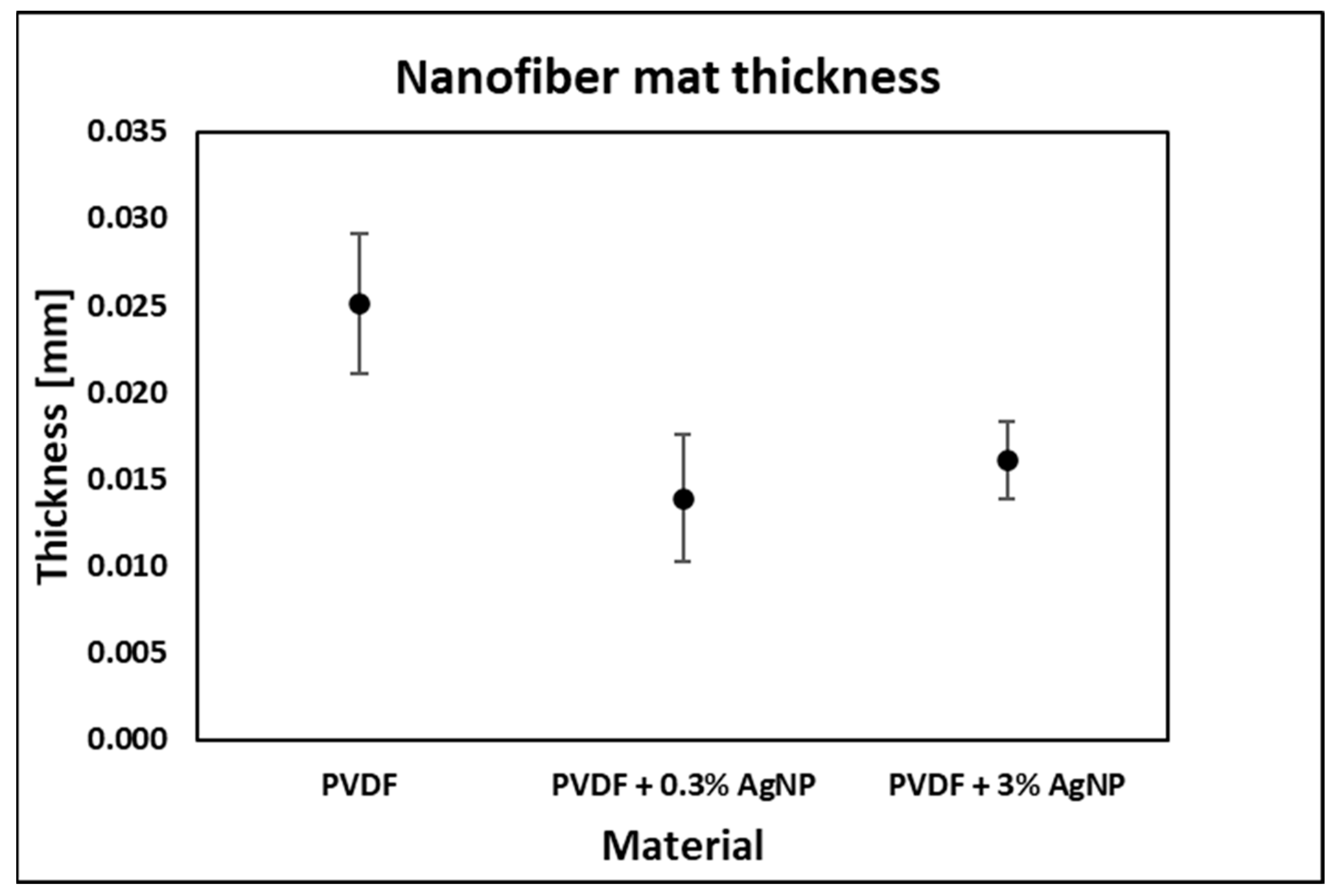
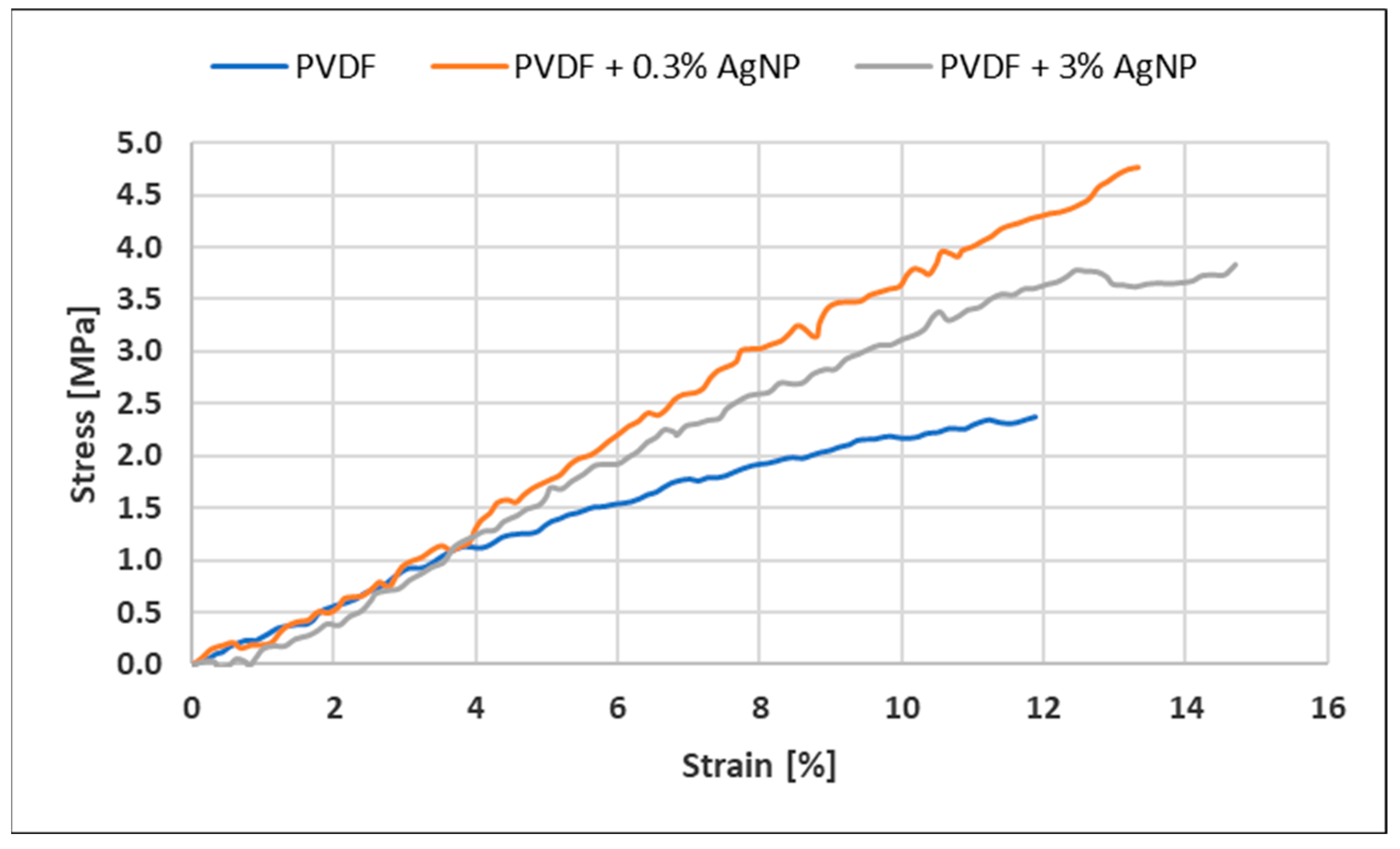
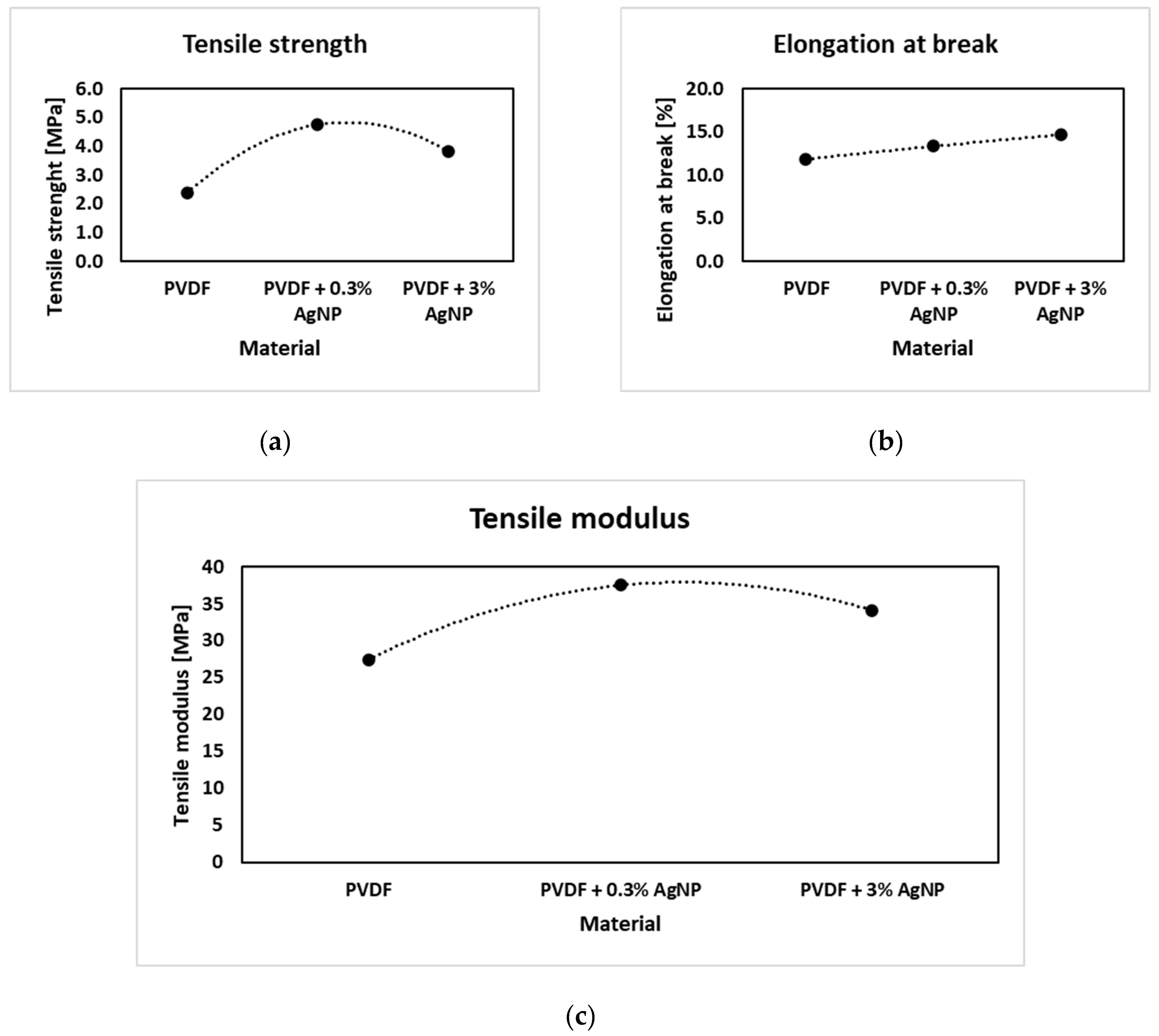
4.3. Mechanical Testing
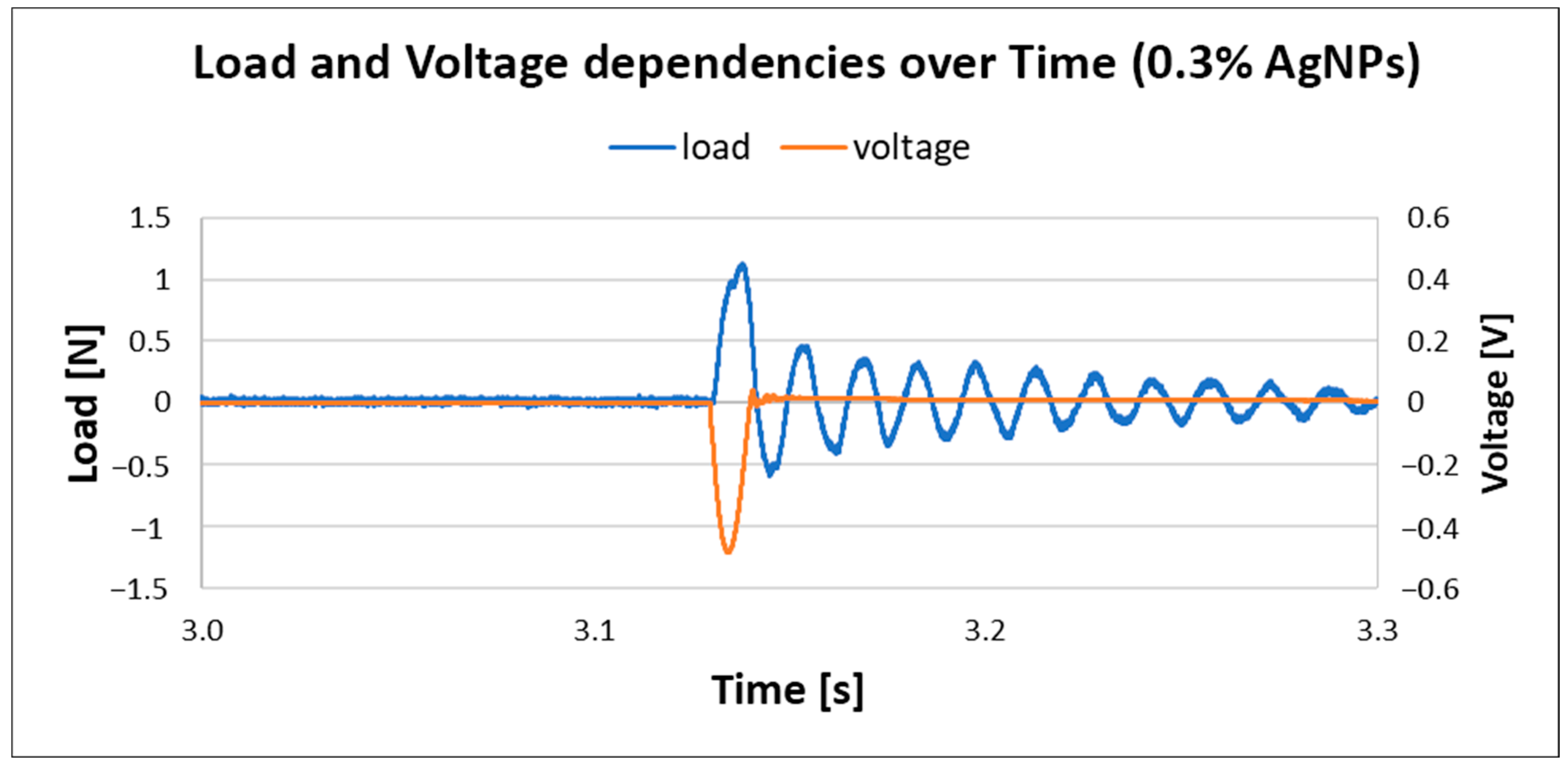
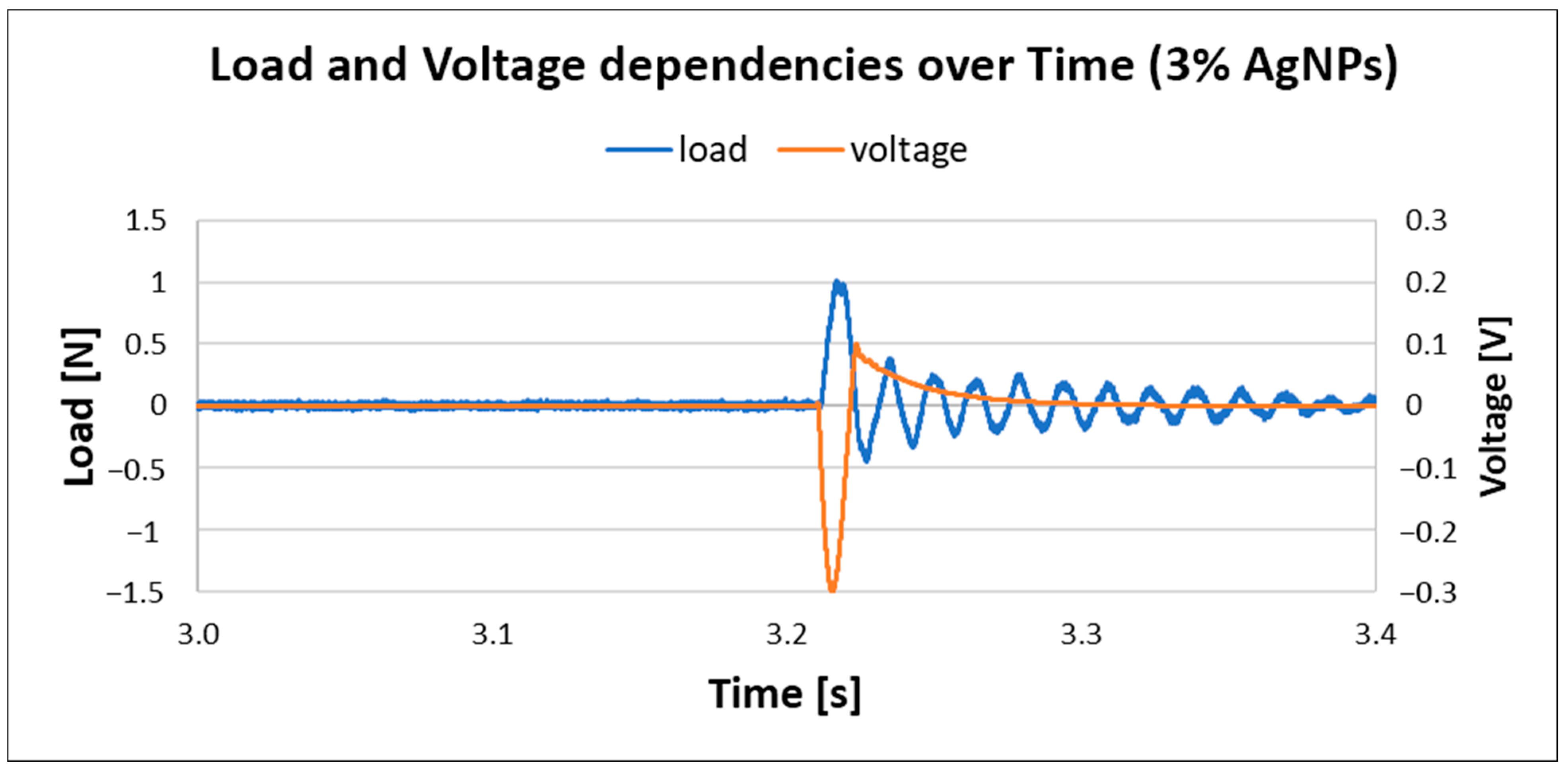
4.4. Measurements Related to Piezoelectric Outputs
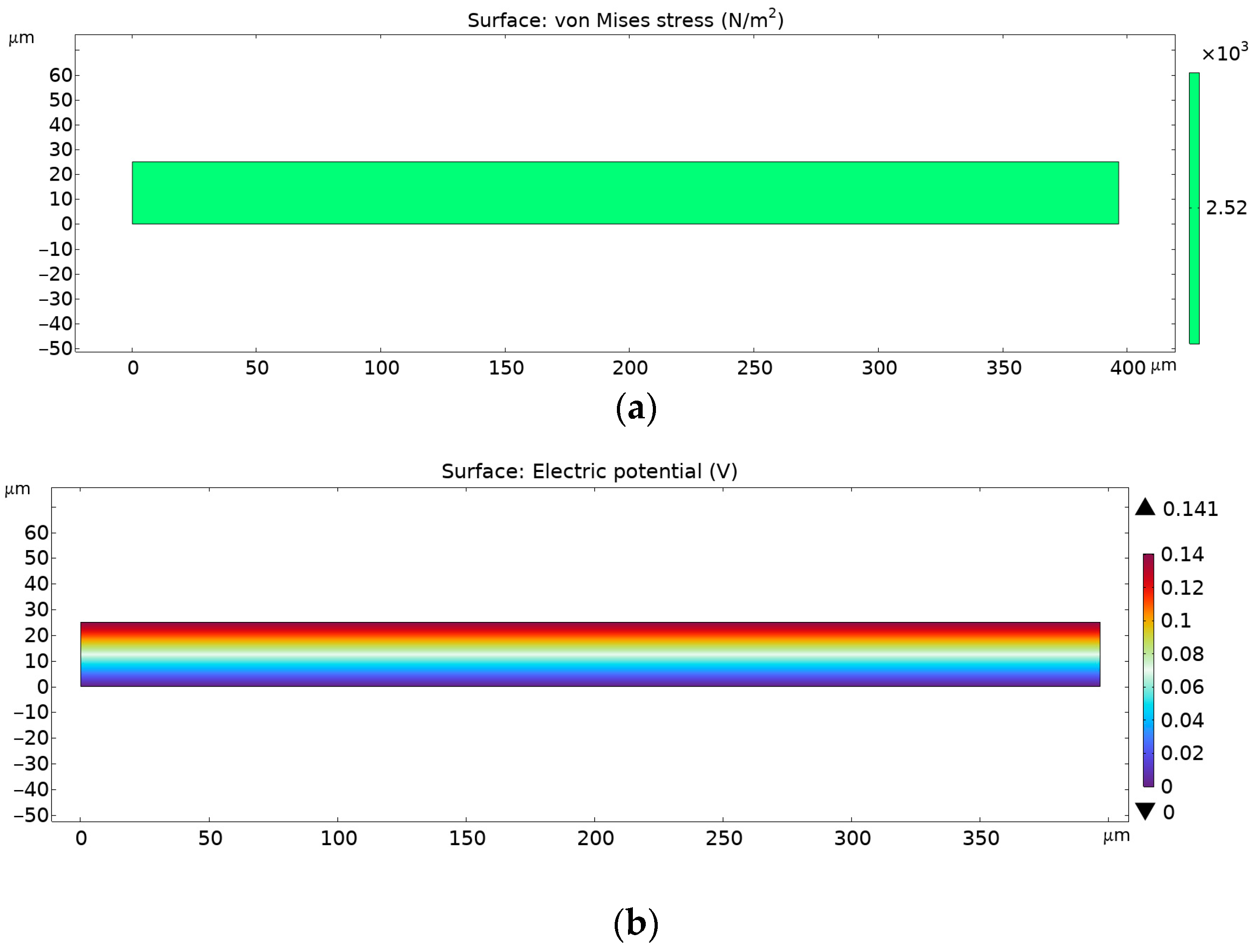
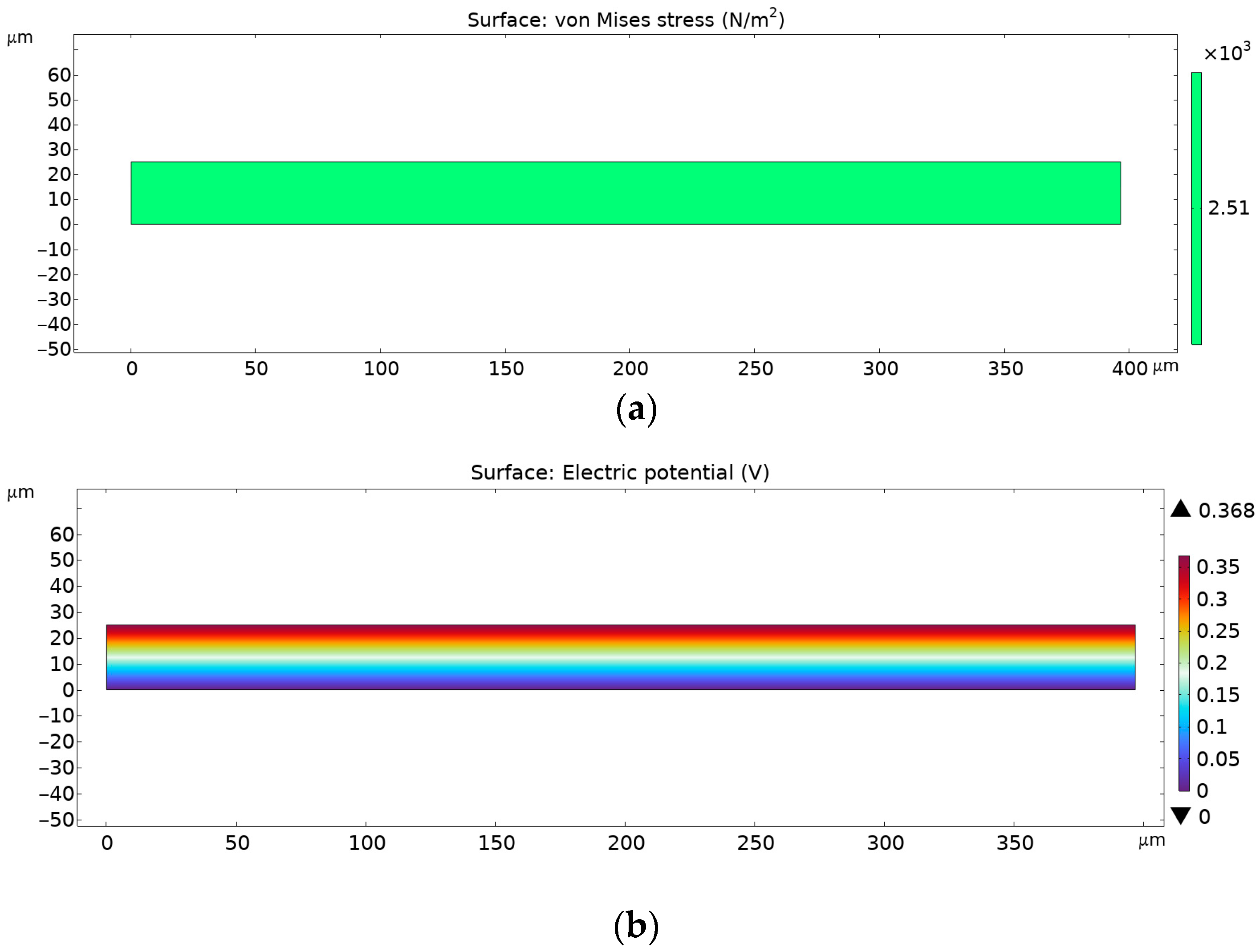
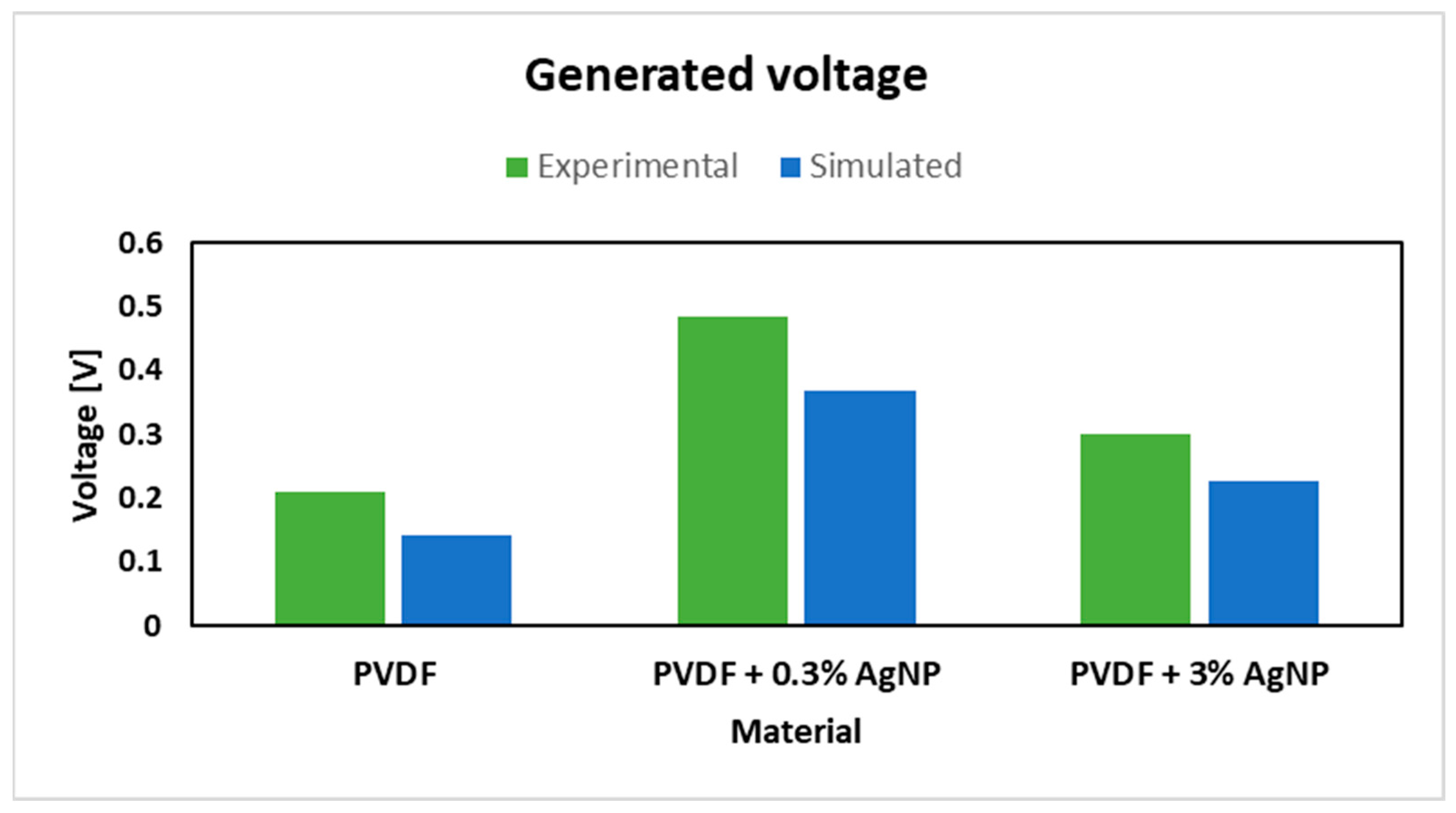
4.5. Finite Element Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ueberschlag, P. PVDF Piezoelectric Polymer. Sens. Rev. 2001, 21, 118–126. [Google Scholar] [CrossRef]
- Milenković, S.; Virijević, K.; Živić, F.; Radojević, I.; Grujović, N. Composite Nanoarchitectonics of Electrospun Piezoelectric PVDF/AgNPs for Biomedical Applications, Including Breast Cancer Treatment. Materials 2024, 17, 3872. [Google Scholar] [CrossRef] [PubMed]
- Anic, M.; Prodanovic, M.; Milenkovic, S.; Filipovic, N.; Grujovic, N.; Zivic, F. The Review of Materials for Energy Harvesting. In Proceedings of the 2021 IEEE 21st International Conference on Bioinformatics and Bioengineering (BIBE), Kragujevac, Serbia, 25 October 2021; IEEE: Kragujevac, Serbia, 2021; pp. 1–6. [Google Scholar]
- Anic, M.; Prodanovic, M.; Milenkovic, S.; Filipovic, N.; Grujovic, N.; Zivic, F. Electrospinning as the fabrication technology for the energy harvesting composites. In Proceedings of the 38th International Conference on Production Engineering of Serbia ICPE-S 2021, Čačak, Serbia, 14 October 2021; Fakultet Tehničkih Nauka u Čačku, Univerziteta u Kragujevcu: Čačak, Serbia, 2021; pp. 167–178. [Google Scholar]
- Fukada, E. History and Recent Progress in Piezoelectric Polymers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 1277–1290. [Google Scholar] [CrossRef] [PubMed]
- Ruan, L.; Yao, X.; Chang, Y.; Zhou, L.; Qin, G.; Zhang, X. Properties and Applications of the β Phase Poly(Vinylidene Fluoride). Polymers 2018, 10, 228. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive Phases of Poly(Vinylidene Fluoride): Determination, Processing and Applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, W.; Wang, T.; Yilmaz, D.E.; Van Duin, A.C.T. C/H/O/F/Al ReaxFF Force Field Development and Application to Study the Condensed-Phase Poly(Vinylidene Fluoride) and Reaction Mechanisms with Aluminum. J. Phys. Chem. C 2022, 126, 11058–11074. [Google Scholar] [CrossRef]
- Marmolejo-Tejada, J.M.; De La Roche-Yepes, J.; Pérez-López, C.A.; Taborda, J.A.P.; Ávila, A.; Jaramillo-Botero, A. Understanding the Origin of Enhanced Piezoelectric Response in PVDF Matrices with Embedded ZnO Nanoparticles, from Polarizable Molecular Dynamics Simulations. J. Chem. Inf. Model. 2021, 61, 4537–4543. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, Z.; Zhu, Y. Study on the Effect of Stretching Behavior on the Properties of PVDF Films and Mechanism. Polymer 2024, 297, 126884. [Google Scholar] [CrossRef]
- Hartono, A.; Satira, S.; Djamal, M.; Ramli, R.; Bahar, H.; Sanjaya, E. Effect of Mechanical Treatment Temperature on Electrical Properties and Crystallite Size of PVDF Film. Adv. Mater. Phys. Chem. 2013, 3, 71–76. [Google Scholar] [CrossRef]
- Patil, Y.; Zhao, J.; Ameduri, B.; Rastogi, S. Tailoring Electroactive β- and γ-Phases via Synthesis in the Nascent Poly(Vinylidene Fluoride) Homopolymers. Macromolecules 2024, 57, 616–627. [Google Scholar] [CrossRef]
- Mukherjee, A.; Dasgupta Ghosh, B.; Ghosh, A.; Roy, S. Polyvinylidene Fluoride Nanocomposites as Piezoelectric Nanogenerator: Properties, Fabrication and Market Applications. Adv. Eng. Mater. 2024, 26, 2400445. [Google Scholar] [CrossRef]
- Bindhu, A.; Arun, A.P.; Pathak, M. Review on Polyvinylidene Fluoride-Based Triboelectric Nanogenerators for Applications in Health Monitoring and Energy Harvesting. ACS Appl. Electron. Mater. 2024, 6, 47–72. [Google Scholar] [CrossRef]
- Virijević, K.; Živanović, M.N.; Nikolić, D.; Milivojević, N.; Pavić, J.; Morić, I.; Šenerović, L.; Dragačević, L.; Thurner, P.J.; Rufin, M.; et al. AI-Driven Optimization of PCL/PEG Electrospun Scaffolds for Enhanced In Vivo Wound Healing. ACS Appl. Mater. Interfaces 2024, 16, 22989–23002. [Google Scholar] [CrossRef] [PubMed]
- Virijević, K.; Živanović, M.; Pavić, J.; Dragačević, L.; Ljujić, B.; Miletić Kovačević, M.; Papić, M.; Živanović, S.; Milenković, S.; Radojević, I.; et al. Electrospun Gelatin Scaffolds with Incorporated Antibiotics for Skin Wound Healing. Pharmaceuticals 2024, 17, 851. [Google Scholar] [CrossRef] [PubMed]
- Purushothaman, S.M.; Tronco, M.F.; Kottathodi, B.; Royaud, I.; Ponçot, M.; Kalarikkal, N.; Thomas, S.; Rouxel, D. A Review on Electrospun PVDF-Based Nanocomposites: Recent Trends and Developments in Energy Harvesting and Sensing Applications. Polymer 2023, 283, 126179. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Jiang, B.; Zhang, Q.; Chen, H.; Shen, Y.; Wang, Z.; Yin, X. Process Investigation on Robust Electrospinning of Non-Aligned and Aligned Polyvinylidene Fluoride Nanofiber Mats for Flexible Piezoelectric Sensors. Polymers 2024, 16, 816. [Google Scholar] [CrossRef]
- Chen, Z.; Guan, M.; Bian, Y.; Yin, X. Multifunctional Electrospun Nanofibers for Biosensing and Biomedical Engineering Applications. Biosensors 2023, 14, 13. [Google Scholar] [CrossRef]
- Kumar, M.; Kulkarni, N.D.; Kumari, P. Piezoelectric Performance Enhancement of Electrospun Functionally Graded PVDF/BaTiO3 Based Flexible Nanogenerators. Mater. Res. Bull. 2024, 174, 112739. [Google Scholar] [CrossRef]
- Salama, M.; Hamed, A.; Noman, S.; Magdy, G.; Shehata, N.; Kandas, I. Boosting Piezoelectric Properties of PVDF Nanofibers via Embedded Graphene Oxide Nanosheets. Sci. Rep. 2024, 14, 16484. [Google Scholar] [CrossRef]
- Pan, C.-T.; Dutt, K.; Yen, C.-K.; Kumar, A.; Kaushik, A.C.; Wei, D.-Q.; Kumar, A.; Wen, Z.-H.; Hsu, W.-H.; Shiue, Y.-L. Characterization of Piezoelectric Properties of Ag-NPs Doped PVDFNanocomposite Fibres Membrane Prepared by Near Field Electrospinning. Comb. Chem. High Throughput Screen. 2022, 25, 720–729. [Google Scholar] [CrossRef]
- Issa, A.; Al-Maadeed, M.; Luyt, A.; Ponnamma, D.; Hassan, M. Physico-Mechanical, Dielectric, and Piezoelectric Properties of PVDF Electrospun Mats Containing Silver Nanoparticles. C 2017, 3, 30. [Google Scholar] [CrossRef]
- Chae, D.W.; Hwang, S.S.; Hong, S.M.; Hong, S.P.; Cho, B.G.; Kim, B.C. Influence of High Contents of Silver Nanoparticles on the Physical Properties of Poly(Vinylidene Fluoride). Mol. Cryst. Liq. Cryst. 2007, 464, 233/[815]–241/[823]. [Google Scholar] [CrossRef]
- Xi, Y.; Pan, W.; Xi, D.; Liu, X.; Yu, J.; Xue, M.; Xu, N.; Wen, J.; Wang, W.; He, H.; et al. Optimization, Characterization and Evaluation of ZnO/Polyvinylidene Fluoride Nanocomposites for Orthopedic Applications: Improved Antibacterial Ability and Promoted Osteoblast Growth. Drug Deliv. 2020, 27, 1378–1385. [Google Scholar] [CrossRef] [PubMed]
- Zaszczyńska, A.; Zabielski, K.; Gradys, A.; Kowalczyk, T.; Sajkiewicz, P. Piezoelectric Scaffolds as Smart Materials for Bone Tissue Engineering. Polymers 2024, 16, 2797. [Google Scholar] [CrossRef]
- Liu, T.; Xie, F.; Geng, L.; He, R.; Sun, M.; Ni, T.; Xu, P.; Xing, C.; Peng, Y.; Chen, K.; et al. Micro-Electro Nanofibrous Dressings Based on PVDF-AgNPs as Wound Healing Materials to Promote Healing in Active Areas. Int. J. Nanomed. 2025, 20, 771–789. [Google Scholar] [CrossRef]
- Mokhtari, F.; Samadi, A.; Rashed, A.O.; Li, X.; Razal, J.M.; Kong, L.; Varley, R.J.; Zhao, S. Recent Progress in Electrospun Polyvinylidene Fluoride (PVDF)-Based Nanofibers for Sustainable Energy and Environmental Applications. Prog. Mater. Sci. 2025, 148, 101376. [Google Scholar] [CrossRef]
- Cai, X.; Lei, T.; Sun, D.; Lin, L. A Critical Analysis of the α, β and γ Phases in Poly(Vinylidene Fluoride) Using FTIR. RSC Adv. 2017, 7, 15382–15389. [Google Scholar] [CrossRef]
- Jiang, Y.; Gong, L.; Hu, X.; Zhao, Y.; Chen, H.; Feng, L.; Zhang, D. Aligned P(VDF-TrFE) Nanofibers for Enhanced Piezoelectric Directional Strain Sensing. Polymers 2018, 10, 364. [Google Scholar] [CrossRef]
- Zeyrek Ongun, M.; Oguzlar, S.; Doluel, E.C.; Kartal, U.; Yurddaskal, M. Enhancement of Piezoelectric Energy-Harvesting Capacity of Electrospun β-PVDF Nanogenerators by Adding GO and rGO. J. Mater. Sci. Mater. Electron. 2020, 31, 1960–1968. [Google Scholar] [CrossRef]
- Kloster, J.T.; Danley, M.J.; Lai, V.K.; Zhao, P. Effects of Porosity on Piezoelectric Characteristics of Polyvinylidene Fluoride Films for Biomedical Applications. BME Front. 2023, 4, 0009. [Google Scholar] [CrossRef]
- Gusarov, B.; Gusarova, E.; Viala, B.; Gimeno, L.; Cugat, O. PVDF Piezoelectric Voltage Coefficient in Situ Measurements as a Function of Applied Stress. J. Appl. Polym. Sci. 2016, 133, app.43248. [Google Scholar] [CrossRef]
- Nair, R.; Mahdi, J.; Amjad, O.; Maree, K.; Jain, A.; Al-Dubai, A.; Jaradat, S.; Shyha, I.; Trabelsi, M.; Alothamn, B.; et al. Parametric Study on PVDF Electrospun Nanofibers: Optical Characteristics, Piezoelectric Analysis, and Correlated Applications. J. Electron. Mater. 2024, 53, 4155–4172. [Google Scholar] [CrossRef]
- Crespo-Miguel, J.; Lucarini, S.; Arias, A.; Garcia-Gonzalez, D. Thermo-Electro-Mechanical Microstructural Interdependences in Conductive Thermoplastics. NPJ Comput. Mater. 2023, 9, 134. [Google Scholar] [CrossRef]
- Dunn, M.L.; Taya, M. Micromechanics Predictions of the Effective Electroelastic Moduli of Piezoelectric Composites. Int. J. Solids Struct. 1993, 30, 161–175. [Google Scholar] [CrossRef]
- Mishra, N.; Das, K. A Mori–Tanaka Based Micromechanical Model for Predicting the Effective Electroelastic Properties of Orthotropic Piezoelectric Composites with Spherical Inclusions. SN Appl. Sci. 2020, 2, 1206. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Machado, M.A.; Vidal, C.; Carvalho, M.S. Modelling Electro-Mechanical Behaviour in Piezoelectric Composites: Current Status and Perspectives on Homogenisation. Adv. Eng. Softw. 2024, 193, 103651. [Google Scholar] [CrossRef]
- Cañamero, F.J.; Buroni, F.C.; Rodríguez-Tembleque, L. Connectivity Patterns in Lead-Free Piezocomposites: A Critical Analysis for 0-3 and 1-3 Configurations. Compos. Struct. 2024, 337, 118062. [Google Scholar] [CrossRef]
- Mackerle, J. Smart Materials and Structures—A Finite Element Approach—An Addendum: A Bibliography (1997–2002). Model. Simul. Mater. Sci. Eng. 2003, 11, 707–744. [Google Scholar] [CrossRef]
- Newnham, R.E.; Skinner, D.P.; Cross, L.E. Connectivity and Piezoelectric-Pyroelectric Composites. Mater. Res. Bull. 1978, 13, 525–536. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Jiménez Segura, N.; Pichler, B.L.A.; Hellmich, C. A Green’s Function-Based Approach to the Concentration Tensor Fields in Arbitrary Elastic Microstructures. Front. Mater. 2023, 10, 1137057. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Jha, D.; Liao, W.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Establishing Structure-Property Localization Linkages for Elastic Deformation of Three-Dimensional High Contrast Composites Using Deep Learning Approaches. Acta Mater. 2019, 166, 335–345. [Google Scholar] [CrossRef]
- Akinpelu, A.; Bhullar, M.; Yao, Y. Discovery of Novel Materials through Machine Learning. J. Phys. Condens. Matter 2024, 36, 453001. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; Bravo-Castillero, J.; Rodríguez-Ramos, R.; Sabina, F.J.; Martínez-Rosado, R. Overall Properties of Piezocomposite Materials 1–3. Mater. Lett. 2001, 48, 93–98. [Google Scholar] [CrossRef]
- Derraz, M.; Ennawaoui, C.; Mastouri, H.; El Hmamssy, Y.; Abouricha, N.; Rjafallah, A.; Laadissi, E.M.; Hajjaji, A. Mathematical Modeling for Predicting Electrical Energy Harvested Using Piezoelectric Composite Materials for Smart System Applications. Micro Nano Eng. 2024, 23, 100253. [Google Scholar] [CrossRef]
- Lv, S.; Li, B.; Zhang, Q.; Shi, Y.; Gao, C. A Finite Deformation Phase Field Model for Electromechanical Fracture of Flexible Piezoelectric Materials. Appl. Math. Model. 2024, 130, 728–748. [Google Scholar] [CrossRef]
- Zhang, J.; Chadwick, A.F.; Chopp, D.L.; Voorhees, P.W. Phase Field Modeling with Large Driving Forces. NPJ Comput. Mater. 2023, 9, 166. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X. Numerical Approximations of Allen-Cahn and Cahn-Hilliard Equations. Discret. Contin. Dyn. Syst. 2010, 28, 1669–1691. [Google Scholar] [CrossRef]
- Wight, C.L.; Zhao, J. Solving Allen-Cahn and Cahn-Hilliard Equations Using the Adaptive Physics Informed Neural Networks. arXiv 2020, arXiv:2007.04542. [Google Scholar]
- Berger, H.; Kari, S.; Gabbert, U.; Rodriguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Diaz, R.; Sabina, F.J.; Maugin, G.A. Unit Cell Models of Piezoelectric Fiber Composites for Numerical and Analytical Calculation of Effective Properties. Smart Mater. Struct. 2006, 15, 451–458. [Google Scholar] [CrossRef]
- Wang, S.Y. A Finite Element Model for the Static and Dynamic Analysis of a Piezoelectric Bimorph. Int. J. Solids Struct. 2004, 41, 4075–4096. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, N.; Das, K.; Roy, A. Effective Electromechanical Properties and Energy Harvesting Response in PMN-0.3PT/PDMS Flexible Piezoelectric Composites: A Combined Experimental and Theoretical Study. J. Phys. Appl. Phys. 2023, 56, 365503. [Google Scholar] [CrossRef]
- Mishra, N.; Das, K. A Comparative Study of Incremental Selfconsistent and Eshelby–Mori–Tanaka Models for Estimating the Electroelastic Properties of Piezoelectric Polymer Composites with an Orthotropic Matrix. Mech. Compos. Mater. 2022, 58, 657–672. [Google Scholar] [CrossRef]
- Wang, S.Y.; Quek, S.T.; Ang, K.K. Vibration Control of Smart Piezoelectric Composite Plates. Smart Mater. Struct. 2001, 10, 637–644. [Google Scholar] [CrossRef]
- Odegard, G. Constitutive Modeling of Nanotube–Reinforced Polymer Composites. Compos. Sci. Technol. 2003, 63, 1671–1687. [Google Scholar] [CrossRef]
- Jagdish, A.K.; Buroni, F.C.; Melnik, R.; Rodriguez-Tembleque, L.; Sáez, A. Flexoelectric Anisotropy and Shear Contributions in Lead-Free Piezocomposites. Mech. Res. Commun. 2024, 140, 104321. [Google Scholar] [CrossRef]
- Knott, E.F. Dielectric Constant of Plastic Foams. IEEE Trans. Antennas Propag. 1993, 41, 1167–1171. [Google Scholar] [CrossRef]
- Furukawa, T.; Fujino, K.; Fukada, E. Electromechanical Properties in the Composites of Epoxy Resin and PZT Ceramics. Jpn. J. Appl. Phys. 1976, 15, 2119–2129. [Google Scholar] [CrossRef]
- Velayutham, T.S.; Halim, N.A.; Majid, W.H.A. Enhanced Functionalities in Flexible Poly (Vinylidene Fluoride-Trifluoroethylene)/Cerium Oxide Doped Sodium Bismuth Titanate [P(VDF-TrFE)/NBT-CeO2] Ceramic Polymer Composite Films: A Comprehensive Investigation of Piezoelectric, Pyroelectric, and Ferroelectric Properties. Next Mater. 2025, 6, 100416. [Google Scholar] [CrossRef]
- Rodrigues-Marinho, T.; Tubio, C.R.; Lanceros-Mendez, S.; Costa, P.F.R. Tailoring the Electrical Response of Polyvinylidene Fluoride Nanocomposites with Electrically Conductive and Dielectric Fillers. Adv. Eng. Mater. 2024, 26, 2301596. [Google Scholar] [CrossRef]
- Voigt, W. Ueber Die Beziehung Zwischen Den Beiden Elasticitätsconstanten Isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A Variational Approach to the Theory of the Elastic Behaviour of Multiphase Materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Affdl, J.C.H.; Kardos, J.L. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Malikan, M.; Dastjerdi, S.; Rucka, M.; Kadkhodayan, M. On Nonlinear 3D Electro-Elastic Numerical Modeling of Two-Phase Inhomogeneous FG Piezocomposites Reinforced with GNPs. Int. J. Eng. Sci. 2025, 207, 104174. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Mikata, Y. Determination of Piezoelectric Eshelby Tensor in Transversely Isotropic Piezoelectric Solids. Int. J. Eng. Sci. 2000, 38, 605–641. [Google Scholar] [CrossRef]
- Kuo, W.-S.; Huang, J.H. On the Effective Electroelastic Properties of Piezoelectric Composites Containing Spatially Oriented Inclusions. Int. J. Solids Struct. 1997, 34, 2445–2461. [Google Scholar] [CrossRef]
- Gandarilla-Pérez, C.A.; Rodríguez-Ramos, R.; Sevostianov, I.; Sabina, F.J.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Lau-Alfonso, L. Extension of Maxwell Homogenization Scheme for Piezoelectric Composites Containing Spheroidal Inhomogeneities. Int. J. Solids Struct. 2018, 135, 125–136. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; Rodríguez-Ramos, R.; López-Realpozo, J.C.; Bravo-Castillero, J.; Otero, J.A.; Sabina, F.J.; Lebon, F.; Dumont, S. Analysis of Fibrous Elastic Composites with Nonuniform Imperfect Adhesion. Acta Mech. 2016, 227, 57–73. [Google Scholar] [CrossRef]
- Odegard, G.M. Constitutive Modeling of Piezoelectric Polymer Composites. Acta Mater. 2004, 52, 5315–5330. [Google Scholar] [CrossRef]
- Kar-Gupta, R.; Venkatesh, T.A. Electromechanical Response of 1–3 Piezoelectric Composites: An Analytical Model. Acta Mater. 2007, 55, 1093–1108. [Google Scholar] [CrossRef]
- Tize Mha, P.; Maréchal, P.; Ntamack, G.E.; Kenmeugne, B. Phenomenological Model for Predicting Thermoelectromechanical Response of 2-2 Piezocomposite. J. Compos. Mater. 2023, 57, 2145–2159. [Google Scholar] [CrossRef]
- Tize Mha, P.; Maréchal, P.; Ntamack, G.E.; Charif d’Ouazzane, S. Homogenized Electromechanical Coefficients and Effective Parameters of 1–3 Piezocomposites for Ultrasound Imaging Transducers. Phys. Lett. A 2021, 408, 127492. [Google Scholar] [CrossRef]
- Chen, Q.; Xiao, C.; Yang, Z.; Tabet, J.; Chen, X. Deep Neural Network Homogenization of Multiphysics Behavior for Periodic Piezoelectric Composites. Compos. Part Appl. Sci. Manuf. 2024, 186, 108421. [Google Scholar] [CrossRef]
- Zheng, B.; Jin, Z.; Hu, G.; Gu, J.; Yu, S.-Y.; Lee, J.-H.; Gu, G.X. Machine Learning and Experiments: A Synergy for the Development of Functional Materials. MRS Bull. 2023, 48, 142–152. [Google Scholar] [CrossRef]
- Yang, Z.; Park, K.; Nam, J.; Cho, J.; Choi, Y.J.; Kim, Y.; Kim, H.; Ryu, S.; Kim, M. Multi-Objective Bayesian Optimization for Laminate-Inspired Mechanically Reinforced Piezoelectric Self-Powered Sensing Yarns. Adv. Sci. 2024, 11, 2402440. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, C.; Huang, B. Searching for Optimal Patterns of Magnetoelectric Multi-Phase Composites with Machine Learning Method. In Proceedings of the 2020 15th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Zhengzhou, China, 16 April 2021; IEEE: Zhengzhou, China, 2021; pp. 85–89. [Google Scholar]
- Zhu, W.; Yang, C.; Huang, B.; Guo, Y.; Xie, L.; Zhang, Y.; Wang, J. Predicting and Optimizing Coupling Effect in Magnetoelectric Multi-Phase Composites Based on Machine Learning Algorithm. Compos. Struct. 2021, 271, 114175. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, N.; Liu, Y.; Chen, W. Prediction of Mechanical Properties of Carbon Fiber Based on Cross-Scale FEM and Machine Learning. Compos. Struct. 2019, 212, 199–206. [Google Scholar] [CrossRef]
- Singh, K.; Adhikari, J.; Roscow, J. Prediction of the Electromechanical Properties of a Piezoelectric Composite Material through the Artificial Neural Network. Mater. Today Commun. 2024, 38, 108288. [Google Scholar] [CrossRef]
- Matos, M.A.S.; Pinho, S.T.; Tagarielli, V.L. Application of Machine Learning to Predict the Multiaxial Strain-Sensing Response of CNT-Polymer Composites. Carbon 2019, 146, 265–275. [Google Scholar] [CrossRef]
- Subeshan, B.; Atayo, A.; Asmatulu, E. Machine Learning Applications for Electrospun Nanofibers: A Review. J. Mater. Sci. 2024, 59, 14095–14140. [Google Scholar] [CrossRef]
- Sarma, S.; Verma, A.K.; Phadkule, S.S.; Saharia, M. Towards an Interpretable Machine Learning Model for Electrospun Polyvinylidene Fluoride (PVDF) Fiber Properties. Comput. Mater. Sci. 2022, 213, 111661. [Google Scholar] [CrossRef]
- Sukpancharoen, S.; Wijakmatee, T.; Katongtung, T.; Ponhan, K.; Rattanachoung, N.; Khojitmate, S. Data-Driven Prediction of Electrospun Nanofiber Diameter Using Machine Learning: A Comprehensive Study and Web-Based Tool Development. Results Eng. 2024, 24, 102826. [Google Scholar] [CrossRef]
- Bai, C.-Y.; Yeh, F.-Y.; Shu, Y.-C. Physics-Informed Neural Network for Parameter Identification in a Piezoelectric Harvester. In Proceedings of the Active and Passive Smart Structures and Integrated Systems XVIII, Long Beach, CA, USA, 9 May 2024; Tol, S., Nouh, M.A., Shahab, S., Yang, J., Huang, G., Li, X., Eds.; SPIE: Long Beach, CA, USA, 2024; p. 39. [Google Scholar]
- Chen, Q.; Wang, G.; Pindera, M.-J. Homogenization and Localization of Nanoporous Composites—A Critical Review and New Developments. Compos. Part B Eng. 2018, 155, 329–368. [Google Scholar] [CrossRef]
- Mourched, B.; Hoxha, M.; Abdelgalil, A.; Ferko, N.; Abdallah, M.; Potams, A.; Lushi, A.; Turan, H.I.; Vrtagic, S. Piezoelectric-Based Sensor Concept and Design with Machine Learning-Enabled Using COMSOL Multiphysics. Appl. Sci. 2022, 12, 9798. [Google Scholar] [CrossRef]
- Stojanovic, B.S.; Svicevic, M.R.; Kaplarevic-Malisic, A.M.; Ivanovic, M.R.; Nedic, D.M.; Filipovic, N.D.; Mijailovich, S.M. Coupling Finite Element and Huxley Models in Multiscale Muscle Modeling. In Proceedings of the 2015 IEEE 15th International Conference on Bioinformatics and Bioengineering (BIBE), Belgrade, Serbia, 2–4 November 2015; IEEE: Belgrade, Serbia, 2015; pp. 1–6. [Google Scholar]
- Milićević, B.; Ivanović, M.; Stojanović, B.; Milošević, M.; Kojić, M.; Filipović, N. Huxley Muscle Model Surrogates for High-Speed Multi-Scale Simulations of Cardiac Contraction. Comput. Biol. Med. 2022, 149, 105963. [Google Scholar] [CrossRef]
- Milicevic, B.; Simic, V.; Milosevic, M.; Ivanovic, M.; Stojanovic, B.; Kojic, M.; Filipovic, N. Integration of Surrogate Huxley Muscle Model into Finite Element Solver for Simulation of the Cardiac Cycle. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11 July 2022; IEEE: Glasgow, UK, 2022; pp. 3943–3946. [Google Scholar]
- Batra, R.; Song, L.; Ramprasad, R. Emerging Materials Intelligence Ecosystems Propelled by Machine Learning. Nat. Rev. Mater. 2020, 6, 655–678. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine Learning in Materials Informatics: Recent Applications and Prospects. NPJ Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Balan, K.K.; Sivanesan, V.; Moorthy, N.; Budhhan, D.; Jeyaseelan, S.; Sundaramoorthy, S. Effect of Thickness of Mat and Testing Parameters on Tensile Strength Variability of Electrospun Nanofibrous Mat. Mater. Today Proc. 2016, 3, 1320–1329. [Google Scholar] [CrossRef]
- Molnar, K.; Vas, L.M.; Czigany, T. Determination of Tensile Strength of Electrospun Single Nanofibers through Modeling Tensile Behavior of the Nanofibrous Mat. Compos. Part B Eng. 2012, 43, 15–21. [Google Scholar] [CrossRef]
- Maccaferri, E.; Cocchi, D.; Mazzocchetti, L.; Benelli, T.; Brugo, T.M.; Giorgini, L.; Zucchelli, A. How Nanofibers Carry the Load: Toward a Universal and Reliable Approach for Tensile Testing of Polymeric Nanofibrous Membranes. Macromol. Mater. Eng. 2021, 306, 2100183. [Google Scholar] [CrossRef]
- Shams Nateri, M.; Azizollah Ganji, B. The Effect of Material Properties on Sensitivity of the Microelectromechanical Systems Piezoelectric Hydrophone. Int. J. Eng. 2017, 30, 1848–1855. [Google Scholar] [CrossRef]
- Moheimani, S.O.R.; Fleming, A.J. Fundamentals of Piezoelectricity. In Piezoelectric Transducers for Vibration Control and Damping; Advances in Industrial Control; Springer: London, UK, 2006; pp. 9–35. ISBN 978-1-84628-331-4. [Google Scholar]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting, 1st ed.; Wiley: New York, NY, USA, 2011; ISBN 978-0-470-68254-8. [Google Scholar]
- Lin, Y.-C.; Huang, Y.-H.; Ma, C.-C.; Chang, C.-K. Experimental and Theoretical Investigations on Sensing and Dynamic Characteristics of PVDF Thin Film. J. Mech. 2020, 37, 1–12. [Google Scholar] [CrossRef]
- Wu, C.M.; Chou, M.H. Acoustic–Electric Conversion and Piezoelectric Properties of Electrospun Polyvinylidene Fluoride/Silver Nanofibrous Membranes. Express Polym. Lett. 2020, 14, 103–114. [Google Scholar] [CrossRef]
- Tariq, A.; Behravesh, A.H.; Utkarsh; Rizvi, G. Statistical Modeling and Optimization of Electrospinning for Improved Morphology and Enhanced β-Phase in Polyvinylidene Fluoride Nanofibers. Polymers 2023, 15, 4344. [Google Scholar] [CrossRef]
- Motamedi, A.S.; Mirzadeh, H.; Hajiesmaeilbaigi, F.; Bagheri-Khoulenjani, S.; Shokrgozar, M. Effect of Electrospinning Parameters on Morphological Properties of PVDF Nanofibrous Scaffolds. Prog. Biomater. 2017, 6, 113–123. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, J.; Yuan, X.; Li, X.; Zhang, Y.; Sheng, J. Preparation and Properties of Electrospun Poly(Vinylidene Fluoride) Membranes. J. Appl. Polym. Sci. 2005, 97, 466–474. [Google Scholar] [CrossRef]
- Felix Swamidoss, V.; Bangaru, M.; Nalathambi, G.; Sangeetha, D.; Selvam, A.K. Silver-Incorporated Poly Vinylidene Fluoride Nanofibers for Bacterial Filtration. Aerosol Sci. Technol. 2019, 53, 196–206. [Google Scholar] [CrossRef]
- Ismail, A.M.; El-Newehy, M.H.; El-Naggar, M.E.; Meera Moydeen, A.; Menazea, A.A. Enhancement the Electrical Conductivity of the Synthesized Polyvinylidene Fluoride/Polyvinyl Chloride Composite Doped with Palladium Nanoparticles via Laser Ablation. J. Mater. Res. Technol. 2020, 9, 11178–11188. [Google Scholar] [CrossRef]
- Tommalieh, M.J.; Ismail, A.M.; Awwad, N.S.; Ibrahium, H.A.; Youssef, M.A.; Menazea, A.A. Investigation of Electrical Conductivity of Gold Nanoparticles Scattered in Polyvinylidene Fluoride/Polyvinyl Chloride via Laser Ablation for Electrical Applications. J. Electron. Mater. 2020, 49, 7603–7608. [Google Scholar] [CrossRef]
- Abdul-Majeed, M.A. Preparation and Characterization of AgNp/PVDF Cmposite Ultrafiltration Membrane. J. Eng. 2018, 24, 50–63. [Google Scholar] [CrossRef]
- Han, G.; Su, Y.; Feng, Y.; Lu, N. Approaches for Increasing the β-Phase Concentration of Electrospun Polyvinylidene Fluoride (PVDF) Nanofibers. ES Mater. Manuf. 2019, 6, 75–80. [Google Scholar] [CrossRef]
- Li, B.; Xu, C.; Zheng, J.; Xu, C. Sensitivity of Pressure Sensors Enhanced by Doping Silver Nanowires. Sensors 2014, 14, 9889–9899. [Google Scholar] [CrossRef] [PubMed]
- Pourbafrani, M.; Azimi, S.; Yaghoobi Nia, N.; Zendehdel, M.; Abolhasani, M.M. The Effect of Electrospinning Parameters on Piezoelectric PVDF-TrFE Nanofibers: Experimental and Simulation Study. Energies 2022, 16, 37. [Google Scholar] [CrossRef]
- Sriyanti, I.; Ramadhani, R.F.; Almafie, M.R.; Ap Idjan, M.K.N.; Syafri, E.; Solihah, I.; Sanjaya, M.R.; Jauhari, J.; Fudholi, A. Physicochemical and Mechanical Properties of Polyvinylidene Fluoride Nanofiber Membranes. Case Stud. Chem. Environ. Eng. 2024, 9, 100588. [Google Scholar] [CrossRef]
- Rahman, M.Z.; Xu, H. Damping under Varying Frequencies, Mechanical Properties, and Failure Modes of Flax/Polypropylene Composites. Polymers 2023, 15, 1042. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy Harvesting from Low Frequency Applications Using Piezoelectric Materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]







| Model Type | Advantages | Limitations |
|---|---|---|
| Micromechanics Models |
|
|
| Models Based on Eshelby’s Equations |
|
|
| Dilute Approximation Models |
|
|
| Mori–Tanaka-Based Models |
|
|
| Extended Mori–Tanaka Models (e.g., Mori–Tanaka–Eshelby) |
|
|
| Self-Consistent Models |
|
|
| Extended Rule of Mixture Models |
|
|
| Models Based on Asymptotic Homogenization (or Periodic Homogenization) |
|
|
| Differential Scheme |
|
|
| Solution | Electrospinning Parameters | |||||
|---|---|---|---|---|---|---|
| PVDF Concentration [%] | Solvent [v/v%] | Voltage [kV] | Needle [Gauge] | Flow Rate [mL/h] | Tip to Collector Distance [cm] | Temperature, Humidity |
| 21% | 75% DMF:25% Ac | 30 | 18 | 0.5 | 15 | 30 °C, 45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milenković, S.; Živić, F.; Grujović, N.; Virijević, K.; Bodić, A.; Petrović, D. Experimental and Numerical Characterization of Electrospun Piezoelectric Polyvinylidene Fluoride Nanocomposites Reinforced with Silver Nanoparticles. Materials 2025, 18, 1467. https://doi.org/10.3390/ma18071467
Milenković S, Živić F, Grujović N, Virijević K, Bodić A, Petrović D. Experimental and Numerical Characterization of Electrospun Piezoelectric Polyvinylidene Fluoride Nanocomposites Reinforced with Silver Nanoparticles. Materials. 2025; 18(7):1467. https://doi.org/10.3390/ma18071467
Chicago/Turabian StyleMilenković, Strahinja, Fatima Živić, Nenad Grujović, Katarina Virijević, Aleksandar Bodić, and Danilo Petrović. 2025. "Experimental and Numerical Characterization of Electrospun Piezoelectric Polyvinylidene Fluoride Nanocomposites Reinforced with Silver Nanoparticles" Materials 18, no. 7: 1467. https://doi.org/10.3390/ma18071467
APA StyleMilenković, S., Živić, F., Grujović, N., Virijević, K., Bodić, A., & Petrović, D. (2025). Experimental and Numerical Characterization of Electrospun Piezoelectric Polyvinylidene Fluoride Nanocomposites Reinforced with Silver Nanoparticles. Materials, 18(7), 1467. https://doi.org/10.3390/ma18071467







