Utilizing 3D Printing and Distributed Optic Fiber to Achieve Temperature-Sensitive Concrete
Abstract
1. Introduction
2. Design Principle of Temperature-Sensitive Concrete System
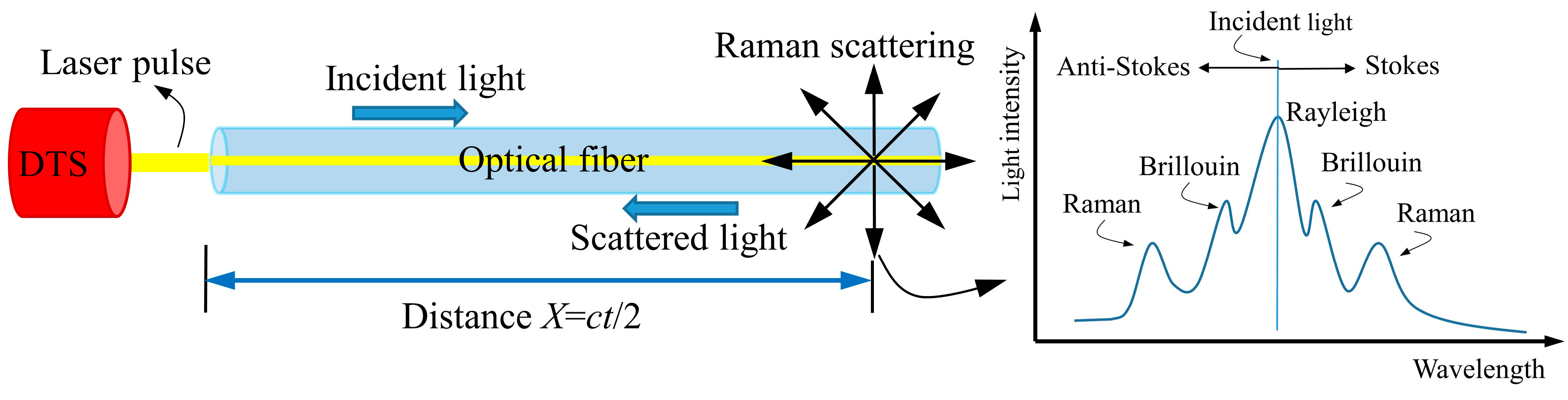
2.1. Principles of the Distributed Temperature System
2.2. Temperature-Sensitive Concrete System
3. Experimental Program
3.1. Mixture Design
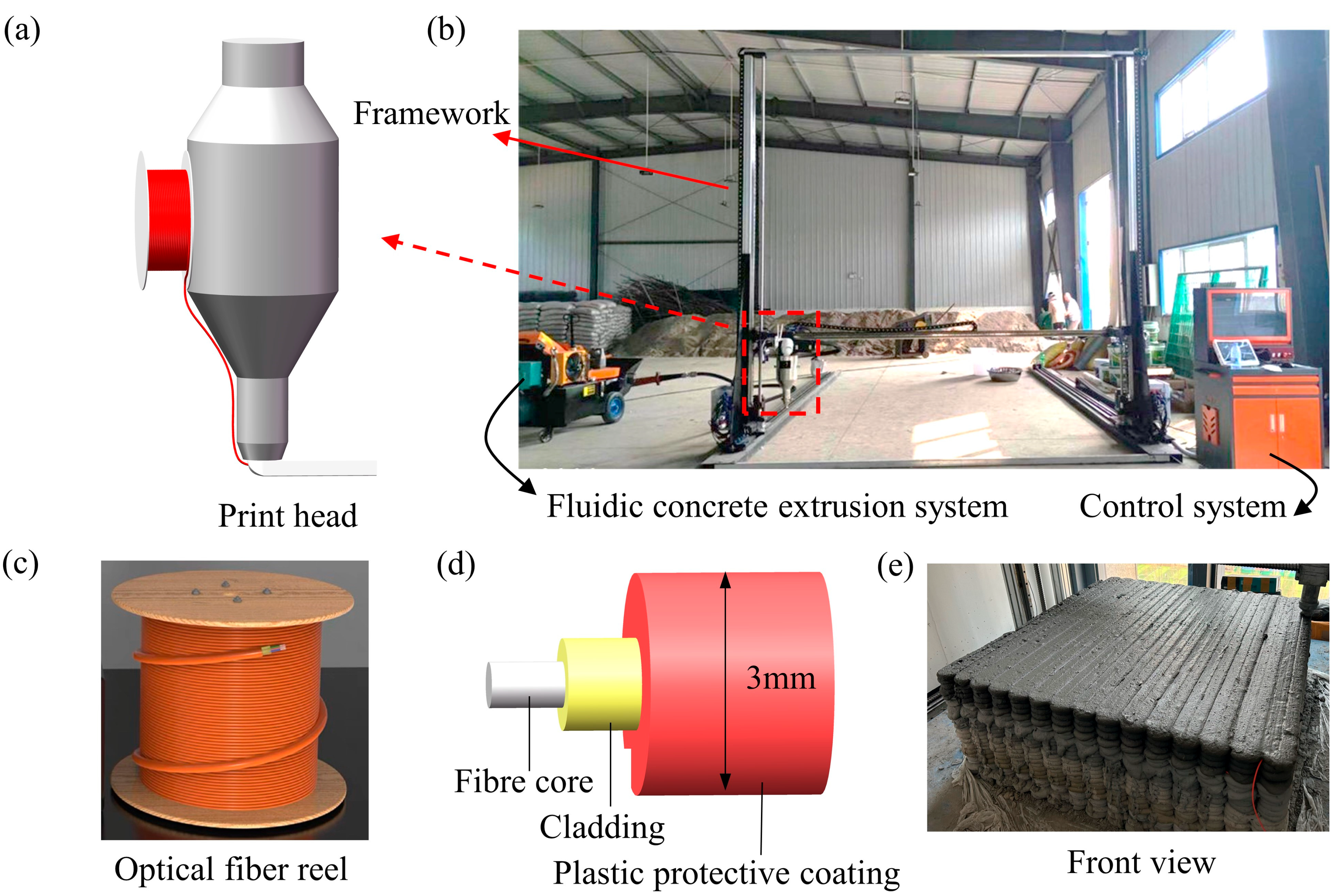
3.2. Optical Fiber Type
3.3. Concrete Mixing and 3D Printing
4. Experimental Study on Temperature-Sensitive Concrete System
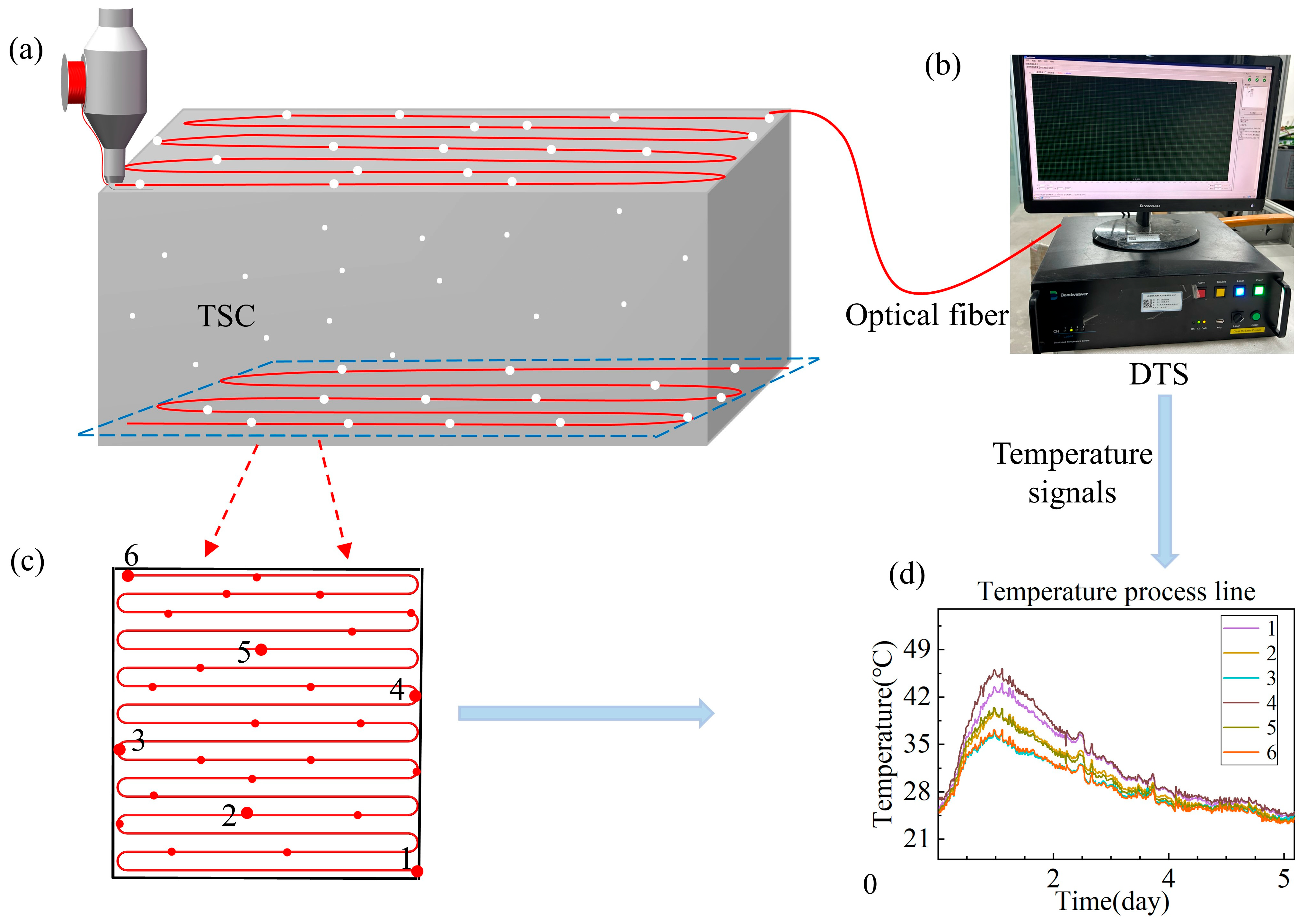
4.1. The Fabrication Method of Temperature-Sensitive Concrete Sample
4.2. Temperature Measurement Test of Temperature-Sensitive Concrete
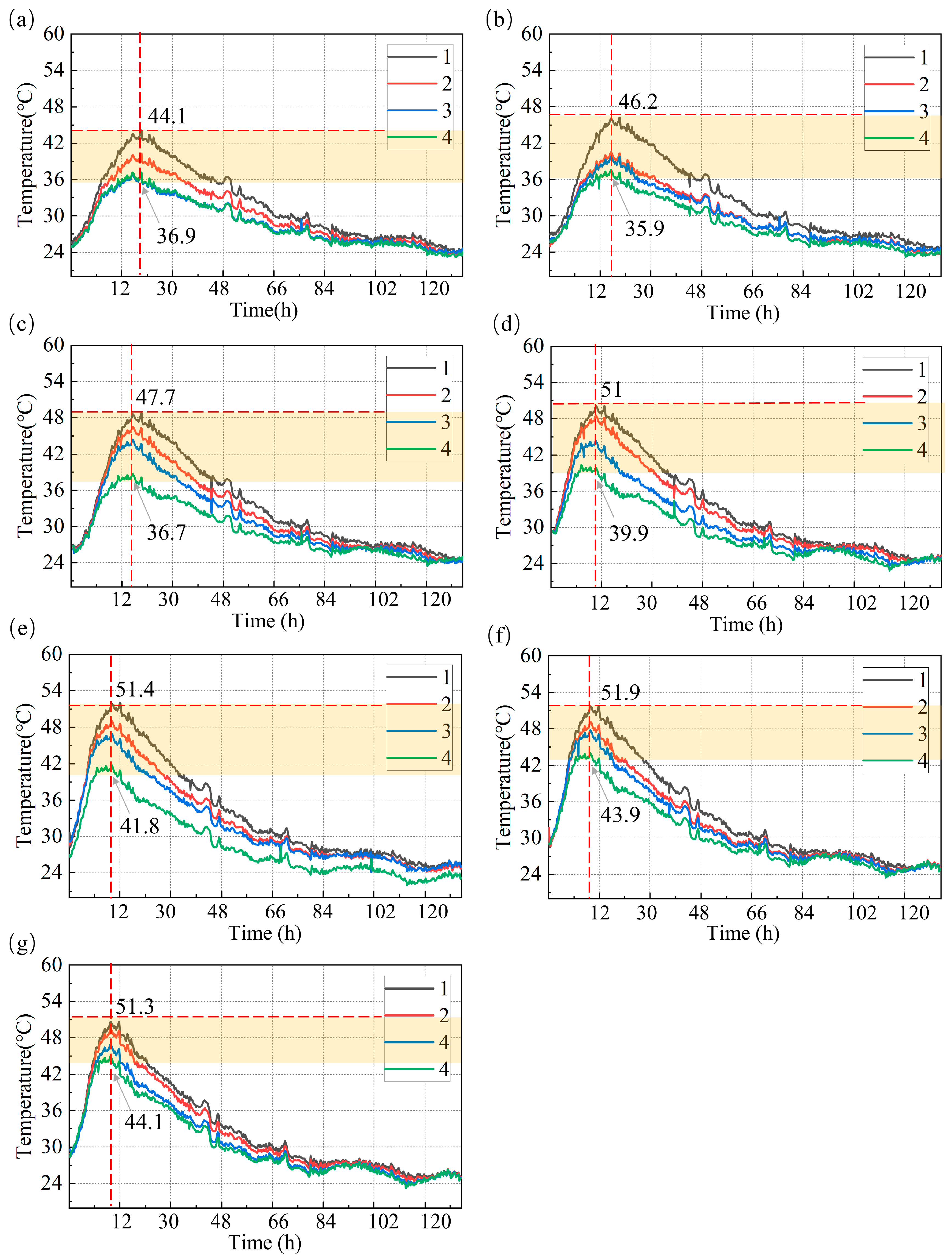
4.3. Test Results and Analysis
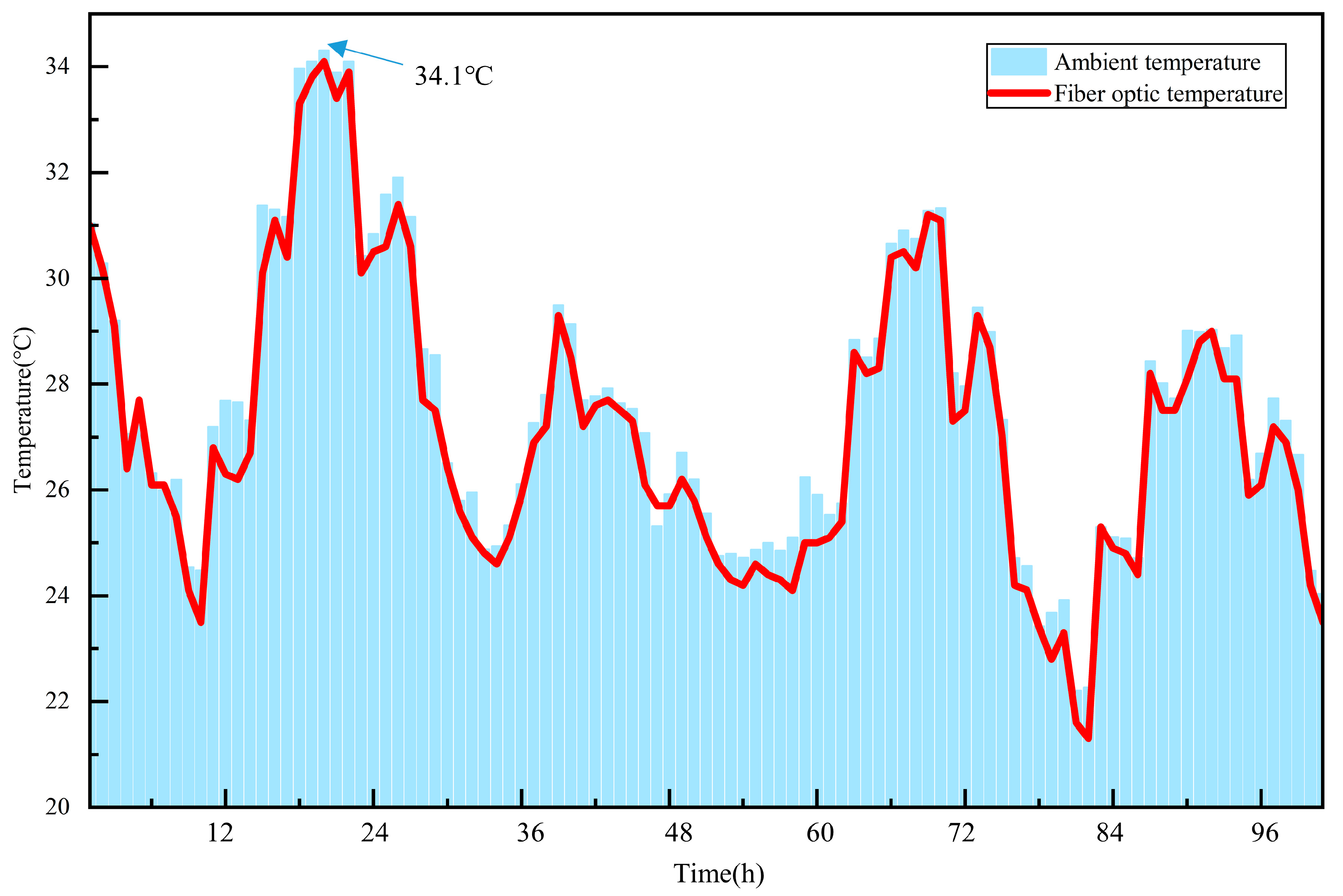
4.3.1. The Influence of Ambient Temperature on Surface 3DPC Temperature
4.3.2. Temperature Process Line Analysis for Different Locations
4.3.3. Temperature Contour Map Analysis for Different Ages
5. Numerical Simulation of Temperature-Sensitive Concrete System
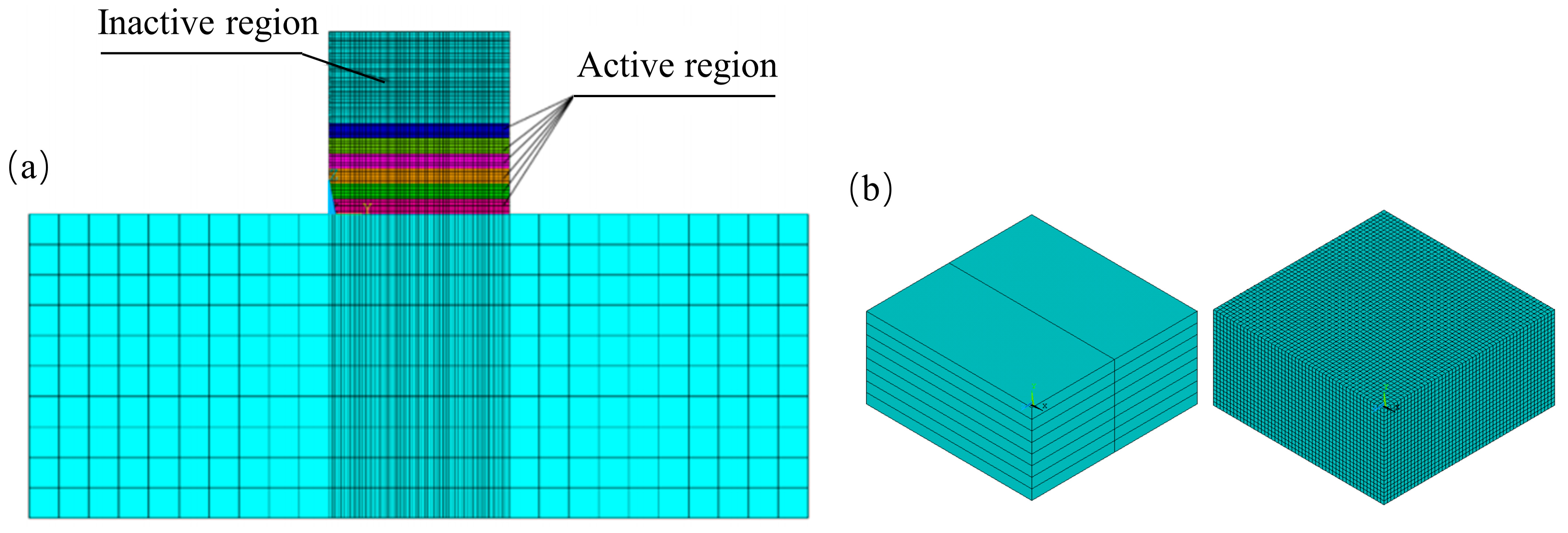
5.1. Simulation of the Concrete Printing Process
5.2. Material Parameters
5.3. Results and Analysis
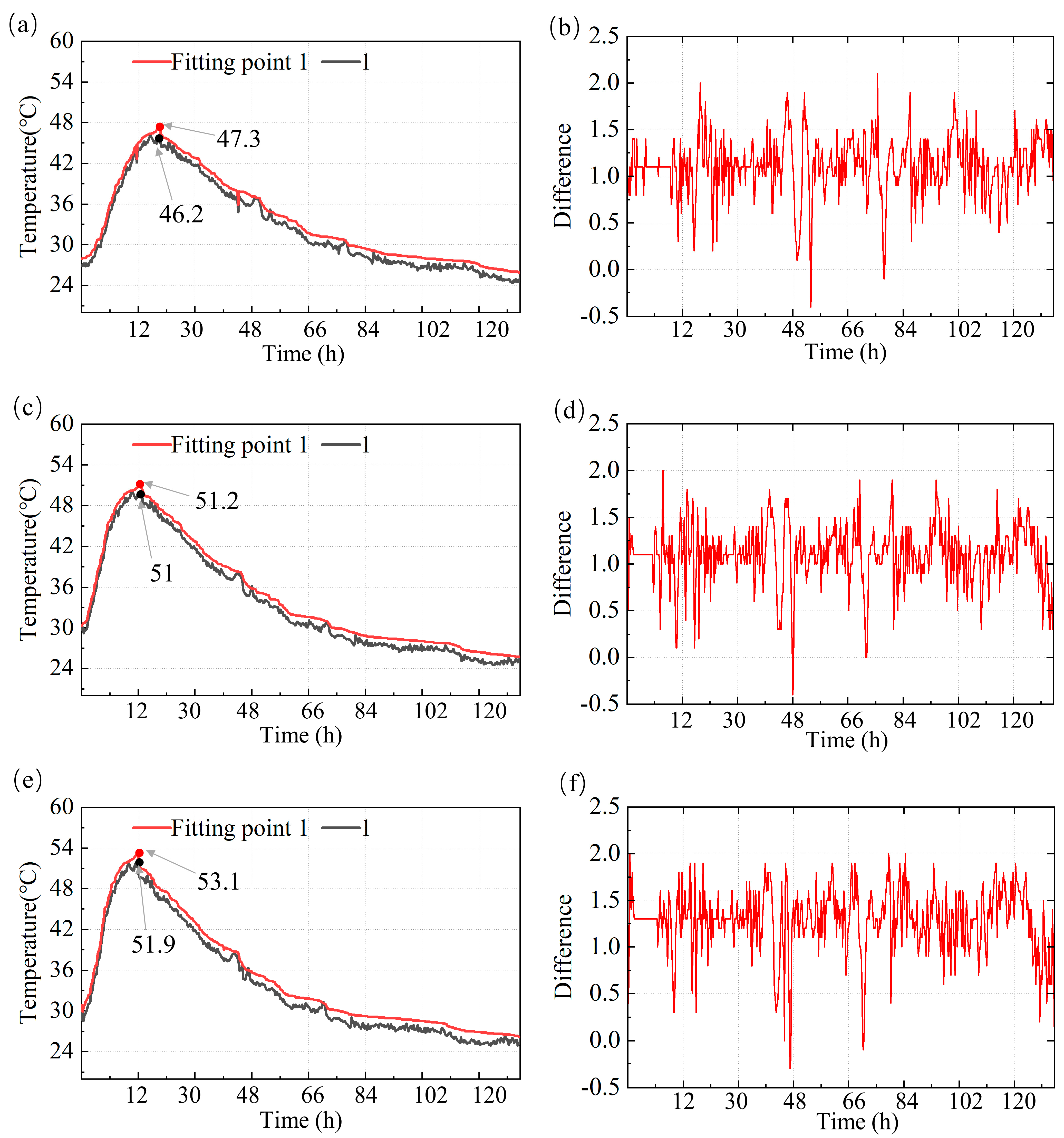
5.3.1. Results Comparison of Experimental and Simulation Temperatures
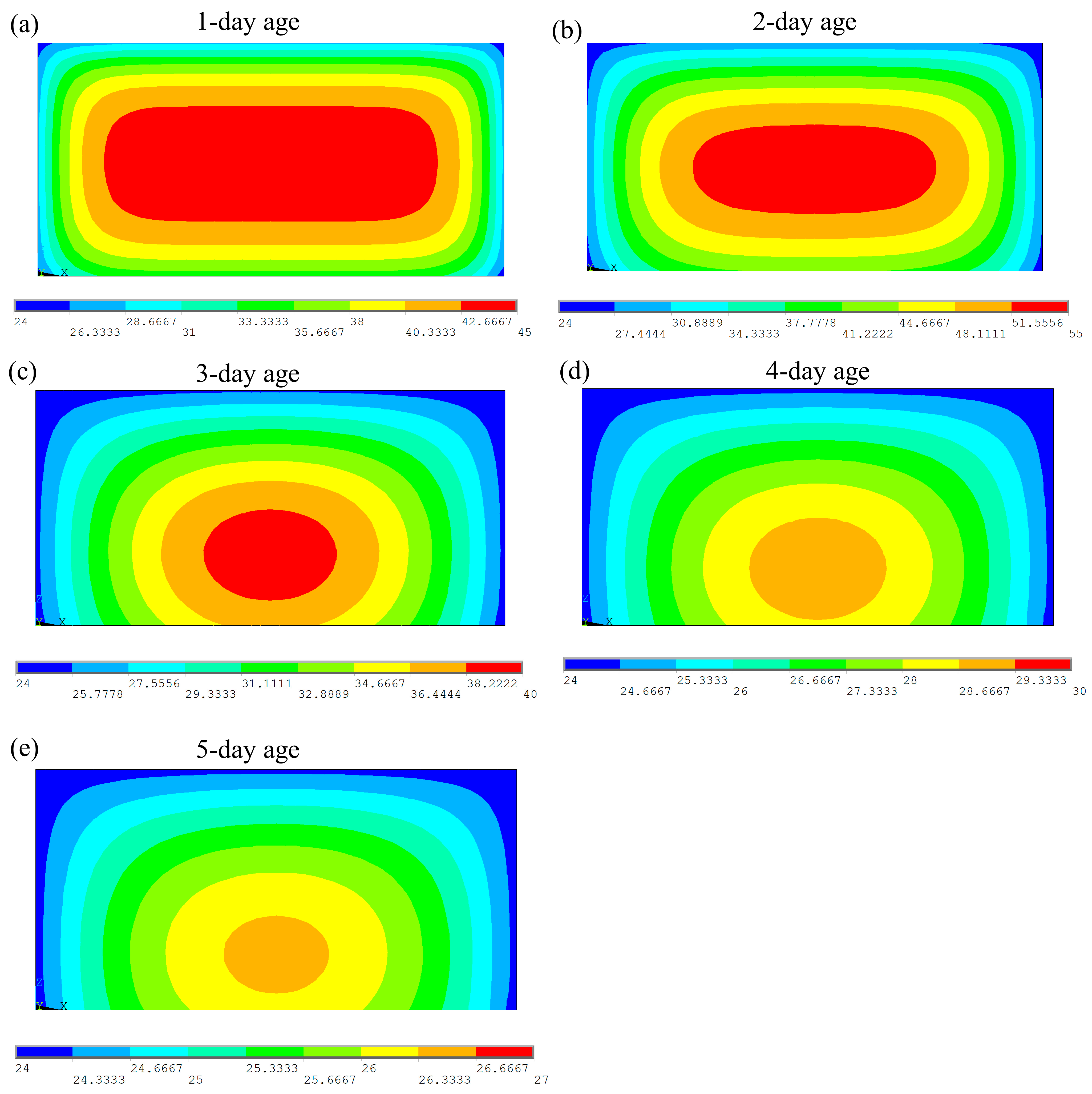
5.3.2. Comparison of Temperature Fields Between Numerical Simulation and Experimental Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3DPC | Three-dimensional printing concrete |
| TSC | Temperature-sensitive concrete |
| TSCS | Temperature-sensitive concrete system |
| DTS | Distributed Temperature Sensing |
| TFE | Temperature field evolution |
References
- Noorzaei, J.; Bayagoob, K.; Thanoon, W.; Jaafar, M. Thermal and stress analysis of Kinta RCC dam. Eng. Struct. 2006, 28, 1795–1802. [Google Scholar] [CrossRef]
- Cha, S.-L.; Jin, S.-S. Prediction of thermal stresses in mass concrete structures with experimental and analytical results. Constr. Build. Mater. 2020, 258, 120367. [Google Scholar] [CrossRef]
- Sheibany, F.; Ghaemian, M. Effects of Environmental Action on Thermal Stress Analysis of Karaj Concrete Arch Dam. J. Eng. Mech. 2006, 132, 532–544. [Google Scholar] [CrossRef]
- Lu, X.; Chen, B.; Tian, B.; Li, Y.; Lv, C.; Xiong, B. A new method for hydraulic mass concrete temperature control: Design and experiment. Constr. Build. Mater. 2021, 302, 124167. [Google Scholar] [CrossRef]
- Dinh, T.H.; Anh, V.T.T.; Nguyen, T.; Le, C.H.; Trung, N.L.; Duc, N.D.; Lin, C.-T. Toward Vision-Based Concrete Crack Detection: Automatic Simulation of Real-World Cracks. IEEE Trans. Instrum. Meas. 2023, 72, 5032015. [Google Scholar] [CrossRef]
- Sharma, B.; Sharma, S.; Reddy, M.S. Monitoring bio-remediation of fine cracks in concrete using ultrasonic wave propagation. J. Build. Eng. 2025, 99, 111550. [Google Scholar] [CrossRef]
- Pouya, M.R.; Sohrabi-Gilani, M.; Ghaemian, M. Thermal analysis of RCC dams during construction considering different ambient boundary conditions at the upstream and downstream faces. J. Civ. Struct. Health Monit. 2022, 12, 487–500. [Google Scholar] [CrossRef]
- Han, Y.; Han, G.; Li, Y.; Yao, X.; Lv, Z. Natural thermometers in concrete: Stability and reliability verification of inclusion decrepitation thermoacoustic thermometry. Constr. Build. Mater. 2023, 409, 133905. [Google Scholar] [CrossRef]
- Fan, Q.; Li, W.; Li, X.; Chen, G.; Yang, H. Application of low heat Portland cement concrete in Hoover Dam and its revelation. Water Power 2016, 42, 46–49. [Google Scholar] [CrossRef]
- Pech-May, N.W.; Oleaga, A.; Mendioroz, A.; Salazar, A. Fast Characterization of the Width of Vertical Cracks Using Pulsed Laser Spot Infrared Thermography. J. Nondestruct. Eval. 2016, 35, 22. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.; Jia, Y.; Tang, L.; Tao, J.; Tian, H. Forward Simulation and Complex Signal Analysis of Concrete Crack Depth Detection Using Tracer Electromagnetic Method. Buildings 2024, 14, 2644. [Google Scholar] [CrossRef]
- Bolhassani, M.; Hamid, A.; Rajaram, S.; Vanniamparambil, P.; Bartoli, I.; Kontsos, A. Failure analysis and damage detection of partially grouted masonry walls by enhancing deformation measurement using DIC. Eng. Struct. 2017, 134, 262–275. [Google Scholar] [CrossRef]
- Bremer, K.; Weigand, F.; Zheng, Y.; Alwis, L.S.; Helbig, R.; Roth, B. Structural Health Monitoring Using Textile Reinforcement Structures with Integrated Optical Fiber Sensors. Sensors 2017, 17, 345. [Google Scholar] [CrossRef]
- Berrocal, C.G.; Fernandez, I.; Rempling, R. Crack monitoring in reinforced concrete beams by distributed optical fiber sensors. Struct. Infrastruct. Eng. 2020, 17, 124–139. [Google Scholar] [CrossRef]
- Tian, Q.; Zhou, J.; Hou, J.; Zhou, Z.; Liang, Z.; Sun, M.; Hu, J.; Huang, J. Building the future: Smart concrete as a key element in next-generation construction. Constr. Build. Mater. 2024, 429, 136364. [Google Scholar] [CrossRef]
- Qiao, H.; Lin, Z.; Sun, X.; Li, W.; Zhao, Y.; Guo, C. Fiber Optic-Based Durability Monitoring in Smart Concrete: A State-of-Art Review. Sensors 2023, 23, 7810. [Google Scholar] [CrossRef]
- Bekzhanova, Z.; Memon, S.A.; Kim, J.R. Self-Sensing Cementitious Composites: Review and Perspective. Nanomaterials 2021, 11, 2355. [Google Scholar] [CrossRef] [PubMed]
- Song, F.; Li, Q.; Xu, S. A review of self-sensing ultra-high performance concrete: Towards next-generation smart structural materials. Cem. Concr. Compos. 2024, 145, 105350. [Google Scholar] [CrossRef]
- Hong, W.; Lv, K.; Jiang, Y.; Yang, C.; Wu, Z.; Hu, X.; Qu, Q. Self-sensing and quantitative assessment of prestressed concrete structures based on distributed long-gauge fiber Bragg grating sensors. J. Intell. Mater. Syst. Struct. 2018, 29, 1974–1985. [Google Scholar] [CrossRef]
- Miclos, S.; Savastru, D.; Savastru, R.; Lancranjan, I. Transverse mechanical stress and optical birefringence induced into single-mode optical fibre embedded in a smart polymer composite material. Compos. Struct. 2019, 218, 15–26. [Google Scholar] [CrossRef]
- Segura, I.; Faneca, G.; Torrents, J.M.; Aguado, A. Self-sensing concrete made from recycled carbon fibres. Smart Mater. Struct. 2019, 28, 105045. [Google Scholar] [CrossRef]
- Cholker, A.K.; Kulkarni, P.; Ravekar, V. Experimental behaviour of smart concrete embedded with micro carbon fibres as a sensing material. J. Phys. Conf. Ser. 2021, 1921, 012095. [Google Scholar] [CrossRef]
- Adresi, M.; Pakhirehzan, F. Evaluating the performance of Self-Sensing concrete sensors under temperature and moisture variations- a review. Constr. Build. Mater. 2023, 404, 132923. [Google Scholar] [CrossRef]
- Tan, X.; Du, J.; Zhang, Q.; Meng, W.; Bao, Y. Monitoring restrained shrinkage and cracks of ultra-high-performance concrete (UHPC) using distributed fiber optic sensors. Constr. Build. Mater. 2024, 422, 135789. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, L.; Zhang, S.; Xiao, J.; Poon, C.S. Advanced measurement techniques for plastic shrinkage and cracking in 3D-printed concrete utilising distributed optical fiber sensor. Addit. Manuf. 2023, 74, 103722. [Google Scholar] [CrossRef]
- Piątek, B.; Howiacki, T.; Kulpa, M.; Siwowski, T.; Sieńko, R.; Bednarski, Ł. Strain, crack, stress and shape diagnostics of new and existing post-tensioned structures through distributed fibre optic sensors. Measurement 2023, 221, 113480. [Google Scholar] [CrossRef]
- Bassil, A.; Chapeleau, X.; Leduc, D.; Abraham, O. Concrete Crack Monitoring Using a Novel Strain Transfer Model for Distributed Fiber Optics Sensors. Sensors 2020, 20, 2220. [Google Scholar] [CrossRef]
- Valvona, F.; Toti, J.; Gattulli, V.; Potenza, F. Effective seismic strengthening and monitoring of a masonry vault by using Glass Fiber Reinforced Cementitious Matrix with embedded Fiber Bragg Grating sensors. Compos. Part B Eng. 2017, 113, 355–370. [Google Scholar] [CrossRef]
- Jipa, A.; Dillenburger, B. 3D Printed Formwork for Concrete: State-of-the-Art, Opportunities, Challenges, and Applications. 3D Print Addit. Manuf. 2022, 9, 84–107. [Google Scholar] [CrossRef]
- Hossain, A.; Zhumabekova, A.; Paul, S.C.; Kim, J.R. A Review of 3D Printing in Construction and its Impact on the Labor Market. Sustainability 2020, 12, 8492. [Google Scholar] [CrossRef]
- Srinivasan, R.; Giannikas, V.; McFarlane, D.; Thorne, A. Customising with 3D printing: The role of intelligent control. Comput. Ind. 2018, 103, 38–46. [Google Scholar] [CrossRef]
- He, X.; Wang, R.; Qi, S.; Cheng, J.; Ye, H.; Li, H.; Chen, S.; Jian, B.; Ge, Q. Vat photopolymerization 3D printing of polymer-derived SiOC ceramics with high precision and high strength. Addit. Manuf. 2023, 78, 103889. [Google Scholar] [CrossRef]
- Han, Y.; Yang, Z.; Ding, T.; Xiao, J. Environmental and economic assessment on 3D printed buildings with recycled concrete. J. Clean. Prod. 2021, 278, 123884. [Google Scholar] [CrossRef]
- Zhu, B.; Pan, J.; Nematollahi, B.; Zhou, Z.; Zhang, Y.; Sanjayan, J. Development of 3D printable engineered cementitious composites with ultra-high tensile ductility for digital construction. Mater. Des. 2019, 181, 108088. [Google Scholar] [CrossRef]
- Markin, S.; Combrinck, R.; Mechtcherine, V. Specifics of plastic shrinkage in 3D-printed concrete elements. Cem. Concr. Res. 2024, 184, 107512. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Zhao, C.; Tang, M. High-Performance Raman Distributed Temperature Sensing Powered by Deep Learning. J. Light. Technol. 2021, 39, 654–659. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Xu, Y.; Zhang, M.; Zhang, J.; Qiao, L.; Promi, M.M.; Wang, T. High-accuracy distributed temperature measurement using difference sensitive-temperature compensation for Raman-based optical fiber sensing. Opt. Express 2019, 27, 36183–36196. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, J.; Yin, H.; Li, Y.B. Numerical simulation and analysis of temperature stress in the dynamic 3D printing process of concrete. Hydropower Water Resour. 2018, 49, 197–203. [Google Scholar] [CrossRef]


| Components | AL2O3 | SiO2 | Fe2O3 | CaO | SO3 | K2O | MgO | TiO2 |
|---|---|---|---|---|---|---|---|---|
| Cement | 5.26 | 22.65 | 3.33 | 59.12 | 2.71 | 0.81 | 2.21 | 0.52 |
| Sand | <1 | 85 | <1 | <1 | - | - | <1 | - |
| Density (g/cm3) | PH Value (23 °C, 40% Concentration) | Total Chloride Ion Content | Alkali Content |
|---|---|---|---|
| 0.40~0.60 | 9.0~12.0 | ≤0.1% | ≤3.0% |
| Cement | Sand | Water | Cement Mortar Lubricant | Accelerator |
|---|---|---|---|---|
| 634.29 | 1268.38 | 253.68 | 2.54 | 41.22 |
| Layer Height (mm) | Print Width (mm) | Fill Density (%) | Fill Pattern | Print Speed (mm/s) | Extrusion Flow Rate (m3/s) |
|---|---|---|---|---|---|
| 15 | 33 | 100 | Concentric circles | 50 | 2.3 |
| Parameters | 3D-Printed TSC |
|---|---|
| Bulk density, γ/kg·m−3 | 2350 |
| Specific heat, C/kJ·(kg·°C)−1 | 1.007 |
| Thermal conductivity, λ/kJ·(m·h·°C)−1 | 9.56 |
| Thermal diffusivity, a/m2·h−1 | 0.0040 |
| Ultimate adiabatic temperature rise, θ0/°C | 49 |
| Poisson’s ratio | 0.17 |
| Coefficient of linear expansion, α/10−6·°C−1 | 7 |
| Ultimate elastic modulus, E0/GPa | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Li, Y.; Huang, Y.; Li, Y.; Yang, Y.; Hu, Y. Utilizing 3D Printing and Distributed Optic Fiber to Achieve Temperature-Sensitive Concrete. Materials 2025, 18, 1897. https://doi.org/10.3390/ma18091897
Zhang Q, Li Y, Huang Y, Li Y, Yang Y, Hu Y. Utilizing 3D Printing and Distributed Optic Fiber to Achieve Temperature-Sensitive Concrete. Materials. 2025; 18(9):1897. https://doi.org/10.3390/ma18091897
Chicago/Turabian StyleZhang, Qiuju, Yujia Li, Yuefan Huang, Yangbo Li, Yahui Yang, and Yutao Hu. 2025. "Utilizing 3D Printing and Distributed Optic Fiber to Achieve Temperature-Sensitive Concrete" Materials 18, no. 9: 1897. https://doi.org/10.3390/ma18091897
APA StyleZhang, Q., Li, Y., Huang, Y., Li, Y., Yang, Y., & Hu, Y. (2025). Utilizing 3D Printing and Distributed Optic Fiber to Achieve Temperature-Sensitive Concrete. Materials, 18(9), 1897. https://doi.org/10.3390/ma18091897










