Mix Design of Pervious Concrete in Geotechnical Engineering Applications
Abstract
1. Introduction
2. Principal Criteria of Permeable Concrete for Geotechnical Applications
2.1. Permeability
2.2. Stability of the Internal Structure
2.3. Resistance to Clogging and Filtering Capacity
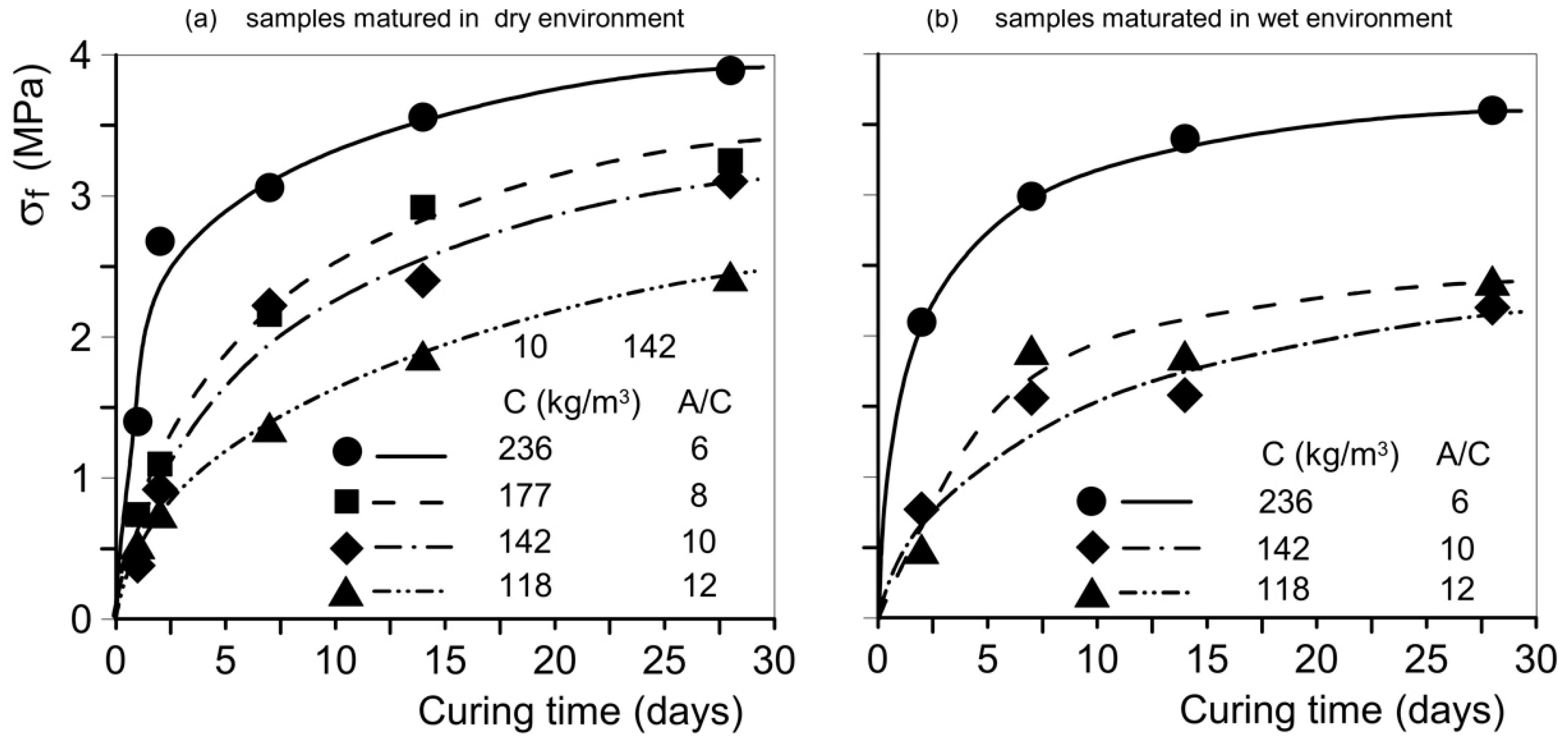
2.4. Strength and Stiffness
2.5. Cast in Place
3. Materials
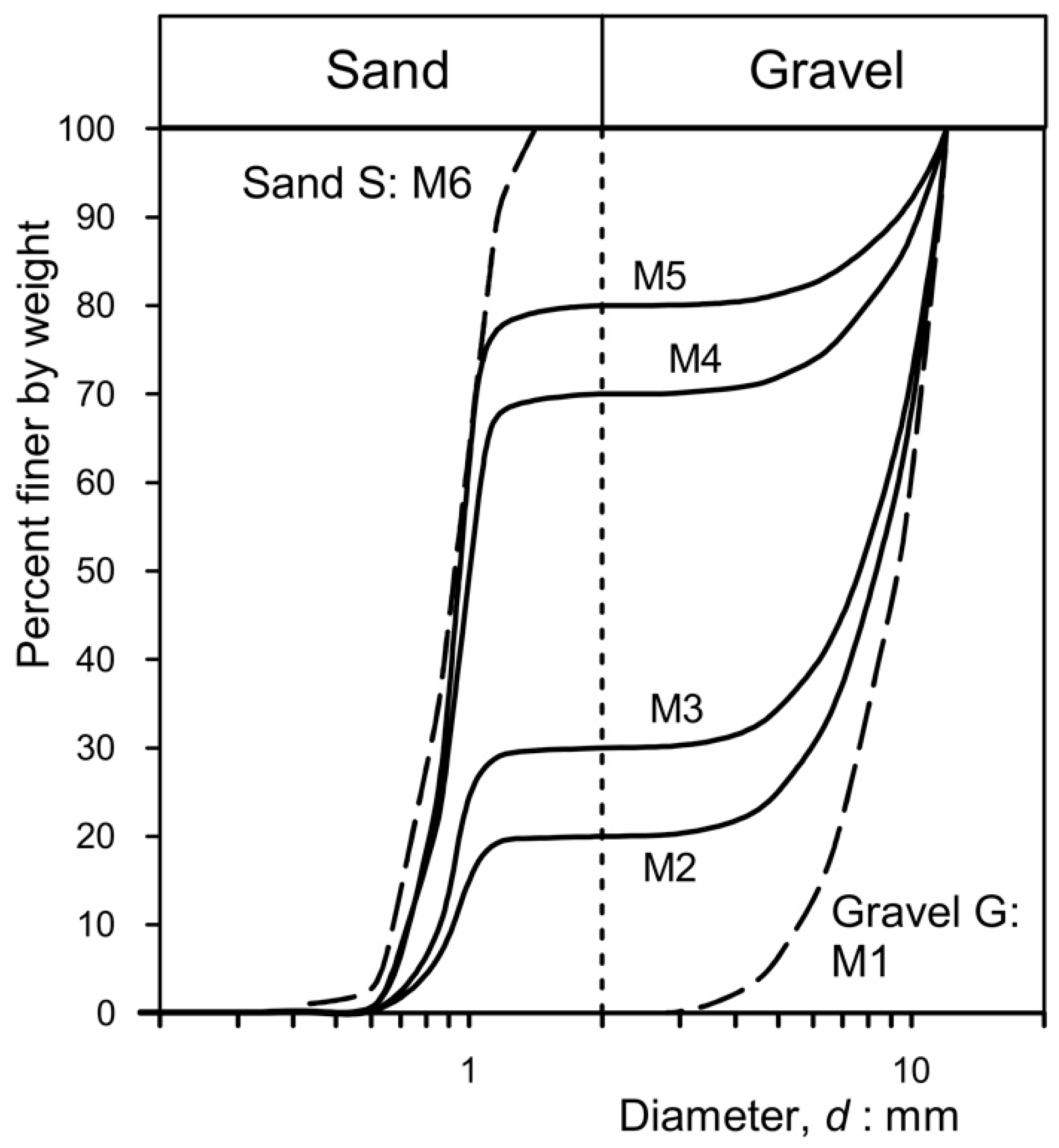
3.1. Aggregates
3.2. Cement
3.3. Water
3.4. Clogging Materials
4. Methods
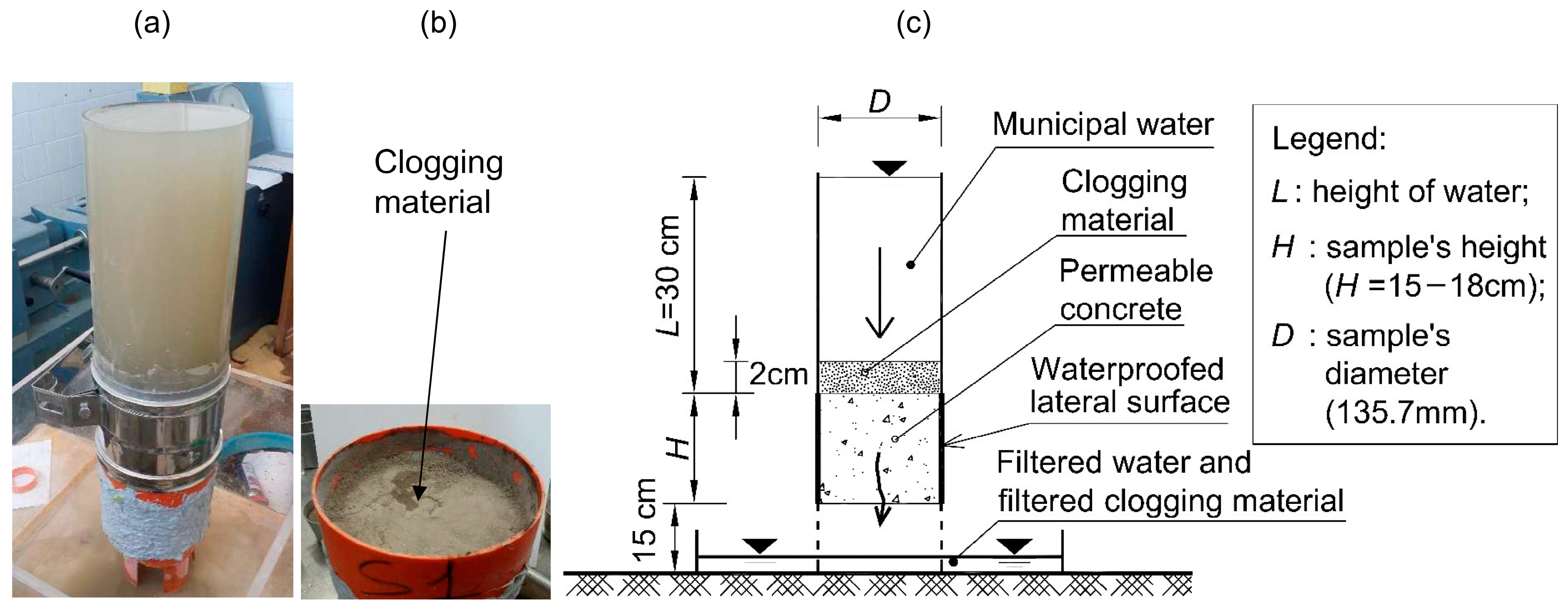
4.1. Tests of Permeability
- -
- A1 and A2 are the cross-sectional areas of the sample and the graduated pipe of the permeameter, respectively (A1 = A2 = πD2/4);
- -
- H is the length of the porous concrete sample;
- -
- h0 is the initial piezometric head, and ht is the current piezometric head at times t0 and t, respectively.
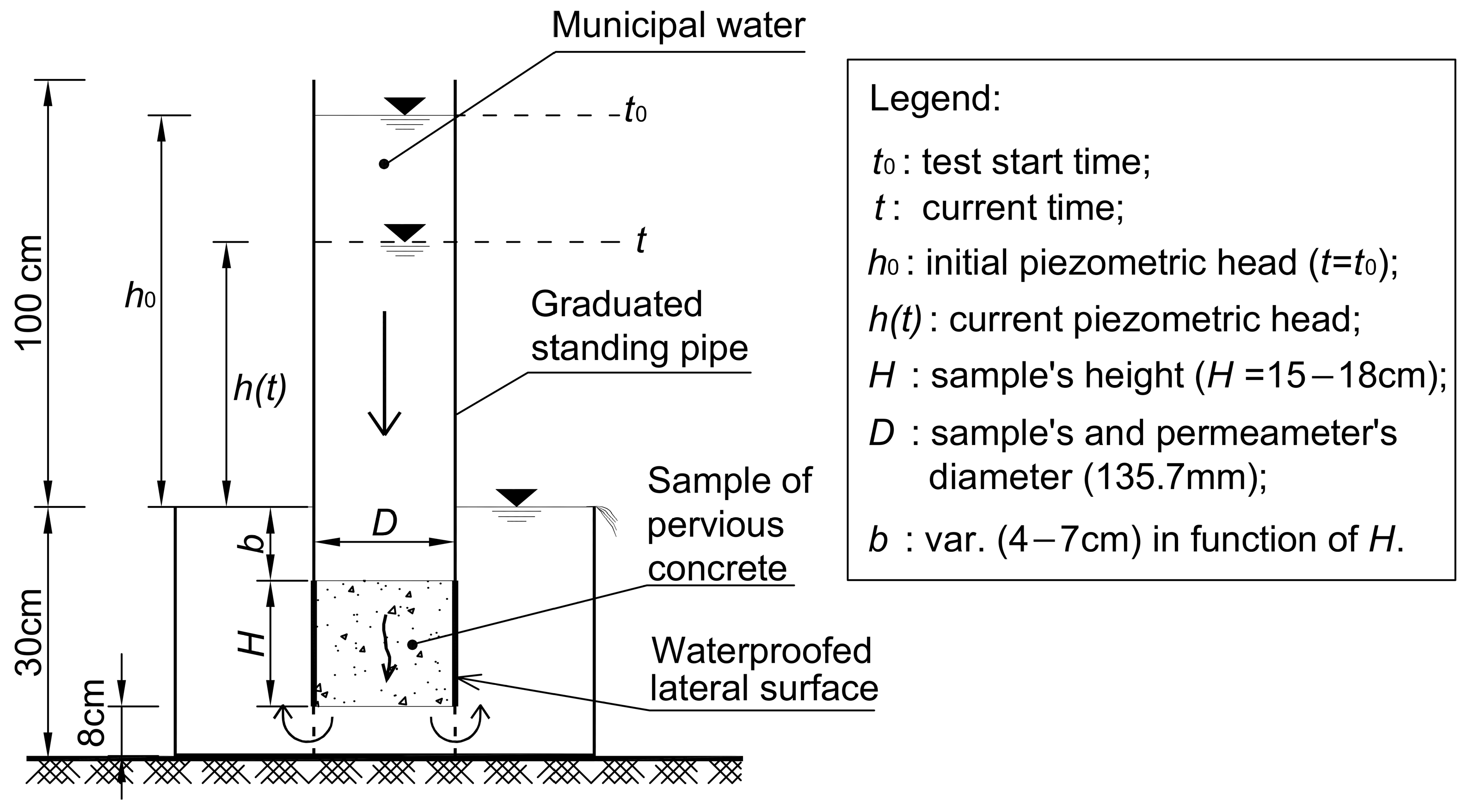
4.2. Clogging Tests
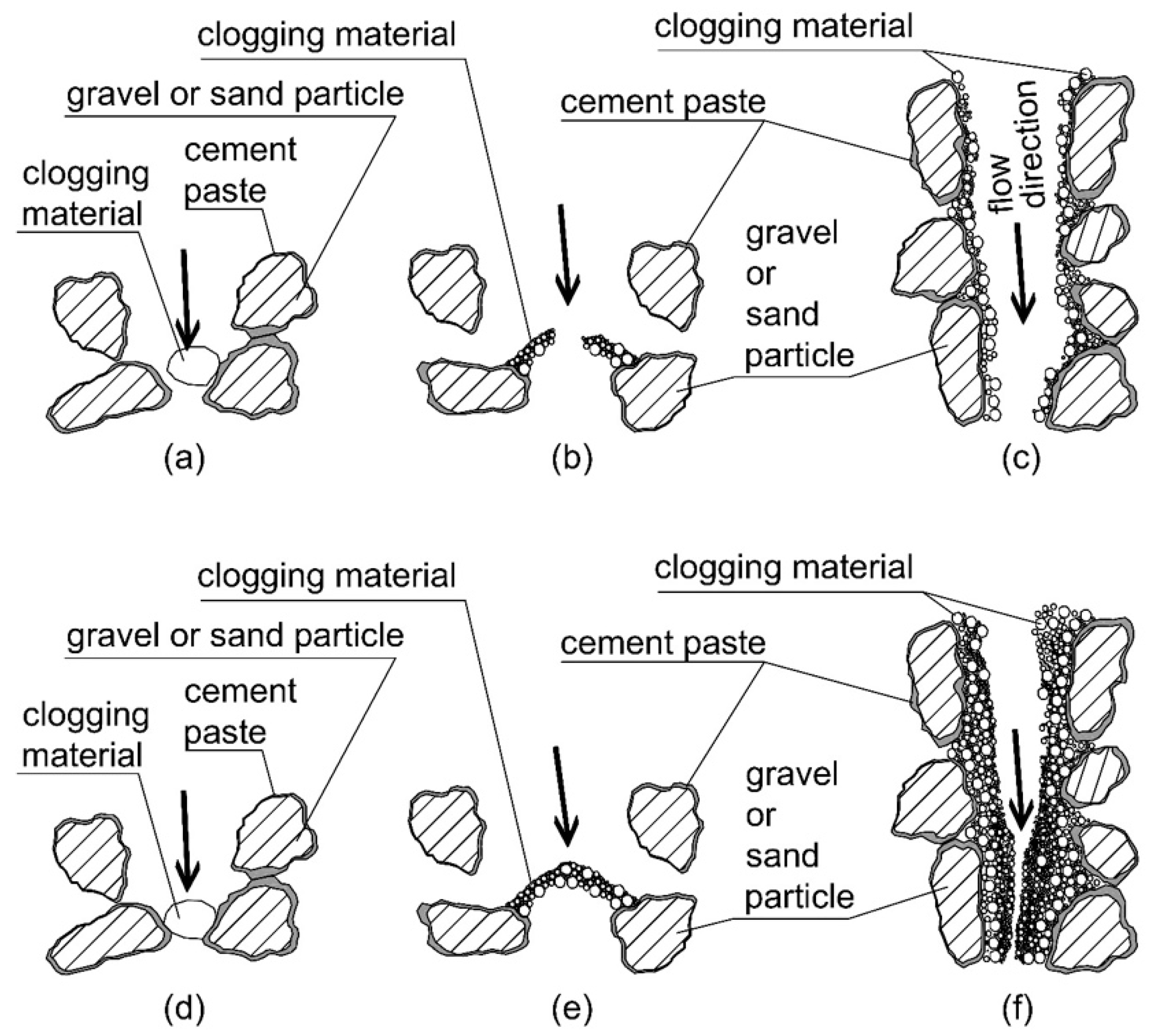
5. Mechanisms of Clogging
6. Results and Discussion
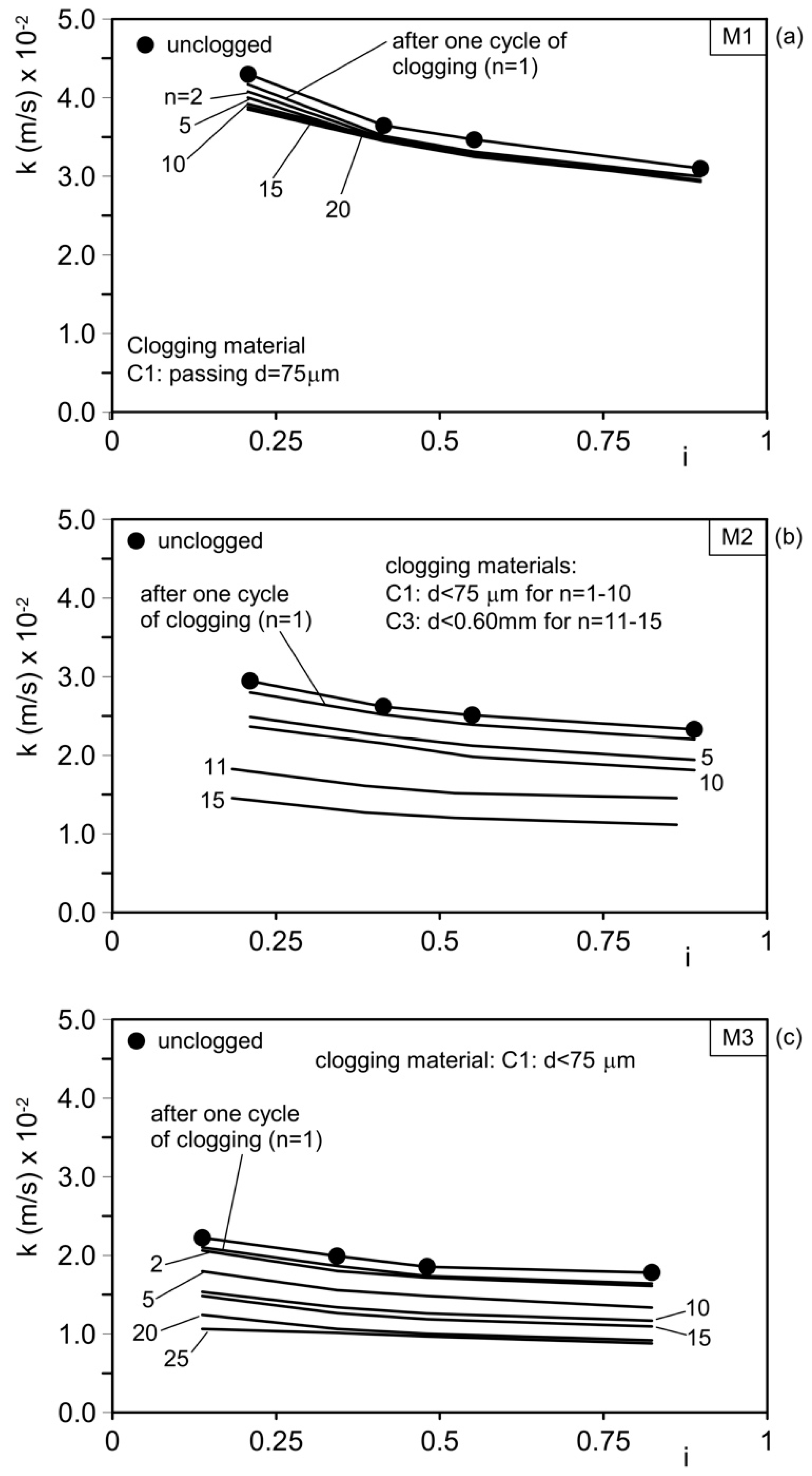
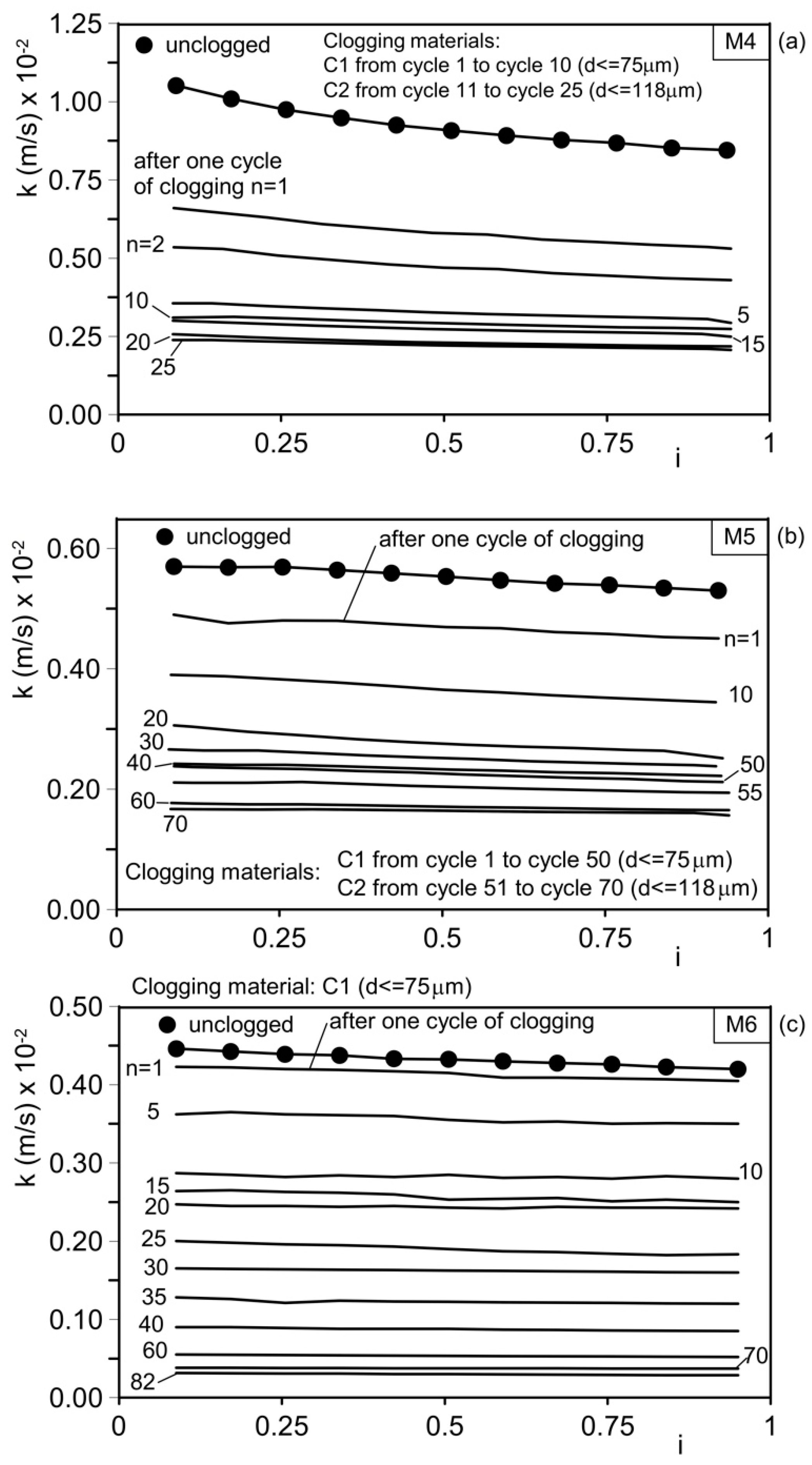
6.1. Hydraulic Conductivity
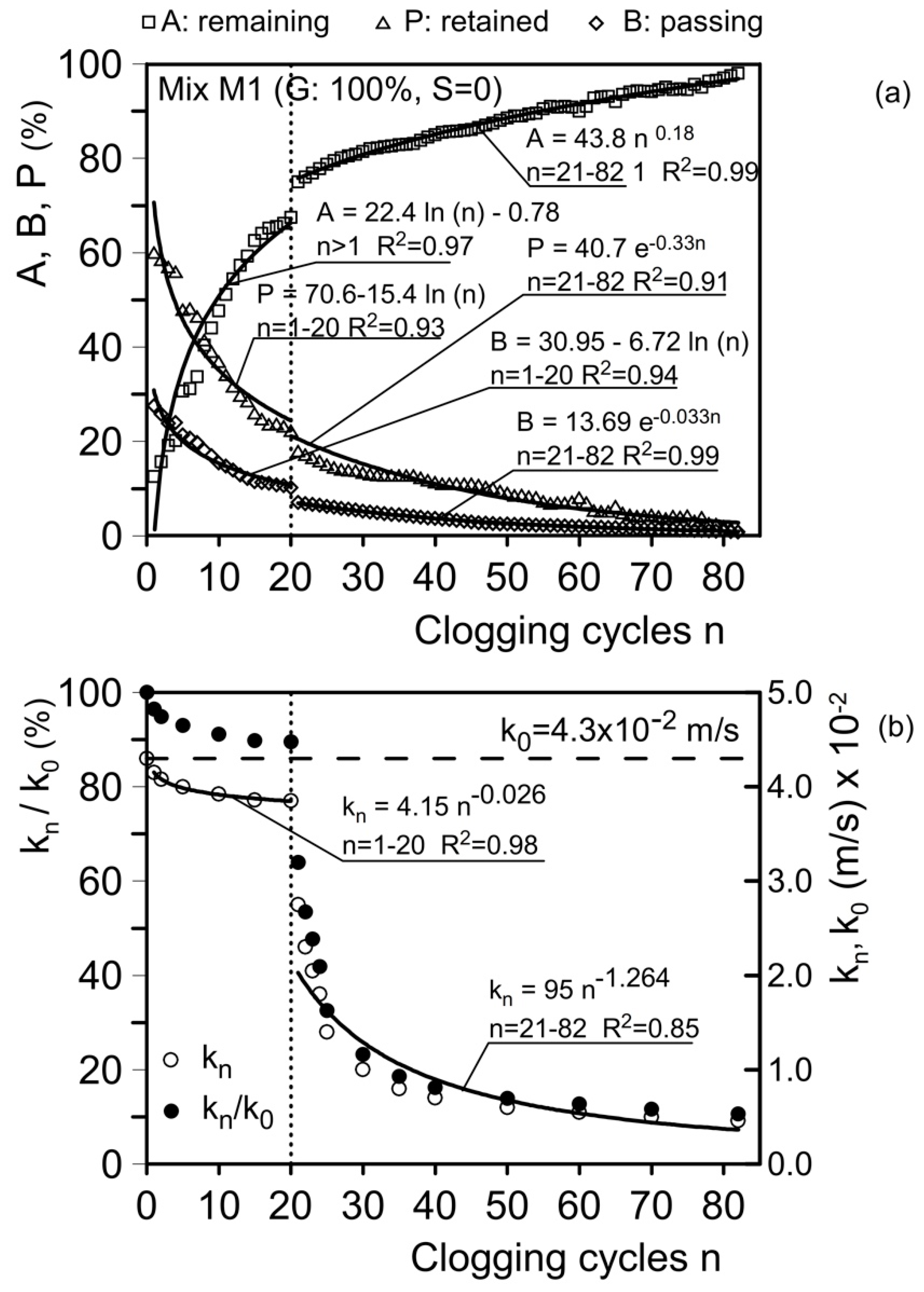
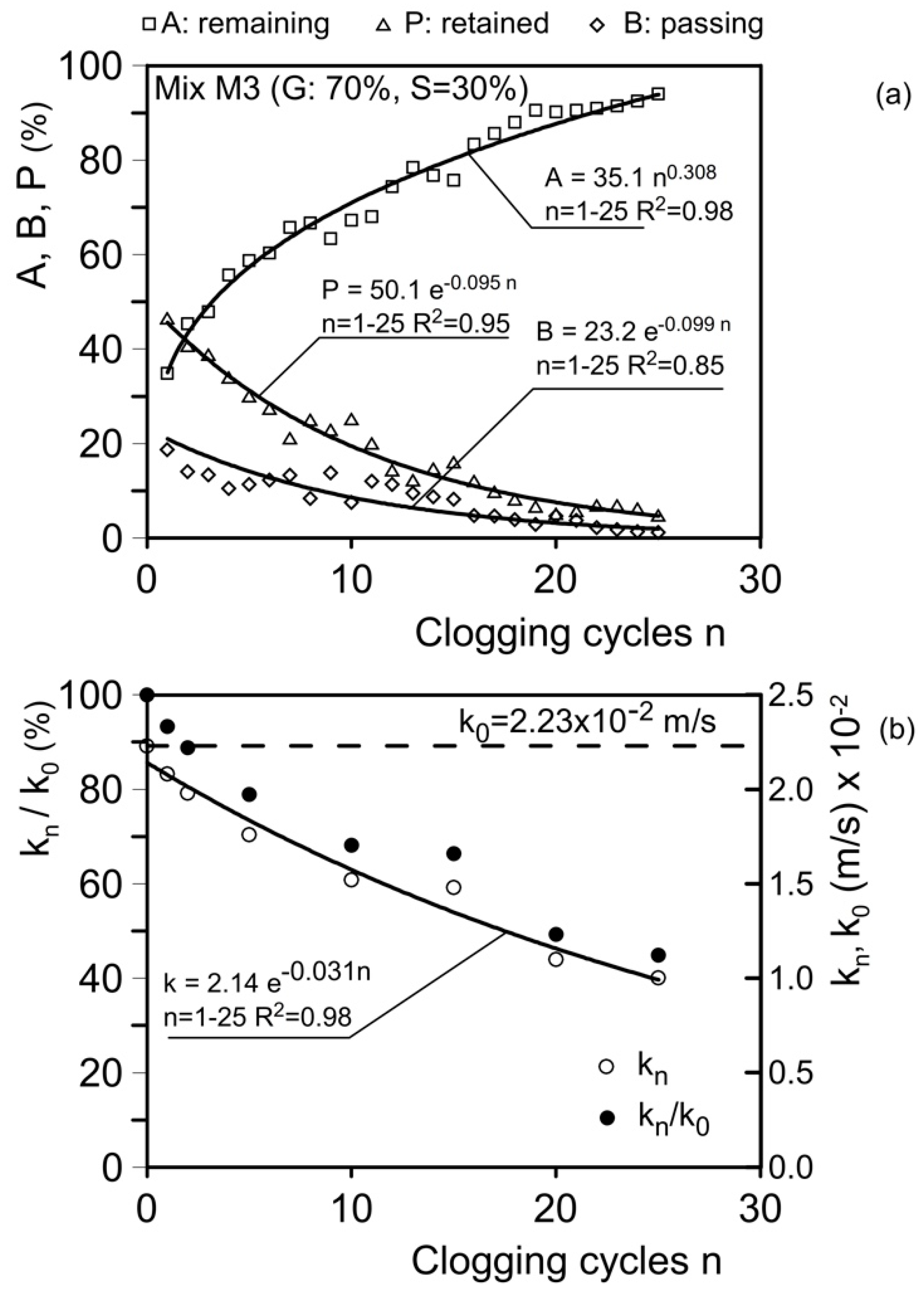
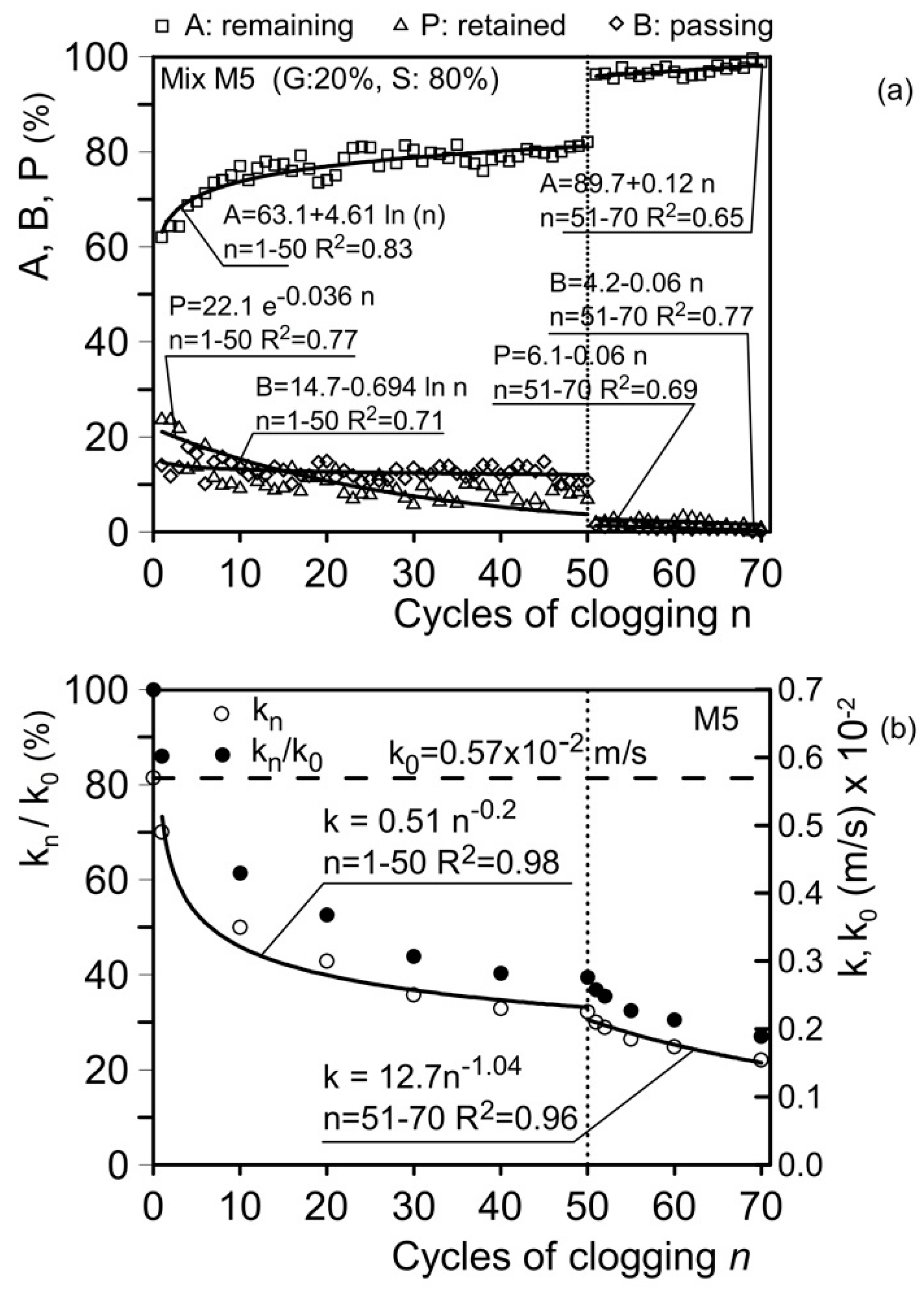
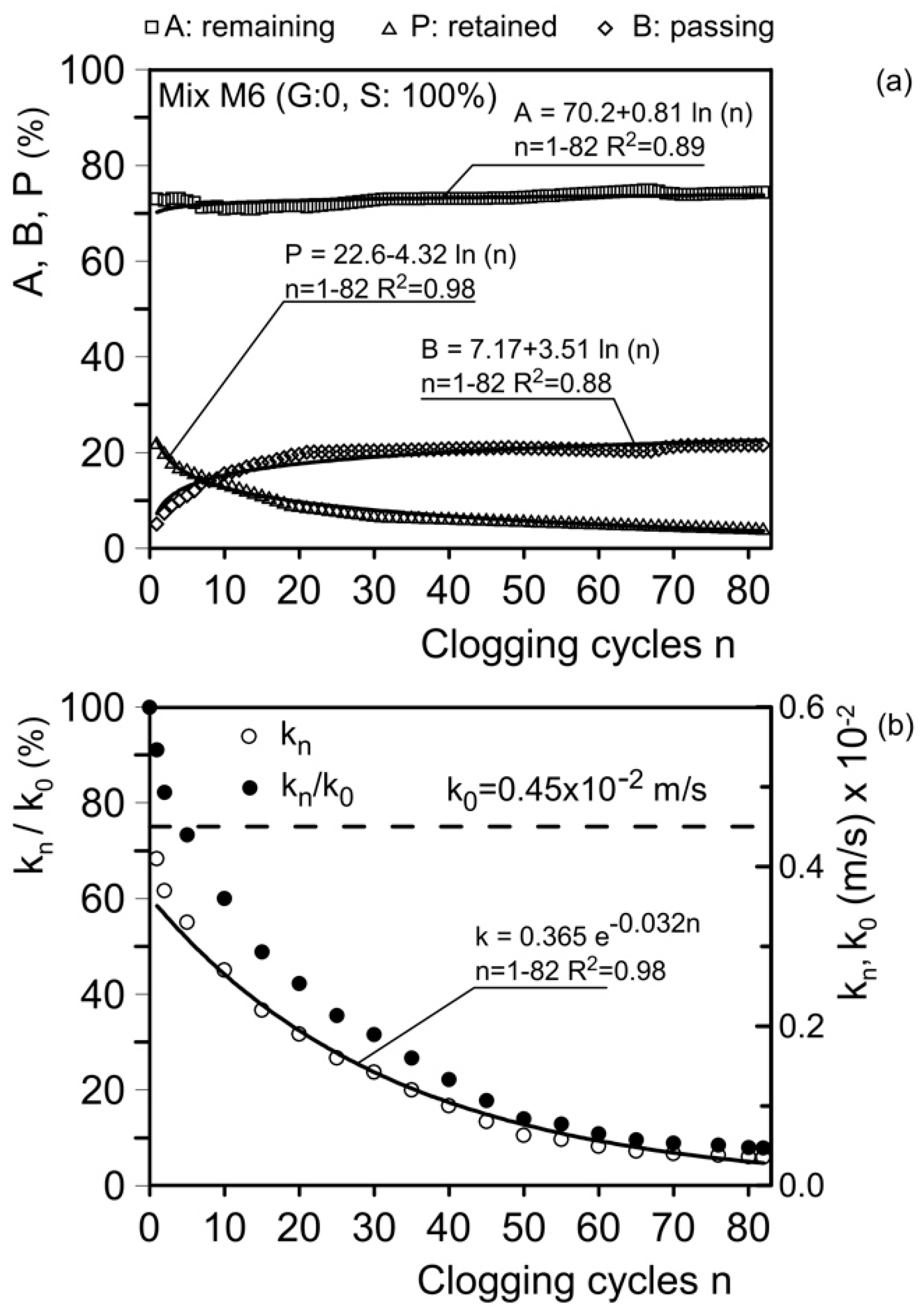
6.2. Study of the Trend of Remaining, Passing, and Retained Material, and a Model of Hydraulic Conductivity with Clogging Cycles
7. Conclusions
- -
- Pervious concretes typically used for roads and other types of pavements (such as no-fines concrete) are ineffective for geotechnical applications.
- -
- The durability and effectiveness of permeable concrete in geotechnical applications strongly depend on its filter properties, specifically, its ability to protect against internal erosion of the base soil while maintaining sufficient residual permeability (in relation to the permeability of the base soil).
- -
- Adding sand to the aggregate mix significantly enhances the filter properties of permeable concrete for cohesionless fine-grained soils, which are the most vulnerable to internal erosion phenomena. This issue is less pertinent in clayey soils, where adhesive forces between particles help reduce internal erosion.
- -
- Residual hydraulic conductivity decreases due to physical clogging. The reduction in permeability increases as the number of clogging cycles rises, and for a very high number of cycles, it can decrease to as low as 10% of its initial (unclogged) value. However, this residual permeability remains sufficient for draining fine cohesionless base soils.
- -
- Additional experimentation is clearly essential to exploring possible scale effects on both the sample geometry and the piezometric gradient, particularly concerning the low gradients commonly observed in soil flow. To generalize the results and enhance the robustness of the findings, it is also necessary to employ various clogging materials, such as clayey and silty–clayey soils.
- -
- To verify these results, it would be useful to conduct experiments in a centrifuge, as well as at a real scale and under actual field conditions.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neville, A.M. Properties of Concrete, Fourth and Final; Longman Group Limited, Ed.; Wiley: Essex, UK, 1995. [Google Scholar]
- Alam, B.; Javed, M.; Ali, Q.; Ahmad, N.; Ibrahim, M. Mechanical properties of no-fines bloated slate aggregate concrete for construction application, experimental study. Int. J. Civ. Struct. Eng. 2012, 3, 302–308. [Google Scholar]
- Yahia, A.; Kabagire, K.D. New approach to proportion pervious concrete. Constr. Build. Mat. 2014, 62, 38–46. [Google Scholar] [CrossRef]
- Zhong, R.; Wille, K. Compression response of normal and high strength pervious concrete. Constr. Build. Mat. 2016, 109, 177–187. [Google Scholar] [CrossRef]
- Adresi, M.; Yamani, A.R.; Tabarestani, M.K.; Rooholamini, H. A comprehensive review on pervious concrete. Constr. Build. Mat. 2023, 407, 133308. [Google Scholar] [CrossRef]
- Xiong, B.; Li, Y.; Chen, B.; Lu, X.; Gao, H.; Jia, S. Influence of distribution of paste coating thickness on performance of pervious concrete. Constr. Build. Mat. 2025, 458, 139602. [Google Scholar] [CrossRef]
- Xiong, B.; Wu, X.; Liu, W.; Lu, X.; Gao, H.; Lv, W. Influence of different aggregate characteristics on pervious concrete. Constr. Build. Mat. 2025, 460, 139789. [Google Scholar] [CrossRef]
- Haselbach, L.; Boyer, M.; Kevern, J.T.; Schaefer, V.R. Cyclic heat island impacts on traditional versus pervious concrete pavement systems. Transp. Res. Rec. J. Transp. Res. Board. 2011, 2240, 107–115. [Google Scholar] [CrossRef]
- Liu, Y.; Li, T.; Yu, L. Urban heat island mitigation and hydrology performance of innovative permeable pavement: A pilot-scale study. J. Clean. Prod. 2020, 244, 118938. [Google Scholar] [CrossRef]
- Ali, M.T.; Rashid, M.H. The effects of coarser sand addition on thermal properties of pervious concrete. Innov. Infrastruct. Solut. 2024, 9, 402. [Google Scholar] [CrossRef]
- Adresi, M.; Yamani, A.R.; Tabarestani, M.K. Evaluating the effectiveness of innovative pervious concrete pavement system for mitigating urban heat island effects, de-icing, and de-clogging. Constr. Build. Mat. 2024, 449, 138361. [Google Scholar] [CrossRef]
- Holmes, R.R.; Hart, M.L.; Kevern, J.T. Enhancing the ability of pervious concrete to remove heavy metals from stormwater. J. Sustain. Water Built Environ. 2017, 3, 04017004. [Google Scholar] [CrossRef]
- Muthu, M.; Santhanam, M.; Kumar, M. Pb removal in pervious concrete filter: Effects of accelerated carbonation and hydraulic retention time. Constr. Build. Mat. 2018, 174, 224–232. [Google Scholar] [CrossRef]
- Shabalala, A.N.; Ekolu, S.O.; Diop, S.; Solomon, F. Pervious concrete reactive barrier for removal of heavy metals from acid mine drainage − column study. J. Hazard. Mat. 2017, 323 Pt B, 641–653. [Google Scholar] [CrossRef]
- Chen, X.; Niu, Z.; Zhang, H.; Lu, M.; Zhou, M.; Li, B. Design of a chitosan modifying alkali-activated slag pervious concrete with the function of water purification. Constr. Build. Mat. 2020, 251, 118979. [Google Scholar] [CrossRef]
- Wijeyawardana, P.; Nanayakkara, N.; Gunasekara, C.; Karunarathna, A.; Law, D.; Pramanik, B.K. Improvement of heavy metal removal from urban runoff using modified pervious concrete. Sci. Tot. Environ. 2022, 815, 152936. [Google Scholar] [CrossRef]
- Horvath, A. Construction materials and the environment. Annu. Rev. Environ. Resour. 2004, 29, 181–204. [Google Scholar] [CrossRef]
- Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. Identification of parameters for embodied energy measurement: A literature review. Energy Build. 2010, 42, 1238–1247. [Google Scholar] [CrossRef]
- Chandrappa, A.K.; Biligiri, K.P. Pervious concrete as a sustainable pavement material—research findings and future prospects: A state-of-the-art review. Constr. Build. Mat. 2016, 111, 262–274. [Google Scholar] [CrossRef]
- Ziccarelli, M.; Ferrari, A.; Rosone, M. The permeable concrete: A low energy consumption solution for deep draining trenches. In Springer Series in Geomechanics and Geoengineering; Ferrari, A., Laloui, L., Eds.; SEG 2018, SSGG; Springer: Cham, Switzerland, 2019; pp. 323–330. ISBN 978-3-319-99669-1. Available online: http://www.springer.com/series/8069 (accessed on 17 April 2025). [CrossRef]
- He, J.; Xu, S.H.S.; Sang, G.C.; Wu, Y.H.; Liu, S. Enhancing the Mechanical Properties and Water Permeability of Pervious Planting Concrete: A Study on Additives and Plant Growth. Materials 2024, 17, 2301. [Google Scholar] [CrossRef]
- Zhuang, P.; Yan, X.; Wang, X.; Liu, J. Study on the Performance Optimization of Plant-Growing Ecological Concrete. Sustainability 2024, 16, 4575. [Google Scholar] [CrossRef]
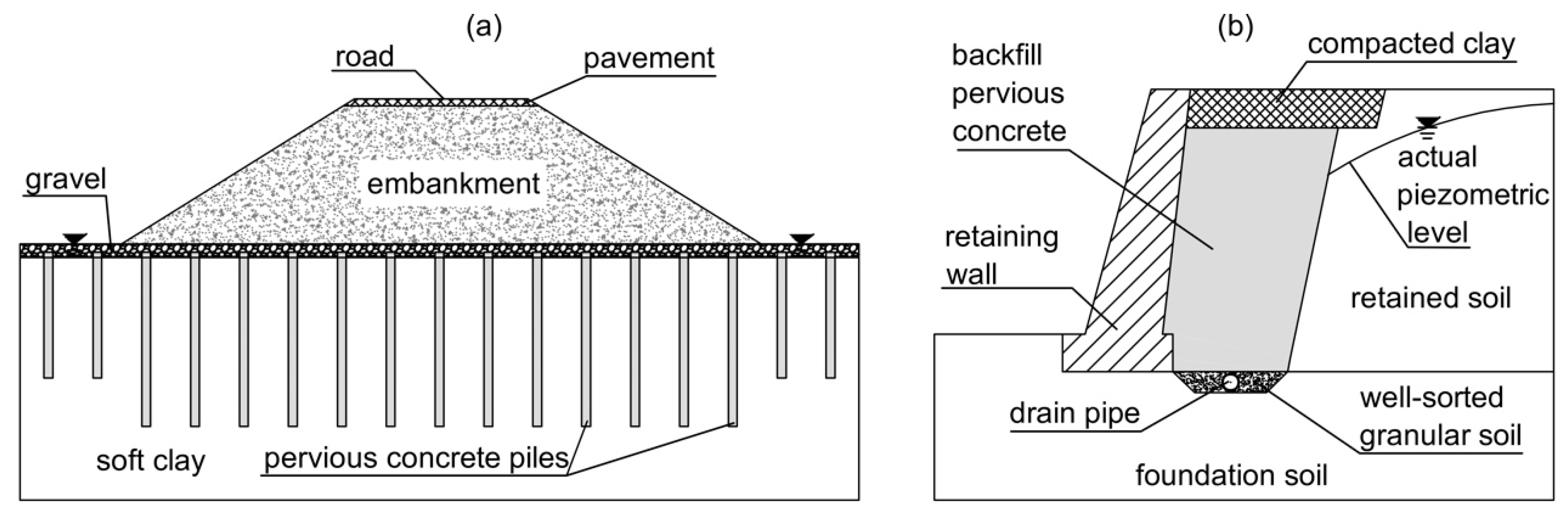
- Ni, L.; Suleiman, M.T.; Raich, A. Pervious Concrete Pile: An Innovation Ground Improvement Alternative. In Proceedings of the Geo-Congress 2013: Stability and Performance of Slopes and Embankments III, ASCE, San Diego, CA, USA, 3–7 March 2013; pp. 2055–2058. [Google Scholar] [CrossRef]
- Suleiman, M.T.; Ni, L.; Raich, A. Development of pervious concrete pile ground-improvement alternative and behavior under vertical loading. J. Geotech. Geoenviron. Eng. 2014, 140, 4014035. [Google Scholar] [CrossRef]
- Ye, G.; Zhang, Q.; Zhang, Z.; Chang, H. Centrifugal modeling of a composite foundation combined with soil-cement columns and prefabricated vertical drains. Soil. Found. 2015, 55, 1259–1269. [Google Scholar] [CrossRef]
- Ni, L.S.; Suleiman, M.T.; Raich, A. Behavior and soil–structure interaction of pervious concrete ground-improvement piles under lateral loading. J. Geotech. Geoenviron. Eng. 2016, 142, 04015071. [Google Scholar] [CrossRef]
- Ni, P.; Mangalathu, S.; Mei, G.; Zhao, Y. Permeable piles: An alternative to improve the performance of driven piles. Comp. Geotech. 2017, 84, 78–87. [Google Scholar] [CrossRef]
- Tiwari, B.; Ajmera, B.; Maw, R.; Cole, R.; Villegas, D.; Palmerson, P. Mechanical Properties of Lightweight Cellular Concrete for Geotechnical Applications. J. Mat. Civ. Eng. 2017, 29, 06017007. [Google Scholar] [CrossRef]
- Ni, P.; Mangalathu, S.; Mei, G.; Zhao, Y. Laboratory investigation of pore pressure dissipation in clay around permeable piles. Can. Geotech. J. 2018, 55, 1257–1267. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, J.; Chen, D.; Li, S.; Jin, Q.; Zheng, Y.; Cui, S. Clogging of pervious concrete pile caused by soil piping: An approximate experimental study. Can. Geotech. J. 2018, 55, 999–1015. [Google Scholar] [CrossRef]
- Amran, M.; Onaizi, A.M.; Fediuk, R.; Danish, A.; Vatin, N.I.; Murali, G.; Abdelgader, H.S.; Mosaberpanah, M.A.; Cecchin, D.; Azevedo, A. An ultra-lightweight cellular concrete for geotechnical applications—A review. Case Stud. Constr. Mat. 2022, 16, e01096. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.-H.; Mei, G.-X.; Xiao, T.; Liu, Z.-Y. Field monitoring of bearing capacity efficiency of permeable pipe pile in clayey soil: A comparative study. Measurement 2021, 186, 110151. [Google Scholar] [CrossRef]
- Cai, J.; Du, G.; Xia, H.; Sun, C. Comparative study on bearing characteristics of pervious concrete piles in silt and clay foundations. Geomech. Eng. 2021, 27, 595–604. [Google Scholar] [CrossRef]
- Xia, H.; Du, G.; Cai, J.; Sun, C. Model tests on the bearing capacity of pervious concrete piles in silt and sand. Geomech. Eng. 2024, 38, 79–91. [Google Scholar] [CrossRef]
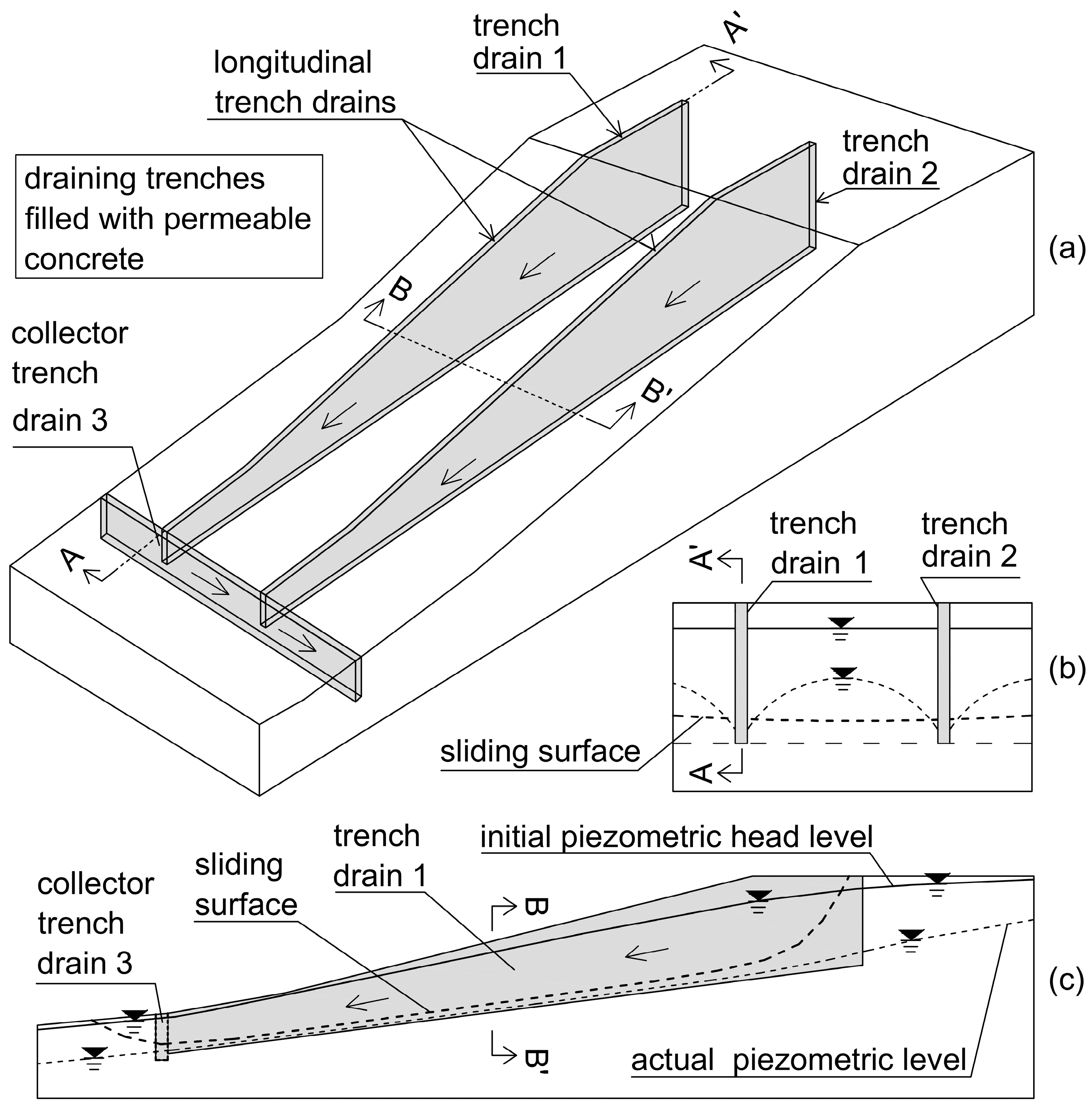
- Valore, C.; Ziccarelli, M.; Muscolino, S.R. An experimental investigation into the permeability and filter properties of pervious concrete for deep draining trenches. Riv. Ital. Geotec. 2018, 52, 7–30. [Google Scholar] [CrossRef]
- Marzulli, V.; Cafaro, F.; Ziccarelli, M. Hydraulic characterization of a pervious concrete for deep draining trenches. J. Mat. Civ. Eng. ASCE 2018, 30, 04018100. [Google Scholar] [CrossRef]
- Ziccarelli, M.; Valore, C. Hydraulic conductivity and strength of pervious concrete for deep trench drains. Geomech. Energy Environ. 2019, 18, 41–55. [Google Scholar] [CrossRef]
- Ziccarelli, M. Influence of Stress-level due to Self-weight on the Hydraulic Conductivity of Permeable Concrete for Geotechnical Applications. Geomech. Energy Environ. 2022, 32, 100409. [Google Scholar] [CrossRef]
- Ziccarelli, M.; Sapienza, G.; Casella, A. Experimental Investigation on Shear Strength at the Permeable Concrete–Fine-Grained Soil Interface for Slope Stabilization Using Deep Socket Counterfort Drains. GeoHazards 2024, 5, 917–931. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, Z.; Li, D.; Zhang, K.; Zhao, L. Mechanical and vegetation performance of porous concrete with recycled aggregate in riparian buffer area. J. Clean. Prod. 2022, 332, 130015. [Google Scholar] [CrossRef]
- Niyomukiza, J.B.; Eisazadeh, A.; Tangtermsirikul, S. Recent advances in slope stabilization using porous vegetation concrete in landslide-prone regions: A review. J. Build. Eng. 2023, 76, 107129. [Google Scholar] [CrossRef]
- Niyomukiza, J.B.; Eisazadeh, A.; Tangtermsirikul, S. Preparation of Porous Concrete Suitable for Vegetation Growth: An Approach Toward Green Infrastructure. In Proceedings of the 8th International Conference on Civil Engineering ICOCE, Singapore, 22–24 March 2024; Lecture Notes in Civil Engineering. Strauss, E., Ed.; Springer: Singapore, 2024; Volume 539, pp. 245–254. [Google Scholar] [CrossRef]
- Zeng, L.; Luo, J.-T.; Yang, Z.-R.; Yu, H.-C.; Wen, W.; Gao, Q.-F.; Zhang, H.-R. Performance evaluation of vegetation concrete with carbonaceous mudstone aggregates in slope protection under wet-dry conditions. Bull. Eng. Geol. Environ. 2024, 83, 1–17. [Google Scholar] [CrossRef]
- Niyomukiza, J.B.; Eisazadeh, A.; Tangtermsirikul, S. Synergistic effect of calcined clay and fly ash on the performance of porous vegetation concrete. Constr. Build. Mat. 2025, 458, 139749. [Google Scholar] [CrossRef]
- Sandoval, G.F.B.; Inocente Jussiani, E.; Campos de Moura, A.; Casanova Andrello, A.; Toralles, B.M. Hydraulic and morphological characterization of clogged pervious concrete (PC). Constr. Build. Mat. 2022, 322, 126464. [Google Scholar] [CrossRef]
- Barnhouse, W.; Srubar III, W.V. Material characterization and hydraulic conductivity modeling of macroporous recycled-aggregate pervious concrete. Constr. Build. Mat. 2016, 110, 89–97. [Google Scholar] [CrossRef]
- Shirke, N.A.; Shuler, S. Cleaning porous pavements using a reverse flush process. J. Transp. Eng. 2009, 135, 832–838. [Google Scholar] [CrossRef]
- Chopra, M.; Kakuturu, S.; Ballock, C.; Spence, J.; Wanielista, M. Effect of rejuvenation methods on the infiltration rates of pervious concrete pavements. J. Hydrol. Eng. 2010, 15, 426–433. [Google Scholar] [CrossRef]
- Hu, N.; Zhang, J.; Xia, S.; Han, R.; Dai, Z.; She, R.; Cui, X.; Meng, B. A field performance evaluation of the periodic maintenance for pervious concrete pavement. J. Clean. Prod. 2020, 263, 121463. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Lv, Q.; Xu, T. Hydrodynamic self-cleaning behaviors of double-layer drainage asphalt pavement. J. Clean. Prod. 2025, 486, 144582. [Google Scholar] [CrossRef]
- Terzaghi, K. Mechanism of Landslides. In Application of Geology to Engineering Practice (Berkey Volume); Paige, S., Ed.; The Geological Society of America: New York, NY, USA, 1950; pp. 83–123. [Google Scholar]
- Hutchinson, J.N. Assessment of the effectiveness of corrective measures in relation to geological conditions and types of slope movement. Bull. Intern. Eng. Geol. 1977, 16, 31–155. [Google Scholar] [CrossRef]
- Bromhead, E.N. An analytical solution to the problem of seepage into counterfort drains. Can. Geotech. J. 1984, 21, 657–662. [Google Scholar] [CrossRef]
- Stanic, B. Influence of draining trenches on slope stability. J. Geotech. Eng. 1984, 110, 1624–1636. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Rahardjo, H.; Hritzuk, K.J.; Leong, E.C.; Rezaur, R.B. Effectiveness of horizontal drains for slope stability. Eng. Geol. 2003, 69, 295–308. [Google Scholar] [CrossRef]
- Rahardjo, H.; Santoso, V.A.; Leong, E.C.; Ng, Y.S.; Hua, C.J. Performance of horizontal drains in residual soil slopes. Soil. Found. 2011, 51, 437–447. [Google Scholar] [CrossRef]
- Lee, M.L.; Ng, K.Y.; Huang, Y.F.; Li, W.C. Rainfall-induced landslides in Hulu Kelang area. Nat. Hazards 2014, 70, 353–375. [Google Scholar] [CrossRef]
- Valore, C.; Ziccarelli, M. The stabilization of a slope-viaduct system without closing traffic. In Proceedings of the European Conference on Soil Mechanics and Geotechnical Engineering, Edinburg, UK, 13–17 September 2015; pp. 367–372. [Google Scholar]
- Wei, Z.L.; Shang, Y.Q.; Sun, H.Y.; Xu, H.D.; Wang, D.F. The effectiveness of a drainage tunnel in increasing the rainfall threshold of a deep-seated landslide. Landslides 2019, 16, 1731–1744. [Google Scholar] [CrossRef]
- Sitarenios, P.; Casini, F.; Askarinejad, A.; Springman, S. Hydro-mechanical analysis of a surficial landslide triggered by artificial rainfall: The Ruedlingen field experiment. Geotechnique 2021, 71, 96–109. [Google Scholar] [CrossRef]
- Amarasinghe, M.P.; Kulathilaka, S.A.S.; Robert, D.J.; Zhou, A.; Jayathissa, H.A.G. Risk assessment and management of rainfall-induced landslides in tropical regions: A review. Nat. Hazards 2024, 120, 2179–2231. [Google Scholar] [CrossRef]
- Di Maio, C.; Vassallo, R. Effects of trench drain systems on pore water pressures in slow, deep, clayey landslides: Influence of hydraulic properties of the slip zone. Eng. Geol. 2025, 347, 107943. [Google Scholar] [CrossRef]
- Moraci, N.; Mandaglio, M.C.; Ielo, D. A new theoretical method to evaluate the internal stability of granular soil. Can. Geotech. J. 2012, 49, 45–58. [Google Scholar] [CrossRef]
- Xantakos, P.P. Slurry Walls as Structural Systems, 2nd ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- ASTM. Standard test methods for maximum index density and unit weight ofsoils using a vibratory table (D4253-00 and D4254-00). In 2004 Annual Book of ASTM Standards; American Society for Testing and Materials: Philadelphia, PA, USA, 2004. [Google Scholar]
- ASTM C192/C C192M–02; Standard Practice for Making and Curing Concrete Test Specimens in the Laboratory. ASTM Standards; American Society for Testing and Materials: Philadelphia, PA, USA, 2002.
- ASTM C1754/C1754M-12; Standard Test Method for Density and Air Void Content of Pervious Concrete. ASTM International: West Conshohocken, PA, USA, 2012.
- UNI EN 197-1:2011; Cement—Composition, Specifications and Conformity Criteria for Common Cements. British Standards Institute: London, UK, 2011.
- Deo, O.; Sumanasooriya, M.; Neithalath, N. Permeability reduction in pervious concretes due to clogging: Experimental and modeling. J. Mat. Civ. Eng. 2010, 22, 741–751. [Google Scholar] [CrossRef]
- Martin, W.D., III; Kaye, N.B.; Putman, B.J. Impact of vertical porosity distribution on the permeability of pervious concrete. Constr. Build. Mat. 2014, 59, 78–84. [Google Scholar] [CrossRef]
- West, D.; Kaye, N.B.; Putman, B.J.; Clark, R. Quantifying the non-linear hydraulic behavior of pervious concrete. J. Test. Eval. ASTM Int. 2016, 44, 2172–2181. [Google Scholar] [CrossRef]
- Montes, F.; Haselbach, L.M. Measuring hydraulic conductivity in pervious concrete. Environ. Eng. Sci. 2006, 23, 960–969. [Google Scholar] [CrossRef]
- Coughlin, J.P.; Campbell, C.D.; Mays, D.C. Infiltration and clogging by sand and clay in a pervious concrete pavement system. J. Hydrol. Eng. 2013, 17, 68–73. [Google Scholar] [CrossRef]
- Kia, A.; Wong, H.S.; Cheeseman, C.R. Clogging of permeable concrete: A review. J. Environ. Manag. 2017, 193, 221–233. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, L.; Yu, W.; Ren, E.; Shi, R. A novel approach to investigate the pore network and clogging of pervious concrete. Case Stud. Constr. Mat. 2025, 22, e04325. [Google Scholar] [CrossRef]
- Maruyama, R.C.; Camarini, G. Properties of Cellular Concrete for Filters. Int. J. Eng. Technol. 2015, 7, 223–228. [Google Scholar] [CrossRef]
- Fell, R.; Mac Gregor, P.; Stapledon, D.; Bell, G.; Foster, M. Chapter 9: Design, specification and construction of filters. In Geotechnical Engineering of Embankment Dams, 2nd ed.; CRC Press: London, UK, 2014; pp. 493–565. [Google Scholar]
- Kevern, J.T. Evaluating permeability and infiltration requirements for pervious concrete. J. Test. Eval. ASTM 2015, 43, 544–553. [Google Scholar] [CrossRef]
- Haselbach, L. Potential for clay clogging of pervious concrete under extreme conditions. J. Hydr. Eng. 2010, 15, 67–69. [Google Scholar]
- Taylor, H.F.; O’Sullivan, C.; Sim, W.W. Geometric and hydraulic void constrictions in granular media. J. Geotech. Geoenviron. Eng. 2016, 142, 04016057. [Google Scholar] [CrossRef]
- Rao, Y.; Zhang, J.; Yang, T.; Feng, J. Effect of Drying on clay clogging of pervious concrete. J. Mat. Civ. Eng. 2021, 33, 04021137. [Google Scholar] [CrossRef]
- Rao, Y.; Fu, H.; Yang, T.; Chen, H.; Zhang, Z.; Ding, H. Comparison between sand and clay clogging mechanisms of pervious concrete pavement. Sci. Rep. 2022, 12, 9258. [Google Scholar] [CrossRef] [PubMed]
- Sandoval, B.; Pieralisi, G.F.; Dall Bello de Souza Risson, K.; Campos de Moura, A.; Toralles, B.M. Clogging phenomenon in Pervious Concrete (PC): A systematic literature review. J. Clean. Prod. 2022, 365, 132579. [Google Scholar] [CrossRef]
- Mata, L.A.; Leming, M.L. Vertical distribution of sediments in pervious concrete pavement systems. ACI Mater. J. 2012, 109, 149–155. [Google Scholar] [CrossRef]
- Fwa, F.; Lim, E.; Tan, H. Comparison of Permeability and Clogging Characteristics of Porous Asphalt and Pervious Concrete Pavements Materials. Transp. Res. Rec. 2014, 2511, 72–80. [Google Scholar] [CrossRef]
- Walsh, S.P.; Rowe, A.; Guo, Q. Laboratory scale study to quantify the effect of sediment accumulation on the hydraulic conductivity of pervious concrete. J. Irrig. Drain. Eng. 2014, 140, 1–7. [Google Scholar] [CrossRef]
- Sandoval, G.; Galobardes, I.; Campos, A.; Toralles, B.M. Assessing the phenomenon of clogging of pervious concrete (Pc): Experimental test and model proposition. J. Build. Eng. 2020, 29, 101203. [Google Scholar] [CrossRef]
- Sandoval, G.F.B.B.; Galobardes, I.; De Moura, A.C.; Toralles, B.M.; Campos, A.; Moura, D.; Toralles, B.M.; De Moura, A.C.; Toralles, B.M. Hydraulic behavior variation of pervious concrete due to clogging. Case Stud. Constr. Mater. 2020, 13, e00354. [Google Scholar] [CrossRef]
- Cai, J.; Chen, J.; Shi, J.; Tian, Q.; Xu, G.; Du, Y. A novel approach to evaluate the clogging resistance of pervious concrete. Case Stud. Constr. Mater. 2022, 16, e00864. [Google Scholar] [CrossRef]





| Material | Gs | γs (kN/m3) |
|---|---|---|
| Sand S | 2.65 | 26 |
| Gravel G | 2.7 | 26.5 |
| Mixture | Gravel G (% in Weight) | Sand S (% in Weight) | dmax (mm) | d60 (mm) | d50 (mm) | d10 (mm) | CU (d60/d10) | Porosity n |
|---|---|---|---|---|---|---|---|---|
| M1 | 100 | 0 | 12 | 10 | 9.20 | 5.60 | 1.41 | 0.42 |
| M2 | 80 | 20 | 12 | 9.11 | 8.31 | 0.92 | 9.90 | 0.40 |
| M3 | 70 | 30 | 12 | 8.91 | 8.62 | 0.86 | 10.36 | 0.39 |
| M4 | 30 | 70 | 12 | 1.11 | 1.00 | 0.75 | 1.48 | 0.39 |
| M5 | 20 | 80 | 12 | 0.99 | 0.95 | 0.73 | 1.36 | 0.38 |
| M6 | 0 | 100 | 1.41 | 0.65 | 0.61 | 0.46 | 1.78 | 0.38 |
| pH | Electrical Conductivity at 20° (μS/cm) | Alkalinity (mg/L) | Sulfates (mg/L) | Potassium (mg/L) | Sodium (mg/L) | Chlorides (mg/L) | Calcium (mg/L) | Nitrates (mg/L) | Magnesium (mg/L) |
|---|---|---|---|---|---|---|---|---|---|
| 7.72 | 100 | 194 | 161 | 4.6 | 4.6 | 48.5 | 99 | 5.9 | 2 |
| Clogging Material | dmax (μm) | d60 (μm) | d50 (μm) | d10 (μm) | CU |
|---|---|---|---|---|---|
| VS | 2000 | 460 | 387 | 129 | 3.57 |
| C1 | 75 | 38.1 | 32 | 7.9 | 4.82 |
| C2 | 180 | 63 | 49 | 8.1 | 7.78 |
| C3 | 600 | 305 | 251 | 101 | 3.02 |
| C4 | 1180 | 390 | 322 | 129 | 3.02 |
| Mixture | Clogging Material | n | kini1 (m/s) × 10−2 | kfin1 (m/s) × 10−2 | kfin1/kini1 (%) | Clogging material | n | kini2 (m/s) × 10−2 | kfin2 (m/s) × 10−2 | kfin2/kini2 (%) | kfin2/kini1 (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | C1 | 1–20 | 4.30 | 3.85 | 89.5 | C4 | 21–82 | 3.98 | 0.47 | 11.8 | 10.9 |
| M2 | C1 | 1–10 | 2.94 | 2.30 | 78.2 | C3 | 11–15 | 2.30 | 1.39 | 60 | 47 |
| M3 | C1 | 1–25 | 2.23 | 1.01 | 45.3 | / | / | / | / | / | / |
| M4 | C1 | 1–10 | 1.05 | 0.31 | 29.5 | C2 | 11–20 | 0.31 | 0.24 | 77.4 | 22.9 |
| M5 | C1 | 1–50 | 0.57 | 0.21 | 36.8 | C2 | 51–70 | 0.21 | 0.17 | 80.9 | 29.8 |
| M6 | C1 | 1–82 | 0.45 | 0.03 | 6.7 | / | / | / | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziccarelli, M. Mix Design of Pervious Concrete in Geotechnical Engineering Applications. Materials 2025, 18, 1909. https://doi.org/10.3390/ma18091909
Ziccarelli M. Mix Design of Pervious Concrete in Geotechnical Engineering Applications. Materials. 2025; 18(9):1909. https://doi.org/10.3390/ma18091909
Chicago/Turabian StyleZiccarelli, Maurizio. 2025. "Mix Design of Pervious Concrete in Geotechnical Engineering Applications" Materials 18, no. 9: 1909. https://doi.org/10.3390/ma18091909
APA StyleZiccarelli, M. (2025). Mix Design of Pervious Concrete in Geotechnical Engineering Applications. Materials, 18(9), 1909. https://doi.org/10.3390/ma18091909







