Formability Assessment of C1100 Pure-Copper Tube Considering an Enhanced Modified Maximum Force Criterion
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Tested Material
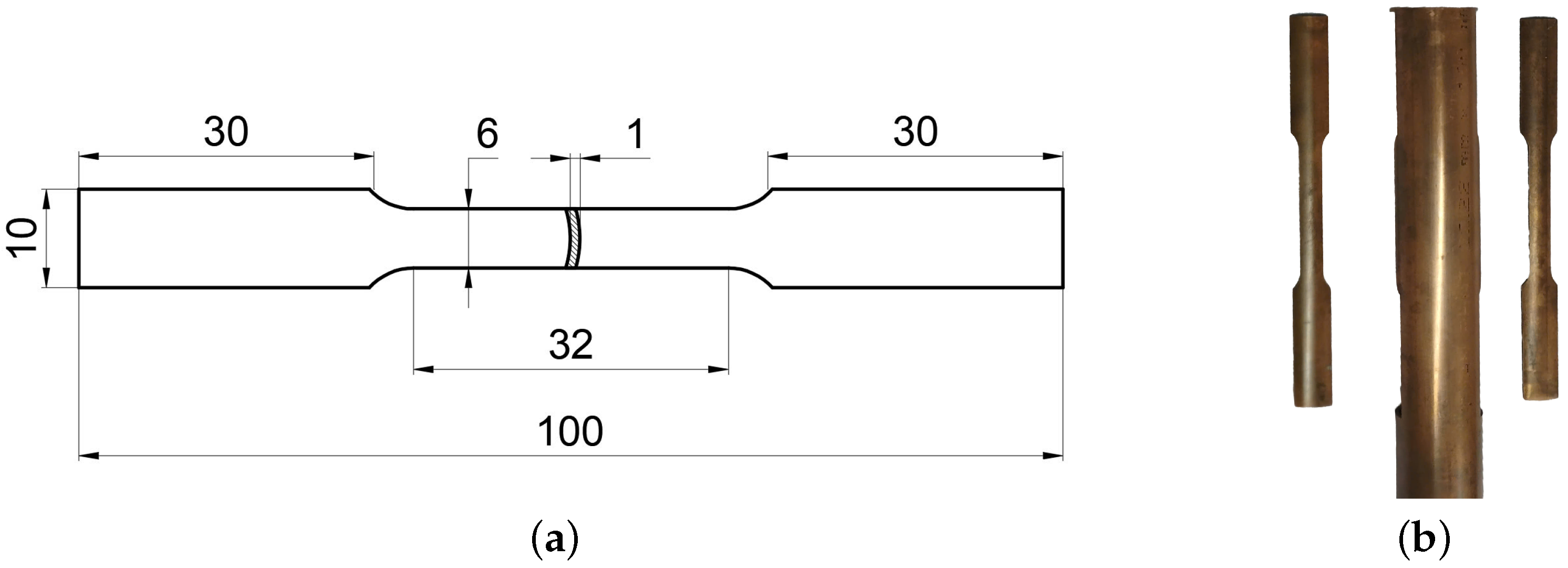
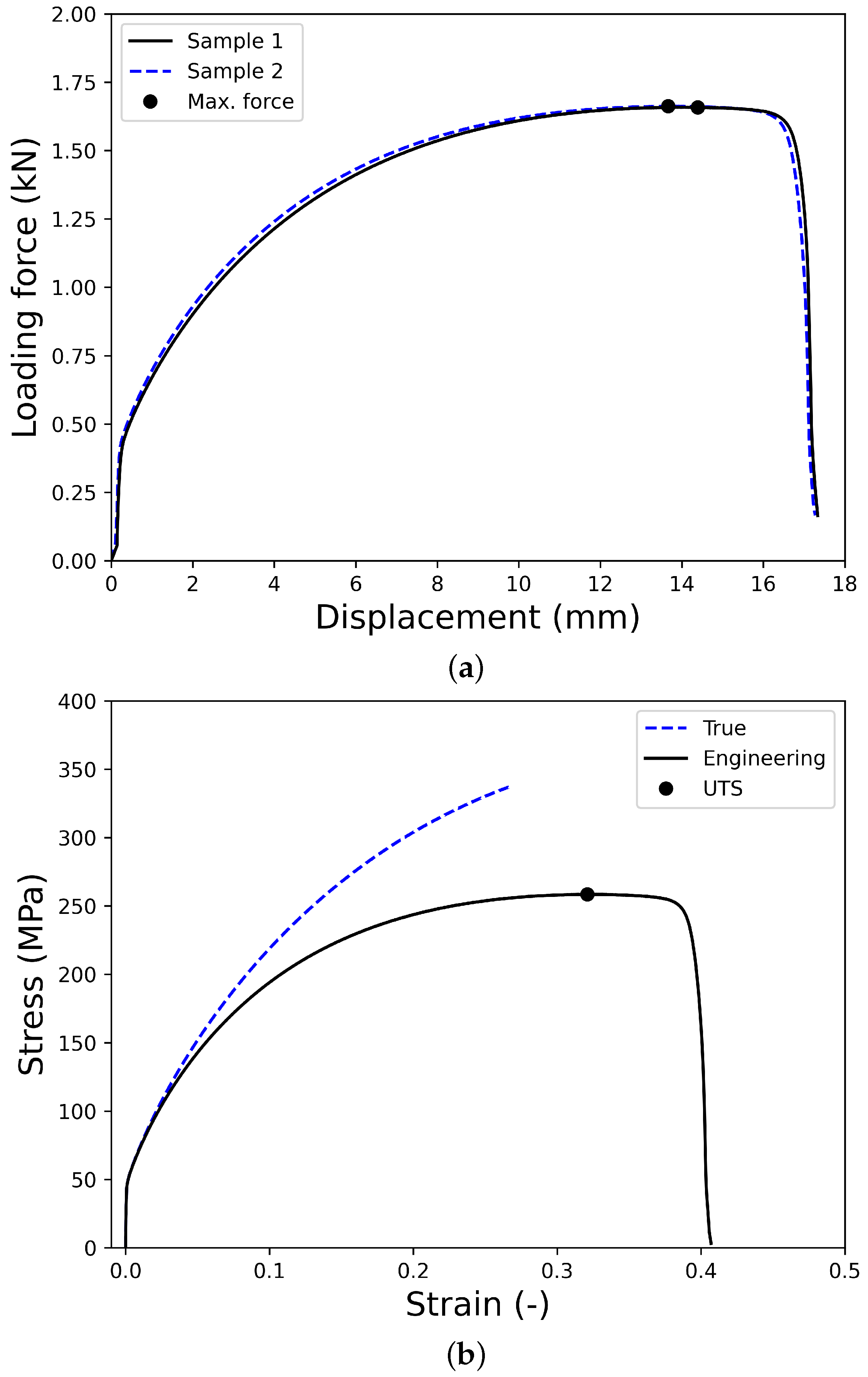
2.2. Uniaxial Tensile Test
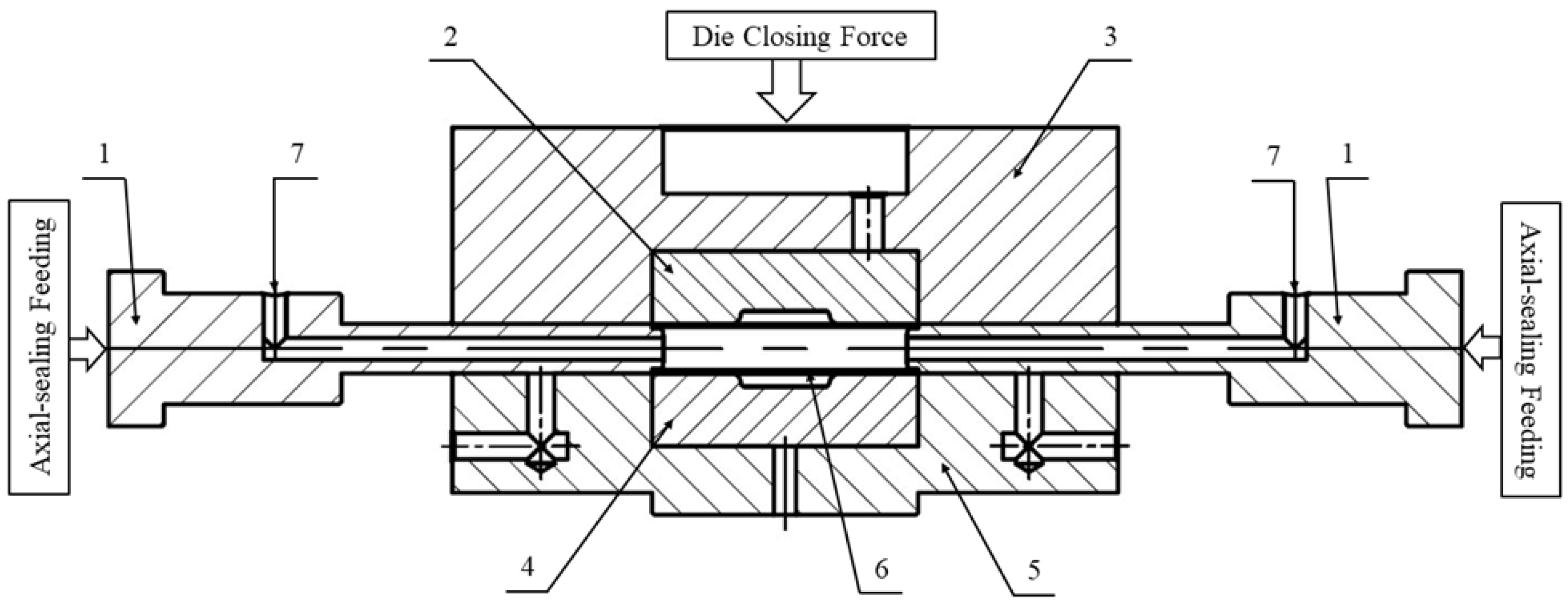
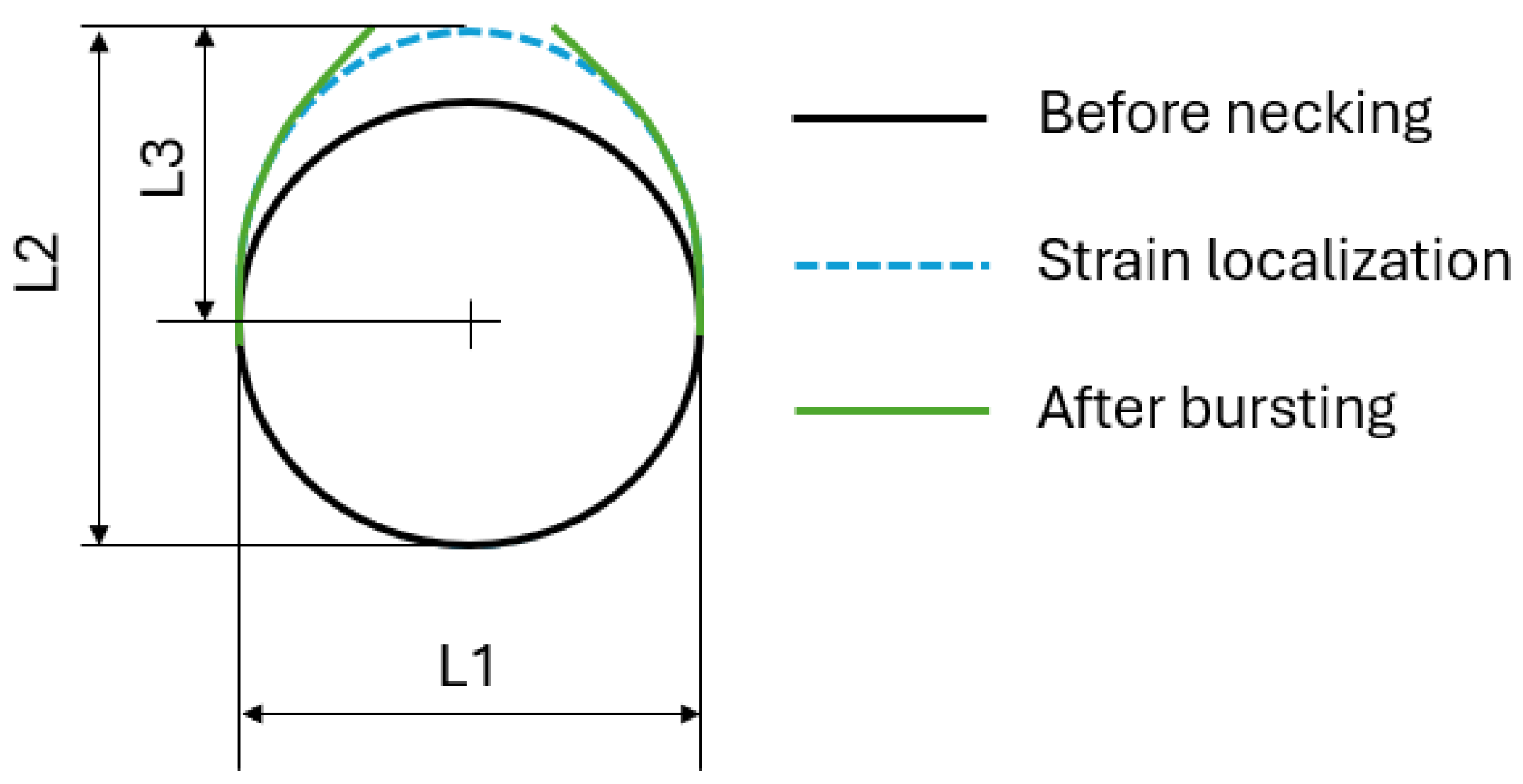
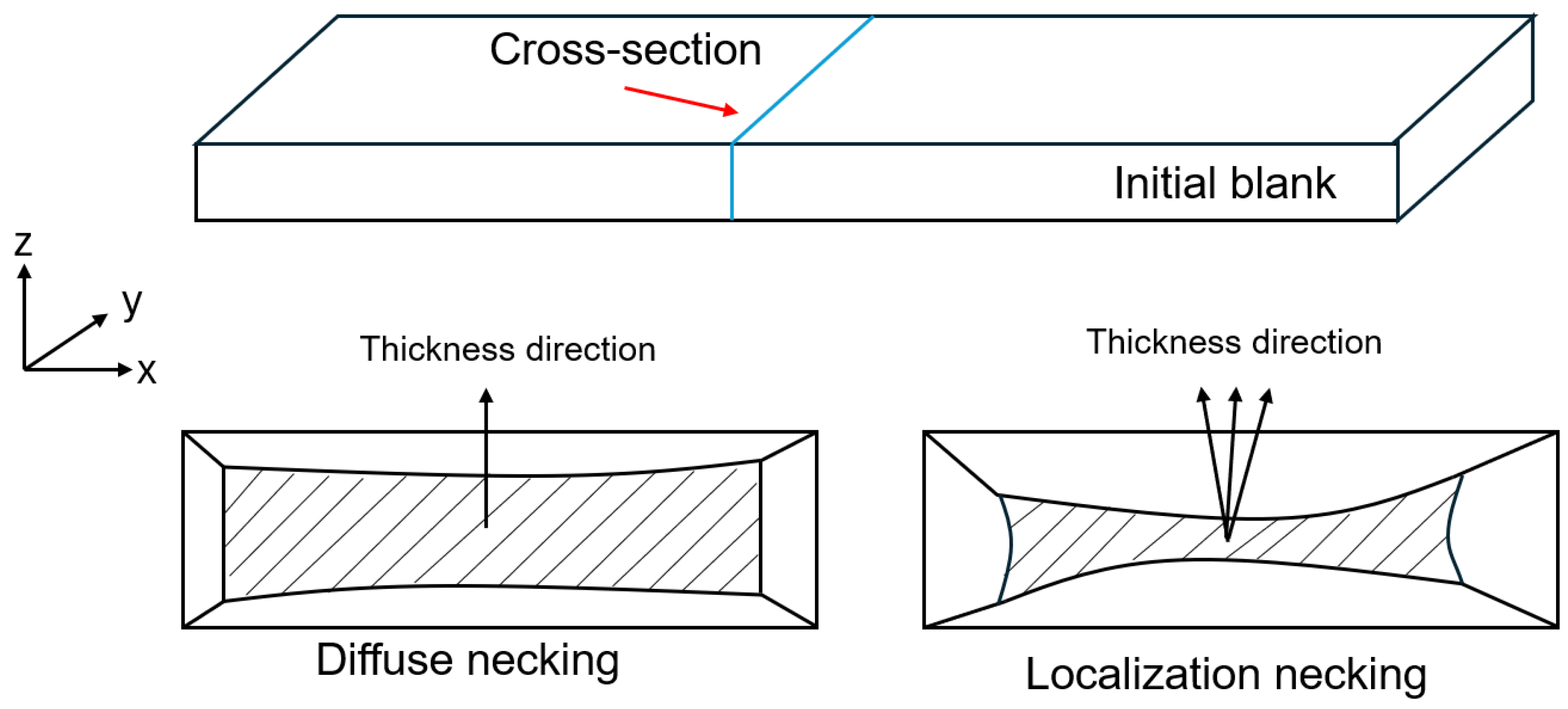
2.3. Tube Expansion Test
3. Theoretical Prediction of the Forming Limit Diagram
3.1. Constitutive Modeling
3.1.1. Constitutive Equations
3.1.2. Validation
3.2. Theoretical Method for Forming Limit Diagram Prediction
3.2.1. MMFC2 Method
3.2.2. MK Method
4. Results and Discussion
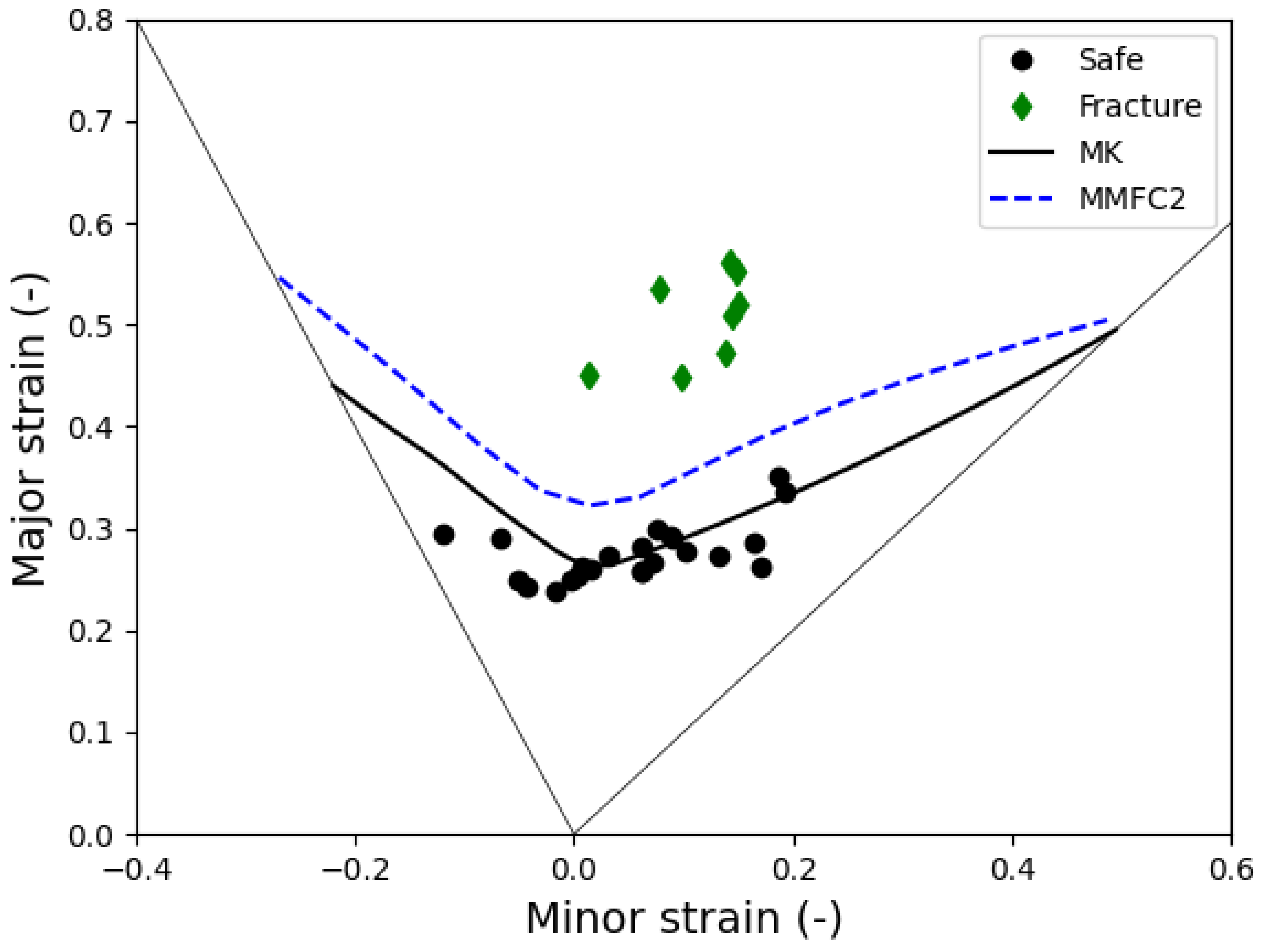
4.1. Comparison of FLD Predictions
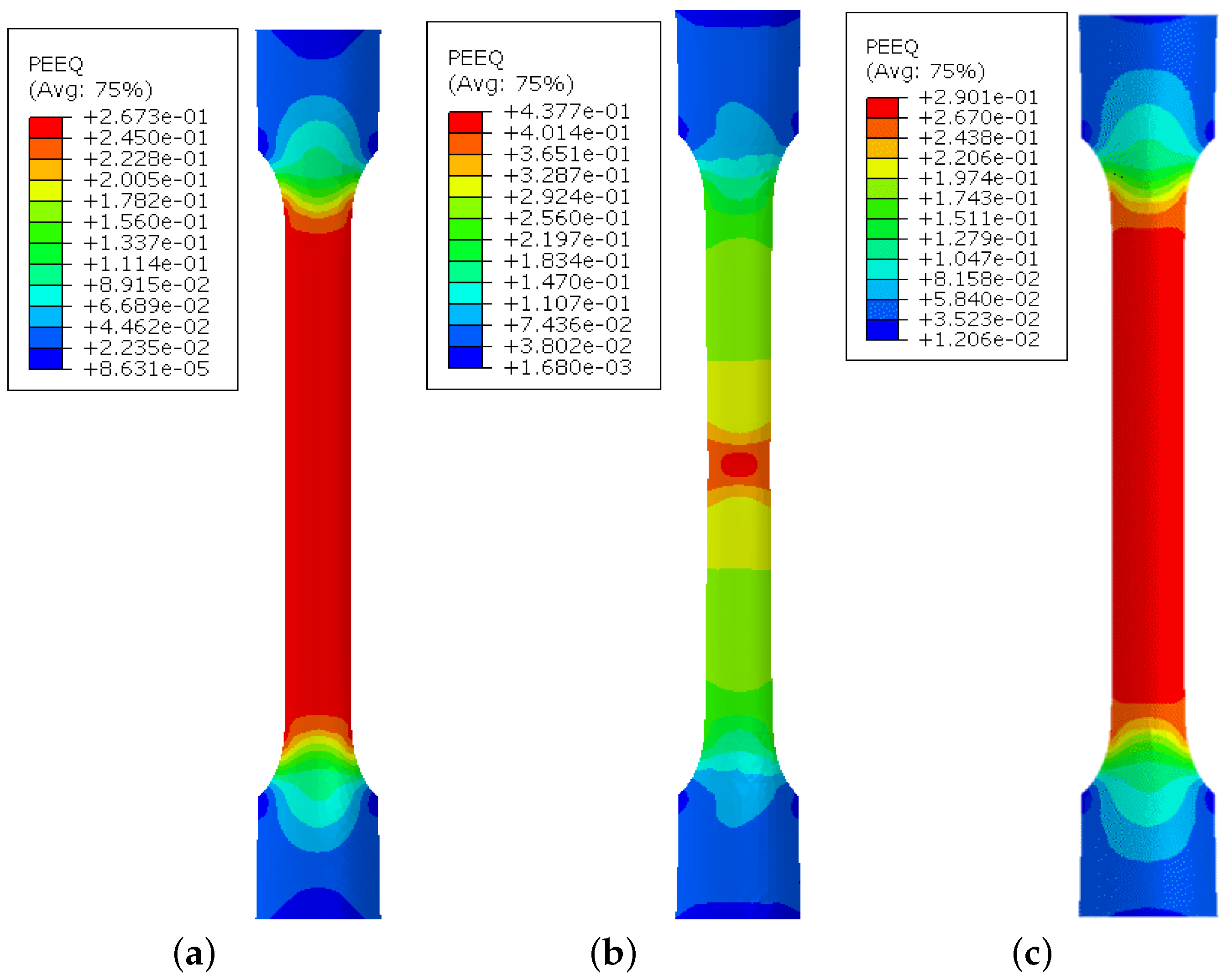
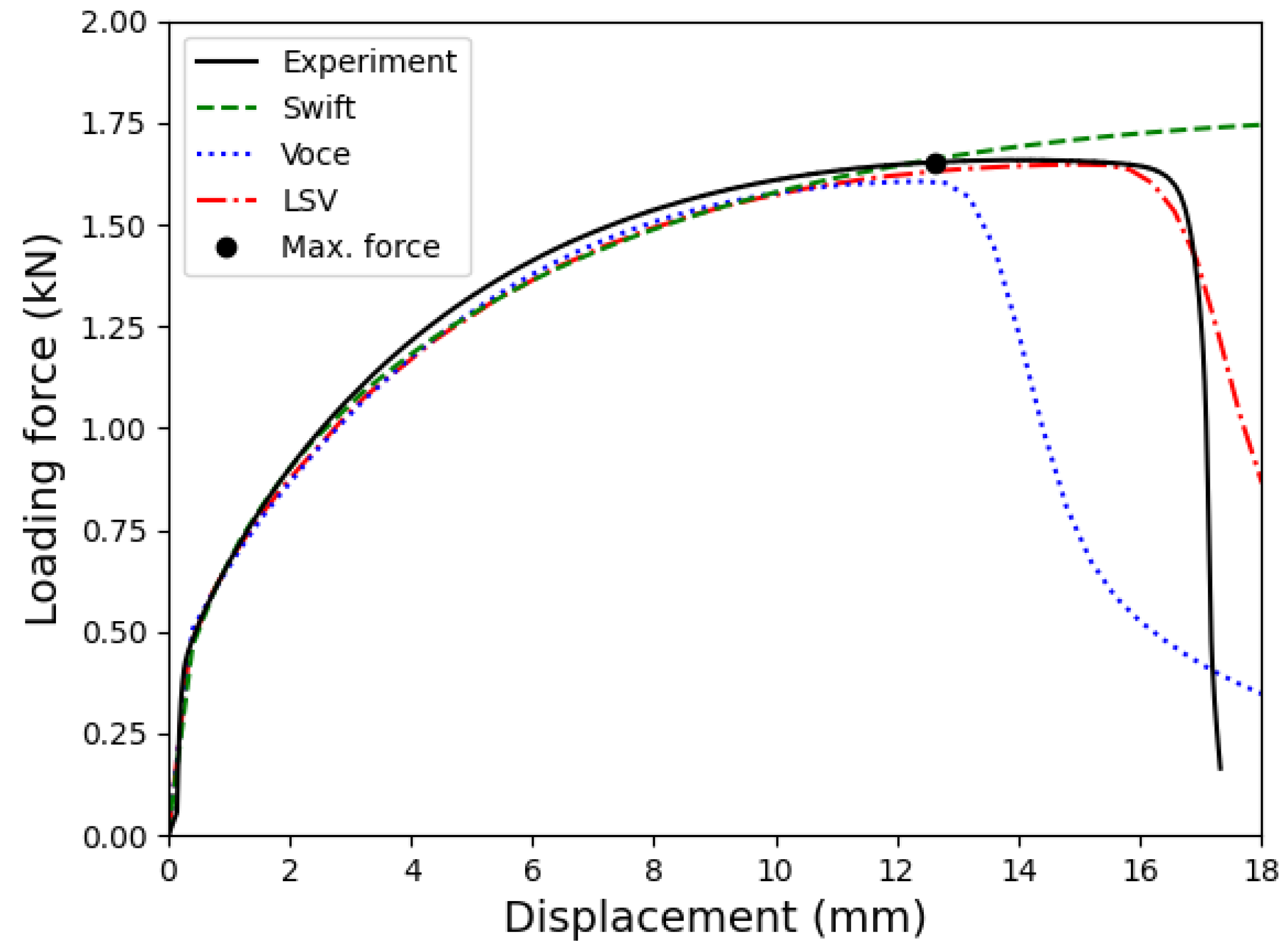
4.2. Application in Finite Element Analysis
5. Conclusions
- Both the Swift and Voce hardening laws effectively capture the hardening behavior of the tested material observed during the uniaxial tensile test. However, both models provide unsatisfactory predictions for the hardening behavior in the post-necking ranges. Fortunately, the LSV model offers an excellent description of the hardening behavior of the C1100 copper tube.
- The calibrated LSV hardening law is used in the MMFC2 and MK models, coupled with the von Mises yield function, to predict the FLD of the tested material. The prediction made by the MMFC2 model is significantly higher than that of the MK model.
- A comparison between experimental and predicted FLDs demonstrates the practical value of the theoretical predictions. The predicted FLD proves to be a useful tool for evaluating failure due to necking that occurs during the hydroforming of the C1100 pure copper tube.
- The predicted FLDs are employed in the FEA of the tube expansion test. It is found that the MK model provides a conservative prediction of the failure of the tube. The prediction of the MMFC2 model is more relevant to the experimental measurements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Xu, X.; Fan, Y.; Wei, L. Loading path design of thin-walled aluminum alloy T-shaped tube hydroforming process based on the control of limit pressure. Int. J. Adv. Manuf. Technol. 2020, 108, 3119–3131. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Dai, W.H.; Chen, C.C. Investigation of punch shape design in tube hydro-piercing processes. Int. J. Adv. Manuf. Technol. 2020, 110, 2211–2220. [Google Scholar] [CrossRef]
- Khalfallah, A.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Constitutive parameter identification of CB2001 yield function and its experimental verification using tube hydroforming tests. Int. J. Mech. Sci. 2020, 185, 105868. [Google Scholar] [CrossRef]
- Wei, C.; Han, Z.; Jia, Z.; Liu, B. An optimization method of wall thickness distributions in T-shaped tube compound-forming method with unconventional tube blank. Thin-Walled Struct. 2024, 200, 111892. [Google Scholar] [CrossRef]
- Koc, M.; Altan, T. Prediction of forming limits and parameters in the tube hydroforming process. Int. J. Mach. Tools Manuf. 2002, 42, 123–138. [Google Scholar] [CrossRef]
- Bell, C.; Corney, J.; Zuelli, N.; Savings, D. A state of the art review of hydroforming technology: Its applications, research areas, history, and future in manufacturing. Int. J. Mater. Form. 2020, 13, 789–828. [Google Scholar] [CrossRef]
- Pramod, K.; Marimuthu, S. Advanced hydroforming process in automotive industry. In Proceedings of the International Conference on Minerals, Materials and Manufacturing Methods (ICMMMM), Coimbatore, India, 19 March 2022; AIP Publishing: Melville, NY, USA, 2023; Volume 2861. [Google Scholar]
- Kim, J.; Kim, S.W.; Song, W.J.; Kang, B.S. Analytical and numerical approach to prediction of forming limit in tube hydroforming. Int. J. Mech. Sci. 2005, 47, 1023–1037. [Google Scholar] [CrossRef]
- Butcher, C.; Chen, Z.; Bardelcik, A.; Worswick, M. Damage-based finite-element modeling of tube hydroforming. Int. J. Fract. 2009, 155, 55–65. [Google Scholar] [CrossRef]
- Yuenyong, J.; Suthon, M.; Kingklang, S.; Thanakijkasem, P.; Mahabunphachai, S.; Uthaisangsuk, V. Formability prediction for tube hydroforming of stainless steel 304 using damage mechanics model. J. Manuf. Sci. Eng. 2018, 140, 011006. [Google Scholar] [CrossRef]
- Liu, C.; Abd El-Aty, A.; Lee, M.G.; Hou, Y.; Xu, Y.; Hu, S.; Cheng, C.; Tao, J.; Guo, X. Predicting the forming limits in the tube hydroforming process by coupling the cyclic plasticity model with ductile fracture criteria. J. Mater. Res. Technol. 2023, 26, 109–120. [Google Scholar] [CrossRef]
- Keshri, S.; Suriyanarayanan, S. Hydroforming: State-of-the-Art Developments and Future Trends. In Analysis and Optimization of Sheet Metal Forming Processes; CRC Press: Boca Raton, FL, USA, 2024; pp. 232–261. [Google Scholar]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Banabic, D.; Kami, A.; Comsa, D.S.; Eyckens, P. Developments of the Marciniak-Kuczynski model for sheet metal formability: A review. J. Mater. Process. Technol. 2021, 287, 116446. [Google Scholar] [CrossRef]
- Dong, G.; Bi, J.; Du, B.; Chen, X.; Zhao, C. Research on AA6061 tubular components prepared by combined technology of heat treatment and internal high pressure forming. J. Mater. Process. Technol. 2017, 242, 126–138. [Google Scholar] [CrossRef]
- Hashemi, R.; Madoliat, R.; Afshar, A. Prediction of forming limit diagrams using the modified MK method in hydroforming of aluminum tubes. Int. J. Mater. Form. 2016, 9, 297–303. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, Y.; Chen, K.; He, Z. Forming Limit Analysis of Thin-Walled Extruded Aluminum Alloy Tubes under Nonlinear Loading Paths Using an Improved MK Model. Materials 2023, 16, 1647. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yang, H.; Lu, R.; Fu, M. Coupled modeling of anisotropy variation and damage evolution for high strength steel tubular materials. Int. J. Mech. Sci. 2016, 105, 41–57. [Google Scholar] [CrossRef]
- Ktari, Z.; Khalfallah, A. Design and validation of a new ring hoop plane strain test for characterizing the anisotropic plastic behavior of tubular materials. Int. J. Solids Struct. 2024, 298, 112869. [Google Scholar] [CrossRef]
- Hora, P.; Tong, L.; Berisha, B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form. 2013, 6, 267–279. [Google Scholar] [CrossRef]
- Krauer, J.; Hora, P.; Tong, L.; Berisha, B. Forming limit prediction of metastable materials with temperature and strain induced martensite transformation. In Materials Processing and Design; Modeling, Simulation and Applications, NUMIFORM ’07, Proceedings of the 9th International Conference on Numerical Methods in Industrial Forming Processes, Porto, Portugal, 17–21 June 2007; AIP: Melville, NY, USA, 2007; Volume 908, pp. 1263–1268. [Google Scholar]
- Paraianu, L.; Dragos, G.; Bichis, I.; Comsa, D.S.; Banabic, D. A new formulation of the modified maximum force criterion (MMFC). Int. J. Mater. Form. 2010, 3, 243–246. [Google Scholar] [CrossRef]
- Manopulo, N.; Hora, P.; Peters, P.; Gorji, M.; Barlat, F. An extended modified maximum force criterion for the prediction of localized necking under non-proportional loading. Int. J. Plast. 2015, 75, 189–203. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, B.H.; Park, K.C.; Kim, Y.S. Influence of the post-necking prediction of hardening law on the theoretical forming limit curve of aluminium sheets. Int. J. Mech. Sci. 2018, 140, 521–536. [Google Scholar] [CrossRef]
- Pham, Q.T.; Islam, M.S.; Sigvant, M.; Caro, L.P.; Lee, M.G.; Kim, Y.S. Improvement of modified maximum force criterion for forming limit diagram prediction of sheet metal. Int. J. Solids Struct. 2023, 273, 112264. [Google Scholar] [CrossRef]
- Seyedkashi, S.; Liaghat, G.H.; Naeini, H.M.; Hoseinpour Gollo, M. Study of Forming Parameters in Hydroforming of a Thin-Walled ASTM C11000 Copper Tube. Adv. Mater. Res. 2010, 83, 133–142. [Google Scholar] [CrossRef]
- Gong, F.; Yang, Z.; Chen, Q.; Xie, Z.; Shu, D.; Yang, J. Influences of lubrication conditions and blank holder force on micro deep drawing of C1100 micro conical–cylindrical cup. Precis. Eng. 2015, 42, 224–230. [Google Scholar] [CrossRef]
- Zahedi, A.; Dariani, B.M.; Mirnia, M.J. Experimental determination and numerical prediction of necking and fracture forming limit curves of laminated Al/Cu sheets using a damage plasticity model. Int. J. Mech. Sci. 2019, 153, 341–358. [Google Scholar] [CrossRef]
- Hashemi, R.; Karajibani, E. Forming limit diagram of Al-Cu two-layer metallic sheets considering the Marciniak and Kuczynski theory. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 848–854. [Google Scholar] [CrossRef]
- Karajibani, E.; Hashemi, R.; Sedighi, M. Forming limit diagram of aluminum-copper two-layer sheets: Numerical simulations and experimental verifications. Int. J. Adv. Manuf. Technol. 2017, 90, 2713–2722. [Google Scholar] [CrossRef]
- Gholami, M.D.; Davoodi, B.; Hashemi, R. Study of forming limit curves and mechanical properties of three-layered brass (CuZn10)/low carbon steel (St14)/brass (CuZn10) composite considering the effect of annealing temperature. J. Mater. Res. Technol. 2022, 18, 4672–4682. [Google Scholar] [CrossRef]
- Bagheri, A.; Shabani, A.; Toroghinejad, M.R.; Taherizadeh, A. Post-rolling annealing of a multilayered Brass/IFS/Brass composite: An evaluation of anisotropy, formability, and mechanical properties. J. Mater. Res. Technol. 2022, 19, 732–746. [Google Scholar] [CrossRef]
- Gallifa-Terricabras, A.; Swieszek, J.S.; Smakulska, D.; Ruiz-Palenzuela, B.; Garlaschè, M. Forming limit diagram of annealed copper OFE thick sheets for optimized hydroforming of superconducting RF cavities. Mater. Des. 2024, 244, 113191. [Google Scholar] [CrossRef]
- Mohammadi, M.; Karami, J.S.; Hashemi, S.J. Forming limit diagram of aluminum/copper bi-layered tubes by bulge test. Int. J. Adv. Manuf. Technol. 2017, 92, 1539–1549. [Google Scholar] [CrossRef]
- ASTM B280; Standard Specification for Seamless Copper Tube for Air Conditioning and Refrigeration Field Service. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM E8; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2019.
- ISO 12004-2:2008; Metallic Materials—Sheet and Strip: Determination of Forming-Limit Curves. Part 2—Determination of Forming-Limit Curves in the Laboratory. International Organization for Standardization: Geneva, Switzerland, 2008.
- Wang, K.; Carsley, J.E.; He, B.; Li, J.; Zhang, L. Measuring forming limit strains with digital image correlation analysis. J. Mater. Process. Technol. 2014, 214, 1120–1130. [Google Scholar] [CrossRef]
- Ahmadi, S.; Eivani, A.; Akbarzadeh, A. Experimental and analytical studies on the prediction of forming limit diagrams. Comput. Mater. Sci. 2009, 44, 1252–1257. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, Y.; Sun, X.; Chen, G.; Luo, Z. Optimization of bi-layered Y-shaped tube hydroforming using RSM. Int. J. Adv. Manuf. Technol. 2024, 133, 521–541. [Google Scholar] [CrossRef]
- Pham, Q.T.; Nguyen-Thoi, T.; Ha, J.; Kim, Y.S. Hybrid fitting-numerical method for determining strain-hardening behavior of sheet metals. Mech. Mater. 2021, 161, 104031. [Google Scholar] [CrossRef]
- Soare, S.C. Theoretical considerations upon the MK model for limit strains prediction: The plane strain case, strain-rate effects, yield surface influence, and material heterogeneity. Eur. J.-Mech.-A/Solids 2010, 29, 938–950. [Google Scholar] [CrossRef]


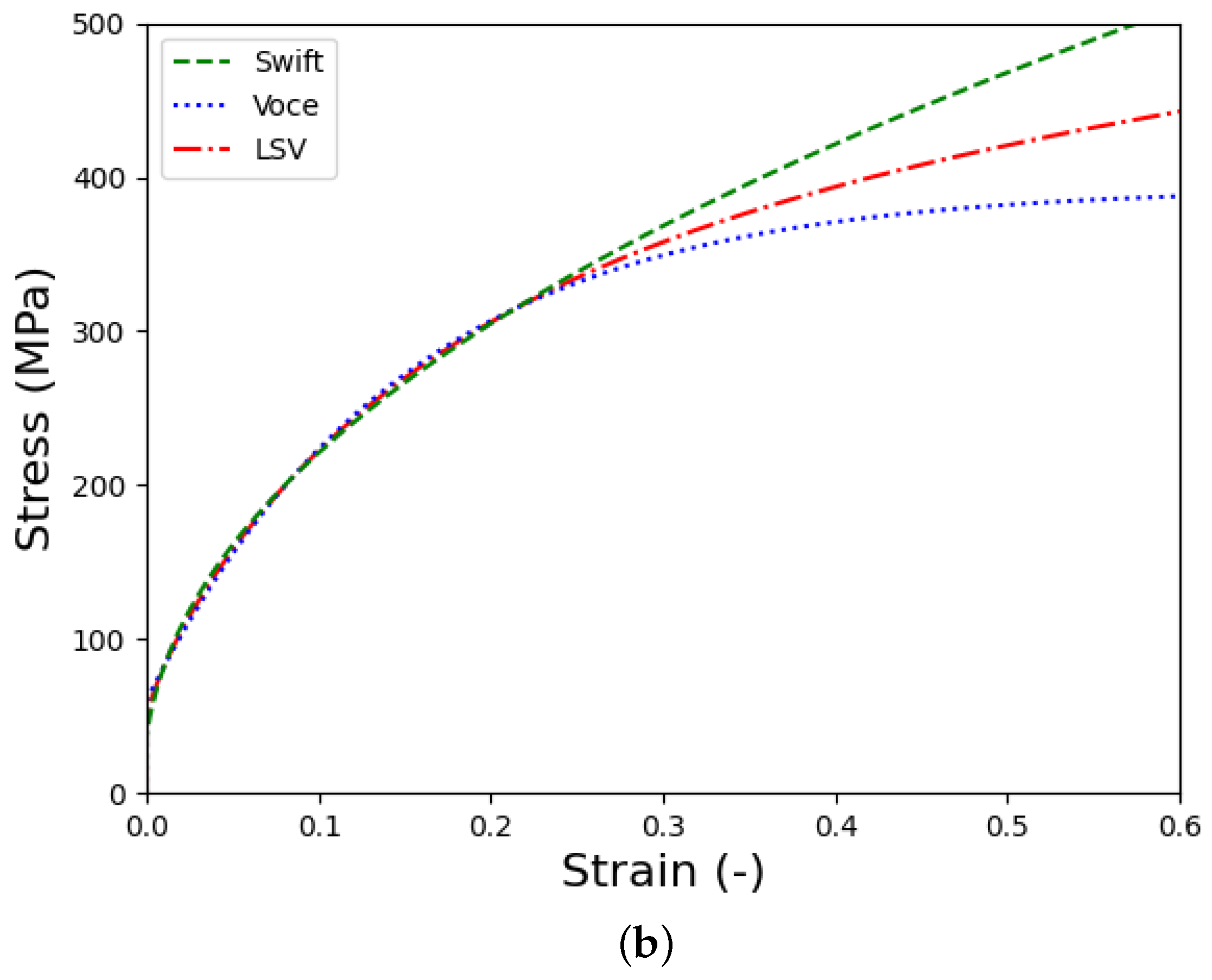




| Hardening Law | Swift | Voce | LSV | ||||
|---|---|---|---|---|---|---|---|
| Parameter | C (MPa) | n | A (MPa) | B (MPa) | k | ||
| Value | 647.42 | 0.00236 | 0.472 | 393.52 | 333.52 | 6.73 | 0.45 |
| Experiment | MK | MMFC2 | ||||
|---|---|---|---|---|---|---|
| # 1 | # 2 | # 3 | Average | |||
| Thickness (mm) | 0.75 | 0.78 | 0.76 | 0.763 | 0.809 | 0.704 |
| Diameter (mm) | 29.1 | 28.3 | 28.8 | 28.73 | 27.08 | 30.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, N.A.; Pham, Q.T.; Dinh, V.D.; Nguyen, D.T.; Nguyen, D.-T.; Hoan, T.D.; Giang, L.D. Formability Assessment of C1100 Pure-Copper Tube Considering an Enhanced Modified Maximum Force Criterion. Materials 2025, 18, 1919. https://doi.org/10.3390/ma18091919
Pham NA, Pham QT, Dinh VD, Nguyen DT, Nguyen D-T, Hoan TD, Giang LD. Formability Assessment of C1100 Pure-Copper Tube Considering an Enhanced Modified Maximum Force Criterion. Materials. 2025; 18(9):1919. https://doi.org/10.3390/ma18091919
Chicago/Turabian StylePham, Ngoc Anh, Quoc Tuan Pham, Van Duy Dinh, Dac Trung Nguyen, Duc-Toan Nguyen, Tran Duc Hoan, and Lai Dang Giang. 2025. "Formability Assessment of C1100 Pure-Copper Tube Considering an Enhanced Modified Maximum Force Criterion" Materials 18, no. 9: 1919. https://doi.org/10.3390/ma18091919
APA StylePham, N. A., Pham, Q. T., Dinh, V. D., Nguyen, D. T., Nguyen, D.-T., Hoan, T. D., & Giang, L. D. (2025). Formability Assessment of C1100 Pure-Copper Tube Considering an Enhanced Modified Maximum Force Criterion. Materials, 18(9), 1919. https://doi.org/10.3390/ma18091919







