Research on the Layout Design of Auxiliary Support Modules for Suppressing Machining Chatter in Thin-Walled Beams
Abstract
:1. Introduction
2. Auxiliary Support Module Layout Design Method
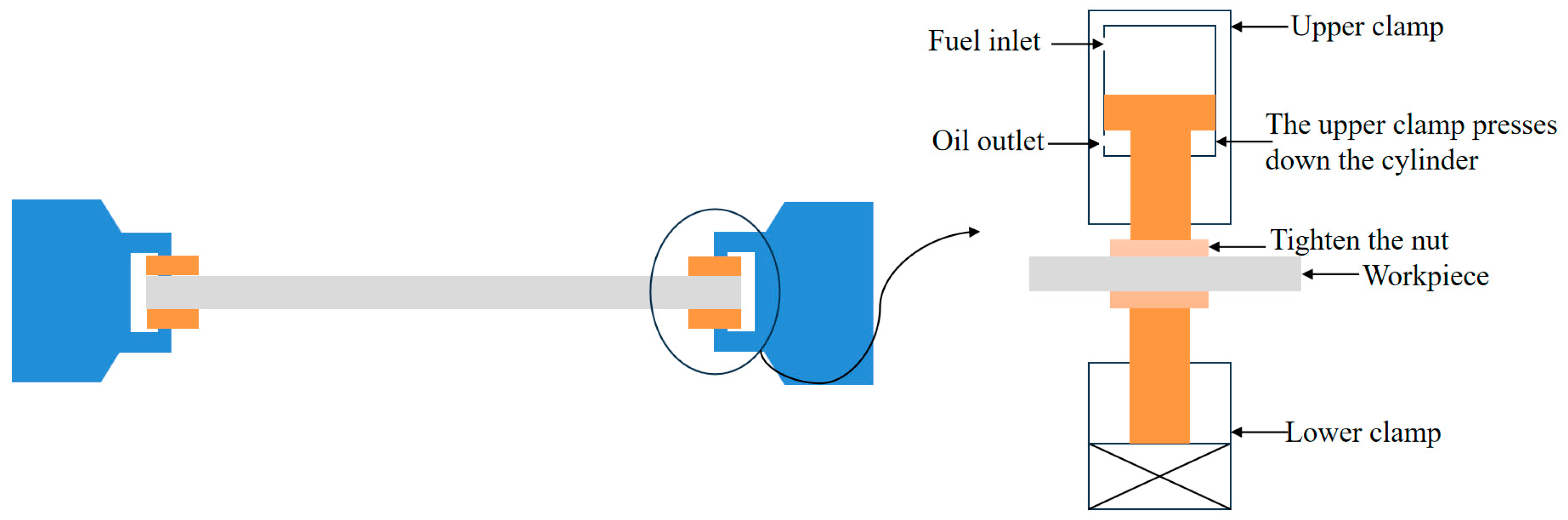
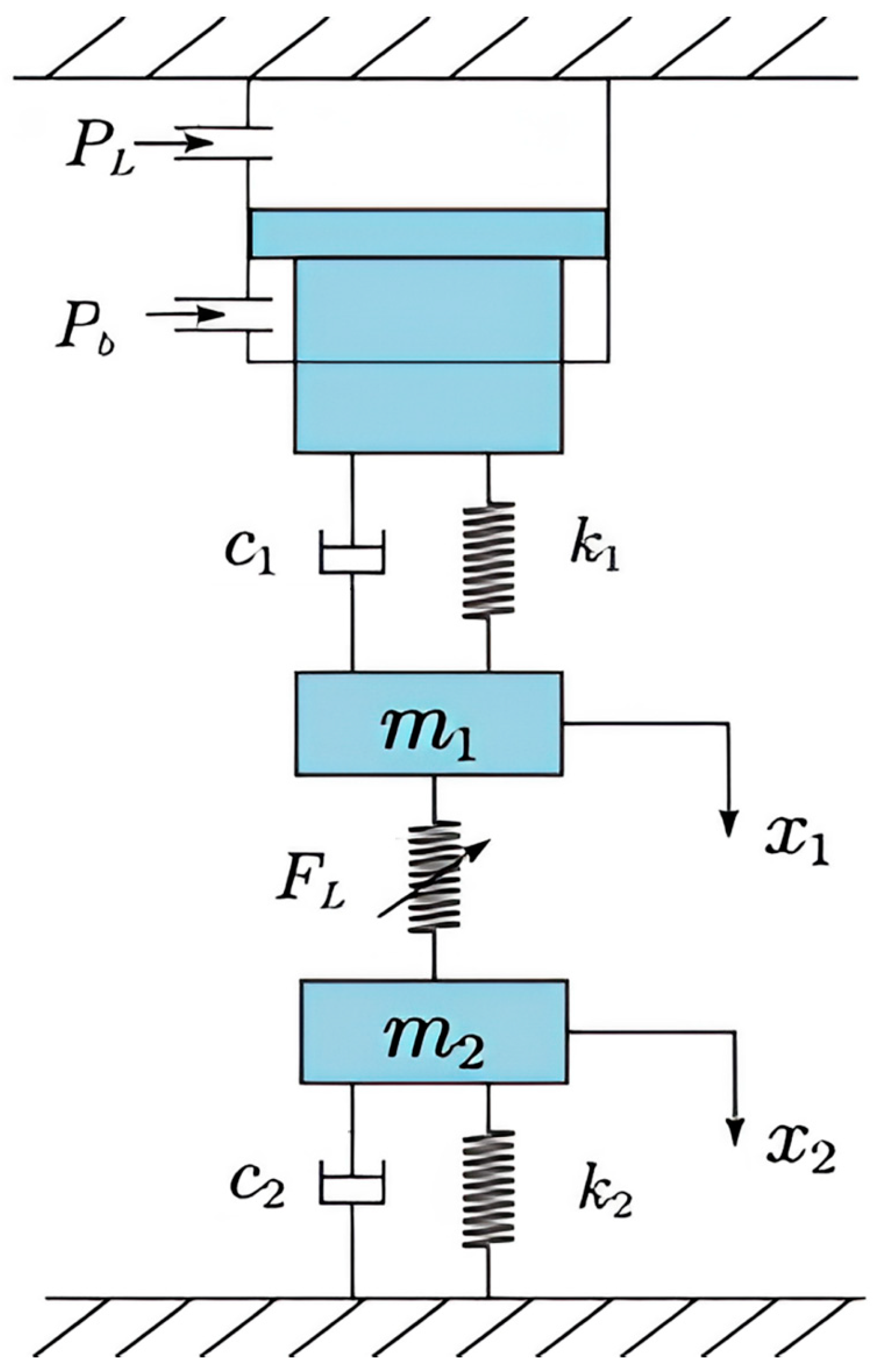
2.1. Mechanical Analysis of Load Vibration of Hydraulic Clamping System
2.2. System Stability Analysis of Hydraulic Floating Clamping Method
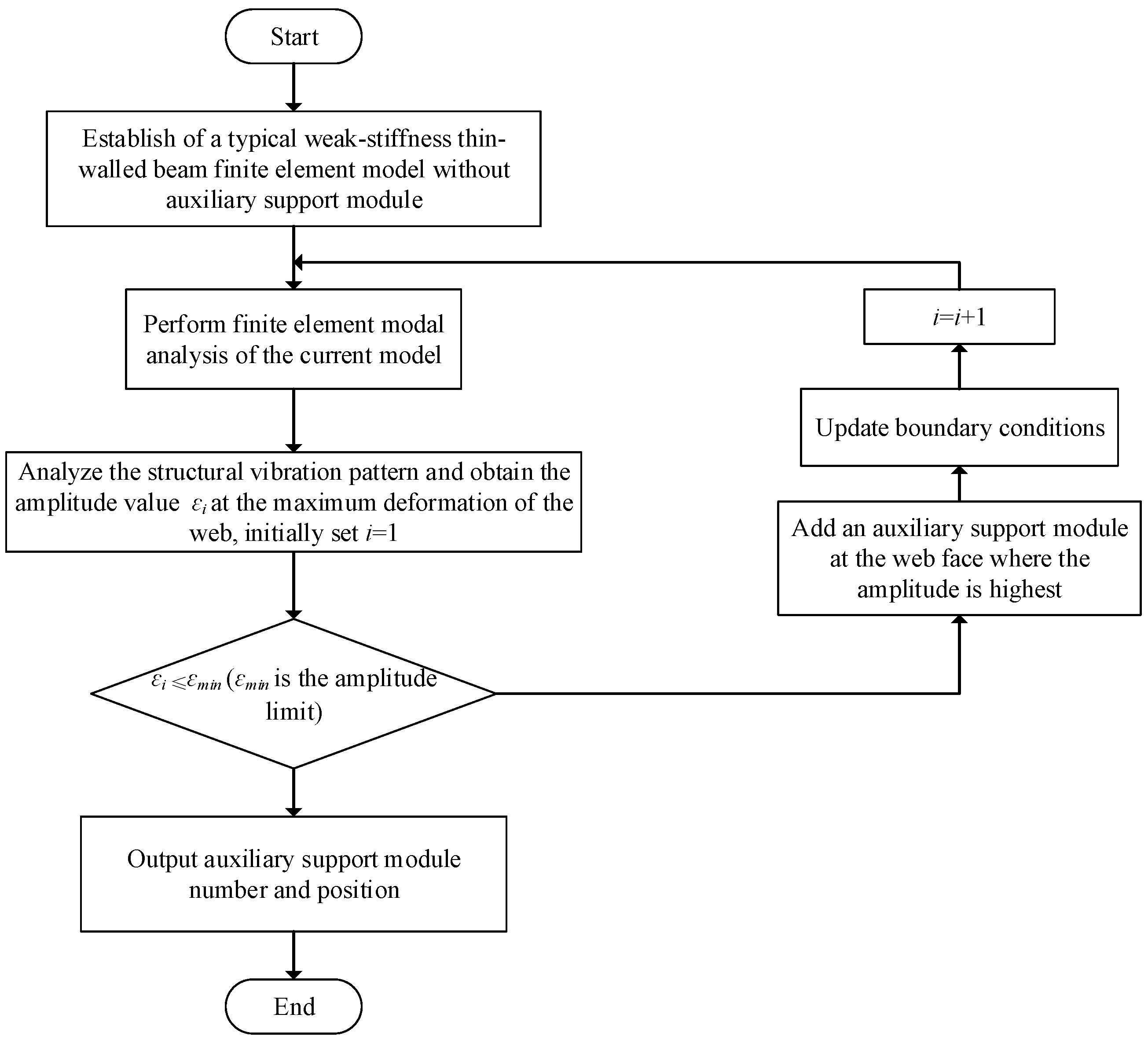
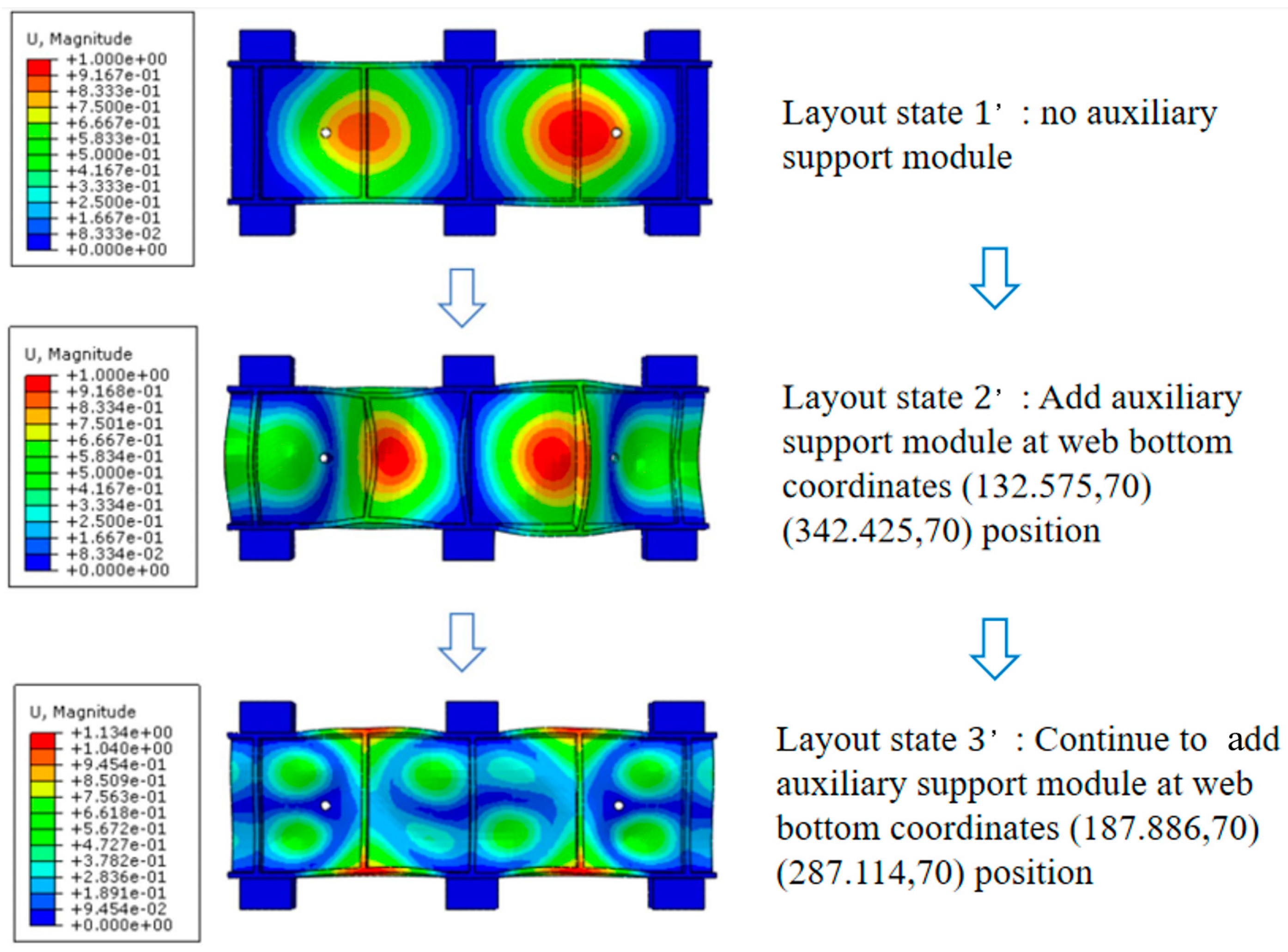
2.3. An Auxiliary Support Module Layout Strategy for Vibration Suppression of Thin-Walled Beams with Weak Stiffness
3. Dynamic Simulation and Experimental Verification of Auxiliary Support Module Layout Design
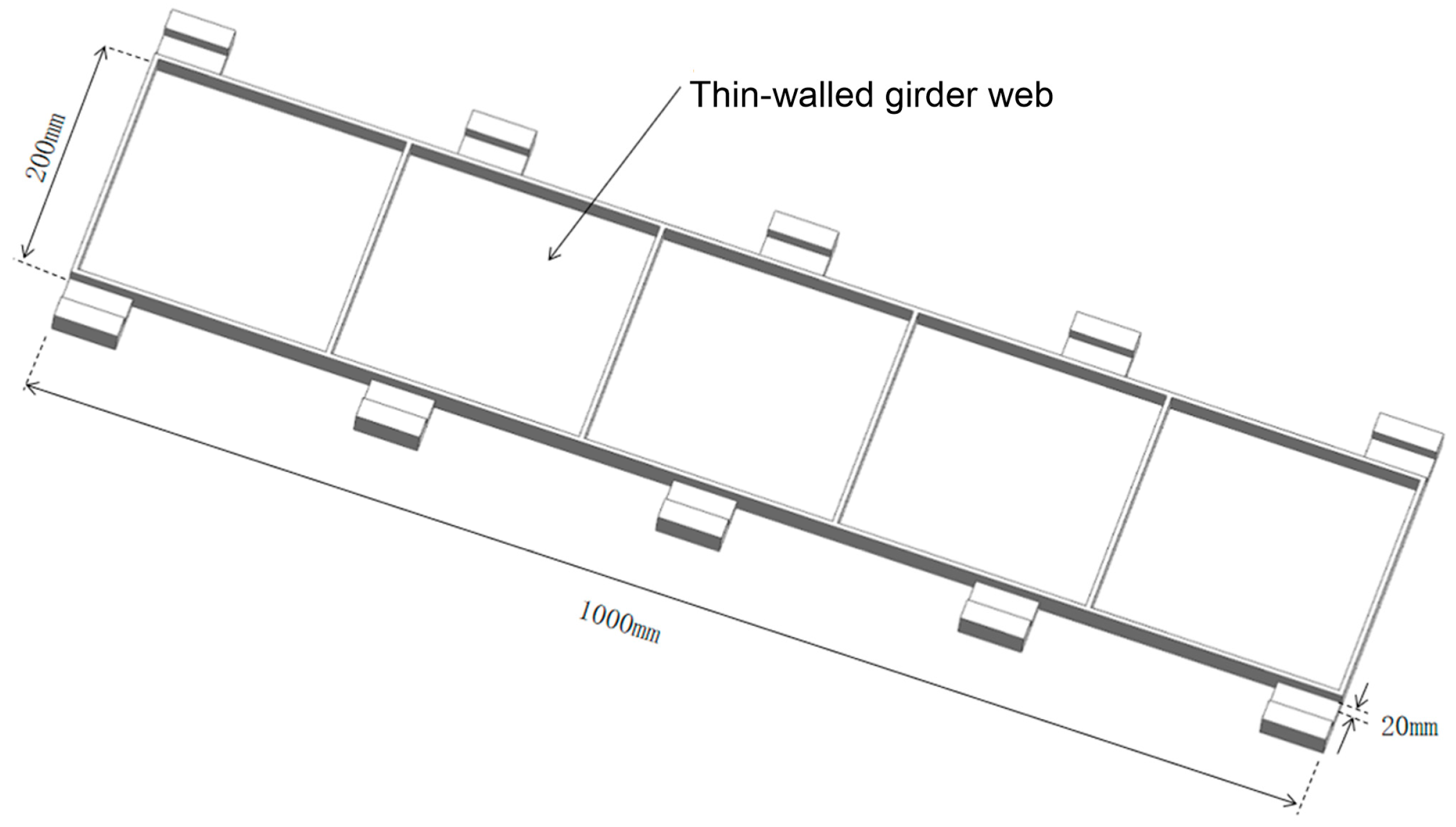
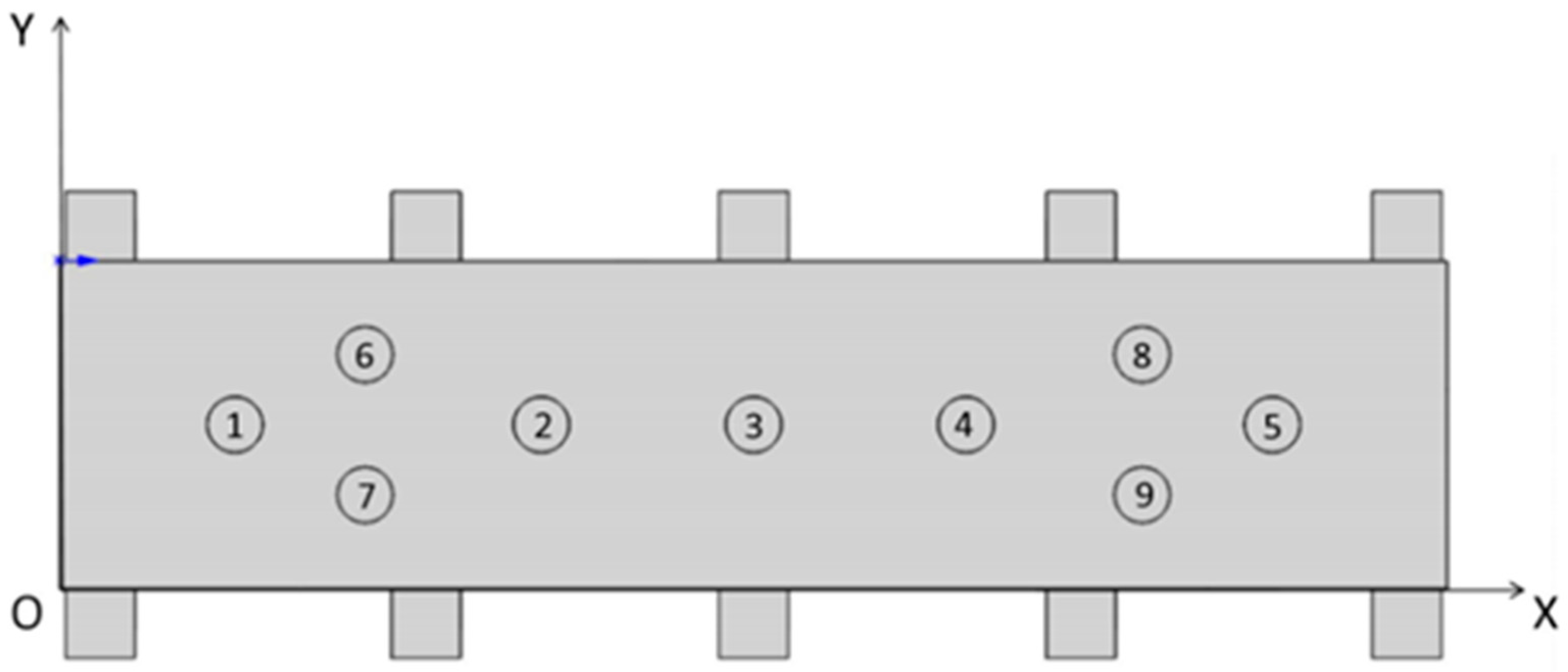
3.1. The Establishment of Simulation Model
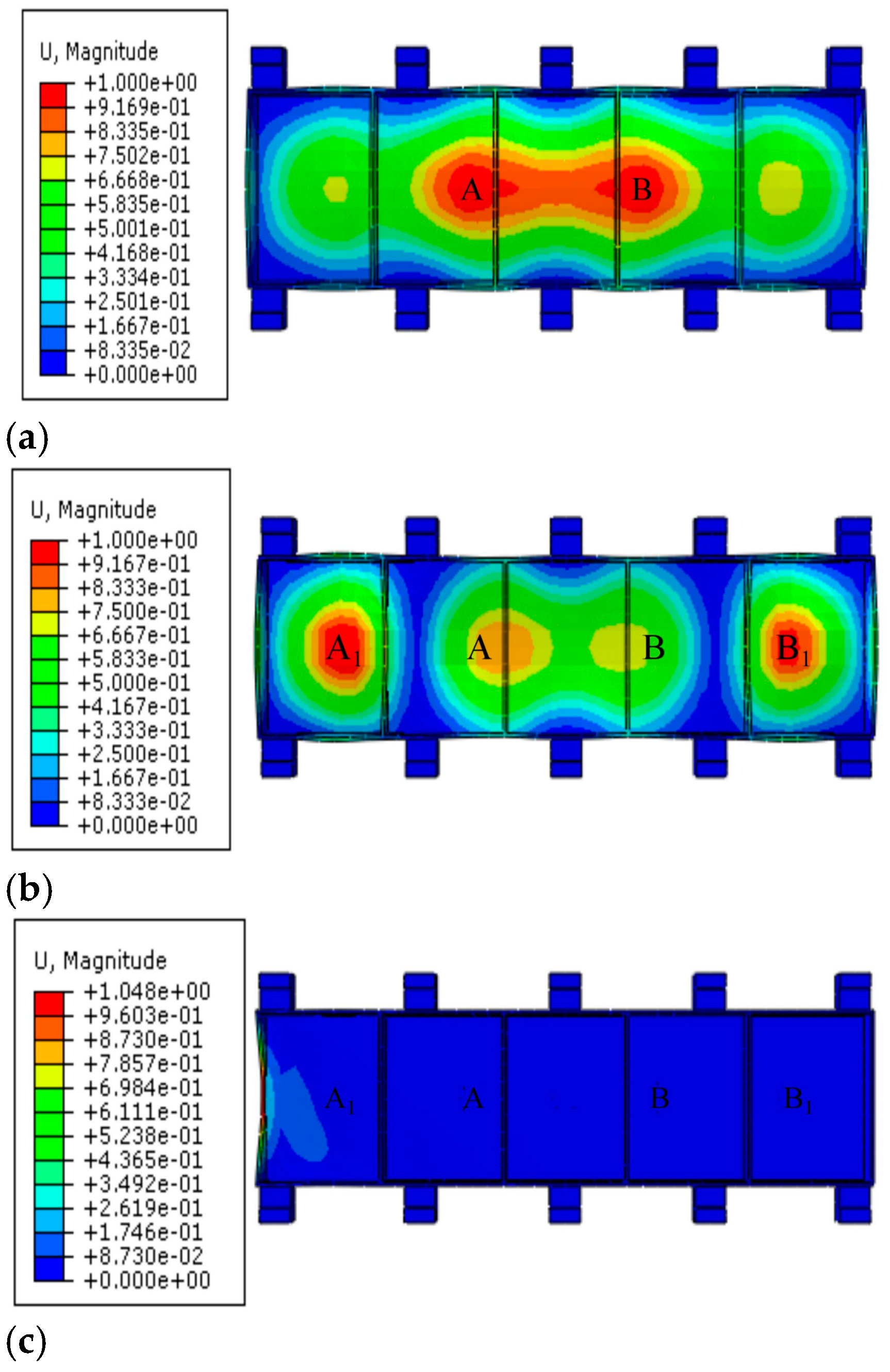
3.2. Analysis of the Simulation Results
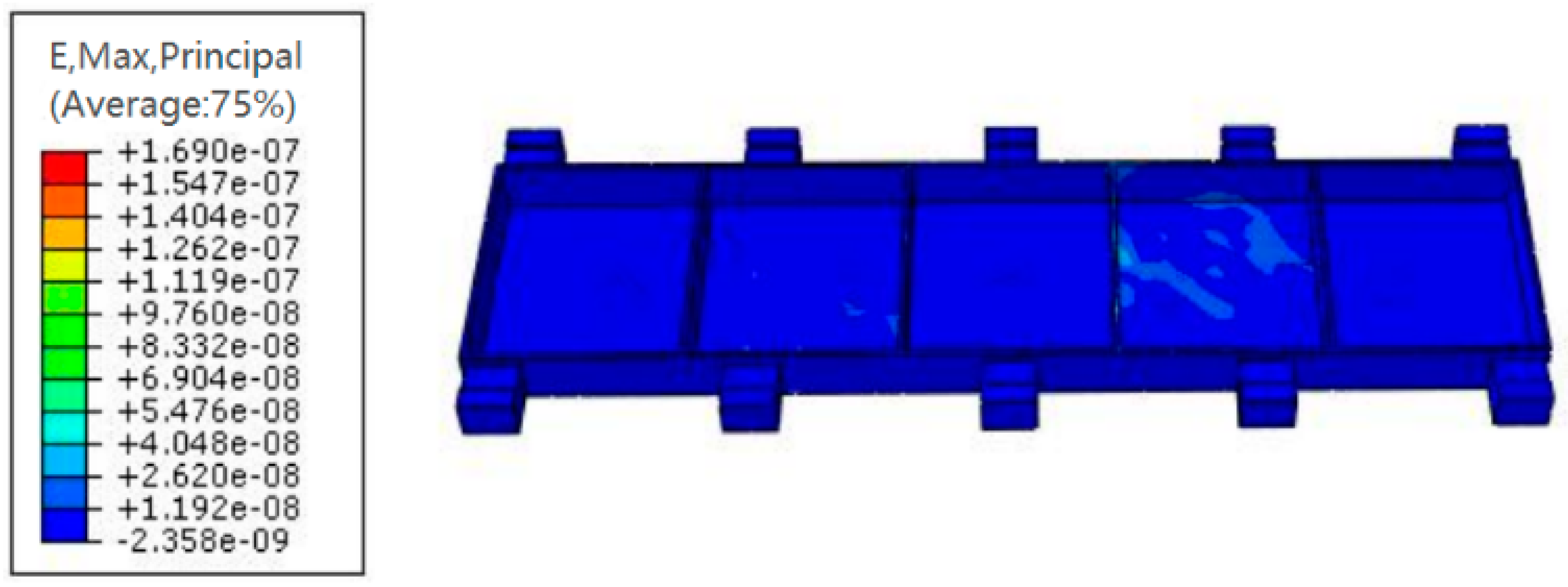
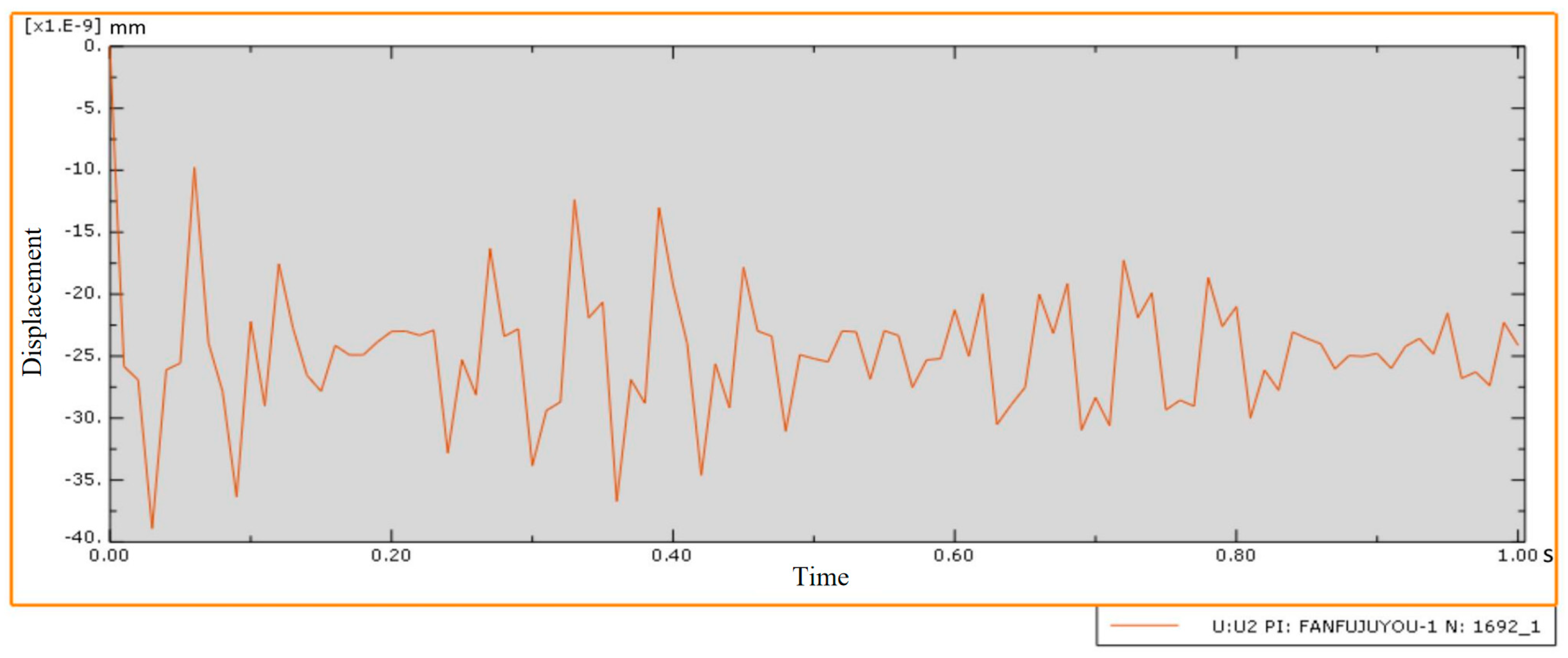
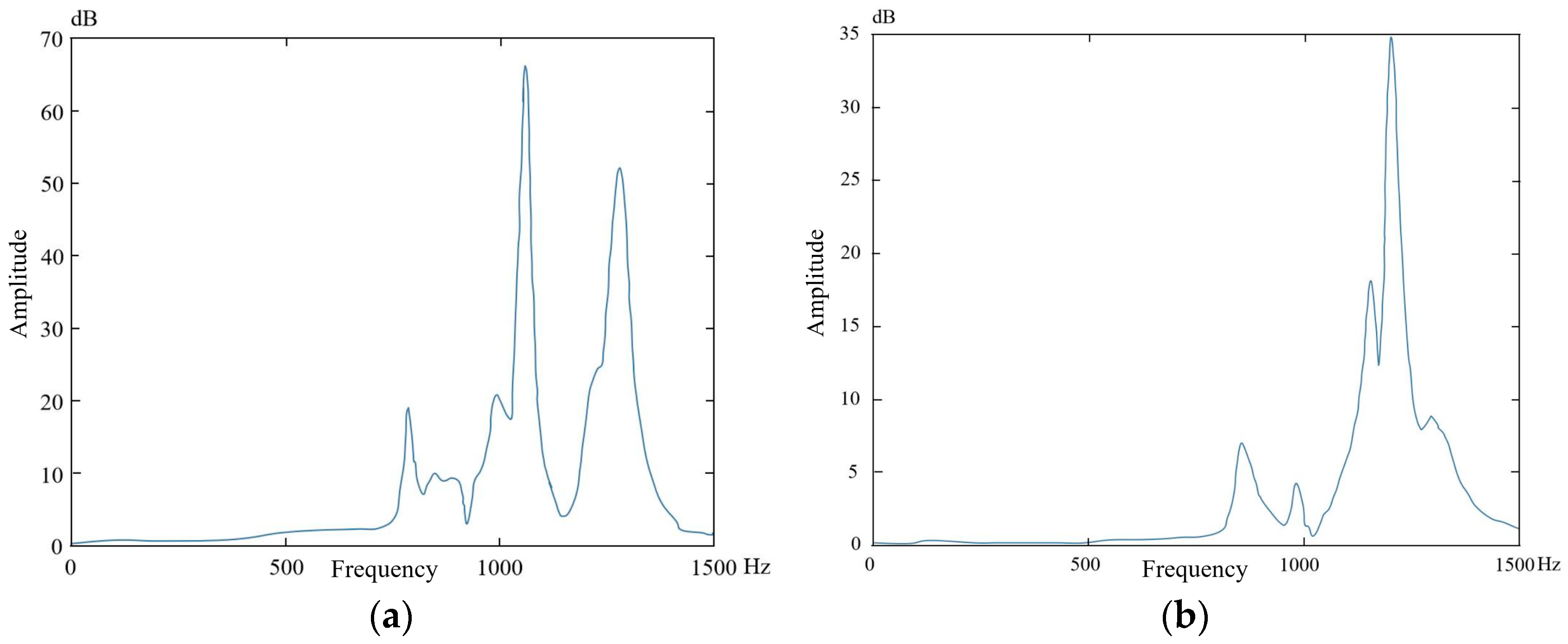
4. Modal Hammering Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Wang, Y. Effect of cryogenic cooling on deformation of milled thin-walled titanium alloy parts. Int. J. Adv. Manuf. Technol. 2022, 122, 3683–3692. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, X.; Chen, T. A review on the simulation and intelligent control of cutting and machining process of difficult-to-machine materials in aerospace. Aerosp. Manuf. Technol. 2023, 66, 14–29. [Google Scholar]
- Staszak, N.; Gajewski, T.; Garbowski, T. Effective Stiffness of Thin-Walled Beams with Local Imperfections. Materials 2022, 15, 7665. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Zhang, Y.; Qiao, H. Milling Mechanism and Chattering Stability of Nickel-Based Superalloy Inconel 718. Materials 2023, 16, 5748. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zheng, M.; Jiang, S.; Zhan, D.; Wang, R. A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts. Machines 2023, 11, 359. [Google Scholar] [CrossRef]
- Ruttanatri, P.; Cole, M.O.T.; Pongvuthithum, R.; Huyanan, S. H-infinity controller design for chatter suppression in machining based on integrated cutting and flexible structure model. Automatica 2021, 130, 109643. [Google Scholar] [CrossRef]
- Du, J.; Long, X. Chatter suppression for milling of thin-walled workpieces based on active modal control. J. Manuf. Process. 2022, 84, 1042–1053. [Google Scholar] [CrossRef]
- Liu, H.-B.; Zhang, H.-Z.; Wang, C.-X.; Miao, H.-H. Vibration suppression of thin-walled parts milling based on additional mass and eddy current damping. Aerosp. Manuf. Technol. 2023, 66, 53–60. [Google Scholar]
- Cai, Y.; Zhang, Z.; Xi, X.; Zhao, D. A Deformation Control Method in Thin-Walled Parts Machining Based on Force and Stiffness Matching Via Cutter Orientation Optimization. J. Manuf. Sci. Eng. 2023, 145, 31007. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, K.; Zhang, J.; Yuan, M.; Wang, X.; Feng, P.; Zhang, M.; Feng, F. Digital modeling-driven chatter suppression for thin-walled part manufacturing. J. Intell. Manuf. 2024, 35, 289–305. [Google Scholar] [CrossRef]
- Wu, Y.; He, Y.; Song, H.-R. A review of research on cutting chatter control of thin-walled parts. Manuf. Technol. Mach. Tools 2021, 11, 49–53. [Google Scholar]
- Shao, L.; Wang, B. Research on vibration control of blade profile machining. Mach. Manuf. 2021, 59, 38–40. [Google Scholar]
- Zheng, Y.; Zhao, Z.; Xu, B.; Yu, Y.; Xu, J. A method to predict chatter stability accurately in milling thin-walled parts by considering force-induced deformation. J. Manuf. Process. 2023, 106, 552–563. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Liu, X.-L.; Li, M.-Y. Intelligent monitoring technology for cutting vibration. J. Mech. Eng. 2020, 56, 1–23. [Google Scholar]
- Liu, Z.-X.; Hu, D.-Z.; Gao, X. Optimization of chatter and cutting parameters for machining thin-walled aerospace magazines. Tool. Technol. 2022, 56, 87–91. [Google Scholar]
- Hou, J.; Wang, B.; Wang, M.; Hao, H. Research on Vibration Evaluation Method for Milling Thin walled Parts. Manuf. Technol. Mach. Tools 2023, 6, 49–54. [Google Scholar]


| (kg/m3) | Young’s Modulus E (Gpa) | Poisson’s Ratio v |
|---|---|---|
| 2800 | 70.3 | 0.33 |
| Degree | Inherent Frequency (Hz) | ||
|---|---|---|---|
| Layout Status 1 | Layout Status 2 | Layout Status 3 | |
| 1 | 1938.2 | 2238.4 | 2290.0 |
| 2 | 2080.6 | 2256.5 | 2895.8 |
| 3 | 2155.3 | 2328.4 | 2911.9 |
| 4 | 2180.5 | 3066.9 | 3066.2 |
| 5 | 2704.8 | 3251.5 | 3363.2 |
| 6 | 2955.1 | 3322.9 | 3420.8 |
| Degree | Inherent Frequency (Hz) | ||
|---|---|---|---|
| Layout Status 1 | Layout Status 2 | Layout Status 3 | |
| 1 | 2115.4 | 2955.3 | 3170.2 |
| 2 | 2133.0 | 3503.5 | 3705.5 |
| 3 | 3512.6 | 3585.2 | 3844.7 |
| 4 | 3570.9 | 3712.1 | 4252.7 |
| 5 | 3642.9 | 4277.7 | 4692.9 |
| 6 | 3681.8 | 4926.7 | 5995.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Gu, Y.; Mu, Z.; Wang, J.; Du, Z.; He, W.; Aw, K.; Yang, Y. Research on the Layout Design of Auxiliary Support Modules for Suppressing Machining Chatter in Thin-Walled Beams. Materials 2025, 18, 1986. https://doi.org/10.3390/ma18091986
Feng J, Gu Y, Mu Z, Wang J, Du Z, He W, Aw K, Yang Y. Research on the Layout Design of Auxiliary Support Modules for Suppressing Machining Chatter in Thin-Walled Beams. Materials. 2025; 18(9):1986. https://doi.org/10.3390/ma18091986
Chicago/Turabian StyleFeng, Junping, Yifei Gu, Zhuang Mu, Jiawei Wang, Zongyang Du, Wenbo He, Kean Aw, and Yinfei Yang. 2025. "Research on the Layout Design of Auxiliary Support Modules for Suppressing Machining Chatter in Thin-Walled Beams" Materials 18, no. 9: 1986. https://doi.org/10.3390/ma18091986
APA StyleFeng, J., Gu, Y., Mu, Z., Wang, J., Du, Z., He, W., Aw, K., & Yang, Y. (2025). Research on the Layout Design of Auxiliary Support Modules for Suppressing Machining Chatter in Thin-Walled Beams. Materials, 18(9), 1986. https://doi.org/10.3390/ma18091986








