The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics
Abstract
:1. Introduction
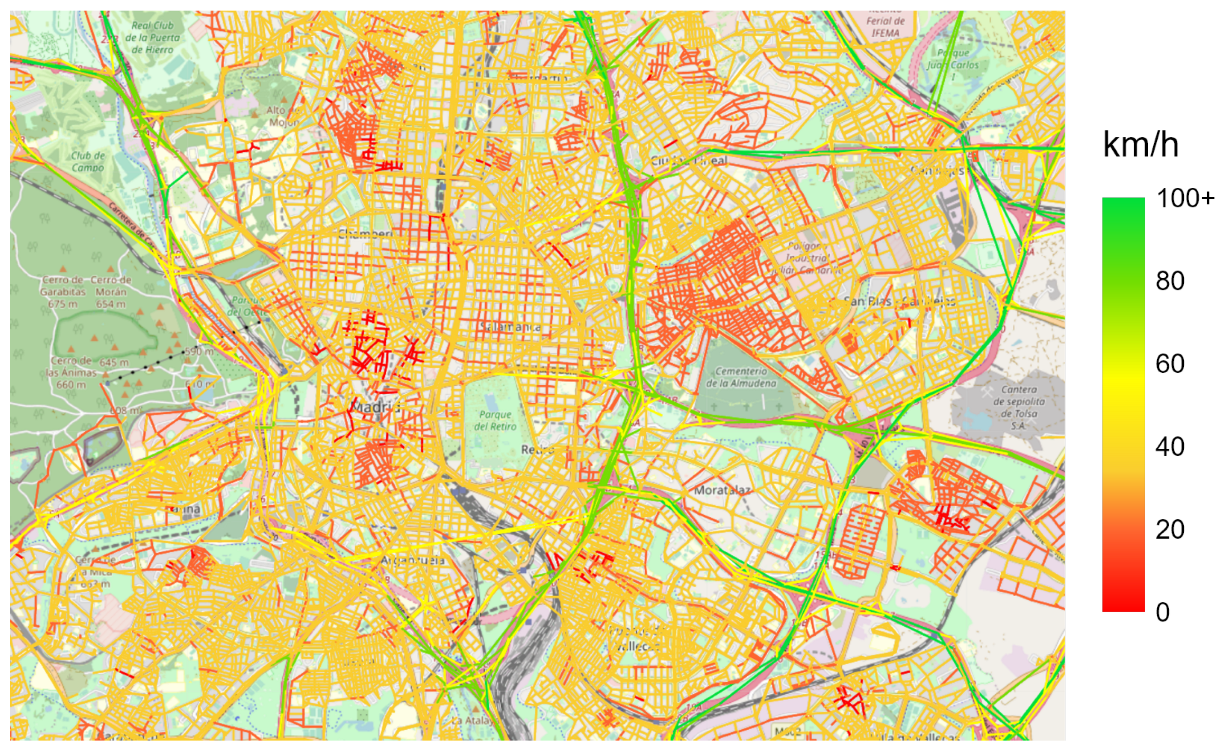
2. Data Acquisition and Integration
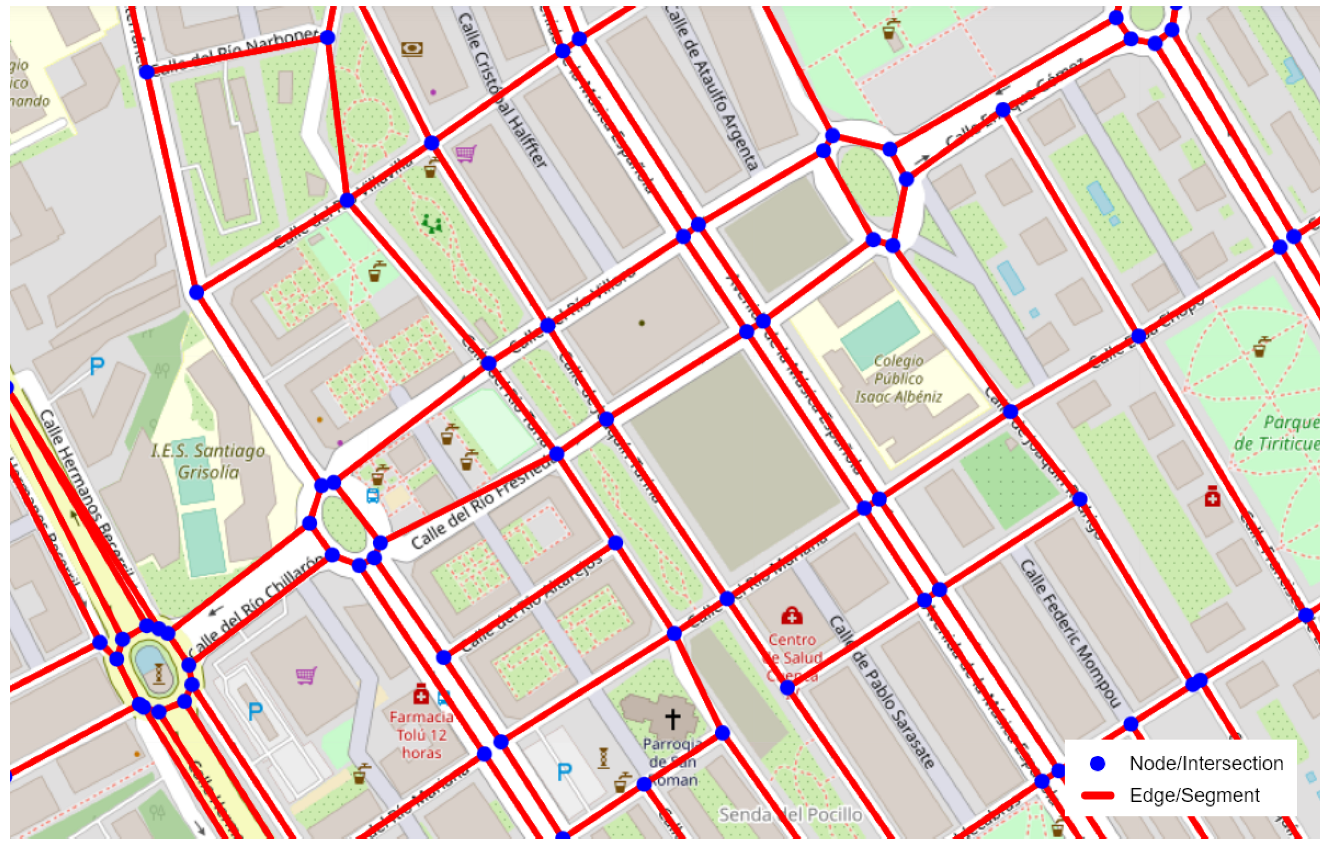
2.1. Construction of the City Graph
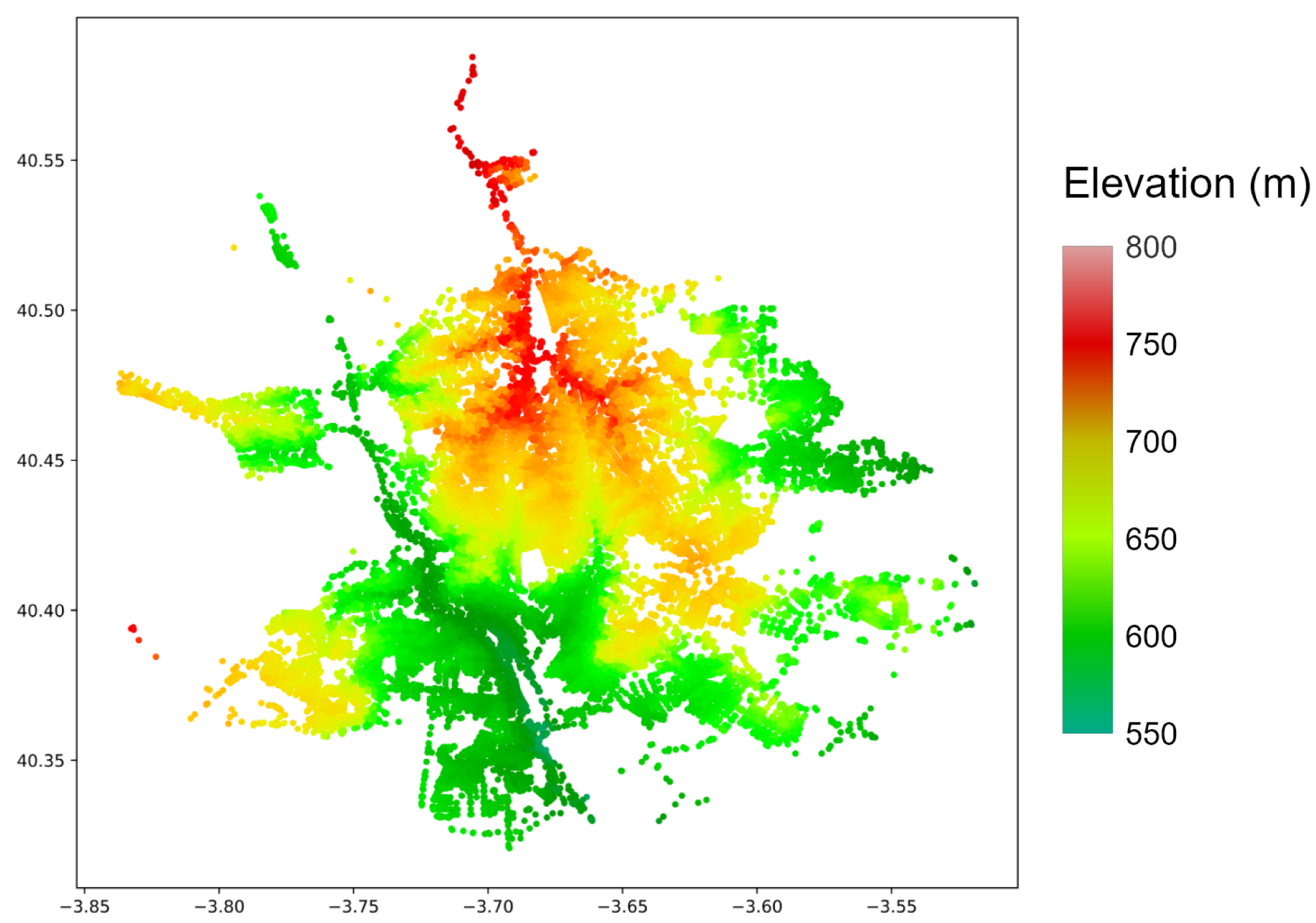
2.2. Integration of Elevation Data
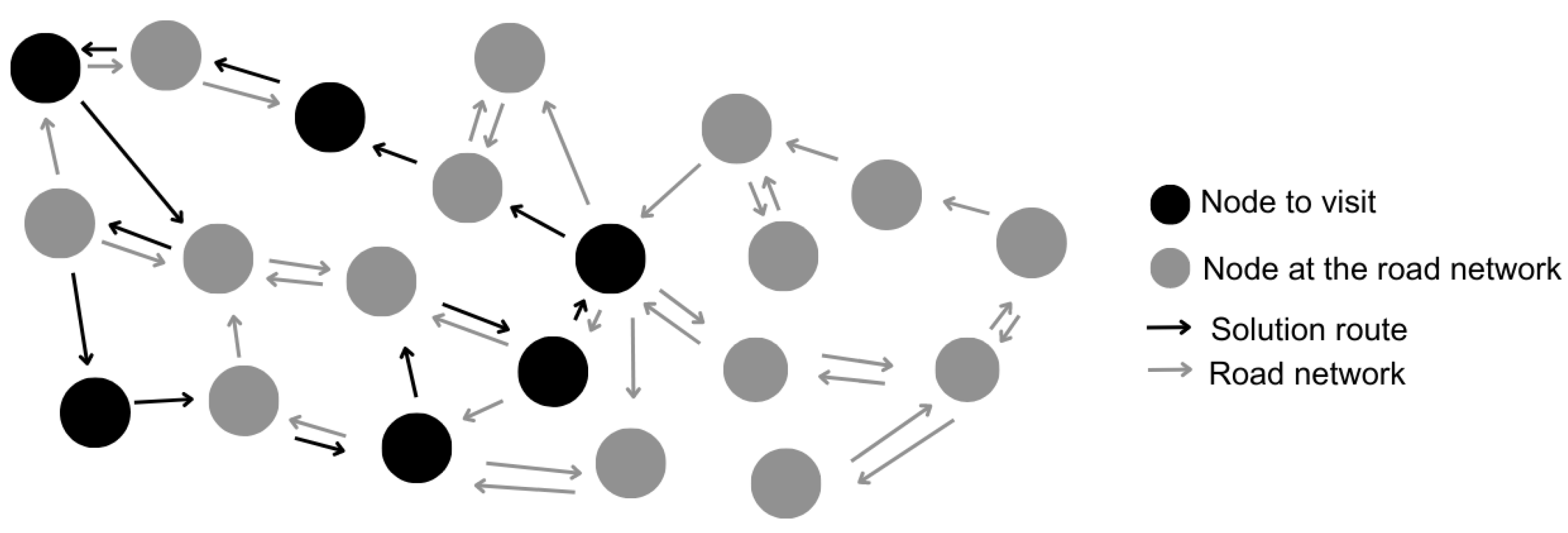
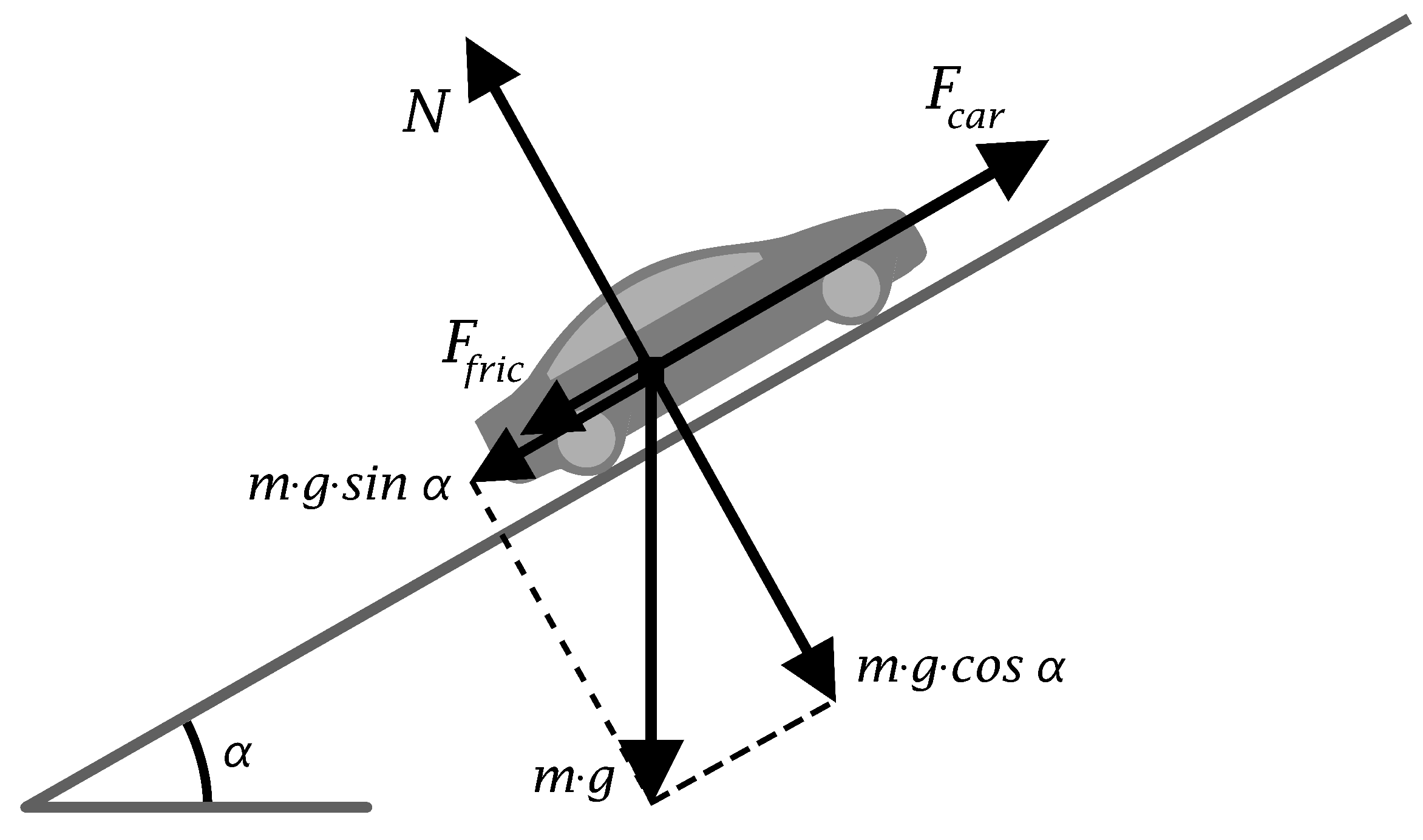
3. Problem Formalization
| Algorithm 1: Electric STSP Algorithm for Energy-Efficient City Touring. |
 |
4. Algorithm Implementation
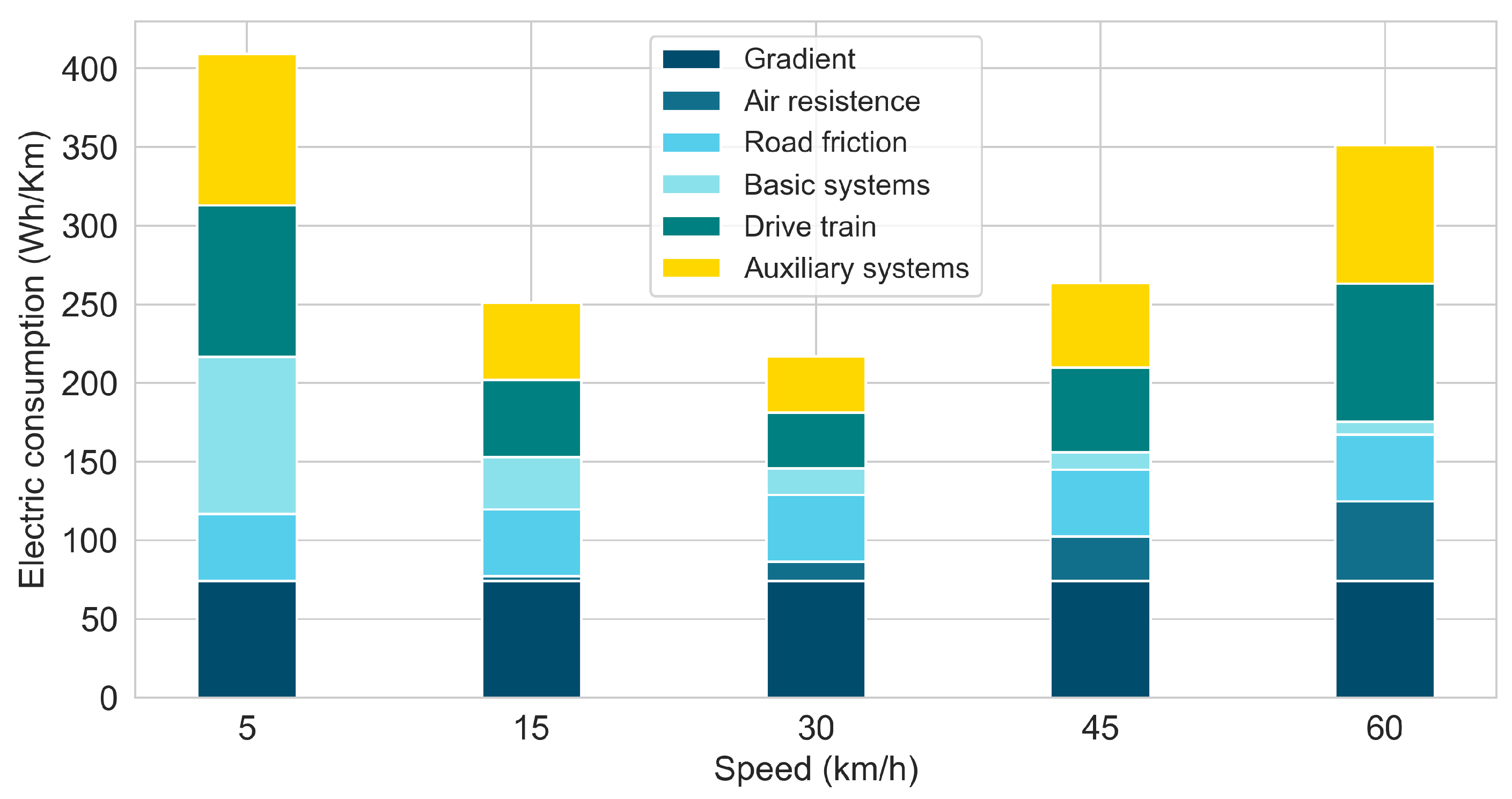
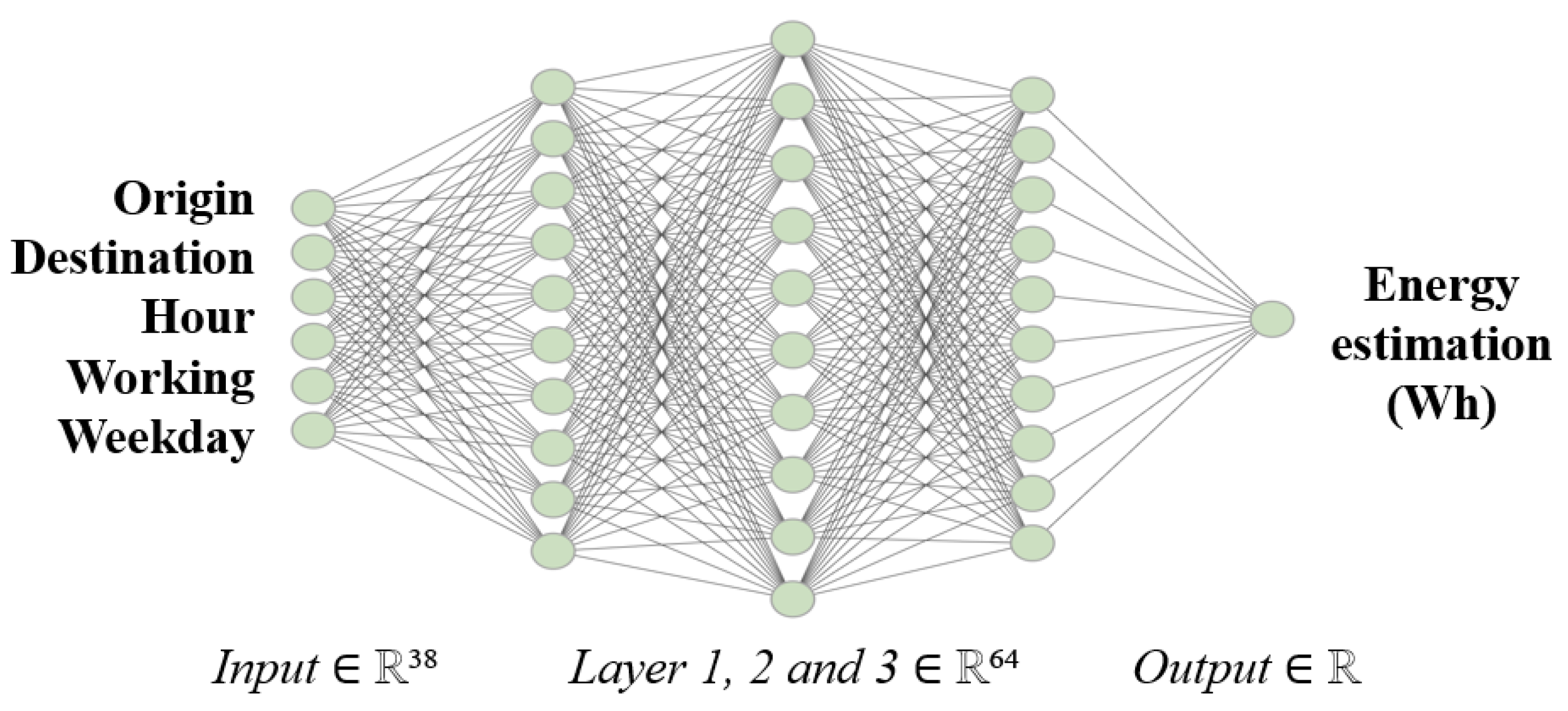
4.1. Estimation of the Energy Consumption through an ANN
4.2. 2-Opt with Nearest Neighbors
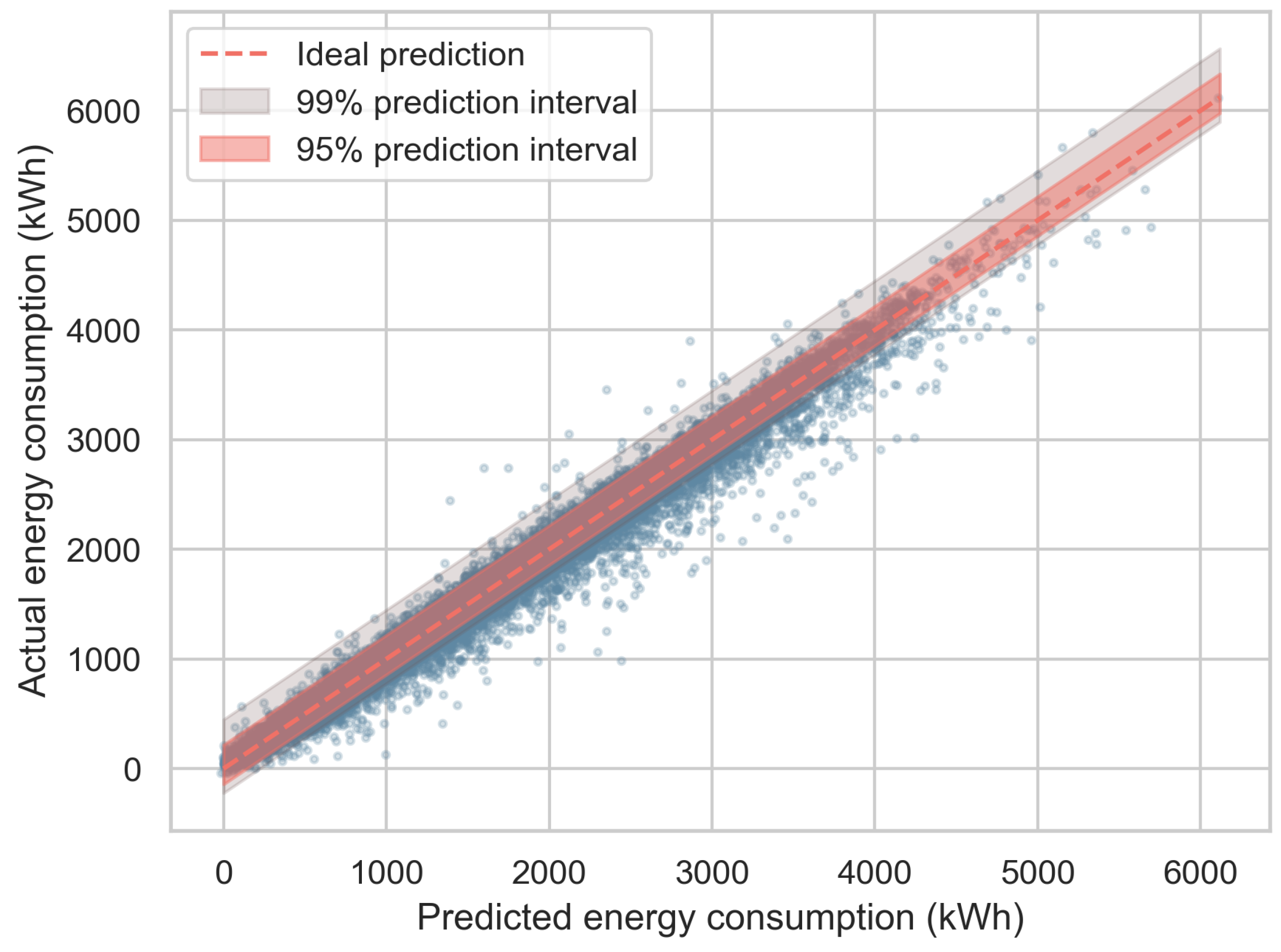
4.3. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| NN | Nearest Neighbor |
| ANN | Artificial Neural Network |
| DEM | Digital Elevation Model |
| TSP | Traveling Salesman Problem |
| STSP | Steiner Traveling Salesman Problem |
| EV-TSP | Electric Vehicle Traveling Salesman Problem |
| EV-STSP | Electric Vehicle Steiner Traveling Salesman Problem |
References
- Basso, R.; Kulcsár, B.; Egardt, B.; Lindroth, P.; Sanchez-Diaz, I. Energy consumption estimation integrated into the electric vehicle routing problem. Transp. Res. D-Transp. Environ. 2019, 69, 141–167. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Trasnp. Res. B-Meth. 2019, 126, 225–255. [Google Scholar] [CrossRef]
- Conejero, J.; Jordán, C.; Sanabria-Codesal, E. An iterative algorithm for the management of an electric car-rental service. J. Appl. Math. 2014, 2014, 483734. [Google Scholar] [CrossRef]
- Conejero, J.; Jordán, C.; Sanabria-Codesal, E. An algorithm for self-organization of driverless vehicles of a car-rental service. Nonlinear Dyn. 2016, 84, 107–114. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Lin, Y.; Tang, T. Electric vehicle’s electricity consumption on a road with different slope. Phys. A 2014, 402, 41–48. [Google Scholar] [CrossRef]
- Graser, A.; Asamer, J.; Dragaschnig, M. How to reduce range anxiety? The impact of digital elevation model quality on energy estimates for electric vehicles. In GI Forum 2014. Geospatial Innovation for Society; Vogler, R., Car, A., Strobl, J., Griesebner, G., Eds.; Wichmann Verl. der Österr. Akad. der Wiss.: Berlin, Germany, 2014; pp. 165–174. [Google Scholar]
- Graser, A.; Asamer, J.; Ponweiser, W. The elevation factor: Digital elevation model quality and sampling impacts on electric vehicle energy estimation errors. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, GA, USA, 3–5 June 2015; pp. 81–86. [Google Scholar]
- Evtimov, I.; Ivanov, R.; Sapundjiev, M. Energy consumption of auxiliary systems of electric cars. MATEC Web Conf. 2017, 133, 06002. [Google Scholar] [CrossRef]
- Muren; Wu, J.; Zhou, L.; Du, Z.; Lv, Y. Mixed steepest descent algorithm for the traveling salesman problem and application in air logistics. Transp. Res. E-Log. 2019, 126, 87–102. [Google Scholar] [CrossRef]
- Baniasadi, P.; Foumani, M.; Smith-Miles, K.; Ejov, V. A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Oper. Res. 2020, 285, 444–457. [Google Scholar] [CrossRef]
- Bay, M.; Limbourg, S. TSP model for electric vehicle deliveries, considering speed, loading and road grades. In Proceedings of the Sixth International Workshop on Freight Transportation and Logistics (ODYSSEUS 2015), Ajaccio, France, 31 May–5 June 2015. [Google Scholar]
- Applegate, D.; Bixby, R.; Chvatál, V.; Cook, W. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Roberti, R.; Wen, M. The electric traveling salesman problem with time windows. Transp. Res. E-Log. 2016, 89, 32–52. [Google Scholar] [CrossRef]
- Doppstadt, C.; Koberstein, A.; Vigo, D. The hybrid electric vehicle–traveling salesman problem. Eur. J. Oper. Res. 2016, 253, 825–842. [Google Scholar] [CrossRef]
- Murakami, K. Formulation and algorithms for route planning problem of plug-in hybrid electric vehicles. Oper. Res. 2018, 18, 497–519. [Google Scholar] [CrossRef]
- Ünal, V.; Soysal, M.; Çimen, M.; Koç, Ç. Dynamic routing optimization with electric vehicles under stochastic battery depletion. Transp. Lett. 2022, in press. [Google Scholar] [CrossRef]
- Baum, M.; Dibbelt, J.; Pajor, T.; Sauer, J.; Wagner, D.; Zündorf, T. Energy-optimal routes for battery electric vehicles. Algorithmica 2020, 82, 1490–1546. [Google Scholar] [CrossRef]
- Rokbani, N.; Kumar, R.; Abraham, A.; Alimi, A.M.; Long, H.V.; Priyadarshini, I.; Son, L. Bi-heuristic ant colony optimization-based approaches for traveling salesman problem. Soft Comput. 2021, 25, 3775–3794. [Google Scholar] [CrossRef]
- Qi, X.; Wu, G.; Boriboonsomsin, K.; Barth, M. Data-driven decomposition analysis and estimation of link-level electric vehicle energy consumption under real-world traffic conditions. Transp. Res. D-Transp. Environ. 2018, 64, 36–52. [Google Scholar] [CrossRef]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Ford, L., Jr. Network Flow Theory; Technical Report; Rand Corp: Santa Monica, CA, USA, 1956. [Google Scholar]
- Jindal, I.; Chen, X.; Nokleby, M.; Ye, J. A unified neural network approach for estimating travel time and distance for a taxi trip. arXiv 2017, arXiv:1710.04350. [Google Scholar]
- Dijkstra, E. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Association for Computing Machinery: New York, NY, USA, 2022; pp. 287–290. [Google Scholar]
- Ahsini, Y.; Díaz-Masa, P.; Inglés, B.; Rubio, A.; Martínez, A.; Magraner, A.; Conejero, J. The electric vehicle travelling salesman problem on digital elevation models for traffic-aware urban logistics Supplementary material. Zenodo 2023. [Google Scholar] [CrossRef]
- Boeing, G. OSMNX: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Centro Nacional de Informción Geográfica. Download Center. Available online: https://centrodedescargas.cnig.es/CentroDescargas/index.jsp (accessed on 1 August 2023).
- NASA. Shuttle Radar Topography Mission (SRTM). 2023. Available online: https://www2.jpl.nasa.gov/srtm/ (accessed on 1 August 2023).
- Open Data Madrid. Madrid’s Historic Traffic Data. 2023. Available online: https://datos.madrid.es (accessed on 1 August 2023).
- Rodriguez Pereira, J.; Fernandez, E.; Laporte, G.; Benavent, E.; Martinez-Sykora, A. The Steiner traveling salesman problem and its extensions. Eur. J. Oper. Res. 2019, 278, 615–628. [Google Scholar] [CrossRef]
- Castaneda, J.; Ghorbani, E.; Ammouriova, M.; Panadero, J.; Juan, A. Optimizing transport logistics under uncertainty with simheuristics: Concepts, review and trends. Logistics 2022, 6, 42. [Google Scholar] [CrossRef]
- Juan, A.; Keenan, P.; Martí, R.; McGarraghy, S.; Panadero, J.; Carroll, P.; Oliva, D. A review of the role of heuristics in stochastic optimisation: From metaheuristics to learnheuristics. Ann. Oper. Res. 2023, 320, 831–861. [Google Scholar] [CrossRef]
- Croes, G. A method for solving traveling-salesman problems. Oper. Res. 1958, 6, 791–812. [Google Scholar] [CrossRef]
- Nuraiman, D.; Ilahi, F.; Dewi, Y.; Hamidi, E.A. A new hybrid method based on nearest neighbor algorithm and 2-OPT algorithm for traveling salesman problem. In Proceedings of the 2018 4th International Conference on Wireless and Telematics (ICWT), Nusa Dua, Bali, 12–13 July 2018; pp. 1–4. [Google Scholar]
- Agarap, A. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yao, Y.; Rosasco, L.; Caponnetto, A. On early stopping in gradient descent learning. Constr. Approx. 2007, 26, 289–315. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant colony optimization for traveling salesman problem based on parameters optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Kizilateş, G.; Nuriyeva, F. On the nearest neighbor algorithms for the traveling salesman problem. In Advances in Computational Science, Engineering and Information Technology, Proceedings of the Third International Conference on Computational Science, Engineering and Information Technology (CCSEIT-2013), Konya, Turkey, 7–9 June 2013; Springer: Cham, Switzerland, 2013; pp. 111–118. [Google Scholar]
- Mohammed, M.; Abd Ghani, M.; Hamed, R.; Mostafa, S.; Ibrahim, D.; Jameel, H.; Alallah, A. Solving vehicle routing problem by using improved K-nearest neighbor algorithm for best solution. J. Comput. Sci. 2017, 21, 232–240. [Google Scholar] [CrossRef]
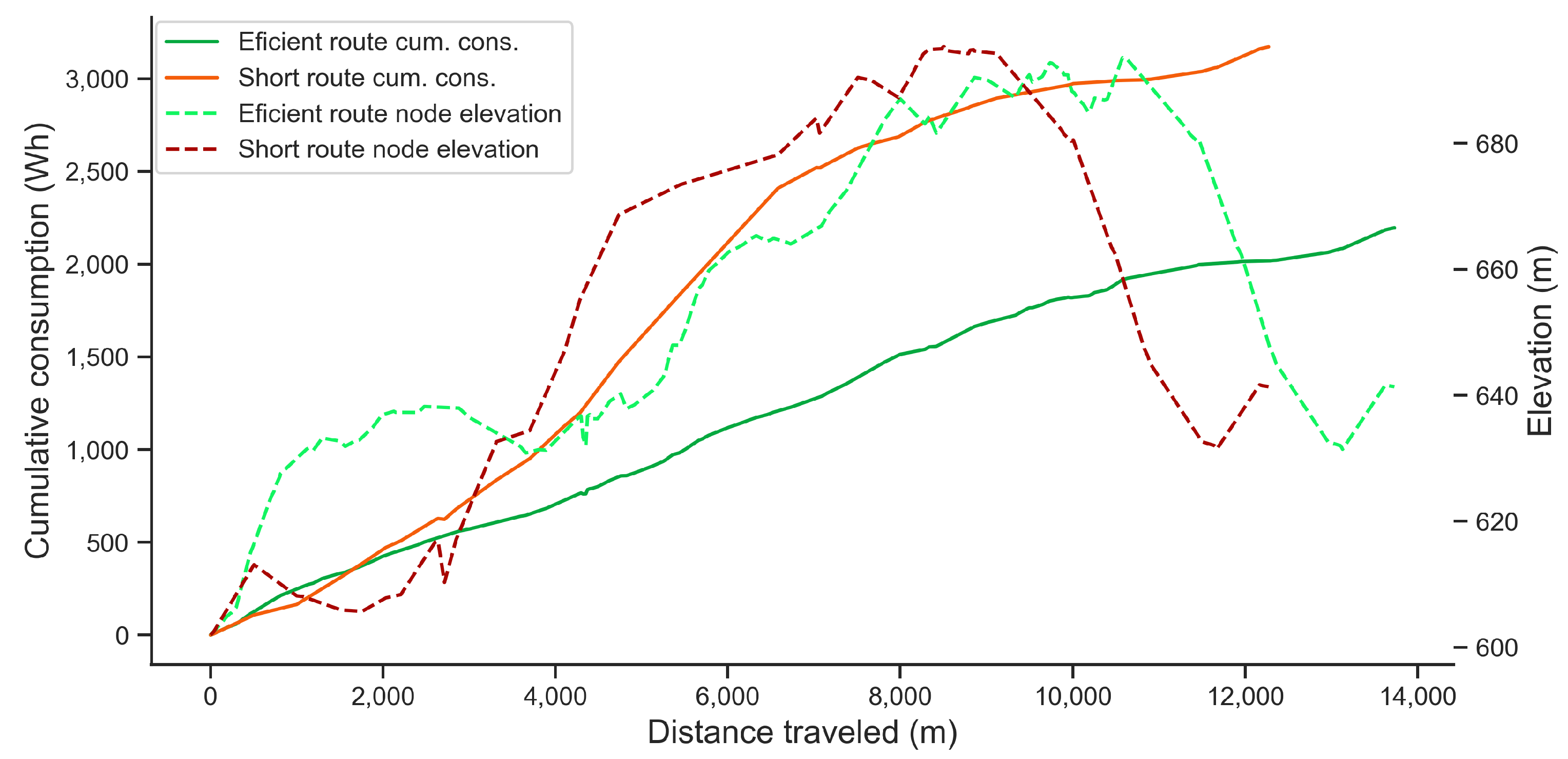
| Bellman–Ford | ANN | Difference | |
|---|---|---|---|
| Average energy consumption (kWh) | 10.966 | 10.969 | 0.0205% |
| Average execution time (s) | 19.25 | 2.25 | −88.28% |
| Madrid5 | Madrid10 | Madrid15 | ||||
|---|---|---|---|---|---|---|
| Energy | Distance | Energy | Distance | Energy | Distance | |
| Travel distance (km) | 44.19 | 41.2 | 69.73 | 64.22 | 89.23 | 83.51 |
| Travel time (min) | 63.99 | 50.15 | 99.57 | 78.38 | 126.24 | 101.53 |
| Average speed (km/h) | 41.43 | 49.29 | 42.02 | 49.16 | 42.38 | 49.35 |
| Energy consumption (kWh) | 6.72 | 8.24 | 10.71 | 12.92 | 13.83 | 16.67 |
| Energy efficiency (km/kWh) | 6.58 | 5 | 6.5 | 4.97 | 6.45 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahsini, Y.; Díaz-Masa, P.; Inglés, B.; Rubio, A.; Martínez, A.; Magraner, A.; Conejero, J.A. The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics. Algorithms 2023, 16, 402. https://doi.org/10.3390/a16090402
Ahsini Y, Díaz-Masa P, Inglés B, Rubio A, Martínez A, Magraner A, Conejero JA. The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics. Algorithms. 2023; 16(9):402. https://doi.org/10.3390/a16090402
Chicago/Turabian StyleAhsini, Yusef, Pablo Díaz-Masa, Belén Inglés, Ana Rubio, Alba Martínez, Aina Magraner, and J. Alberto Conejero. 2023. "The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics" Algorithms 16, no. 9: 402. https://doi.org/10.3390/a16090402
APA StyleAhsini, Y., Díaz-Masa, P., Inglés, B., Rubio, A., Martínez, A., Magraner, A., & Conejero, J. A. (2023). The Electric Vehicle Traveling Salesman Problem on Digital Elevation Models for Traffic-Aware Urban Logistics. Algorithms, 16(9), 402. https://doi.org/10.3390/a16090402










