Advanced Fault Detection in Power Transformers Using Improved Wavelet Analysis and LSTM Networks Considering Current Transformer Saturation and Uncertainties
Abstract
:1. Introduction
1.1. Research Importance
1.2. Research Literature Review
1.3. Shortcoming of Previous Research
- Dependence on Time Domain Features:
- -
- Susceptibility to Noise: Features extracted from the differential current in the time domain can be highly sensitive to noise [3].
- Intelligent Techniques for Internal Fault Detection
- -
- Artificial Neural Networks:
- -
- Support Vector Machines:
- Signal Analysis Tools
- -
- Wavelet Transform:
- -
- -
- -
- S-Transform:
- -
- Shortcomings of Harmonic Blocking and Restraint Techniques
- -
- Harmonic Restraint:
- -
- Low Security: Often lacks security when dealing with inrush currents that have low harmonic content [21].
- -
- Unexpected Blocking: Can unexpectedly block the relay during the energization of a faulty transformer, especially with high harmonics in healthy phases [21].
- -
- Harmonic Cross-Blocking:
- -
- Low Reliability: Exhibits low reliability during the energization of a faulty transformer [21].
- -
- -
- Modern Transformers:
- -
- Low Harmonic Ratios: Modern power transformers may exhibit very low second harmonic ratios during energization, challenging harmonic-based methods [21].
- Challenges with New Techniques
- -
- Artificial Intelligence and Signal Processing Methods:
- -
- -
- -
- -
- Machine Learning Algorithms:
- -
- Advanced Signal Processing Techniques:
- -
- Hybrid Approaches:
1.4. Research Contribution
- Introduction of Advanced Feature Extraction:
- ○
- Utilizes wavelet transform analysis to derive novel features from the differential current, significantly enhancing fault detection accuracy.
- Integration with Deep Learning for Real-Time Application
- ○
- Implements long short-term memory (LSTM) networks for training, thereby boosting the system’s capability to accurately identify internal transformer faults in real time.
- ○
- Comprehensive Fault Detection:
- ○
- Integrates differential current amplitude and bias current in the detection process, resulting in a more robust and reliable fault detection mechanism.
- Consideration of CT Saturation and Measurement Uncertainty
- ○
- Addresses the challenges posed by CT saturation and measurement uncertainties, often overlooked in traditional methods.
- Improved Relay Operations
- ○
- Mitigates issues caused by even harmonics and DC components during CT saturation, thereby reducing the likelihood of incorrect relay activations.
- Enhanced Reliability and Security
- ○
- Demonstrates superior performance in detecting internal faults in power transformers, even under challenging conditions such as CT saturation.
1.5. Research Structure
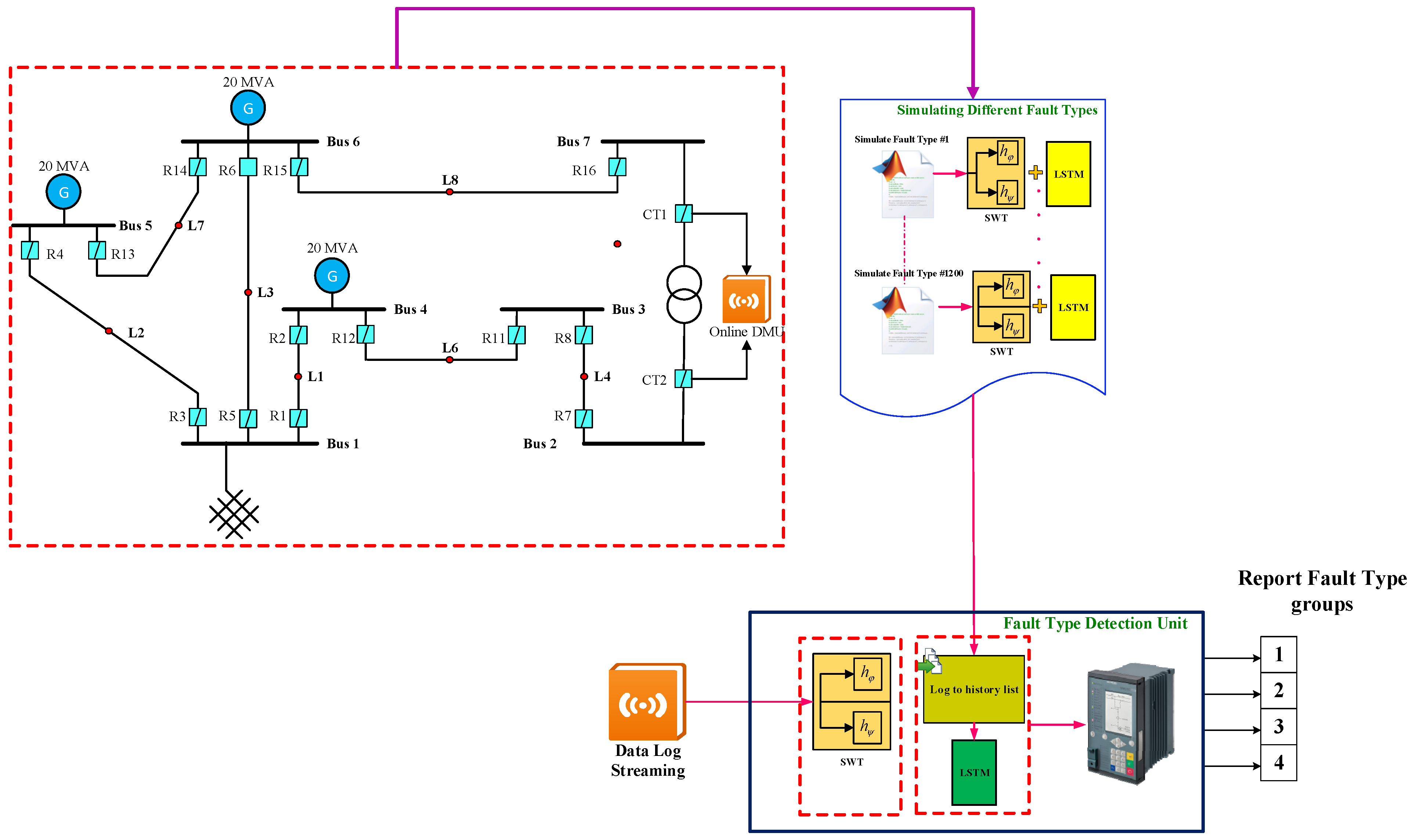
2. Conceptual Model and Problem Procedure
| Algorithm 1. Procedure of the Proposed Framework for Internal Fault Detection in Power Transformers |
| 1. Training Stage: |
| 1.1. For k = 1:2000 |
| 1.2. If k ≤ 500 |
| 1.3. Run the Simulation file for sampling the differential currents of external fault |
| 1.4. SignalVector = Differential currents of external fault |
| 1.5. ElseIf 500 < k ≤ 1000 |
| 1.6. Run the Simulation file for sampling the differential currents of inrush current |
| 1.7. SignalVector = Differential currents of inrush current |
| 1.8. ElseIf 1000 < k ≤ 1500 |
| 1.9. Run the Simulation file for sampling the differential currents of internal fault without CT saturation |
| 1.10. SignalVector = Differential currents of inrush current internal fault without CT saturation |
| 1.11. ElseIf 1500 < k ≤ 2000 |
| 1.12. Run the Simulation file for sampling the differential currents of internal fault with CT saturation |
| SignalVector = Differential currents of inrush current internal fault with CT saturation |
| 1.13. Call the Improved RTBSWT Function () |
|
|
| 1.14. End Call RTBSWT Function |
| 1.15. Call Proposed LSTM Network Function |
| |
| 1.16. End LSTM Function |
| 1.17. End for (K = 2000) |
| 2. Test and Verification Stage |
| 2.1. Call an unknown differential current (, ) |
| 2.2. Call the Improved RTBSWT Function () 2.3. Feature selection of using the 1.13.1 and 1.13.2 |
| 2.4. End Call RTBSWT Function |
| 2.5. Call Proposed LSTM Network Function |
| 2.6. = predict the signal type using the trained LSTM Network |
| 2.7. End LSTM Function |
| 2.8. Calculate the RSME (, ) |
| 2.9. End Stage 2 |
3. Problem Statement and Mathematical Formulation
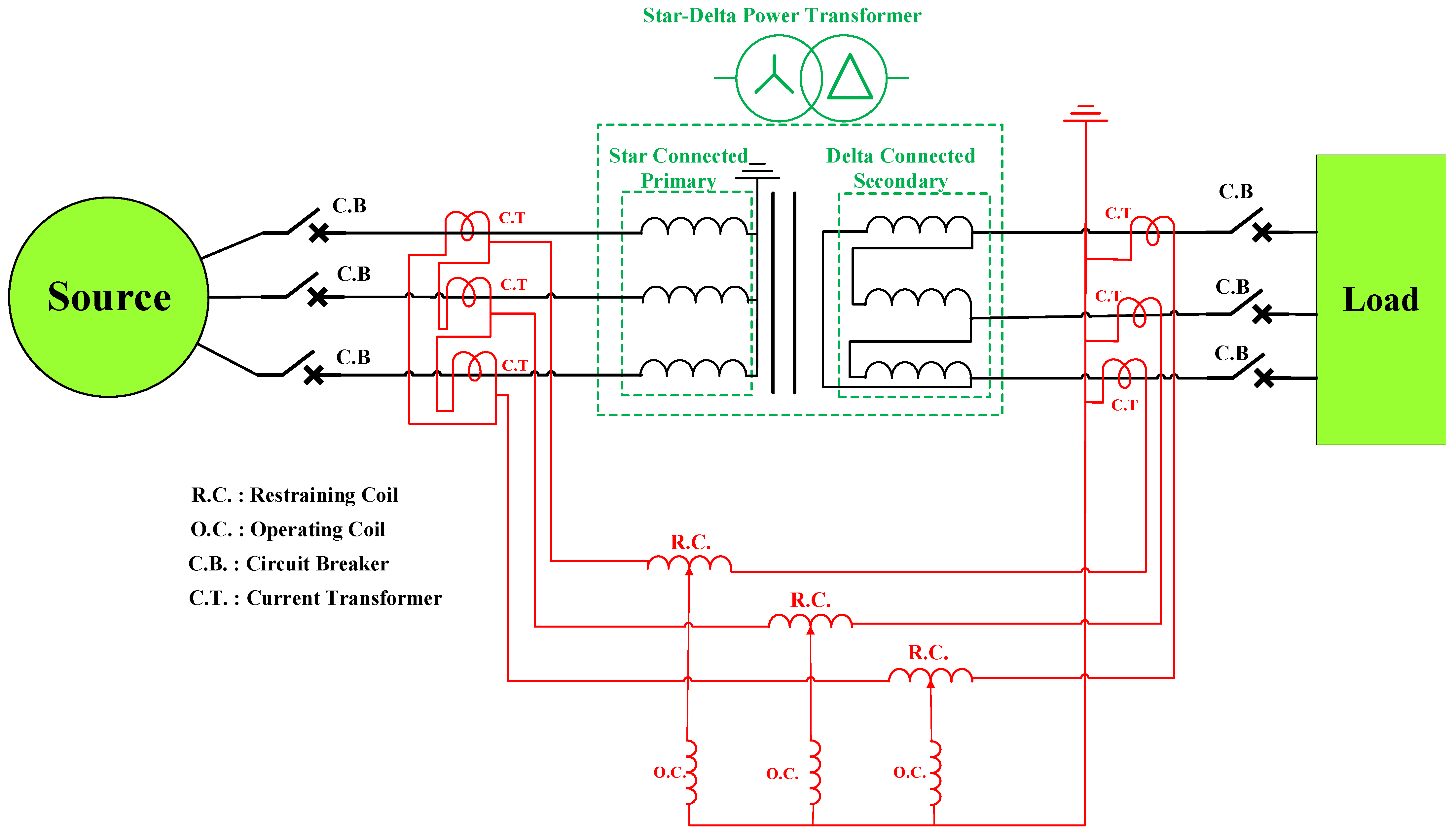
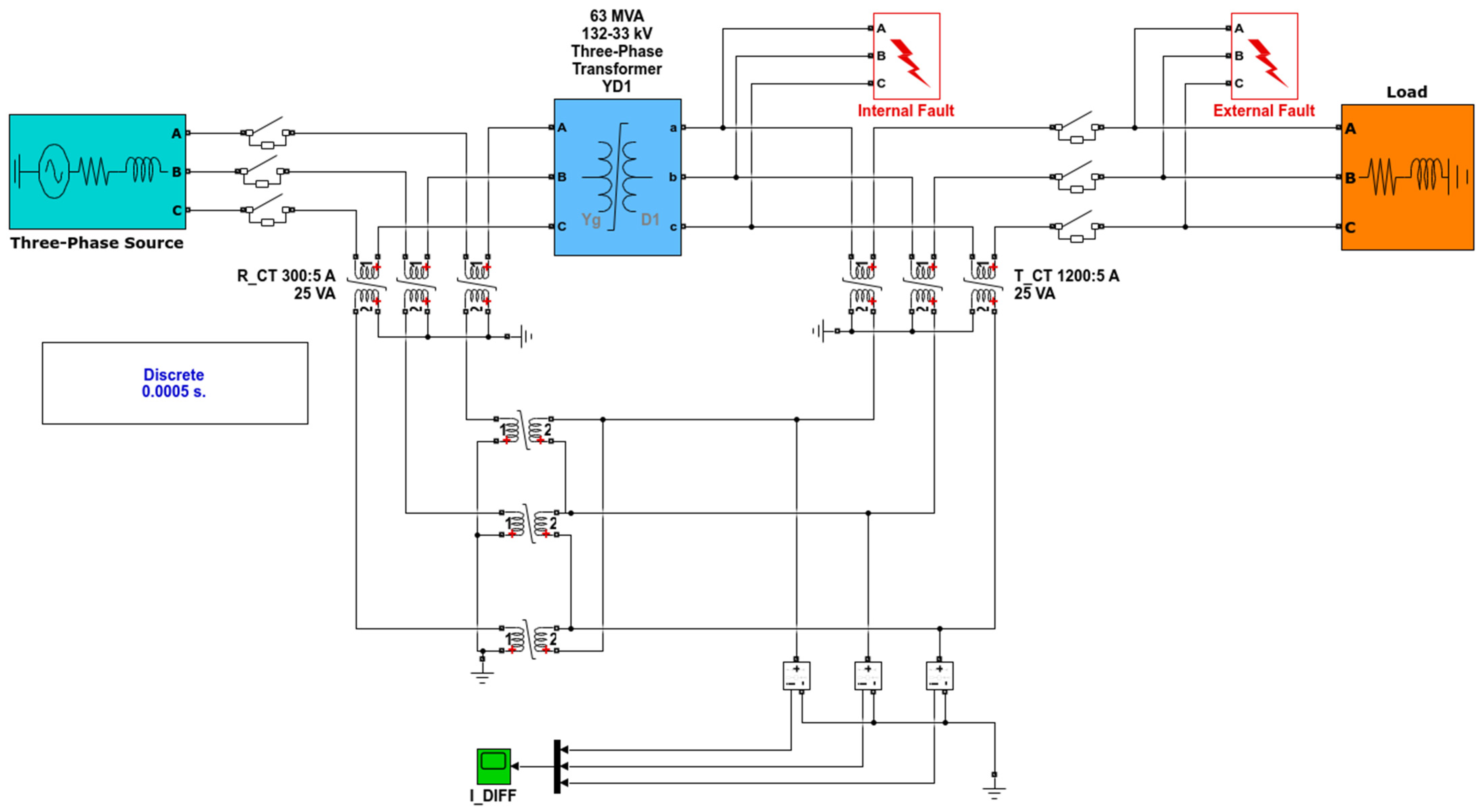
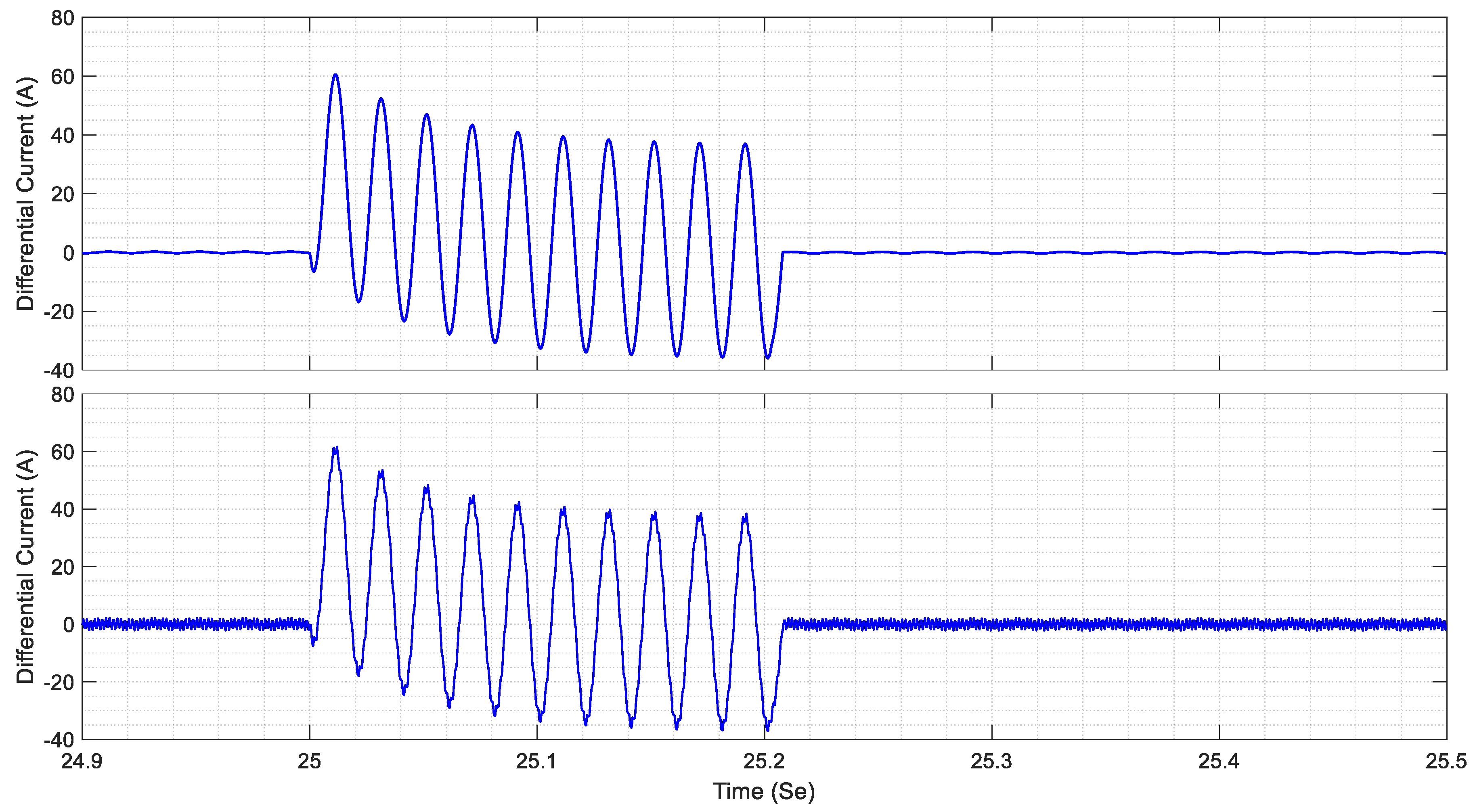
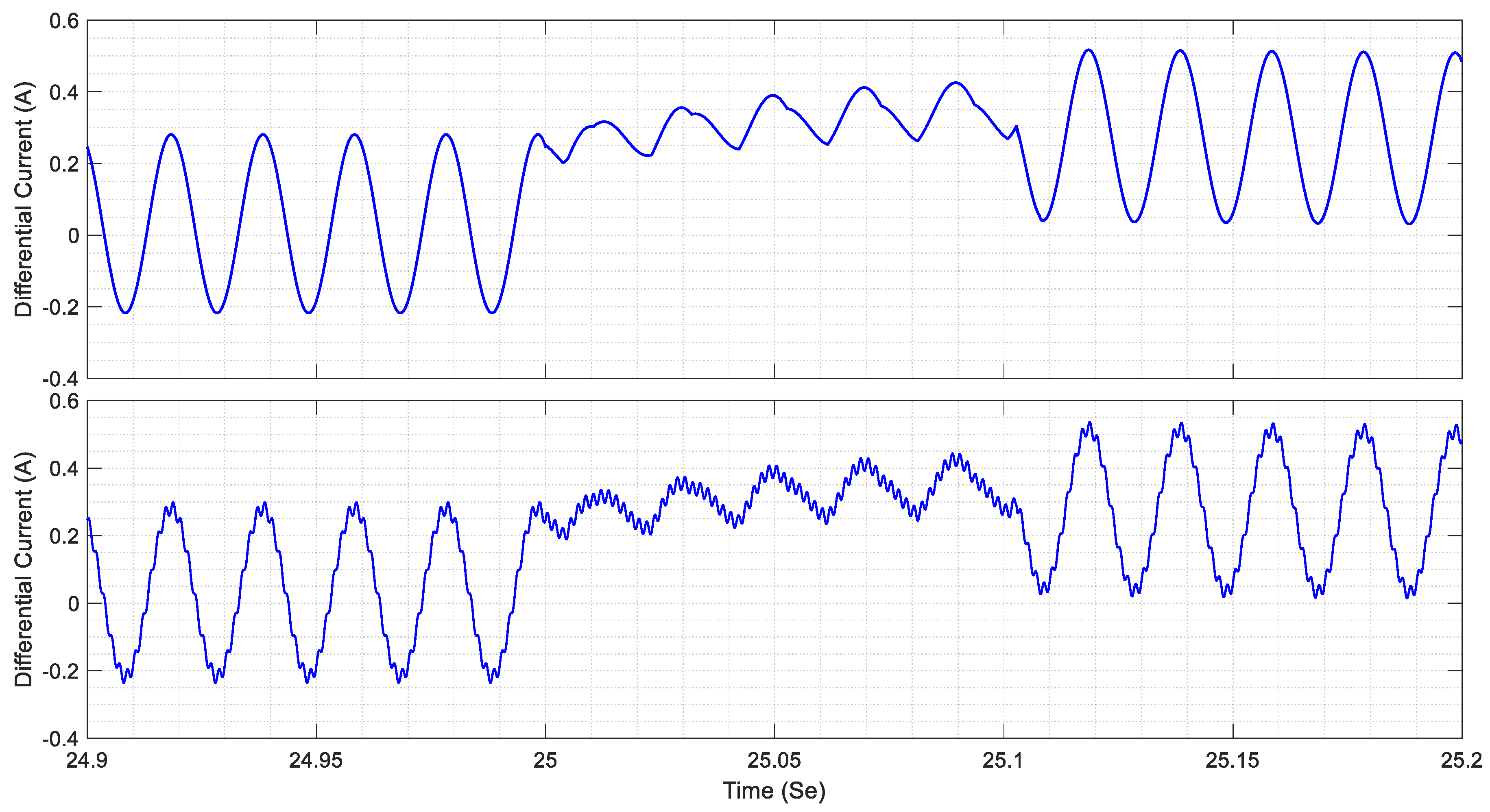
3.1. Structure of Differential Current Measuring
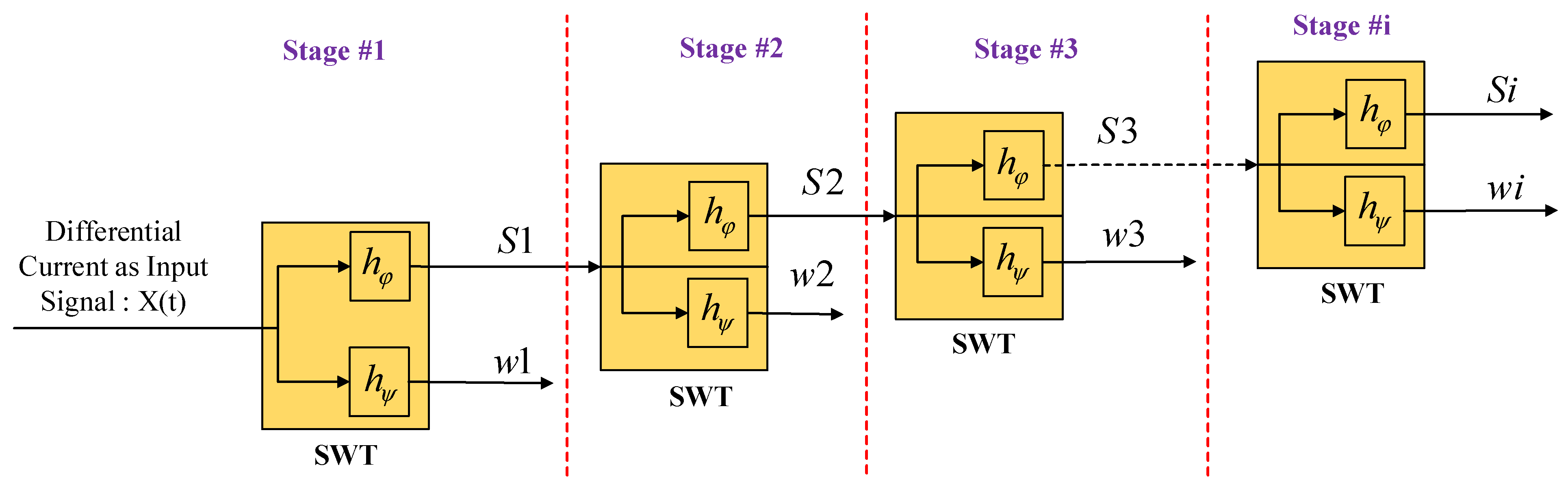
3.2. Wavelet Transform (Stationary State)—SWT
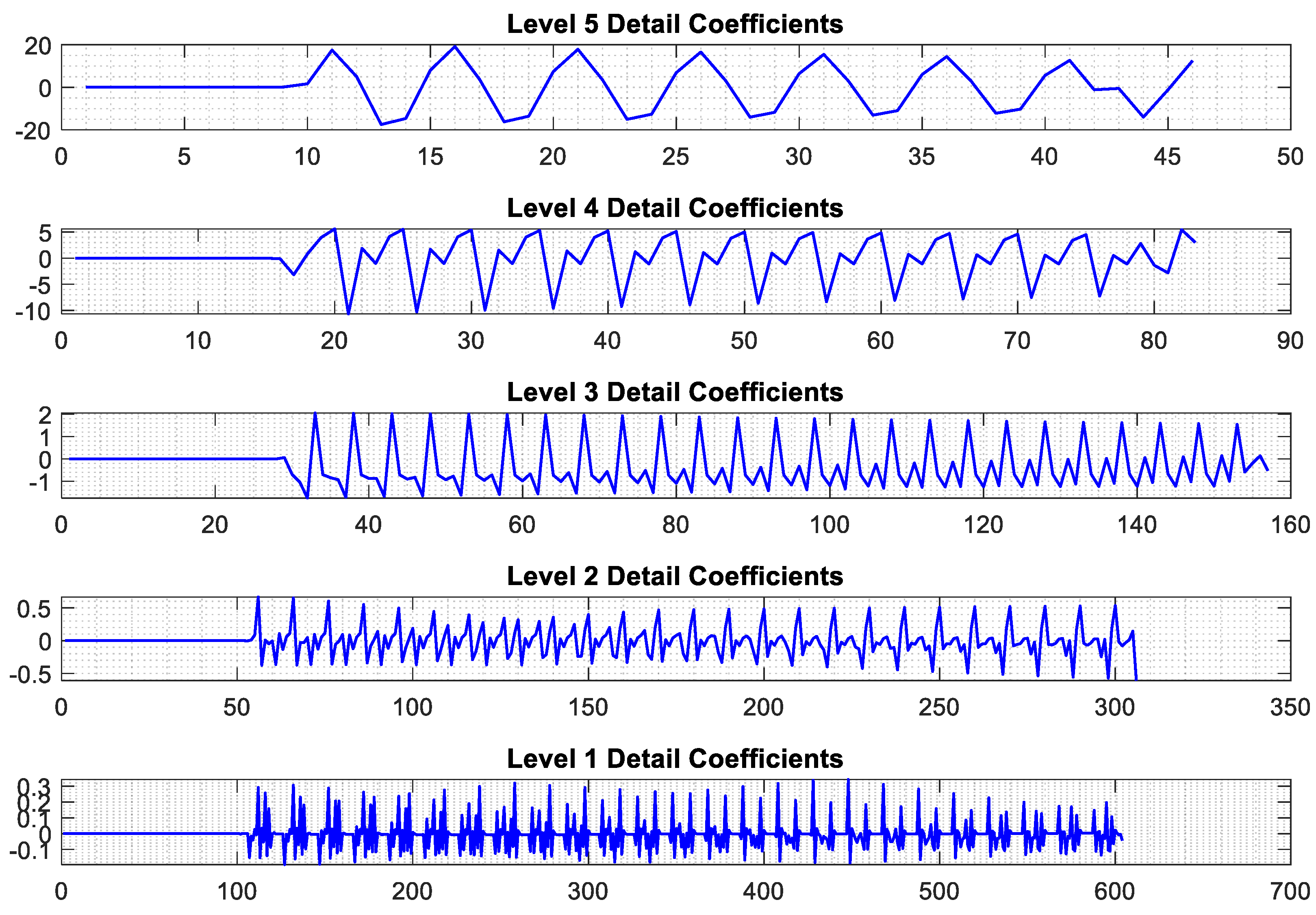
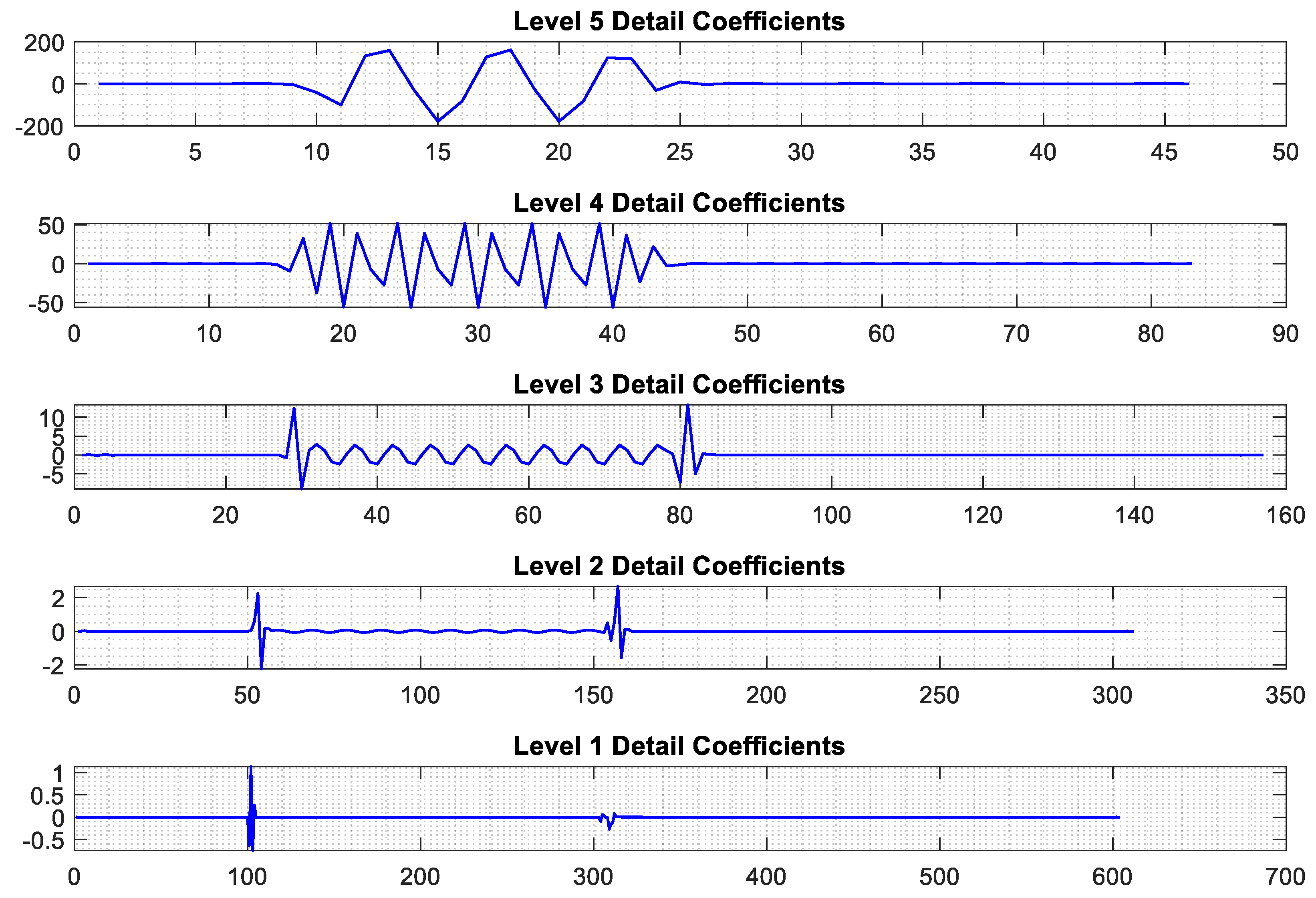
3.2.1. Real-Time Stationary Wavelet Transform (RT-SWT)
3.2.2. Improved Wavelet Transform (Real-Time Boundary Stationary)
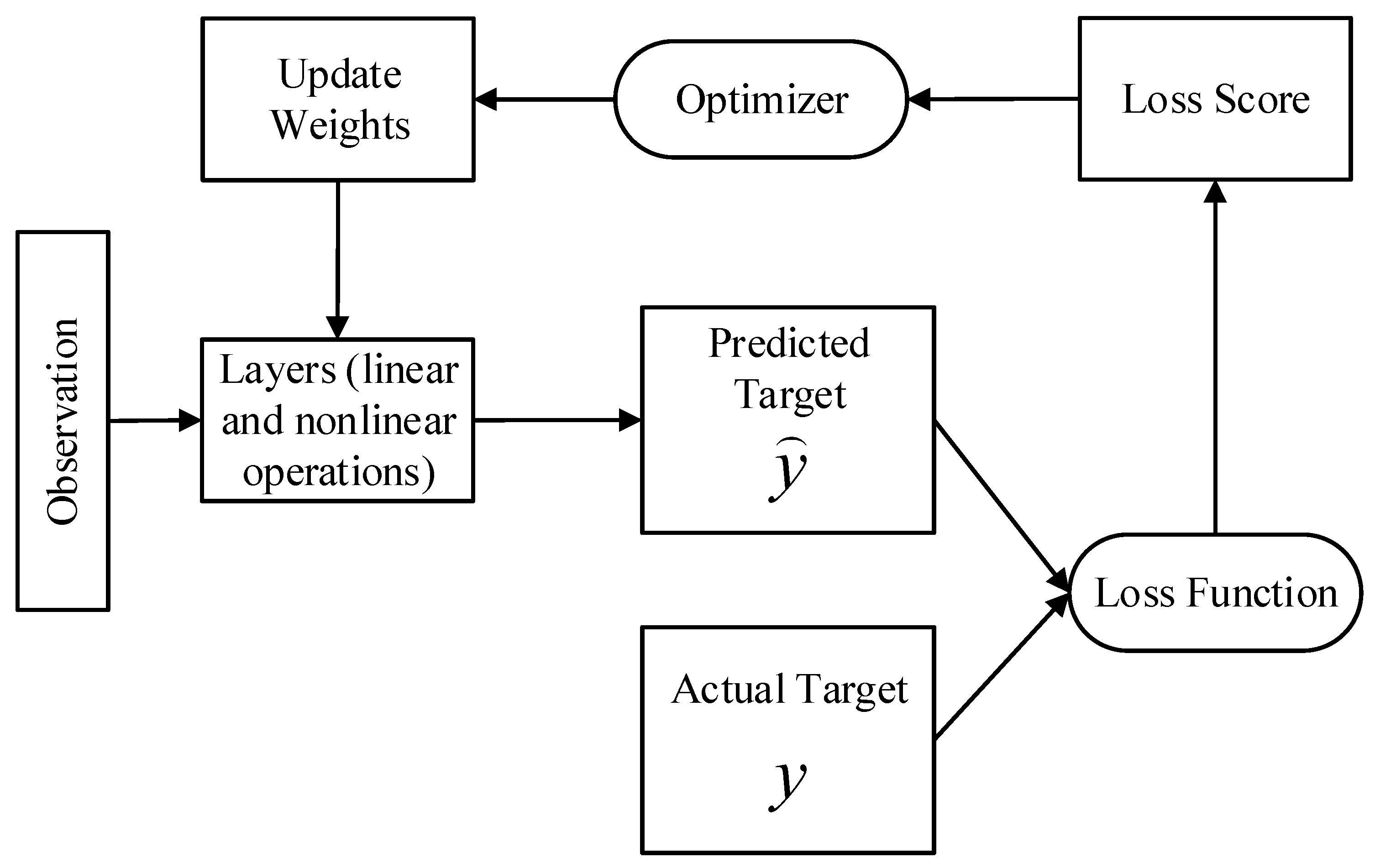
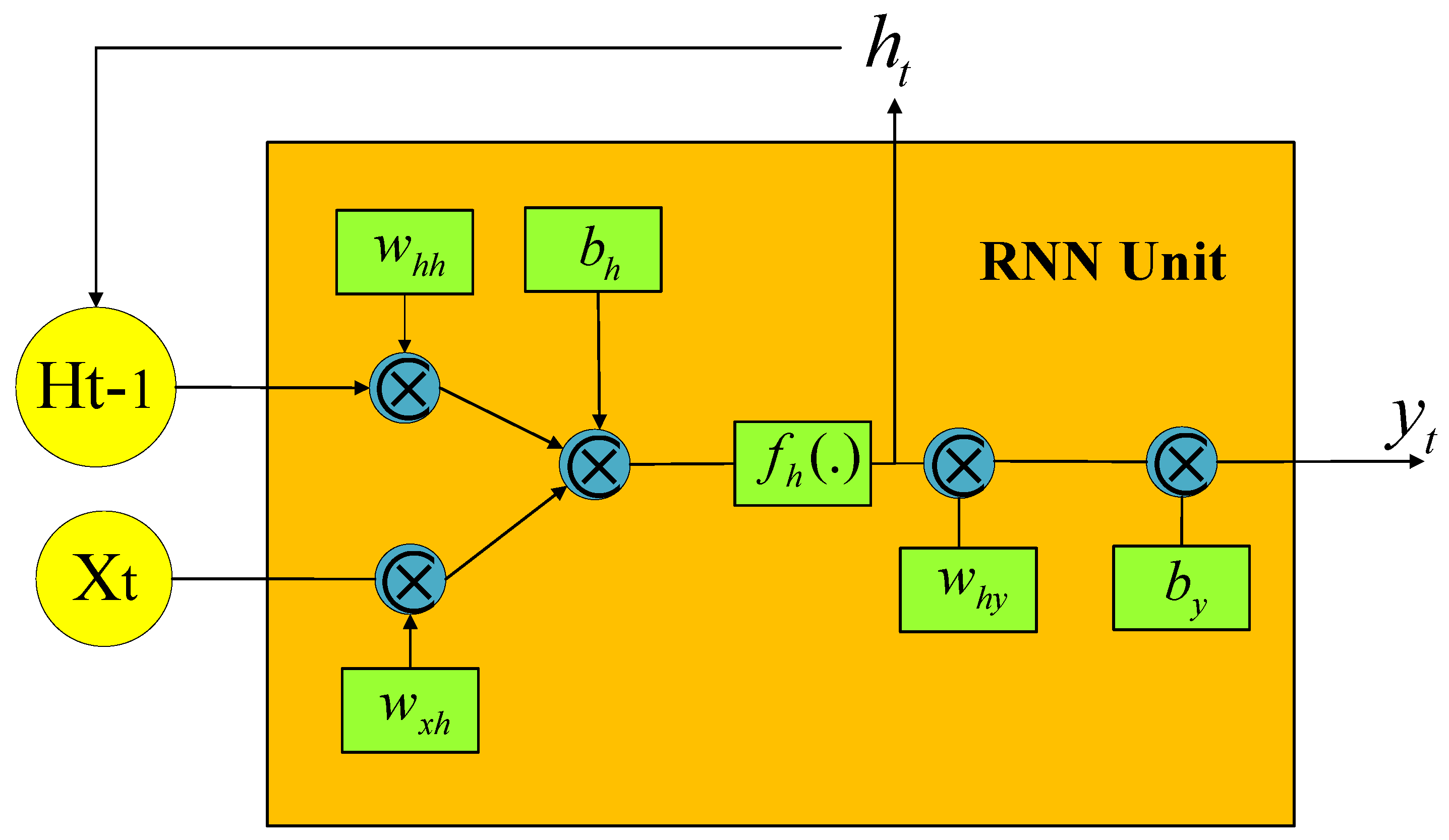
3.3. Enhanced LSTM Neural Network
- : Binary coding vector using (0,1) for various types of faults in power transformers.
4. Result Analysis and Discussion
- Running the power system with varying power supply phase angles (0–360°).
- Modifying fault ground resistance within a range (0.001, 0.01, 0.1, 1, 2, 10, …, 75, 125, 150).
- Adjusting transformer load from 5 MVA to 33 MVA.
- Manipulating fault location timing on both the LV side (33 kV) and HV side (132 kV) as per the provided table.
| Cases | Power Source Phase Angle | Number of Cases | Fault Location | Fault Ground Resistance | Transformer Load |
|---|---|---|---|---|---|
| Inrush current | (0–360°) | 500 | - | - | - |
| Internal faults with and without CT saturation | (0–360°) | 500 | HV and LV | (0.001, 0.01, 0.1, …, 75), | (5 MVA to 33 MVA) |
| 500 | HV and LV | ||||
| External faults under CT saturation | (0–360°) | 250 | HV | (0.001, 0.01, 0.1, …, 75, 125, 150), | (5 MVA to 33 MVA) |
| 250 | LV |
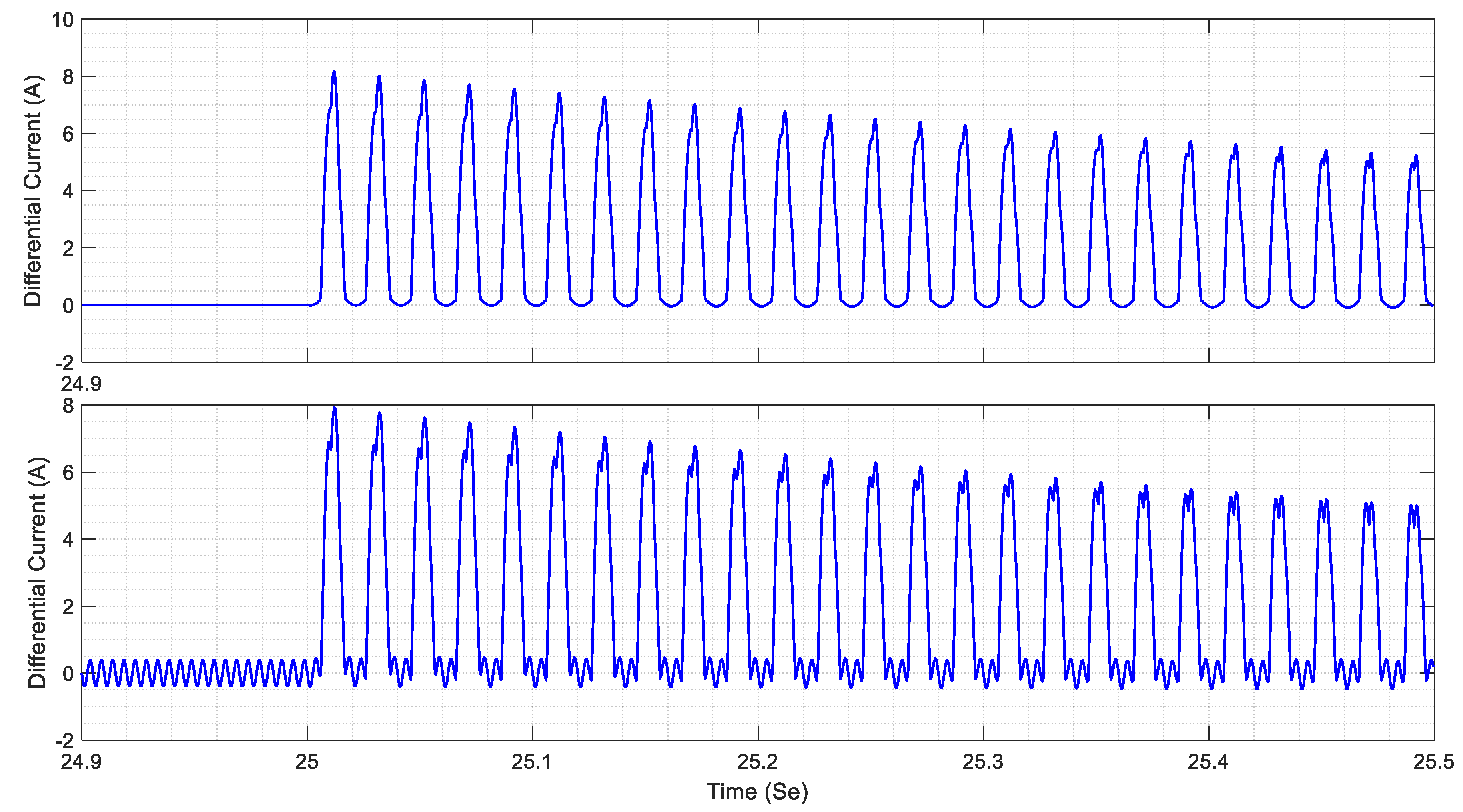
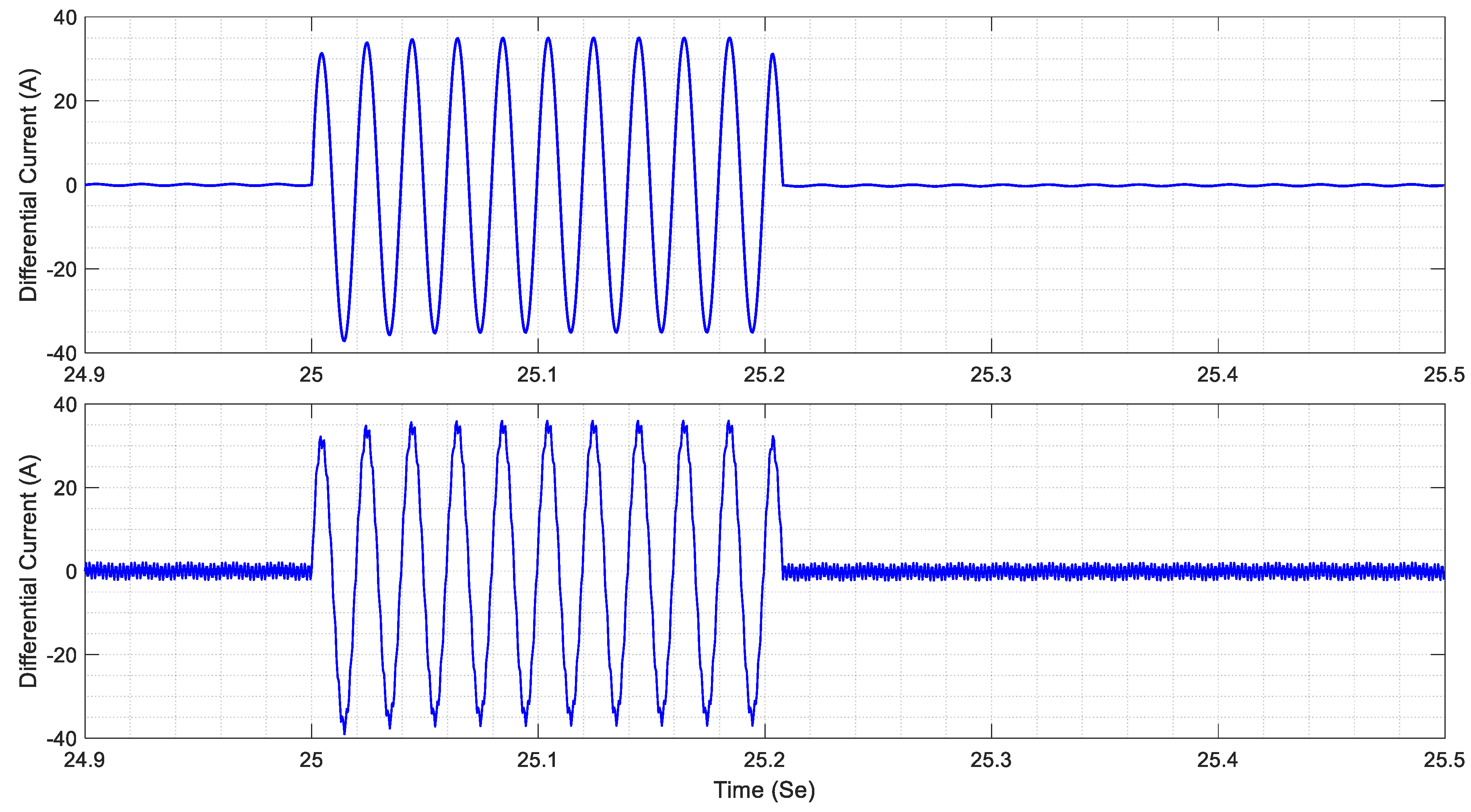
4.1. Feature Extraction Using Improved RBSWT
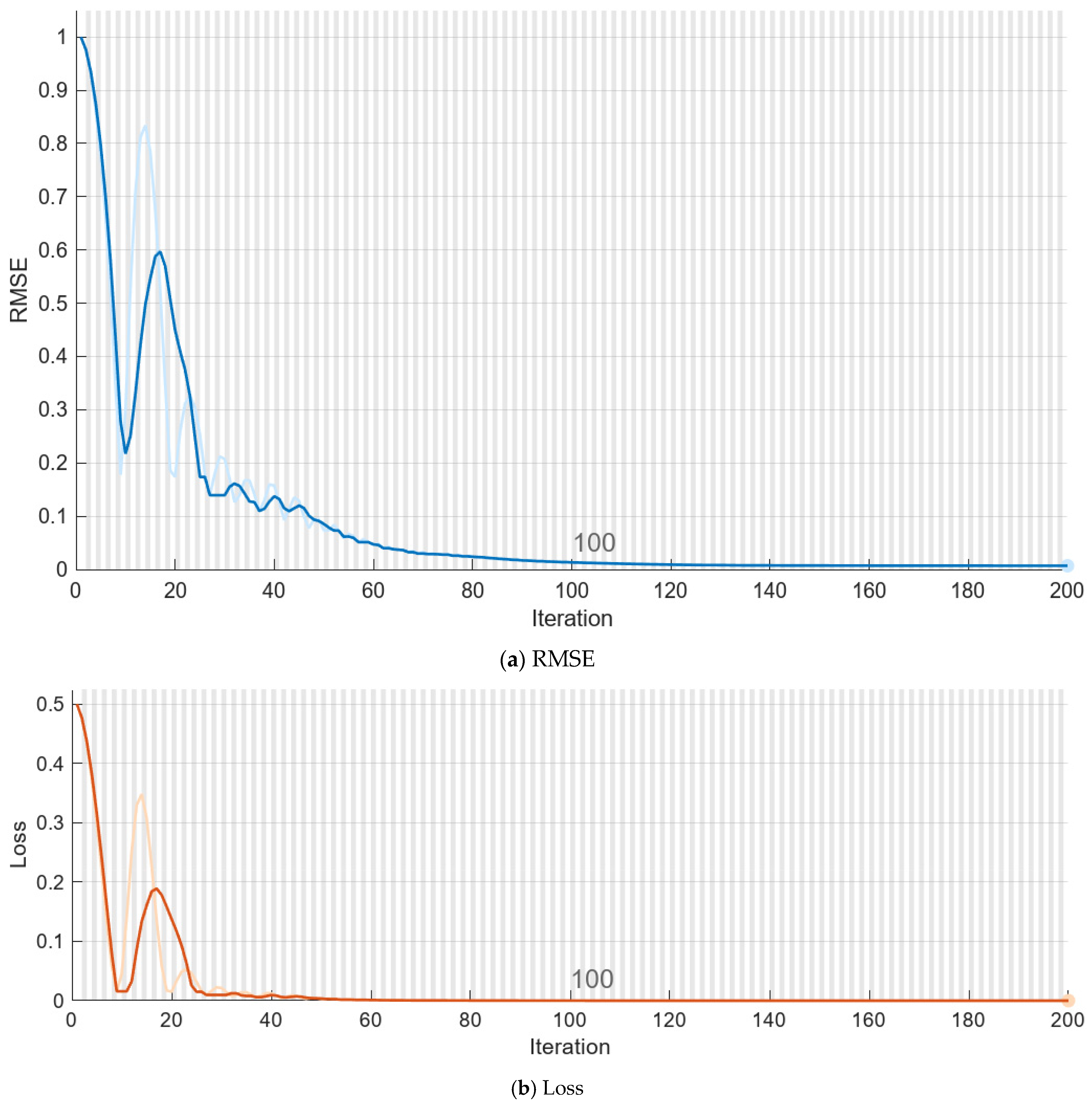
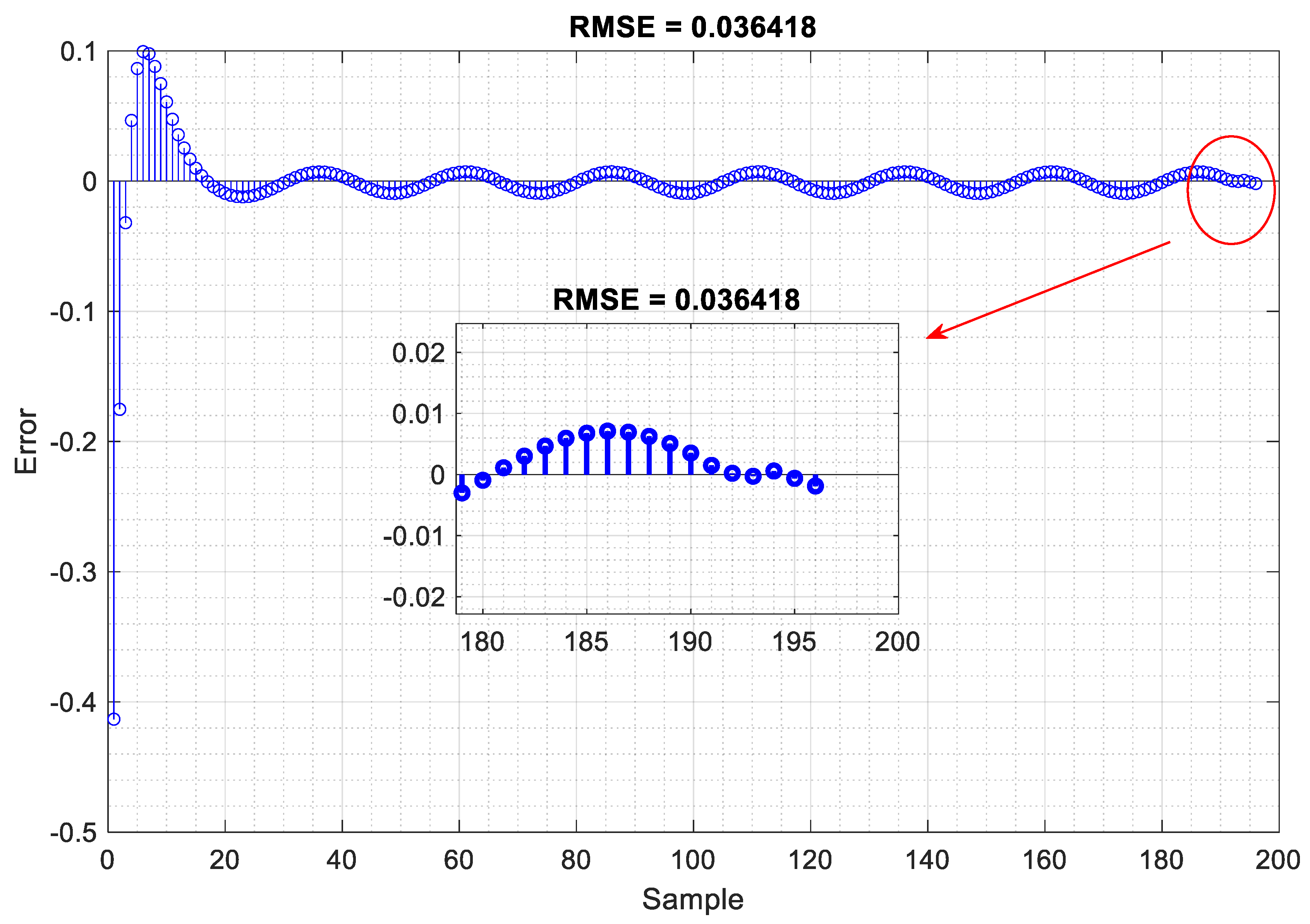
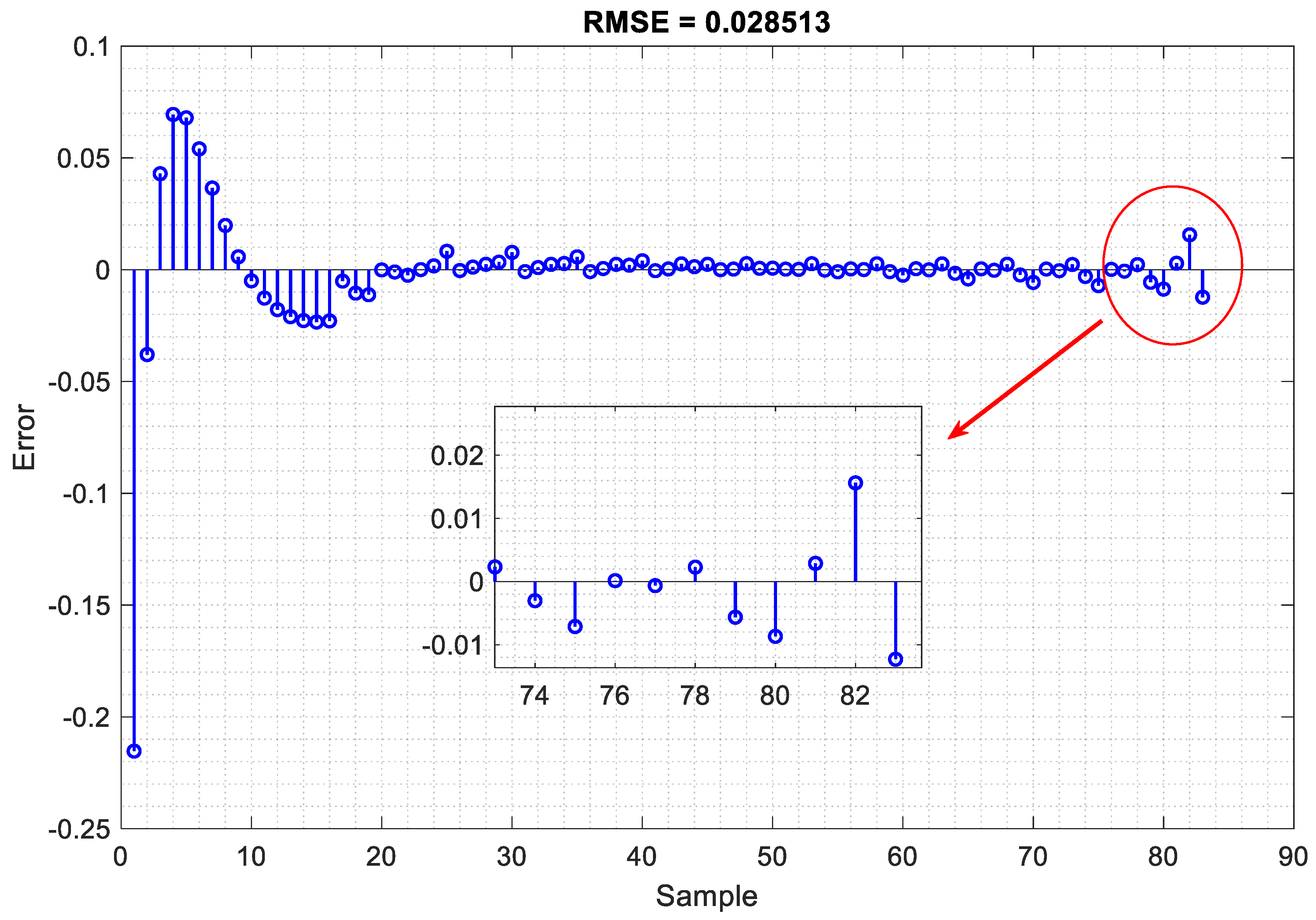
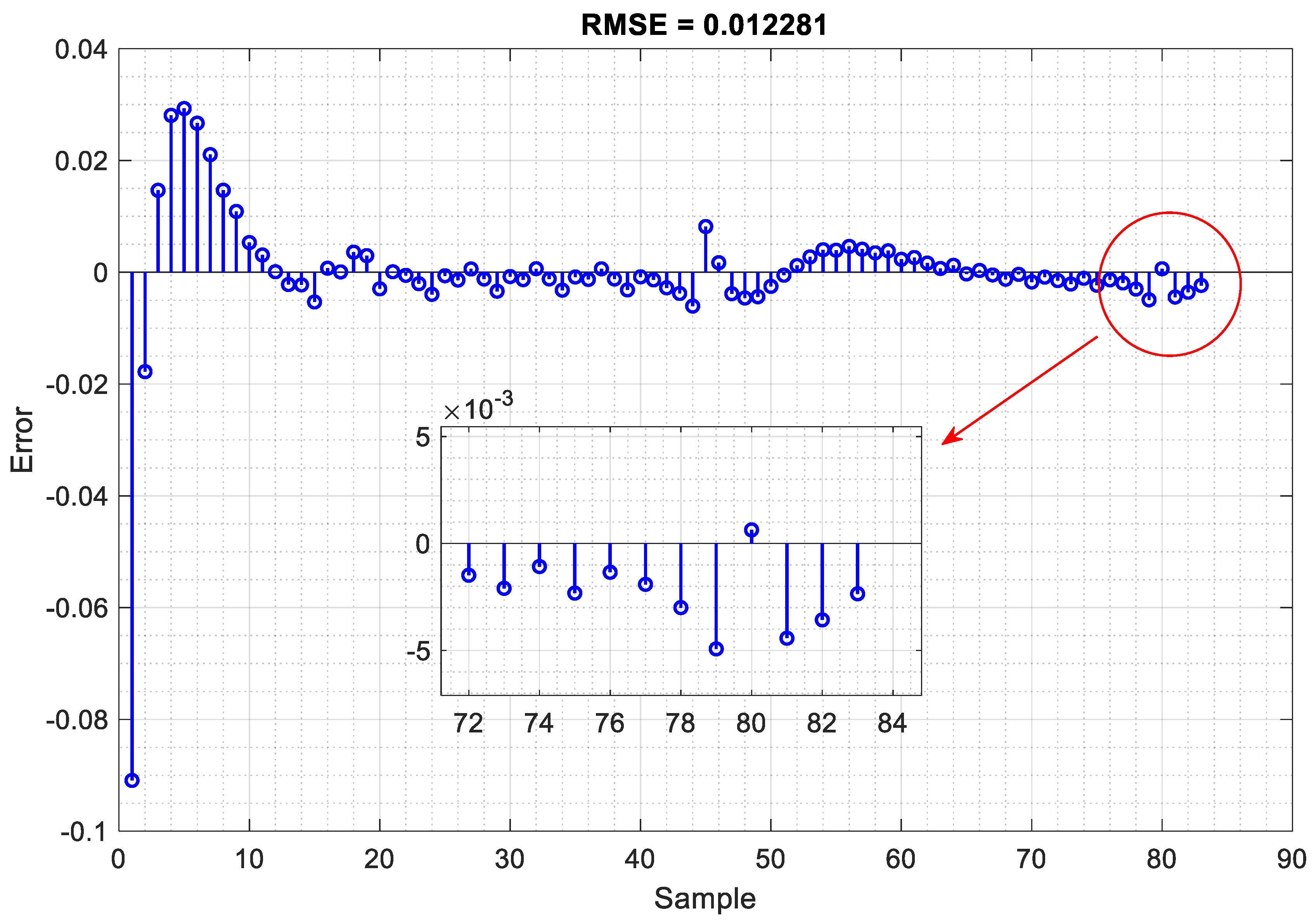
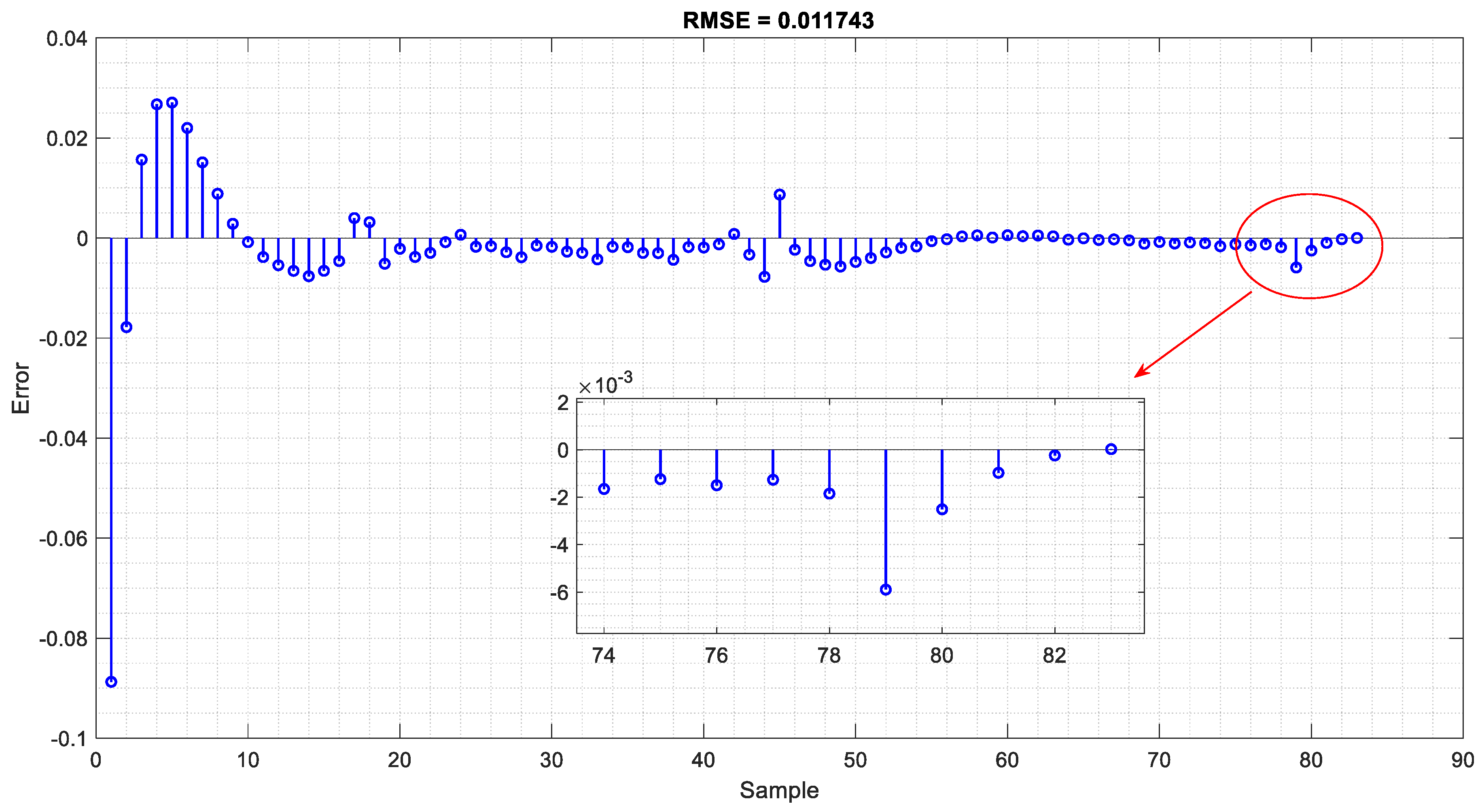
4.2. Training and Verification of the Proposed LSTM Neural Network
4.3. Analysis of Results and Comparison with State-of-the-Art Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSTM | Long Short-Term Memory | ELSTM | Enhanced Long Short-Term Memory |
| RT-SWT | Real-Time Stationary Wavelet Transform | GRU | Gated Recurrent Unit |
| RTBSWT | Real-Time Boundary Stationary Wavelet Transform | BPTT | Backpropagation Through Time |
| ANN | Artificial Neural Network | SMOTE | Synthetic Minority Over-Sampling Technique |
| DNN | Deep Neural Network | RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
References
- Ameli, A.; Ghafouri, M.; Zeineldin, H.H.; Salama, M.M.; El-Saadany, E.F. Accurate fault diagnosis in transformers using an auxiliary current-compensation-based framework for differential relays. IEEE Trans. Instrum. Meas. 2021, 70, 9004214. [Google Scholar] [CrossRef]
- Abbasi, A.R. Fault detection and diagnosis in power transformers: A comprehensive review and classification of publications and methods. Electr. Power Syst. Res. 2022, 209, 107990. [Google Scholar] [CrossRef]
- Nair, K. Power and Distribution Transformers: Practical Design Guide; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- AlOmari, A.A.; Smadi, A.A.; Johnson, B.K.; Feilat, E.A. Combined approach of LST-ANN for discrimination between transformer inrush current and internal fault. In Proceedings of the 2020 52nd North American Power Symposium (NAPS), Tempe, AZ, USA, 11–13 April 2021; pp. 1–6. [Google Scholar]
- He, A.; Jiao, Z.; Li, Z.; Liang, Y. Discrimination between internal faults and inrush currents in power transformers based on the discriminative-feature-focused CNN. Electr. Power Syst. Res. 2023, 223, 109701. [Google Scholar] [CrossRef]
- Key, S.; Son, G.-W.; Nam, S.-R. Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies 2024, 17, 963. [Google Scholar] [CrossRef]
- Chiradeja, P.; Pothisarn, C.; Phannil, N.; Ananwattananporn, S.; Leelajindakrairerk, M.; Ngaopitakkul, A.; Thongsuk, S.; Pornpojratanakul, V.; Bunjongjit, S.; Yoomak, S. Application of probabilistic neural networks using high-frequency components’ differential current for transformer protection schemes to discriminate between external faults and internal winding faults in power transformers. Appl. Sci. 2021, 11, 10619. [Google Scholar] [CrossRef]
- Moravej, Z.; Ebrahimi, A.; Pazoki, M.; Barati, M. Time domain differential protection scheme applied to power transformers. Int. J. Electr. Power Energy Syst. 2023, 154, 109465. [Google Scholar] [CrossRef]
- Shanu, T.; Mishra, A. Wavelet Scattering and Multiclass Support Vector Machine (WS_MSVM) for Effective Fault Classification in Transformers: A Real-time Experimental Approach. Eng. Res. Express 2024, 6, 035302. [Google Scholar] [CrossRef]
- Talware, D.; Kulkarni, D.; Gawande, P.G.; Patil, M.S.; Raut, K.; Mathurkar, P.K. Transformer protection improvement using fuzzy logic. Eur. Chem. Bull. 2023, 12, 54–67. [Google Scholar]
- Wong, S.Y.; Ye, X.; Guo, F.; Goh, H.H. Computational intelligence for preventive maintenance of power transformers. Appl. Soft Comput. 2022, 114, 108129. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, A.E.; Rivas-Araiza, E.A.; Garduño-Aparicio, M.; Tovar-Arriaga, S.; Rodriguez-Resendiz, J.; Toledano-Ayala, M. A Novel Methodology for Classifying Electrical Disturbances Using Deep Neural Networks. Technologies 2023, 11, 82. [Google Scholar] [CrossRef]
- Obakpolor, F.E.; Saha, A.K. Discriminating Between Magnetizing Inrush Current and Fault Current in Power Transformer Protection using Wavelet Transform. In Proceedings of the 2021 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Potchefstroom, South Africa, 27–29 January 2021; pp. 1–6. [Google Scholar]
- Yi, T.; Xie, Y.; Zhang, H.; Kong, X. Insulation fault diagnosis of disconnecting switches based on wavelet packet transform and PCA-IPSO-SVM of electric fields. IEEE Access 2020, 8, 176676–176690. [Google Scholar] [CrossRef]
- Babaei, Z.; Moradi, M. Novel method for discrimination of transformers faults from magnetizing inrush currents using wavelet transform. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 803–813. [Google Scholar] [CrossRef]
- Moosavi, S.M.L.; Damchi, Y.; Assili, M. A new fast method for improvement of power transformer differential protection based on discrete energy separation algorithm. Int. J. Electr. Power Energy Syst. 2022, 136, 107759. [Google Scholar] [CrossRef]
- Chavez, J.J.; Popov, M.; López, D.; Azizi, S.; Terzija, V. S-Transform based fault detection algorithm for enhancing distance protection performance. Int. J. Electr. Power Energy Syst. 2021, 130, 106966. [Google Scholar] [CrossRef]
- Nazari, A.A.; Hosseini, S.A.; Taheri, B. Improving the performance of differential relays in distinguishing between high second harmonic faults and inrush current. Electr. Power Syst. Res. 2023, 223, 109675. [Google Scholar] [CrossRef]
- Ahmadzadeh-Shooshtari, B.; Rezaei-Zare, A. Comparison of harmonic blocking methods in transformer differential protection under GIC conditions. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 22–31 October 2021; pp. 498–503. [Google Scholar]
- Baiceanu, F.; Beniuga, O.; Beniuga, R.; Diac, E. Quality Assessment of Power Transformers Differential Protection Behavior Using Harmonic Restraint Techniques. In Proceedings of the 2020 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 22–23 October 2020; pp. 680–684. [Google Scholar]
- Hamilton, R. Analysis of transformer inrush current and comparison of harmonic restraint methods in transformer protection. IEEE Trans. Ind. Appl. 2013, 49, 1890–1899. [Google Scholar] [CrossRef]
- Guzmán, A.; Fischer, N.; Labuschagne, C. Improvements in transformer protection and control. In Proceedings of the 2009 62nd Annual Conference for Protective Relay Engineers, College Station, TX, USA, 30 March–2 April 2009; pp. 563–579. [Google Scholar]
- Vazquez, E.; Mijares, I.I.; Chacon, O.L.; Conde, A. Transformer differential protection using principal component analysis. IEEE Trans. Power Deliv. 2007, 23, 67–72. [Google Scholar] [CrossRef]
- Li, Z.; Jiao, Z.; He, A. Dynamic differential current-based transformer protection using convolutional neural network. CSEE J. Power Energy Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Hosseinimoghadam, S.M.S.; Dashtdar, M.; Dashtdar, M. Improving the differential protection of power transformers based on clarke transform and fuzzy systems. J. Control. Autom. Electr. Syst. 2022, 33, 610–624. [Google Scholar] [CrossRef]
- Peng, F.; Gao, H.; Huang, J.; Guo, Y.; Liu, Y.; Zhang, Y. Power differential protection for transformer based on fault component network. IEEE Trans. Power Deliv. 2023, 38, 2464–2477. [Google Scholar] [CrossRef]
- Silva, A.F.; Silveira, E.G.; Alipio, R. Artificial neural network applied to differential protection of power transformers. J. Control Autom. Electr. Syst. 2021, 33, 850–857. [Google Scholar] [CrossRef]
- Medeiros, R.P.; Costa, F.B.; Silva, K.M.; Muro, J.D.J.C.; Júnior, J.R.L.; Popov, M. A clarke-wavelet-based time-domain power transformer differential protection. IEEE Trans. Power Deliv. 2021, 37, 317–328. [Google Scholar] [CrossRef]
- Suliman, M.Y.; Al-Khayyat, M.T. Discrimination Between Inrush and Internal Fault Currents in Protection Based Power Transformer using DWT. Int. J. Electr. Eng. Inform. 2021, 13, 1–20. [Google Scholar] [CrossRef]
- Kumar, V.; Magdum, P.; Lekkireddy, R.; Shah, K. Comprehensive Approaches for the Differential Protection of Power Transformers Using Advanced Classification Techniques. In Proceedings of the 2024 IEEE/IAS 60th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 19–23 May 2024; pp. 1–7. [Google Scholar]
- Xiaojun, L.; Feng, X.; Wang, X.; Li, Z. New Method of Transformer Differential Protection Based on Graph Fourier Transform. Electr. Power Compon. Syst. 2023, 51, 1251–1265. [Google Scholar] [CrossRef]
- Bagheri, S.; Safari, F.; Shahbazi, N. Detection and Classification of Cross-Country Faults, Internal and External Electrical Faults and Inrush Current in Power Transformers Using Maximum Overlap Discrete Wavelet Transform. J. Nonlinear Syst. Electr. Eng. 2022, 8, 117–137. [Google Scholar]
- Shahbazi, N.; Bagheri, S.; Gharehpetian, G. Identification and classification of cross-country faults in transformers using K-NN and tree-based classifiers. Electr. Power Syst. Res. 2022, 204, 107690. [Google Scholar] [CrossRef]
- Costa, F.; Souza, B.; Brito, N. Real-time detection of voltage sags based on wavelet transform. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), Sao Paulo, Brazil, 8–10 November 2010; pp. 537–542. [Google Scholar]
- Costa, F.B. Fault-induced transient detection based on real-time analysis of the wavelet coefficient energy. IEEE Trans. Power Deliv. 2013, 29, 140–153. [Google Scholar] [CrossRef]
- Costa, F.B. Boundary wavelet coefficients for real-time detection of transients induced by faults and power-quality disturbances. IEEE Trans. Power Deliv. 2014, 29, 2674–2687. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Bagheri, M.; Zollanvari, A.; Nezhivenko, S. Transformer fault condition prognosis using vibration signals over cloud environment. IEEE Access 2018, 6, 9862–9874. [Google Scholar] [CrossRef]
- Bifet, A.; Gavalda, R.; Holmes, G.; Pfahringer, B. Machine Learning for Data Streams: With Practical Examples in MOA. MIT Press: Cambridge, MA, USA, 2023. [Google Scholar]
- Gori, M.; Betti, A.; Melacci, S. Machine Learning: A Constraint-Based Approach; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Jordan, M.I. Attractor dynamics and parallelism in a connectionist sequential machine. In Artificial Neural Networks: Concept Learning; IEEE Press: Piscataway, NJ, USA, 1990; pp. 112–127. [Google Scholar]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Carver, R.; Andrychowicz, M.; Hickey, J. Deep learning for twelve hour precipitation forecasts. Nat. Commun. 2022, 13, 5145. [Google Scholar] [CrossRef] [PubMed]
- Fauvel, K.; Lin, T.; Masson, V.; Fromont, É.; Termier, A. Xcm: An explainable convolutional neural network for multivariate time series classification. Mathematics 2021, 9, 3137. [Google Scholar] [CrossRef]
- Oruh, J.; Viriri, S.; Adegun, A. Long short-term memory recurrent neural network for automatic speech recognition. IEEE Access 2022, 10, 30069–30079. [Google Scholar] [CrossRef]
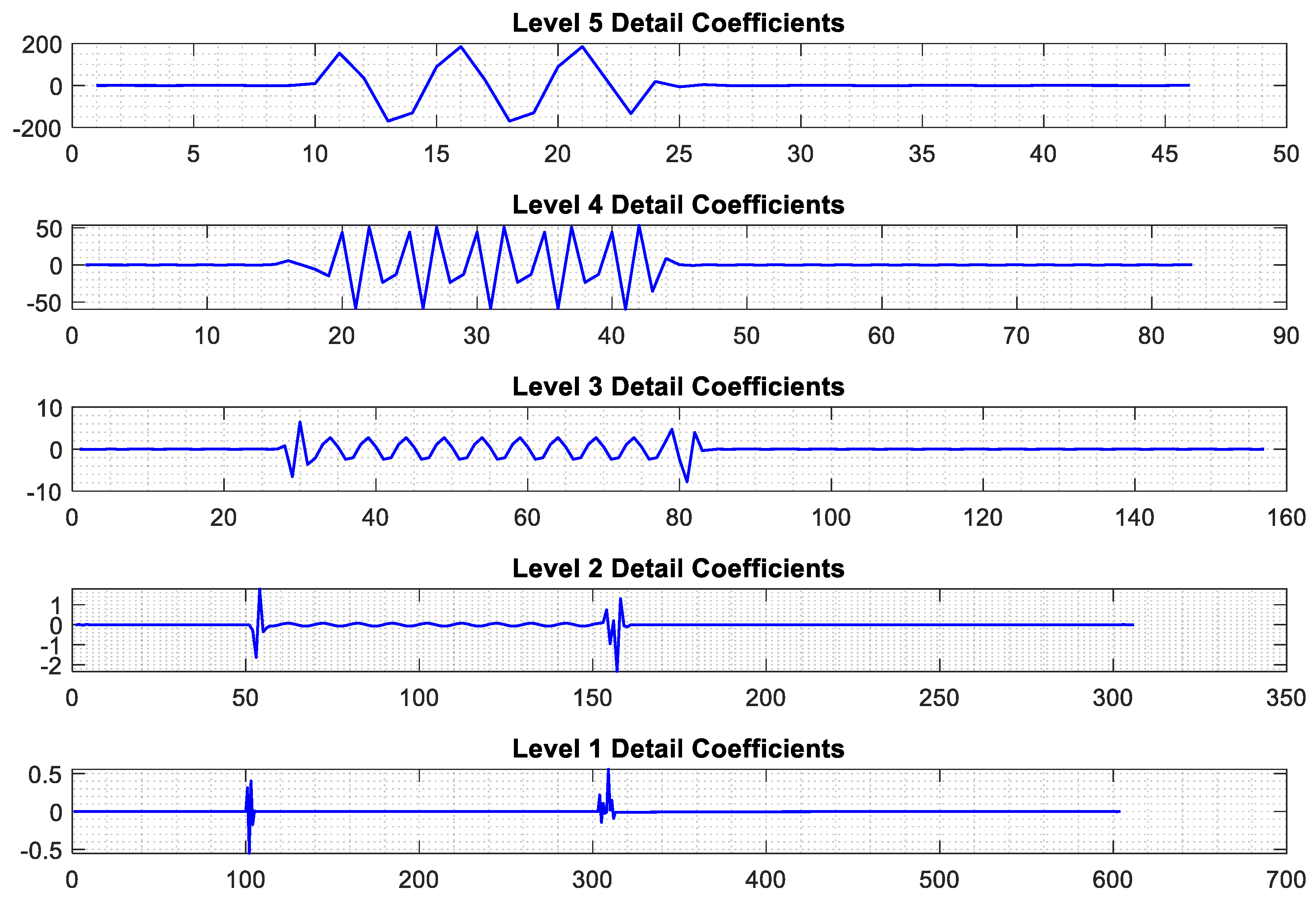
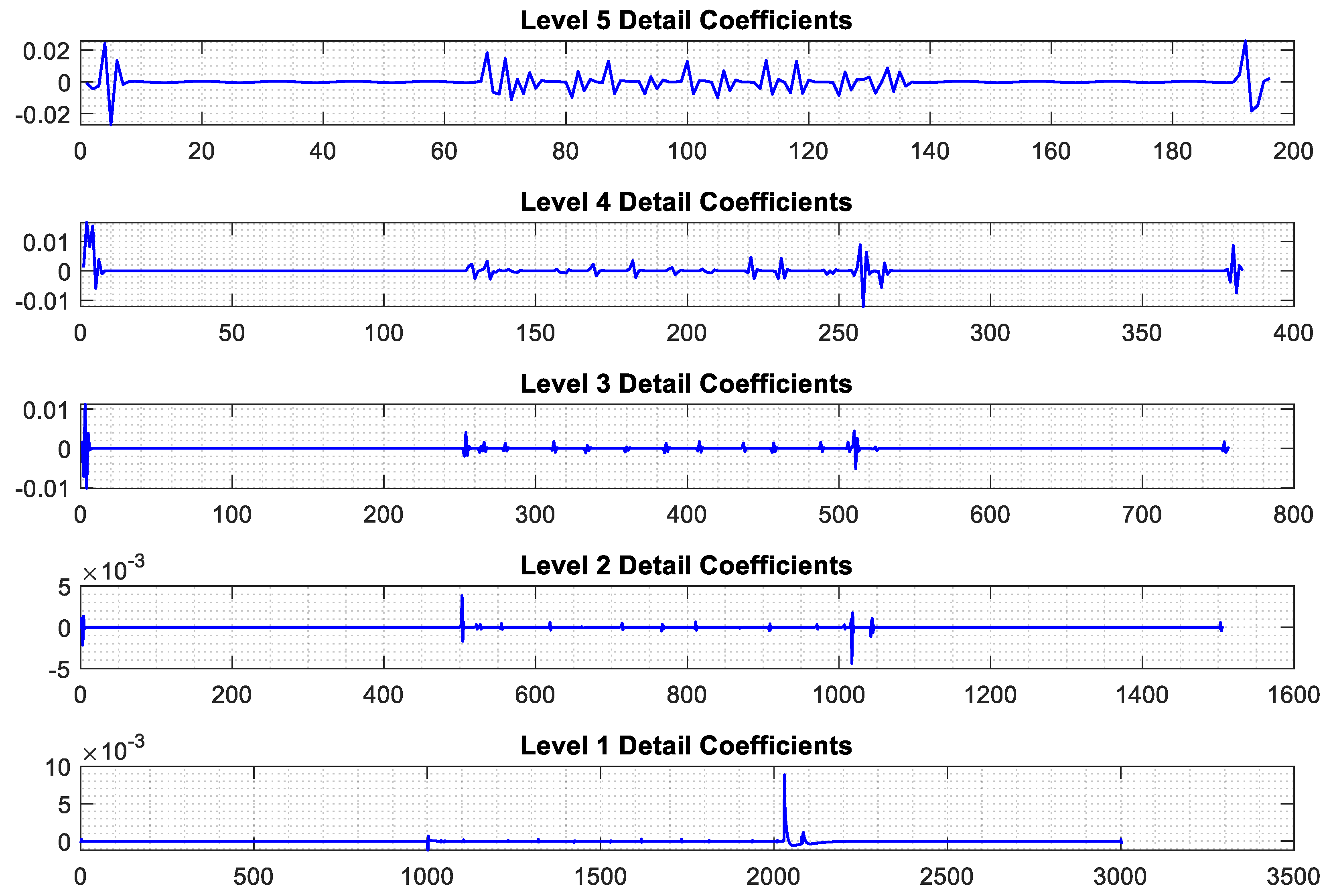
| Fault Type | Binary Code |
|---|---|
| Internal faults | (0,0) |
| External faults | (0,1) |
| Inrush current | (1,0) |
| Internal faults and inrush current (under CT saturation) | (1,1) |
| Connection of Transformer | YnD11 |
|---|---|
| Nominal apparent power (MVA) | 63 |
| Voltage ratio (kV) | 132/33 |
| Rated frequency (Hz) | 50 |
| Percentage impedance (%) | 10 |
| CT ratio primary side | 300:5 |
| CT ratio secondary side | 1200:5 |
| Epoch | Iteration | Time Elapsed (hh:mm:ss) | Mini-Batch RMSE | Mini-Batch Loss | Base Learning Rate |
|---|---|---|---|---|---|
| 1 | 1 | 00:00:03 | 191 × 10−2 | 18 × 10−1 | 1 × 10−2 |
| 50 | 50 | 00:00:04 | 7 × 10−2 | 26 × 10−4 | 1 × 10−2 |
| 100 | 100 | 00:00:05 | 3 × 10−2 | 4 × 10−4 | 1 × 10−2 |
| 150 | 150 | 00:00:06 | 1 × 10−2 | 57 × 10−7 | 1 × 10−3 |
| 200 | 200 | 00:00:07 | 933 × 10−5 | 44 × 10−7 | 1 × 10−3 |
| Fault Type | Analysis of Correct Diagnosis by Different Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [5,24,27] | [10,25] | [9,14] | Present Method | ||||||
| Internal fault | Number of cases | Number | % | Number | % | Number | % | Number | % |
| 500 | 489 | 97 | 476 | 95 | 482 | 96 | 498 | 99 | |
| Average detection time (ms) | 340 | 380 | 410 | 130 | |||||
| External fault | Number of cases | Number | % | Number | % | Number | % | Number | % |
| 500 | 469 | 93 | 471 | 94 | 463 | 92 | 499 | 99 | |
| Average detection time (ms) | 362 | 310 | 510 | 110 | |||||
| Inrush currents | Number of cases | Number | % | Number | % | Number | % | Number | % |
| 500 | 486 | 97 | 477 | 95 | 471 | 94 | 497 | 99 | |
| Average detection time (ms) | 360 | 379 | 525 | 120 | |||||
| Internal faults with CT saturation | Number of cases | Number | % | Number | % | Number | % | Number | % |
| 500 | 462 | 92 | 420 | 84 | 431 | 86 | 496 | 99 | |
| Average detection time (ms) | 390 | 428 | 610 | 170 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhamd, Q.; Saniei, M.; Seifossadat, S.G.; Mashhour, E. Advanced Fault Detection in Power Transformers Using Improved Wavelet Analysis and LSTM Networks Considering Current Transformer Saturation and Uncertainties. Algorithms 2024, 17, 397. https://doi.org/10.3390/a17090397
Alhamd Q, Saniei M, Seifossadat SG, Mashhour E. Advanced Fault Detection in Power Transformers Using Improved Wavelet Analysis and LSTM Networks Considering Current Transformer Saturation and Uncertainties. Algorithms. 2024; 17(9):397. https://doi.org/10.3390/a17090397
Chicago/Turabian StyleAlhamd, Qusay, Mohsen Saniei, Seyyed Ghodratollah Seifossadat, and Elaheh Mashhour. 2024. "Advanced Fault Detection in Power Transformers Using Improved Wavelet Analysis and LSTM Networks Considering Current Transformer Saturation and Uncertainties" Algorithms 17, no. 9: 397. https://doi.org/10.3390/a17090397
APA StyleAlhamd, Q., Saniei, M., Seifossadat, S. G., & Mashhour, E. (2024). Advanced Fault Detection in Power Transformers Using Improved Wavelet Analysis and LSTM Networks Considering Current Transformer Saturation and Uncertainties. Algorithms, 17(9), 397. https://doi.org/10.3390/a17090397






