Modification Model of Glued-In Rods Splice Connection Using Statistical Analysis for Mengkulang Glulam Timber
Abstract
:1. Introduction
2. Materials and Methods
2.1. Glued-In Rods Preparation
2.2. Moisture Content Experimental Work
2.3. Glue Tensile Test
2.4. Statistical Analysis
2.4.1. Development of GRPS Models Equation
2.4.2. Relationship between DV versus IVs
2.4.3. Correlation and Relationship among the Parameters
- (i)
- Pearson’s product-moment correlation coefficient, r
- (ii)
- Kendall’s τ-b
- (iii)
- Spearman rank correlation test.
2.4.4. Multiple Linear Regression Analysis
- (i)
- Based on the coefficient of determination or R2 values
- (ii)
- Mean square error MSE(p) for a p variable(s) equation
- (iii)
- model testing using new experimental data for verification
3. Results
3.1. Moisture Content, Density and Glue Tensile Strength
3.2. Pull-out Performance Behaviour after Testing
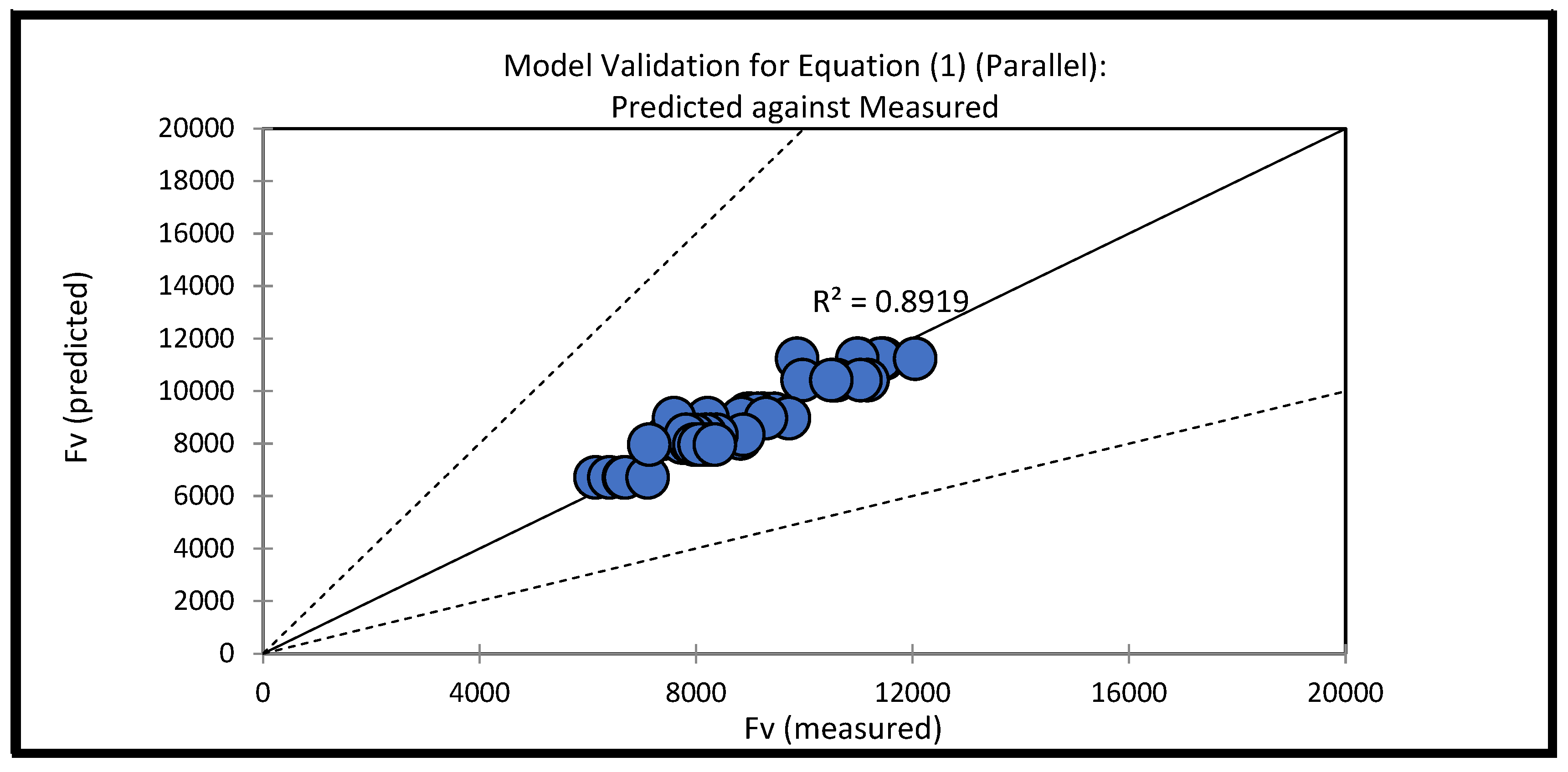
3.3. Accuracy and Validation of Developed GRPS Models
3.4. Model Testing of Developed GRPS Models with New Experimental Data
3.5. Validation Data Predicted against Measured Data for Parallel GRPS0° and Perpendicular GRPS90°
4. Conclusions
- (i)
- coefficient of determination (R2),
- (ii)
- mean square error (MSE) and
- (iii)
- model testing using new experimental data for verification.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kangas, J. Joints of Glulam Structures Based on Glued-In Ribbed Steel, 196; VTT Publications: Espoo, Finland, 1994. [Google Scholar]
- Riberholt, H. Glued bolts in glulam—Proposals for CIB code. In Proceedings of the 21st Conference of CIB-W18, Parksville, BC, Canada, September 1988. [Google Scholar]
- Ansell, M.P.; Smedley, D. Bonded-in technology for structural timber. Proc. ICE–Constr. Mater. 2007, 160, 95–98. [Google Scholar] [CrossRef]
- Itany, R.Y.; Faherty, K.F. Structural Wood Research, State-of-the-Art and Research Needs; ASCE: New York, NY, USA, 1984; p. 210. [Google Scholar]
- Bouchaīr, A.; Racher, P.; Bocquet, J.F. Analysis of dowelled timber to timber moment-resisting joints. Mater. Struct. 2007, 40, 1127–1141. [Google Scholar] [CrossRef]
- Bouchaïr, A. Modélisation non Linéaire du Comportement Local des Assemblages Bois. Ph.D. Thesis, Blaise Pascal University, Clermont-Ferrand, France, 1993. (Only Available In French). [Google Scholar]
- DS 413:1982; Code of Practice for The Structural Use of Timber. British Standards Institution (BSI): London, UK, 1982.
- EN 1995-2; (English): Eurocode 5: Design of timber structures—Part 2: Bridges [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- MS 544-9; Fire-Resistance of Timber Structures: Section 1: Method of Calculating Fire Resistance of Timber Members. Department of Standards Malaysia, SIRIM: Shah Alam, Malaysia, 2001.
- EN 1995-1-1; Design of Timber Structures Part 1 (Vol. 144, Issue 6). European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1995:1-2; Eurocode 5: Design of Timber Structures. European Committee for Standardization: Brussels, Belgium, 2004.
- Shakimon, M.N.; Hassan, R.; Malek, N.J.A.; Zainal, A.; Awaludin, A.; Hamid, N.H.A.; Lum, W.C.; Salit, M.S. European Yield Model Exponential Decay Constant Modification for Glulam after Fire Exposure. Forests 2022, 13, 2012. [Google Scholar] [CrossRef]
- Yeboah, D.; Taylor, S.; McPolin, D.; Gilfillan, R.; Gilbert, S. Behaviour of joints with bonded-in steel bars loaded parallel to the grain of timber elements. Constr. Build. Mater. 2011, 25, 2312–2317. [Google Scholar] [CrossRef]
- Stepinac, M.; Hunger, F.; Tomasi, R.; Serrano, E. Comparison of design rules for glued-in rods and design rule proposal for implementation in European standards. Working commision W18_timber structures comparison of design rules for glued-in rods and european standards. In Proceedings of the 46th Conference Of CIB-W18–Timber Structures of the International Council for Research and Innovation in Building and Construction, Vancouver, BC, Canada, 26–29 August 2013. [Google Scholar]
- Hussin, T.A.R.; Boss, S.; Hassan, R. Pull-out behaviour of two different glue lines thickness glued-in steel dowel for kempas species. Malays. Constr. Res. J. 2018, 25, 75–83. [Google Scholar]
- Mohamad, W.N.N.; Suliman, N.H.; Kamarudin, M.K.; Mohd-Amin, N.; Hassan, R. Pull-out strength steel rods bonded into mengkulang (Tarrietia Javanica) Glulam at five different angles to the grain. J. Trop. For. Sci. 2018, 30, 67–74. [Google Scholar]
- Kasim, M.; Quenneville, J.H.P. Effect of row spacing on the capacity of bolted timber connections loaded perpendicular-to-grain. In Proceedings of the CIBW18 Conference, Kyoto, Japan, September 2002. Paper 35-7-6. [Google Scholar]
- Gustafsson, P.J.; Serrano, E.; Aicher, S.; Johansson, C.J. A strength design equation for glued-in rods. Proc. Int. Relem’s 2001, 22, 324–327. [Google Scholar]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 2003; 703p, ISBN 0-8058-2223-2. [Google Scholar]
- Faghani, P. Investigations on Pull-Out Strength of Timber Joints with Glued-In Rods. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2013. [Google Scholar]
- EN 1995:2001; Eurocode 5: Design of Timber Structures—Part 1-1: General-Common rules and rules for buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2019.
- BS EN 26891; Timber Structures-Joints Made with Mechanical Fasteners–General Principles for the Determination of Strength and Deformation Characteristics. British Standards Institution: London, UK, 1991.
- MS758: 2001; Glued Laminated Timber. Performance Requirements and Minimum Production Requirements. Department of Standards Malaysia (SIRIM): Shah Alam, Malaysia, 2001.
- prEN 1995-2; Eurocode 5-Design of Timber Structures, Part 2: Bridges. Final Project Team Draft (Stage 34). Document CEN/TC 250/SC 5: N 198. European Committee for Standardization CEN: Brussels, Belgium, 2003.
- Feligioni, L.; Lavisci, P.; Duchanois, G.; De Ciechi, M.; Spinelli, P. Influence of glue rheology and joints thickness on the strength of bonded-in rods. Holz Als Roh-Und Werkst 2003, 61, 281–287. [Google Scholar]
- Steiger, R.; Serrano, E.; Stepinac, M.; Rajčić, V.; O’Neill, C.; McPolin, D.; Widmann, R. Strengthening of timber structures with glued-in rods. Constr. Build. Mater. 2015, 97, 90–105. [Google Scholar] [CrossRef] [Green Version]
- Rossignon, A.; Espion, B. Experimental assessment of the pull-out strength of single rods bonded in glulam parallel to the grain. Eur. J. Wood Wood Prod. 2008, 66, 419–432. [Google Scholar] [CrossRef]
- Hair, J.F.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
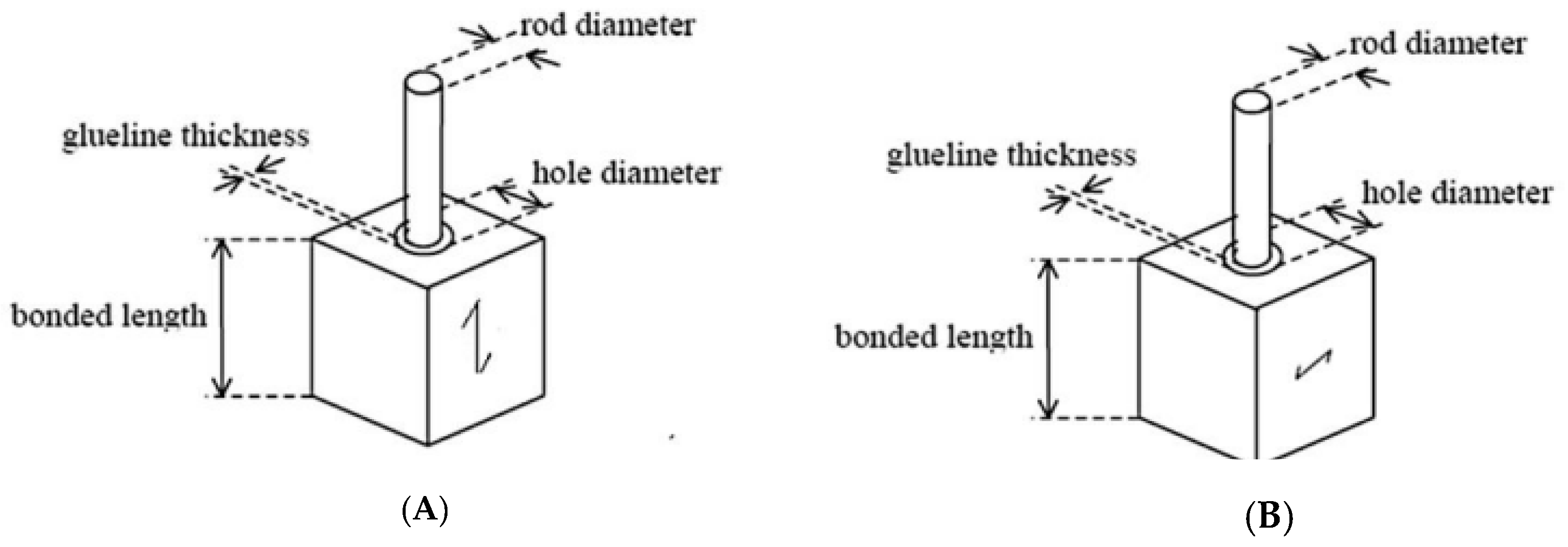
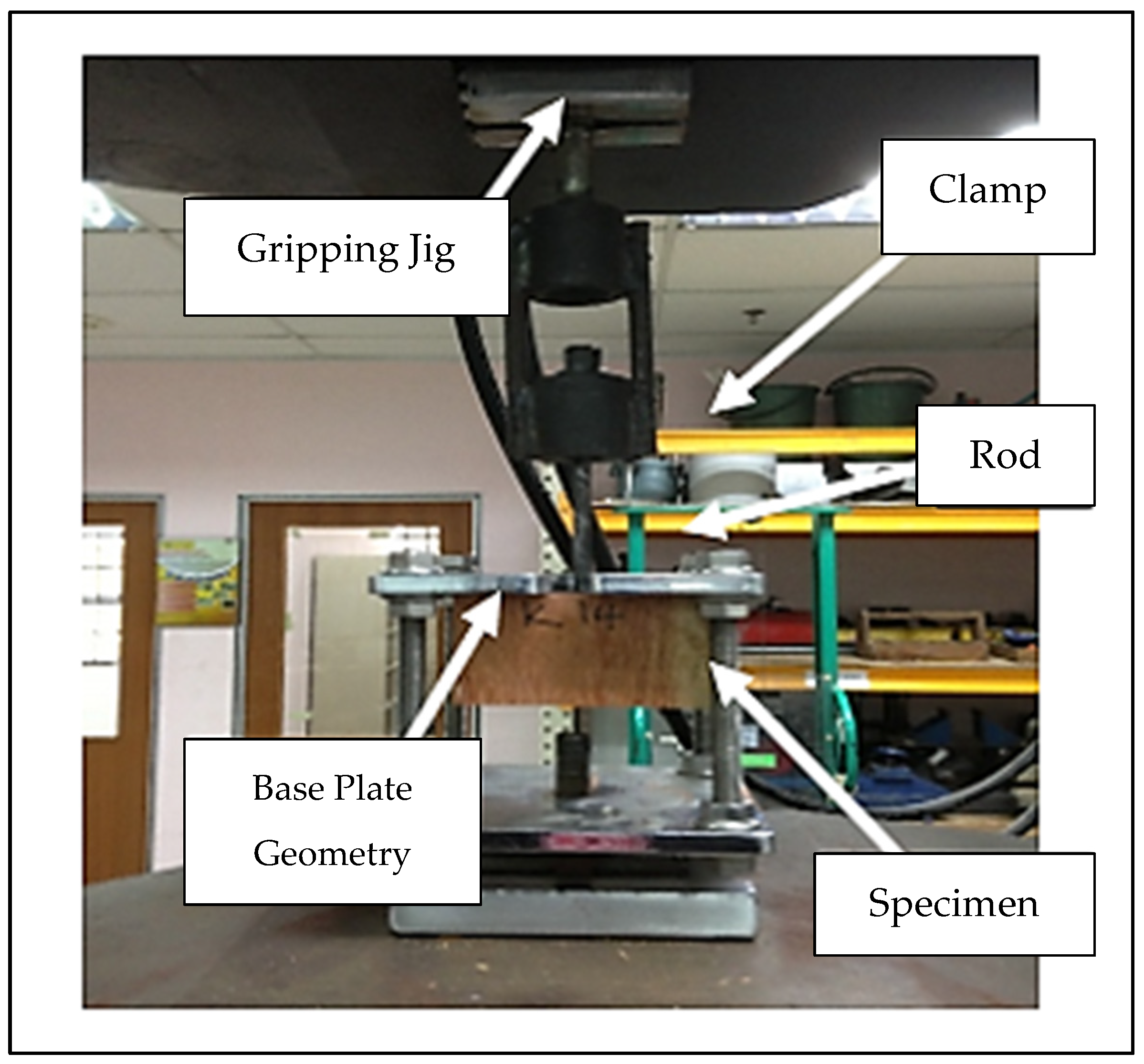


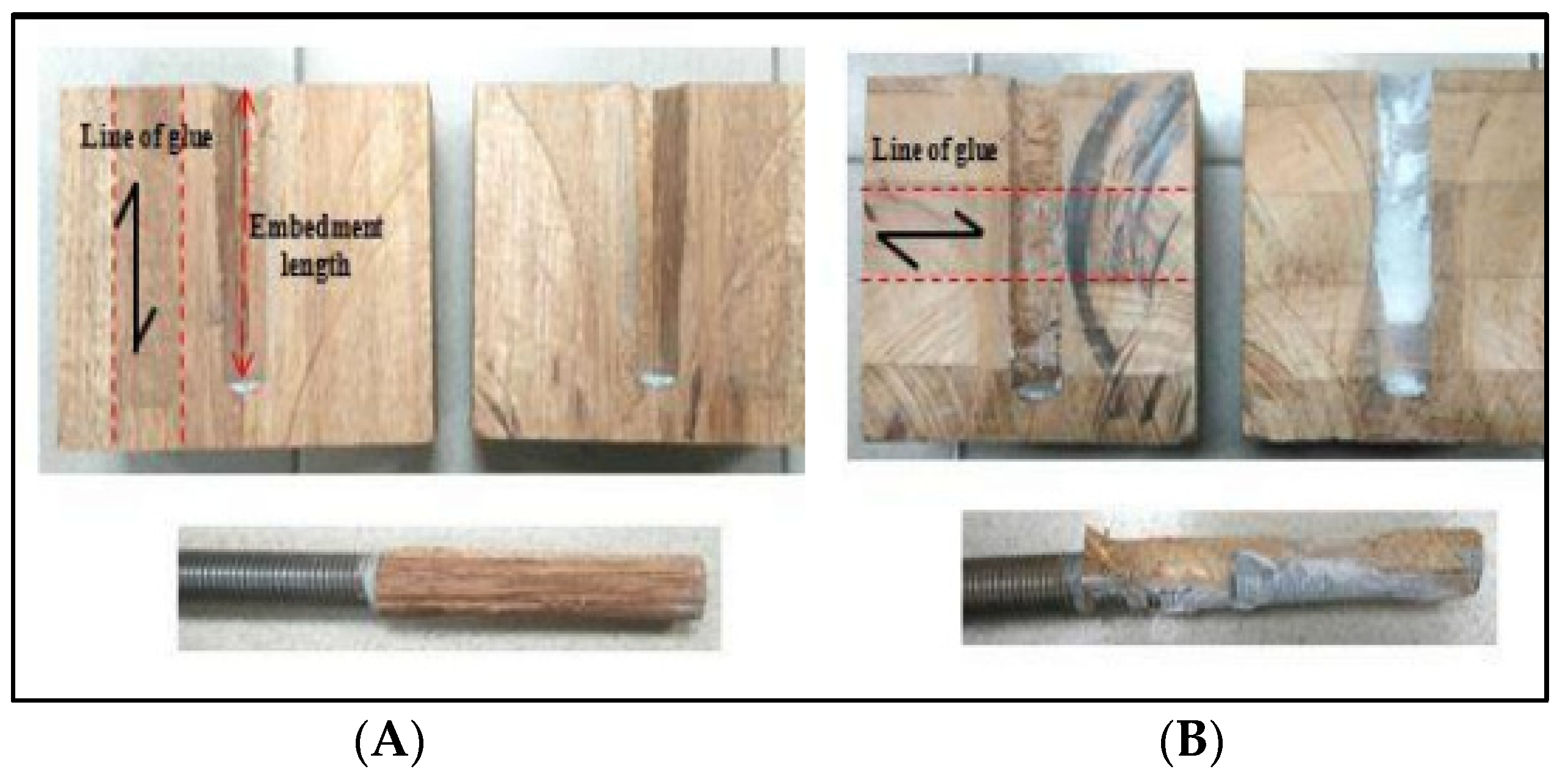

| Rod Size | Glue Line Thickness | No of Samples | Sample Size | |
|---|---|---|---|---|
| Parallel | Perpendicular | |||
| 12 | 2 | 18 | 18 | 100 × 100 × 100 |
| 16 | 3 | 17 | 18 | 115 × 115 × 115 |
| 20 | 4 | 18 | 18 | 170 × 170 × 170 |
| Total samples | 53 | 54 | ||
| Investigators | Main Equation | Shear Strength/Additional Parameters |
|---|---|---|
| [2] | ||
| [24] | ||
| [25] | ||
| [26] | ||
| [27] |
| Parameters | Coefficient of Determination, R2 | |
|---|---|---|
| Parallel (GRPS0°) | Perpendicular (GRPS90°) | |
| Density | 0.8611 | 0.9457 |
| Moisture Content | 0.8682 | 0.8682 |
| Area | 0.8637 | 0.8447 |
| Ratio | 0.807 | 0.9464 |
| Glue Thickness | 0.9584 | 0.8637 |
| Embedded Length | 0.255 | 0.1841 |
| Rod Diameter | 0.2823 | 0.0925 |
| Correlation | Negative | Positive |
|---|---|---|
| Small | −0.29 to −0.10 | 0.10 to 0.29 |
| Medium | −0.49 to −0.30 | 0.30 to 0.49 |
| Large | −1.00 to −0.50 | 0.50 to 1.00 |
| Rod Diameter (mm) | 12 | 16 | 20 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glue-Thickness (mm) | Load Carrying Capacity | Strength | Load Carrying Capacity | Strength | Load Carrying Capacity | Strength | |||||||
| Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | ||
| 2 | Mean (kN) | 51.82 | 13.36 | 5.65 | 0.11 | 91.15 | 7.44 | 6.11 | 0.08 | 121.86 | 8.20 | 4.96 | 0.05 |
| 3 | 51.52 | 6.43 | 6.22 | 0.08 | 83.93 | 5.99 | 7.65 | 0.08 | 120.49 | 8.71 | 5.75 | 0.05 | |
| 4 | 47.25 | 5.72 | 5.57 | 0.07 | 86.39 | 5.86 | 7.26 | 0.07 | 152.52 | 7.22 | 5.82 | 0.05 | |
| Rod Diameter (mm) | 12 | 16 | 20 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glue-Thickness (mm) | Load Carrying Capacity | Strength | Load Carrying Capacity | Strength | Load Carrying Capacity | Strength | |||||||
| Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | Load (kN) | Disp. (mm) | Stress (MPa) | Strain (%) | ||
| 2 | Mean (kN) | 42.93 | 5.80 | 4.68 | 0.06 | 73.27 | 7.18 | 2.98 | 0.04 | 120.04 | 7.41 | 4.89 | 0.05 |
| 3 | 247.06 | 5.62 | 5.13 | 0.06 | 65.77 | 6.25 | 2.67 | 0.04 | 134.70 | 8.71 | 5.48 | 0.05 | |
| 4 | 50.25 | 6.46 | 5.47 | 0.07 | 75.13 | 7.25 | 3.06 | 0.04 | 140.57 | 7.72 | 5.72 | 0.05 | |
| Model | Regression Method | Equation No | Model Performance | |||
|---|---|---|---|---|---|---|
| GRPS Equations | % Error | MSE (%) | R2 | |||
| GRPS0° | Multiple Linear | GRPS0°-1 | fv,0 | 0.672 | 0.163 | 0.945 |
| GRPS90° | Multiple Linear | GRPS90°-1 | fv,90 | 0.677 | 0.610 | 0.250 |
| Model Equations | Discrepancy | Percentage (%) Different |
|---|---|---|
| GRPS0°-1 | 1.30 | 20.32 |
| GRPS0°-1 | 1.02 | 12.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raja Hussin, T.A.; Hassan, R.; Anshari, B.; Md Nor, A.; Sapuan, S.M. Modification Model of Glued-In Rods Splice Connection Using Statistical Analysis for Mengkulang Glulam Timber. Forests 2023, 14, 491. https://doi.org/10.3390/f14030491
Raja Hussin TA, Hassan R, Anshari B, Md Nor A, Sapuan SM. Modification Model of Glued-In Rods Splice Connection Using Statistical Analysis for Mengkulang Glulam Timber. Forests. 2023; 14(3):491. https://doi.org/10.3390/f14030491
Chicago/Turabian StyleRaja Hussin, Tengku Anita, Rohana Hassan, Buan Anshari, Azman Md Nor, and S. M. Sapuan. 2023. "Modification Model of Glued-In Rods Splice Connection Using Statistical Analysis for Mengkulang Glulam Timber" Forests 14, no. 3: 491. https://doi.org/10.3390/f14030491
APA StyleRaja Hussin, T. A., Hassan, R., Anshari, B., Md Nor, A., & Sapuan, S. M. (2023). Modification Model of Glued-In Rods Splice Connection Using Statistical Analysis for Mengkulang Glulam Timber. Forests, 14(3), 491. https://doi.org/10.3390/f14030491







