Site Index Model for Southern Subtropical Masson Pine Forests Using Stand Dominant Height
Abstract
:1. Introduction
2. Materials and Method
2.1. Study Sites and Data
2.2. One-Way ANOVA
2.3. Generalized Algebraic Difference Equations
2.4. Bayesian Approach
2.5. Nonlinear Mixed-Effects Models
2.6. Model Evaluation
3. Results
3.1. One-Way ANOVA of Different Densities and Management Modes on the Dominant Height of Forest Stands
3.2. Basic GADA Model Selection
3.3. Site Index Model with Different Random Effects
3.4. Comparison of Three Methods
4. Discussion
4.1. The Effect of Stand Density on the Dominant Height of Forests
4.2. The Effect of Management Mode on the Dominant Height of Forests
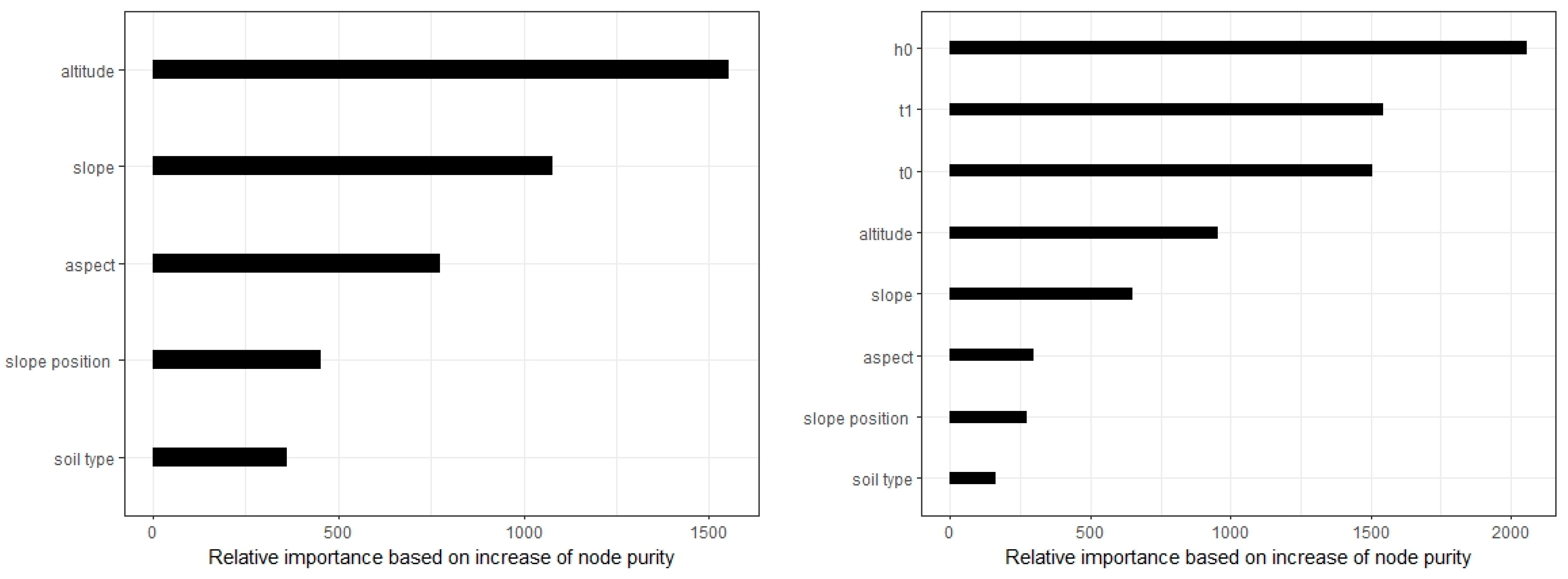
4.3. Model Comparison and the Influence of Terrain Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- #Code for NLME in R partially references the article: http://doi.org/10.3390/rs12071066.
- #Code for Bayesian estimation using STAN function package in R.
- TBB_LIB_DIR = “D:/oneapi-tbb-2021.9.0-win/oneapi-tbb-2021.9.0/lib/intel64”
- Sys.setenv(LIB_TBB = TBB_LIB_DIR)
- Sys.setenv(PKG_LIBS = Sys.getenv(“LOCAL_LIBS”))
- library(StanHeaders)
- library(brms)
- library(rstudioapi)
- library(rstan)
- options(mc.cores = parallel::detectCores())
- rstan_options(auto_write = TRUE)
- data_bys <- list(
- N = plot_number,
- t1 = data_training$t1,
- t0 = data_training$t0,
- h0 = data_training$h0,
- h1 = data_training$h1
- )
- model_code <- “
- data {
- int<lower=0> N;
- vector[N] t0;
- vector[N] t1;
- vector[N] h0;
- vector[N] h1;
- }
- parameters {
- real b1;
- real b2;
- real c;
- }
- transformed parameters {
- vector[N] h1_pred;
- for (i in 1:N) {
- h1_pred[i]=exp((log(h0[i])+b1*(t0[i]^(-c)))/(1-b2*(t0[i]^(-c))))*exp(-(b1+b2*((log(h0[i])+b1*(t0[i]^(-c)))/(1-b2*(t0[i]^(-c)))))*(t1[i]^(-c)));
- }
- }
- model {
- b1 ~ normal(-9.911901, 13.780287776761);
- b2 ~ normal(2.911217, 1.258677560464);
- c ~ normal(0.271303, 0.009979410609);
- h1 ~ normal(h1_pred, 1);
- }
- “
- stan_model <- stan_model(model_code = model_code) # Compiling a Stan model
- fit <- sampling(stan_model, data = data_bys, iter = 500000, warmup = 100000, control = list(max_treedepth = 15))
- print(fit)
References
- Carmean, W.H. Forest site quality evaluation in the United States. Adv. Agron. 1975, 27, 209–269. [Google Scholar]
- Li, F.R. Forest Mensuration, 4th ed.; China Forestry Publishing House: Beijing, China, 2019; pp. 135–159. (In Chinese) [Google Scholar]
- Pretzsch, H.; Grote, R.; Reineking, B.; Rötzer, T.; Seifert, S. Models for forest ecosystem management: A European perspective. Ann. Bot. 2008, 101, 1065–1087. [Google Scholar] [CrossRef]
- Englin, J.; Mendelsohn, R. A hedonic travel cost analysis for valuation of multiple components of site quality: The recreation value of forest management. J. Environ. Econ. Manag. 1991, 21, 275–290. [Google Scholar] [CrossRef]
- Carmean, W.H. Site index curves for upland oaks in the Central States. For. Sci. 1972, 18, 109–120. [Google Scholar]
- Monserud, R.A. Height growth and site index curves for inland Douglas-fir based on stem analysis data and forest habitat type. For. Sci. 1984, 30, 943–965. [Google Scholar]
- Seynave, I.; Gégout, J.-C.; Hervé, J.-C.; Dhôte, J.-F.; Drapier, J.; Bruno, É.; Dumé, G. Picea abies site index prediction by environmental factors and understorey vegetation: A two-scale approach based on survey databases. Can. J. For. Res. 2005, 35, 1669–1678. [Google Scholar] [CrossRef]
- Nothdurft, A.; Wolf, T.; Ringeler, A.; Böhner, J.; Saborowski, J. Spatio-temporal prediction of site index based on forest inventories and climate change scenarios. For. Ecol. Manag. 2012, 279, 97–111. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway. Scand. J. For. Res. 2012, 27, 619–636. [Google Scholar] [CrossRef]
- Bailey, R.L.; Clutter, J.L. Base-age invariant polymorphic site curves. For. Sci. 1974, 20, 155–159. [Google Scholar]
- Duan, G.; Lei, X.; Zhang, X.; Liu, X. Site index modeling of Larch using a mixed-effects model across regional site types in Northern China. Forests 2022, 13, 815. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, S.; Chhin, S.; Zhang, X.; He, P. Modelling site index of Chinese fir plantations using a random effects model across regional site types in Hunan province, China. For. Ecol. Manag. 2019, 446, 143–150. [Google Scholar] [CrossRef]
- Palahí, M.; Tomé, M.; Pukkala, T.; Trasobares, A.; Montero, G. Site index model for Pinus sylvestris in north-east Spain. For. Ecol. Manag. 2004, 187, 35–47. [Google Scholar] [CrossRef]
- Jordan, L.; Souter, R.; Parresol, B.; Daniels, R.F. Application of the algebraic difference approach for developing self-referencing specific gravity and biomass equations. For. Sci. 2006, 52, 81–92. [Google Scholar]
- Zobel, J.M.; Schubert, M.R.; Granger, J.J. Shortleaf Pine (Pinus echinata) Site Index Equation for the Cumberland Plateau, USA. For. Sci. 2022, 68, 259–269. [Google Scholar] [CrossRef]
- Cieszewski, C.J.; Bailey, R. Generalized algebraic difference approach: Theory based derivation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Bravo-Oviedo, A.; Del Río, M.; Montero, G. Site index curves and growth model for Mediterranean maritime pine (Pinus pinaster Ait.) in Spain. For. Ecol. Manag. 2004, 201, 187–197. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; Tome, M.; Bravo, F.; Montero, G.; Del Rio, M. Dominant height growth equations including site attributes in the generalized algebraic difference approach. Can. J. For. Res. 2008, 38, 2348–2358. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; del Río, M.; Montero, G. Geographic variation and parameter assessment in generalized algebraic difference site index modelling. For. Ecol. Manag. 2007, 247, 107–119. [Google Scholar] [CrossRef]
- Sun, X.; He, Z.; Kabrick, J. Bayesian spatial prediction of the site index in the study of the Missouri Ozark Forest Ecosystem Project. Comput. Stat. Data Anal. 2008, 52, 3749–3764. [Google Scholar] [CrossRef]
- Berger, J.O.; De Oliveira, V.; Sansó, B. Objective Bayesian analysis of spatially correlated data. J. Am. Stat. Assoc. 2001, 96, 1361–1374. [Google Scholar] [CrossRef]
- Fang, Z.; Bailey, R.L. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments. For. Sci. 2001, 47, 287–300. [Google Scholar]
- Calegario, N.; Daniels, R.F.; Maestri, R.; Neiva, R. Modeling dominant height growth based on nonlinear mixed-effects model: A clonal Eucalyptus plantation case study. For. Ecol. Manag. 2005, 204, 11–21. [Google Scholar] [CrossRef]
- Ling, Y.; Zhao, J.; Wang, H.; Liu, Y. Diagnosis of Potential Geographical Distribution of Pinus massoniana under Climate Change. Chin. J. Agrometeorol. 2023, 44, 144. (In Chinese) [Google Scholar]
- Wang, M.; Borders, B.E.; Zhao, D. An empirical comparison of two subject-specific approaches to dominant heights modeling: The dummy variable method and the mixed model method. For. Ecol. Manag. 2008, 255, 2659–2669. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, J.; Zeng, J.; Ming, A.; Liu, X.; Jia, H.; Lei, X.; Lu, Y. Analysis on the Effect of Close-to-nature Transformation of Pinus massoniana Pure Forest Plantation. For. Res. 2023, 36, 31–38. (In Chinese) [Google Scholar]
- Xing, H.; Lu, Y.; Liu, X.; Wang, X.; Jia, H.; Zeng, J. A Study on the Competition Intensity of Masson Pine Forest Stand Based on Near-Natural Transformation. J. Beijing For. Univ. 2016, 38, 42–54. (In Chinese) [Google Scholar]
- Lu, Y.C. The Theory and Practice of Near Natural Forest Management, 1st ed.; Beijing Science and Technology Press: Beijing, China, 2006; pp. 1–10. (In Chinese) [Google Scholar]
- GB/T 26424-2010; Technical Regulations for Inventory for Forest Management Planning and Design. State Forestry Bureau: Beijing, China, 2010.
- Gea-Izquierdo, G.; Cañellas, I.; Montero, G. Site index in agroforestry systems: Age-dependent and age-independent dynamic diameter growth models for Quercus ilex in Iberian open oak woodlands. Can. J. For. Res. 2008, 38, 101–113. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J. Bayesian statistics and modelling. Nat. Rev. Methods Primers 2021, 1, 1. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.A.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar] [CrossRef]
- Drew, T.J.; Flewelling, J.W. Stand density management: An alternative approach and its application to Douglas-fir plantations. For. Sci. 1979, 25, 518–532. [Google Scholar]
- Meredieu, C.; Perret, S.; Dreyfus, P. Modelling dominant height growth: Effect of stand density. In Proceedings of the Modelling Forest Systems. Workshop on the Interface between Reality, Modelling and the Parameter Estimation Processes, Sesimbra, Portugal, 2–5 June 2002; pp. 111–121. [Google Scholar]
- Pienaar, L.V.; Shiver, B.D. The effect of planting density on dominant height in unthinned slash pine plantations. For. Sci. 1984, 30, 1059–1066. [Google Scholar]
- Tymińska-Czabańska, L.; Hawryło, P.; Socha, J. Assessment of the effect of stand density on the height growth of Scots pine using repeated ALS data. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102763. [Google Scholar] [CrossRef]
- Wang, X.P.; Lu, Y.C.; Qin, Y.S.; Peiset, C. Beijing Near Natural Forest Management Technical Guidelines, 1st ed.; China Forestry Publishing House: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Lu, Y.C.; Zhang, W.H.; Cao, X.P. Technical Guidelines for Near Natural Cultivation and Management of Pinus tabulaeformis Forests on the Loess Plateau, 1st ed.; China Forestry Publishing House: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Woodruff, D.R.; Bond, B.J.; Ritchie, G.A.; Scott, W. Effects of stand density on the growth of young Douglas-fir trees. Can. J. For. Res. 2002, 32, 420–427. [Google Scholar] [CrossRef]
- Vallet, P.; Perot, T. Tree diversity effect on dominant height in temperate forest. For. Ecol. Manag. 2016, 381, 106–114. [Google Scholar] [CrossRef]
- Assmann, E. The Principles of Forest Yield Study: Studies in the Organic Production, Structure, Increment and Yield of Forest Stands; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Plauborg, K. Analysis of radial growth responses to changes in stand density for four tree species. For. Ecol. Manag. 2004, 188, 65–75. [Google Scholar] [CrossRef]
- Lu, L.; Wang, H.; Chhin, S.; Duan, A.; Zhang, J.; Zhang, X. A Bayesian Model Averaging approach for modelling tree mortality in relation to site, competition and climatic factors for Chinese fir plantations. For. Ecol. Manag. 2019, 440, 169–177. [Google Scholar] [CrossRef]
- Nothdurft, A. Climate sensitive single tree growth modeling using a hierarchical Bayes approach and integrated nested Laplace approximations (INLA) for a distributed lag model. For. Ecol. Manag. 2020, 478, 118497. [Google Scholar] [CrossRef]
- Jiang, S.; Jomaa, S.; Büttner, O.; Meon, G.; Rode, M. Multi-site identification of a distributed hydrological nitrogen model using Bayesian uncertainty analysis. J. Hydrol. 2015, 529, 940–950. [Google Scholar] [CrossRef]
- Harrison, X.A.; Donaldson, L.; Correa-Cano, M.E.; Evans, J.; Fisher, D.N.; Goodwin, C.E.; Robinson, B.S.; Hodgson, D.J.; Inger, R. A brief introduction to mixed effects modelling and multi-model inference in ecology. PeerJ 2018, 6, e4794. [Google Scholar] [CrossRef]
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.-S.S. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef]
- Stage, A.R. An expression for the effect of aspect, slope, and habitat type on tree growth. For. Sci. 1976, 22, 457–460. [Google Scholar]
- Lihui, M.; Xiaoli, L.; Jie, C.; Youke, W.; Jingui, Y. Effects of slope aspect and rainfall on belowground deep fine root traits and aboveground tree height. Front. Plant Sci. 2021, 12, 684468. [Google Scholar] [CrossRef] [PubMed]
- Méndez-Toribio, M.; Meave, J.A.; Zermeño-Hernández, I.; Ibarra-Manríquez, G. Effects of slope aspect and topographic position on environmental variables, disturbance regime and tree community attributes in a seasonal tropical dry forest. J. Veg. Sci. 2016, 27, 1094–1103. [Google Scholar] [CrossRef]
- Cai, Q.; Liu, Y.; Qian, H.; Liu, R. Inverse effects of recent warming on trees growing at the low and high altitudes of the Dabie Mountains, subtropical China. Dendrochronologia 2020, 59, 125649. [Google Scholar] [CrossRef]
- Zhuang, L.; Axmacher, J.C.; Sang, W. Different radial growth responses to climate warming by two dominant tree species at their upper altitudinal limit on Changbai Mountain. J. For. Res. 2017, 28, 795–804. [Google Scholar] [CrossRef]
- Xing, X.; Qian, J.; Chen, X.; Chen, C.; Sun, J.; Wei, S.; Yimamaidi, D.; Zhanar, Z. Analysis of effects of recent changes in hydrothermal conditions on vegetation in central Asia. Land 2022, 11, 327. [Google Scholar] [CrossRef]
- Ni, Y.; Xiao, W.; Liu, J.; Jian, Z.; Li, M.; Xu, J.; Lei, L.; Zhu, J.; Li, Q.; Zeng, L. Radial growth-climate correlations of Pinus massoniana in natural and planted forest stands along a latitudinal gradient in subtropical central China. Agric. For. Meteorol. 2023, 334, 109422. [Google Scholar] [CrossRef]
- Fekedulegn, D.; Hicks, R.R., Jr.; Colbert, J. Influence of topographic aspect, precipitation and drought on radial growth of four major tree species in an Appalachian watershed. For. Ecol. Manag. 2003, 177, 409–425. [Google Scholar] [CrossRef]
- Johansson, B.; Chen, D. The influence of wind and topography on precipitation distribution in Sweden: Statistical analysis and modelling. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 1523–1535. [Google Scholar] [CrossRef]
- Pang, S.; Wang, X.; Melching, C.S.; Feger, K.-H. Development and testing of a modified SWAT model based on slope condition and precipitation intensity. J. Hydrol. 2020, 588, 125098. [Google Scholar] [CrossRef]





| Variable | Training Set (70%) | Validation Set (30%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean | Std. | Min. | Max. | Mean | Std. | |
| Age/year | 3.00 | 40.00 | 20.31 | 6.75 | 4.00 | 36.00 | 19.73 | 6.94 |
| Dominant height/m | 4.43 | 25.80 | 16.51 | 3.83 | 4.95 | 26.60 | 16.18 | 4.37 |
| Altitude/m | 169.00 | 800.00 | 378.70 | 121.52 | 179.00 | 800.00 | 405.90 | 150.72 |
| Slope/° | 0.00 | 42.00 | 23.52 | 9.63 | 0.00 | 42.00 | 25.89 | 8.86 |
| Stand Density/trees/ha | 125.00 | 1775.00 | 733.25 | 380.41 | 75.00 | 1625.00 | 765.66 | 362.30 |
| Site Factors | Class | |||||
|---|---|---|---|---|---|---|
| Altitude | 4 classes by 200 m (0–800 m) | |||||
| Slope | 15° | ° | ° | |||
| Aspect | Sunny slope | Semi-sunny slope | Shady and semi-shady slope | None slope | ||
| Slope position | Ridge | Upper slope | Middle slope | Lower slope | Valley | Flat |
| Soil type | Red earth | Brick-red earth | Purple earth | Yellow earth | Lateritic red soil | |
| Base Equation | Free Parameters | GADA Dynamic Equation | No. | |
|---|---|---|---|---|
| Gompertz: | E1 | |||
| E2 | ||||
| Hossfeld IV: | E3 | |||
| Korf: | E4 | |||
| E5 | ||||
| Richards: | E6 | |||
| E7 |
| Df | Sum Sq | Mean Sq | F Value | ) | |
|---|---|---|---|---|---|
| Density | 2 | 7.265 | 3.633 | 3.496 | 0.075 |
| Residuals | 9 | 9.351 | 1.039 |
| Df | Sum Sq | Mean Sq | F Value | ) | |
|---|---|---|---|---|---|
| Management mode | 1 | 1.995 | 1.995 | 0.770 | 0.395 |
| Residuals | 14 | 36.284 | 2.592 |
| No. | Parameters | Estimate | Std. Error | p-Value | R2 | RMSE | MAE | AIC |
|---|---|---|---|---|---|---|---|---|
| M1 | b | 0.068639 | 0.007925 | <0.001 | 0.9134 | 1.1963 | 0.9369 | 627.83 |
| c2 | 0.621136 | 0.030307 | <0.001 | |||||
| M2 | b | 0.067648 | 0.007848 | <0.001 | 0.9225 | 1.1320 | 0.8967 | 602.47 |
| c2 | 7.280496 | 0.399721 | <0.001 | |||||
| M3 | a1 | 22.281017 | 0.824898 | <0.001 | 0.9317 | 1.0625 | 0.8915 | 550.01 |
| b | 1.274450 | 0.110856 | <0.001 | |||||
| c1 | −0.001802 | 0.000218 | <0.001 | |||||
| c2 | 5.184688 | 2.183751 | 0.019 | |||||
| M4 | b1 | −9.911901 | 3.712181 | 0.008 | 0.9341 | 1.0435 | 0.8521 | 563.14 |
| b2 | 2.911217 | 1.121908 | 0.010 | |||||
| c | 0.271303 | 0.099897 | 0.007 | |||||
| M5 | a1 | 1.045529 | 0.012011 | <0.001 | 0.9192 | 1.1554 | 0.9167 | 604.51 |
| c | 0.100515 | 0.069586 | 0.150 | |||||
| M6 | b | 0.031715 | 0.010543 | 0.003 | 0.8896 | 1.3511 | 1.0693 | 661.8762 |
| c1 | −0.797494 | 0.122048 | <0.001 | |||||
| c2 | 0.484051 | 0.072742 | <0.001 | |||||
| M7 | b | 0.014400 | 0.011646 | 0.218 | 0.9260 | 1.1061 | 0.8753 | 586.15 |
| c2 | 3.290686 | 0.189392 | <0.001 |
| Random Effects | Random Effects Construct Variables | Levels | 1 | Std. Error | Std. Error | Std. Error | R² | RMSE | MAE | AIC | No. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Altitude | 4 | −8.465137 | 3.157405 | 2.476417 | 0.955311 | 0.228937 | 0.099898 | 0.9347 | 1.0387 | 0.8447 | 564.88 | M4.1 | |
| Slope | 3 | −9.749985 | 2.824700 | 2.890913 | 0.840261 | 0.273461 | 0.074471 | 0.9352 | 1.0351 | 0.8499 | 569.06 | M4.2 | |
| Aspect | 4 | −8.636531 | 3.177930 | 2.562699 | 0.973702 | 0.242117 | 0.100209 | 0.9366 | 1.0242 | 0.8381 | 568.23 | M4.3 | |
| Altitude × Slope | 11 | −9.910294 | 3.711532 | 2.910942 | 1.121779 | 0.271305 | 0.099903 | 0.9341 | 1.0435 | 0.8520 | 569.14 | M4.4 | |
| Altitude × Aspect | 11 | −7.186774 | 2.646211 | 2.127407 | 0.802359 | 0.193630 | 0.098107 | 0.9356 | 1.0315 | 0.8390 | 565.06 | M4.5 | |
| Slope × Aspect | 10 | −9.468011 | 3.565104 | 2.782777 | 1.076361 | 0.260356 | 0.100196 | 0.9346 | 1.0401 | 0.8490 | 565.15 | M4.6 | |
| Altitude × Slope × Aspect | 23 | −8.978159 | 3.380999 | 2.635419 | 1.019855 | 0.246411 | 0.100142 | 0.9348 | 1.0386 | 0.8479 | 565.20 | M4.7 |
| Method | Parameters | Estimate | Std. Error | p-Value | R2 | RMSE | MAE | AIC |
|---|---|---|---|---|---|---|---|---|
| Nonlinear Least Squares (M4) | −9.911901 | 3.712181 | 0.008 | 0.9341 | 1.0435 | 0.8521 | 563.14 | |
| 2.911217 | 1.121908 | 0.010 | ||||||
| 0.271303 | 0.099897 | 0.007 | ||||||
| Bayesian Approach (M4.8) | 9.407929 | 0.007374 | - | 0.9220 | 1.1357 | 0.8975 | - | |
| −0.738057 | 0.001373 | - | ||||||
| 0.268599 | 0.000014 | - | ||||||
| Nonlinear Mixed-Effects Model (M4.3) | −8.636531 | 3.177930 | 0.007 | 0.9366 | 1.0242 | 0.8381 | 568.23 | |
| 2.562699 | 0.973702 | 0.009 | ||||||
| 0.242117 | 0.100209 | 0.017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, K.; Duan, G.; Wu, Y.; Wang, Z.; Liu, X. Site Index Model for Southern Subtropical Masson Pine Forests Using Stand Dominant Height. Forests 2024, 15, 87. https://doi.org/10.3390/f15010087
Zou K, Duan G, Wu Y, Wang Z, Liu X. Site Index Model for Southern Subtropical Masson Pine Forests Using Stand Dominant Height. Forests. 2024; 15(1):87. https://doi.org/10.3390/f15010087
Chicago/Turabian StyleZou, Kailun, Guangshuang Duan, You Wu, Zhanyin Wang, and Xianzhao Liu. 2024. "Site Index Model for Southern Subtropical Masson Pine Forests Using Stand Dominant Height" Forests 15, no. 1: 87. https://doi.org/10.3390/f15010087
APA StyleZou, K., Duan, G., Wu, Y., Wang, Z., & Liu, X. (2024). Site Index Model for Southern Subtropical Masson Pine Forests Using Stand Dominant Height. Forests, 15(1), 87. https://doi.org/10.3390/f15010087





