Enhancement Method Based on Multi-Strategy Improved Pelican Optimization Algorithm and Application to Low-Illumination Forest Canopy Images
Abstract
1. Introduction
- Aiming at the defects of the POA, which is slow in convergence, weak in exploitation, and easily falls into local optimum, it is improved using nonlinear decreasing coefficients, the Hardy–Weinberg principle, and diversity variation operation, respectively.
- MIPOA is used to determine the optimal parameters of IBF, which overcomes the low efficiency of IBF parameter selection and effectively improves the contrast of low-illumination forest canopy images.
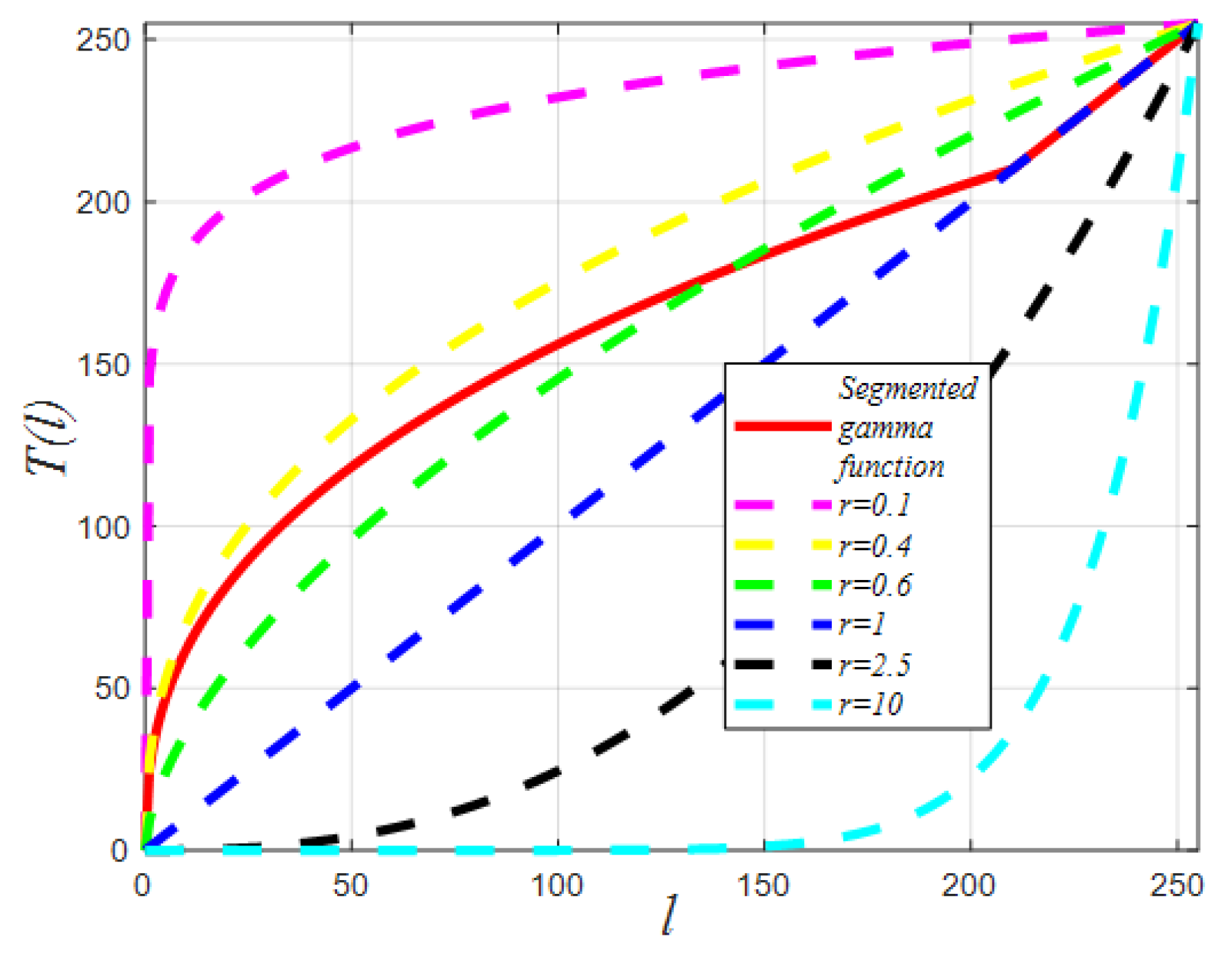
- Owing to the uneven brightness distribution of forest canopy images, a segmented gamma correction function was designed to equalize the brightness of low-illumination forest canopy images.
- We investigated the performance of the MIPOA and MIPOA-based enhancement methods on the benchmark function and low-illumination forest canopy image problem, respectively.
- We compared MIPOA with five POA-variant algorithms. MIPOA performed better than the other POA-variant algorithms. The enhancement results show that the MIPOA-based enhancement method effectively improves enhancement quality.
2. Establishment of the POA Model
2.1. The Standard POA
2.1.1. Initialization
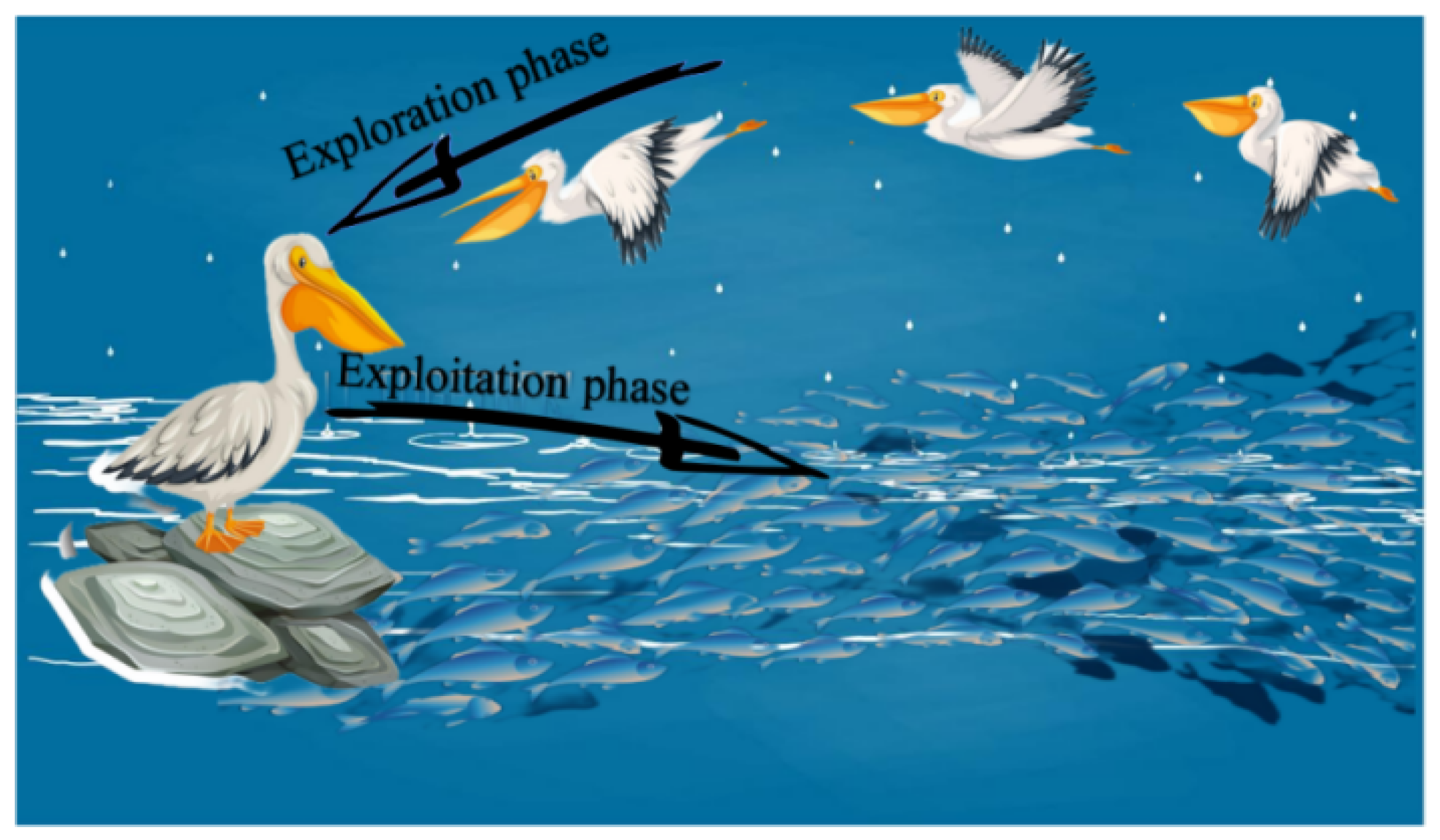
2.1.2. Exploration Phase
2.1.3. Exploitation Phase
2.2. MIPOA
| Algorithm 1 Pseudo-code of POA |
|
2.2.1. Dynamic Nonlinear Decreasing Factor
2.2.2. Hardy–Weinberg Principle
2.2.3. Diversity Variation Perturbation
- 1.
- Set the population aggregation threshold d.
- 2.
- Calculate the degree of population aggregation .
- 3.
- Judge whether is less than the threshold d. If less, execute step 4; otherwise, jump to step 2.
- 4.
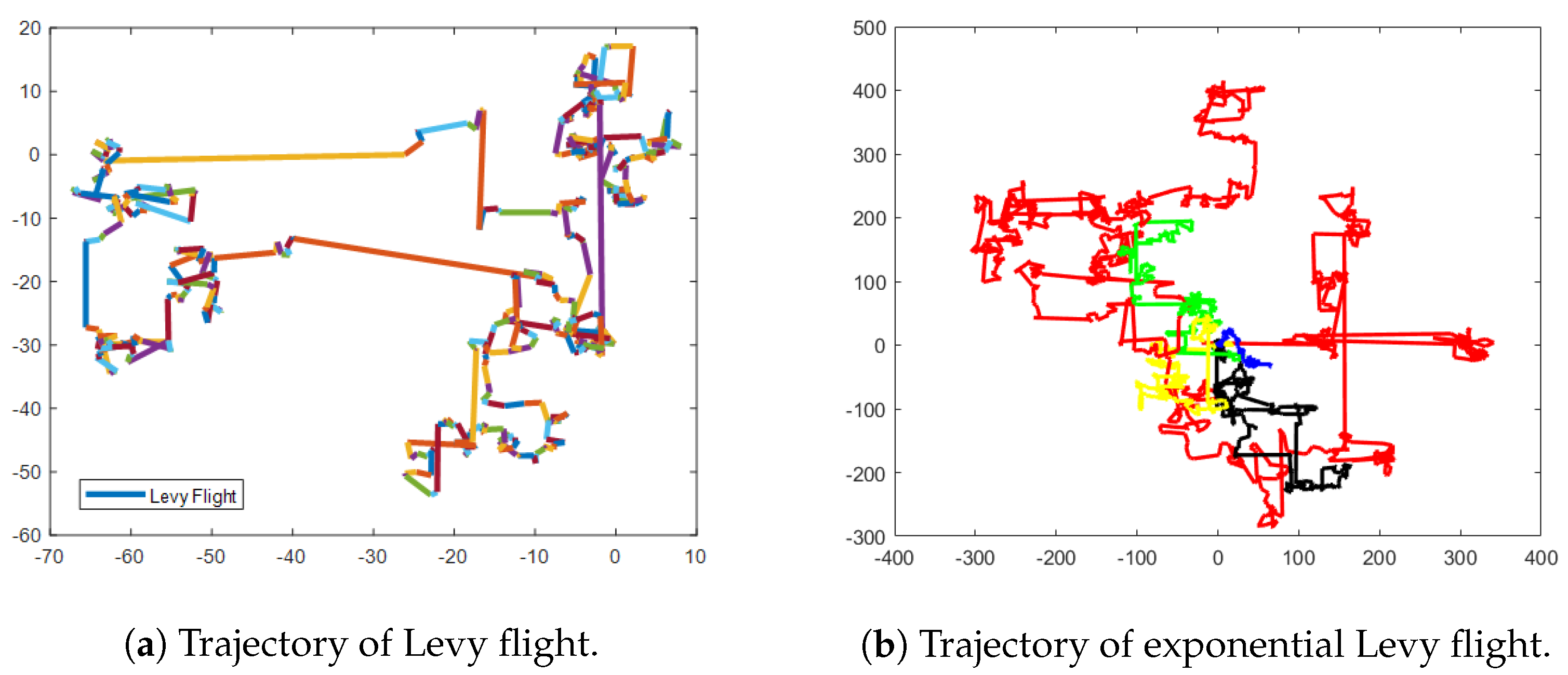
- Randomly selected population particles for exponential Levy flight.
2.2.4. The Framework of the MIPOA
| Algorithm 2 Pseudo-code of MIPOA |
|
3. Low-Illumination Forest Canopy Image Enhancement Based on the MIPOA
3.1. Data Sources and Analysis
3.2. IBF
3.3. Segmented Gamma Function
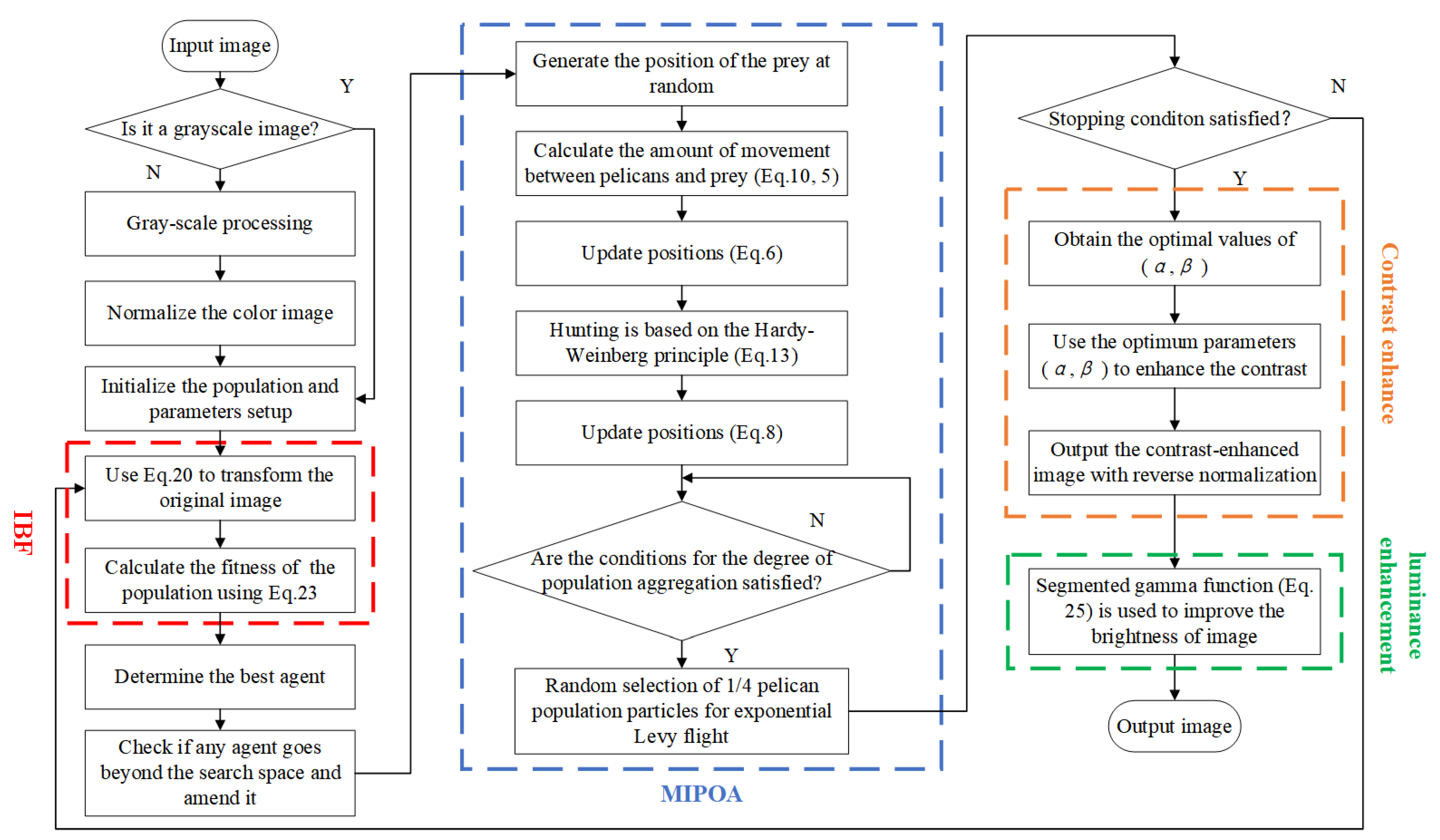
3.4. Algorithm Implementation
- 1.
- Input the image to be enhanced.
- 2.
- Judge whether the input image is a grayscale image. If this is true, then normalization is performed directly. If it is a color image, then grayscale processing is performed first followed by normalization.
- 3.
- Generate the population and parameters of MIPOA.
- 4.
- Apply (20) to achieve image contrast enhancement.
- 5.
- Calculate the fitness value of the population using (23).
- 6.
- Update the best agent.
- 7.
- Check whether the agent goes beyond the search space.
- 8.
- Generate the position of the prey at random.
- 9.
- Calculate the amount of movement between the pelicans and prey .
- 10.
- Update new positions (6).
- 11.
- Perform hunting based on the Hardy–Weinberg principle (13).
- 12.
- Update new positions (8).
- 13.
- Determine whether the aggregation of populations satisfies these requirements.
- 14.
- If the conditions are met, perform random selection of pelican population particles for exponential Levy flight.
- 15.
- Repeat Steps 3–14 until the algorithm meets the stop condition.
- 16.
- Output the result of MIPOA as the optimal values of for IBF.
- 17.
- Use the optimum parameters found in Step 16 to enhance the contrast of the input image.
- 18.
- Output the contrast-enhanced image with reverse normalization.
- 19.
- Use the segmented gamma function to improve the brightness of the image (25).
- 20.
- Output the enhanced image.
4. Performance Testing and Analysis of the MIPOA
4.1. Benchmark Test Functions
4.2. Experimental Setup
4.3. Comparative Results and Analysis of the MIPOA with POA Variants
4.3.1. Effect of the Value of the Threshold Parameter redd on the Performance of the Algorithm
4.3.2. Optimization Accuracy Analysis
4.3.3. Stability Analysis
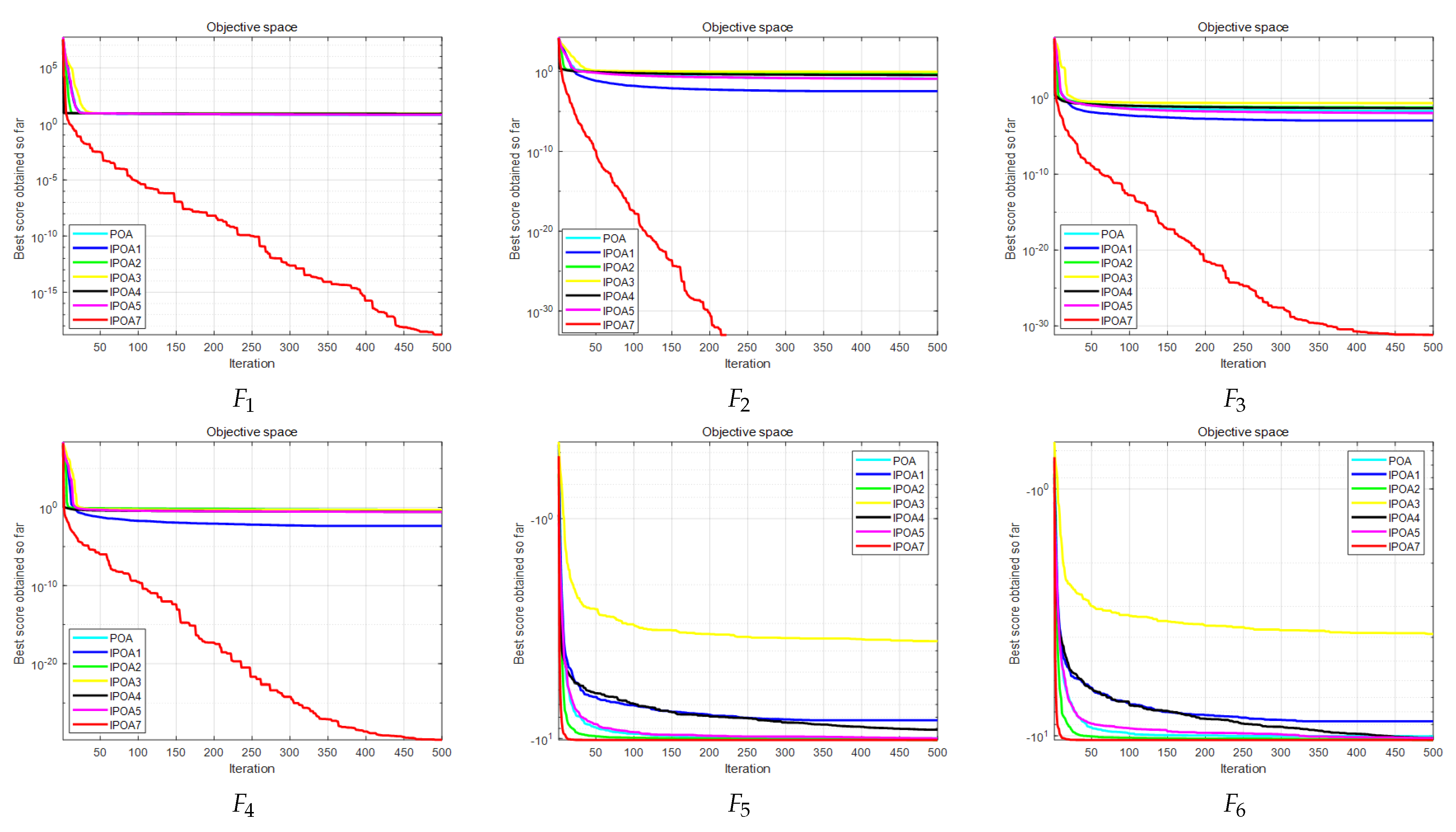
4.3.4. Convergence Analysis
4.3.5. Statistical Analysis
- (1)
- The distribution is free, and assuming that the sample data follows a normal distribution is unnecessary.
- (2)
- Strong stability; not affected by outliers.
- (3)
- Simple, convenient, intuitive, and understandable.
5. Results and Discussion of MIPOA-Based Enhancement Algorithm
5.1. Evaluation Indicators
5.1.1. FSIM
5.1.2. Entropy
5.1.3. CII
5.1.4. Average Gradient
5.1.5. Pixel Mean
5.2. Analysis of IBF Parameter Optimization Experiment Results
5.3. Experimental Results and Analysis of Low-Illumination Forest Canopy Images
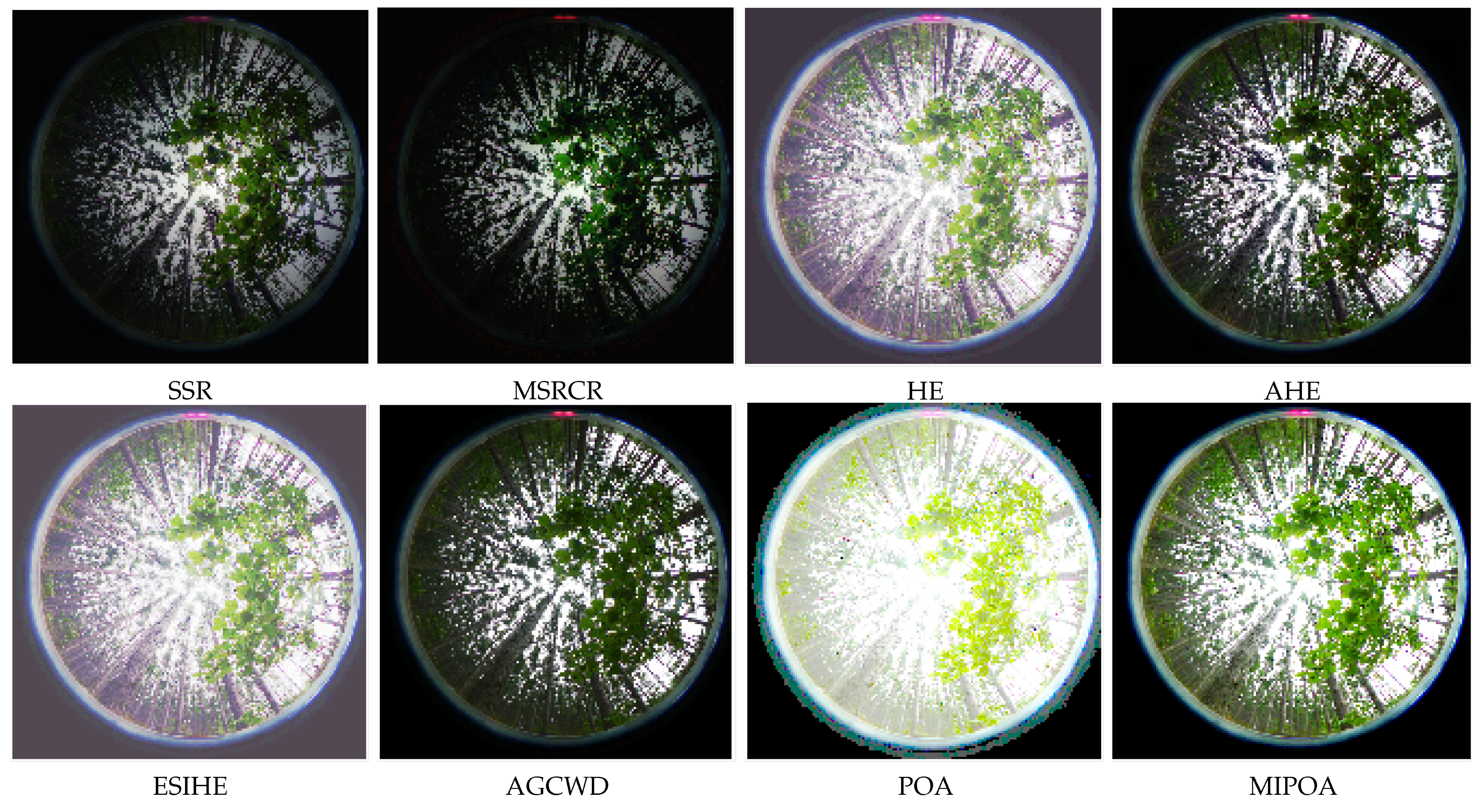
5.3.1. Subjective Evaluation Analysis
5.3.2. Objective Evaluation Analysis
6. Conclusions and Outlook
- The nonlinear decreasing coefficient, Hardy–Weinberg theorem, and diversity variant operation are incorporated into the POA mathematical model to further enhance the algorithm’s ability to explore, exploit, and escape local optimal solutions. The experimental results of the benchmarking function demonstrate that the performance of MIPOA is comprehensively improved and surpasses the five POA variant algorithms in terms of optimization search accuracy, stability, convergence, and statistical analysis.
- IBF is an effective method for improving the contrast of an image; however, its parameters require manual configuration, and parameter selection is inefficient. In IBF parameter optimization, the MIPOA outperforms PSO, ChOA, FAG, HWOA, and POA in FSIM, entropy, and CII. This indicates that the MIPOA algorithm improves the optimization accuracy of the IBF parameters such that the enhanced canopy image exhibits less distortion, contains rich information, and demonstrates effectively enhanced contrast.
- Based on the characteristics of low brightness and uneven distribution of forest canopy images, a segmented gamma correction function was designed to increase the brightness of dark areas while avoiding over-enhancement of the bright regions. In low-light forest canopy image enhancement, the MIPOA-based enhancement method achieves moderate pixel averages and high average gradients, which are superior to those of six traditional image enhancement methods: SSR, MSRCR, HE, AHE, ESIHE, and AGCWD.
- Nevertheless, this study has certain limitations. To prevent overexposure of the bright regions, the segmented gamma correction function does not perform any processing on the bright areas. This preserved the brightness of the bright regions. In the event that the image is exposed and conceals its details, the processing effect of the proposed method, although superior to traditional enhancement algorithms, is not as effective as that of the canopy image with low and normal illumination. Therefore, further development of the segmented gamma correction function is necessary to expose the high-brightness areas. Additionally, the MIPOA algorithm demonstrates strong superiority in the benchmark function, which can be applied to practical engineering problems, such as structural optimization.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Woldamanuel, E.M. Grayscale Image Enhancement Using Water Cycle Algorithm. IEEE Access 2023, 11, 86575–86596. [Google Scholar] [CrossRef]
- Sengupta, D.; Biswas, A.; Gupta, P. Non-linear weight adjustment in adaptive gamma correction for image contrast enhancement. Multimed. Tools Appl. 2021, 80, 3835–3862. [Google Scholar] [CrossRef]
- Prakash, A.; Bhandari, A.K. Cuckoo search constrained gamma masking for MRI image contrast enhancement. Multimed. Tools Appl. 2023, 82, 40129–40148. [Google Scholar] [CrossRef]
- Asiri, A.A.; Soomro, T.A.; Shah, A.A.; Pogrebna, G.; Irfan, M.; Alqahtani, S. Optimized Brain Tumor Detection: A Dual-Module Approach for MRI Image Enhancement and Tumor Classification. IEEE Access 2024, 12, 42868–42887. [Google Scholar] [CrossRef]
- Mishra, A.K.; Choudhry, M.S.; Kumar, M. Underwater image enhancement using multiscale decomposition and gamma correction. Multimed. Tools Appl. 2023, 82, 15715–15733. [Google Scholar] [CrossRef]
- Zhang, W.; Zhuang, P.; Sun, H.H.; Li, G.; Kwong, S.; Li, C. Underwater Image Enhancement via Minimal Color Loss and Locally Adaptive Contrast Enhancement. IEEE Trans. Image Process. 2022, 31, 3997–4010. [Google Scholar] [CrossRef] [PubMed]
- Sreeshan, K.; Dinesh, R.; Renji, K. Nondestructive inspection of aerospace composite laminate using thermal image processing. SN Appl. Sci. 2020, 2, 1830. [Google Scholar] [CrossRef]
- Bhandari, A.K. A logarithmic law based histogram modification scheme for naturalness image contrast enhancement. J. Ambient Intell. Humaniz. Comput. 2020, 11, 1605–1627. [Google Scholar] [CrossRef]
- Stark, J.A. Adaptive image contrast enhancement using generalizations of histogram equalization. IEEE Trans. Image Process. 2000, 9, 889–896. [Google Scholar] [CrossRef]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vision Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Liu, J. Research on Low Illumination Image Enhancement Based on Metaheuristic Algorithm; Tongfang Knowledge Network (Beijing) Technology Co., Ltd.: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Zuiderveld, K.J. Contrast Limited Adaptive Histogram Equalization. In Graphics Gems; Academic Press: Cambridge, MA, USA, 1994; pp. 474–485. [Google Scholar] [CrossRef]
- Huang, S.C.; Cheng, F.C.; Chiu, Y.S. Efficient Contrast Enhancement Using Adaptive Gamma Correction With Weighting Distribution. IEEE Trans. Image Process. 2013, 22, 1032–1041. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, H.; Kong, N.S.P. Brightness Preserving Dynamic Histogram Equalization for Image Contrast Enhancement. IEEE Trans. Consum. Electron. 2007, 53, 1752–1758. [Google Scholar] [CrossRef]
- Singh, K.; Kapoor, R. Image enhancement using Exposure based Sub Image Histogram Equalization. Pattern Recognit. Lett. 2014, 36, 10–14. [Google Scholar] [CrossRef]
- Senthamarai, G.; Santhi, K. Dynamic multi-histogram equalisation for image contrast enhancement with improved brightness preservation. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; pp. 1205–1209. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Liu, A.; Wu, Q.; Bi, L. Global and Adaptive Contrast Enhancement for Low Illumination Gray Images. IEEE Access 2019, 7, 163395–163411. [Google Scholar]
- Choi, D.H.; Jang, I.H.; Kim, M.H.; Kim, N.C. Color image enhancement using single-scale retinex based on an improved image formation model. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 7–18. [Google Scholar]
- Rahman, Z.; Jobson, D.J.; Woodell, G.A. Multi-scale retinex for color image enhancement. In Proceedings of the ICIP (3), Lausanne, Switzerland, 19 September 1996; pp. 1003–1006. [Google Scholar] [CrossRef]
- Jobson, D.J.; Rahman, Z.; Woodell, G.A. A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef]
- Du, N.; Luo, Q.; Du, Y.; Zhou, Y. Color Image Enhancement: A Metaheuristic Chimp Optimization Algorithm. Neural Process. Lett. 2022, 54, 4769–4808. [Google Scholar] [CrossRef]
- Qu, X.; Yu, Y.; Bian, S.; Xiao, C. Design of a Contrast Enhancement Algorithm for Visual Communication Images Based on PSO. In Proceedings of the 2023 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 25–27 September 2023; pp. 445–449. [Google Scholar] [CrossRef]
- Song, W.; Lin, C.B. Improved adaptive image enhancement algorithm based on SSA. In Proceedings of the 2023 IEEE International Conference on Control, Electronics and Computer Technology (ICCECT), Jilin, China, 28–30 April 2023; pp. 54–57. [Google Scholar] [CrossRef]
- Asokan, A.; Popescu, D.E.; Anitha, J.; Hemanth, D.J. Algorithm Based Non-linear Contrast Stretching for Satellite Image Enhancement. Geosciences 2020, 10, 78. [Google Scholar] [CrossRef]
- Braik, M. Hybrid enhanced whale optimization algorithm for contrast and detail enhancement of color images. Clust. Comput. 2024, 27, 231–267. [Google Scholar] [CrossRef]
- Shen, R.; Zhou, M.; Ling, S. Image Enhancement Technology Based on Improved FA Algorithm and Incomplete Beta Function. J. Chongqing Technol. Bus. Univ. Nat. Sci. Ed. 2023, 40, 57–63. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Zhou, J.; Zheng, R.; Hou, H. Improved pelican algorithm for optimizing LSTM based temperature prediction of reheating furnace billets. Foreign Electron. Meas. Technol. 2023, 42, 174–179. [Google Scholar] [CrossRef]
- Ye, Y.; Wei, W. Feature selection method based on pelican optimization algorithm integrated with multi-strategies. Microelectron. Comput. 2023, 40, 19–25. [Google Scholar] [CrossRef]
- Yang, G.; Hu, H.; Wang, X.; Feng, S.; Wang, F.; Sun, J. Research on Image Matching Method Based on Mass Perturbation Pelican Optimization Algorithm. J. Zhengzhou Univ. Nat. Sci. Ed. 2023, 47, 1–7. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, T.; Li, C.; Jie, J.; Shi, H.; Yang, H. Improved Pelican Optimization Algorithm Fused with Multi-Strategy. Control Eng. China 2023, 05, 1–15. [Google Scholar] [CrossRef]
- Tuerxun, W.; Xu, C.; Haderbieke, M.; Guo, L.; Cheng, Z. A Wind Turbine Fault Classification Model Using Broad Learning System Optimized by Improved Pelican Optimization Algorithm. Machines 2022, 10, 407. [Google Scholar] [CrossRef]
- Igel, C.; Toussaint, M. Recent results on no-free-lunch theorems for optimization. arXiv 2003, arXiv:cs/0303032. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Saari, M.M.; Daniyal, H. Barnacles Mating Optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103330. [Google Scholar] [CrossRef]
- Chawla, M.; Duhan, M. Levy flights in Metaheuristics Optimization Algorithms-A Review. Appl. Artif. Intell. 2018, 32, 802–821. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Song, W.; Lang, C.; Xing, Z.; Sun, K. Multiverse Optimization Algorithm Based on Lévy Flight Improvement for Multithreshold Color Image Segmentation. IEEE Access 2019, 7, 32805–32844. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Song, W.; Oliva, D.; Lang, C.; Li, Y. Masi Entropy for Satellite Color Image Segmentation Using Tournament-Based Lévy Multiverse Optimization Algorithm. Remote Sens. 2019, 11, 942. [Google Scholar] [CrossRef]
- Zhao, X.; Zhu, L.; Wu, B. An improved mayfly algorithm based on Kapur entropy for multilevel thresholding color image segmentation. J. Intell. Fuzzy Syst. 2023, 44, 365–380. [Google Scholar] [CrossRef]
- Su, M.; Zhao, X.; Hongluan, Z.; Wei, Z.; Xiaojun, L. Improvement of Traffic Signal Timing Based on Harris Hawks Optimization Algorithm with Multiple Strategies. Comput. Technol. Dev. 2023, 33, 101–107. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Z.; Li, Z.; Wu, Z. 3D Path Planning of Unmanned Aerial Vehicle Based on Enhanced Sand Cat Swarm Optimization Algorithm. Acta Armamentarii 2023, 44, 3382–3393. [Google Scholar] [CrossRef]
- Wei, Z.; Li, X.; Wang, L. Improved TDOA3d positioning algorithm based on adaptive Levy flight. J. Hebei Univ. Nat. Sci. Ed. 2023, 43, 207–215. [Google Scholar] [CrossRef]
- Zhu, L.; Shao, S.; Jing, W.; Liu, L. PSO-Optimized-Fast Segmentation Algorithm for 3D Otsu Forest Canopy Image. J. Harbin Univ. Sci. Technol. 2019, 24, 128–133. [Google Scholar] [CrossRef]
- Li, C.; Li, M.; Iizuka, K.; Liu, J.; Chen, K.; Li, Y. Effects of Forest Canopy Structure on Forest Aboveground Biomass Estimation Using Landsat Imagery. IEEE Access 2021, 9, 5285–5295. [Google Scholar] [CrossRef]
- Brusa, A.; Bunker, D.E. Increasing the precision of canopy closure estimates from hemispherical photography: Blue channel analysis and under-exposure. Agric. For. Meteorol. 2014, 195–196, 102–107. [Google Scholar] [CrossRef]
- Li, K.; Huang, X.; Zhang, J.; Sun, Z.; Huang, J.; Sun, C.; Xie, Q.; Song, W. A New Method for Forest Canopy Hemispherical Photography Segmentation Based on Deep Learning Forests. Forests 2020, 11, 1366. [Google Scholar] [CrossRef]
- Li, T.; Lin, J.; Wu, W.; Jiang, R. Effects of Illumination Conditions on Individual Tree Height Extraction Using UAV LiDAR: Pilot Study of a Planted Coniferous Stand. Forests 2024, 15, 758. [Google Scholar] [CrossRef]
- Du, Z.; Zheng, G.; Shen, G.; Moskal, L.M. Characterizing spatiotemporal variations of forest canopy gaps using aerial laser scanning data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102588. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J. Adaptive Enhancement of Optoelectronic Images Based on ISSA and Incomplete Beta Function. J. Chifeng Univ. Nat. Sci. Ed. 2021, 37, 25–29. [Google Scholar] [CrossRef]
- Fan, X.; Sun, Z.; Tian, E.; Yin, Z.; Cao, G. Medical image contrast enhancement based on improved sparrow search algorithm. Int. J. Imaging Syst. Technol. 2023, 33, 389–402. [Google Scholar] [CrossRef]
- Shen, R.; Zhou, M. Image Enhancement Based on Improved MCLPSO Algorithm and Non-Complete Beta Function. J. Heilongjiang Univ. Technol. Compr. Ed. 2023, 23, 71–78. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Wu, Q.; Bi, L. An adaptive enhancement method for low illumination color images. Appl. Intell. 2021, 51, 202–222. [Google Scholar] [CrossRef]
- Majumdar, P.; Das, S.; Bhattacharya, D. Honey Badger algorithm using lens opposition based learning and local search algorithm. Evol. Syst. 2024, 15, 335–360. [Google Scholar] [CrossRef]
- Akl, D.T.; Saafan, M.M.; Haikal, A.Y.; El-Gendy, E.M. IHHO: An improved Harris Hawks optimization algorithm for solving engineering problems. Neural Comput. Applic. 2024, 36, 12185–12298. [Google Scholar] [CrossRef]
- Nasab, S.T.M.; Abualigah, L. Improve Harris Hawkes optimizer algorithm via Laplace crossover. J. Ambient Intell. Humaniz. Comput. 2024, 15, 2057–2072. [Google Scholar] [CrossRef]
- Abualigah, L.; Habash, M.; Hanandeh, E.S.; Hussein, A.M.; Shinwan, M.A.; Zitar, R.A.; Jia, H. Improved Reptile Search Algorithm by Salp Swarm Algorithm for Medical Image Segmentation. J. Bionic Eng. 2023, 20, 1766–1790. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.; Wei, X.; Huang, H. A chaotic adaptive butterfly optimization algorithm. Evol. Intel. 2024, 17, 493–511. [Google Scholar] [CrossRef]
- Wu, B.; Zhu, L.; Li, X. Giza pyramids construction algorithm with gradient contour approach for multilevel thresholding color image segmentation. Appl Intell. 2023, 53, 21248–21267. [Google Scholar] [CrossRef]
- Abualigah, L.; Oliva, D.; Jia, H.; Gul, F.; Khodadadi, N.; Hussien, A.G.; Shinwan, M.A.; Ezugwu, A.E.; Abuhaija, B.; Zitar, R.A. Improved prairie dog optimization algorithm by dwarf mongoose optimization algorithm for optimization problems. Multim. Tools Appl. 2024, 83, 32613–32653. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, L.; Wu, B.; Wang, J.; Zhao, X.; Ryspayev, A. An efficient multilevel thresholding segmentation method based on improved chimp optimization algorithm. J. Intell. Fuzzy Syst. 2023, 44, 4693–4715. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, M.; Liu, Y.; Chen, Y.; He, K.; Liu, Z. A modified shuffled frog leaping algorithm with inertia weight. Sci. Rep. 2024, 14, 4146. [Google Scholar] [CrossRef]
- Qu, P.; Yuan, Q.; Du, F.; Gao, Q. An improved manta ray foraging optimization algorithm. Sci. Rep. 2024, 14, 10301. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yuan, Q.; Shi, H.; Han, M. Multi-strategy Improved Seagull Optimization Algorithm. Int. J. Comput. Intell. Syst. 2023, 16, 154. [Google Scholar] [CrossRef]
- Chauhan, S.; Vashishtha, G.; Abualigah, L.; Kumar, A. Boosting salp swarm algorithm by opposition-based learning concept and sine cosine algorithm for engineering design problems. Soft Comput. 2023, 27, 18775–18802. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Zhang, W.; Bi, L. Mine image enhancement using adaptive bilateral gamma adjustment and double plateaus histogram equalization. Multim. Tools Appl. 2022, 81, 12643–12660. [Google Scholar] [CrossRef]
- Dai, L.; Qi, P.; Lu, H. Image Enhancement Method in Underground Coal Mines Based on an Improved Particle Swarm Optimization Algorithm. Appl. Sci. 2023, 13, 3254. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Z.; Yuan, X.; Wu, X. Adaptive image enhancement method for correcting low-illumination images. Inf. Sci. 2019, 496, 25–41. [Google Scholar] [CrossRef]
- Bhateja, V.; Misra, M.; Urooj, S. Non-Linear Polynomial Filters for Edge Enhancement of Mammograms. Comput. Methods Programs Biomed. 2016, 129, 125–134. [Google Scholar] [CrossRef]






| No. | Method | Algorithm Performance Improvement |
|---|---|---|
| [28] | Introducing the sine–cosine algorithm and linear weights w in the POA exploratory phase | Improving the population’s optimization accuracy |
| Perturbing the new individuals after the population iteration is completed | Increasing the convergence accuracy of the population | |
| [29] | Good point set initialization populations | Improving exploration capabilities |
| Inverse computation of pelican positions using reverse difference evolutionary algorithm | Fast approach to the optimal solution | |
| Introducing an adaptive t-variation perturbation strategy near the optimal solution | Improving convergence accuracy and avoiding falling into local optimal solutions | |
| [30] | A new quality perturbation method is introduced. The principle is to converge to a better solution by detecting points near the distribution points | Effectively improves the convergence accuracy of the POA algorithm when dealing with multi-peak functions |
| [31] | Tent chaotic and refractive reverse learning strategies to initializing pelican populations | Increasing the diversity of populations |
| Nonlinear inertia weighting factors | Improving the convergence speed of the algorithm | |
| Leader strategy of the salp swarm algorithm | Coordinate algorithm exploitation and exploration capabilities | |
| [32] | Initialization of pelican populations using Tent chaos mapping | Improving the algorithm’s global search capability |
| The dynamic weighting factor helps the pelican particles to update their positions constantly | The algorithm is motivated to perform a better localized search while speeding up convergence |
| Style | Functions | Dim | Range | |
|---|---|---|---|---|
| Unimodal | 30 | [−30,30] | 0 | |
| 30 | [−100,100] | 0 | ||
| Multimodal | 30 | [−50,50] | 0 | |
| 30 | [−50,50] | 0 | ||
| Fixed- dimension | 4 | [0,10] | −10.1532 | |
| 4 | [0,10] | −10.4028 |
| d | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| −10.1532 | −10.1532 | −10.1532 | −10.1532 | −10.1532 | −10.1532 | |
| −10.4028 | −10.4028 | −10.4028 | −10.4028 | −10.4028 | −10.4028 |
| Function | IPOA1 | IPOA2 | IPOA3 | IPOA4 | IPOA5 | POA | MIPOA |
|---|---|---|---|---|---|---|---|
| 6.845 | 7.7161 | 8.0252 | 7.7614 | 6.4686 | 6.3346 | ||
| 0.50931 | 0.93683 | 0.24565 | 0.10587 | 0.14188 | 0 | ||
| 0.24127 | |||||||
| 0.52224 | 0.49832 | 0.2703 | 0.23057 | 0.33185 | |||
| −7.4037 | −10.151 | −3.824 | −8.4475 | −9.471 | −9.6433 | −10.1532 | |
| −8.152 | −10.4008 | −3.6839 | −9.8673 | −10.2244 | −8.9854 | −10.4028 |
| Function | IPOA1 | IPOA2 | IPOA3 | IPOA4 | IPOA5 | POA | MIPOA |
|---|---|---|---|---|---|---|---|
| 0.38883 | 0.8502 | 0.24278 | 0.18844 | 0.57132 | 0.68305 | ||
| 0.2642 | 0.1496 | 0.19721 | 0.14571 | 0.15422 | 0 | ||
| 0.24374 | 0.10386 | 0.20668 | 0.1758 | 0.19504 | |||
| 2.4497 | 0.5296 | 2.4398 | 1.7617 | 1.5555 | |||
| 2.5498 | 0.77742 | 1.6205 | 0.97018 | 2.3906 |
| Function | MIPOA vs. IPOA1 | MIPOA vs. IPOA2 | MIPOA vs. IPOA3 | MIPOA vs. IPOA4 | MIPOA vs. IPOA5 | MIPOA vs. POA |
|---|---|---|---|---|---|---|
| Image | PSO | ChOA | FAG | HWOA | POA | MIPOA |
|---|---|---|---|---|---|---|
| L1 | 0.4196 | 0.7409 | 0.6450 | 0.6457 | 0.6444 | 0.7409 |
| L2 | 0.7891 | 0.7542 | 0.7863 | 0.7866 | 0.7861 | 0.7872 |
| L3 | 0.4715 | 0.8729 | 0.4715 | 0.4715 | 0.4715 | 0.8729 |
| L4 | 0.6813 | 0.7544 | 0.6763 | 0.6855 | 0.6762 | 0.7782 |
| N1 | 0.4545 | 0.5574 | 0.4545 | 0.4545 | 0.4545 | 0.5574 |
| N2 | 0.4541 | 0.6955 | 0.6368 | 0.6352 | 0.6398 | 0.6955 |
| N3 | 0.4208 | 0.7366 | 0.6578 | 0.6641 | 0.6589 | 0.7366 |
| N4 | 0.4578 | 0.6834 | 0.6192 | 0.7465 | 0.6286 | 0.6834 |
| S1 | 0.6611 | 0.6728 | 0.6623 | 0.6624 | 0.6623 | 0.6728 |
| S2 | 0.7171 | 0.7072 | 0.7023 | 0.7024 | 0.7059 | 0.7072 |
| S3 | 0.7228 | 0.7472 | 0.7232 | 0.7453 | 0.7318 | 0.7472 |
| S4 | 0.4702 | 0.52775 | 0.6731 | 0.50391 | 0.6722 | 0.6735 |
| Image | PSO | ChOA | FAG | HWOA | POA | MIPOA |
|---|---|---|---|---|---|---|
| L1 | 0.6020 | 0.6095 | 0.6093 | 0.6095 | 0.6020 | 0.9963 |
| L2 | 1.0496 | 1.0491 | 1.0329 | 1.0329 | 1.0329 | 1.0680 |
| L3 | 0.7238 | 0.7238 | 0.7238 | 0.7238 | 0.7238 | 1.2062 |
| L4 | 1.0906 | 1.0998 | 0.9876 | 1.1006 | 6.1894 | 5.4951 |
| N1 | 0.7525 | 0.7525 | 0.7525 | 0.7525 | 0.7525 | 0.7525 |
| N2 | 0.6889 | 0.6889 | 0.6889 | 0.6889 | 0.6889 | 0.7093 |
| N3 | 0.6552 | 0.6657 | 0.6717 | 0.6717 | 0.6717 | 1.0131 |
| N4 | 0.7021 | 0.7021 | 0.7021 | 0.9493 | 0.7021 | 0.7223 |
| S1 | 0.8912 | 0.8117 | 0.8117 | 0.8117 | 0.8117 | 0.8999 |
| S2 | 1.0237 | 0.8814 | 0.9114 | 0.9390 | 0.9463 | 0.9464 |
| S3 | 0.9510 | 0.9933 | 0.9510 | 0.9777 | 0.9643 | 0.9977 |
| S4 | 0.5689 | 0.6231 | 0.6206 | 0.6206 | 0.6206 | 0.6206 |
| Image | PSO | ChOA | FAG | HWOA | POA | MIPOA |
|---|---|---|---|---|---|---|
| L1 | 0.13413 | 0.36543 | 0.35405 | 0.35655 | 0.35253 | 0.75717 |
| L2 | 0.8621 | 0.87318 | 0.83681 | 0.83871 | 0.83548 | 0.87162 |
| L3 | 0.23288 | 0.23288 | 0.23288 | 0.23288 | 0.23288 | 0.7.552 |
| L4 | 0.52004 | 0.53058 | 0.50119 | 0.53536 | 0.36867 | 0.56017 |
| N1 | 0.27333 | 0.27333 | 0.27333 | 0.27333 | 0.27333 | 0.32986 |
| N2 | 0.24185 | 0.24149 | 0.35872 | 0.35621 | 0.36104 | 0.46825 |
| N3 | 0.18988 | 0.42405 | 0.43598 | 0.45027 | 0.43841 | 0.72213 |
| N4 | 0.25192 | 0.25148 | 0.37194 | 0.35515 | 0.38255 | 0.49493 |
| S1 | 0.55991 | 0.54769 | 0.53967 | 0.54102 | 0.54045 | 0.58361 |
| S2 | 0.81039 | 0.66821 | 0.69807 | 0.70201 | 0.72416 | 0.73274 |
| S3 | 0.70063 | 0.61153 | 0.70229 | 0.82281 | 0.74441 | 0.82672 |
| S4 | 0.13844 | 0.52775 | 0.48658 | 0.50391 | 0.48261 | 0.48858 |
| Image | SSR | MSRCR | HE | AHE | ESIHE | AGCWD | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|
| L1 | 0.1738 | 0.13045 | 131.8026 | 67.8067 | 146.486 | 62.3378 | 136.4606 | 109.3775 |
| L2 | 0.1719 | 0.13563 | 133.5489 | 68.4875 | 146.1617 | 67.1037 | 110.8766 | 111.2707 |
| L3 | 0.15534 | 0.12036 | 134.7179 | 64.849 | 148.5695 | 62.4672 | 168.6012 | 120.3972 |
| L4 | 0.18598 | 0.22468 | 131.4676 | 72.198 | 146.7958 | 65.8371 | 116.2406 | 101.3712 |
| N1 | 0.15872 | 0.1227 | 135.4125 | 66.5866 | 150.6597 | 61.5617 | 188.433 | 102.1638 |
| N2 | 0.17623 | 0.12525 | 133.672 | 72.8189 | 150.8542 | 62.2017 | 152.6776 | 99.47 |
| N3 | 0.18877 | 0.13811 | 132.7017 | 75.5299 | 150.6192 | 65.7029 | 136.6966 | 122.2561 |
| N4 | 0.17676 | 0.11069 | 133.8923 | 71.693 | 150.8456 | 62.4132 | 150.3798 | 97.7514 |
| S1 | 0.20991 | 0.13783 | 130.432 | 76.9887 | 144.8233 | 59.4392 | 109.4696 | 116.9768 |
| S2 | 0.22319 | 0.15324 | 129.6689 | 78.1447 | 143.5475 | 64.6676 | 89.5116 | 95.4927 |
| S3 | 0.25879 | 0.18499 | 131.1036 | 87.7792 | 149.5625 | 67.4396 | 105.4981 | 105.9425 |
| S4 | 0.18871 | 0.129 | 131.9709 | 69.6043 | 144.9612 | 59.1859 | 97.461 | 113.904 |
| Image | SSR | MSRCR | HE | AHE | ESIHE | AGCWD | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|
| L1 | 0.21476 | 0.20568 | 69.1124 | 89.4665 | 61.4729 | 77.6979 | 79.9959 | 99.7079 |
| L2 | 0.19032 | 0.18063 | 56.2363 | 75.94 | 50.707 | 67.689 | 73.2809 | 73.0566 |
| L3 | 0.17349 | 0.1756 | 57.4847 | 76.2796 | 51.3378 | 68.4572 | 46.9917 | 76.4251 |
| L4 | 0.22796 | 0.22468 | 64.5598 | 91.166 | 56.9781 | 79.205 | 96.3159 | 103.6209 |
| N1 | 0.19555 | 0.1966 | 59.3725 | 86.5276 | 52.35 | 75.8051 | 20.6108 | 90.2516 |
| N2 | 0.24722 | 0.22833 | 77.0218 | 103.7641 | 66.945 | 89.3605 | 72.1111 | 122.0603 |
| N3 | 0.26527 | 0.24528 | 80.1178 | 112.7574 | 69.2948 | 95.1207 | 99.7179 | 115.1481 |
| N4 | 0.24952 | 0.19933 | 79.3524 | 106.9948 | 69.2884 | 91.052 | 77.5816 | 126.5218 |
| S1 | 0.23557 | 0.20088 | 64.1875 | 85.7273 | 57.2292 | 67.9809 | 90.4239 | 93.6418 |
| S2 | 0.22838 | 0.19447 | 59.6667 | 83.6017 | 53.9296 | 63.4942 | 87.7947 | 87.8751 |
| S3 | 0.32679 | 0.30519 | 77.4858 | 109.9073 | 67.0062 | 94.2225 | 123.0046 | 123.2372 |
| S4 | 0.22359 | 0.19739 | 58.668 | 83.7094 | 52.9611 | 69.3839 | 86.7325 | 96.788 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Zhu, L.; Wang, J.; Mohamed, A.M.E. Enhancement Method Based on Multi-Strategy Improved Pelican Optimization Algorithm and Application to Low-Illumination Forest Canopy Images. Forests 2024, 15, 1783. https://doi.org/10.3390/f15101783
Zhao X, Zhu L, Wang J, Mohamed AME. Enhancement Method Based on Multi-Strategy Improved Pelican Optimization Algorithm and Application to Low-Illumination Forest Canopy Images. Forests. 2024; 15(10):1783. https://doi.org/10.3390/f15101783
Chicago/Turabian StyleZhao, Xiaohan, Liangkuan Zhu, Jingyu Wang, and Alaa M. E. Mohamed. 2024. "Enhancement Method Based on Multi-Strategy Improved Pelican Optimization Algorithm and Application to Low-Illumination Forest Canopy Images" Forests 15, no. 10: 1783. https://doi.org/10.3390/f15101783
APA StyleZhao, X., Zhu, L., Wang, J., & Mohamed, A. M. E. (2024). Enhancement Method Based on Multi-Strategy Improved Pelican Optimization Algorithm and Application to Low-Illumination Forest Canopy Images. Forests, 15(10), 1783. https://doi.org/10.3390/f15101783





