Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview
- (1)
- Transition to continuous-cover forestry (CCFt) starting with planting at year 0 with regulated harvesting, non-declining carbon stock and revenue from carbon up to age 40–45 (when carbon reaches an upper threshold) under the carbon stock-change method. The simulation was run over a 300-year planning horizon.
- (2)
- Steady-state CCF with a start point at 150 years along the planning horizon once the forest estate consists of a mixed-age class distribution, which represents the long-term steady-state (CCFs). This scenario is equivalent to the second half of scenario 1 (years 150–300) assuming that year 150 becomes year 0.
- (3)
- Traditional rotational forest management, with revenue from carbon up to years 20–25 (long-term carbon mid-point) under the carbon averaging method and unregulated harvesting of timber (RFMt).
- (4)
- Steady state of the above traditional RFM, with a start point at 150 years (RFMs) when trees are at mid-rotation. Starting the RFMs at mid-rotation represents a point at which a fair comparison can be made with CCFs as this reduces the time period to receive revenue, which increases profitability. This scenario is equivalent to the second half of scenario 3 (years 150–300) assuming that year 150 along the planning horizon becomes year 0.
- (5)
- Permanent carbon forest (PCF) with only income from carbon under the carbon stock-change method over the entire 300-year simulation.
2.2. Forest Harvest Scheduling Model
- -
- Indices
- t = Index of time periods;
- j = Index of age classes.
- -
- Parameters
- T = Total number of periods;
- J = Total number of age classes;
- Pj = Net price per cubic meter (NZD/m3) of timber harvested from age class j;
- ϕ = Net price per tonne of CO2 stored (NZD/tonne CO2);
- Vj = Merchantable yield per hectare (m3/ha) in age class j;
- Sj = Carbon stock (tonnes CO2/ha) in age class j;
- r = Discount rate (as decimal number);
- aj = area (ha) of age class j at the beginning of the planning horizon;
- E = variable cost of establishing and tending 1 ha that was harvested.
- -
- Decision variables
- ytj = area (ha) harvested in period t from age class j
- -
- Auxiliary variables
- -
- Objective Function
- -
- Area constraints
- (i)
- The area harvested must be immediately replanted (Rt).
- (ii)
- The area planted in any period (Rt) must be subsequently harvested.
- (iii)
- The area at the beginning of the planning horizon in each age class must subsequently be cut.
- -
- Management constraints
- Minimum and maximum age of harvest. Trees are allowed to be harvested between ages 35 and 100 years, i.e.,
- 2
- Minimum canopy cover. This ensures that 50% of the forest estate should be age 20 years or older, which is an age at which canopy closure can be assumed in redwood at the final crop stand density. That is,
- 3
- Non-declining carbon stock. This constraint ensures that carbon stock does not decline so that revenue from carbon is received but does not have to be returned.
- 4
- Timber flow constraints. These can be stated as relationships between one given period and the next, allowing a maximum increase (α) and decrease (β) in the flow. Notice that α and β are proportions of the unit, meaning that from one period to the next, the volume harvested must not vary by more than that proportion.
2.3. Solving the Optimisation Problem
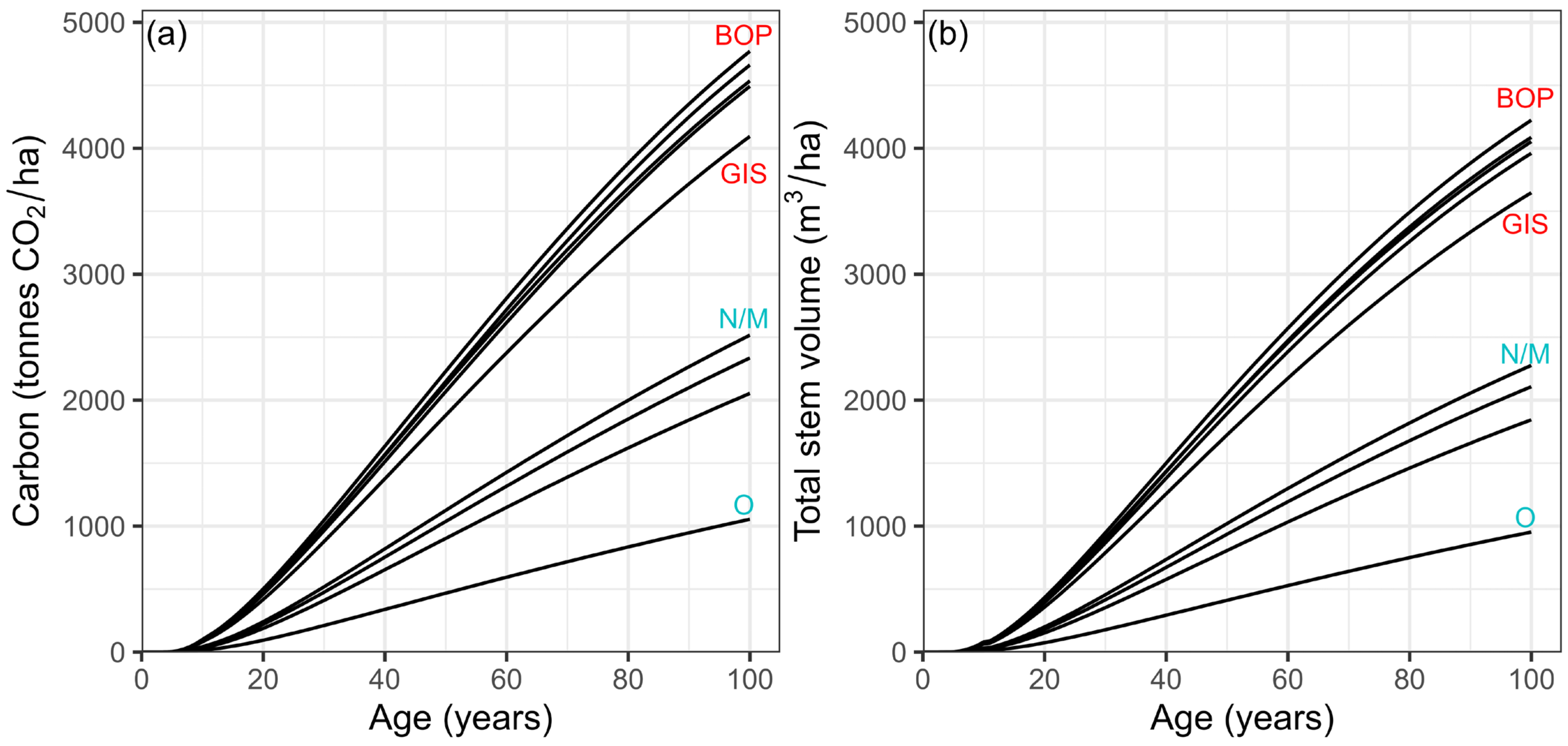
2.4. Estimates of Carbon and Total Stem Volume
2.5. Timber Value and Harvesting Costs
2.6. Establishment, Silviculture and Management Costs
2.7. Carbon Value
2.8. Sensitivity Analyses
3. Results
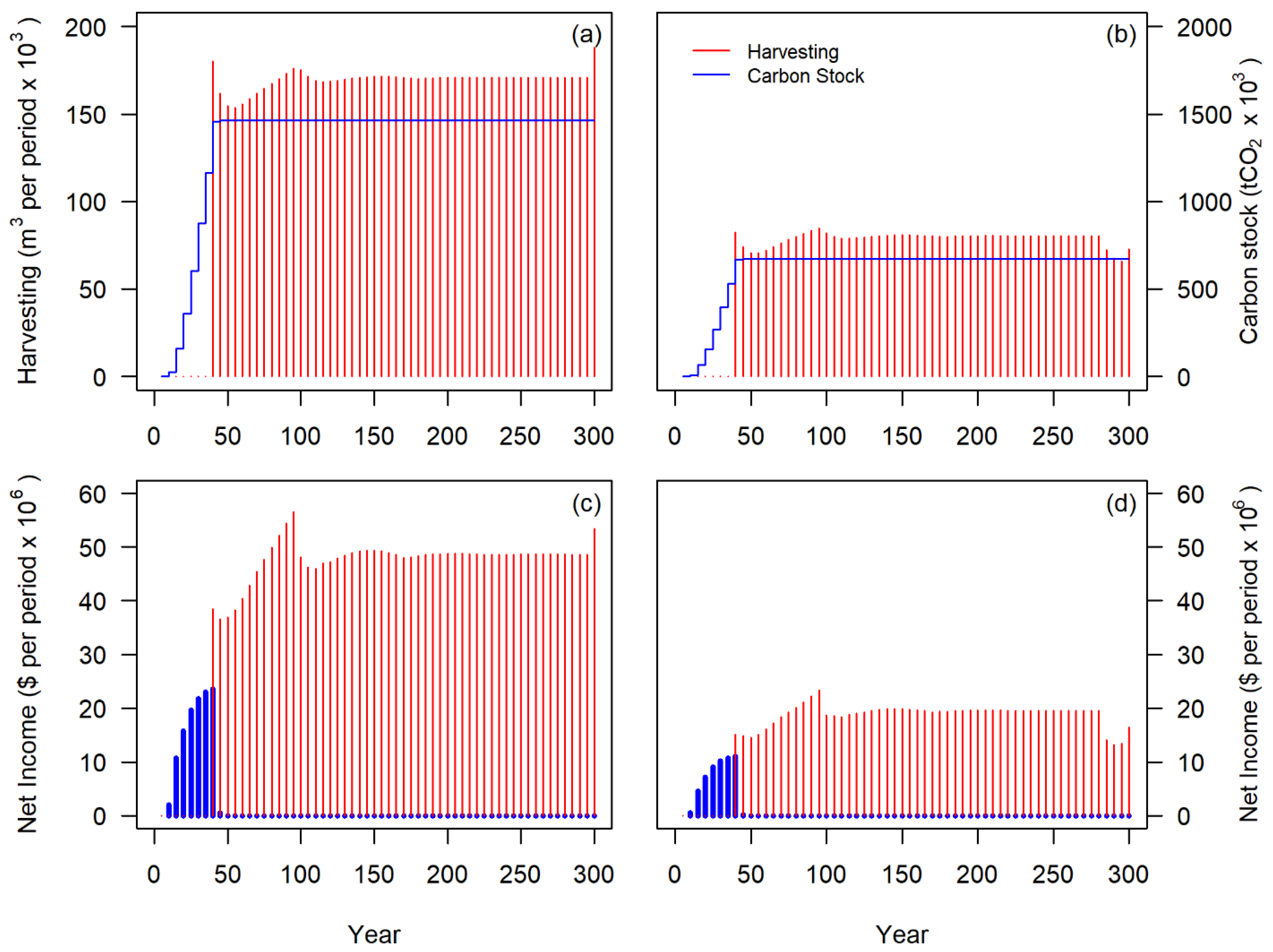
3.1. Regime Comparison of Forest Structure, Timber Flow and Carbon Accumulation
3.1.1. Variation under Baseline Conditions
3.1.2. Sensitivity Analyses
3.2. Financial Comparison of Regimes
3.3. Sensitivity Analyses
3.3.1. Carbon
3.3.2. Timber Price and Yield
3.3.3. Discount Rate
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Regime 1 (CCFt) | Regime 2 (CCFs) | Regime 3 (RFMt) | Regime 4 (RFMs) | Regime 5 (PCF) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NI | SI | NI | SI | NI | SI | NI | SI | NI | SI | ||
| m3/ha per year | m3/ha at harvest, age 37.5 years | ||||||||||
| Carbon Price (NZD/t CO2) | 0 | 32,798 | 13,064 | 34,419 | 13,494 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - |
| 35 | 32,798 | 13,050 | 34,419 | 13,648 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| 80 | 32,798 | 12,763 | 34,419 | 12,790 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| 160 | 31,256 | 11,837 | 33,141 | 13,834 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| Timber Price | −20% | 32,792 | 12,382 | 33,788 | 12,702 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - |
| base | 32,798 | 12,763 | 34,419 | 12,790 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| 20% | 32,798 | 12,960 | 34,419 | 12,965 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| Yield | −50% | 16,151 | 6227 | 16,092 | 6246 | 519,826 | 200,263 | 519,826 | 200,263 | - | - |
| −20% | 26,236 | 10,032 | 27,529 | 9934 | 831,722 | 320,421 | 831,722 | 320,421 | - | - | |
| base | 32,798 | 12,763 | 34,419 | 12,790 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| 20% | 39,358 | 15,631 | 41,303 | 16,059 | 1,247,583 | 480,632 | 1,247,583 | 480,632 | - | - | |
| 50% | 49,198 | 19,700 | 51,629 | 20,299 | 1,559,478 | 600,790 | 1,559,478 | 600,790 | - | - | |
| Discount rate | 4% | 32,798 | 12,574 | 34,419 | 14,185 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - |
| 6% | 32,798 | 12,763 | 34,419 | 12,790 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| 8% | 28,643 | 10,574 | 28,020 | 10,416 | 1,039,652 | 400,526 | 1,039,652 | 400,526 | - | - | |
| Regime 1 (CCFt) | Regime 2 (CCFs) | Regime 3 (RFMt) | Regime 4 (RFMs) | Regime 5 (PCF) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NI | SI | NI | SI | NI | SI | NI | SI | NI | SI | ||
| Carbon stock (tonnes CO2/ha) by region | |||||||||||
| Carbon Price (NZD/t CO2) | 0 | 1374 | 567 | 1374 | 567 | 515 | 207 | 543 | 219 | 5968 | 2905 |
| 35 | 1374 | 569 | 1374 | 569 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| 80 | 1374 | 583 | 1374 | 583 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| 160 | 1604 | 870 | 1604 | 870 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| Timber Price | −20% | 1383 | 619 | 1383 | 619 | 515 | 207 | 543 | 219 | 5968 | 2905 |
| base | 1374 | 583 | 1374 | 583 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| 20% | 1374 | 575 | 1374 | 575 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| Yield | −50% | 691 | 301 | 691 | 301 | 258 | 104 | 272 | 109 | 2984 | 1452 |
| −20% | 1099 | 471 | 1099 | 471 | 412 | 166 | 435 | 175 | 4775 | 2324 | |
| base | 1374 | 583 | 1374 | 583 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| 20% | 1648 | 704 | 1648 | 704 | 618 | 249 | 652 | 263 | 7162 | 3486 | |
| 50% | 2060 | 878 | 2060 | 878 | 773 | 311 | 815 | 328 | 8952 | 4357 | |
| Discount rate | 4% | 1374 | 611 | 1374 | 611 | 515 | 207 | 543 | 219 | 5968 | 2905 |
| 6% | 1374 | 583 | 1374 | 583 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
| 8% | 1700 | 839 | 1700 | 839 | 515 | 207 | 543 | 219 | 5968 | 2905 | |
References
- Pommerening, A.; Murphy, S. A review of the history, definitions and methods of continuous cover forestry with special attention to afforestation and restocking. Forestry 2004, 77, 27–44. [Google Scholar] [CrossRef]
- Schütz, J.-P. Close-to-nature silviculture: Is this concept compatible with species diversity? Forestry 1999, 72, 359–366. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Hasenauer, H.; Kindermann, G. Sustainability in multi-aged stands: An analysis of long-term plenter systems. Forestry 2007, 80, 163–181. [Google Scholar] [CrossRef]
- United Nations. Convention on Biological Diversity; United Nations: Montreal, QC, Canada, 2011; Available online: https://www.cbd.int/doc/legal/cbd-en.pdf (accessed on 15 December 2023).
- Mason, W.L.; Diaci, J.; Carvalho, J.; Valkonen, S. Continuous cover forestry in Europe: Usage and the knowledge gaps and challenges to wider adoption. For. Int. J. For. Res. 2022, 95, 1–12. [Google Scholar] [CrossRef]
- Matthews, J.D. Silvicultural Systems; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Thompson, I.; Mackey, B.; McNulty, S.; Mosseler, A. Forest Resilience, Biodiversity, and Climate Change. In A Synthesis of the Biodiversity/Resilience/Stability Relationship in Forest Ecosystems; Technical Series No. 43; Secretariat of the Convention on Biological Diversity: Montreal, QC, Canada, 2009; 67p. [Google Scholar]
- Knoke, T.; Paul, C.; Gosling, E.; Jarisch, I.; Mohr, J.; Seidl, R. Assessing the economic resilience of different management systems to severe forest disturbance. Environ. Resour. Econ. 2023, 84, 343–381. [Google Scholar] [CrossRef] [PubMed]
- Pukkala, T.; Laiho, O.; Lähde, E. Continuous cover management reduces wind damage. For. Ecol. Manag. 2016, 372, 120–127. [Google Scholar] [CrossRef]
- Pukkala, T. Which type of forest management provides most ecosystem services? For. Ecosyst. 2016, 3, 9. [Google Scholar] [CrossRef]
- Tahvonen, O. Economics of rotation and thinning revisited: The optimality of clearcuts versus continuous cover forestry. For. Policy Econ. 2016, 62, 88–94. [Google Scholar] [CrossRef]
- Tahvonen, O.; Pukkala, T.; Laiho, O.; Lähde, E.; Niinimäki, S. Optimal management of uneven-aged Norway spruce stands. For. Ecol. Manag. 2010, 260, 106–115. [Google Scholar] [CrossRef]
- Andreassen, K.; Øyen, B.H. Economic consequences of three silvicultural methods in uneven-aged mature coastal spruce forests of central Norway. Forestry 2002, 75, 483–488. [Google Scholar] [CrossRef]
- Assmuth, A.; Rämö, J.; Tahvonen, O. Economics of size-structured forestry with carbon storage. Can. J. For. Res. 2018, 48, 11–22. [Google Scholar] [CrossRef]
- Purser, P.; Ó’Tuama, P.; Vítková, L.; Dhubháin, Á.N. Factors affecting the economic assessment of continuous cover forestry compared with rotation based management. Ir. For. 2015, 72, 150–165. [Google Scholar]
- Brown, J.E. Monarchs of the Mist: The Story of Redwood National Park and the Coast Redwoods; Coastal Parks Association: Pyrmont, Australia, 1982. [Google Scholar]
- Earle, C.J. Sequoia sempervirens. The Gymnosperm Database. 2018. Available online: https://www.conifers.org/cu/Sequoia.php (accessed on 22 June 2023).
- Sillett, S.C.; Van Pelt, R.; Carroll, A.L.; Campbell-Spickler, J.; Antoine, M.E. Aboveground biomass dynamics and growth efficiency of Sequoia sempervirens forests. For. Ecol. Manag. 2020, 458, 117740. [Google Scholar] [CrossRef]
- Bain, J.; Nicholas, I. Health. In Best Practice with Farm Forestry Timber Species; Nicholas, I., Ed.; No. 3: Redwoods—NZFFA Electronic Handbook Series No. 3. New Zealand Farm Forestry Associtaion: Wellington, New Zealand, 2008; Available online: https://www.nzffa.org.nz/system/assets/2080/Redwoods_Handbook.pdf (accessed on 22 June 2023).
- Peters, T.; Hardaker, A.; Dauksta, D.; Newman, G.; Lellig, C.; Healey, J. Top Five Alternative Conifer Tree Species in Great Britain: Main Report and Executive Summary. Welsh Government. 2021. Available online: https://woodknowledge.wales/wkw-resource/forestry/top-five-alternative-conifer (accessed on 22 June 2023).
- Brown, I.; Low, C.; McConnochie, R.; Nicholas, I.; Webster, R. Site Selection. In Best Practice with Farm Forestry Timber Species; Nicholas, I., Ed.; No. 3: Redwoods, NZFFA Electronic Handbook Series No. 3. New Zealand Farm Forestry Associtaion: Wellington, New Zealand, 2008; pp. 19–21. Available online: https://www.nzffa.org.nz/system/assets/2080/Redwoods_Handbook.pdf (accessed on 22 June 2023).
- Rapley, S. Redwood in New Zealand. New Zealand J. For. 2018, 63, 29–33. [Google Scholar]
- Jacobs, D.F.; Cole, D.W.; McBride, J.R. Fire history and perpetuation of natural coast redwood ecosystems. J. For. 1985, 83, 494–497. [Google Scholar]
- Stuart, J.D. Fire history of an old-growth forest of Sequoia sempervirens (Taxodiaceae) forest in Humboldt Redwoods State Park, California. Madrono 1987, 34, 128–141. [Google Scholar]
- Olson, D.F.; Roy, D.F.; Walters, G.A. Sequoia sempervirens (D. Don) Endl. Redwood. Silv. North Am. 1990, 1, 541–551. [Google Scholar]
- Knowles, F.B.; Miller, J.T. Introduced Forest Trees in New Zealand: Recognition, Role, and Seed Source; No. 13 The Redwoods. FRI Bulletin No. 124; New Zealand Forest Research Institute: Rotorua, New Zealand, 1993. [Google Scholar]
- Toral, I.; Caru, M.; Herrera, M.A.; Gonzalez, L.; Martin, L.M.; Miranda, J.; Navarro-Cerrillo, R.M. Clones identification of Sequoia sempervirens (D. Don) Endl. in Chile by using PCR-RAPDs technique. J. Zhejiang Univ. 2009, 10, 112–119. [Google Scholar] [CrossRef]
- Arnaud, Y.; Franclet, A.; Tranvan, H.; Jacques, M. Micropropagation and rejuvenation of Sequoia sempervirens (Lamb) Endl: A review. Ann. Des Sci. For. 1993, 50, 273–295. [Google Scholar] [CrossRef][Green Version]
- Breidenbach, N.; Gailing, O.; Krutovsky, K.V. Genetic structure of coast redwood (Sequoia sempervirens [D. Don] Endl.) populations in and outside of the natural distribution range based on nuclear and chloroplast microsatellite markers. PLoS ONE 2020, 15, e0243556. [Google Scholar] [CrossRef]
- SWP Research Partnership. The Specialty Woods Products Research Partnership. Final Report. 2015–2023. 2023. Available online: https://fgr.nz/documents/download/10702 (accessed on 7 October 2023).
- Watt, M.S.; Kimberley, M.O. Spatial comparisons of carbon sequestration for redwood and radiata pine within New Zealand. For. Ecol. Manag. 2022, 513, 120190. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O.; Rapley, S.; Webster, R. Comparing volume productivity of redwood and radiata pine plantations in New Zealand. For. Ecol. Manag. 2021, 500, 119628. [Google Scholar] [CrossRef]
- NZFOA. New Zealand Forestry Industry, Facts and Figures 2021/2022. New Zealand Plantation Forest Industry. New Zealand Forest Owners Association, Wellington. 2022. Available online: https://www.nzfoa.org.nz/resources/publications/facts-and-figures (accessed on 4 July 2023).
- Bayne, K.; Edwards, P.; Payn, T. Media coverage of recent New Zealand storm events. NZ J. For. 2019, 64, 17. [Google Scholar]
- Jones, A.G.; Cridge, A.; Fraser, S.; Holt, L.; Klinger, S.; McGregor, K.F.; Paul, T.; Payn, T.; Scott, M.B.; Yao, R.T. Transitional forestry in New Zealand: Re-evaluating the design and management of forest systems through the lens of forest purpose. Biol. Rev. 2023. [Google Scholar] [CrossRef]
- Manley, B. Impact of carbon price on the relative profitability of production forestry and permanent forestry for New Zealand plantations. For. Policy Econ. 2023, 156, 103057. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O.; Steer, B.S.C.; Neumann, A. Financial comparison of afforestation using redwood and radiata pine under carbon regimes within New Zealand. Trees For. People 2023, 13, 100422. [Google Scholar] [CrossRef]
- Watt, M.S.; Kimberley, M.O. Financial Comparison of Afforestation Using Redwood and Radiata Pine within New Zealand for Regimes That Derive Value from Timber and Carbon. Forests 2023, 14, 2262. [Google Scholar] [CrossRef]
- ICAP. Emissions Trading Worldwide: Status Report 2023; International Carbon Action Partnership: Berlin, Germany, 2023; Available online: https://icapcarbonaction.com/en/publications/emissions-trading-worldwide-2023-icap-status-report (accessed on 30 November 2023).
- García, O. FOLPI, a forestry-oriented linear programming interpreter. In Proceedings IUFRO Symposium on Forest Management Planning and Managerial Economics, Tokyo, Japan, 15–19 October 1984; Nagumo, H., Ed.; University of Tokyo: Tokyo, Japan, 1984; pp. 293–305. [Google Scholar]
- Cown, D.; Marshall, H.; Silcock, P.; Meason, D. Sawn timber grade recovery from a planted coast redwood stand growing in New Zealand. New Zealand J. For. Sci. 2013, 43, 8. [Google Scholar] [CrossRef]
- Mason, A.J. OpenSolver—An Open Source Add-in to Solve Linear and Integer Progammes in Excel. In Operations Research Proceedings 2011; Klatte, D., Lüthi, H.-J., Schmedders, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 401–406. [Google Scholar]
- Kimberley, M.O.; Watt, M.S. A Novel Approach to Modelling Stand-Level Growth of an Even-Aged Forest Using a Volume Productivity Index with Application to New Zealand-Grown Coast Redwood. Forests 2021, 12, 1155. [Google Scholar] [CrossRef]
- IPCC. Good Practice Guidance for Land Use, Land Use Change and Forestry; Penman, J., Gytarsky, M., Hiraishi, T., Krug, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., et al., Eds.; Institute for Global Environmental Strategies (IGES): Kanagawa, Japan, 2003. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 2 November 2023).
- Manley, B. Afforestation Economic Modelling. Report Prepared for MPI; University of Canterbury: Canterbury, New Zealand, 2021. Available online: https://www.mpi.govt.nz/dmsdocument/50302-Afforestation-Economic-Modelling-Report (accessed on 22 June 2023).
- Perry, C.; Bloomberg, M.; Evison, D. Economic analysis of a target diameter harvesting system in radiata pine. New Zealand J. For. 2013, 60, 31–37. Available online: https://ir.canterbury.ac.nz/server/api/core/bitstreams/adea2612-91f4-4f72-873b-def815a9e79a/content (accessed on 30 October 2023).
- Ministry for Primary Industries. Managing Exotic Afforestation Incentives: Regulatory Impact Statement. 2022. Available online: https://www.mpi.govt.nz/dmsdocument/53992-Managing-Permanent-Exotic-Afforestation-Incentives-Regulatory-Impact-Statement (accessed on 22 June 2023).
- Climate Change Commission. Ināia Tonu Nei: A Low Emissions Future for Aotearoa. 2021. Available online: https://www.climatecommission.govt.nz/our-work/advice-to-government-topic/inaia-tonu-nei-a-low-emissions-future-for-aotearoa/ (accessed on 22 June 2023).
- Pukkala, T.; Lahde, E.; Laiho, O. Optimizing the structure and management of uneven-sized stands of Finland. Forestry 2010, 83, 129–142. [Google Scholar] [CrossRef]
- Orois, S.a.S.; Chang, S.J.; von Gadow, K. Optimal residual growing stock and cutting cycle in mixed uneven-aged maritime pine stands in Northwestern Spain. For. Policy Econ. 2004, 6, 145–152. [Google Scholar] [CrossRef]
- Bates, C.G.; Roeser, J. Light intensities required for growth of coniferous seedlings. Am. J. Bot. 1928, 15, 185–194. [Google Scholar] [CrossRef]
- Roy, D.F. Silvical Characteristics of Redwood (Sequoia sempervirens D. Don Endl.); Res. Paper PSW-RP-28; Pacific Southwest Forest & Range Experiment Station Forest Service, U.S. Department of Agriculture: Berkeley, CA, USA, 1966; 20p. [Google Scholar]
- Boldenow, R.W.; McBride, J.R. Redwood Seedling Responses to Light Patterns and Intensities; General Technical Report PSW-GTR-258; U.S. Department of Agriculture, Forest Service, Pacific Southwest Research Station: Albany, CA, USA, 2016. [Google Scholar]
- Jameson, M.J.; Robards, T.A. Coast redwood regeneration survival and growth in Mendocino County, California. West. J. Appl. For. 2007, 22, 171–175. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Stancioiu, P.T.; Spencer, M.A. Understory stump sprout development under variable canopy density and leaf area in coast redwood. For. Ecol. Manag. 2007, 244, 76–85. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Berrill, J.-P. Dynamics of coast redwood sprout clump development in variable light environments. J. For. Res. 2010, 15, 131–139. [Google Scholar] [CrossRef]
- Beaudet, M.; Harvey, B.D.; Messier, C.; Coates, K.D.; Poulin, J.; Kneeshaw, D.D.; Brais, S.; Bergeron, Y. Managing understory light conditions in boreal mixedwoods through variation in the intensity and spatial pattern of harvest: A modelling approach. For. Ecol. Manag. 2011, 261, 84–94. [Google Scholar] [CrossRef]
- Knoke, T.; Plusczyk, N. On economic consequences of transformation of a spruce (Picea abies (L.) Karst.) dominated stand from regular into irregular age structure. For. Ecol. Manag. 2001, 151, 163–179. [Google Scholar] [CrossRef]
- Weaver, S. Carbon economics of natural regeneration at scale. New Zealand J. For. 2023, 67, 35–47. [Google Scholar]
- Manley, B. Trends in discount rates used for forest valuation in New Zealand. New Zealand J. For. Sci. 2019, 49. [Google Scholar]
- Ramírez-Martínez, A.; Gonzalez-Guillen, M.d.J.; De Los Santos-Posadas, H.M.; Ángeles-Pérez, G.; Santiago-García, W. Forest management with carbon scenarios in the central region of Mexico. iforest-Biogeosciences For. 2021, 14, 413. [Google Scholar] [CrossRef]
- Kula, E.; Gunalay, Y. Carbon sequestration, optimum forest rotation and their environmental impact. Environ. Impact Assess. Rev. 2012, 37, 18–22. [Google Scholar] [CrossRef]
- Ekholm, T. Optimal forest rotation under carbon pricing and forest damage risk. For. Policy Econ. 2020, 115, 102131. [Google Scholar] [CrossRef]
- Hou, G.; Delang, C.O.; Lu, X.; Olschewski, R. Optimizing rotation periods of forest plantations: The effects of carbon accounting regimes. For. Policy Econ. 2020, 118, 102263. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Rodriguez, L.C.E. Optimal rotations on Eucalyptus plantations including carbon sequestration—A comparison of results in Brazil and Spain. For. Ecol. Manag. 2006, 229, 247–258. [Google Scholar] [CrossRef]
- Bateman, I.J.; Lovett, A.A. Estimating and valuing the carbon sequestered in softwood and hardwood trees, timber products and forest soils in Wales. J. Environ. Manag. 2000, 60, 301–323. [Google Scholar] [CrossRef]
- Stavins, R.; Richards, K. The cost of U.S. forest-based carbon sequestration. Pew Center on Global Climate Change, Arlington, VA, US. 2005, 52p. Available online: https://www.c2es.org/wp-content/uploads/2005/01/cost-us-forest-based-carbon-sequestration.pdf (accessed on 3 December 2023).
- Foltyn-Zarychta, M.; Buła, R.; Pera, K. Discounting for energy transition policies—Estimation of the social discount rate for Poland. Energies 2021, 14, 741. [Google Scholar] [CrossRef]
- Freeman, M.C.; Groom, B. How certain are we about the certainty-equivalent long term social discount rate? J. Environ. Econ. Manag. 2016, 79, 152–168. [Google Scholar] [CrossRef]
- Davies, O.; Kerr, G. Comparing the costs and revenues of transformation to continuous cover forestry for sitka spruce in Great Britain. Forests 2015, 6, 2424–2449. [Google Scholar] [CrossRef]
- Burdon, R.D. Is coast redwood an answer to the Mangatu problem? New Zealand J. For. 1975, 20, 148–152. [Google Scholar]
- Phillips, C.J.; Marden, M.; Lambie, S.; Watson, A.; Ross, C.; Fraser, S. Observations of below-ground characteristics of young redwood trees (Sequoia sempervirens) from two sites in New Zealand–implications for erosion control. Plant Soil 2013, 363, 33–48. [Google Scholar] [CrossRef]
- Marden, M. The tolerance of Sequoia sempervirens to sedimentation, East Coast region, New Zealand. New Zealand For. 1993, 38, 22–24. [Google Scholar]
- Garrett, L.G.; Clinton, P.W. Erosion mitigation and carbon. In Coast Redwood (Sequoia sempervirens) Development Plan; Scion (New Zealand Forest Research Institute Limited): Rotorua, New Zealand, 2013; Available online: https://www.researchgate.net/publication/327634451_New_Zealand%27s_Coast_Redwood_Forestry_Development_Plan (accessed on 4 August 2023).

| SED | Log Values (NZD/m3) | |
|---|---|---|
| Class (cm) | Pruned | Unpruned |
| 10 | - | 51 |
| 20 | - | 153 |
| 30 | 295 | 167 |
| 40 | 428 | 242 |
| 50 | 460 | 274 |
| 60 | 515 | 330 |
| 70 | 609 | 423 |
| 80 | 611 | 425 |
| 90 | 614 | 428 |
| 100 | 614 | 428 |
| Region | 35 yr | 40 yr | 50 yr | 60 yr | 70 yr | 80 yr | 90 yr | 100 yr |
|---|---|---|---|---|---|---|---|---|
| At Mill Gate NZD/m3 | ||||||||
| Auckland | 294 | 304 | 324 | 346 | 364 | 382 | 397 | 409 |
| Waikato/Taranaki | 314 | 327 | 349 | 369 | 390 | 408 | 421 | 434 |
| Bay of Plenty | 305 | 313 | 338 | 358 | 378 | 395 | 411 | 422 |
| Gisborne | 299 | 312 | 329 | 350 | 368 | 387 | 400 | 414 |
| Hawkes Bay/Southern NI | 309 | 321 | 342 | 363 | 383 | 401 | 415 | 428 |
| Nelson/Marlborough | 280 | 293 | 305 | 324 | 333 | 350 | 366 | 376 |
| Canterbury/West Coast | 267 | 288 | 322 | 325 | 340 | 359 | 370 | 378 |
| Otago | 194 | 221 | 242 | 272 | 289 | 292 | 298 | 307 |
| Southland | 273 | 297 | 306 | 325 | 340 | 348 | 365 | 381 |
| Item | Continuous-Cover Forestry (CCF) | Rotational Forest Manage (RFM) | Permanent Carbon Forests (PCF) | |||
|---|---|---|---|---|---|---|
| Cost (NZD/ha) | Year | Cost (NZD/ha) | Year | Cost (NZD/ha) | Year | |
| Land prep, silvicultural costs | ||||||
| Tracking, land preparation | 100 | Year established | 100 | Year established | 100 | 0 * |
| Pre-plant spray | 184 | 0 * | 184 | 0 * | 184 | 0 * |
| Seedlings, planting | 2425 | 0 * | 2425 | 0 * | 2425 | 0 * |
| Release spraying | 400 | 0 * | 400 | 0 * | 400 | 0 * |
| Mapping | 50 | 0 * | 50 | 0 * | 50 | 0 * |
| Pruning | 2329 | 6, 8, 10 | 2329 | 6, 8, 10 | - | - |
| Thinning to waste | 900 | 11 * | 900 | 11 * | - | - |
| Thinning coppiced sprouts | 2000 | 2nd rotation onwards year 11 | 2000 | 2nd rotation onwards year 11 | - | - |
| Harvesting costs | ||||||
| Harvest planning | 150 | 2 yrs before harv. | 150 | 2 yrs before harv. | - | - |
| Road construction (first rotation) | 5000 | 1 yr before harv. | 5000 | 1 yr before harv. | - | - |
| Road rehabilitation (2nd + rotations) | 1500 | 1 yr before harv. | 1500 | 1 yr before harv. | - | - |
| Periodic costs | ||||||
| Carbon administration for Field Measurement Approach | 71 | Every 5 yrs to 45 years | 71 | Every 5 yrs to 25 years | 71 | Every 5 yrs in perpetuity |
| Maintenance roads, tracks, fences | 50 | Every 5 yrs | 50 | Every 5 yrs | 50 | Every 5 yrs |
| Animal control | 100 | 0, 1, 2, 3, 4, 5, then every 5 yrs | 100 | 0, 1, 2, 3, 4, 5, then every 5 yrs | 100 | 0, 1, 2, 3, 4, 5, then every 5 yrs |
| Annual costs | ||||||
| Forest Management | 60 | 40 | 40 | |||
| Rates, insurance, administration | 42 | 42 | 42 | |||
| Costs (NZD/m3) | Year | Costs (NZD/m3) | Year | |||
| Harvesting costs | ||||||
| Log harvesting | 60 | Yr of harvest | 48 | Yr of harvest | - | - |
| Cartage | 19 | Yr of harvest | 19 | Yr of harvest | - | - |
| Road maintenance | 3.75 | Yr of harvest | 3 | Yr of harvest | - | - |
| Post-harvest ancillary costs | 1.88 | Yr of harvest | 1.5 | Yr of harvest | - | - |
| Harvest management Fee | 5.63 | Yr of harvest | 4.5 | Yr of harvest | - | - |
| Forest growers levy | 0.33 | Yr of harvest | 0.33 | Yr of harvest | - | - |
| Regime | Metric | Units | AK | W/T | BOP | GIS | H/SNI | N/M | C/W | O | S |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 CCFt | SEV | NZD/ha | 34,579 | 35,991 | 37,045 | 29,187 | 33,947 | 11,732 | 6882 | −2789 | 9866 |
| IRR | % | 12.8 | 12.8 | 13.1 | 12.0 | 12.6 | 9.0 | 7.9 | 5.0 | 8.6 | |
| Forest Cover | % | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 71 | |
| min-max | 53–84 | 52–83 | 52–83 | 52–83 | 52–83 | 52–83 | 53–86 | 56–87 | 52–83 | ||
| Carbon stock | t CO2/ha | 1399 | 1403 | 1465 | 1232 | 1352 | 754 | 601 | 324 | 672 | |
| Timber Flow | min | 30,041 | 30,288 | 30,725 | 26,495 | 29,114 | 15,410 | 11,816 | 5174 | 13,193 | |
| (m3 per year) | max | 36,875 | 36,967 | 37,580 | 32,509 | 35,670 | 19,225 | 14,428 | 7341 | 16,957 | |
| 2 CCFs | SEV | NZD/ha | 131,960 | 144,765 | 141,433 | 117,526 | 136,064 | 59,359 | 47,618 | 16,746 | 55,288 |
| Forest Cover | % | 72 | 73 | 72 | 73 | 73 | 73 | 72 | 71 | 71 | |
| min-max | 72–73 | 72–73 | 72–73 | 72–73 | 72–73 | 72–73 | 63–73 | 57–74 | 55–73 | ||
| Timber Flow | min | 33,423 | 33,506 | 34,065 | 29,461 | 32,329 | 15,727 | 12,598 | 5836 | 13,193 | |
| (m3 per year) | max | 36,875 | 36,967 | 37,580 | 32,509 | 35,670 | 19,225 | 13,907 | 6942 | 16,185 | |
| 3 RFMt | SEV | NZD/ha | 34,008 | 36,057 | 36,525 | 28,679 | 33,766 | 10,636 | 5250 | −4538 | 8629 |
| IRR | % | 12.6 | 12.7 | 12.9 | 11.8 | 12.4 | 8.8 | 7.5 | 4.0 | 8.3 | |
| Forest Cover | % | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | |
| min-max | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | ||
| Carbon stock | t CO2/ha | 527 | 526 | 551 | 461 | 507 | 270 | 213 | 108 | 247 | |
| Timber Flow | min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| (m3 at harvest) | max | 1,072,000 | 1,061,000 | 1,091,000 | 929,000 | 1,023,000 | 533,000 | 408,000 | 200,000 | 485,000 | |
| 4 RFMs | SEV | NZD/ha | 78,300 | 85,335 | 83,556 | 69,386 | 80,174 | 34,483 | 24,159 | 4908 | 30,802 |
| IRR | % | 26.1 | 26.6 | 26.5 | 25.4 | 26.2 | 21.2 | 19.3 | 11.8 | 20.6 | |
| Forest Cover | % | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | 47 | |
| min-max | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | ||
| Carbon stock | t CO2/ha | 555 | 554 | 580 | 486 | 534 | 285 | 225 | 115 | 261 | |
| Timber Flow | min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| (m3 at harvest) | max | 1,072,000 | 1,061,000 | 1,091,000 | 929,000 | 1,023,000 | 533,000 | 408,000 | 200,000 | 485,000 | |
| 5 PCF | SEV | NZD/ha | 34,021 | 33,396 | 35,785 | 28,310 | 31,933 | 12,467 | 7501 | −1019 | 10,486 |
| IRR | % | 13.9 | 13.7 | 14.2 | 12.9 | 13.5 | 9.6 | 8.3 | 5.6 | 9.1 | |
| Forest Cover | % | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| min-max | 100–100 | 100–100 | 100–100 | 100–100 | 100–100 | 100–100 | 100–100 | 100–100 | 100–100 | ||
| Carbon stock | t CO2/ha | 6035 | 6059 | 6242 | 5521 | 5910 | 3648 | 3022 | 1588 | 3405 |
| Regime 1 (CCFt) | Regime 2 (CCFs) | Regime 3 (RFMt) | Regime 4 (RFMs) | Regime 5 (PCF) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NI | SI | NI | SI | NI | SI | NI | SI | NI | SI | ||
| SEV (NZD/ha) by region | |||||||||||
| Carbon Price (NZD/t CO2) | 0 | 4056 | −5944 | 136,126 | 44,133 | 15,255 | −2571 | 80,353 | 23,182 | −10,503 | −10,503 |
| 35 | 17,344 | −611 | 136,126 | 44,205 | 23,526 | 642 | 80,353 | 23,182 | 8418 | −2786 | |
| 80 | 34,430 | 6267 | 136,126 | 44,714 | 34,161 | 4773 | 80,353 | 23,182 | 32,746 | 7137 | |
| 160 | 65,201 | 18,751 | 136,126 | 44,714 | 53,067 | 12,118 | 80,353 | 23,182 | 75,995 | 24,777 | |
| Timber Price | −20% | 31,404 | 5292 | 108,158 | 36,323 | 28,892 | 3070 | 63,454 | 17,717 | 32,746 | 7137 |
| base | 34,430 | 6267 | 136,126 | 44,714 | 34,161 | 4773 | 80,353 | 23,182 | 32,746 | 7137 | |
| 20% | 37,455 | 7283 | 164,093 | 53,877 | 39,430 | 6477 | 97,252 | 28,646 | 32,746 | 7137 | |
| Yield | −50% | 11,680 | −2395 | 66,206 | 20,973 | 11,535 | −3159 | 38,106 | 9520 | 11,121 | −1683 |
| −20% | 25,330 | 2801 | 108,159 | 35,444 | 25,111 | 1601 | 63,454 | 17,717 | 24,096 | 3609 | |
| base | 34,430 | 6267 | 136,126 | 44,714 | 34,161 | 4773 | 80,353 | 23,182 | 32,746 | 7137 | |
| 20% | 43,530 | 9733 | 164,093 | 54,399 | 43,211 | 7946 | 97,252 | 28,646 | 41,396 | 10,665 | |
| 50% | 57,179 | 14,932 | 206,044 | 68,921 | 56,787 | 12,706 | 122,600 | 36,843 | 54,370 | 15,957 | |
| Discount rate | 4% | 81,258 | 23,159 | 213,192 | 73,200 | 77,352 | 18,639 | 135,619 | 40,200 | 65,356 | 21,141 |
| 6% | 34,430 | 6267 | 136,126 | 44,714 | 34,161 | 4773 | 80,353 | 23,182 | 32,746 | 7137 | |
| 8% | 15,794 | −649 | 97,452 | 31,479 | 15,560 | −1357 | 51,535 | 14,308 | 17,020 | 546 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bown, H.E.; Watt, M.S. Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand. Forests 2024, 15, 344. https://doi.org/10.3390/f15020344
Bown HE, Watt MS. Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand. Forests. 2024; 15(2):344. https://doi.org/10.3390/f15020344
Chicago/Turabian StyleBown, Horacio E., and Michael S. Watt. 2024. "Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand" Forests 15, no. 2: 344. https://doi.org/10.3390/f15020344
APA StyleBown, H. E., & Watt, M. S. (2024). Financial Comparison of Continuous-Cover Forestry, Rotational Forest Management and Permanent Carbon Forest Regimes for Redwood within New Zealand. Forests, 15(2), 344. https://doi.org/10.3390/f15020344






