Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme
Abstract
1. Introduction
2. Materials and Methods
2.1. Growth Models
2.2. Growth Data
2.3. Prediction of Productivity Indices
2.3.1. Extraction of Productivity Indices and Predictor Variables
2.3.2. Modelling Approach
2.3.3. Extraction of 300 Index and Site Index for Spatial Predictions of Carbon
2.4. Predictions of Carbon
2.4.1. Overview
2.4.2. Redwood Carbon Predictions
2.4.3. Cypress spp. Carbon Predictions
2.4.4. Predictions of Total Carbon and Residual Carbon for Redwood and Cypresses
3. Results
3.1. Productivity Models for Redwood
3.2. Productivity Models for Cypresses
3.3. Spatial Predictions of 300 Index and Site Index
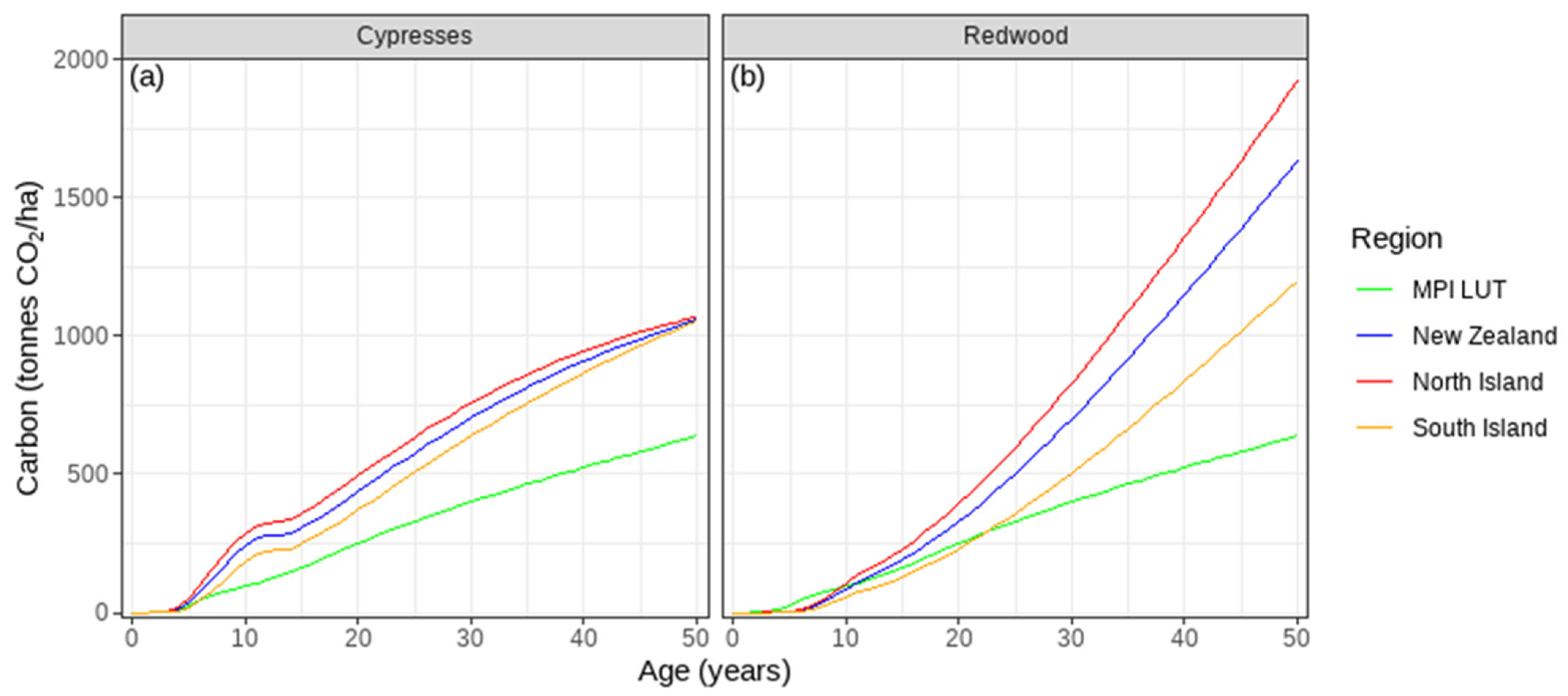
3.4. Differences Between Species and Islands in Post-1989 Carbon
3.5. Comparisons of Post-1989 Carbon with Existing Lookup Tables
3.6. Regional Variation in Predicted Post-1989 Carbon
3.7. Comparisons of Age of Average Carbon to Current MPI Averaging Age
3.8. Regional Variation in Pre-1990 Carbon
3.9. National, Island and Regional Estimates of the LUT for Redwood and Cypresses
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ETS | New Zealand’s Emissions Trading Scheme |
| FMA | Field measurement approach |
| LUT | Lookup table |
| MTH | Mean top height (mean height of the 100 largest diameter trees per hectare) |
| MPI | Ministry for Primary Industries |
| RFE | Recursive feature elimination |
| RMSE | Root mean square error |
| PSP | Permanent sample plot |
Appendix A
| Variable | Units | Abbreviation | Reference |
|---|---|---|---|
| Climatic variables | |||
| Air temperature—mean, max, min. | °C | Tmean, Tmin, Tmax | [41] |
| Degree ground frost (frosts/month) | days | DGF | [40] |
| Growing degree days | Degree days | GDD | [40] |
| Rainfall | mm | Rain | [41] |
| Rainfall days | days year−1 | Rain days | [41] |
| Relative Humidity at 9 am | % | RH | [41] |
| Solar radiation | MJ m−2 day−1 | S Rad | [41] |
| Sunshine hours | hours | Sun hours | [41] |
| Windspeed | km hr−1 | Wind | [41] |
| Water balance | |||
| Annual water deficit | mm | AWD | [45,70] |
| Drainage | mm | Drain | [45,70] |
| Gravel content | % | GC | [44] |
| Percentage root zone water balance | % | Wbal | [42] |
| Plant rooting depth | mm | PRD | [44] |
| Profile available water content | mm | PAW | [44] |
| Profile readily available water | mm | PRAW | [44] |
| Rainfall/Potential evapotranspiration | RPet | [45,70] | |
| Topographic wetness index | TWI | [71] | |
| Edaphic variables | |||
| Carbon: Nitrogen ratio | CN ratio | [43] | |
| Macroporosity | % | Macro | [44] |
| Particle size | [45,70] | ||
| pH | pH | [44] | |
| Phosphorus retention | % | P retention | [44] |
| Topographic and landscape | |||
| Aspect | ° | Aspect | [45,70] |
| Distance to stream | m | DTS | [46] |
| Elevation | m | Elev | [47] |
| Multiresolution ridge top flatness | MrRFT | [72] | |
| Multiresolution valley bottom flatness | MrVBF | [72] | |
| Profile curvature | Profc | [72] | |
| Slope | ° | Slope | [46] |
References
- Manley, B. Impact of carbon price on the relative profitability of production forestry and permanent forestry for New Zealand plantations. For. Policy Econ. 2023, 156, 103057. [Google Scholar]
- ICAP. Emissions Trading Worldwide: Status Report 2023. 2023. Available online: https://icapcarbonaction.com/en/publications/emissions-trading-worldwide-2023-icap-status-report (accessed on 17 January 2025).
- Ministry for Primary Industries. Registering in the ETS with Post-1989 Forest Land. 2023. Available online: https://www.mpi.govt.nz/forestry/forestry-in-the-emissions-trading-scheme/joining-the-ets/registering-in-the-ets-with-post-1989-forest-land/ (accessed on 23 January 2025).
- Leining, C. A Guide to the New Zealand Emissions Trading Scheme: 2022 Update. 2022. Available online: https://www.motu.nz/assets/Documents/our-research/environment/climate-change-mitigation/emissions-trading/A-Guide-to-the-New-Zealand-Emissions-Trading-System-2022-Update-Motu-Research.pdf (accessed on 15 February 2025).
- NZFOA. New Zealand Forestry Industry, Facts and Figures 2022/2023. New Zealand Plantation Forest Industry. New Zealand Forest Owners Association, Wellington. 2023. Available online: https://www.nzfoa.org.nz/images/Facts_and_Figures_2022-2023_-_WEB.pdf (accessed on 11 March 2024).
- Kearns, V. New Zealand Cypress Strategy. 2024–2044. Available online: https://www.nzffa.org.nz/system/assets/8345/SWP-T138.pdf (accessed on 10 June 2024).
- Brown, J.E. Monarchs of the Mist: The Story of Redwood National Park and the Coast Redwoods; Coastal Parks Association: Point Reyes Station, CA, USA, 1982. [Google Scholar]
- Earle, C.J. Sequoia sempervirens. The Gymnosperm Database. 2018. Available online: https://www.conifers.org/cu/Sequoia.php (accessed on 22 June 2023).
- Sillett, S.C.; Van Pelt, R.; Carroll, A.L.; Campbell-Spickler, J.; Antoine, M.E. Aboveground biomass dynamics and growth efficiency of Sequoia sempervirens forests. For. Ecol. Manag. 2020, 458, 117740. [Google Scholar]
- Bain, J.; Nicholas, I. Health. In Best Practice with Farm Forestry Timber Species; Nicholas, I., Ed.; No. 3: Redwoods—NZFFA Electronic Handbook Series No. 3; NZFFA: Wellington, New Zealand, 2008; Available online: https://www.nzffa.org.nz/system/assets/2080/Redwoods_Handbook.pdf (accessed on 22 June 2023).
- Peters, T.; Hardaker, A.; Dauksta, D.; Newman, G.; Lellig, C.; Healey, J. Top Five Alternative Conifer Tree Species in Great Britain: Main Report and Executive Summary. Welsh Government. 2021. Available online: https://woodknowledge.wales/wp-content/uploads/5-Alternative-conifer-species-final-corrected-EN.pdf (accessed on 22 June 2023).
- Brown, I.; Low, C.; McConnochie, R.; Nicholas, I.; Webster, R. Site Selection. In Best Practice with Farm Forestry Timber Species; Nicholas, I., Ed.; No. 3: Redwoods—NZFFA Electronic Handbook Series No. 3; NZFFA: Wellington, New Zealand, 2008; pp. 19–21. Available online: https://www.nzffa.org.nz/system/assets/2080/Redwoods_Handbook.pdf (accessed on 22 June 2023).
- Rapley, S. Redwood in New Zealand. N. Z. J. For. 2018, 63, 29–33. [Google Scholar]
- Jacobs, D.F.; Cole, D.W.; McBride, J.R. Fire history and perpetuation of natural coast redwood ecosystems. J. For. 1985, 83, 494–497. [Google Scholar]
- Stuart, J.D. Fire history of an old-growth forest of Sequoia sempervirens (Taxodiaceae) forest in Humboldt Redwoods State Park, California. Madrono 1987, 34, 128–141. [Google Scholar]
- Olson, D.F.; Roy, D.F.; Walters, G.A. Sequoia sempervirens (D. Don) Endl. Redwood. Silv. N. Am. 1990, 1, 541–551. [Google Scholar]
- Knowles, F.B.; Miller, J.T. Introduced Forest Trees in New Zealand: Recognition, Role, and Seed Source; No. 13 The Redwoods; FRI Bulletin No. 124; New Zealand Forest Research Institute: Rotorua, New Zealand, 1993. [Google Scholar]
- Toral, I.; Caru, M.; Herrera, M.A.; Gonzalez, L.; Martin, L.M.; Miranda, J.; Navarro-Cerrillo, R.M. Clones identification of Sequoia sempervirens (D. Don) Endl. in Chile by using PCR-RAPDs technique. J. Zhejiang Univ. Sci. B 2009, 10, 112–119. [Google Scholar] [CrossRef]
- Arnaud, Y.; Franclet, A.; Tranvan, H.; Jacques, M. Micropropagation and rejuvenation of Sequoia sempervirens (Lamb) Endl: A review. Ann. Sci. For. 1993, 50, 273–295. [Google Scholar] [CrossRef][Green Version]
- Breidenbach, N.; Gailing, O.; Krutovsky, K.V. Genetic structure of coast redwood (Sequoia sempervirens [D. Don] Endl.) populations in and outside of the natural distribution range based on nuclear and chloroplast microsatellite markers. PLoS ONE 2020, 15, e0243556. [Google Scholar]
- SWP Research Partnership. The Specialty Woods Products Research Partnership. Final Report. 2015–2023. 2023. Available online: https://fgr.nz/wp-content/uploads/2024/03/SWP-T170-Final-Report-DIGITAL-final.pdf (accessed on 7 October 2023).
- Watt, M.S.; Kimberley, M.O. Spatial comparisons of carbon sequestration for redwood and radiata pine within New Zealand. For. Ecol. Manag. 2022, 513, 120190. [Google Scholar]
- Watt, M.S.; Kimberley, M.O.; Rapley, S.; Webster, R. Comparing volume productivity of redwood and radiata pine plantations in New Zealand. For. Ecol. Manag. 2021, 500, 119628. [Google Scholar]
- Kimberley, M.O.; Watt, M.S. A Novel Approach to Modelling Stand-Level Growth of an Even-Aged Forest Using a Volume Productivity Index with Application to New Zealand-Grown Coast Redwood. Forests 2021, 12, 1155. [Google Scholar] [CrossRef]
- Hogan, C.M.; Frankis, M.P. Monterey Cypress, Cupressus macrocarpa; Stromberg, N., Ed.; Global Twitcher. Com.: Degerhamn, Sweden, 2009. [Google Scholar]
- Axelrod, D.I. Age and origin of the Monterey endemic area. Madrono 1982, 29, 127–147. [Google Scholar]
- Little, E.L. Names of new world cypresses (Cupressus). Phytologia 1970, 20, 429–445. [Google Scholar]
- Felger, R.S.; Johnson, M.B.; Wilson, M.F. The Trees of Sonora, Mexico; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Rzedowski, J.; Huerta, L. Vegetación de México; Limusa, Noriega Editores México: Mexico City, Mexico, 1994. [Google Scholar]
- Farjon, A. “Cupressus lusitanica”. IUCN Red List of Threatened Species. 2013: E.T42221A2962663. 2013. Available online: https://www.iucnredlist.org/species/42221/2962663 (accessed on 16 January 2025).
- Haslett, A.N. Properties and utilisation of exotic speciality timbers grown in New Zealand. Part III: Cypresses. Chamaecyparis lawsoniana (A. Murr.) Parl.,× Cupressocyparis leylandii (Jacks et Dall.) Dall., Cupressus lusitanica Mill., Cupressus macrocarpa Hartw. FRI Bull. For. Res. Inst. N. Z. 1986, 119, 12. [Google Scholar]
- Kimberley, M.O.; West, G.; Dean, M.; Knowles, L. Site Productivity: The 300 Index—A volume productivity index for radiata pine. N. Z. J. For. 2005, 50, 13–18. [Google Scholar]
- Kimberley, M.O.; Watt, M.S. Growth Models for Even-Aged Stands of Hesperocyparis macrocarpa and Hesperocyparis lusitanica. Forests 2023, 14, 105. [Google Scholar] [CrossRef]
- Assmann, E. Die Bedeutung des „erweiterten Eichhorn’schen Gesetzes “für die Konstruktion von Fichten-Ertragstafeln. Forstwiss. Cent. 1955, 74, 321–330. [Google Scholar]
- Hasenauer, H.; Burkhart, H.E.; Sterba, H. Variation in potential volume yield of loblolly pine plantations. For. Sci. 1994, 40, 162–176. [Google Scholar]
- Vanclay, J.K.; Skovsgaard, J.P.; Hansen, C.P. Assessing the quality of permanent sample plot databases for growth modelling in forest plantations. For. Ecol. Manag. 1995, 71, 177–186. [Google Scholar]
- Skovsgaard, J.P. Management of Sitka spruce Without Thinnings: An Analysis of Stand Structure and Volume Production of Unthinned Stands of Sitka spruce (Picea sitchensis (Bong.) Carr.) in Denmark; 8789822781; Forskningscentret for Skov og Landskab: Hørsholm, Denmark, 1997. [Google Scholar]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. For. Int. J. For. Res. 2008, 81, 13–31. [Google Scholar]
- Watt, M.S.; Kimberley, M.O.; Steer, B.S.C.; Holdaway, A. Spatial comparisons of productivity and carbon sequestration for Cupressus lusitanica and macrocarpa within New Zealand. For. Ecol. Manag. 2023, 536, 120829. [Google Scholar]
- Leathwick, J.R.; Wilson, G.; Stephens, R.T.T. Climate Surfaces for New Zealand, Landcare Research Contract Report LC9798/126; Landcare Research: Hamilton, New Zealand, 1998; p. 22. [Google Scholar]
- Wratt, D.S.; Tait, A.; Griffiths, G.; Espie, P.; Jessen, M.; Keys, J.; Ladd, M.; Lew, D.; Lowther, W.; Mitchell, N.; et al. Climate for crops: Integrating climate data with information about soils and crop requirements to reduce risks in agricultural decision-making. Meteorol. Appl. 2006, 13, 305–315. [Google Scholar] [CrossRef]
- Palmer, D.J.; Watt, M.S.; Hock, B.K.; Lowe, D.J. A dynamic framework for spatial modelling Pinus radiata soil water balance (SWatBal) across New Zealand. Scion Bull. 2009, 234, 93. [Google Scholar]
- Watt, M.S.; Palmer, D.J. Use of regression kriging to develop a Carbon: Nitrogen ratio surface for New Zealand. Geoderma 2012, 183, 49–57. [Google Scholar]
- Newsome, P.F.J.; Wilde, R.H.; Willoughby, E.J. Land Resource Information System Spatial Data Layers: Data Dictionary. Landcare Research report; LandCare Research: Palmerston North, New Zealand, 2008; p. 75. [Google Scholar]
- Leathwick, J.; Morgan, F.; Wilson, G.; Rutledge, D.; McLeod, M.; Johnston, K. Land Environments of New Zealand: A Technical Guide; Ministry for the Environment and Manaaki Whenua Landcare Research: Lincoln, New Zealand, 2002; p. 244. [Google Scholar]
- Palmer, D.J.; Höck, B.K.; Dunningham, A.G.; Lowe, D.J.; Payn, T.W. Developing national-scale terrain attributes for New Zealand (TANZ). For. Res. Bull. 2009, 232, 1–81. [Google Scholar]
- Barringer, J.R.F.; Pairman, D.; McNeill, S.J. Development of a High Resolution Digital Elevation Model for New Zealand; Landcare Research Contract Report (LC0102/170); Landcare Research: Lincoln, New Zealand, 2002. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Woodall, C.W.; Heath, L.S.; Domke, G.M.; Nichols, M.C. Methods and Equations for Estimating Aboveground Volume, Biomass, and Carbon for Trees in the US Forest Inventory, 2010; General Technical Report NRS-88; US Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2011; Volume 88, pp. 1–30. 30p. [Google Scholar]
- Miles, P.D.; Smith, W.B. Specific Gravity and Other Properties of Wood and Bark for 156 Tree Species Found in North America; US Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2009; Volume 38. [Google Scholar]
- Kizha, A.R.; Han, H.-S. Predicting aboveground biomass in second growth coast redwood: Comparing localized with generic allometric models. Forests 2016, 7, 96. [Google Scholar] [CrossRef]
- IPCC. Good Practice Guidance for Land Use, Land Use Change and Forestry; Penman, J., Gytarsky, M., Hiraishi, T., Krug, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., et al., Eds.; Institute for Global Environmental Strategies (IGES): Kanagawa, Japan, 2003. [Google Scholar]
- Pillers, M.D.; Stuart, J.D. Leaf-litter accretion and decomposition in interior and coastal old-growth redwood stands. Can. J. For. Res. 1993, 23, 552–557. [Google Scholar] [CrossRef]
- Busing, R.T.; Fujimori, T. Biomass, production and woody detritus in an old coast redwood (Sequoia sempervirens) forest. Plant Ecol. 2005, 177, 177–188. [Google Scholar] [CrossRef]
- Beets, P.N.; Roberston, K.A.; Ford-Robertson, J.B.; Gordon, J.; Maclaren, J.P. Description and validation of C_Change: A model for simulating carbon content in managed Pinus radiata stands. N. Z. J. For. Sci. 1999, 29, 409–427. [Google Scholar]
- Van Pelt, R.; Sillett, S.C.; Kruse, W.A.; Freund, J.A.; Kramer, R.D. Emergent crowns and light-use complementarity lead to global maximum biomass and leaf area in Sequoia sempervirens forests. For. Ecol. Manag. 2016, 375, 279–308. [Google Scholar] [CrossRef]
- Wilson, P.L.; Funck, J.W.; Avery, R.B. Fuelwood Characteristics of Northwestern Conifers and Hardwoods; General Technical Report PNW-GTR-810; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2010; Volume 810, 50p. [Google Scholar]
- Jones, D.A.; O’Hara, K.L. Carbon density in managed coast redwood stands: Implications for forest carbon estimation. Forestry 2012, 85, 99–110. [Google Scholar] [CrossRef]
- McKinley, R.B.; Shelbourne, C.J.A.; Harris, J.M.; Young, G.D. Variation in whole-tree basic wood density for a range of plantation species grown in New Zealand. N. Z. J. For. Sci. 2000, 30, 436–446. [Google Scholar]
- Beets, P.N.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; Graham, J.D.; Henley, D.; Meason, D.F. Plantation species-specific adjustment functions for the Forest Carbon Predictor in New Zealand. N. Z. J. For. Sci. 2018, 48, 1–17. [Google Scholar]
- Watt, M.S.; Kimberley, M.O. Comparing regional variation in carbon sequestration for radiata pine and redwood throughout New Zealand. N. Z. J. For. 2022, 67, 12–21. [Google Scholar]
- Te Uru Rākau. Additional Proposed Amendments to the Climate Change (Forestry Sector) Regulations 2008. 2021. Available online: https://www.mpi.govt.nz/dmsdocument/44176-Additional-proposed-amendments-to-the-Climate-Change-Forestry-Sector-Regulations-2008-Discussion-document (accessed on 28 January 2025).
- Maclaren, P. Realistic alternatives to radiata pine in New Zealand—A critical review. New Zealand J. For. 2005, 50, 3–10. [Google Scholar]
- Miller, J.T.; Knowles, F.B. Introduced Forest Trees in New Zealand: Recognition, Role, and Seed Source: Volume 19 The Cypresses (Revised Edition); FRI Bulletin No. 124; NZ Forest Research Institute: Rotorua, New Zealand, 1992; 33p. [Google Scholar]
- Nicholas, I. Best Practice with Farm Forestry Timber Species, No.1: Cypresses—NZFFA Electronic Handbook Series No. 1. 2007. Available online: www.nzffa.org.nz (accessed on 28 January 2025).
- West, G.G. Douglas fir, Japanese Larch and European Larch in pure and mixed stands. N. Z. J. For. Sci. 1991, 21, 3–9. [Google Scholar]
- NZFFA. Cedar—Japanese Cedar, Cryptomeria japonica. 2024. Available online: https://www.nzffa.org.nz/farm-forestry-model/species-selection-tool/species/cedar/japanese-cedar/#:~:text=Growth%20rates%20vary%20around%20the,each%20cm%20of%20diameter%20growth (accessed on 9 June 2024).
- Leathwick, J.; Wilson, G.; Rutledge, D.; Wardle, P.; Morgan, F.; Johnston, K.; McLeod, M.; Kirkpatrick, R. Land Environments of New Zealand; Bateman: Auckland, New Zealand, 2003; p. 184. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2000. [Google Scholar]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 1–14. [Google Scholar]







| Region | Cypresses | Redwood | |
|---|---|---|---|
| C. lusitanica | C. macrocarpa | S. sempervirens | |
| All data | |||
| North Island | 324 | 92 | 435 |
| South Island | 104 | 313 | 134 |
| New Zealand | 428 | 405 | 569 |
| PSP data | |||
| North Island | 159 | 53 | 147 |
| South Island | 21 | 106 | 44 |
| New Zealand | 180 | 159 | 191 |
| FMA data | |||
| North Island | 165 | 39 | 288 |
| South Island | 83 | 207 | 90 |
| New Zealand | 248 | 246 | 378 |
| Pre-1990 forests | |||
| North Island | 68 | 27 | 61 |
| South Island | 8 | 81 | 10 |
| New Zealand | 76 | 108 | 71 |
| Post-1989 forests | |||
| North Island | 256 | 65 | 374 |
| South Island | 96 | 232 | 124 |
| New Zealand | 352 | 297 | 498 |
| Regions | |||
| Auckland | 52 | 7 | 10 |
| Waikato/Taupo | 65 | 22 | 157 |
| Bay of Plenty | 115 | 26 | 39 |
| Gisborne | 41 | 13 | 76 |
| Hawke’s Bay/Southern Nth Island | 51 | 24 | 153 |
| Nelson/Marlborough | 20 | 28 | 6 |
| Canterbury/West Coast | 83 | 151 | 115 |
| Otago | 1 | 119 | 12 |
| Southland | 0 | 15 | 1 |
| 300 Index | Site Index | ||
|---|---|---|---|
| Variable | Importance | Variable | Importance |
| CN ratio | 0.172 | Tavg March | 0.394 |
| Tmax Dec. | 0.136 | Tmax Dec. | 0.105 |
| Wind Summer | 0.104 | CN ratio | 0.0641 |
| Tmin June | 0.0997 | Drainage June | 0.0524 |
| No. frosts June | 0.0862 | Water balance Feb. | 0.0519 |
| No. frosts Feb. | 0.0693 | Wind Summer | 0.0471 |
| 300 Index | Site Index | ||
|---|---|---|---|
| Variable | Importance | Variable | Importance |
| C. lusitanica | C. lusitanica | ||
| Tavg autumn | 0.199 | Growing degree days | 0.219 |
| Solar rad. January | 0.110 | Annual rain days | 0.132 |
| Solar rad. December | 0.084 | Tmin June | 0.098 |
| VPD spring | 0.063 | Solar rad. December | 0.087 |
| Tmin June | 0.063 | Annual solar rad. | 0.055 |
| Annual rain days | 0.062 | Solar rad. September | 0.053 |
| C. macrocarpa | C. macrocarpa | ||
| Solar rad. Autumn | 0.122 | Tmax January | 0.259 |
| Solar rad. June | 0.111 | Annual rainfall | 0.131 |
| Water balance June | 0.103 | Foliar Nitrogen | 0.124 |
| CN ratio | 0.088 | Establishment year | 0.121 |
| Aspect | 0.072 | Elevation | 0.103 |
| Profile curvature | 0.064 | Aspect | 0.100 |
| Region | Redwood | Cypresses | ||||||
|---|---|---|---|---|---|---|---|---|
| 300 Index (m3 ha−1 yr−1) | Site Index (m) | 300 Index (m3 ha−1 yr−1) | Site Index (m) | |||||
| Mean | CV | Mean | CV | Mean | CV | Mean | CV | |
| Auckland | 19.8 | 19.5 | 27.8 | 7.7 | 17.0 | 11.5 | 26.5 | 5.1 |
| Waikato/Taupo | 19.1 | 40.9 | 28.3 | 21.1 | 14.6 | 14.7 | 24.5 | 9.4 |
| Bay of Plenty | 19.4 | 31.8 | 29.7 | 17.8 | 14.6 | 15.4 | 25.6 | 10.3 |
| Gisborne | 18.7 | 31.7 | 27.0 | 18.2 | 17.1 | 19.6 | 26.7 | 12.8 |
| Hawke’s Bay/Southern NI | 20.0 | 35.4 | 27.9 | 17.4 | 13.8 | 15.7 | 23.9 | 10.2 |
| Nelson/Marlborough | 12.7 | 52.5 | 23.2 | 23.6 | 11.7 | 19.4 | 23.2 | 9.4 |
| Canterbury/West Coast | 11.8 | 57.2 | 20.6 | 25.4 | 11.3 | 16.8 | 21.9 | 8.7 |
| Otago | 13.7 | 56.6 | 19.0 | 13.6 | 12.3 | 14.7 | 22.2 | 9.2 |
| Southland | 9.0 | 51.8 | 19.3 | 10.2 | 13.1 | 14.0 | 23.4 | 5.7 |
| North Island | 19.7 | 28.1 | 14.9 | 24.9 | ||||
| South Island | 11.9 | 20.3 | 12.0 | 22.4 | ||||
| New Zealand | 16.6 | 25.0 | 13.6 | 23.8 | ||||
| Region | Redwood | Cypresses | ||
|---|---|---|---|---|
| Carbon (Tonnes CO2 ha−1) | Carbon (Tonnes CO2 ha−1) | |||
| Age 30 | Age 50 | Age 30 | Age 50 | |
| Island/national means | ||||
| North Island | 831 | 1920 | 755 | 1068 |
| South Island | 504 | 1198 | 638 | 1052 |
| New Zealand | 701 | 1633 | 702 | 1061 |
| % Island differences | ||||
| Nth Island/Sth Island | 64.8 | 60.3 | 18.3 | 1.5 |
| Regional means | ||||
| Auckland | 838 | 1936 | 838 | 1144 |
| Waikato/Taupo | 810 | 1868 | 744 | 1059 |
| Bay of Plenty | 829 | 1905 | 747 | 1060 |
| Gisborne | 792 | 1836 | 840 | 1146 |
| Hawke’s Bay/SN Isl. | 847 | 1956 | 712 | 1028 |
| Nelson/Marlborough | 546 | 1278 | 632 | 1047 |
| Canterbury/West Coast | 502 | 1191 | 610 | 1019 |
| Otago | 566 | 1360 | 650 | 1065 |
| Southland | 390 | 926 | 689 | 1111 |
| Range regional diff (%) | ||||
| North Island | 6.9 | 6.6 | 18.1 | 11.4 |
| South Island | 45.3 | 46.9 | 12.9 | 9.1 |
| MPI LUT | 400 | 641 | 400 | 641 |
| % Estimates/MPI LUT | ||||
| North Island | 108 | 200 | 89 | 67 |
| South Island | 26 | 87 | 60 | 64 |
| New Zealand | 75 | 155 | 76 | 65 |
| Region | Redwood | Cypresses | ||||
|---|---|---|---|---|---|---|
| Rotation Length (Years) | Rotation Length (Years) | |||||
| 40 | 45 | 50 | 40 | 45 | 50 | |
| Island/national means | ||||||
| North Island | 24 | 26 | 29 | 21 | 23 | 25 |
| South Island | 24 | 27 | 29 | 22 | 24 | 26 |
| New Zealand | 24 | 26 | 29 | 22 | 24 | 26 |
| Regional means | ||||||
| Auckland | 24 | 26 | 29 | 21 | 23 | 25 |
| Waikato/Taupo | 24 | 26 | 29 | 21 | 23 | 25 |
| Bay of Plenty | 24 | 26 | 29 | 21 | 23 | 25 |
| Gisborne | 24 | 26 | 29 | 21 | 23 | 24 |
| Hawke’s Bay/SN Isl. | 24 | 26 | 29 | 21 | 23 | 25 |
| Nelson/Marlborough | 24 | 26 | 29 | 22 | 24 | 26 |
| Canterbury/West Coast | 24 | 27 | 29 | 22 | 24 | 26 |
| Otago | 24 | 27 | 29 | 22 | 24 | 26 |
| Southland | 24 | 27 | 29 | 22 | 24 | 26 |
| Current LUT age | 22 | 22 | 22 | 22 | 22 | 22 |
| Difference averaging age | ||||||
| North Island | 2 | 4 | 7 | -1 | 1 | 3 |
| South Island | 2 | 5 | 7 | 0 | 2 | 4 |
| New Zealand | 2 | 4 | 7 | 0 | 2 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watt, M.S.; Kimberley, M.O.; Steer, B.S.C.; Scholer, M.N. Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme. Forests 2025, 16, 598. https://doi.org/10.3390/f16040598
Watt MS, Kimberley MO, Steer BSC, Scholer MN. Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme. Forests. 2025; 16(4):598. https://doi.org/10.3390/f16040598
Chicago/Turabian StyleWatt, Michael S., Mark O. Kimberley, Benjamin S. C. Steer, and Micah N. Scholer. 2025. "Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme" Forests 16, no. 4: 598. https://doi.org/10.3390/f16040598
APA StyleWatt, M. S., Kimberley, M. O., Steer, B. S. C., & Scholer, M. N. (2025). Carbon Sequestration Estimates for Minor Exotic Softwood Species for Use in New Zealand’s Emissions Trading Scheme. Forests, 16(4), 598. https://doi.org/10.3390/f16040598







