The Challenge of Die Filling in Rotary Presses—A Systematic Study of Material Properties and Process Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Powder Characterization
2.2.2. Powder Blending
2.2.3. Die Filling/Tableting Experiments
3. Theoretical Background
3.1. Definition of Terms
3.2. Detailed Process Description
- PS1—powder feeding from the hopper into the feed frame;
- PS2—powder transport by the feeding wheel (into the filling area);
- PS3—die filling;
- PS4—dosing out: reduction of die fill volume (by ).
4. Results and Discussion
4.1. Powder Characteristics—Flow Behavior
4.2. Impact of Process Parameters on Filling Yield
4.2.1. Impact of Turret Speed on the Filling Yield
4.2.2. Impact of Paddle Speed on the Filling Yield
4.2.3. Impact of Turret Speed and Paddle Speed on the Tablet Weight Variation Coefficient
4.2.4. Impact of the Fill Depth
4.2.5. Impact of the Dosing Depth
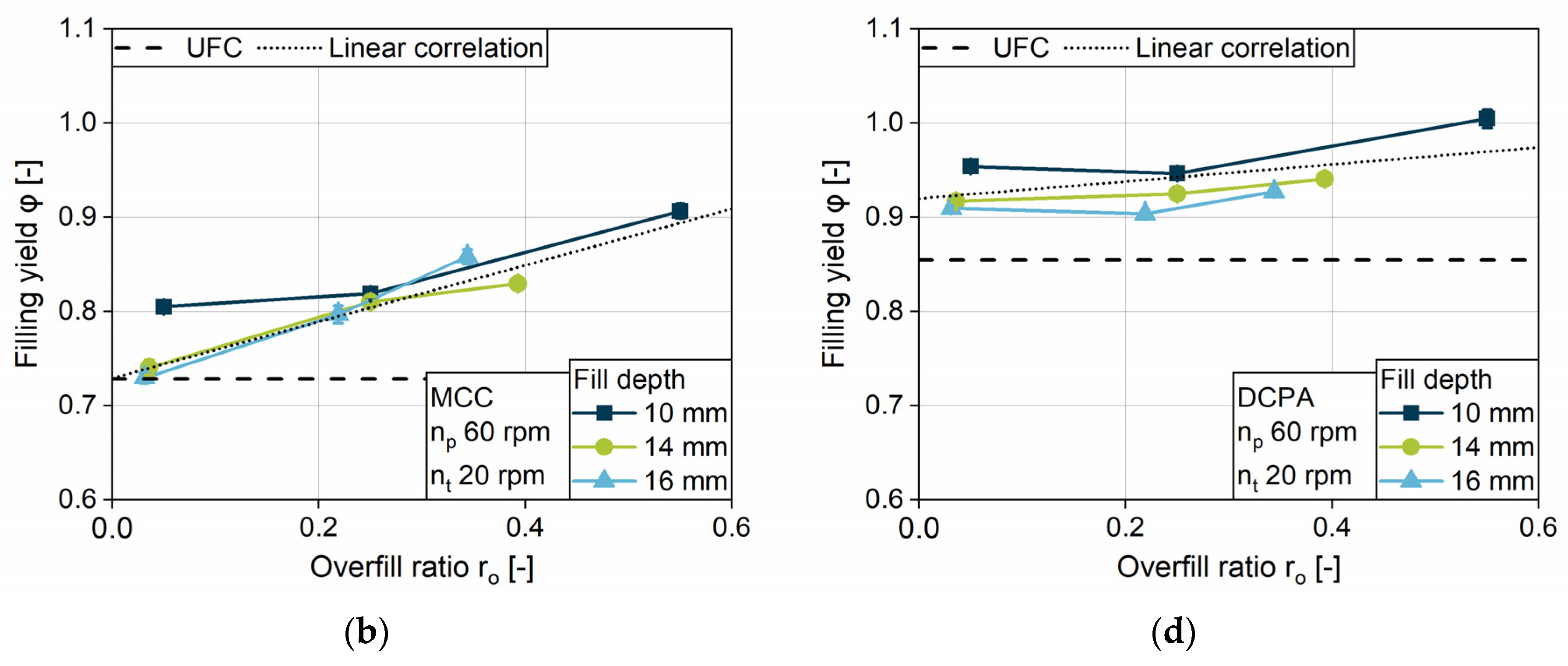
4.2.6. Impact of Overfill
4.3. Impact of Material Properties on the Filling Yield
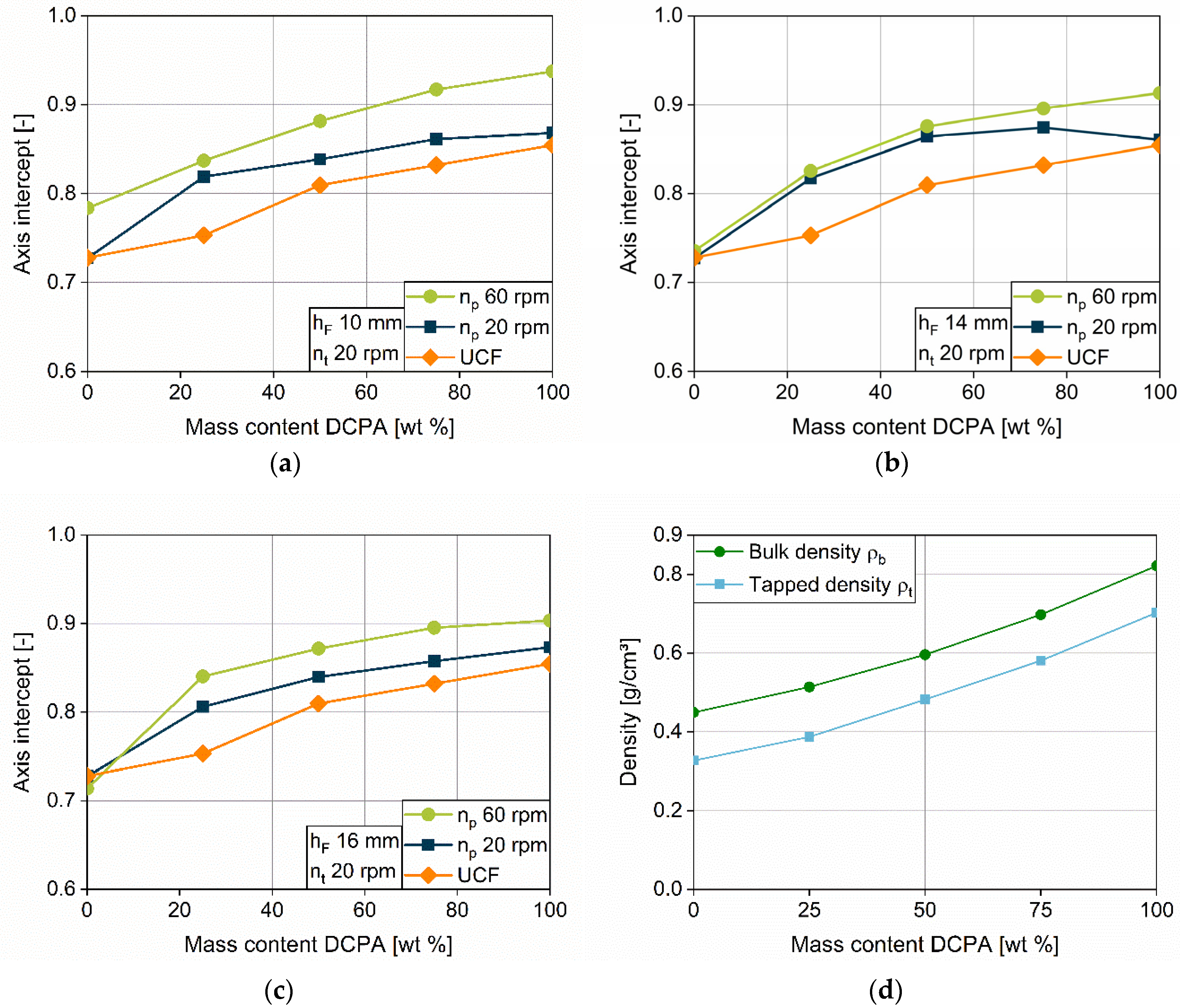
4.3.1. Impact of the Material Properties on the Densification
4.3.2. Impact of Flow Properties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chatterjee, S.; Food and Drug Administration CDER. Guidance for Industry, Q8 Pharmaceutical Development; Food and Drug Administration CDER: White Oak, MD, USA, 2006. [Google Scholar]
- Jackson, S.; Sinka, I.C.; Cocks, A.C.F. The effect of suction during die fill on a rotary tablet press. Eur. J. Pharm. Biopharm. 2007, 65, 253–256. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Dihoru, L.; Cocks, A.C.F. The flow of powder into simple and stepped dies. Powder Technol. 2003, 134, 24–39. [Google Scholar] [CrossRef]
- Mateo-Ortiz, D.; Colon, Y.; Romañach, R.J.; Méndez, R. Analysis of powder phenomena inside a Fette 3090 feed frame using in-line NIR spectroscopy. J. Pharm. Biomed. Anal. 2014, 100, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Peeters, E.; de Beer, T.; Vervaet, C.; Remon, J.-P. Reduction of tablet weight variability by optimizing paddle speed in the forced feeder of a high-speed rotary tablet press. Drug Dev. Ind. Pharm. 2015, 41, 530–539. [Google Scholar] [CrossRef]
- Xie, X.; Puri, V.M. Uniformity of Powder Die Filling Using a Feed Shoe: A Review. Particul. Sci. Technol. 2006, 24, 411–426. [Google Scholar] [CrossRef]
- Baserinia, R.; Sinka, I.C. Mass flow rate of fine and cohesive powders under differential air pressure. Powder Technol. 2018, 334, 173–182. [Google Scholar] [CrossRef]
- Baserinia, R.; Sinka, I.C. Powder die filling under gravity and suction fill mechanisms. Int. J. Pharm. 2019, 563, 135–155. [Google Scholar] [CrossRef]
- Schneider, L.C.R.; Sinka, I.C.; Cocks, A.C.F. Characterisation of the flow behaviour of pharmaceutical powders using a model die–shoe filling system. Powder Technol. 2007, 173, 59–71. [Google Scholar] [CrossRef]
- Sinka, I.C.; Cocks, A.C.F. Evaluating the flow behaviour of powders for die fill performance. Powder Metall. 2009, 52, 8–11. [Google Scholar] [CrossRef]
- Goh, H.P.; Heng, P.W.S.; Liew, C.V. Understanding effects of process parameters and forced feeding on die filling. Eur. J. Pharm. Sci. 2018, 122, 105–115. [Google Scholar] [CrossRef]
- Sinka, I.C.; Schneider, L.C.R.; Cocks, A.C.F. Measurement of the flow properties of powders with special reference to die fill. Int. J. Pharm. 2004, 280, 27–38. [Google Scholar] [CrossRef]
- Bierwisch, C.; Kraft, T.; Riedel, H.; Moseler, M. Die filling optimization using three-dimensional discrete element modeling. Powder Technol. 2009, 196, 169–179. [Google Scholar] [CrossRef]
- Bierwisch, C.; Kraft, T.; Riedel, H.; Moseler, M. Three-dimensional discrete element models for the granular statics and dynamics of powders in cavity filling. J. Mech. Phys. Solids 2009, 57, 10–31. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.-Y.; Kafui, K.D.; Thornton, C. 3D DEM/CFD analysis of size-induced segregation during die filling. Powder Technol. 2011, 206, 177–188. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.-Y.; Thornton, C. The effects of air and particle density difference on segregation of powder mixtures during die filling. Chem. Eng. Sci. 2011, 66, 661–673. [Google Scholar] [CrossRef]
- Nwose, E.N.; Pei, C.; Wu, C.-Y. Modelling die filling with charged particles using DEM/CFD. Particuology 2012, 10, 229–235. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Cocks, A.C.F. Numerical and experimental investigations of the flow of powder into a confined space. Mech. Mater. 2006, 38, 304–324. [Google Scholar] [CrossRef]
- Ketterhagen, W.R. Simulation of powder flow in a lab-scale tablet press feed frame: Effects of design and operating parameters on measures of tablet quality. Powder Technol. 2015, 275, 361–374. [Google Scholar] [CrossRef]
- Furukawa, R.; Shiosaka, Y.; Kadota, K.; Takagaki, K.; Noguchi, T.; Shimosaka, A.; Shirakawa, Y. Size-induced segregation during pharmaceutical particle die filling assessed by response surface methodology using discrete element method. J. Drug. Deliv. Sci. Technol. 2016, 35, 284–293. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Guo, Y. Numerical modelling of suction filling using DEM/CFD. Chem. Eng. Sci. 2012, 73, 231–238. [Google Scholar] [CrossRef]
- Hildebrandt, C.; Gopireddy, S.R.; Scherließ, R.; Urbanetz, N.A. Investigation of powder flow within a pharmaceutical tablet press force feeder—A DEM approach. Powder Technol. 2019, 345, 616–632. [Google Scholar] [CrossRef]
- Tsunazawa, Y.; Shigeto, Y.; Tokoro, C.; Sakai, M. Numerical simulation of industrial die filling using the discrete element method. Chem. Eng. Sci. 2015, 138, 791–809. [Google Scholar] [CrossRef]
- Gopireddy, S.R.; Hildebrandt, C.; Urbanetz, N.A. Numerical simulation of powder flow in a pharmaceutical tablet press lab-scale gravity feeder. Powder Technol. 2016, 302, 309–327. [Google Scholar] [CrossRef]
- Zakhvatayeva, A.; Zhong, W.; Makroo, H.A.; Hare, C.; Wu, C.Y. An experimental study of die filling of pharmaceutical powders using a rotary die filling system. Int. J. Pharm. 2018, 553, 84–96. [Google Scholar] [CrossRef]
- Mendez, R.; Muzzio, F.; Velazquez, C. Study of the effects of feed frames on powder blend properties during the filling of tablet press dies. Powder Technol. 2010, 200, 105–116. [Google Scholar] [CrossRef]
- Goh, H.P.; Sia Heng, P.W.; Liew, C.V. The Effects of Feed Frame Parameters and Turret Speed on Mini-Tablet Compression. J. Pharm. Sci. 2019, 108, 1161–1171. [Google Scholar] [CrossRef]
- Yaginuma, Y.; Ozeki, Y.; Kakizawa, M.; Gomi, S.-I.; Watanabe, Y. Effects of powder flowability on die-fill properties in rotary compression. J. Drug. Deliv. Sci. Technol. 2007, 17, 205–210. [Google Scholar] [CrossRef]
- van Snick, B.; Grymonpré, W.; Dhondt, J.; Pandelaere, K.; Di Pretoro, G.; Remon, J.P.; de Beer, T.; Vervaet, C.; Vanhoorne, V. Impact of blend properties on die filling during tableting. Int. J. Pharm. 2018, 549, 476–488. [Google Scholar] [CrossRef]
- Dühlmeyer, K.P.; Özcoban, H.; Leopold, C.S. A novel method for determination of the filling level in the feed frame of a rotary tablet press. Drug Dev. Ind. Pharm. 2018, 44, 1744–1751. [Google Scholar] [CrossRef]
- Dühlmeyer, K.P.; Özcoban, H.; Leopold, C.S. Inline monitoring of the powder filling level within a rotary tablet press feed frame. Powder Technol. 2019, 351, 134–143. [Google Scholar] [CrossRef]
- Dühlmeyer, K.P.; Özcoban, H.; Leopold, C.S. Comparison of two paddle wheel geometries within the filling chamber of a rotary tablet press feed frame with regard to the distribution behavior of a model powder and the influence on the resulting tablet mass. Drug Dev. Ind. Pharm. 2019, 45, 1233–1241. [Google Scholar] [CrossRef]
- Grymonpré, W.; Vanhoorne, V.; van Snick, B.; Blahova Prudilova, B.; Detobel, F.; Remon, J.P.; de Beer, T.; Vervaet, C. Optimizing feed frame design and tableting process parameters to increase die-filling uniformity on a high-speed rotary tablet press. Int. J. Pharm. 2018, 548, 54–61. [Google Scholar] [CrossRef]
- Schulze, D. Powders an Bulk Solids. Behavior, Characterization, Storage and Flow; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-73767-4. [Google Scholar]


















| Material | x10 [µm] | x50 [µm] | x90 [µm] | ρs[g/cm3] | ρb[g/cm3] | ρt[g/cm3] |
|---|---|---|---|---|---|---|
| MCC | 28 | 110 | 243 | 1.56 | 0.327 | 0.449 |
| 25 wt % DCPA | 29 | 117 | 258 | 0.387 | 0.514 | |
| 50 wt % DCPA | 31 | 136 | 284 | 0.483 | 0.596 | |
| 75 wt % DCPA | 31 | 148 | 298 | 0.581 | 0.698 | |
| DCPA | 38 | 178 | 322 | 2.83 | 0.703 | 0.822 |
| Blend | wt % MCC | wt % DCPA + 1% MgSt |
|---|---|---|
| 25 wt % DCPA | 75 | 25 |
| 50 wt % DCPA | 50 | 50 |
| 75 wt % DCPA | 25 | 75 |
| Fill Depth (mm) | Dosing Depth (mm) | Turret Speed (rpm) | Paddle Speed (rpm) |
|---|---|---|---|
| 10 | 4.5 8.5 9.5 | 20, 40, 60 | 5, 20, 40, 60 |
| 14 | 8.5 10.5 13.5 | 20, 40, 60 | 5, 20, 40, 60 |
| 10.5 | 20, 40, 60 | 5, 20, 40, 60 | |
| 16 | 13.5 | ||
| 15.5 | 20, 30, 40, 50, 60 | 5, 20, 40, 60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schomberg, A.K.; Kwade, A.; Finke, J.H. The Challenge of Die Filling in Rotary Presses—A Systematic Study of Material Properties and Process Parameters. Pharmaceutics 2020, 12, 248. https://doi.org/10.3390/pharmaceutics12030248
Schomberg AK, Kwade A, Finke JH. The Challenge of Die Filling in Rotary Presses—A Systematic Study of Material Properties and Process Parameters. Pharmaceutics. 2020; 12(3):248. https://doi.org/10.3390/pharmaceutics12030248
Chicago/Turabian StyleSchomberg, Ann Kathrin, Arno Kwade, and Jan Henrik Finke. 2020. "The Challenge of Die Filling in Rotary Presses—A Systematic Study of Material Properties and Process Parameters" Pharmaceutics 12, no. 3: 248. https://doi.org/10.3390/pharmaceutics12030248
APA StyleSchomberg, A. K., Kwade, A., & Finke, J. H. (2020). The Challenge of Die Filling in Rotary Presses—A Systematic Study of Material Properties and Process Parameters. Pharmaceutics, 12(3), 248. https://doi.org/10.3390/pharmaceutics12030248







