Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. PK Data
2.2. Data Analysis
2.2.1. Clustering
2.2.2. Population Pharmacokinetic Modeling
2.2.3. Structural PK Model
2.2.4. Variability Model
2.2.5. Model Evaluation
3. Results
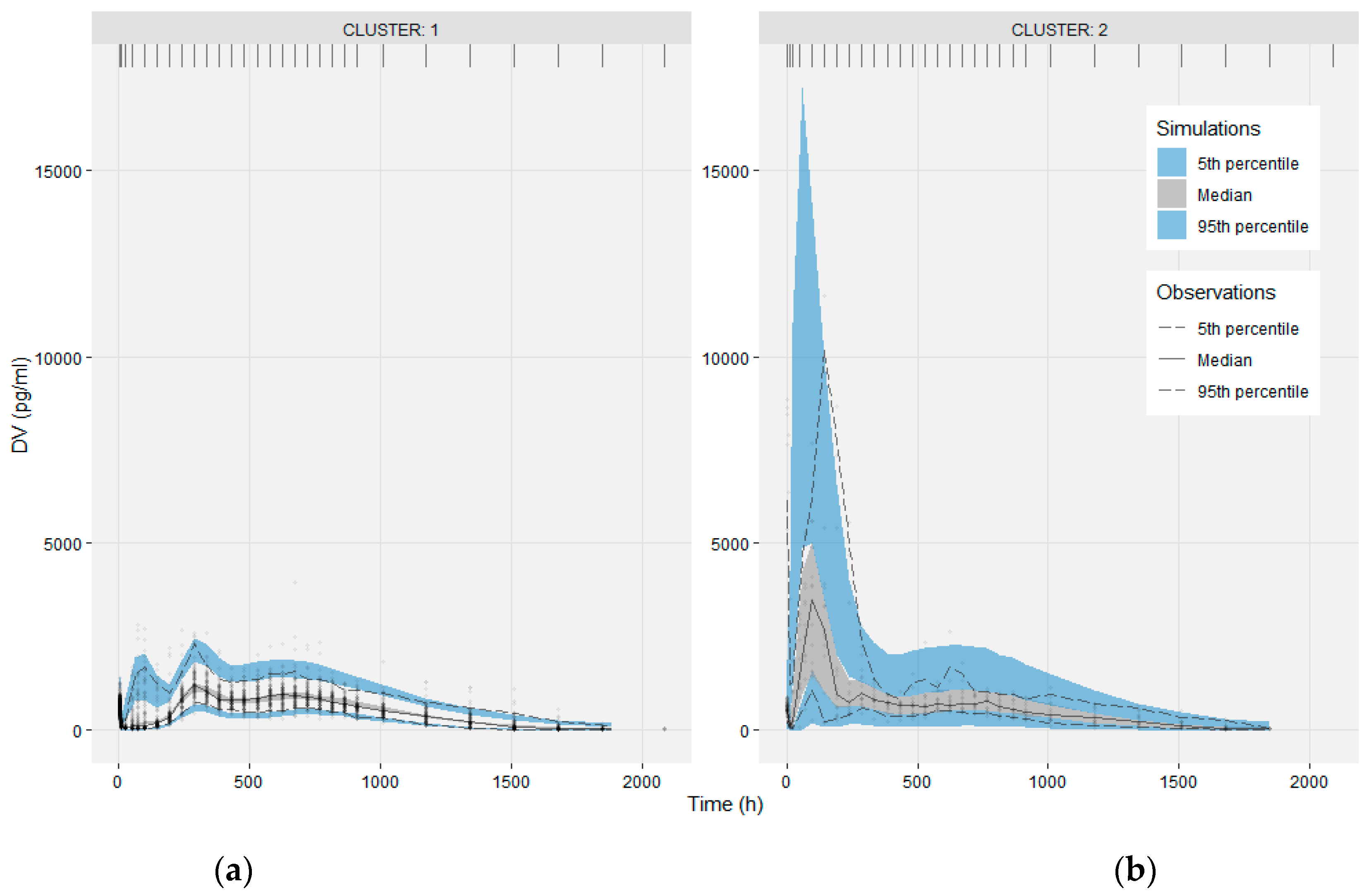
3.1. Clustering
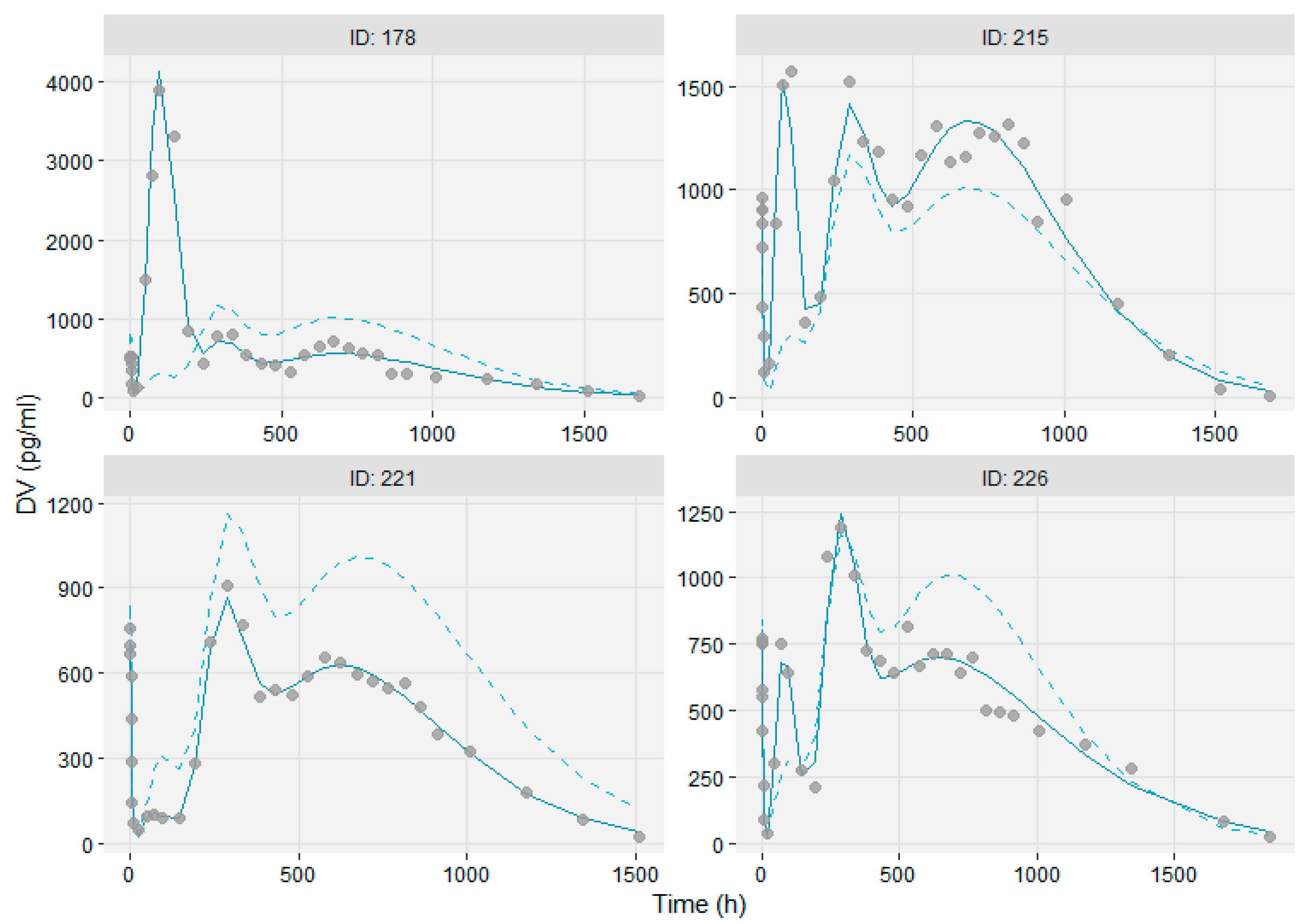
3.2. Population PK Model
3.3. Modeling the Sub-Populations of Cluster Analysis
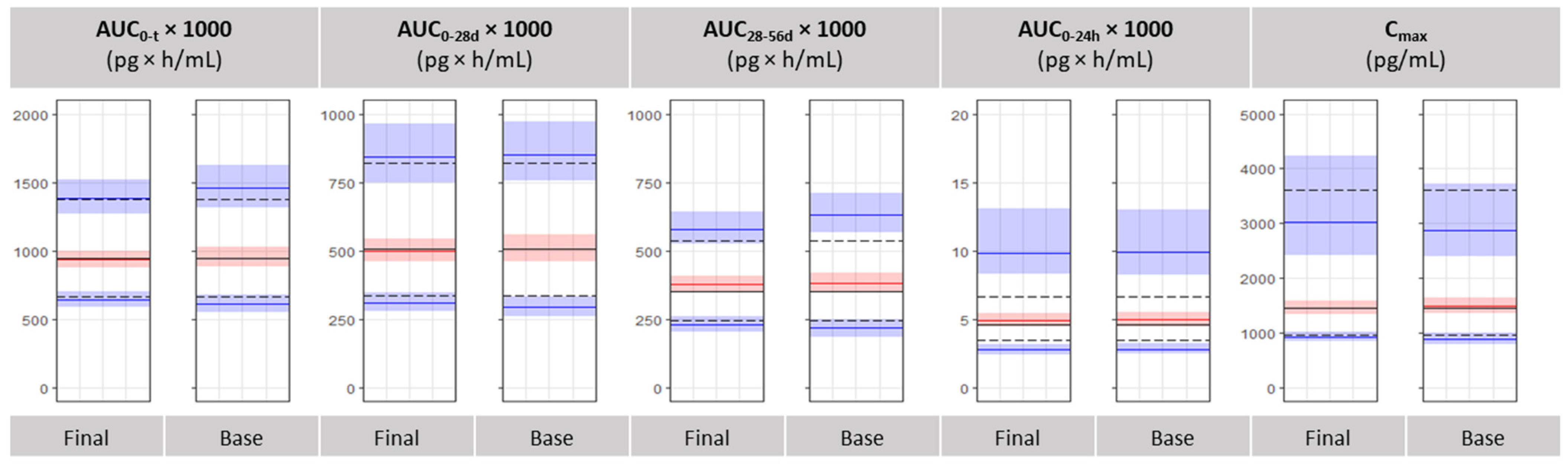
3.4. Bioequivalence Metrics Evaluation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stueven, A.K.; Kayser, A.; Wetz, C.; Amthauer, H.; Wree, A.; Tacke, F.; Wiedenmann, B.; Roderburg, C.; Jann, H. Somatostatin analogues in the treatment of neuroendocrine tumors: Past, present and future. Int. J. Mol. Sci. 2019, 20, 3049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Comets, E.; Mentré, F.; Kawai, R.; Nimmerfall, F.; Marbach, P.; Vonderscher, J. Modeling the Kinetics of Release of Octreotide from Long-Acting Formulations Injected Intramuscularly in Rabbits. J. Pharm. Sci. 2000, 89, 1123–1133. [Google Scholar] [CrossRef]
- Park, K.; Skidmore, S.; Hadar, J.; Garner, J.; Park, H.; Otte, A.; Soh, B.K.; Yoon, G.; Yu, D.; Yun, Y.; et al. Injectable, long-acting PLGA formulations: Analyzing PLGA and understanding microparticle formation. J. Control. Release 2019, 304, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Chen, T.-L.; Marino, M.; Lau, H.; Miller, T.; Kalafsky, G.; McLeod, J.F. Population PK and PK/PD modelling of microencapsulated octreotide acetate in healthy subjects. Br. J. Clin. Pharmacol. 2000, 50, 543–552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Genolini, C.; Ecochard, R.; Benghezal, M.; Driss, T.; Andrieu, S.; Subtil, F. KmlShape: An efficient method to cluster longitudinal data (Time-Series) according to their shapes. PLoS ONE 2016, 11, e0150738. [Google Scholar] [CrossRef]
- Bauer, R.J. NONMEM Tutorial Part I: Description of Commands and Options, With Simple Examples of Population Analysis. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 525–537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bauer, R.J. NONMEM Tutorial Part II: Estimation Methods and Advanced Examples. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 538–556. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibiansky, L.; Gibiansky, E.; Bauer, R. Comparison of Nonmem 7.2 estimation methods and parallel processing efficiency on a target-mediated drug disposition model. J. Pharmacokinet. Pharmacodyn. 2012, 39, 17–35. [Google Scholar] [CrossRef] [PubMed]
- Keizer, R.J.; Karlsson, M.O.; Hooker, A. Modeling and simulation workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e50. [Google Scholar] [CrossRef] [PubMed]
- Lindbom, L.; Ribbing, J.; Jonsson, E.N. Perl-speaks-NONMEM (PsN)—A Perl module for NONMEM related programming. Comput. Methods Programs Biomed. 2004, 75, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Savic, R.M.; Jonker, D.M.; Kerbusch, T.; Karlsson, M.O. Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies. J. Pharmacokinet. Pharmacodyn. 2007, 34, 711–726. [Google Scholar] [CrossRef] [PubMed]
- Shivva, V.; Korell, J.; Tucker, I.G.; Duffull, S.B. An approach for identifiability of population pharmacokinetic- pharmacodynamic models. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Tsamandouras, N.; Wendling, T.; Rostami-Hodjegan, A.; Galetin, A.; Aarons, L. Incorporation of stochastic variability in mechanistic population pharmacokinetic models: Handling the physiological constraints using normal transformations. J. Pharmacokinet. Pharmacodyn. 2015, 42, 349–373. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.T.; Mouksassi, M.S.; Holford, N.; Al-Huniti, N.; Freedman, I.; Hooker, A.C.; John, J.; Karlsson, M.O.; Mould, D.R.; Perez Ruixo, J.J.; et al. Model evaluation of continuous data pharmacometric models: Metrics and graphics. CPT Pharmacomet. Syst. Pharmacol. 2017, 6, 87–109. [Google Scholar] [CrossRef]
- Kim, H.; Han, S.; Cho, Y.-S.; Yoon, S.-K.; Bae, K.-S. Development of R packages: ‘NonCompart’ and ‘ncar’ for noncompartmental analysis (NCA). Transl. Clin. Pharmacol. 2018, 26, 10. [Google Scholar] [CrossRef] [Green Version]
- European Medicines Agency. EMA/MB/69923/2010—Annual Report of the European Medicines Agency 2009. Available online: https://www.ema.europa.eu/en/documents/scientific-guideline/octreotide-acetate-depot-powder-solvent-suspension-injection-10-mg-20-mg-30-mg-product-specific_en.pdf (accessed on 30 March 2021).
- Shivva, V.; Korell, J.; Tucker, I.G.; Duffull, S.B. Parameterisation affects identifiability of population models. J. Pharmacokinet. Pharmacodyn. 2014, 41, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Jaber, M.M.; Al-Kofahi, M.; Sarafoglou, K.; Brundage, R.C. Individualized Absorption Models in Population Pharmacokinetic Analyses. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 307–309. [Google Scholar] [CrossRef] [PubMed]
- Hadar, J.; Skidmore, S.; Garner, J.; Park, H.; Park, K.; Wang, Y.; Qin, B.; Jiang, X. Characterization of branched poly(lactide-co-glycolide) polymers used in injectable, long-acting formulations. J. Control. Release 2019, 304, 75–89. [Google Scholar] [CrossRef] [PubMed]



| Demographics | Median (Q1–Q3) |
|---|---|
| Subjects, n | 118 |
| Age, years | 28 (23–37) |
| Height, cm | 175 (170–178) |
| Weight, kg | 75 (66–86) |
| BMI, kg/m2 | 24.75 (22.4–27.7) |
| Clustering | |
| Cluster 1, n | 103 |
| Cluster 2, n | 15 |
| Non-Compartmental Analysis | Mean (±SD) |
| AUC0–t (pg × h/mL) | 988.7 × 103 (±327.9 × 103) |
| Cluster 1 | 944.0 × 103 (±284.0 × 103) |
| Cluster 2 | 1295.2 × 103 (±442.1 × 103) |
| Cmax (pg/mL) | 1891.1 (±1622.6) |
| Cluster 1 | 1433.3 (±497.4) |
| Cluster 2 | 5034.8 (±2840.6) |
| Parameter | Estimate (RSE%) | Bootstrap | Workflow Bootstrap | ||||
|---|---|---|---|---|---|---|---|
| Median | 95% CI | RSE (%) | Median | 95% CI | RSE (%) | ||
| ka | 0.27 (2.2) | 0.27 | 0.26–0.28 | 2 | 0.27 | 0.26–0.28 | 2 |
| V | 15.3 (7.7) | 15.1 | 13.5–16.8 | 6 | 15.1 | 13.6–17.1 | 6 |
| CL Cluster effect: | 32.7 (5.8) −8.61 (34) | 32.7 −9.32 | 31.0–34.4 −14.32 to −3.66 | 3 48 | 32.6 −9.24 | 30.8–34.8 −13.95 to −3.57 | 3 38 |
| YF1 | −5.18 (1.8) | −5.19 | −5.24 to −5.11 | 1 | −5.19 | −5.24 to −5.11 | 1 |
| YF2 Cluster effect: | −3.36 (7.9) 3.06 (33) | −3.35 3.01 | −3.62 to −3.03 2.52–3.46 | 4 8 | −3.34 3.02 | −3.69 to −3.02 2.02–3.55 | 5 14 |
| YF3 Cluster effect: | −1.54 (2.8) −0.523 (26.8) | −1.54 −0.468 | −1.64 to −1.42 −0.704 to −0.291 | 4 22 | −1.55 −0.47 | −1.65 to −1.44 −0.715–0.01 | 4 35 |
| YMTT1 | −0.421 (21.8) | −0.41 | −0.554 to −0.244 | 20 | −0.41 | −0.562 to −0.253 | 20 |
| MTT2 | 181 (3.3) | 180 | 166–191 | 5 | 179 | 167–191 | 4 |
| MTT3 | 506 (3.8) | 508 | 486–530 | 4 | 508 | 481–534 | 3 |
| N1 | 3.42 (15) | 3.43 | 2.67–4.07 | 10 | 3.44 | 2.80–4.10 | 9 |
| N2 | 17.9 (6) | 18.0 | 15.1–20.2 | 7 | 18.0 | 15.9–20.3 | 7 |
| N3 | 5.08 (5) | 5.00 | 4.57–5.62 | 5 | 5.03 | 4.58–5.57 | 5 |
| Proportional Residual Error | 0.143 (1.3) | 0.143 | 0.128–0.155 | 5 | 0.14 | 0.127–0.156 | 5 |
| Additive Residual Error | 28.4 (3.7) | 28.2 | 22.9–33.8 | 10 | 28.8 | 23.6–35.2 | 10 |
| Inter-Individual Variability | Estimate (RSE%) [Shrinkage %] | Median | 95% CI | RSE (%) | Median | 95% CI | RSE (%) |
| IIVV | 39.4 (13) [16.3] | 39.9 | 33.4–46.5 | 17 | 39.7 | 32.1–46.1 | 13 |
| IIVCL | 28.2 (8) [1] | 28.3 | 24.2–34.6 | 30 | 28.3 | 23.4–32.7 | 22 |
| IIVYF1 | 28.9 (7) [3.4] | 25.8 | 14.1–50.1 | 65 | 28.1 | 13.9–48.2 | 50 |
| IIVYF2 | 128.8 (16) [4] | 128.4 | 112.5–141.3 | 6 | 129.2 | 110.9–143.7 | 6 |
| IIVYF3 | 20.5 (18) [30.3] | 21.0 | 13.1–35.0 | 30 | 21.1 | 14.1–37.2 | 25 |
| IIVYMTT1 | 60.1 (12) [12] | 59.6 | 48.5–70.7 | 10 | 60.6 | 49.5–73.6 | 10 |
| IIVMTT2 | 17.3 (20) [17.6] | 18.2 | 14.4–26.3 | 68 | 18.7 | 14.3–28.8 | 50 |
| IIVMTT3 | 20.2 (9) [1.7] | 20.7 | 16.9–31.2 | 74 | 20.6 | 16.6–30.0 | 54 |
| IIVN1 | 71.2 (10) [22] | 70.2 | 36.0–101.5 | 25 | 69.2 | 36.0–106.1 | 23 |
| IIVN2 | 26.2 (21) [31.2] | 26.3 | 16.0–33.6 | 32 | 26.5 | 16.9–34.1 | 26 |
| IIVN3 | 31.4 (12) [9.3] | 29.7 | 24.0–41.5 | 14 | 31 | 24.2–42.2 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapralos, I.; Dokoumetzidis, A. Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis. Pharmaceutics 2021, 13, 1578. https://doi.org/10.3390/pharmaceutics13101578
Kapralos I, Dokoumetzidis A. Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis. Pharmaceutics. 2021; 13(10):1578. https://doi.org/10.3390/pharmaceutics13101578
Chicago/Turabian StyleKapralos, Iasonas, and Aristides Dokoumetzidis. 2021. "Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis" Pharmaceutics 13, no. 10: 1578. https://doi.org/10.3390/pharmaceutics13101578
APA StyleKapralos, I., & Dokoumetzidis, A. (2021). Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis. Pharmaceutics, 13(10), 1578. https://doi.org/10.3390/pharmaceutics13101578







