A Novel Method for Predicting the Human Inherent Clearance and Its Application in the Study of the Pharmacokinetics and Drug–Drug Interaction between Azidothymidine and Fluconazole Mediated by UGT Enzyme
Abstract
:1. Introduction
2. Materials and Methods
2.1. Construction of CLint QSAR Model
2.1.1. Data Collection and Processing
2.1.2. QSAR Model Construction
2.1.3. QSAR Model Evaluation
2.2. Bio-PK Metabolic System
2.2.1. Standards and Reagents
2.2.2. Preparation of Human Liver Microsome-Hydrogel (HLM-Gel) System
2.2.3. HPLC Analysis Method
2.2.4. Microsomal Incubation Assay
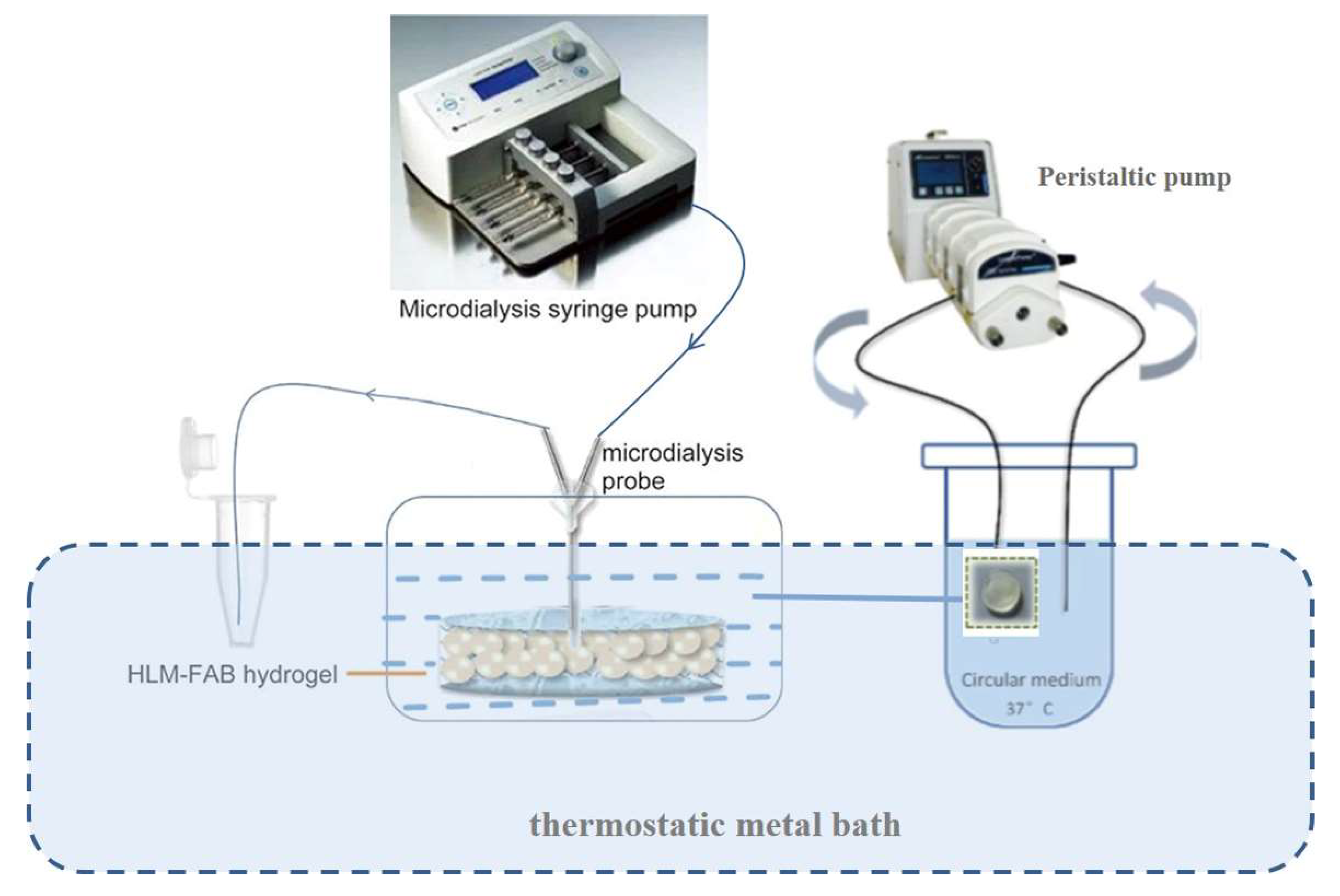
2.2.5. Bio-PK Metabolic System Construction
2.2.6. Metabolism of AZT in the Bio-PK Metabolic System
2.2.7. Interaction of AZT and FCZ in the Bio-PK Metabolic System
2.2.8. PBPK Model Construction
3. Results
3.1. QSAR Model of CLint
3.2. HPLC Method Validation
3.3. Incubation Time of HLM-Gel System
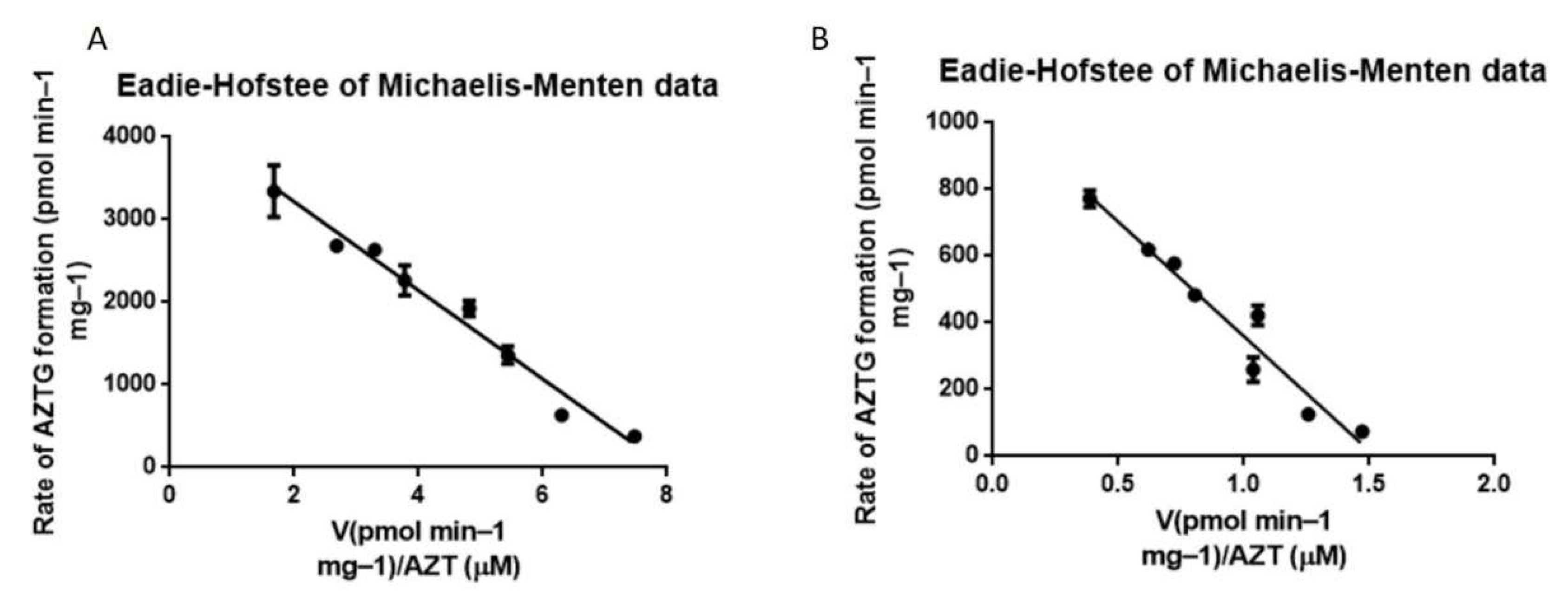
3.4. Metabolism via HLM and HLM-Gel
3.5. Bio-PK Metabolic System
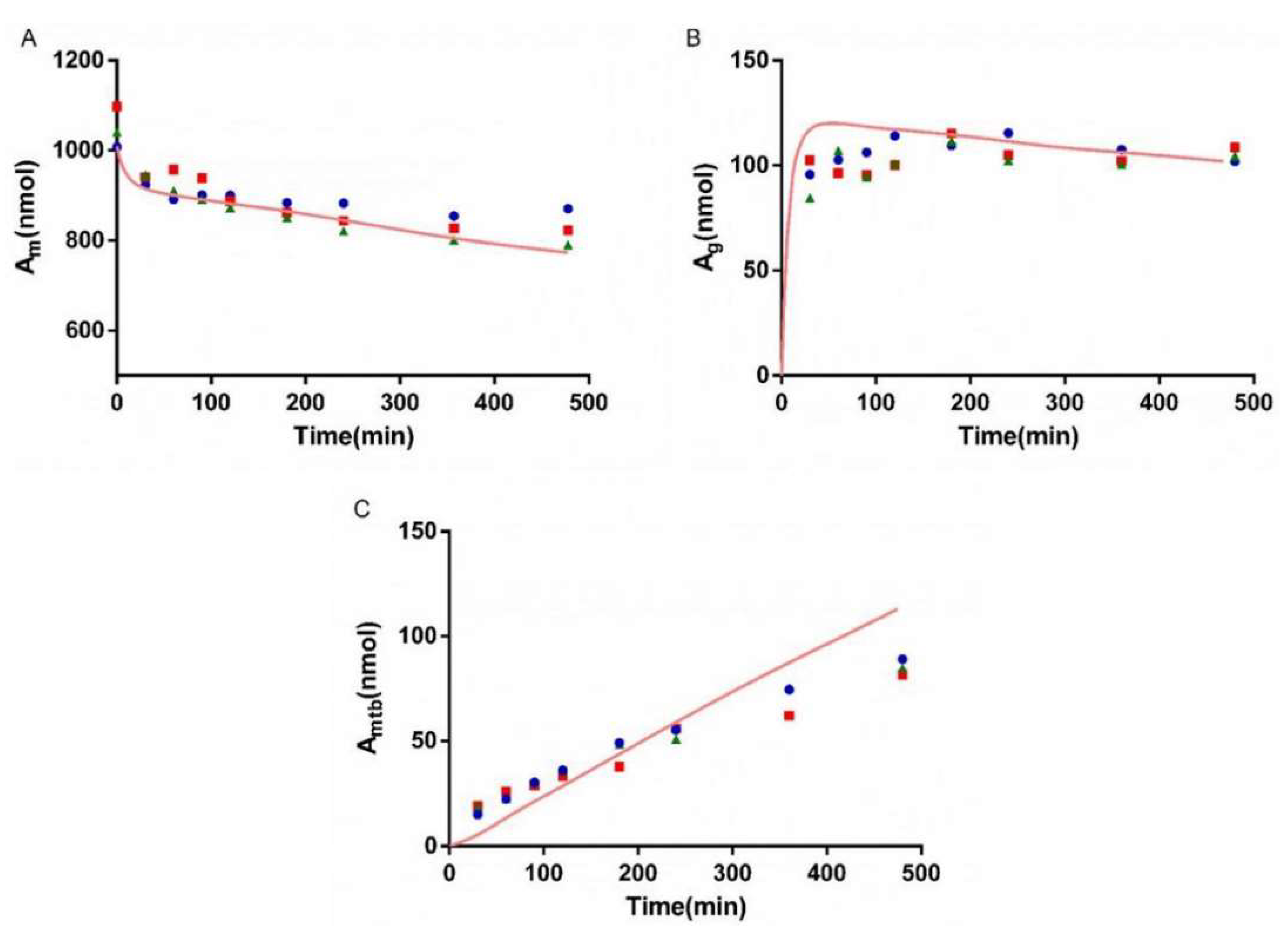
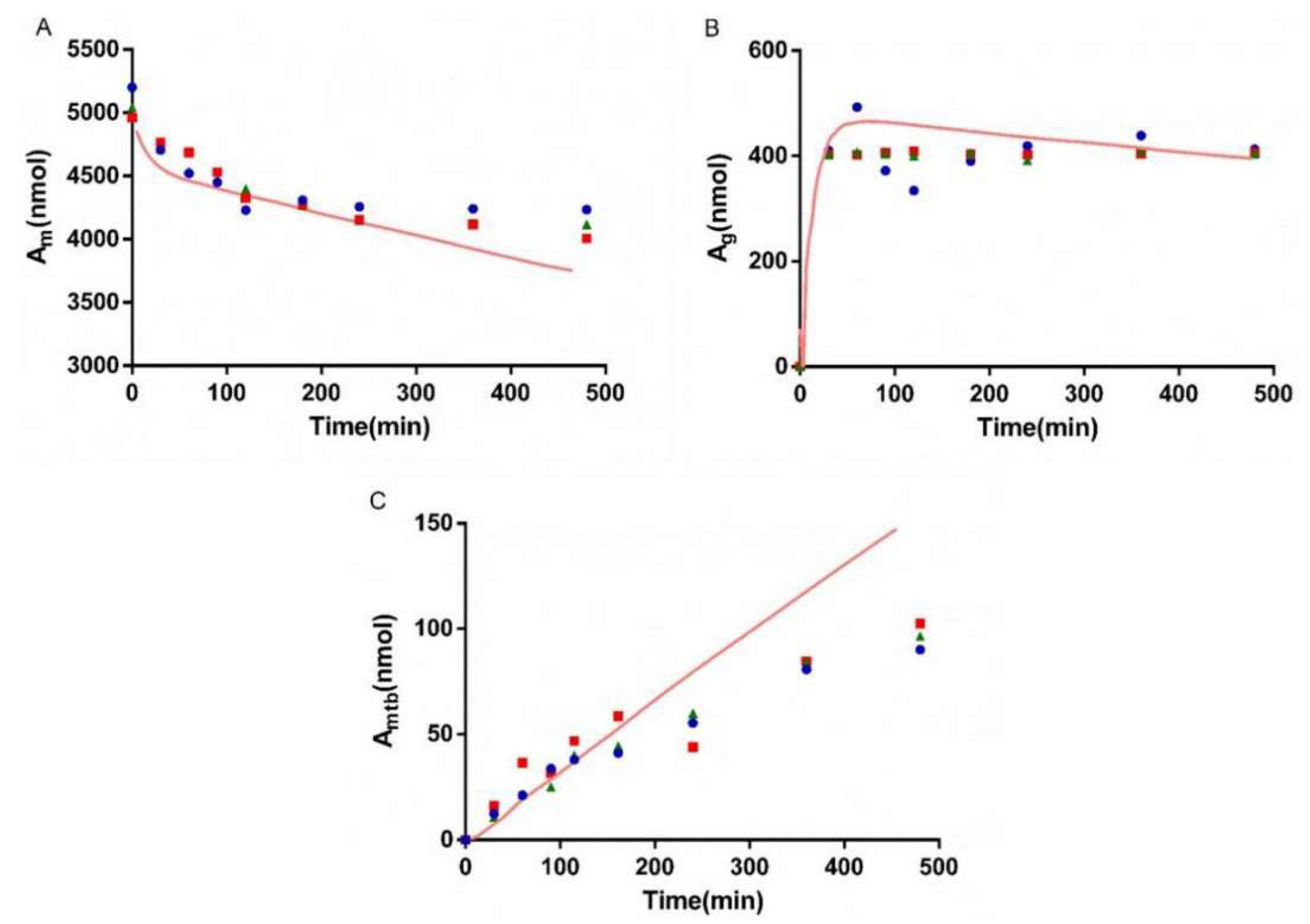
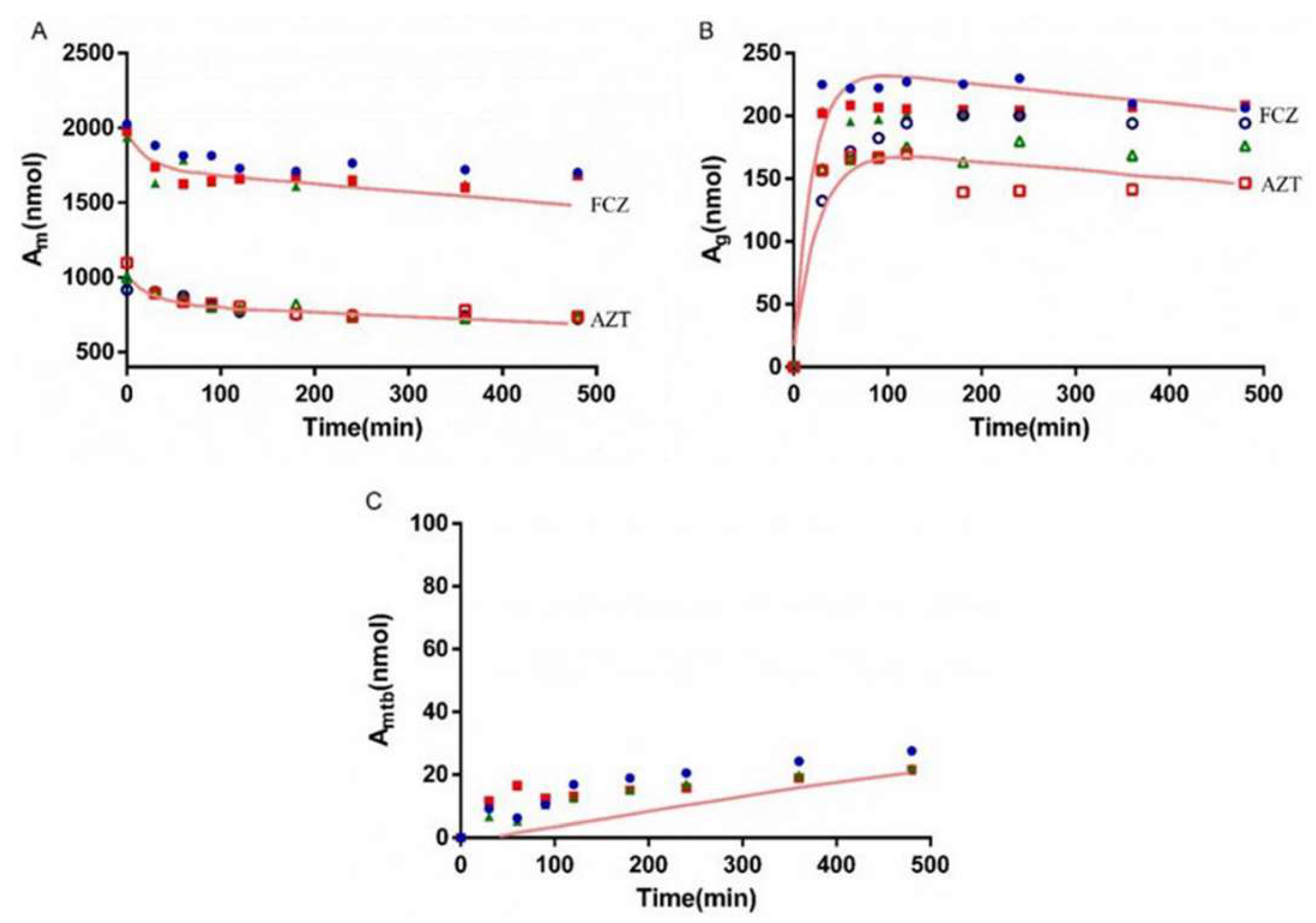
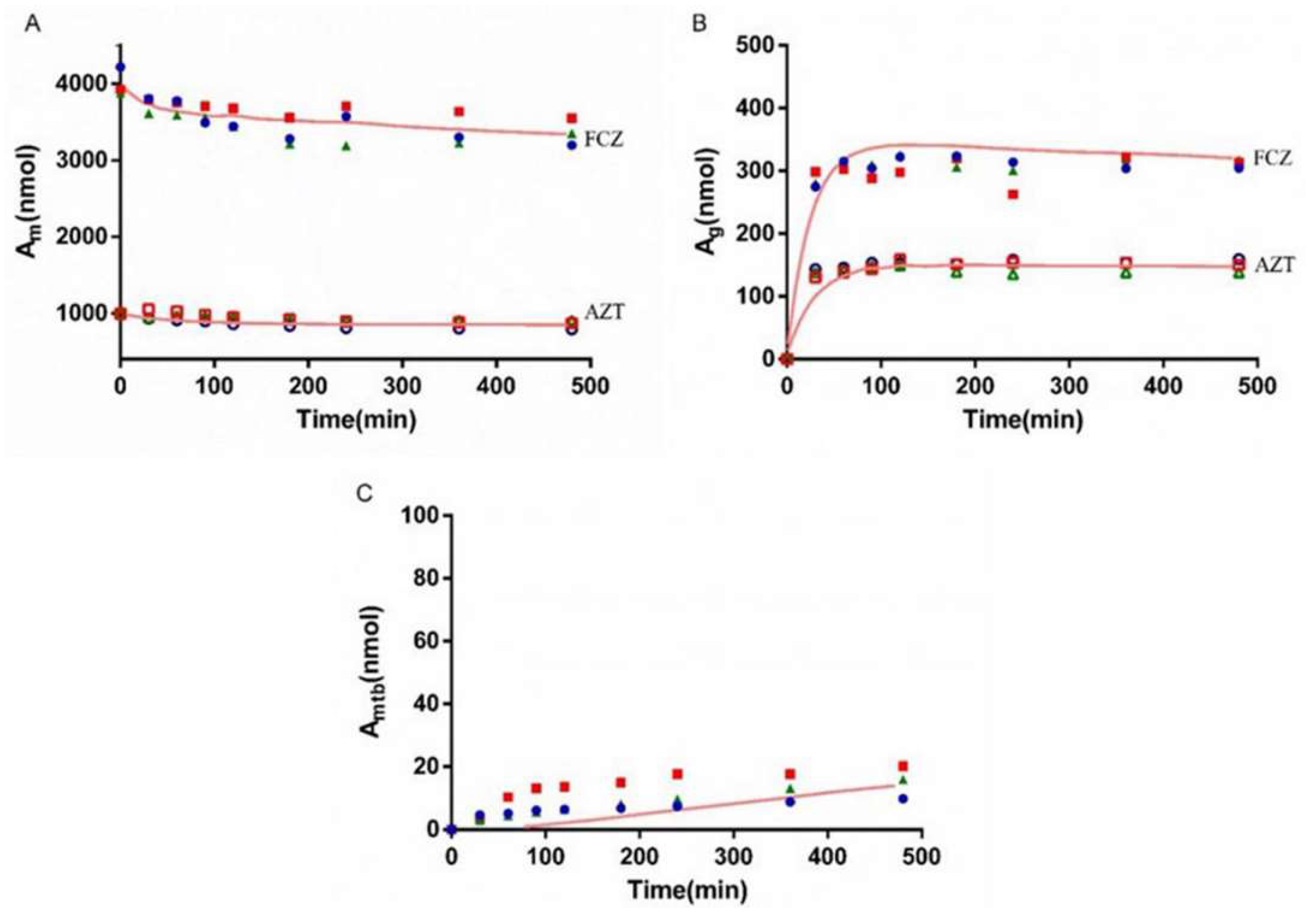
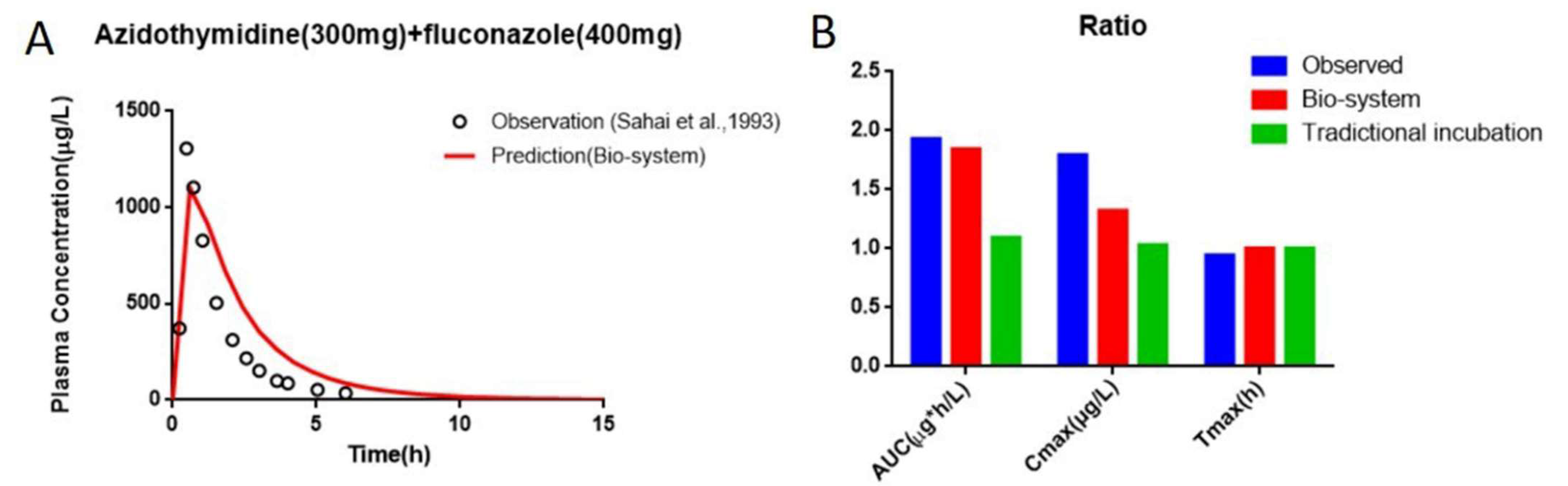
3.6. Interaction Study of AZT and FCZ
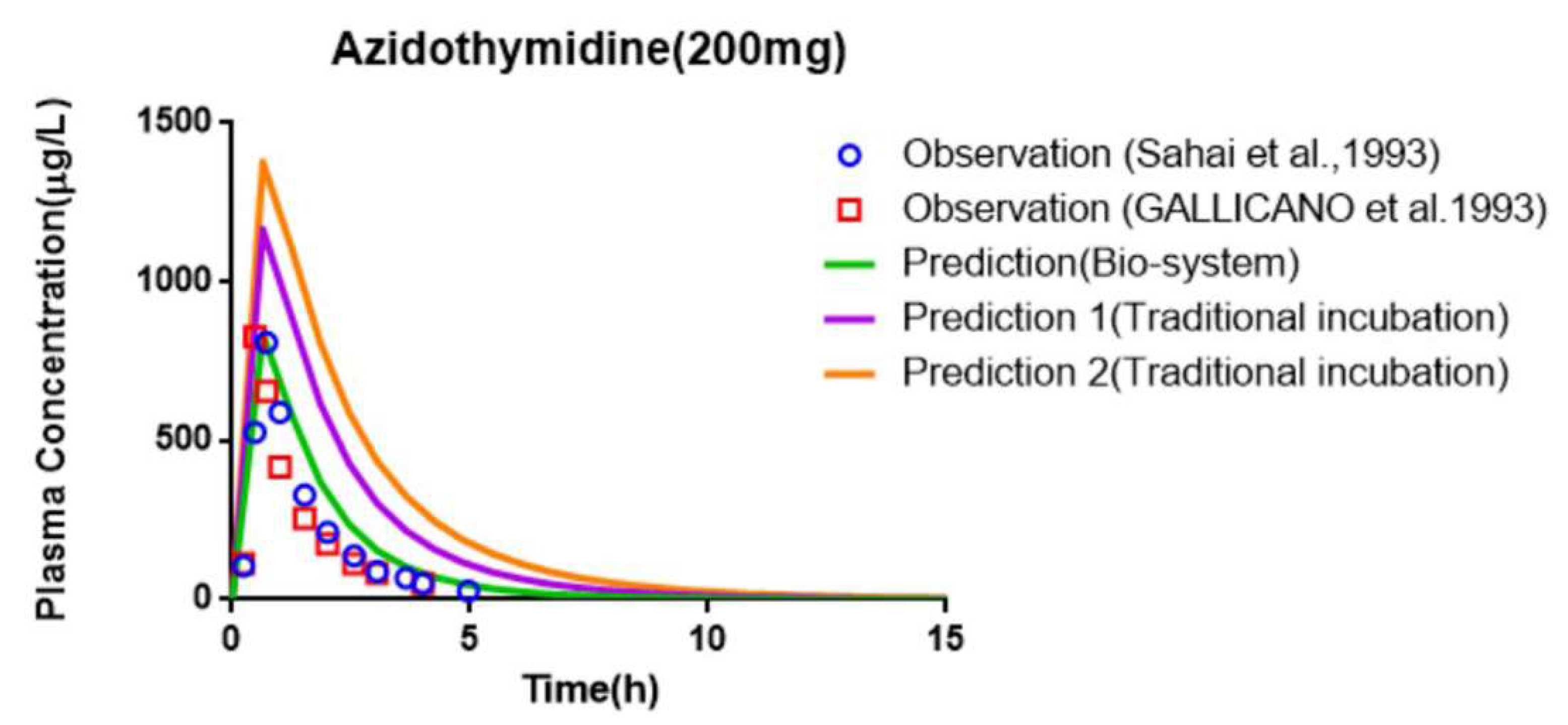
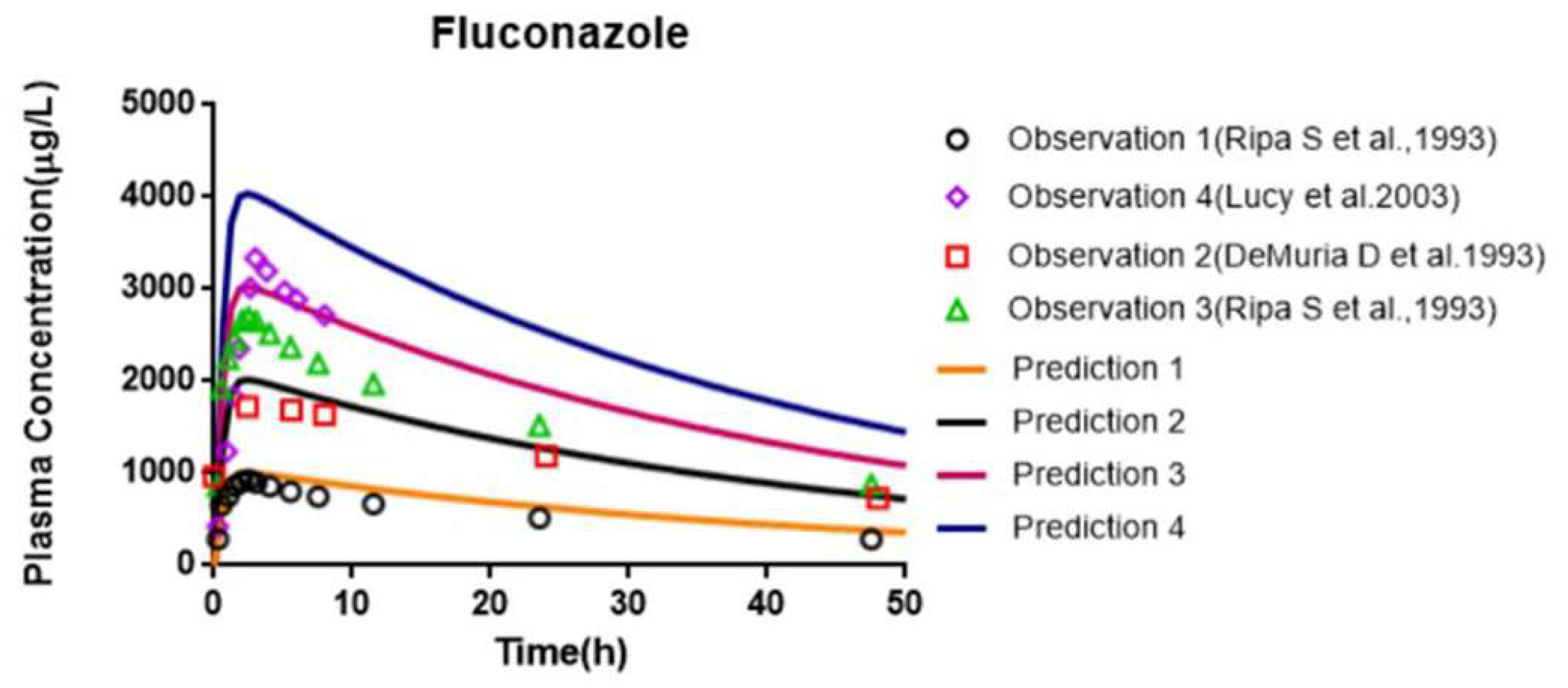
3.7. Prediction of PK and Interaction Results from PBPK Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Prentis, R.; Lis, Y.; Walker, S. Pharmaceutical innovation by the seven UK-owned pharmaceutical companies (1964–1985). Br. J. Clin. Pharmacol. 1988, 25, 387–396. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.H.; Lu, A.Y. Role of pharmacokinetics and metabolism in drug discovery and development. Pharmacol. Rev. 1997, 49, 403. [Google Scholar]
- Fowler, S.; Chen, W.L.K.; Duignan, D.B.; Gupta, A.; Hariparsad, N.; Kenny, J.R.; Lai, W.G.; Liras, J.; Phillips, J.A.; Gan, J. Microphysiological systems for ADME-related applications: Current status and recommendations for system development and characterization. Lab Chip 2020, 20, 446–467. [Google Scholar] [CrossRef] [PubMed]
- Fabre, K.; Berridge, B.; Proctor, W.R.; Ralston, S.; Will, Y.; Baran, S.W.; Yoder, G.; Van Vleet, T.R. Introduction to a manuscript series on the characterization and use of microphysiological systems (MPS) in pharmaceutical safety and ADME applications. Lab Chip 2020, 20, 1049–1057. [Google Scholar] [CrossRef] [PubMed]
- Wetmore, B.A. Quantitative in vitro-to-in vivo extrapolation in a high-throughput environment. Toxicology 2015, 332, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Raunio, H.; Taavitsainen, P.; Honkakoski, P.; Juvonen, R.; Pelkonen, O. In Vitro Methods in the Prediction of Kinetics of Drugs: Focus on Drug Metabolism. Altern. Lab. Anim. 2004, 32, 425–430. [Google Scholar] [CrossRef]
- van de Kerkhof, E.; de Graaf, I.; Groothuis, G. In Vitro Methods to Study Intestinal Drug Metabolism. Curr. Drug Metab. 2007, 8, 658–675. [Google Scholar] [CrossRef]
- Hariparsad, N.; Sane, R.; Strom, S.; Desai, P. In vitro methods in human drug biotransformation research: Implications for cancer chemotherapy. Toxicol. Vitr. 2006, 20, 135–153. [Google Scholar] [CrossRef]
- Pelkonen, O.; Turpeinen, M. In vitro–in vivoextrapolation of hepatic clearance: Biological tools, scaling factors, model assumptions and correct concentrations. Xenobiotica 2007, 37, 1066–1089. [Google Scholar] [CrossRef] [PubMed]
- Cascone, S.; Lamberti, G.; Marra, F.; Titomanlio, G.; D’Amore, M.; Barba, A.A. Gastrointestinal behavior and ADME phenomena: I. In vitro simulation. J. Drug Deliv. Sci. Technol. 2016, 35, 272–283. [Google Scholar] [CrossRef]
- Boase, S.; Miners, J.O. In vitro-in vivo correlations for drugs eliminated by glucuronidation: Investigations with the model substrate zidovudine. Br. J. Clin. Pharmacol. 2002, 54, 493–503. [Google Scholar] [CrossRef] [Green Version]
- Uchaipichat, V.; Winner, L.K.; Mackenzie, P.I.; Elliot, D.J.; Williams, J.A.; Miners, J.O. Quantitative prediction ofin vivoinhibitory interactions involving glucuronidated drugs fromin vitrodata: The effect of fluconazole on zidovudine glucuronidation. Br. J. Clin. Pharmacol. 2006, 61, 427–439. [Google Scholar] [CrossRef] [Green Version]
- Court, M.H.; Krishnaswamy, S.; Hao, Q.; Duan, S.X.; Patten, C.J.; Von Moltke, L.L.; Greenblatt, D.J. Evaluation of 3′-azido-3′-deoxythymidine, morphine, and codeine as probe substrates for UDP-glucuronosyltransferase 2B7 (UGT2B7) in human liver microsomes: Specificity and influence of the UGT2B7*2 polymorphism. Drug Metab. Dispos. 2003, 31, 1125–1133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdullah, N.H.; Ismail, S. Inhibition of UGT2B7 Enzyme Activity in Human and Rat Liver Microsomes by Herbal Constituents. Molecule 2018, 23, 2696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Hong, X.; Yao, Z.; Dai, Y.; Zhao, G.; Qin, Z.; Wu, B.; Gonzalez, F.J.; Yao, X. Glucuronidation of icaritin by human liver microsomes, human intestine microsomes and expressed UDP-glucuronosyltransferase enzymes: Identification of UGT1A3, 1A9 and 2B7 as the main contributing enzymes. Xenobiotica 2018, 48, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Rowland, A.; Gaganis, P.; Elliot, D.J.; Mackenzie, P.I.; Knights, K.M.; Miners, J.O. Binding of Inhibitory Fatty Acids Is Responsible for the Enhancement of UDP-Glucuronosyltransferase 2B7 Activity by Albumin: Implications for in Vitro-in Vivo Extrapolation. J. Pharmacol. Exp. Ther. 2007, 321, 137–147. [Google Scholar] [CrossRef] [Green Version]
- Rowland, A.; Knights, K.M.; MacKenzie, P.I.; Miners, J.O. Characterization of the Binding of Drugs to Human Intestinal Fatty Acid Binding Protein (IFABP): Potential Role of IFABP as an Alternative to Albumin for in Vitro-in Vivo Extrapolation of Drug Kinetic Parameters. Drug Metab. Dispos. 2009, 37, 1395–1403. [Google Scholar] [CrossRef] [Green Version]
- Mano, Y.; Usui, T.; Kamimura, H. Inhibitory potential of nonsteroidal anti-inflammatory drugs on UDP-glucuronosyltransferase 2B7 in human liver microsomes. Eur. J. Clin. Pharmacol. 2007, 63, 211–216. [Google Scholar] [CrossRef]
- Engtrakul, J.J.; Foti, R.S.; Strelevitz, T.J.; Fisher, M.B. Altered AZT (3′-azido-3′-deoxythymidine) glucuronidation kinetics in liver microsomes as an explanation for underprediction of in vivo clearance: Comparison to hepatocytes and effect of incubation environment. Drug Metab. Dispos. 2005, 33, 1621–1627. [Google Scholar] [CrossRef] [Green Version]
- Tong, S.; Sun, H.; Xue, C.; Chen, H.; Liu, J.; Yang, H.; Zhou, N.; Xiang, X.; Cai, W. Establishment and assessment of a novel in vitro bio-PK/PD system in predicting the in vivo pharmacokinetics and pharmacodynamics of cyclophosphamide. Xenobiotica 2018, 48, 368–375. [Google Scholar] [CrossRef]
- Xue, C.-F.; Zhang, Z.; Jin, Y.; Zhu, B.; Xing, J.-F.; Ma, G.; Xiang, X.-Q.; Cai, W.-M. Novel in vitro dynamic metabolic system for predicting the human pharmacokinetics of tolbutamide. Acta Pharmacol. Sin. 2018, 39, 1522–1532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Zheng, Y.; Zhao, B.; Shao, T.; Shi, Q.; Zhou, N.; Cai, W. Encapsulation of liver microsomes into a thermosensitive hydrogel for characterization of drug metabolism and toxicity. Biomaterials 2013, 34, 9770–9778. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ma, G.; Xue, C.; Sun, H.; Wang, Z.; Xiang, X.; Cai, W. Establishment of rat liver microsome-hydrogel system for in vitro phase II metabolism and its application to study pharmacological effects of UGT substrates. Drug Metab. Pharmacokinet. 2019, 34, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Li, J.; Zheng, Y.; Zhou, L.; Tong, S.; Zhao, B.; Cai, W. Drug activity screening based on microsomes-hydrogel system in predicting metabolism induced antitumor effect of oroxylin A. Sci. Rep. 2016, 6, 21604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, N.; Zheng, Y.; Xing, J.; Yang, H.; Chen, H.; Xiang, X.; Liu, J.; Tong, S.; Zhu, B.; Cai, W. Application of a New Dynamic Model to Predict the In Vitro Intrinsic Clearance of Tolbutamide Using Rat Microsomes Encapsulated in a Fab Hydrogel. Drug Metab. Dispos. 2015, 44, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Peyret, T.; Krishnan, K. QSARs for PBPK modelling of environmental contaminants. SAR QSAR Environ. Res. 2011, 22, 129–169. [Google Scholar] [CrossRef] [PubMed]
- Nair, P.C.; McKinnon, R.; Miners, J.O. A Fragment-Based Approach for the Computational Prediction of the Nonspecific Binding of Drugs to Hepatic Microsomes. Drug Metab. Dispos. 2016, 44, 1794–1798. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, F.; Hashida, M. In Silico Approaches for Predicting ADME Properties of Drugs. Drug Metab. Pharmacokinet. 2004, 19, 327–338. [Google Scholar] [CrossRef] [Green Version]
- Lombardo, F.; Desai, P.V.; Arimoto, R.; Desino, K.E.; Fischer, H.; Keefer, C.E.; Petersson, C.; Winiwarter, S.; Broccatelli, F. In Silico Absorption, Distribution, Metabolism, Excretion, and Pharmacokinetics (ADME-PK): Utility and Best Practices. An Industry Perspective from the International Consortium for Innovation through Quality in Pharmaceutical Development. J. Med. Chem. 2017, 60, 9097–9113. [Google Scholar] [CrossRef]
- Ekins, S.; Waller, C.L.; Swaan, P.W.; Cruciani, G.; Wrighton, S.A.; Wikel, J.H. Progress in predicting human ADME parameters in silico. J. Pharmacol. Toxicol. Methods 2000, 44, 251–272. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, W.; Chen, K.; Jiang, H. New technologies in computer-aided drug design: Toward target identification and new chemical entity discovery. Drug Discov. Today: Technol. 2006, 3, 307–313. [Google Scholar] [CrossRef] [PubMed]
- Zhivkova, Z.D. Quantitative Structure —Pharmacokinetics Relationships for Plasma Protein Binding of Basic Drugs. J. Pharm. Pharm. Sci. 2017, 20, 349–359. [Google Scholar] [CrossRef]
- Pirovano, A.; Brandmaier, S.; Huijbregts, M.; Ragas, A.M.; Veltman, K.; Hendriks, A.J. QSARs for estimating intrinsic hepatic clearance of organic chemicals in humans. Environ. Toxicol. Pharmacol. 2016, 42, 190–197. [Google Scholar] [CrossRef] [PubMed]
- Aliagas, I.; Gobbi, A.; Heffron, T.; Lee, M.-L.; Ortwine, D.F.; Zak, M.; Khojasteh, S.C. A probabilistic method to report predictions from a human liver microsomes stability QSAR model: A practical tool for drug discovery. J. Comput. Mol. Des. 2015, 29, 327–338. [Google Scholar] [CrossRef] [PubMed]
- Miners, J.O.; Mackenzie, P.I.; Knights, K.M. The prediction of drug-glucuronidation parameters in humans: UDP-glucuronosyltransferase enzyme-selective substrate and inhibitor probes for reaction phenotyping andin vitro–in vivoextrapolation of drug clearance and drug-drug interaction potential. Drug Metab. Rev. 2010, 42, 196–208. [Google Scholar] [CrossRef]
- Nikolic, K.; Agababa, D. Prediction of hepatic microsomal intrinsic clearance and human clearance values for drugs. J. Mol. Graph. Model. 2009, 28, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Ekins, S.; Obach, R.S. Three-dimensional quantitative structure activity relationship computational approaches for prediction of human in vitro intrinsic clearance. J. Pharmacol. Exp. Ther. 2000, 295, 463–473. [Google Scholar]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, S.; Jeong, S.-P. Decision Tree Application to Classification Problems with Boosting Algorithm. Electronics 2021, 10, 1903. [Google Scholar] [CrossRef]
- Sun, J.; Zhong, G.; Huang, K.; Dong, J. Banzhaf random forests: Cooperative game theory based random forests with consistency. Neural Netw. 2018, 106, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Yuen, S.C.; Liang, X.; Zhu, H.; Jia, Y.; Leung, S.-W. Prediction of differentially expressed microRNAs in blood as potential biomarkers for Alzheimer’s disease by meta-analysis and adaptive boosting ensemble learning. Alzheimer’s Res. Ther. 2021, 13, 1–30. [Google Scholar] [CrossRef]
- Hou, N.; Li, M.; He, L.; Xie, B.; Wang, L.; Zhang, R.; Yu, Y.; Sun, X.; Pan, Z.; Wang, K. Predicting 30-days mortality for MIMIC-III patients with sepsis-3: A machine learning approach using XGboost. J. Transl. Med. 2020, 18, 1–14. [Google Scholar] [CrossRef]
- Yan, J.; Xu, Y.; Cheng, Q.; Jiang, S.; Wang, Q.; Xiao, Y.; Ma, C.; Yan, J.; Wang, X. LightGBM: Accelerated genomically designed crop breeding through ensemble learning. Genome Biol. 2021, 22, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Yang, H.; Li, J.; Wang, T.; Li, W.; Liu, G.; Tang, Y. In Silico Prediction of Compounds Binding to Human Plasma Proteins by QSAR Models. ChemMedChem 2018, 13, 572–581. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Yu, J.; Huang, T.; Li, C.; Li, C. Average Quasi-Consensus Algorithm for Distributed Constrained Optimization: Impulsive Communication Framework. IEEE Trans. Cybern. 2018, 50, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Sahai, J.; Gallicano, K.; Pakuts, A.; Cameron, D.W. Effect of Fluconazole on Zidovudine Pharmacokinetics in Patients Infected with Human Immunodeficiency Virus. J. Infect. Dis. 1994, 169, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Gallicano, K.; Sahai, J.; Ormsby, E.; Cameron, D.; Pakuts, A.; McGilveray, I. Pharmacokinetics of zidovudine after the initial single dose and during chronic-dose therapy in HIV-infected patients. Br. J. Clin. Pharmacol. 1993, 36, 128–131. [Google Scholar] [CrossRef] [Green Version]
- Ripa, S.; Ferrante, L.; Prenna, M. Pharmacokinetics of Fluconazole in Normal Volunteers. Chemotherapy 1993, 39, 6–12. [Google Scholar] [CrossRef]
- DeMuria, D.; Forrest, A.; Rich, J.; Scavone, J.M.; Cohen, L.G.; Kazanjian, P.H. Pharmacokinetics and bioavailability of fluconazole in patients with AIDS. Antimicrob. Agents Chemother. 1993, 37, 2187–2192. [Google Scholar] [CrossRef] [Green Version]
- Sasongko, L.; Williams, K.M.; Day, R.; McLachlan, A.J. Human subcutaneous tissue distribution of fluconazole: Comparison of microdialysis and suction blister techniques. Br. J. Clin. Pharmacol. 2003, 56, 551–561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lučić, B.; Batista, J.; Bojović, V.; Lovrić, M.; Kržić, A.S.; Bešlo, D.; Nadramija, D.; Vikić-Topić, D. Estimation of Random Accuracy and its Use in Validation of Predictive Quality of Classification Models within Predictive Challenges. Croat. Chem. Acta 2019, 92, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Ekins, S. In silico approaches to predicting drug metabolism, toxicology and beyond. Biochem. Soc. Trans. 2003, 31, 611–614. [Google Scholar] [CrossRef] [Green Version]





| Data | Metric | RF | ADA | XG | LGB | Consensus (Average) |
|---|---|---|---|---|---|---|
| 5-CV | MAE (μL/min/mg) | 35.48 | 32.87 | 35.31 | 36.27 | 33.32 |
| RMSE (μL/min/mg) | 77.41 | 83.92 | 77.08 | 76.58 | 75.88 | |
| R2 | 0.56 | 0.48 | 0.56 | 0.57 | 0.58 | |
| r | 0.75 | 0.71 | 0.75 | 0.76 | 0.76 | |
| Test | MAE (μL/min/mg) | 35.16 | 32.95 | 35.84 | 37.28 | 33.52 |
| RMSE (μL/min/mg) | 84.28 | 88.70 | 84.66 | 86.72 | 83.59 | |
| R2 | 0.50 | 0.44 | 0.49 | 0.47 | 0.50 | |
| r | 0.71 | 0.68 | 0.70 | 0.69 | 0.71 |
| Parameters | AZT | AZTG | FCZ |
|---|---|---|---|
| Linearity equation (n = 8 points) | y = 5.1548x + 21.2189 | y = 5.2534x + 3.3663 | y = 0.1899x + 4.5826 |
| Correlation coefficient | 0.999 | 1 | 1 |
| LLOQ (μM) | 10 | 1 | 50 |
| Intra-day precision (%) * (n = 5) | 5 ± 2 | 7.3 ± 1.5 | 5.6 ± 1.3 |
| Inter-day precision (%) * (n = 5) | 9.5 ± 3.6 | 6.8 ± 2.6 | 3.9 ± 1.9 |
| Intra-day accuracy (%) * (n = 5) | 104 ± 2 | 98 ± 1 | 100.8 ± 2.5 |
| Inter-day accuracy (%) * (n = 5) | 104 ± 1 | 99.5 ± 2.2 | 100.6 ± 0.1 |
| Experimentation | Km (μM) | Vmax (pmol/min/mg Microsomal Protein) | CLint (μL/min/mg Protein) |
|---|---|---|---|
| HLM | 536 | 4287 | 8.1 |
| HLM-Gel | 686 | 1045 | 1.52 |
| Time (min) | 500 μM | 1000 μM | 2500 μM |
|---|---|---|---|
| 30 | 100.07% | 101.32% | 103.26% |
| 60 | 99.78% | 98.09% | 100.84% |
| 90 | 99.14% | 97.39% | 98.16% |
| 120 | 98.02% | 96.38% | 94.81% |
| 180 | 97.64% | 96.52% | 94.66% |
| 240 | 96.49% | 96.85% | 92.90% |
| 360 | 95.57% | 97.98% | 93.24% |
| 480 | 97.15% | 98.73% | 92.48% |
| Time (min) | AZT | FCZ | ||||
|---|---|---|---|---|---|---|
| 500-1 | 500-2 | 500-3 | 500 | 1000 | 2000 | |
| 30 | 101.61% | 105.58% | 101.46% | 96.37% | 98.05% | 100.35% |
| 60 | 100.8% | 103.56% | 101.36% | 96.38% | 97.5% | 100.17% |
| 90 | 99.54% | 99.63% | 99.97% | 94.02% | 95.38% | 97% |
| 120 | 97.32% | 98.21% | 98% | 91.84% | 94.69% | 95.74% |
| 180 | 96.35% | 95.80% | 95.26% | 89.99% | 93.82% | 91.51% |
| 240 | 95.01% | 93.92% | 93.51% | 91.42% | 94.87% | 94.38% |
| 360 | 94.28% | 93.92% | 93.1% | 91.43% | 92.85% | 92.37% |
| 480 | 94.82% | 92.74% | 92.86% | 93.48% | 94.96% | 91.79% |
| AZT (200 mg) | AUC (μg⋅h/L) | Cmax (μg/L) | Tmax (h) | CL (L/h) | |
|---|---|---|---|---|---|
| Observed [47,48] | 1020 ± 390 | 1042 ± 632 | 0.8 ± 0.3 | 194 ± 53 | |
| 1078 ± 257 | 1093 ± 679 | 0.6 ± 0.2 | 183 ± 53 | ||
| Traditional incubation | Predicted 1 [12] | 2570.08 | 1163.65 | 0.63 | 84.33 ± 36.88 |
| Fold error | 2.52 | 1.12 | 1.26 | 2.30 | |
| 2.38 | 1.06 | 1.10 | 2.17 | ||
| Predicted 2 | 3501 | 1374.73 | 0.65 | 61.96 ± 25.23 | |
| Fold error | 3.43 | 1.32 | 1.24 | 3.13 | |
| 3.25 | 1.26 | 1.13 | 2.95 | ||
| Bio-system | Predicted | 1529.21 | 833.94 | 0.6 | 143.26 ± 67.98 |
| Fold error | 1.5 | 1.25 | 1.33 | 1.36 | |
| 1.42 | 1.31 | 1.04 | 1.27 | ||
| FCZ | AUC (μg⋅h/L) | Cmax (μg/L) | Tmax (h) |
|---|---|---|---|
| Observation 1 [49] (50 mg) | 39,810 ± 6460 | 930 ± 130 | 2.5 |
| Prediction 1 (50 mg) | 45,424.77 | 1010.38 | 2.41 |
| Fold error | 1.14 | 1.09 | 1.04 |
| Observation 2 [50] (100 mg) | 99,300 | 2080 | 2 |
| Prediction 2 (100 mg) | 90,849.33 | 2020.77 | 2.41 |
| Fold error | 1.09 | 1.03 | 1.21 |
| Observation 3 [49] (150 mg) | 114,150 ± 19,730 | 2690 ± 430 | 2.5 |
| Prediction 3 (150 mg) | 136,273.8 | 3031.14 | 2.41 |
| Fold error | 1.19 | 1.13 | 1.04 |
| Observation 4 [51] (200 mg) | 207,000 ± 55,700 | 3580 ± 140 | 3.2 ± 0.8 |
| Prediction 4 (200 mg) | 181,698.11 | 4041.49 | 2.41 |
| Fold error | 1.14 | 1.13 | 1.32 |
| Parameters | AUC (μg⋅h/L) | Cmax (μg/L) | Tmax (h) |
|---|---|---|---|
| AZT alone | 1020 ± 390 | 1042 ± 632 | 0.8 ± 0.3 |
| AZT + FCZ | 1965 ± 838 | 1864 ± 958 | 0.8 ± 0.3 |
| Ratio | 1.93 | 1.79 | 0.94 |
| Predicted (AZT alone) | 2570.08 | 1163.65 | 0.63 |
| Fold error | 2.52 | 1.12 | 1.26 |
| Predicted(AZT + FCZ) | 2812.57 | 1203.61 | 0.63 |
| Fold error | 1.43 | 1.55 | 1.19 |
| Ratio | 1.09 | 1.03 | 1 |
| Fold error | 1.76 | 1.73 | 1.06 |
| Predicted(AZT alone) | 1529.21 | 833.94 | 0.6 |
| Fold error | 1.5 | 1.25 | 1.33 |
| Predicted (AZT + FCZ) | 2809.52 | 1101.02 | 0.6 |
| Fold error | 1.43 | 1.69 | 1.25 |
| Ratio | 1.84 | 1.32 | 1 |
| Fold error | 1.05 | 1.36 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Zhang, J.; Fang, B.; Xiang, X.; Ma, G.; Zhang, S.; Zhu, B.; Cai, W. A Novel Method for Predicting the Human Inherent Clearance and Its Application in the Study of the Pharmacokinetics and Drug–Drug Interaction between Azidothymidine and Fluconazole Mediated by UGT Enzyme. Pharmaceutics 2021, 13, 1734. https://doi.org/10.3390/pharmaceutics13101734
Yuan Y, Zhang J, Fang B, Xiang X, Ma G, Zhang S, Zhu B, Cai W. A Novel Method for Predicting the Human Inherent Clearance and Its Application in the Study of the Pharmacokinetics and Drug–Drug Interaction between Azidothymidine and Fluconazole Mediated by UGT Enzyme. Pharmaceutics. 2021; 13(10):1734. https://doi.org/10.3390/pharmaceutics13101734
Chicago/Turabian StyleYuan, Yawen, Jun Zhang, Boyu Fang, Xiaoqiang Xiang, Guo Ma, Shunguo Zhang, Bin Zhu, and Weimin Cai. 2021. "A Novel Method for Predicting the Human Inherent Clearance and Its Application in the Study of the Pharmacokinetics and Drug–Drug Interaction between Azidothymidine and Fluconazole Mediated by UGT Enzyme" Pharmaceutics 13, no. 10: 1734. https://doi.org/10.3390/pharmaceutics13101734
APA StyleYuan, Y., Zhang, J., Fang, B., Xiang, X., Ma, G., Zhang, S., Zhu, B., & Cai, W. (2021). A Novel Method for Predicting the Human Inherent Clearance and Its Application in the Study of the Pharmacokinetics and Drug–Drug Interaction between Azidothymidine and Fluconazole Mediated by UGT Enzyme. Pharmaceutics, 13(10), 1734. https://doi.org/10.3390/pharmaceutics13101734






