Integrating Elastic Tensor and PC-SAFT Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions
Abstract
:1. Introduction
2. Materials and Methods
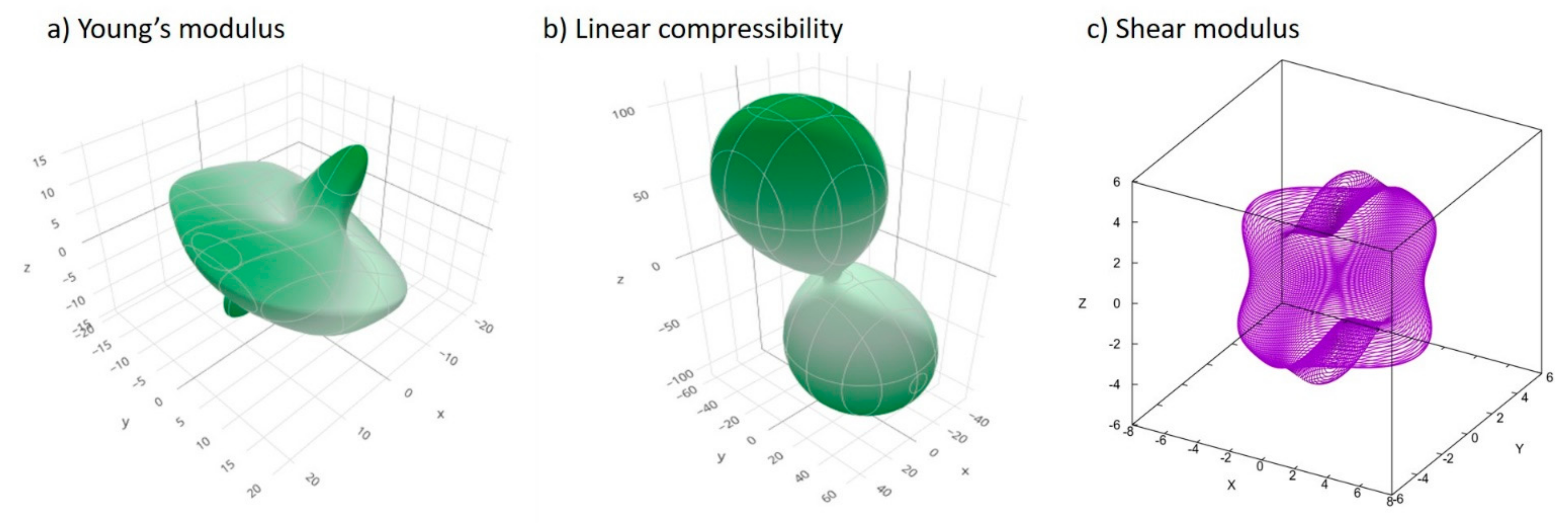
2.1. Mechanical Properties Calculation by Elastic Constants Simulations
2.2. PC-SAFT Model Implementation
2.3. Process Model
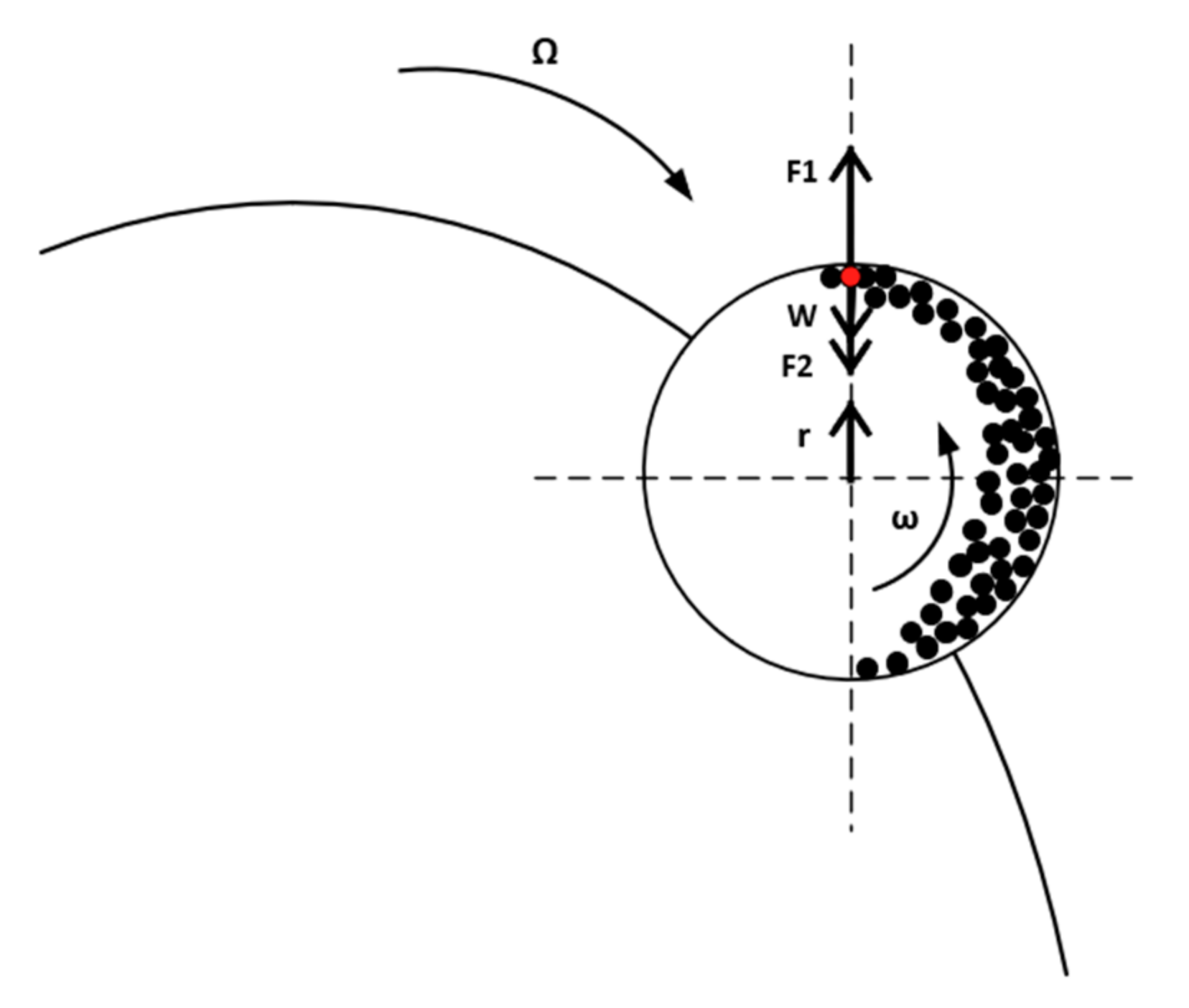
2.3.1. Predicting the Ball Mill Key Process Parameters and the Output Quality Material Attributes
2.3.2. Distribution Functions
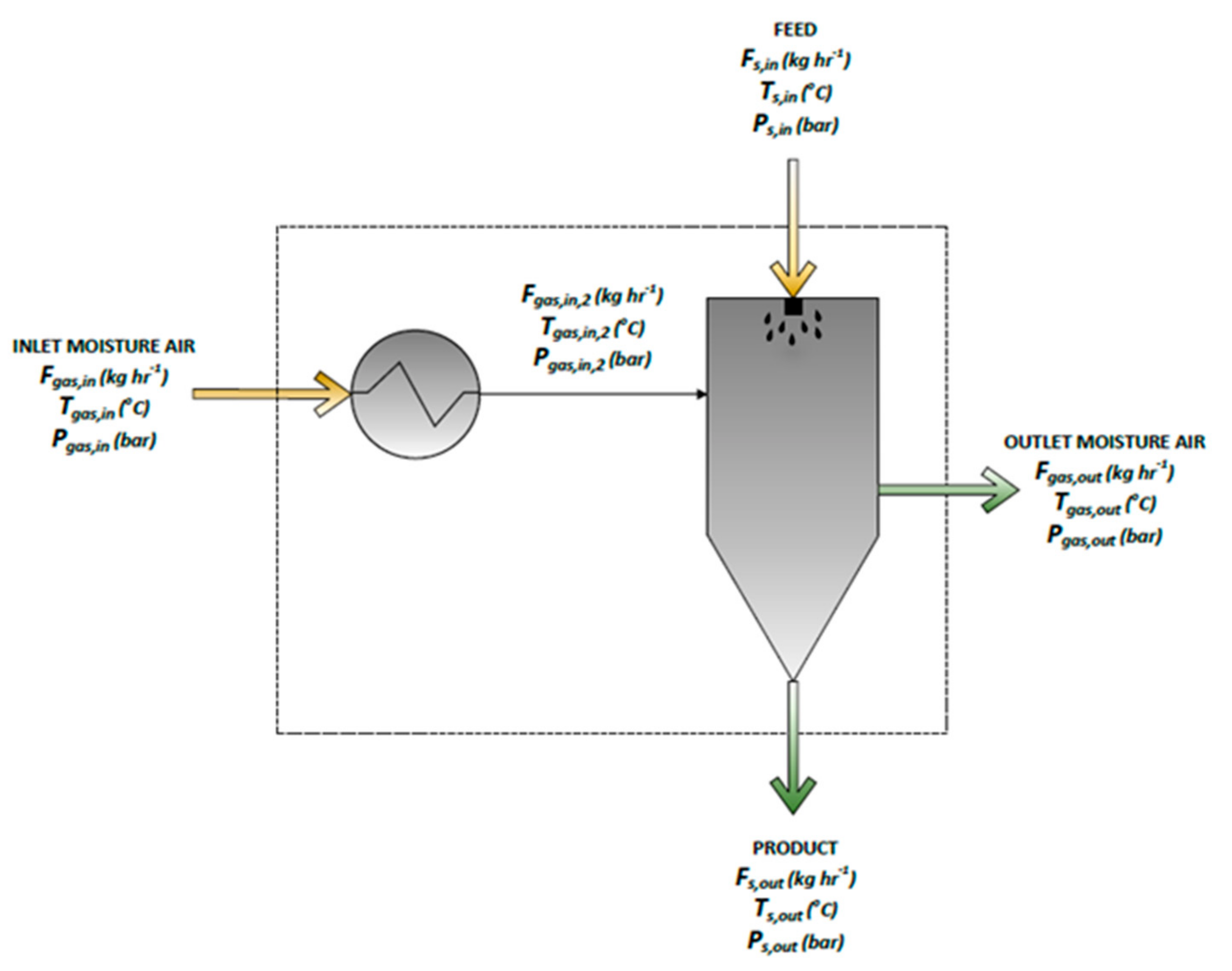
2.3.3. Process SD Model
2.3.4. SD Evaporation Model
2.3.5. SD Particle Formation Model
2.4. Phase Equilibria Model
2.5. Gibbs Energy Enhancement and Solubility Model Implementation
3. Results
3.1. Mechanical Properties
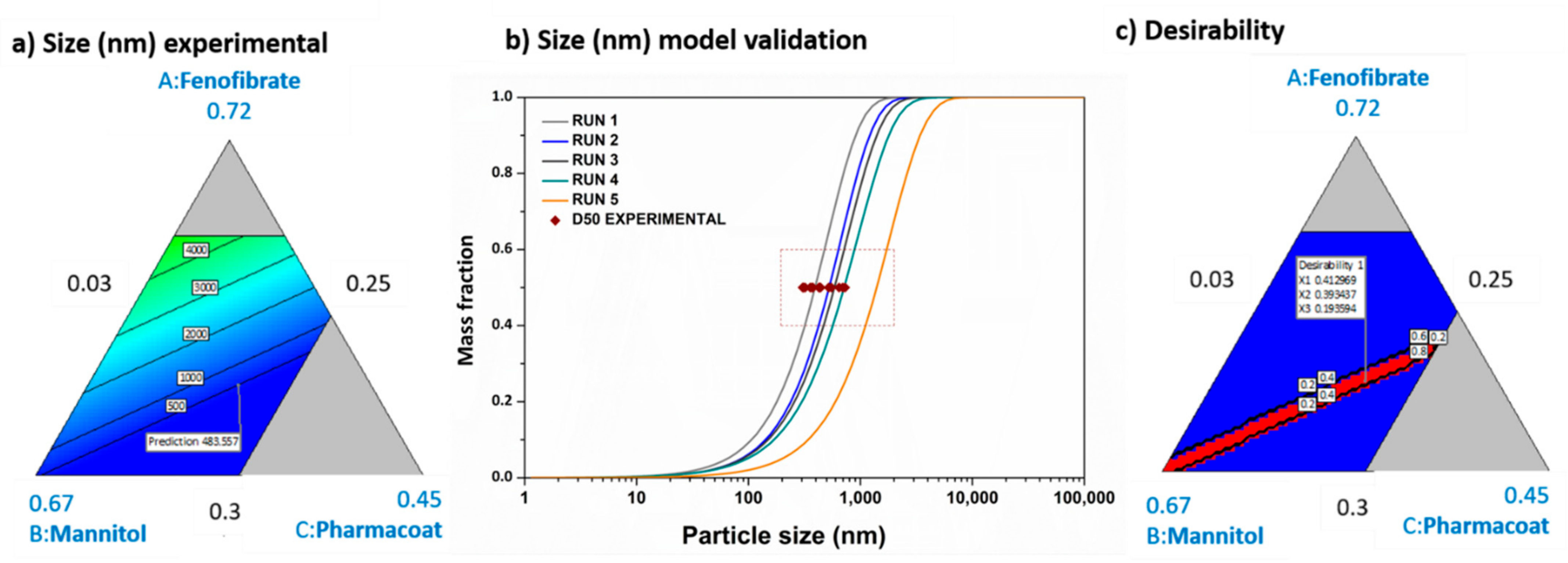
3.2. WMM Model Expansion and Experimental Validation
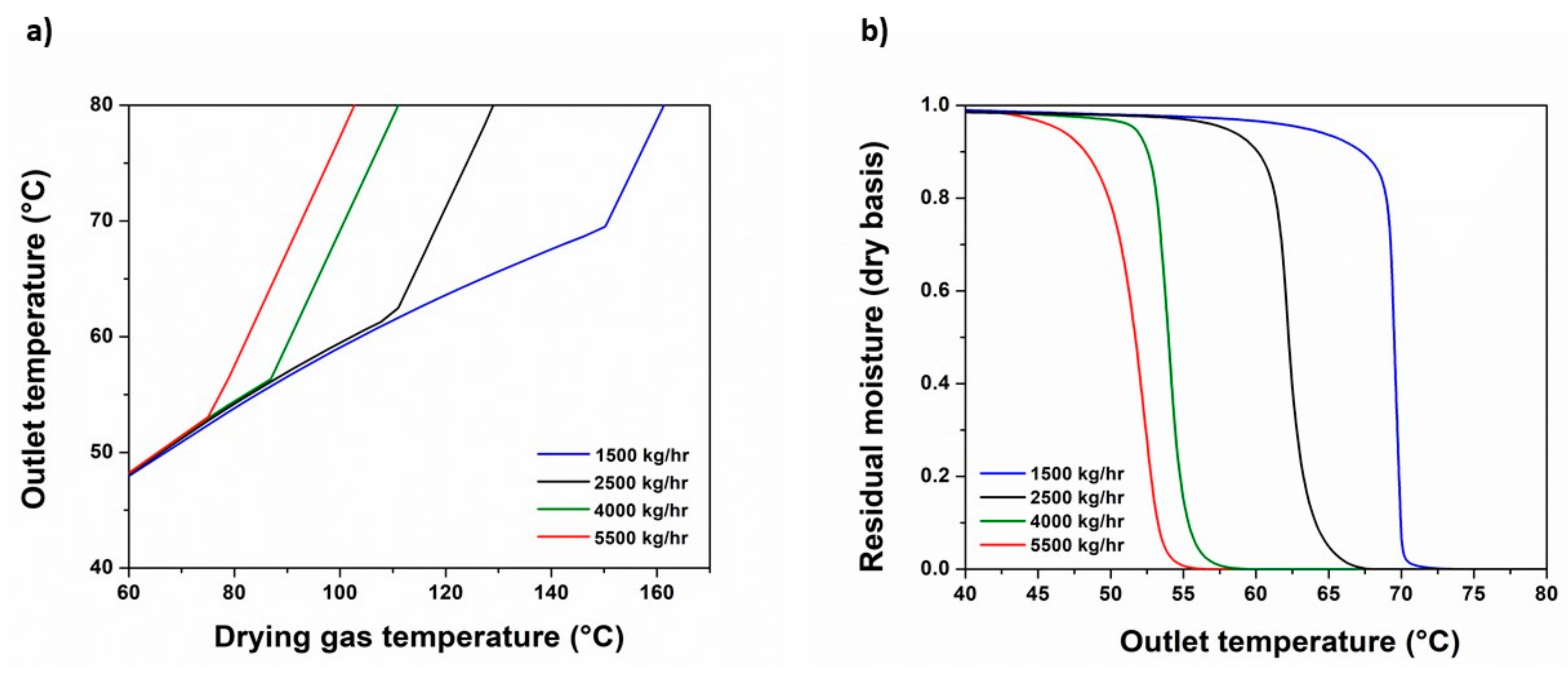
3.3. SD Modeling Expansion and Experimental Validation
3.4. Solubility Enhancement Prediction and Experimental Validation
4. Discussion
- (a)
- BWI integration in systems-based pharmaceutics powder simulation.
- (b)
- Equation-based numerical solution method development for predicting process design (grinding mass medium, diameter mill, centrifugal acceleration, residual moisture and drying gas temperature), and end-product material specifications (size, solubility) of WMM and SD of ternary crystalline API suspensions.
- (c)
- Applicability of the platform for any given BCSII API ternary formulation, currently accounting for 40% of new drug formulations.
- (d)
- Solubility prediction and dependencies solving, regarding the particle size distribution and temperature of nanocomposite material systems, crucial factors to be taken into consideration towards process development implementation and product performance assessments.
- (e)
- Unification of the energy and mass balance processes governing equations with macroscale statistical and quantum mechanics material system data, offering exciting novel applications, especially since high-performance computing currently makes the estimation of elastic constants a viable reality.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ouranidis, A.; Gkampelis, N.; Vardaka, E.; Karagianni, A.; Tsiptsios, D.; Nikolakakis, I.; Kachrimanis, K. Overcoming the solubility barrier of ibuprofen by the rational process design of a nanocrystal formulation. Pharmaceutics 2020, 12, 969. [Google Scholar] [CrossRef]
- Manca, M.L.; Lai, F.; Pireddu, R.; Valenti, D.; Schlich, M.; Pini, E.; Ailuno, G.; Fadda, A.M.; Sinico, C. Impact of nanosizing on dermal delivery and antioxidant activity of quercetin nanocrystals. J. Drug Deliv. Sci. Technol. 2020, 55, 101482. [Google Scholar] [CrossRef]
- Pireddu, R.; Schlich, M.; Marceddu, S.; Valenti, D.; Pini, E.; Fadda, A.M.; Lai, F.; Sinico, C. Nanosuspensions and microneedles roller as a combined approach to enhance diclofenac topical bioavailability. Pharmaceutics 2020, 12, 1140. [Google Scholar] [CrossRef] [PubMed]
- Eskin, D.; Zhupanska, O.; Hamey, R.; Moudgil, B.; Scarlett, B. Microhydrodynamics of stirred media milling. Powder Technol. 2005, 156, 95–102. [Google Scholar] [CrossRef]
- Lu, G.; Duan, Y.-Y.; Wang, X.-D. Surface tension, viscosity, and rheology of water-based nanofluids: A microscopic interpretation on the molecular level. J. Nanopart. Res. 2014, 16, 2564. [Google Scholar] [CrossRef]
- Peltonen, L.; Hirvonen, J. Pharmaceutical nanocrystals by nanomilling: Critical process parameters, particle fracturing and stabilization methods. J. Pharm. Pharmacol. 2010, 62, 1569–1579. [Google Scholar] [CrossRef]
- Longest, P.W.; Farkas, D.; Hassan, A.; Hindle, M. Computational Fluid Dynamics (CFD) Simulations of Spray Drying: Linking Drying Parameters with Experimental Aerosolization Performance. Pharm. Res. 2020, 37, 101. [Google Scholar] [CrossRef]
- Arpagaus, C. Pharmaceutical Particle Engineering via Nano Spray Drying—Process Parameters and Application Examples on the Laboratory-Scale. Int. J. Med. Nano Res. 2018, 5, 26. [Google Scholar] [CrossRef]
- Morris, K.R.; Griesser, U.J.; Eckhardt, C.J.; Stowell, J.G. Theoretical approaches to physical transformations of active pharmaceutical ingredients during manufacturing processes. Adv. Drug Deliv. Rev. 2001, 48, 91–114. [Google Scholar] [CrossRef]
- Rietveld, I.B.; Céolin, R. Rotigotine: Unexpected Polymorphism with Predictable Overall Monotropic Behavior. J. Pharm. Sci. 2015, 104, 4117–4122. [Google Scholar] [CrossRef]
- Shah, D.A.; Murdande, S.B.; Dave, R.H. A Review: Pharmaceutical and Pharmacokinetic Aspect of Nanocrystalline Suspensions. J. Pharm. Sci. 2016, 105, 10–24. [Google Scholar] [CrossRef]
- Seager, R.J.; Acevedo, A.J.; Spill, F.; Zaman, M.H. Solid dissolution in a fluid solvent is characterized by the interplay of surface area-dependent diffusion and physical fragmentation. Sci. Rep. 2018, 8, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kiely, E.; Zwane, R.; Fox, R.; Reilly, A.M.; Guerin, S. Density functional theory predictions of the mechanical properties of crystalline materials. CrystEngComm 2021, 23, 5697–5710. [Google Scholar] [CrossRef]
- Yalameha, S.; Nourbakhsh, Z.; Vashaee, D. ElATools: A tool for analyzing anisotropic elastic properties of the 2D and 3D materials. arXiv 2021, arXiv:2105.07279. [Google Scholar]
- Ge, K.; Ji, Y.; Lu, X. A novel interfacial thermodynamic model for predicting solubility of nanoparticles coated by stabilizers. Chinese, J. Chem. Eng. 2021, 31, 103–112. [Google Scholar] [CrossRef]
- Ouranidis, A.; Gkampelis, N.; Markopoulou, C.; Nikolakakis, I.; Kachrimanis, K. Development of a nanocrystal formulation of a low melting point api following a quality by design approach. Processes 2021, 9, 954. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
- Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 1–11. [Google Scholar] [CrossRef]
- Gent, M.; Menendez, M.; Toraño, J.; Torno, S. A correlation between Vickers Hardness indentation values and the Bond Work Index for the grinding of brittle minerals. Powder Technol. 2012, 224, 217–222. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Reply to Comment on “perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules”. Ind. Eng. Chem. Res. 2019, 58, 5744–5745. [Google Scholar] [CrossRef] [Green Version]
- Tumakaka, F.; Sadowski, G. Application of the Perturbed-Chain SAFT equation of state to polar systems. Fluid Phase Equilib. 2004, 217, 233–239. [Google Scholar] [CrossRef]
- Yousaf, A.M.; Kim, D.W.; Oh, Y.K.; Yong, C.S.; Kim, J.O.; Choi, H.G. Enhanced oral bioavailability of fenofibrate using polymeric nanoparticulated systems: Physicochemical characterization and in vivo investigation. Int. J. Nanomed. 2015, 10, 1819–1830. [Google Scholar]
- Murdande, S.B.; Shah, D.A.; Dave, R.H. Impact of nanosizing on solubility and dissolution rate of poorly soluble pharmaceuticals. J. Pharm. Sci. 2015, 104, 2094–2102. [Google Scholar] [CrossRef] [PubMed]
- Brinkmann, J.; Huxoll, F.; Luebbert, C.; Sadowski, G. Solubility of pharmaceutical ingredients in triglycerides. Eur. J. Pharm. Biopharm. 2019, 145, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Iemtsev, A.; Hassouna, F.; Mathers, A.; Klajmon, M.; Dendisová, M.; Malinová, L.; Školáková, T.; Fulem, M. Physical stability of hydroxypropyl methylcellulose-based amorphous solid dispersions: Experimental and computational study. Int. J. Pharm. 2020, 589, 119845. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, G.; Alphazan, T.; Wildeboer, W.J.; Meesters, G.M.H. Thermo-physical characterization of Pharmacoat® 603, Pharmacoat® 615 and Mowiol® 4-98. J. Therm. Anal. Calorim. 2012, 109, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Chapman, W.G.; Jackson, G.; Gubbins, K.E. Phase equilibria of associating fluids chain molecules with multiple bonding sites. Mol. Phys. 1988, 65, 1057–1079. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosd, M. Saftfirstpaper. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilibria 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Prausnitz, J.M. Thermodynamic and Transport Properties of Coal Liquids. Fluid Phase Equilib. 1987, 35, 316–318. [Google Scholar] [CrossRef]
- Garzón, L.C.; Martínez, F. Temperature dependence of solubility for ibuprofen in some organic and aqueous solvents. J. Solution Chem. 2004, 33, 1379–1395. [Google Scholar] [CrossRef]
- Buckton, G.; Beezer, A.E. The relationship between particle size and solubility. Int. J. Pharm. 1992, 82, 7–10. [Google Scholar] [CrossRef]
- Kojima, T.; Karashima, M.; Yamamoto, K.; Ikeda, Y. Combination of NMR Methods to Reveal the Interfacial Structure of a Pharmaceutical Nanocrystal and Nanococrystal in the Suspended State. Mol. Pharm. 2018, 15, 3901–3908. [Google Scholar] [CrossRef] [PubMed]
- Van Eerdenbrugh, B.; Vermant, J.; Martens, J.A.; Froyen, L.; Humbeeck, J.V.; Van Den Mooter, G.; Augustijns, P. Solubility increases associated with crystalline drug nanoparticles: Methodologies and significance. Mol. Pharm. 2010, 7, 1858–1870. [Google Scholar] [CrossRef]
- French, A.D. Idealized powder diffraction patterns for cellulose polymorphs. Cellulose 2014, 21, 885–896. [Google Scholar] [CrossRef]
- Hadjittofis, E.; Isbell, M.A.; Karde, V.; Varghese, S.; Ghoroi, C.; Heng, J.Y.Y. Influences of Crystal Anisotropy in Pharmaceutical Process Development. Pharm. Res. 2018, 35, 100. [Google Scholar] [CrossRef] [Green Version]
- Cairns, A.B.; Goodwin, A.L. Negative linear compressibility. Phys. Chem. Chem. Phys. 2015, 17, 20449–20465. [Google Scholar] [CrossRef] [Green Version]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Magdalinović, N.M. Calculation of energy required for grinding in a ball mill. Int. J. Miner. Process. 1989, 25, 41–46. [Google Scholar] [CrossRef]
- Neikov, O.D. Mechanical Crushing and Grinding; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 2; pp. 47–62. ISBN 9781856174220. [Google Scholar]
- Mio, H.; Kano, J.; Saito, F. Scale-up method of planetary ball mill. Chem. Eng. Sci. 2004, 59, 5909–5916. [Google Scholar] [CrossRef]
- Wisniewski, R. Spray Drying Technology Review. Available online: https://ttu-ir.tdl.org/bitstream/handle/2346/64598/ICES_2015_submission_68.pdf?sequence=1 (accessed on 12 September 2021).
- Both, E.M.; Boom, R.M.; Schutyser, M.A.I. Particle morphology and powder properties during spray drying of maltodextrin and whey protein mixtures. Powder Technol. 2020, 363, 519–524. [Google Scholar] [CrossRef]
- Kajiyama, T.; Park, K.J. Influence of Air Parameters on Spray Drying Energy Consumption. Rev. Bras. Prod. Agroind. Camp. Gd. 2010, 12, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Dohrn, S.; Rawal, P.; Luebbert, C.; Lehmkemper, K.; Kyeremateng, S.O.; Degenhardt, M.; Sadowski, G. Predicting process design spaces for spray drying amorphous solid dispersions. Int. J. Pharm. X 2021, 3, 100072. [Google Scholar] [PubMed]
- Teleki, A.; Nylander, O.; Bergström, C.A.S. Intrinsic dissolution rate profiling of poorly water-soluble compounds in biorelevant dissolution media. Pharmaceutics 2020, 12, 493. [Google Scholar] [CrossRef] [PubMed]
- Watterson, S.; Hudson, S.; Svärd, M.; Rasmuson, Å.C. Thermodynamics of fenofibrate and solubility in pure organic solvents. Fluid Phase Equilib. 2014, 367, 143–150. [Google Scholar] [CrossRef] [Green Version]
- Valavi, M.; Ukrainczyk, M.; Dehghani, M.R. Prediction of solubility of active pharmaceutical ingredients by semi- predictive Flory Huggins/Hansen model. J. Mol. Liq. 2017, 246, 166–172. [Google Scholar] [CrossRef]




| Substance | mi (-) | σi (Å) | εi k−1 (K) | εAiBi k−1 (K) | κAiBi (-) | Indexed |
|---|---|---|---|---|---|---|
| Fenofibrate | 3.85 | 4.76 | 0 | 0 | 0.02 | [25] |
| HPMC (Pharmacoat 603) | 595.4 | 2.88 | 298 | 1602.3 | 0.02 | [26,27] |
| Water | 1 | 3 | 366 | 2500.7 | 0.035 | [22] |
| i–j | kij |
|---|---|
| Fenofibrate-HPMC | 0.01 |
| Fenofibrate-Water | 0 |
| HPMC-Water | 0.08 |
| Nanomechanical Stability and Anisotropy Properties | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tool | Elastic Properties | Bulk Mod. (GPa) | Shear Mod. (GPa) | Young Mod. (GPa) | Poisson’s Ratio | Pugh Ratio | Linear Compressibility (TPa−1) | UAI | Hardness (GPa) | Vickers Hardness | Fracture Toughness (MPa/m2) |
| Elate | Average | 9.44 | 4.63 | 11.94 | 0.289 | 0.12 | 4.94 | 0.61 | 0.02 | ||
| ElaTools | Voigt | 10.45 | 6.11 | 15.34 | 0.2554 | 1.7106 | 108.475 | 4.9368 | 0.901 | ||
| ElaTools | Reuss | 8.43 | 3.15 | 8.404 | 0.363 | 2.6754 | −4.513 | 0.465 | |||
| ElaTools | Average (Hill) | 9.44 | 4.63 | 11.872 | 0.3092 | 2.0388 | 0.683 | ||||
| Process Parameters | Aspen Plus V9 | Experimental |
|---|---|---|
| Mill diameter | 15 cm | 14 cm |
| Rotation speed | 691 rpm | 450 rpm |
| Solution material mass | 10 g | 10 g |
| Grinding balls mass | 68 g | 70 g |
| D80 initial | 100 ± 25 μm | 100 μm |
| Centrifugal acceleration | 95G | 95G |
| Final size range | 300–500 nm | 300–500 nm |
| Parameters | Run 1 | Run 2 | Run 3 | Run 4 | Run 5 |
|---|---|---|---|---|---|
| Fair, 1 (kg/h) | 2500 | 2500 | 1500 | 2500 | 1500 |
| Tair,1 (°C) | 116 | 116 | 145 | 116 | 116 |
| Dn (mm) | 0.007 | 0.007 | 0.007 | 0.03 | 0.007 |
| Pair,1 (bar) | 6 | 4.5 | 4.5 | 4.5 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouranidis, A.; Davidopoulou, C.; Kachrimanis, K. Integrating Elastic Tensor and PC-SAFT Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions. Pharmaceutics 2021, 13, 1771. https://doi.org/10.3390/pharmaceutics13111771
Ouranidis A, Davidopoulou C, Kachrimanis K. Integrating Elastic Tensor and PC-SAFT Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions. Pharmaceutics. 2021; 13(11):1771. https://doi.org/10.3390/pharmaceutics13111771
Chicago/Turabian StyleOuranidis, Andreas, Christina Davidopoulou, and Kyriakos Kachrimanis. 2021. "Integrating Elastic Tensor and PC-SAFT Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions" Pharmaceutics 13, no. 11: 1771. https://doi.org/10.3390/pharmaceutics13111771
APA StyleOuranidis, A., Davidopoulou, C., & Kachrimanis, K. (2021). Integrating Elastic Tensor and PC-SAFT Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions. Pharmaceutics, 13(11), 1771. https://doi.org/10.3390/pharmaceutics13111771







