Microwell Plate-Based Dynamic Light Scattering as a High-Throughput Characterization Tool in Biopharmaceutical Development
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation of Lysozyme Formulations
2.3. High-Throughput Preparation of Peptide-12 Formulations
2.4. Determination of Protein and Peptide Concentration
2.5. Determination of Denaturation Temperature (Tm) by Intrinsic Fluorescence Spectroscopy (IFS)
2.6. Molecular Weight (Mw) and Purity of Lysozyme by UHPLC-RP/UV-MS
2.7. Surface Tension Measurements by Wilhelmy Plate Method
2.8. Dynamic Viscosity Measurements
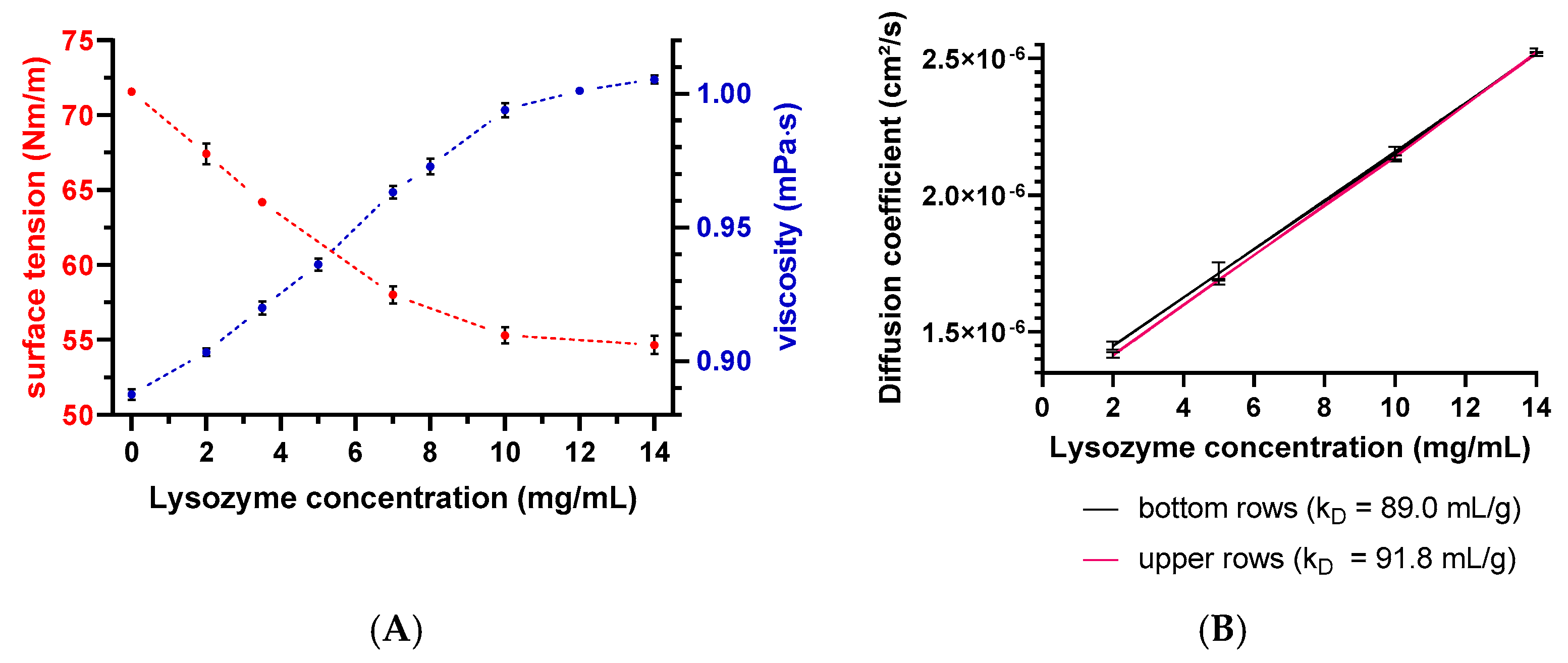
2.9. Plate-Based DLS Measurement of the Diffusion Self-Interaction Parameter (kD)
2.10. Variability and Statistics of Plate-Based DLS Measurements
3. Results and Discussion
3.1. Variability and Statistics of Plate-Based DLS Measurements
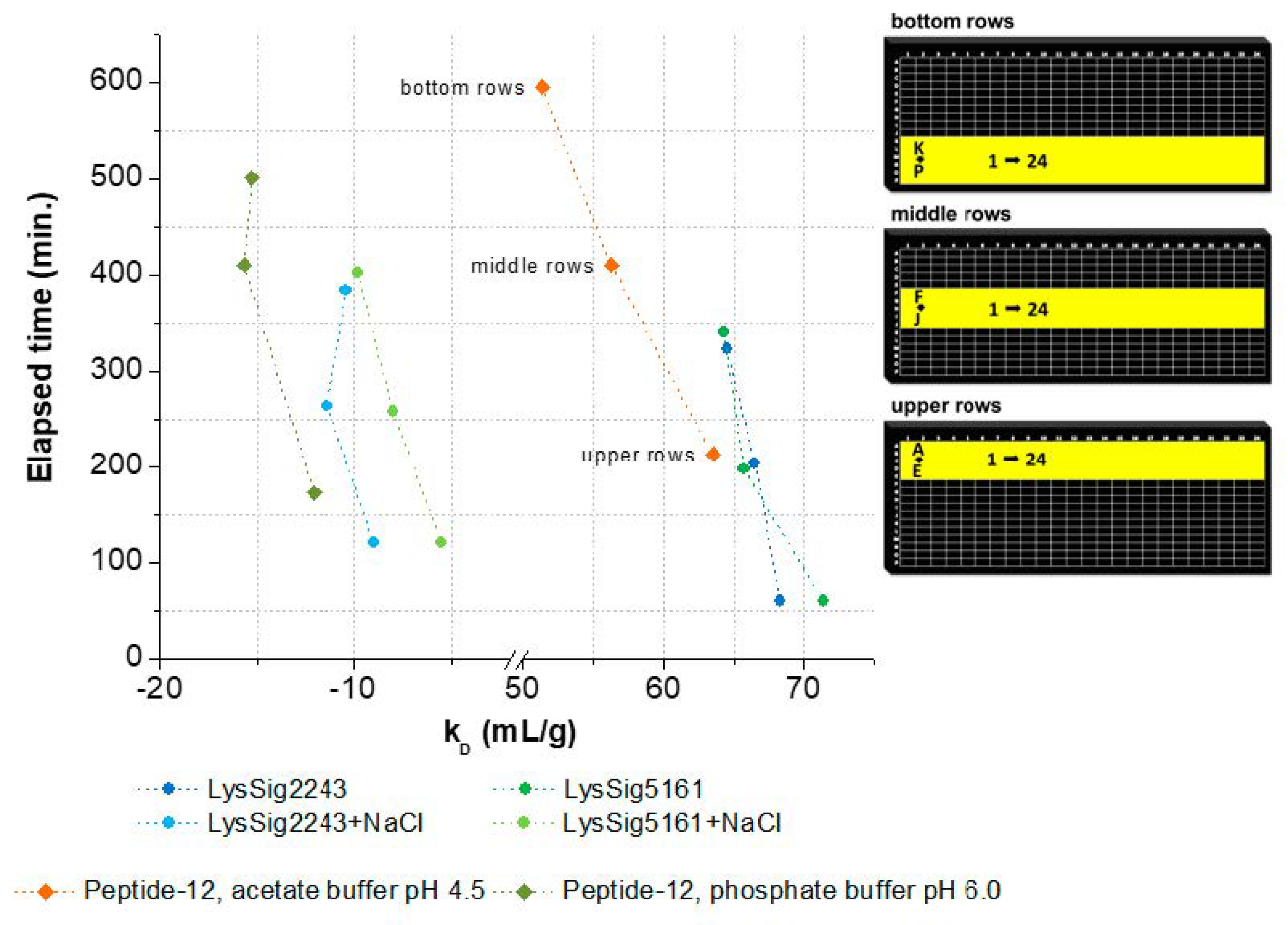
3.2. kD Measurement as a Function of Plate Position and Elapsed Time
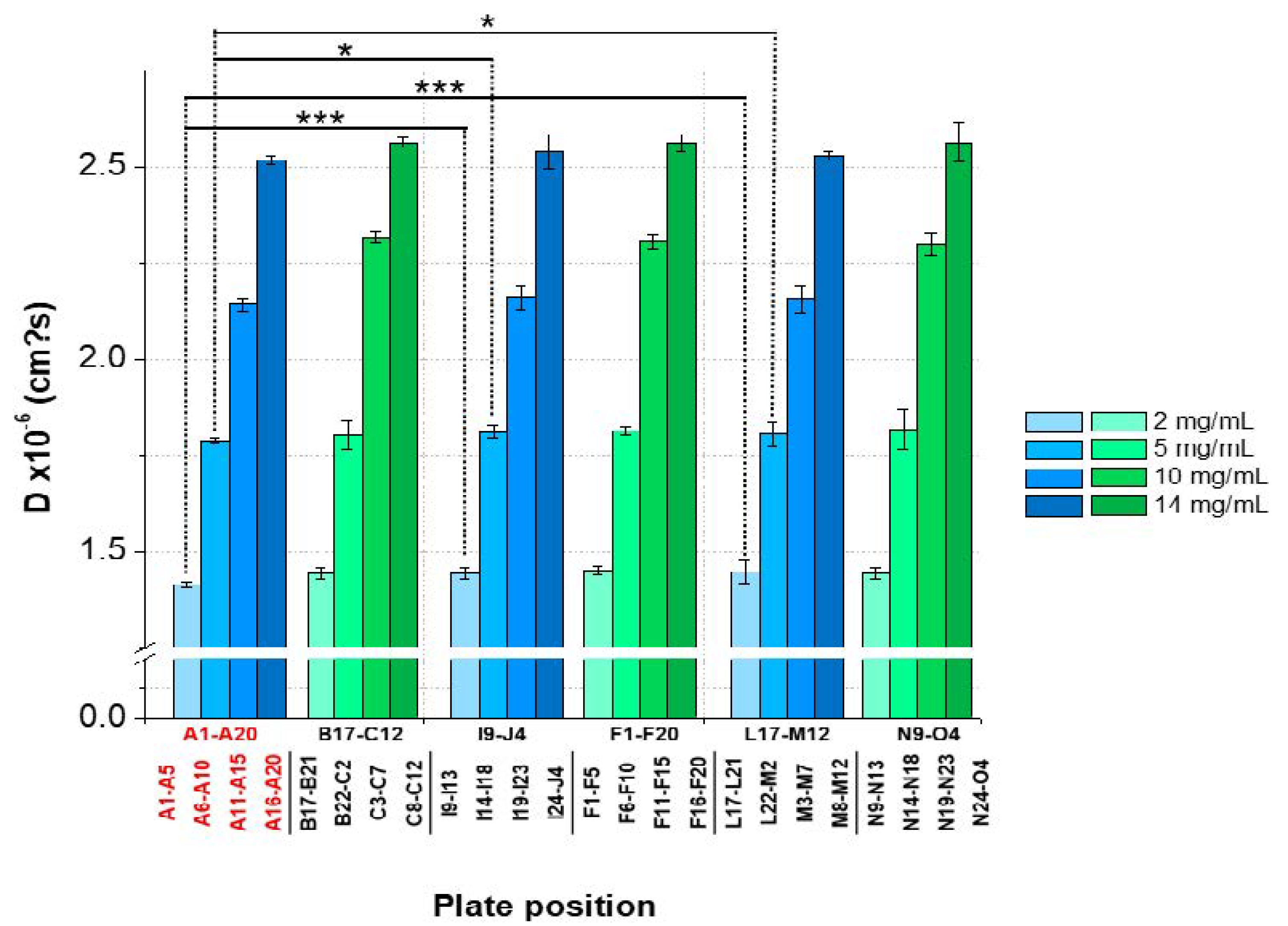
3.3. Intra-Plate Variability of Plate-Based DLS Measurements
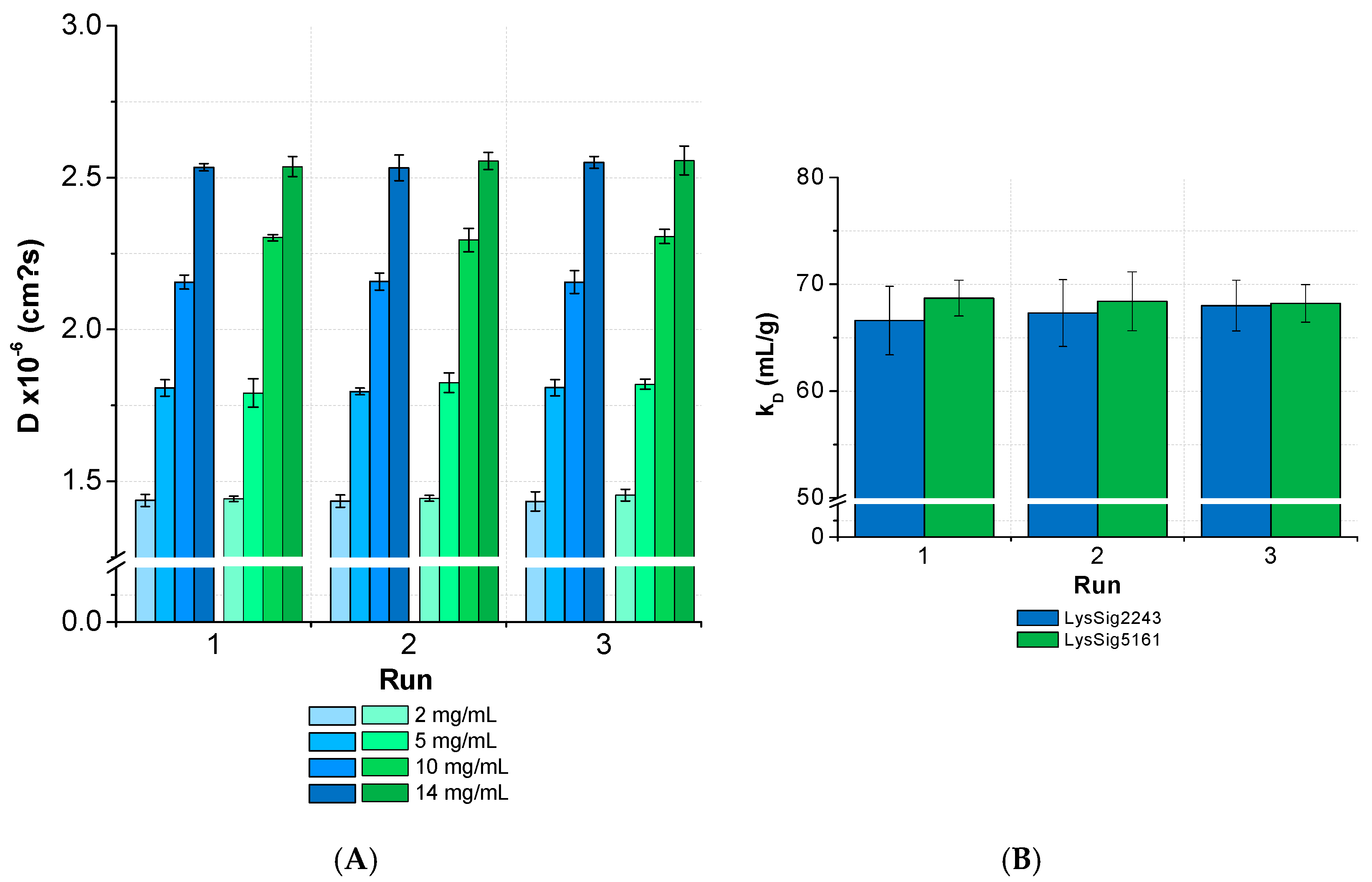
3.4. Inter-Plate Variability of Plate-Based DLS Measurements
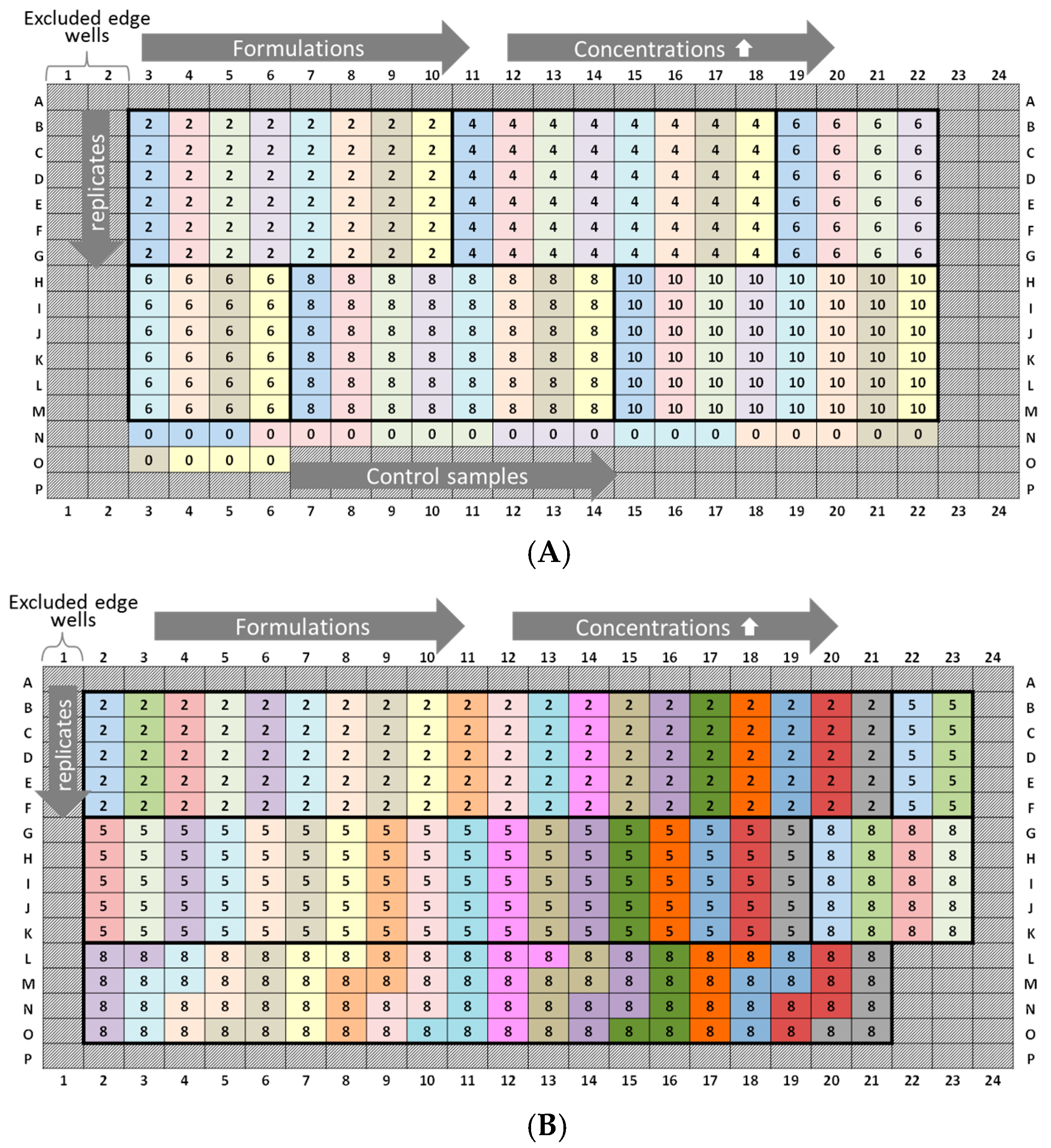
3.5. Plate Design Recommendations for High-Throughput Formulation Screening
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
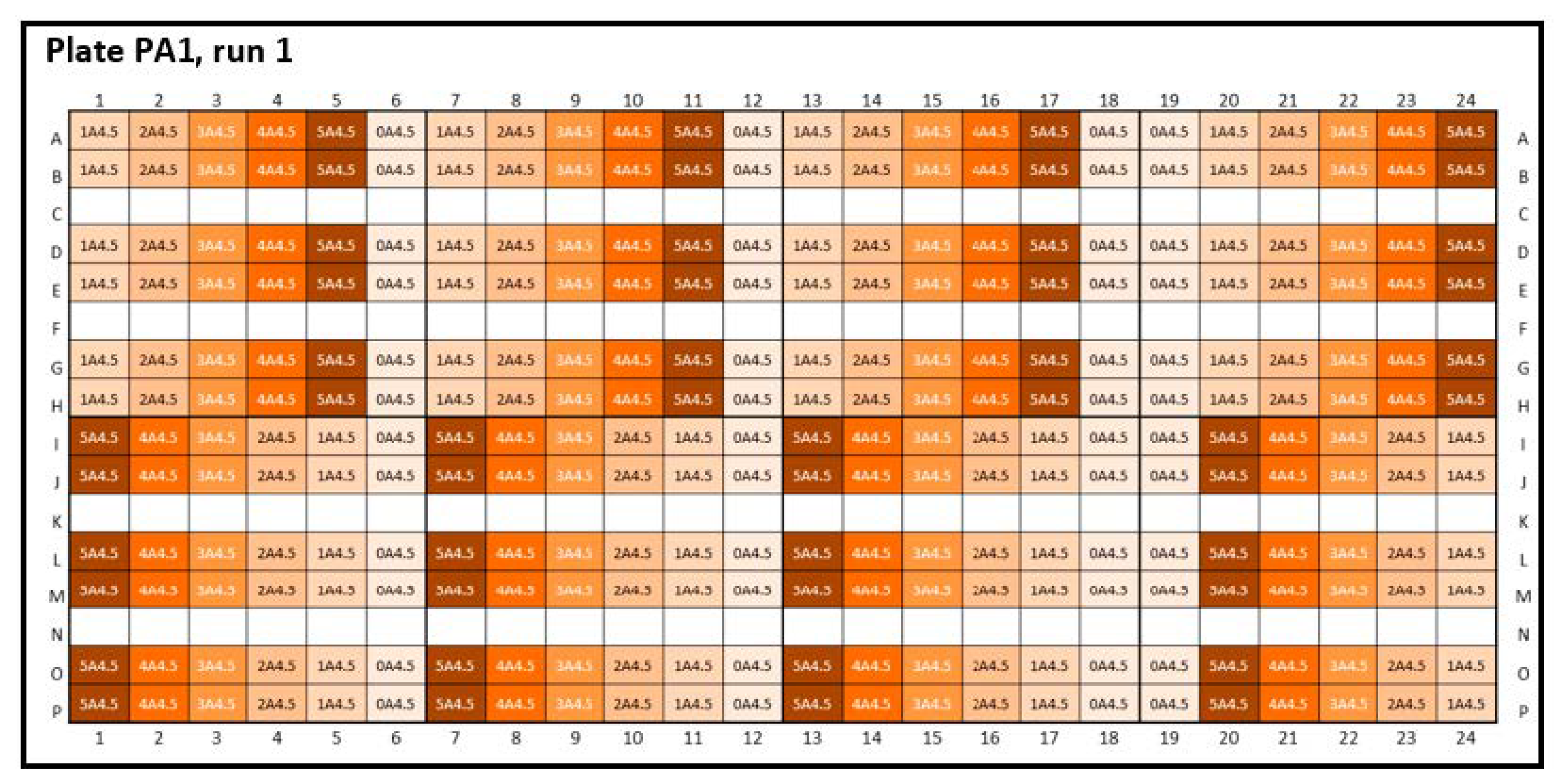
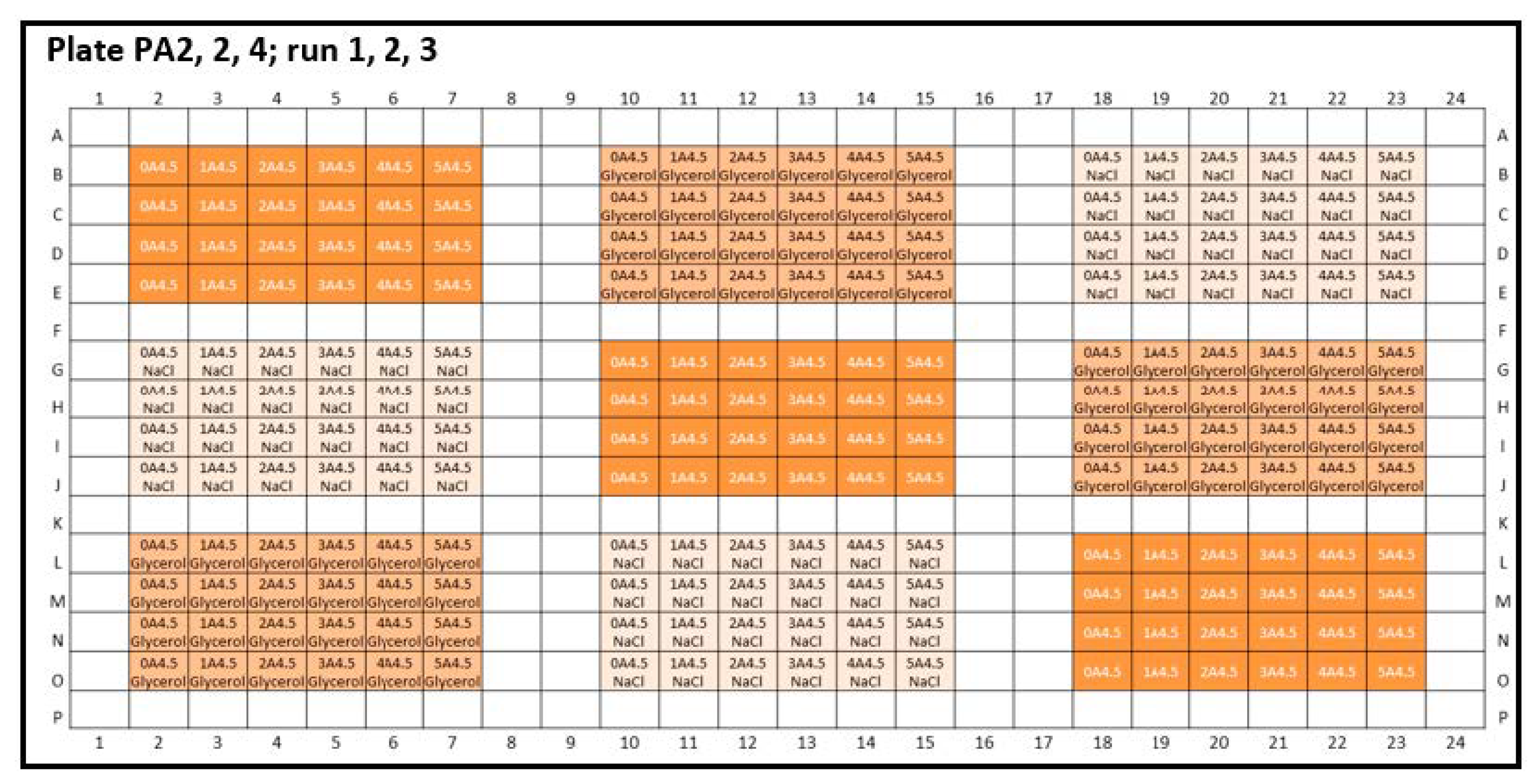
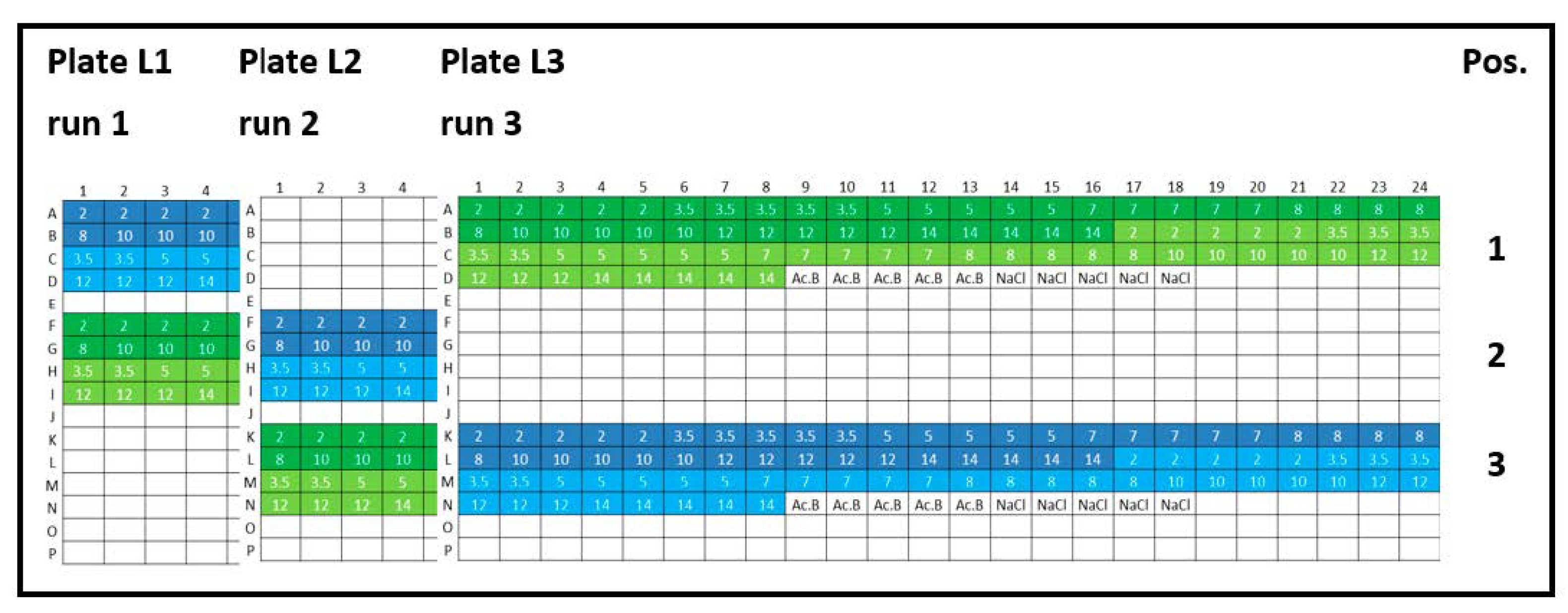
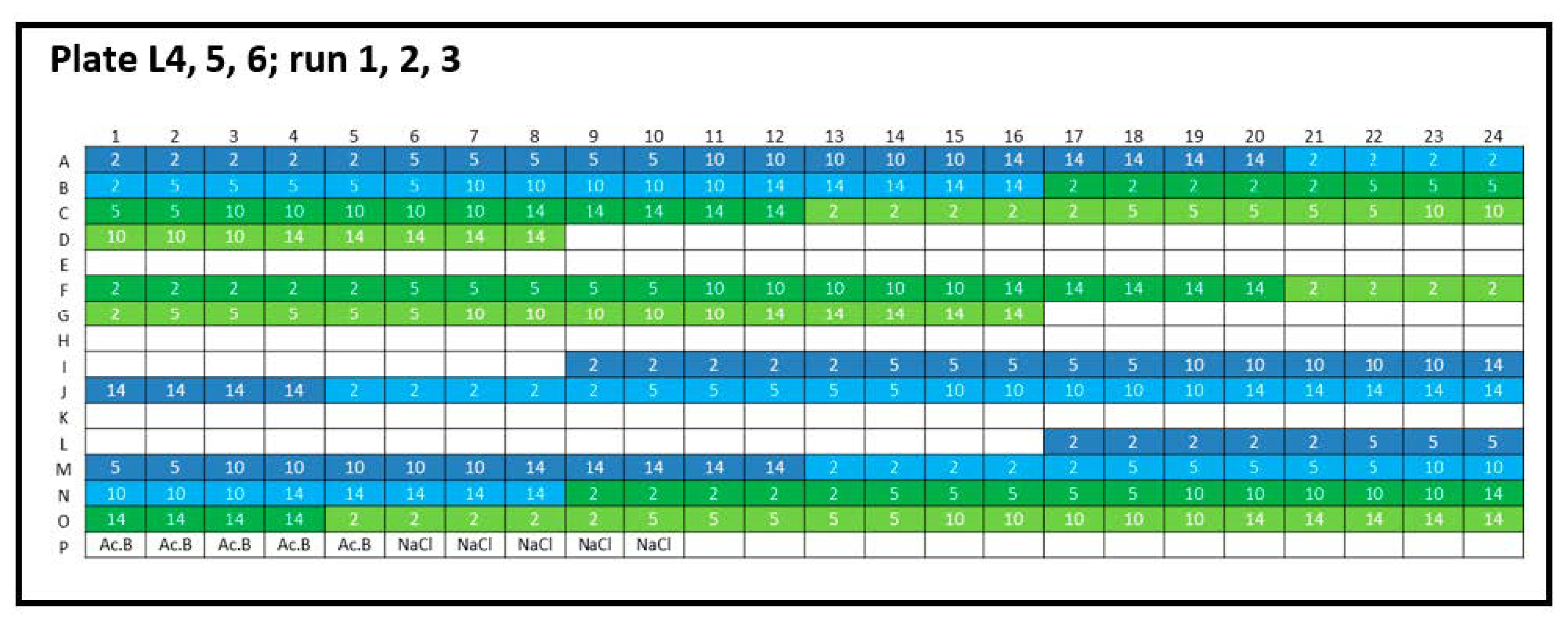
Appendix B
References
- Lau, J.L.; Dunn, M.K. Therapeutic peptides: Historical perspectives, current development trends, and future directions. Bioorg. Med. Chem. 2018, 26, 2700–2707. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, M.; Gieseler, H. Predictive Screening Tools Used in High-Concentration Protein Formulation Development. J. Pharm. Sci. 2018, 107, 772–777. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.U.I.; Graf, O.; Milovic, N.; Luan, X.; Bluemel, M.; Smolny, M.; Forrer, K. Formulation Development of Antibodies Using Robotic System and High-Throughput Laboratory (HTL). J. Pharm. Sci. 2010, 99, 2279–2294. [Google Scholar] [CrossRef] [PubMed]
- Mahler, H.-C.; Friess, W.; Grauschopf, U.; Kiese, S. Protein Aggregation: Pathways, Induction Factors and Analysis. J. Pharm. Sci. 2009, 98, 2909–2934. [Google Scholar] [CrossRef]
- Ratanji, K.D.; Derrick, J.P.; Dearman, R.J.; Kimber, I. Immunogenicity of therapeutic proteins: Influence of aggregation. J. Immunotoxicol. 2013, 11, 99–109. [Google Scholar] [CrossRef] [Green Version]
- Sorret, L.L.; Dewinter, M.A.; Schwartz, D.K.; Randolph, T.W. Challenges in Predicting Protein-Protein Interactions from Measurements of Molecular Diffusivity. Biophys. J. 2016, 111, 1831–1842. [Google Scholar] [CrossRef] [Green Version]
- Mayr, L.M.; Bojanic, D. Novel trends in high-throughput screening. Curr. Opin. Pharmacol. 2009, 9, 580–588. [Google Scholar] [CrossRef]
- Hofmann, M.; Winzer, M.; Weber, C.; Gieseler, H. A Low-Volume Screening Tool to Optimize Colloidal Stability for Highly Concentrated Protein Formulations. Am. Pharm. Rev. 2014, 17, 1–5. [Google Scholar]
- Razinkov, V.I.; Kleemann, G.R. High-Throughput Formulation Development of Biopharmaceuticals; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; ISBN 9781907568640. [Google Scholar]
- Inglese, J.; Auld, D.S. High Throughput Screening (HTS) Techniques: Applications in Chemical Biology. Wiley Encycl. Chem. Biol. 2008. [Google Scholar] [CrossRef]
- Shekarchi, I.C.; Sever, J.L.; Lee, Y.J.; Castellano, G.; Madden, D.L. Evaluation of various plastic microtiter plates with measles, toxoplasma, and gamma globulin antigens in enzyme-linked immunosorbent assays. J. Clin. Microbiol. 1984, 19, 89–96. [Google Scholar] [CrossRef] [Green Version]
- Lilyanna, S.; Ng, E.M.W.; Moriguchi, S.; Chan, S.P.; Kokawa, R.; Huynh, S.H.; Chong, P.C.J.; Ng, Y.X.; Richards, A.M.; Ng, T.W.; et al. Variability in Microplate Surface Properties and Its Impact on ELISA. J. Appl. Lab. Med. 2018, 2, 687–699. [Google Scholar] [CrossRef] [Green Version]
- Capelle, M.A.H.; Gurny, R.; Arvinte, T. High throughput screening of protein formulation stability: Practical considerations. Eur. J. Pharm. Biopharm. 2007, 65, 131–148. [Google Scholar] [CrossRef] [PubMed]
- Reed, G.F.; Lynn, F.; Meade, B.D. Use of Coefficient of Variation in Assessing Variability of Quantitative Assays. Clin. Vaccine Immunol. 2002, 9, 1235–1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- U.S. Department of Health and Human Services; Food and Drug Administration; Center for Drug Evaluation and Research (CDER); Center for Veterinary Medicine (CVM). Guidance for Industry, Bioanalytical Method Validation; Department of Health and Human Services; Food and Drug Administration: Rockville, MD, USA, 2018.
- DeSilva, B.; Smith, W.; Weiner, R.; Kelley, M.; Smolec, J.; Lee, B.; Khan, M.; Tacey, R.; Hill, H.; Celniker, A. Recommendations for the Bioanalytical Method Validation of Ligand-Binding Assays to Support Pharmacokinetic Assessments of Macromolecules. Pharm. Res. 2003, 20, 1885–1900. [Google Scholar] [CrossRef]
- Bevan, C.D.; Lloyd, R.S. A High-Throughput Screening Method for the Determination of Aqueous Drug Solubility Using Laser Nephelometry in Microtiter Plates. Anal. Chem. 2000, 72, 1781–1787. [Google Scholar] [CrossRef]
- Berg, M.; Undisz, K.; Thiericke, R.; Zimmermann, P.; Moore, T.; Posten, C. Evaluation of Liquid Handling Conditions in Microplates. J. Biomol. Screen. 2001, 6, 47–56. [Google Scholar] [CrossRef]
- Matthews, C.Z.; Woolf, E.J.; Matuszewski, B.K. Improved procedure for the the determination of rofecoxib in human plasma involving 96-well solid-phase extraction and fluorescence detection. J. Chromatogr. A 2002, 949, 83–89. [Google Scholar] [CrossRef]
- Lundholt, B.K.; Scudder, K.M.; Pagliaro, L. A Simple Technique for Reducing Edge Effect in Cell-Based Assays. J. Biomol. Screen. 2003, 8, 566–570. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, S.S. Variance Components of an Enzyme-linked Immunosorbent Assay for Detection of IgG Antibodies in Milk Samples to Mycobacterium avium subspecies paratuberculosis in Dairy Cattle. J. Vet. Med. Ser. B 2002, 49, 384–387. [Google Scholar] [CrossRef]
- Paweska, J.T.; Jansen van Vuren, P.; Swanepoel, R. Validation of an indirect ELISA based on a recombinant nucleocapsid protein of Rift Valley fever virus for the detection of IgG antibody in humans. J. Virol. Methods 2007, 146, 119–124. [Google Scholar] [CrossRef]
- Gaines Das, R.E. Assessment of Assay Precision: A Case Study of an ELISA for Anti-pertussis Antibody. Biologicals 1999, 27, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Uchida, M.; Cheung, J.; Antochshuk, V.; Shameem, M. Method qualification and application of diffusion interaction parameter and virial coefficient. Int. J. Biol. Macromol. 2013, 62, 487–493. [Google Scholar] [CrossRef] [PubMed]
- Evers, A.; Pfeiffer-Marek, S.; Bossart, M.; Heubel, C.; Stock, U.; Tiwari, G.; Gebauer, B.; Elshorst, B.; Pfenninger, A.; Lukasczyk, U.; et al. Peptide Optimization at the Drug Discovery-Development Interface: Tailoring of Physicochemical Properties Toward Specific Formulation Requirements. J. Pharm. Sci. 2019, 108, 1404–1414. [Google Scholar] [CrossRef] [PubMed]
- Evers, A.; Bossart, M.; Pfeiffer-Marek, S.; Elvert, R.; Schreuder, H.; Kurz, M.; Stengelin, S.; Lorenz, M.; Herling, A.; Konkar, A.; et al. Dual Glucagon-like Peptide 1 (GLP-1)/Glucagon Receptor Agonists Specifically Optimized for Multidose Formulations. J. Med. Chem. 2018, 61, 5580–5593. [Google Scholar] [CrossRef] [PubMed]
- Wilhelmy, L. Ueber die Abhängigkeit der Capillaritäts-Constanten des Alkohols von Substanz und Gestalt des benetzten festen Körpers. Ann. Phys. Chem. 1863, 195, 177–217. [Google Scholar] [CrossRef] [Green Version]
- Harding, S.E.; Johnson, P. The concentration-dependence of macromolecular parameters. Biochem. J. 1985, 231, 543–547. [Google Scholar] [CrossRef] [Green Version]
- Parmar, A.S.; Muschol, M. Hydration and Hydrodynamic Interactions of Lysozyme: Effects of Chaotropic versus Kosmotropic Ions. Biophys. J. 2009, 97, 590–598. [Google Scholar] [CrossRef] [Green Version]
- Eberstein, W.; Georgalis, Y.; Saenger, W. Molecular interactions in crystallizing lysozyme solutions studied by photon correlation spectroscopy. J. Cryst. Growth 1994, 143, 71–78. [Google Scholar] [CrossRef]
- Nikfarjam, S.; Jouravleva, E.V.; Anisimov, M.A.; Woehl, T.J. Effects of Protein Unfolding on Aggregation and Gelation in Lysozyme Solutions. Biomolecules 2020, 10, 1262. [Google Scholar] [CrossRef]
- Aslam, M. Introducing Grubbs’s test for detecting outliers under neutrosophic statistics—An application to medical data. J. King Saud Univ. Sci. 2020, 32, 2696–2700. [Google Scholar] [CrossRef]
- Wiegmann, V.; Martinez, C.B.; Baganz, F. A simple method to determine evaporation and compensate for liquid losses in small-scale cell culture systems. Biotechnol. Lett. 2018, 40, 1029–1036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carreón, Y.J.P.; Ríos-Ramírez, M.; Moctezuma, R.E.; González-Gutiérrez, J. Texture analysis of protein deposits produced by droplet evaporation. Sci. Rep. 2018, 8, 9580. [Google Scholar] [CrossRef] [Green Version]
- Noskov, B.; Mikhailovskaya, A. Adsorption kinetics of globular proteins and protein/surfactant complexes at the liquid–gas interface. Soft Matter 2013, 9, 9392. [Google Scholar] [CrossRef]
- Carreón, Y.J.P.; González-Gutiérrez, J.; Pérez-Camacho, M.I.; Mercado-Uribe, H. Patterns produced by dried droplets of protein binary mixtures suspended in water. Colloids Surfaces B Biointerfaces 2018, 161, 103–110. [Google Scholar] [CrossRef]
- Amrhein, S.; Bauer, K.C.; Galm, L.; Hubbuch, J. Non-invasive high throughput approach for protein hydrophobicity determination based on surface tension. Biotechnol. Bioeng. 2015, 112, 2485–2494. [Google Scholar] [CrossRef]
- Szymańska, A.; Ślósarek, G. Light Scattering Studies of Hydration and Structural Transformations of Lysozyme. Acta Phys. Pol. A 2012, 121, 694–698. [Google Scholar] [CrossRef]
- Roberts, D.; Keeling, R.; Tracka, M.; van der Walle, C.F.; Uddin, S.; Warwicker, J.; Curtis, R. The Role of Electrostatics in Protein–Protein Interactions of a Monoclonal Antibody. Mol. Pharm. 2014, 11, 2475–2489. [Google Scholar] [CrossRef]
- Pindrus, M.A.; Shire, S.J.; Yadav, S.; Kalonia, D.S. The Effect of Low Ionic Strength on Diffusion and Viscosity of Monoclonal Antibodies. Mol. Pharm. 2018, 15, 3133–3142. [Google Scholar] [CrossRef]
- Bauer, K.C.; Göbel, M.; Schwab, M.-L.; Schermeyer, M.-T.; Hubbuch, J. Concentration-dependent changes in apparent diffusion coefficients as indicator for colloidal stability of protein solutions. Int. J. Pharm. 2016, 511, 276–287. [Google Scholar] [CrossRef]
- Saluja, A.; Fesinmeyer, R.M.; Hogan, S.; Brems, D.N.; Gokarn, Y.R. Diffusion and Sedimentation Interaction Parameters for Measuring the Second Virial Coefficient and Their Utility as Predictors of Protein Aggregation. Biophys. J. 2010, 99, 2657–2665. [Google Scholar] [CrossRef] [Green Version]
- Yadav, S.; Scherer, T.M.; Shire, S.J.; Kalonia, D.S. Use of dynamic light scattering to determine second virial coefficient in a semidilute concentration regime. Anal. Biochem. 2011, 411, 292–296. [Google Scholar] [CrossRef] [PubMed]
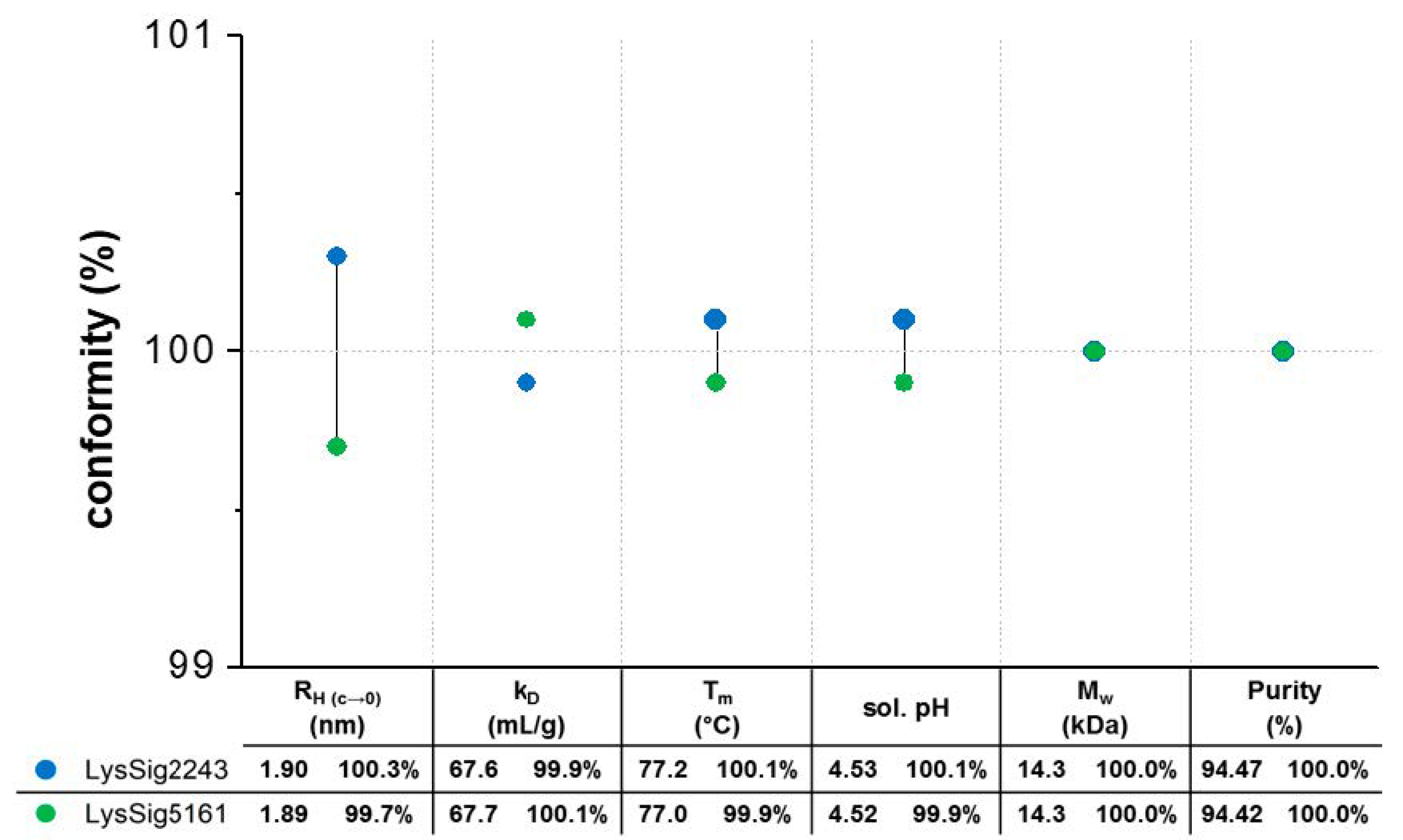
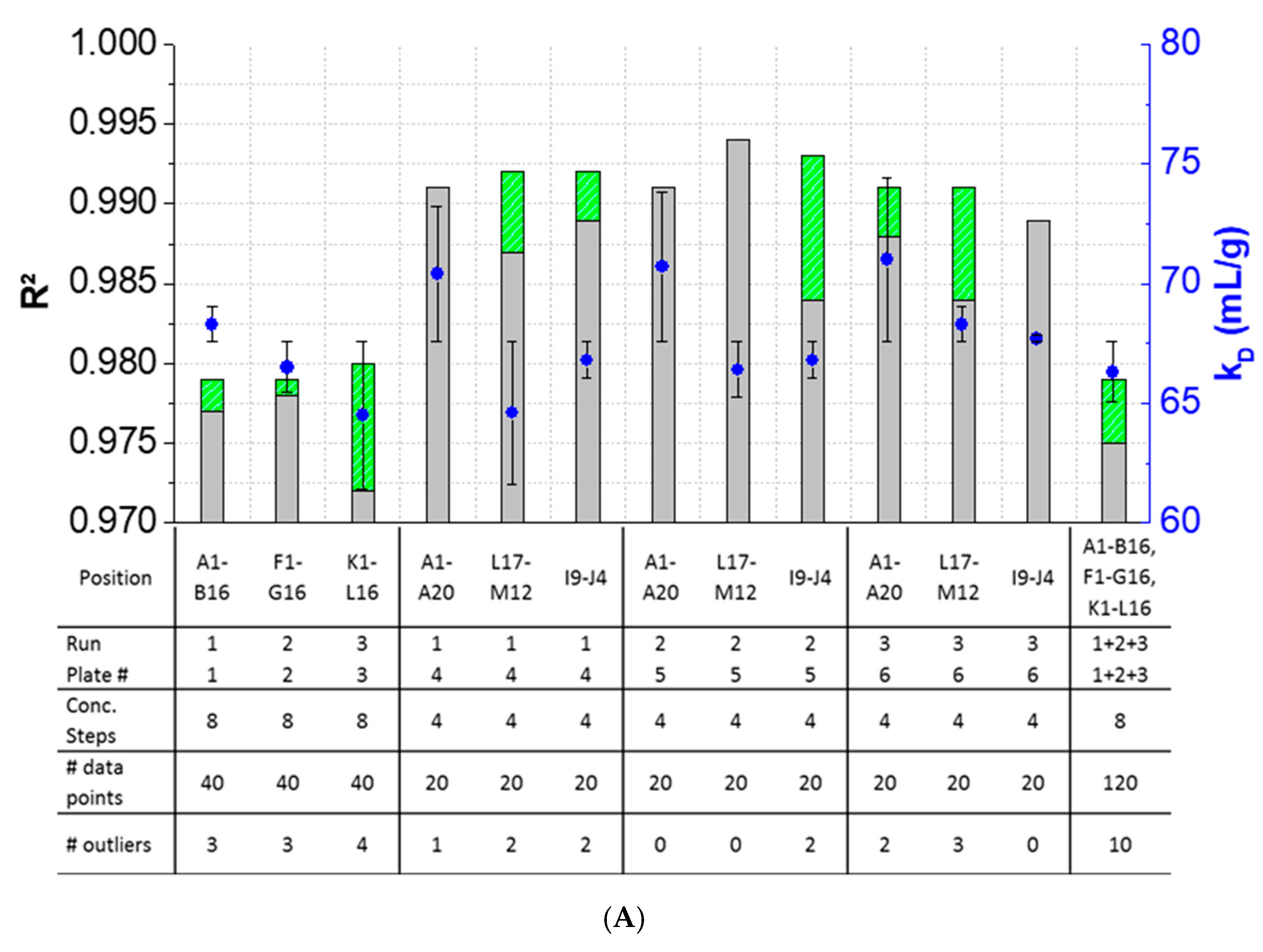
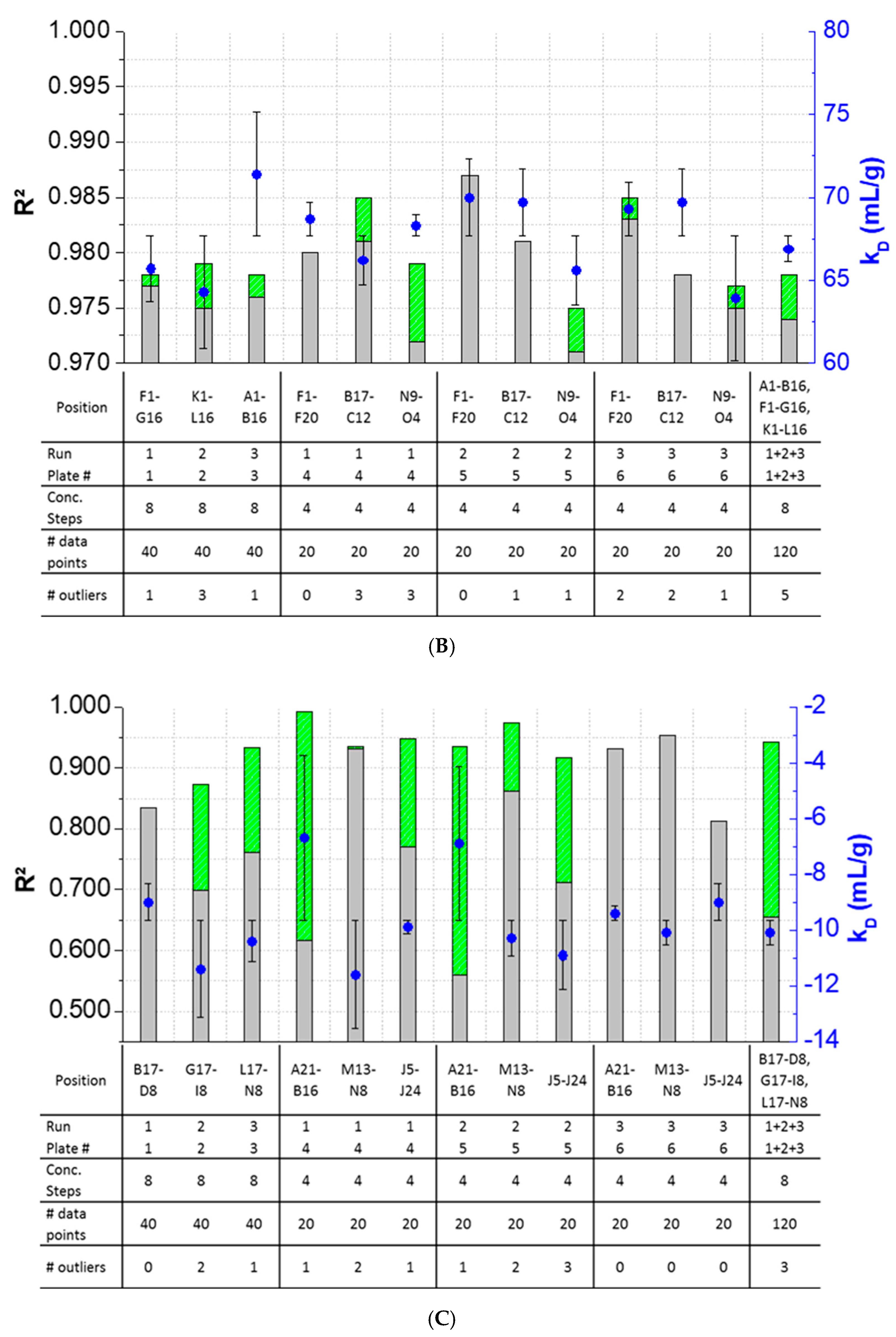
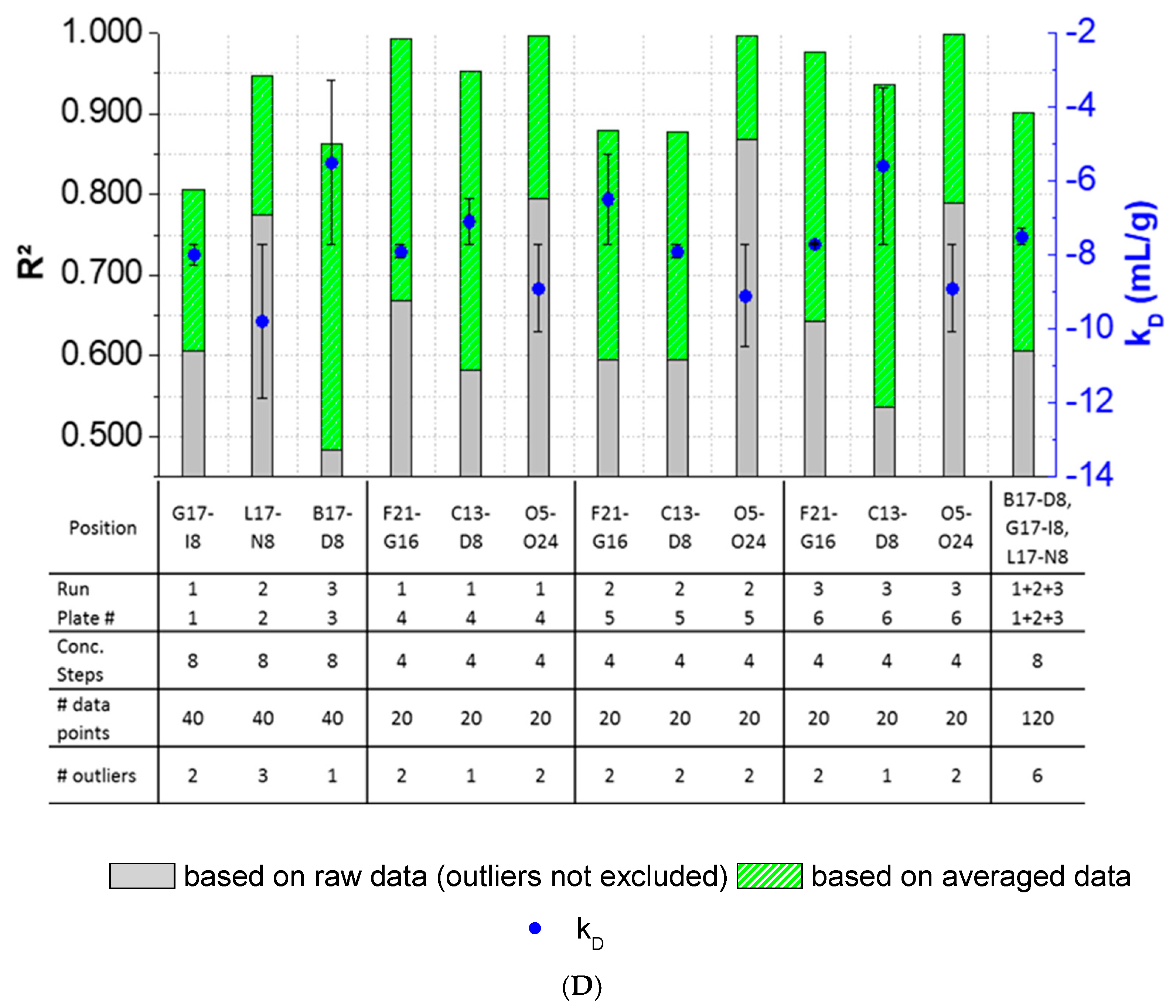


| Approach Ac | |||||||||
| A | B | C | D | E | F | G | H | Av. | |
| Average kD (mL/g) | 59.8 | 56.3 | 55.6 | 57.4 | 57.1 | 54.7 | 56.4 | 55.7 | 57.0 |
| SDkD (mL/g) | 5.4 | 3.8 | 0.9 | 6.0 | 8.1 | 4.8 | 5.2 | 5.2 | 5.1 |
| # single kD | 8 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 34 |
| # data points (single kD) | 30 | 120 | 64/56 | 64/56 | 30 | 30 | 60 | 60 | n.a. |
| CV(%) | 9.0 | 6.8 | 1.6 | 10.4 | 14.1 | 8.7 | 9.2 | 9.4 | 8.9 |
| Span kD (%) | 25.8 | 9.1 | 3.7 | 21.0 | 24.5 | 17.9 | 16.9 | 20.6 | 39.2 |
| Approach Ph | |||||||||
| A | B | C | D | E | F | G | H | Av. | |
| Average kD (mL/g) | −14.8 | −15.6 | −14.5 | −14.7 | −14.1 | −15.8 | −14.7 | −14.5 | −14.8 |
| SD kD(mL/g) | 2.5 | 0.6 | 2.0 | 2.3 | 2.9 | 1.6 | 2.0 | 1.5 | 2.0 |
| # single kD | 8 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 34 |
| # data points (single kD) | 30 | 120 | 64/56 | 64/56 | 30 | 30 | 60 | 60 | n.a. |
| CV (%) | 16.8 | 4.0 | 13.5 | 15.6 | 20.4 | 10.2 | 13.7 | 10.6 | 13.4 |
| Span kD (%) | 37.6 | 5.4 | 26.7 | 30.8 | 33.2 | 22.2 | 26.7 | 19.7 | 37.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dauer, K.; Pfeiffer-Marek, S.; Kamm, W.; Wagner, K.G. Microwell Plate-Based Dynamic Light Scattering as a High-Throughput Characterization Tool in Biopharmaceutical Development. Pharmaceutics 2021, 13, 172. https://doi.org/10.3390/pharmaceutics13020172
Dauer K, Pfeiffer-Marek S, Kamm W, Wagner KG. Microwell Plate-Based Dynamic Light Scattering as a High-Throughput Characterization Tool in Biopharmaceutical Development. Pharmaceutics. 2021; 13(2):172. https://doi.org/10.3390/pharmaceutics13020172
Chicago/Turabian StyleDauer, Katharina, Stefania Pfeiffer-Marek, Walter Kamm, and Karl G. Wagner. 2021. "Microwell Plate-Based Dynamic Light Scattering as a High-Throughput Characterization Tool in Biopharmaceutical Development" Pharmaceutics 13, no. 2: 172. https://doi.org/10.3390/pharmaceutics13020172
APA StyleDauer, K., Pfeiffer-Marek, S., Kamm, W., & Wagner, K. G. (2021). Microwell Plate-Based Dynamic Light Scattering as a High-Throughput Characterization Tool in Biopharmaceutical Development. Pharmaceutics, 13(2), 172. https://doi.org/10.3390/pharmaceutics13020172









