Protein–Mineral Composite Particles with Logarithmic Dependence of Anticancer Cytotoxicity on Concentration of Montmorillonite Nanoplates with Adsorbed Cytochrome c
Abstract
:1. Introduction
1.1. Cytochrome c as a Proapoptotic Agent
1.2. Montmorillonite Nanoplates as a Drug-Delivery-Bearer
1.3. Conditions for Proapoptotic Effectiveness
1.4. Unsolved Problems and Aims of the Investigation
1.5. Experimental Approach
2. Materials and Methods
2.1. Materials
2.2. Static and Electric Light Scattering
2.3. Microelectrophoreses
2.4. Cytotoxicity
2.5. Computer Techniques
3. Results and Interpretation
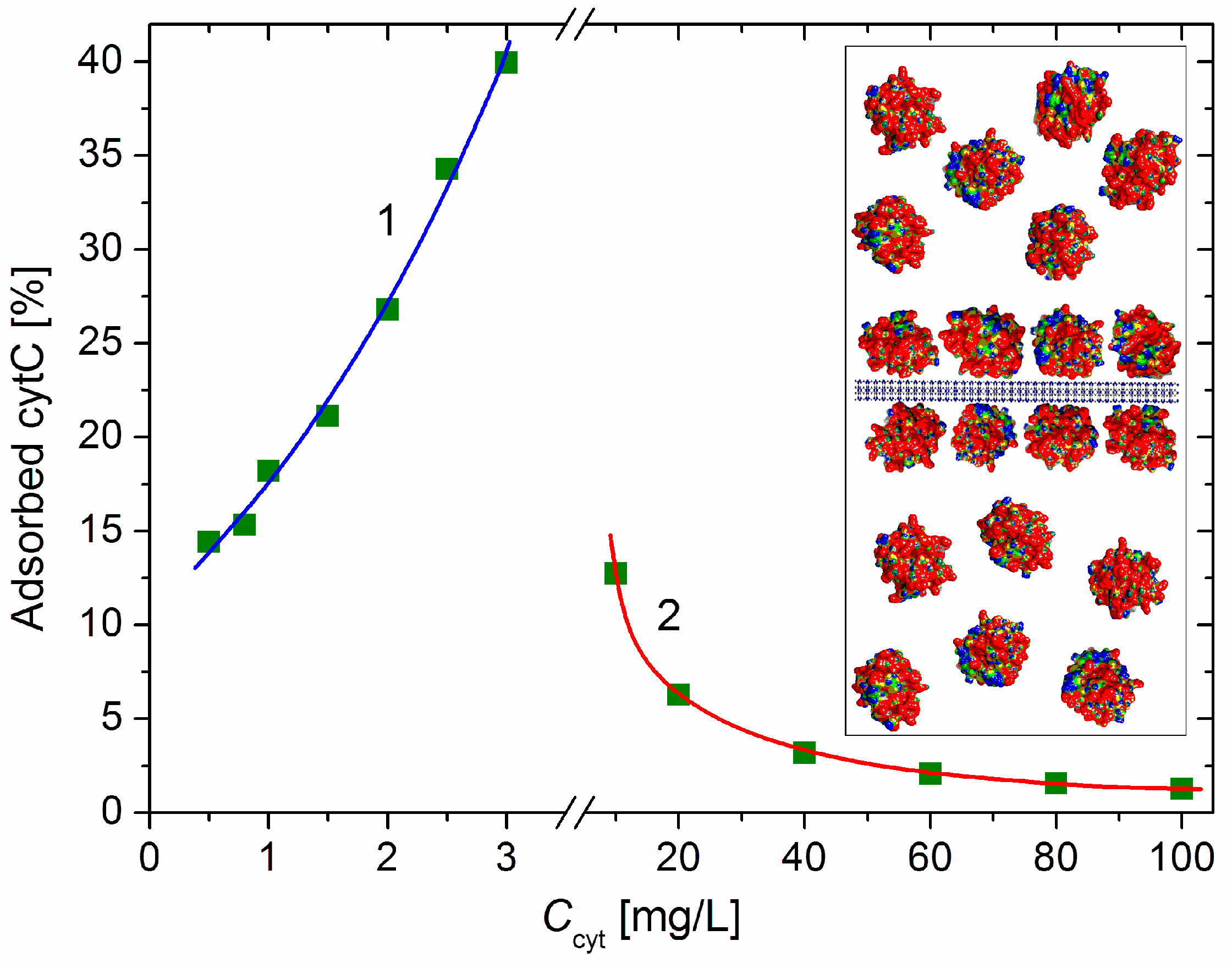
3.1. Adsorption of cytC on MM Plates
3.2. Mass Increment
3.3. Adsorbed Protein Fraction
3.4. Protein Density on Monoplate Surface
3.5. cytC Globules per MM Lamella
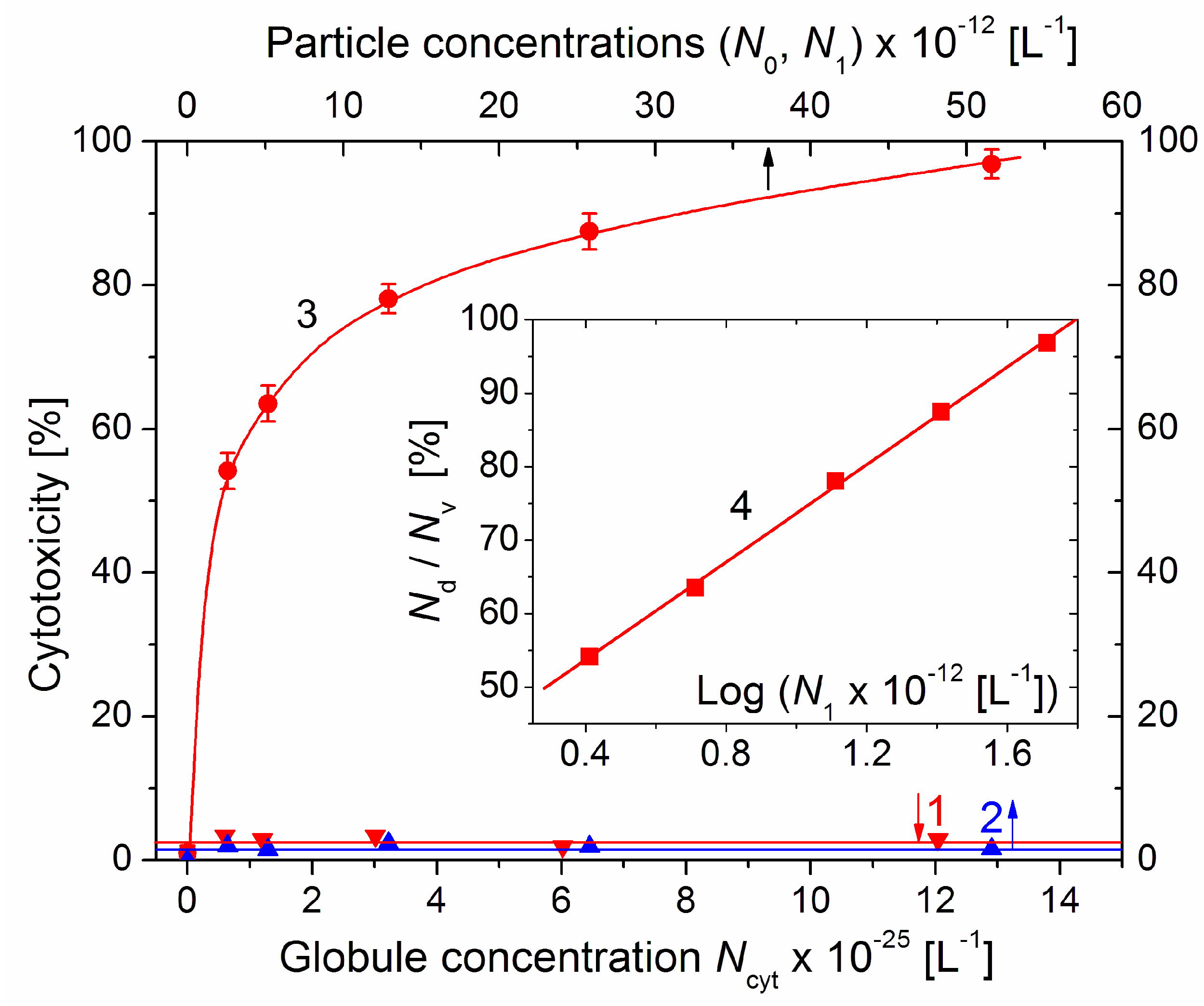
3.6. Concentration of cytC–MM Particles
3.7. Particle–Concentration Dependence of the Cytotoxicity
4. Discussion
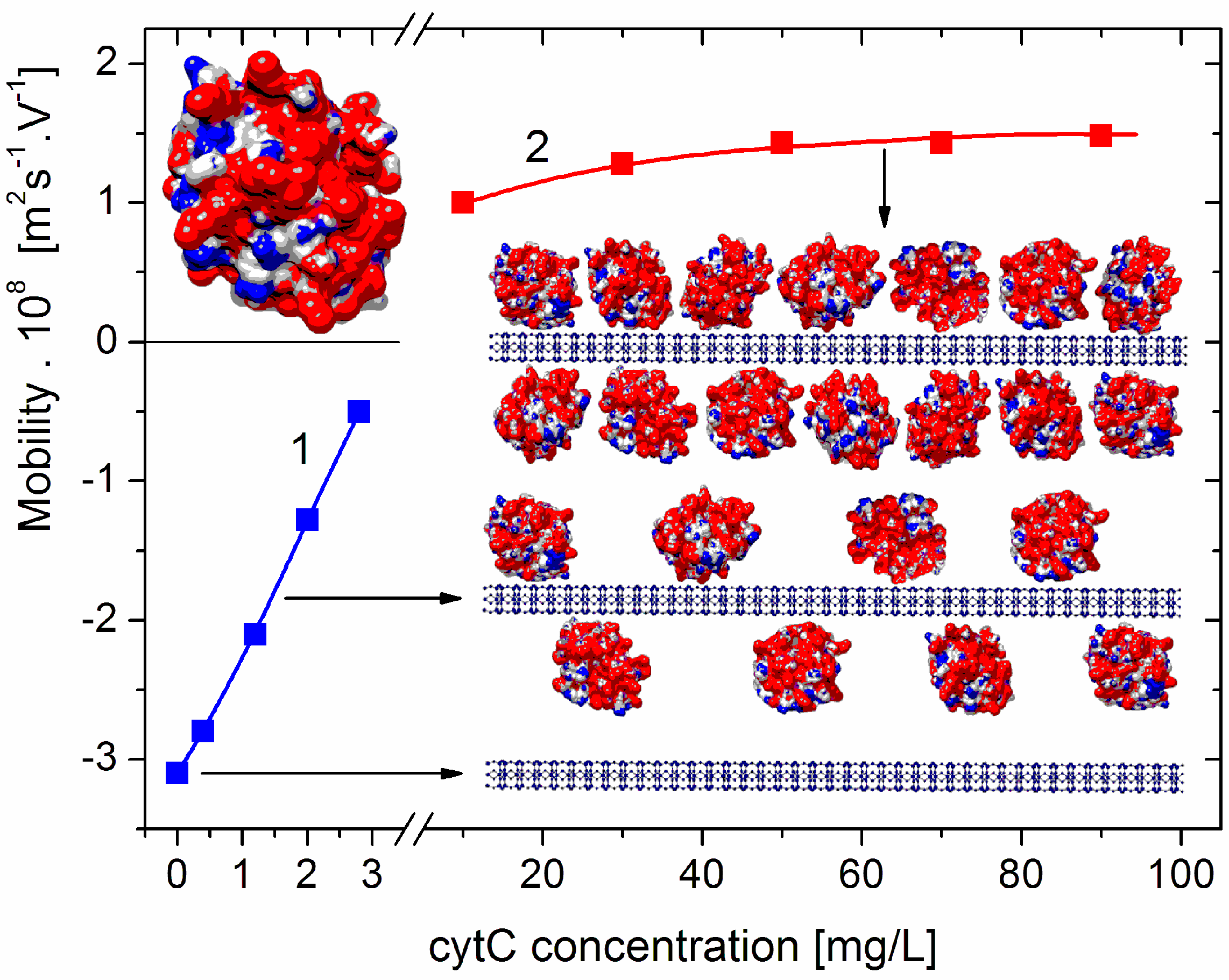
4.1. Electrokinetic Potential
4.2. Light Scattering Coefficient
4.3. Coagulation Stability
4.4. Protein/Mineral Ratio
4.5. Surface Protein Density
4.6. MM as a Protein Barer
4.7. Adsorbed Protein Detection
4.8. Cytotoxicity Definition
4.9. Cytochrome-Carrier Composite Particles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, D.R.; Reed, J.C. Mitochondria and apoptosis. Science 1998, 281, 1309–1312. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wang, X. Cytochrome c-mediated apoptosis. Ann. Rev. Biochem. 2004, 73, 87–106. [Google Scholar] [CrossRef] [PubMed]
- Vaughn, A.; Deshmukh, M. Glucose metabolism inhibits apoptosis in neurons and cancer cells by redox inactivation of cytochrome c. Nat. Cell Biol. 2008, 10, 1477–1483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heiden, M.V.; Cantley, L.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gatenby, R.; Gillies, R. Why do cancers have high aerobic glycolysis. Nat. Rev. Cancer 2004, 4, 891–899. [Google Scholar] [CrossRef]
- Zhivotovsky, B.; Orrenius, S.; Brustugun, O.; Døskeland, S. Injected cytochrome c induces apoptosis. Nature 1998, 391, 449–450. [Google Scholar] [CrossRef]
- Hristova, S.; Zhivkov, A. Isoelectric point of free and adsorbed cytochrome c determined by various methods. Colloids Surf. B: Biointerfaces 2019, 174, 87–94. [Google Scholar] [CrossRef]
- Hristova, S.; Zhivkov, A. Electrooptical determination of the isoelectric point of globular proteins: Cytochrome c adsorbed on montmorillonite nanoplates. Colloids Surf. B Biointerfaces 2019, 176, 480–487. [Google Scholar] [CrossRef]
- Nadeau, P. The physical dimensions of fundamental clay particles. Clay Miner. 1985, 20, 499–514. [Google Scholar] [CrossRef]
- Whalley, W.; Mullins, C. Effect of saturating cation on tactoid size distribution in bentonite suspensions. Clay Miner. 1991, 26, 11–17. [Google Scholar] [CrossRef]
- Murray, H. 2D-structure and composition of the clay minerals and their physical and chemical properties. In Developments in Clay Science; Elsevier: Amsterdam, The Netherlands, 2006; pp. 7–31. [Google Scholar]
- Schoonheydt, R.; Johnston, C.; Bergaya, F. Clay minerals and their surfaces. In Developments in Clay Science; Schoonheydt, R., Johnston, C.T., Bergaya, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–21. [Google Scholar]
- Cain, K.; Langlais, C.; Sun, X.; Brown, D.; Cohen, G. Physiological concentrations of K+ inhibit cytochrome c-dependent formation of the apoptosome. J. Biol. Chem. 2001, 276, 41985–41990. [Google Scholar] [CrossRef] [Green Version]
- Hristova, S.; Zhivkov, A. Adsorption of cytochrome c on montmorillonite nanoplates: Protein concentration dependence. J. Colloid Interface Sci. 2015, 446, 252–262. [Google Scholar] [CrossRef]
- Cortez, C.; Tomaskovic-Crook, E.; Johnston, A.; Scott, A.; Nice, E.; Heath, J.; Caruso, F. Influence of size, surface, cell line, and kinetic properties on the specific binding of A33 antigen-targeted multilayered particles and capsules to colorectal cancer cells. ACS Nano 2007, 1, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Win, K.Y.; Feng, S. Effects of particle size and surface coating on cellular uptake of polymeric nanoparticles for oral delivery of anticancer drugs. Biomaterials 2005, 26, 2713–2722. [Google Scholar] [CrossRef]
- Hristova, S.; Zhivkov, A. Cytotoxic effect of exogenous cytochrome c adsorbed on montmorillonite colloid particles on colon cancer cell culture. Compt. Rend Acad. bulg. Sci. 2019, 72, 198–203. [Google Scholar]
- Hristova, S.; Zhivkov, A.M. Montmorillonite colloid plates with adsorbed cytochrome c: In vitro cytotoxic effect on colon cancer cell culture. Cancer Nanotechnol. 2021, 12, 23. [Google Scholar] [CrossRef]
- Santra, S.; Kaittanis, C.; Perez, J.M. Cytochrome c encapsulating theranostic nanoparticles: A novel bifunctional system for targeted delivery of therapeutic membrane-impermeable proteins to tumors and imaging of cancer therapy. Mol. Pharm. 2010, 7, 1209–1222. [Google Scholar] [CrossRef] [Green Version]
- Ng, D.; Fahrer, J.; Wu, Y.; Eisele, K.; Kuan, S.; Barth, H.; Weil, T. Efficient delivery of p53 and cytochrome c by supramolecular assembly of a dendritic multi-domain delivery system. Adv. Healthc. Mater. 2013, 2, 1620–1629. [Google Scholar] [CrossRef]
- Malekigorji, M.; Hoskins, C.; Curtis, T.; Enhancement, G.V. of the cytotoxic effect of anticancer agent by cytochrome c functionalized hybrid nano-particles in hepatocellular cancer cells. J. Nanomed. Res. 2014, 1, 1–8. [Google Scholar]
- Méndez, J.; Morales Cruz, M.; Delgado, Y.; Figueroa, C.M.; Orellano, E.A.; Morales, M.; Monteagudo, A.; Griebenow, K. Delivery of chemically glycosylated cytochrome c immobilized in mesoporous silica nanoparticles induces apoptosis in HeLa cancer cells. Mol. Pharm. 2013, 11, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Koo, A.; Min, K.; Lee, H.; Jegal, J.; Lee, J.; Lee, S. Calcium carbonate mineralized nanoparticles as an intracellular transporter of cytochrome c for cancer therapy. Chem. Asian J. 2015, 10, 2380–2387. [Google Scholar] [CrossRef] [PubMed]
- Al-Shakarchi, W.; Alsuraifi, A.; Abed, M.; Abdullah, M.; Richardson, A.; Curtis, A.; Hoskins, C. Combined effect of anticancer agents and cytochrome C decorated hybrid nanoparticles for liver cancer therapy. Pharmaceutics 2018, 10, 48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macone, A.; Masciarelli, S.; Palombarini, F.; Quaglio, D.; Boffi, A.; Trabuco, M.C.; Baiocco, P.; Fazi, F.; Bonamore, A. Ferritin nanovehicle for targeted delivery of cytochrome C to cancer cells. Sci. Rep. 2019, 9, 11749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.; Lee, W.; Park, S.; Choi, D.; Kim, S.; Park, N. Reversibly pH-responsive gold nanoparticles and their applications for photothermal cancer therapy. Sci. Rep. 2019, 9, 20180. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhang, F.; Wen, H.; Shi, W.; Huang, Q.; Huang, Y.; Xie, J.; Li, P.; Chen, J.; Qin, L.; et al. Tumor- and mitochondria-targeted nanoparticles eradicate drug resistant lung cancer through mitochondrial pathway of apoptosis. J. Nanobiotechnol. 2020, 18, 8. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Y.; Li, Y.; Zhang, L.; Jiang, H.; Tao, J. Zhu Gold nanoparticle-guarded large-pore mesoporous silica nanocomposites for delivery and controlled release of cytochrome c. J. Colloid Interface Sci. 2021, 589, 34–44. [Google Scholar] [CrossRef]
- Eskin, B. Light Scattering by Polymer Solutions and Macromolecule Properties; Nauka: Moscow, Russia, 1986. [Google Scholar]
- van de Hulst, H. Light Scattering by Small Particles; John Wiley: New York, NY, USA, 1957. [Google Scholar]
- Stoylov, S. Colloid Electro-Optics–Theory, Techniques and Applications; Acad. Press: London, UK, 1991. [Google Scholar]
- Dukhin, S.; Deryagin, B. Electrophoresis; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Hunter, R. Zeta Potential in Colloid Science; Academic press: London, UK, 1981. [Google Scholar]
- Dolinsky, T.; Nielsen, J.; McCammon, J.; Baker, N.A. PDB2PQR: An automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004, 32, W665–W667. [Google Scholar] [CrossRef]
- Li, H.; Robertson, A.; Jensen, J. Very fast empirical prediction and rationalization of protein pKa values. Proteins Struct. Funct. Bioinform. 2005, 61, 704–721. [Google Scholar] [CrossRef]
- Pettersen, E.; Goddard, T.; Huang, C.; Couch, G.; Greenblatt, D.; Meng, E.; Ferrin, T. UCSF Chimera–A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [Green Version]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hristova, S.H.; Zhivkov, A.M. Protein–Mineral Composite Particles with Logarithmic Dependence of Anticancer Cytotoxicity on Concentration of Montmorillonite Nanoplates with Adsorbed Cytochrome c. Pharmaceutics 2023, 15, 386. https://doi.org/10.3390/pharmaceutics15020386
Hristova SH, Zhivkov AM. Protein–Mineral Composite Particles with Logarithmic Dependence of Anticancer Cytotoxicity on Concentration of Montmorillonite Nanoplates with Adsorbed Cytochrome c. Pharmaceutics. 2023; 15(2):386. https://doi.org/10.3390/pharmaceutics15020386
Chicago/Turabian StyleHristova, Svetlana H., and Alexandar M. Zhivkov. 2023. "Protein–Mineral Composite Particles with Logarithmic Dependence of Anticancer Cytotoxicity on Concentration of Montmorillonite Nanoplates with Adsorbed Cytochrome c" Pharmaceutics 15, no. 2: 386. https://doi.org/10.3390/pharmaceutics15020386
APA StyleHristova, S. H., & Zhivkov, A. M. (2023). Protein–Mineral Composite Particles with Logarithmic Dependence of Anticancer Cytotoxicity on Concentration of Montmorillonite Nanoplates with Adsorbed Cytochrome c. Pharmaceutics, 15(2), 386. https://doi.org/10.3390/pharmaceutics15020386







