The Effect of Particle Shape on the Compaction of Realistic Non-Spherical Particles—A Multi-Contact DEM Study
Abstract
:1. Introduction
2. Theory
2.1. Hertz–Mindlin Contact Model
2.2. Multi-Contact Adhesive Elastic–Plastic Model
2.3. Bonded Multi-Sphere Model (BMS)
2.4. Conventional Multi-Sphere Model (CMS)
3. DEM Simulations of the Uniaxial Compression of a Single Rubber Sphere
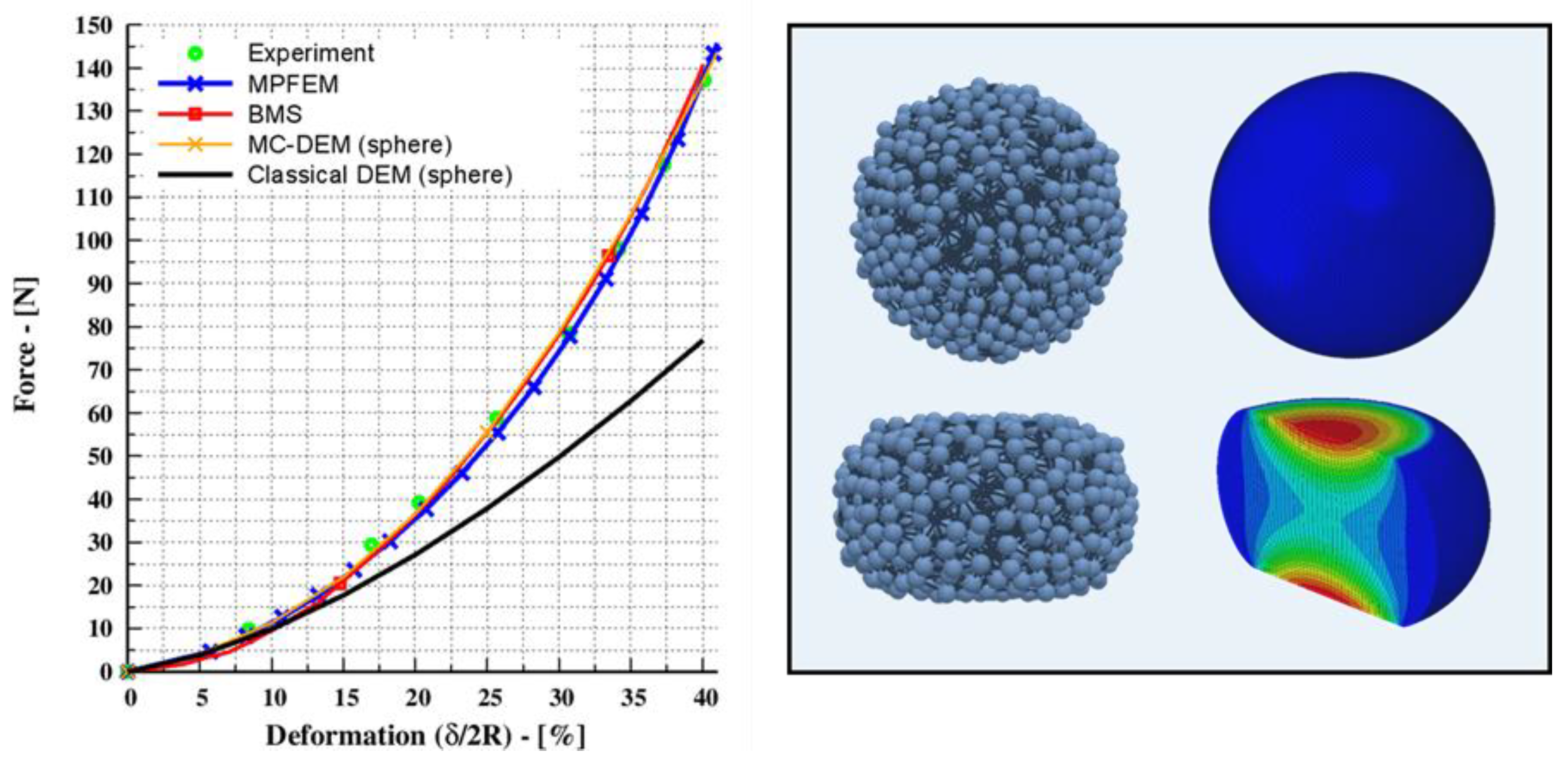
3.1. The Bonded Multi-Sphere Approach (BMS) and the Multiple-Particle Finite Element Method (MPFEM)
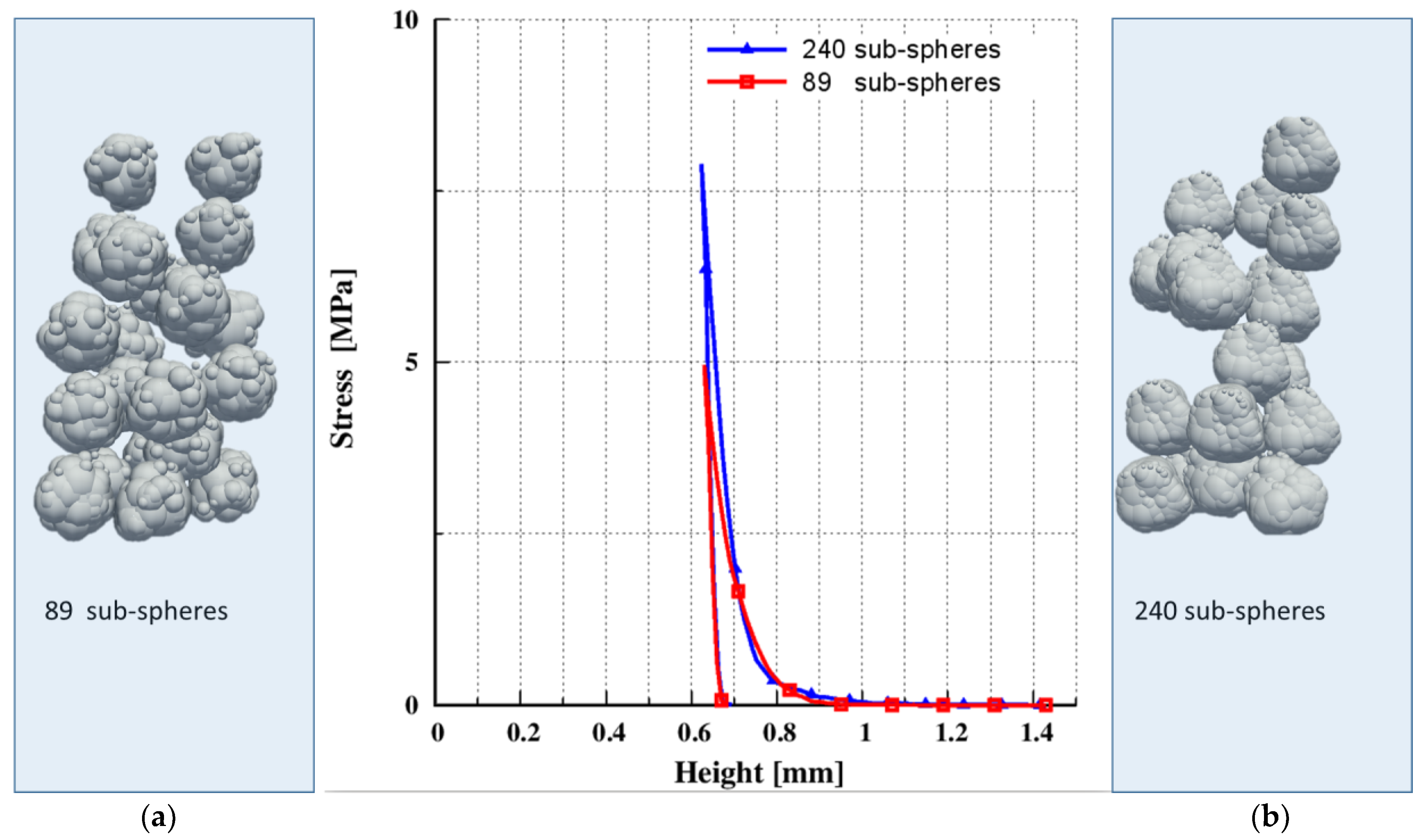
3.2. Sensitivity Analysis of BMS and MPFEM Approach
3.3. The Conventional Multi-Sphere (CMS)
4. Realistic Particle Modeling with the CMS and BMS Approach
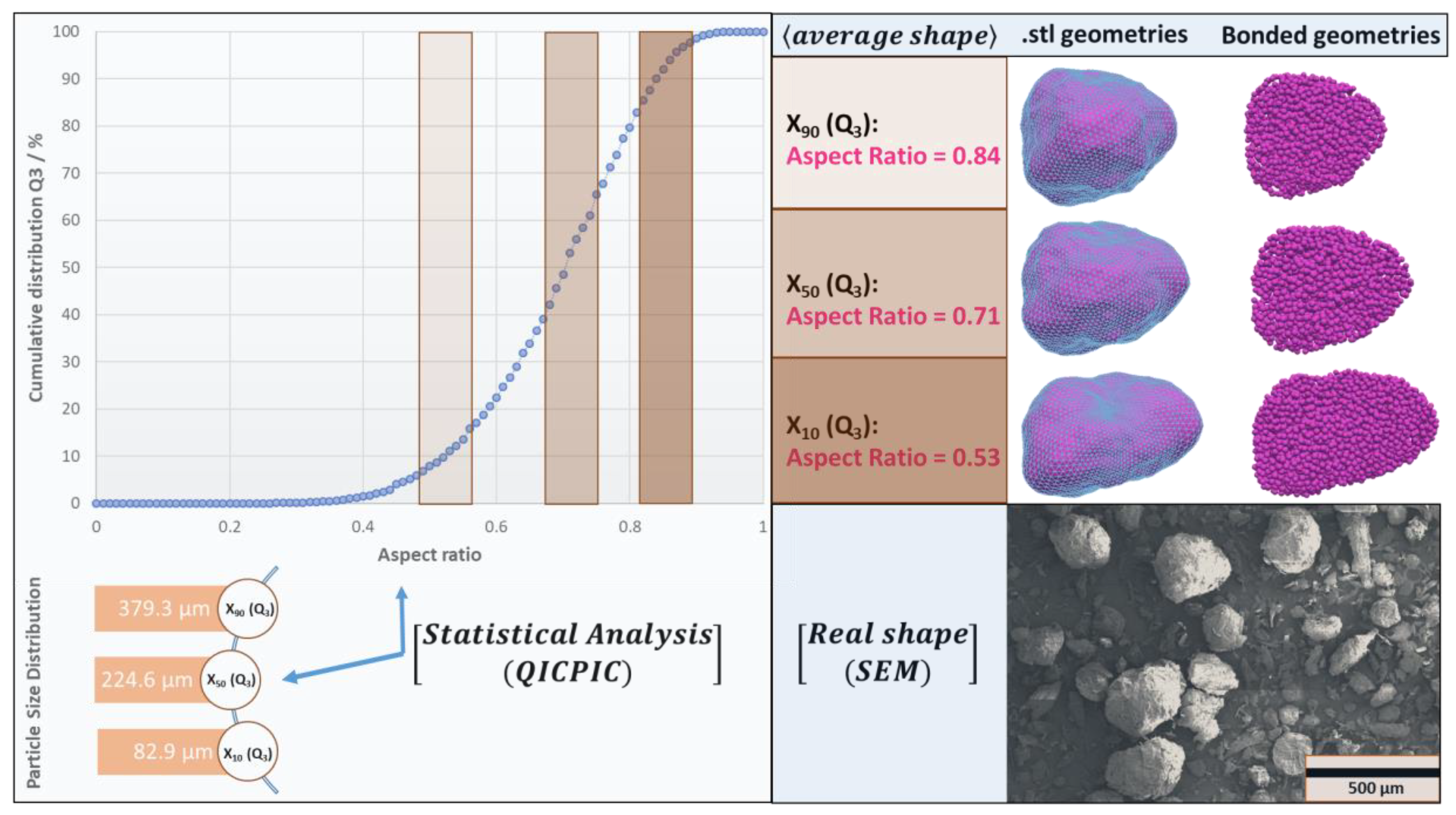
4.1. Materials
4.2. Experimental Methods
4.3. Numerical Example with the CMS Approach
4.4. Modeling Compaction of Avicel® PH 200 with BMS Approach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- He, Y.; Evans, T.J.; Shen, Y.S.; Yu, A.B.; Yang, R.Y. Discrete modelling of the compaction of non-spherical particles using a multi-sphere approach. Miner. Eng. 2018, 117, 108–116. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, F.; Xu, N.W.; Liu, Y.; Xu, Y.J.G.M. A composite particle model for non-spherical particles in DEM simulations. Granul. Matter 2015, 17, 763–774. [Google Scholar] [CrossRef]
- Giannis, K.; Schilde, C.; Finke, J.H.; Kwade, A. Modeling of high-density compaction of pharmaceutical tablets using multi-contact discrete element method. Pharmaceutics 2021, 13, 2194. [Google Scholar] [CrossRef]
- Grohn, P.; Weis, D.; Thommes, M.; Heinrich, S.; Antonyuk, S. Contact Behavior of Microcrystalline Cellulose Pellets Depending on their Water Content. Chem. Eng. Technol. 2020, 43, 887–895. [Google Scholar] [CrossRef] [Green Version]
- Wensrich, C.M.; Katterfeld, A. Rolling friction as a technique for modelling particle shape in DEM. Powder Technol. 2012, 217, 409–417. [Google Scholar] [CrossRef]
- Dosta, M.; Costa, C.; Al-Qureshi, H. Numerical investigation of compaction of deformable particles with bonded-particle model. In Proceedings of the 8th International Conference on Micromechanics on Granular Media, Montpellier, France, 3–7 July 2017; Volume 140, p. 15021. [Google Scholar]
- Jiménez-Herrera, N.; Barrios, G.K.; Tavares, L.M. Comparison of breakage models in DEM in simulating impact on particle beds. Adv. Powder Technol. 2018, 29, 692–706. [Google Scholar] [CrossRef]
- Shi, C.; Li, D.J.; Xu, W.Y.; Wang, R. Discrete element cluster modeling of complex mesoscopic particles for use with the particle flow code method. Granul. Matter 2015, 17, 377–387. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Kloss, C.; Pirker, S.; Ooi, J.Y.; Papanicolopulos, S.A. Influence of various DEM shape representation methods on packing and shearing of granular assemblies. Granul. Matter 2021, 23, 26. [Google Scholar] [CrossRef]
- Höhner, D.; Wirtz, S.; Kruggel-Emden, H.; Scherer, V. Comparison of the multi-sphere and polyhedral approach to simulate non-spherical particles within the discrete element method: Influence on temporal force evolution for multiple contacts. Powder Technol. 2011, 208, 643–656. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, W.Y.; Liu, Q.Y.; Liu, Q.Y.; Meng, Q.X. A novel non-overlapping approach to accurately represent 2D arbitrary particles for DEM modelling. J. Cent. South Univ. 2017, 24, 190–202. [Google Scholar] [CrossRef]
- Podlozhnyuk, A.; Pirker, S.; Kloss, C. Efficient implementation of superquadric particles in discrete element method within an open-source framework. Comput. Part Mech. 2017, 4, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Irazábal, J.; Salazar, F.; Oñate, E. Numerical modelling of granular materials with spherical discrete particles and the bounded rolling friction model. Application to railway ballast. Comput. Geotech. 2017, 85, 220–229. [Google Scholar] [CrossRef]
- Benjamin, N.; Thomas, L.; Meinhard, K. Polyhedral particles for the discrete element method. Granul. Matter 2013, 15, 85–93. [Google Scholar]
- Liu, Z.; Ma, H.; Zhao, Y. CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed. Energies 2021, 14, 4939. [Google Scholar] [CrossRef]
- Eliáš, J. Simulation of railway ballast using crushable polyhedral particles. Powder Technol. 2014, 264, 458–465. [Google Scholar] [CrossRef]
- O’Sullivan, C. Particulate Discrete Element Modelling: A Geomechanics Perspective; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Thornton, C. Granular dynamics, contact mechanics and particle system simulations. A DEM study. In Particle Technology Series; Springer: Cham, Switzerland; New York, NY, USA, 2015; Volume 24. [Google Scholar]
- Giannis, K.; Schilde, C.; Finke, J.H.; Kwade, A.; Celigueta, M.A.; Taghizadeh, K.; Luding, S. Stress based multi-contact model for discrete-element simulations. Granul. Matter 2021, 23, 17. [Google Scholar] [CrossRef]
- Brodu, N.; Dijksman, J.A.; Behringer, R.P. Multiple-contact discrete-element model for simulating dense granular media. Phys. Rev. E 2015, 91, 032201. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, M.; Cuitiño, A.M. A nonlocal contact formulation for confined granular systems. J. Mech. Phys. Solids 2012, 60, 333–350. [Google Scholar] [CrossRef] [Green Version]
- Schramm, M.; Tekeste, M.Z.; Plouffe, C.; Harby, D. Estimating bond damping and bond Young’s modulus for a flexible wheat straw discrete element method model. Biosyst. Eng. 2019, 186, 349–355. [Google Scholar] [CrossRef]
- Guo, Y.; Wassgren, C.; Hancock, B.; Ketterhagen, W.; Curtis, J.J.P.T. Validation and time step determination of discrete element modeling of flexible fibers. Powder Technol. 2013, 249, 386–395. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. In Band 92; De Gruyter: Berlin, Germany, 2021; pp. 156–171. [Google Scholar]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granul. Matter 2008, 10, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Thakur, S.C. Mesoscopic Discrete Element Modelling of Cohesive Powders for Bulk Handling Applications. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2014. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Xia, Y.; Lai, Z.; Westover, T.; Klinger, J.; Huang, H.; Chen, Q. Discrete element modeling of deformable pin-ewood chips in cyclic loading test. Powder Technol. 2019, 345, 1–14. [Google Scholar] [CrossRef]
- Chen, X.; Peng, D.; Morrissey, J.P.; Ooi, J.Y. A comparative assessment and unification of bond models in DEM simulations. Granul. Matter 2022, 24, 29. [Google Scholar] [CrossRef]
- Parteli, E.J. DEM simulation of particles of complex shapes using the multisphere method: Application for additive manufacturing. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2013; Volume 1542, pp. 185–188. [Google Scholar]
- Saeed, M.K.; Siraj, M.S. Mixing study of non-spherical particles using DEM. Powder Technol. 2019, 344, 617–627. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Rickelt, S.; Wirtz, S.; Scherer, V. A study on the validity of the multi-sphere Discrete Element Method. Powder Technol. 2008, 188, 153–165. [Google Scholar] [CrossRef]
- Amberger, S.; Friedl, M.; Goniva, C.; Pirker, S.; Kloss, C. Approximation of objects by spheres for multisphere simulations in DEM. In Proceedings of the ECCOMAS-2012, Vienna, Austria, 10–14 September 2012; pp. 5446–5458. [Google Scholar]
- Tatara, Y. Extensive Theory of Force-Approach Relations of Elastic Spheres in Compression and in Impact. J. Eng. Mater. Technol. 1989, 111, 163–168. [Google Scholar] [CrossRef]
- Gethin, D.T.; Lewis, R.W.; Ransing, R.S. A discrete deformable element approach for the compaction of powder systems. Model. Simul. Mater. Sci. Eng. 2002, 11, 101. [Google Scholar] [CrossRef]
- Procopio, A.T.; Zavaliangos, A. Simulation of multi-axial compaction of granular media from loose to high relative densities. J. Mech. Phys. Solids 2005, 53, 1523–1551. [Google Scholar] [CrossRef]
- Agarwal, A.; Gonzalez, M. Contact radius and curvature corrections to the nonlocal contact formulation accounting for multi-particle interactions in elastic confined granular systems. Int. J. Eng. Sci. 2018, 133, 26–46. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, S.; Bier, W. High-order time integration applied to metal powder plasticity. Int. J. Plast. 2008, 24, 17–54. [Google Scholar] [CrossRef]
- Hartmann, P.; Thoeni, K.; Rojek, J. A generalised multi-scale Peridynamics–DEM framework and its application to rigid–soft particle mixtures. Comput. Mech. 2022, 71, 107–126. [Google Scholar] [CrossRef]
- Schomberg, A.K.; Diener, A.; Wünsch, I.; Finke, J.H.; Kwade, A. The use of X-ray microtomography to inves-tigate the microstructure of pharmaceutical tablets: Potentials and comparison to common physical methods. Interna-Tional J. Pharm. X 2021, 3, 100090. [Google Scholar]
- Pourtavakoli, H.; Parteli, E.J.; Pöschel, T. Granular dampers: Does particle shape matter? New J. Phys. 2016, 18, 073049. [Google Scholar] [CrossRef] [Green Version]
- Tamadondar, M.R.; de Martín, L.; Rasmuson, A. Agglomerate breakage and adhesion upon impact with complex-shaped particles. AIChE J. 2019, 65, e16581. [Google Scholar] [CrossRef]
- Mollon, G.; Zhao, J. Fourier-Voronoi-based generation of realistic samples for discrete modelling of granular materials. Granul. Matter 2012, 14, 621. [Google Scholar] [CrossRef]
- Gao, Y.; De Simone, G.; Koorapaty, M. Calibration and verification of DEM parameters for the quantitative simulation of pharmaceutical powder compression process. Powder Technol. 2021, 378, 160–171. [Google Scholar] [CrossRef]
- Pham-Ba, S.; Molinari, J.F. Adhesive wear with a coarse-grained discrete element model. Comput. Methods Appl. Mech. Eng. 2022, 397, 115124. [Google Scholar] [CrossRef]
- Kozhar, S.; Dosta, M.; Antonyuk, S.; Heinrich, S.; Bröckel, U. DEM simulations of amorphous irregular shaped micrometer-sized titania agglomerates at compression. Adv. Powder Technol. 2015, 26, 767–777. [Google Scholar] [CrossRef]




| Parameter | Symbol | Values | Units |
|---|---|---|---|
| Young’s modulus—particle (p) | E | 18.5 | MPa |
| Young’s modulus—particle (w) | E | 1 | GPa |
| Particle density | ρ | 2000 | kg/m3 |
| Poisson’s ratio | ν | 0.46 | - |
| Coefficient of restitution | COR | 0.7 | - |
| Friction coefficient | f | 0.5 | - |
| Bond normal stiffness | N/m3 | ||
| Bond tangential stiffness | N/m3 | ||
| Empirical prefactor | β | 1.71 | - |
| Material | Span (-) | ||||
|---|---|---|---|---|---|
| Avicel® PH 200 | 82.9 | 224.6 | 379.3 | 1.32 | 1541.1 |
| Property | Symbol | Values | Units |
|---|---|---|---|
| Young’s modulus—particle (p) | E | MPa | |
| Young’s modulus—wall (w) | E | MPa | |
| Poisson’s ratio—particle | ν | 0.30 | - |
| Poisson’s ratio—wall | ν | 0.31 | - |
| Coefficient of restitution particle | COR (p-p) | 0.352 | - |
| Coefficient of restitutio—wall | COR (p-w) | 0.352 | - |
| Coefficient of sliding friction—(p-p) | μs(pp) | 0.561 | - |
| Coefficient of sliding friction—(p-w) | μs(pw) | 0.707 | - |
| Coefficient of rolling friction—(p-p) | μr(pp) | 0.3 | - |
| Coefficient of rolling friction—(p-w) | μr(pp) | 0.01 | - |
| Density | ρ | 1541.1 | kg/m3 |
| Property | Symbol | Values | Units |
|---|---|---|---|
| Young’s modulus—particle(p) | E | MPa | |
| Young’s modulus—wall(w) | E | MPa | |
| Poisson’s ratio—particle | ν | 0.30 | - |
| Poisson’s ratio—wall | ν | 0.31 | - |
| Coefficient of restitution particle | COR (p-p) | 0.352 | - |
| Coefficient of restitutio—wall | COR (p-w) | 0.352 | - |
| Coefficient of sliding friction—(p-p) | μs(pp) | 0.561 | - |
| Coefficient of sliding friction—(p-w) | μs(pw) | 0.707 | - |
| Coefficient of rolling friction—(p-p) | μr(pp) | 0.3 | - |
| Coefficient of rolling friction—(p-w) | μr(pp) | 0.01 | - |
| Density | ρ | 1541.1 | kg/m3 |
| Bond normal stiffness | N/m3 | ||
| Bond tangential stiffness | N/m3 | ||
| Empirical prefactor | β | 1.3 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannis, K.; Kwade, A.; Finke, J.H.; Schilde, C. The Effect of Particle Shape on the Compaction of Realistic Non-Spherical Particles—A Multi-Contact DEM Study. Pharmaceutics 2023, 15, 909. https://doi.org/10.3390/pharmaceutics15030909
Giannis K, Kwade A, Finke JH, Schilde C. The Effect of Particle Shape on the Compaction of Realistic Non-Spherical Particles—A Multi-Contact DEM Study. Pharmaceutics. 2023; 15(3):909. https://doi.org/10.3390/pharmaceutics15030909
Chicago/Turabian StyleGiannis, Kostas, Arno Kwade, Jan Henrik Finke, and Carsten Schilde. 2023. "The Effect of Particle Shape on the Compaction of Realistic Non-Spherical Particles—A Multi-Contact DEM Study" Pharmaceutics 15, no. 3: 909. https://doi.org/10.3390/pharmaceutics15030909
APA StyleGiannis, K., Kwade, A., Finke, J. H., & Schilde, C. (2023). The Effect of Particle Shape on the Compaction of Realistic Non-Spherical Particles—A Multi-Contact DEM Study. Pharmaceutics, 15(3), 909. https://doi.org/10.3390/pharmaceutics15030909








