The Key Role of Wettability and Boundary Layer in Dissolution Rate Test
Abstract
1. Introduction
2. Materials and Methods
2.1. Drugs
2.2. Wettability
2.3. Particle Size
2.4. DRT Test
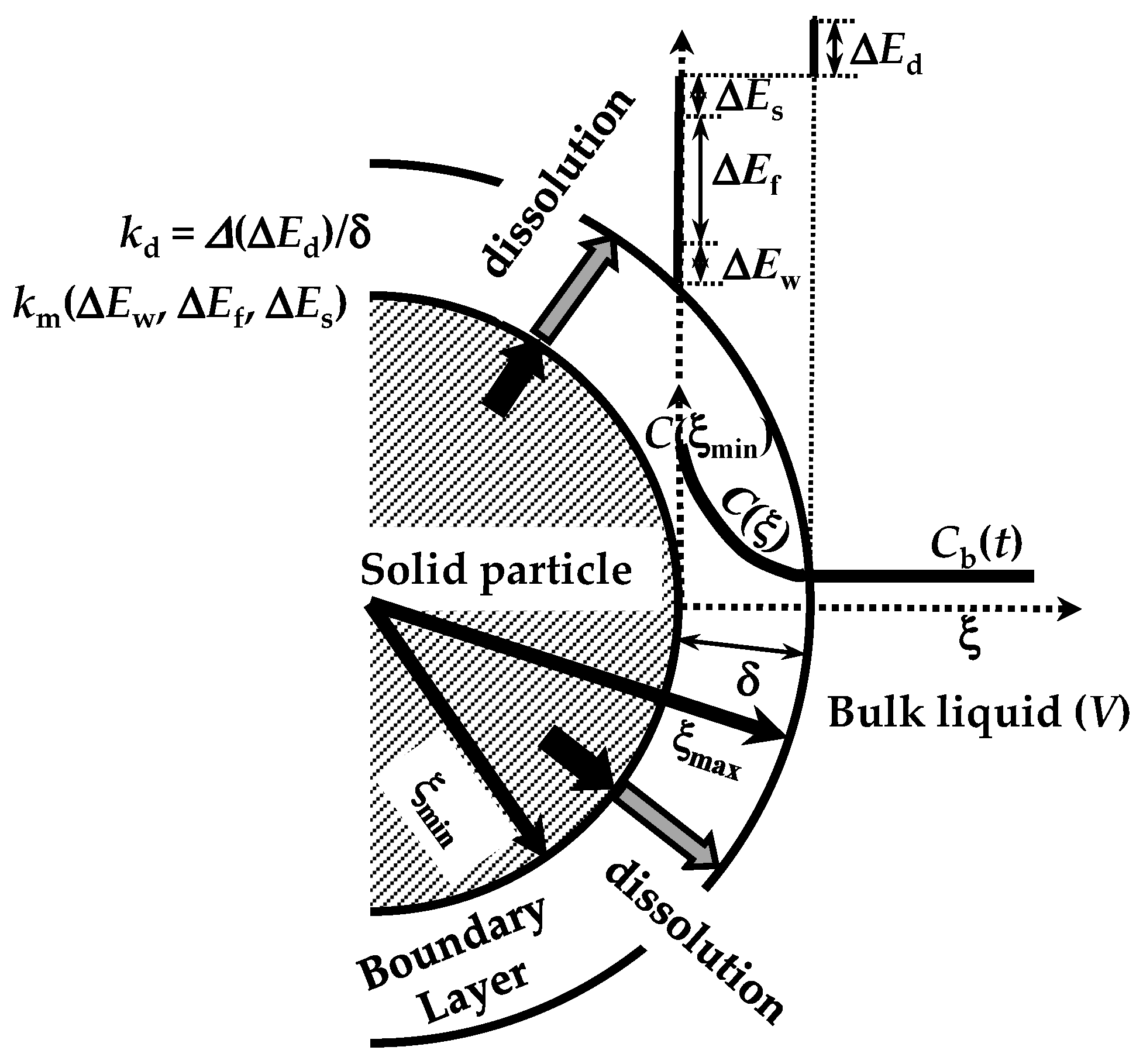
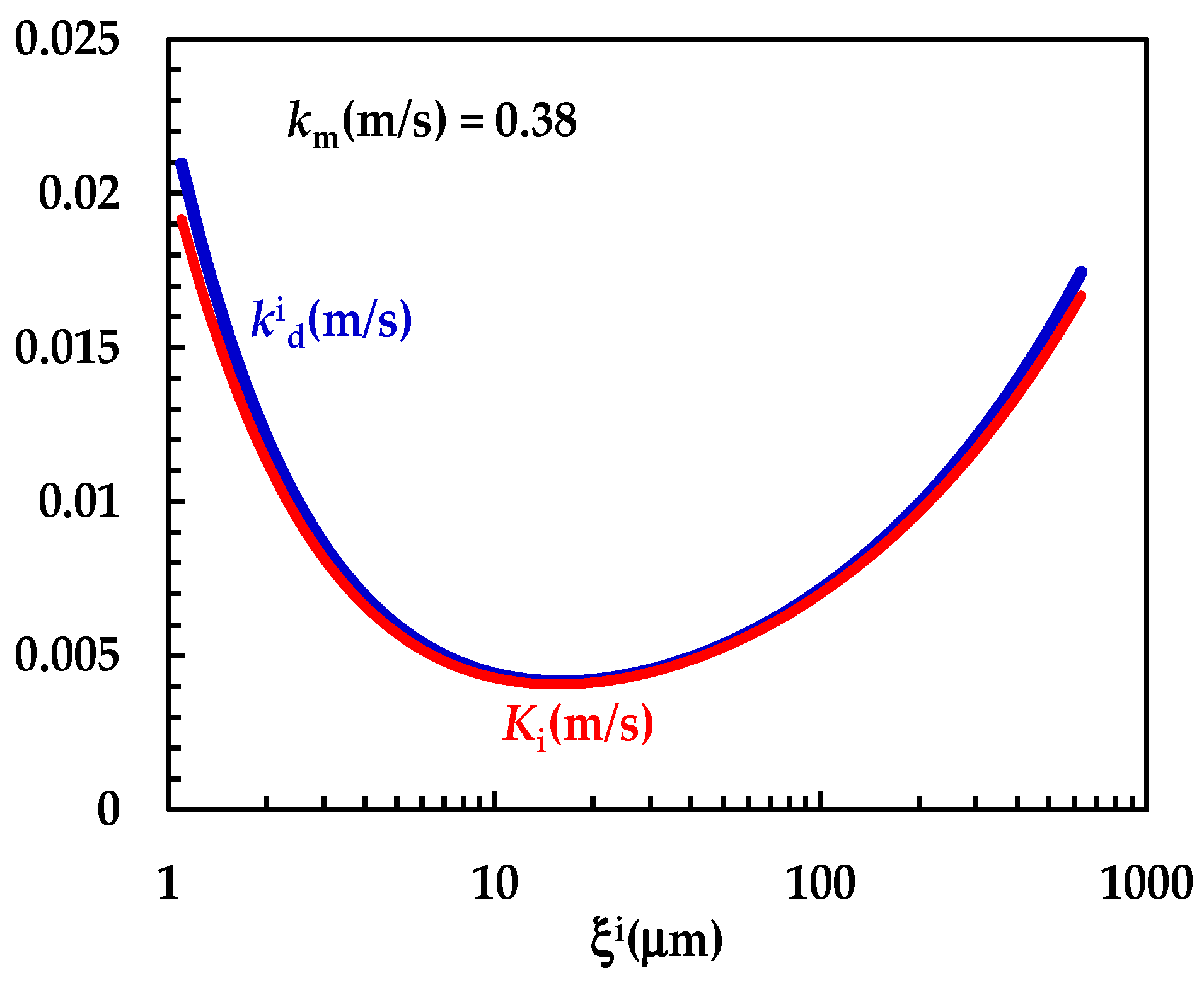
3. Mathematical Modelling
4. Results and Discussion
4.1. Microscopic Results
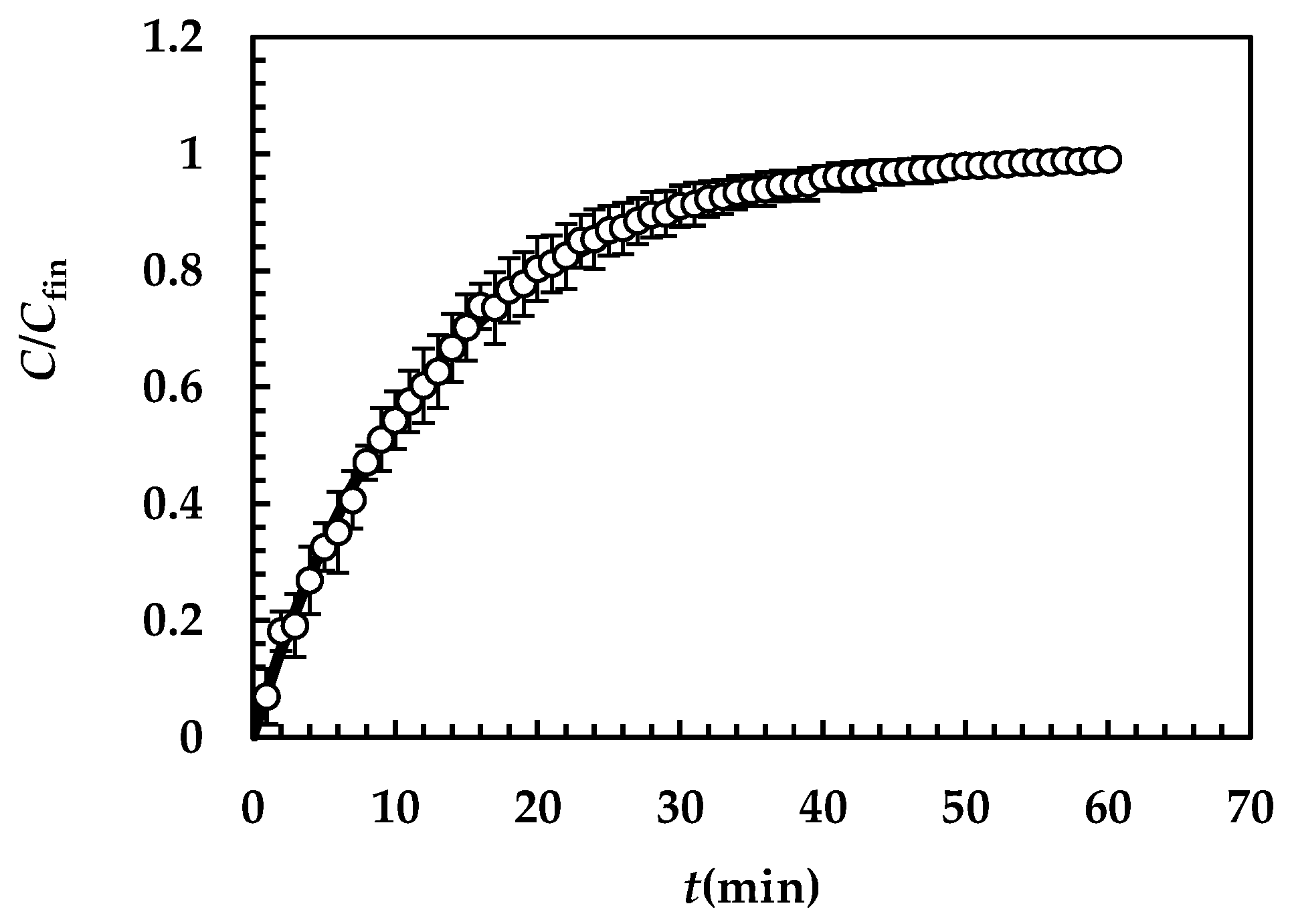
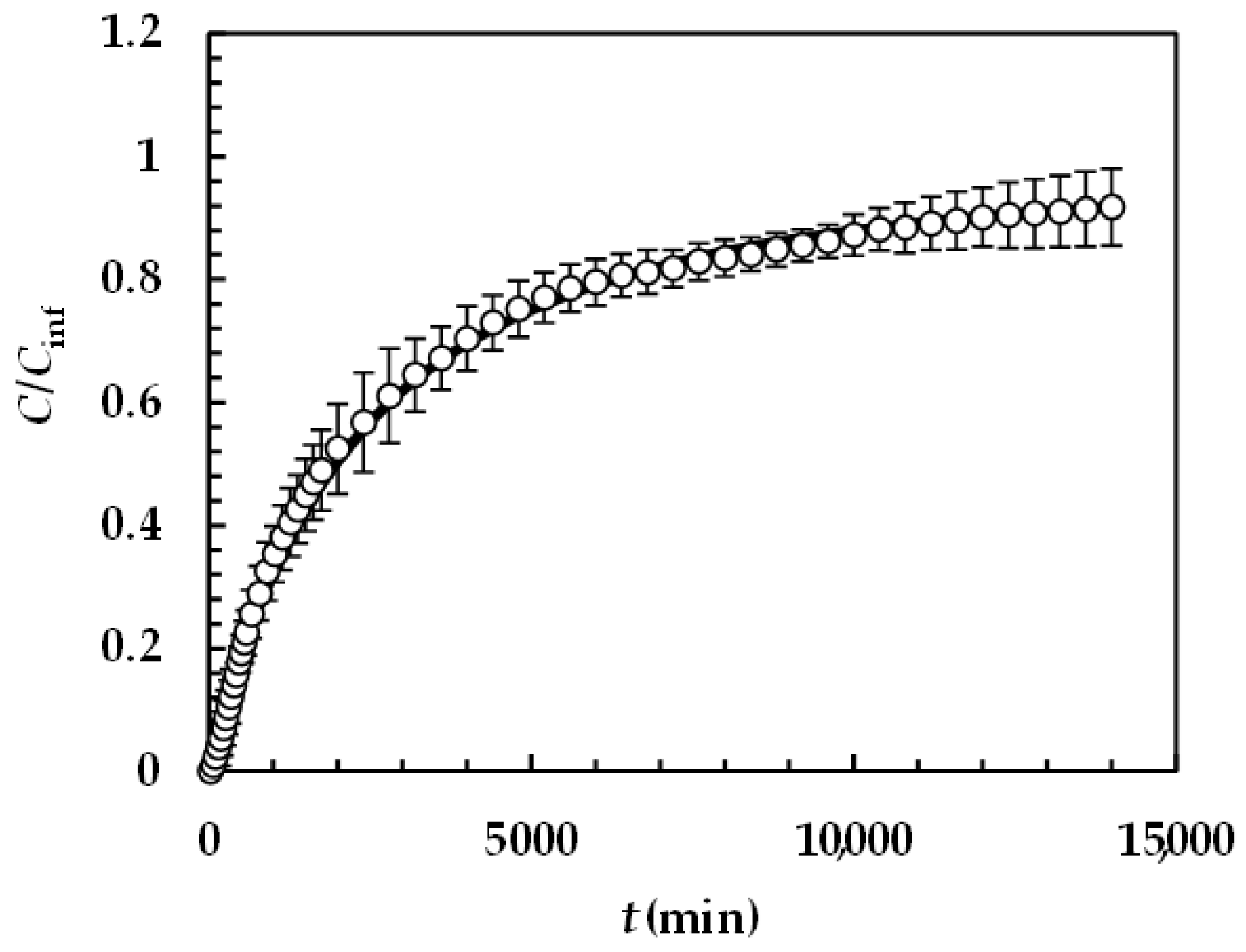
4.2. Macroscopic Results: Data Fitting
4.2.1. Theophylline
4.2.2. Praziquantel
4.2.3. Comparison Between Drugs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
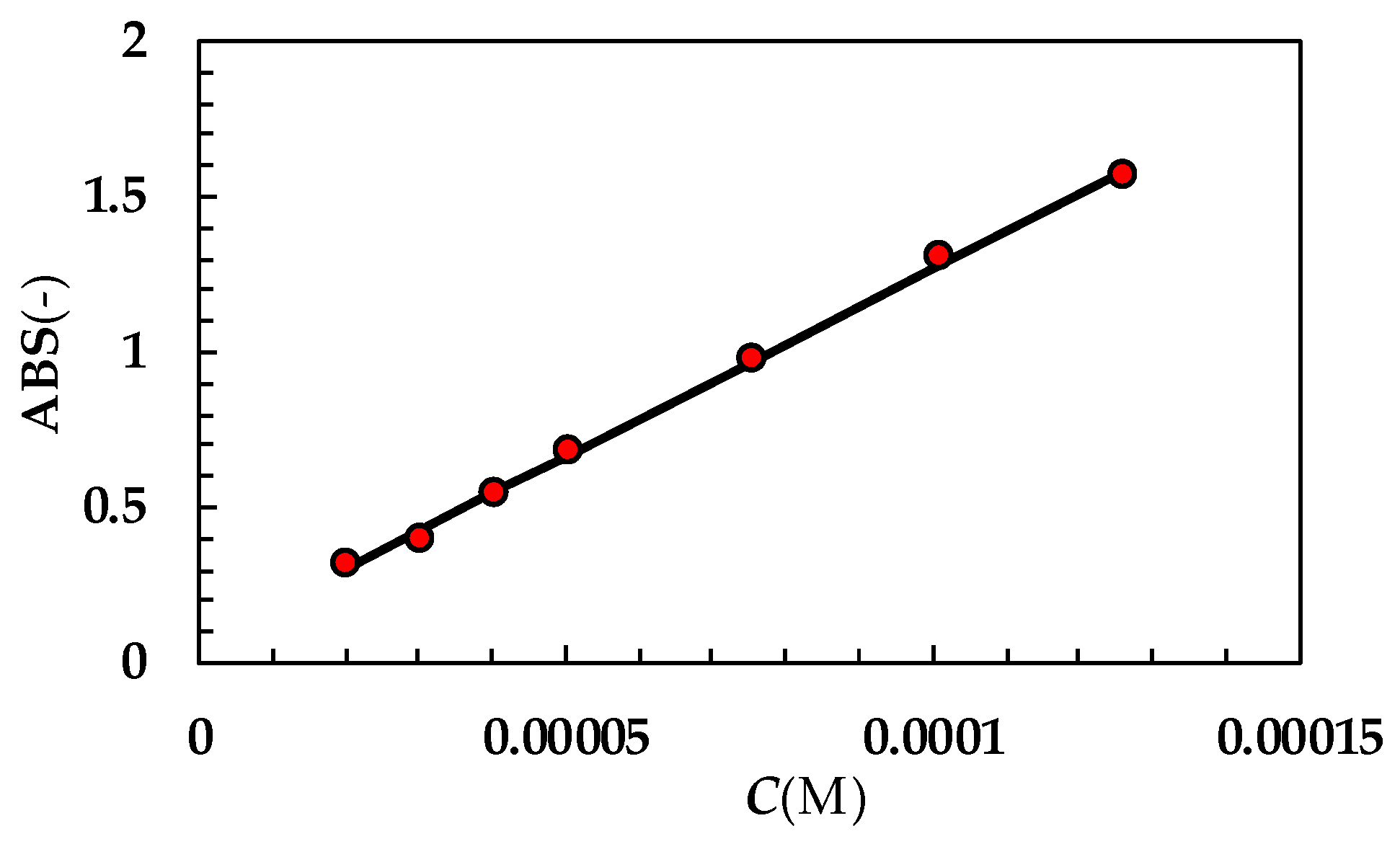
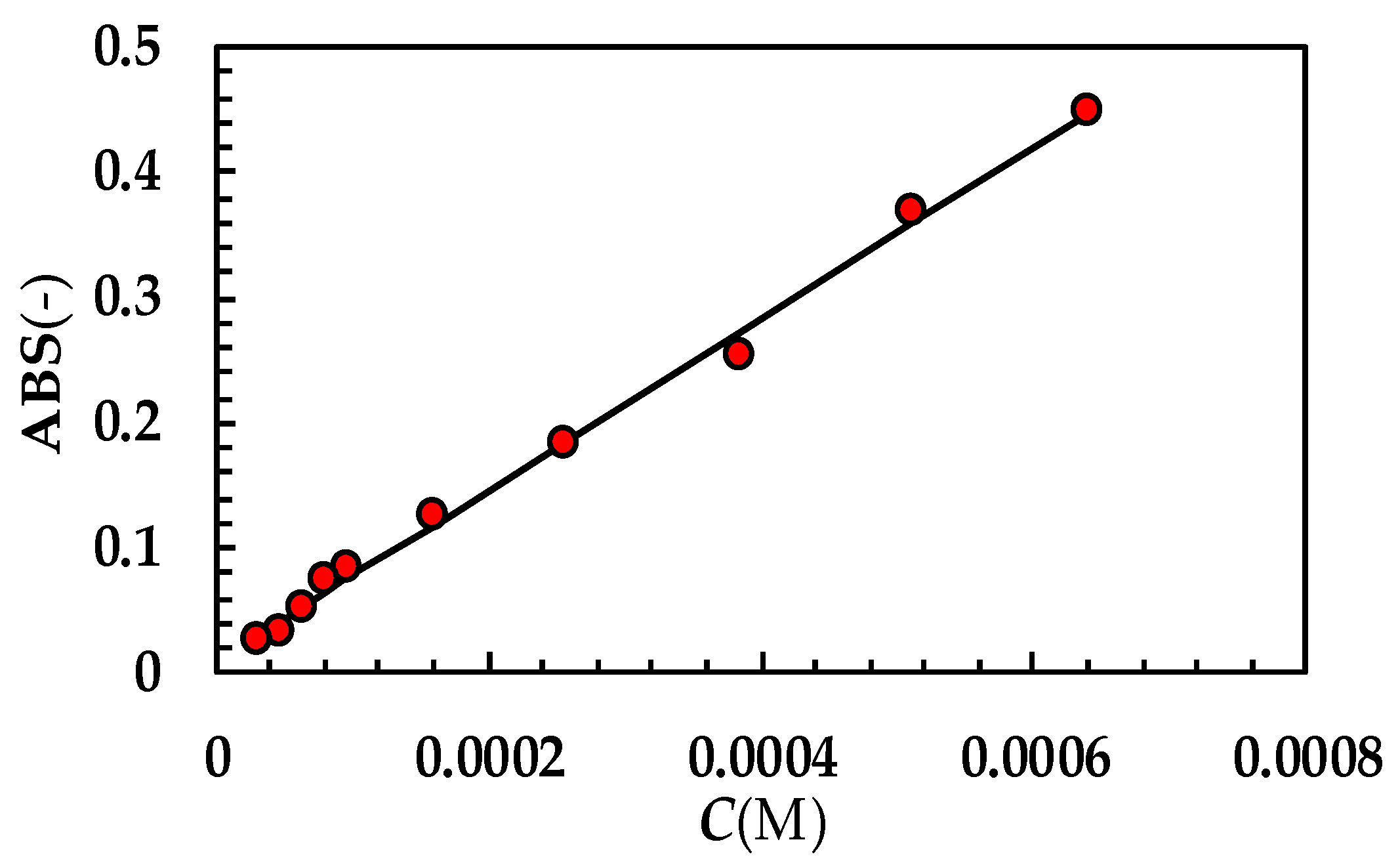
Appendix B
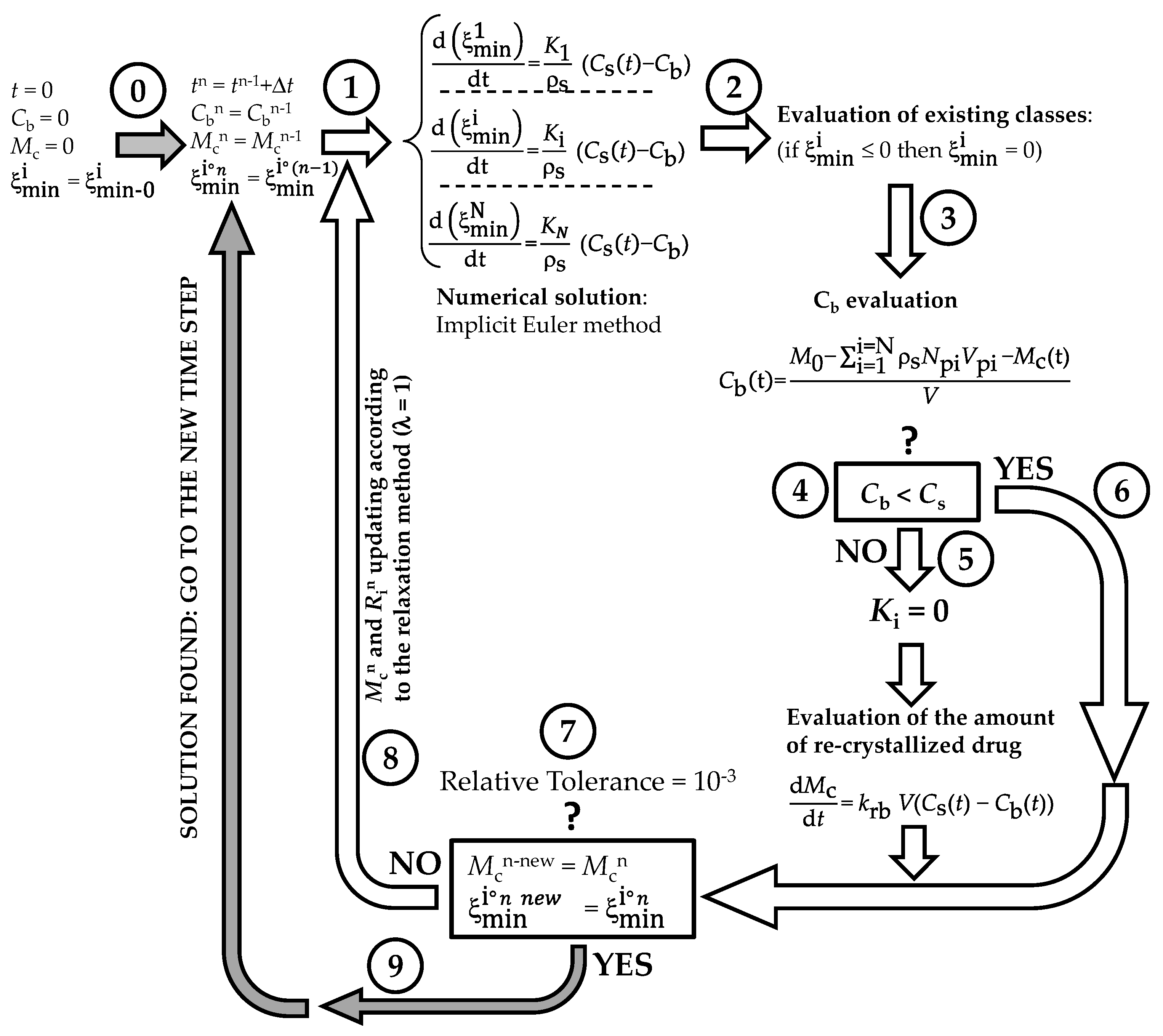
References
- Laitinen, R.; Lahtinen, J.; Silfsten, P.; Vartiainen, E.; Jarho, P.; Ketolainen, J. An optical method for continuous monitoring of the dissolution rate of pharmaceutical powders. J. Pharm. Biomed. Anal. 2010, 52, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Stukelj, J.; Agopov, M.; Yliruusi, J.; Stachan, C.J. Image-based dissolution analysis for tracking the surface stability of amorphous powders. ADMET DMPK 2020, 8, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Kwan, K.C. Oral bioavailability and first pass effects. Drug Metab. Dispos. 1997, 25, 1329–1336. [Google Scholar] [PubMed]
- Naidu, R.; Semple, K.T.; Megharaj, M.; Juhasz, A.L.; Bolan, N.S.; Gupta, S.K.; Clothier, B.E.; Schulin, R. Bioavailability: Definition, assessment and implications for risk assessment. Dev. Soil Sci. 2008, 32, 39–51. [Google Scholar] [CrossRef]
- Loftsson, T.; Brewster, M.E. Pharmaceutical applications of cyclodextrins: Basic science and product development. J. Pharm. Pharmacol. 2010, 62, 1607–1621. [Google Scholar] [CrossRef]
- Davis, M.; Walker, G. Recent strategies in spray drying for the enhanced bioavailability of poorly water-soluble drugs. J. Contr. Rel. 2018, 269, 110–127. [Google Scholar] [CrossRef]
- Gigliobianco, M.R.; Casadidio, C.; Censi, R.; Di Martino, P. Nanocrystals of Poorly Soluble Drugs: Drug Bioavailability and Physicochemical Stability. Pharmaceutics 2018, 10, 134. [Google Scholar] [CrossRef]
- Bertoni, S.; Albertini, B.; Passerini, N. Spray Congealing: An Emerging Technology to Prepare Solid Dispersions with Enhanced Oral Bioavailability of Poorly Water Soluble Drugs. Molecules 2019, 24, 3471. [Google Scholar] [CrossRef]
- Hixson, W.; Crowell, J.H. Dependence of reaction velocity upon surface and agitation I. Theoretical consideration. Ind. Eng. Chem. 1931, 23, 923–931. [Google Scholar] [CrossRef]
- Hixson, W.; Crowell, J.H. Dependence of reaction velocity upon surface and agitation II. Experimental procedure in study surface. Ind. Eng. Chem. 1931, 23, 1002–1009. [Google Scholar] [CrossRef]
- Hixson, W.; Crowell, J.H. Dependence of reaction velocity upon surface and agitation III. Experimental procedure in study of agitation. Ind. Eng. Chem. 1931, 23, 1160–1169. [Google Scholar] [CrossRef]
- Niebergall, P.J.; Milosovich, G. Dissolution of particles under conditions of rapid agitation. J. Pharm. Sci. 1963, 52, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, V.P.; Brown, K.F. Dissolution profile in relation to initial particle distribution. J. Pharm. Sci. 1975, 64, 1192–1195. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, V.P.; Brown, K.F. Size distribution effects in multiparticulate dissolution. J. Pharm. Sci. 1975, 64, 1981–1986. [Google Scholar] [CrossRef]
- Pedersen, V.P.; Brown, K.F. General class of multiparticulate dissolution models. J. Pharm. Sci. 1977, 66, 1435–1438. [Google Scholar] [CrossRef]
- Pedersen, V.P.; Myrick, J.W. Versatile kinetic approach to analysis of dissolution data. J. Pharm. Sci. 1978, 67, 1450–1455. [Google Scholar] [CrossRef]
- Hsu, J.P.; Liu, B.T. Dissolution of solid particles in liquids: A reaction-diffusion model. Colloids Surf. 1993, 69, 229–238. [Google Scholar] [CrossRef]
- Grassi, M.; Grassi, G.; Lapasin, R.; Colombo, I. Understanding Drug Release and Absorption Mechanisms: A Physical and Mathematical Approach; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Guo, N.; Hou, B.; Wang, N.; Xiao, Y.; Hiang, J.; Guo, Y.; Zong, S.; Hao, H. In situ monitoring and modeling of the solution-mediated polymorphic transformation of rifampicin: From form II to form I. J. Pharm. Sci. 2018, 107, 344–352. [Google Scholar] [CrossRef]
- Abrami, M.; Grassi, L.; di Vittorio, R.; Hasa, D.; Perissutti, B.; Voinovich, D.; Grassi, G.; Colombo, I.; Grassi, M. Dissolution of an ensemble of differently shaped poly-dispersed drug particles undergoing solubility reduction: Mathematical modelling. ADMET DMPK 2020, 8, 297–313. [Google Scholar] [CrossRef]
- Thormann, D.U.; De Mieri, M.; Neuburger, M.; Verjee, S.; Altmann, P.; Hamburger, M.; Imanidis, G. Mechanism of chemical degradation and determination of solubility by kinetic modeling of the highly unstable sesquiterpene lactone nobilin in different media. J. Pharm. Sci. 2014, 103, 3139–3152. [Google Scholar] [CrossRef]
- Mosharraf, M.; Nyström, C. The effect of particle size and shape on the surface specific dissolution rate of micronized practically insoluble drugs. Int. J. Pharm. 1995, 122, 35–47. [Google Scholar] [CrossRef]
- Hirai, D.; Iwao, Y.; Kimura, S.I.; Noguchi, S.; Itai, S. Mathematical model to analyze the dissolution behaviour of metastable crystals or amorphous drug accompanied with solid-liquid interface reaction. Int. J. Pharm. 2017, 522, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Hsu, S.-Y.; Wu, C.-W. Effects of particle shape in mass-diffusion-controlled dissolution process. Int. Comm. Heat Mass Transf. 2021, 125, 105321. [Google Scholar] [CrossRef]
- Yuan, Q.; Jia, X.; Williams, R.A. Validation of a multi-component digital dissolution model for irregular particles. Powder Technol. 2013, 240, 25–30. [Google Scholar] [CrossRef]
- Hsu, J.P.; Lin, D.L.; Lin, M.J. Dissolution of solid particles in liquids: A surface layer model. Colloids Surf. 1991, 61, 35–47. [Google Scholar] [CrossRef]
- Wang, J.; Flanagan, D.R. General solution for diffusion controlled dissolution of spherical particles 1. Theory. J. Pharm. Sci. 1999, 88, 731–738. [Google Scholar] [CrossRef]
- Hasa, D.; Perissutti, B.; Voinovich, D.; Abrami, M.; Farra, R.; Fiorentino, S.M.; Grassi, G.; Grassi, M. Drug Nanocrystals: Theoretical Background of Solubility Increase and Dissolution Rate Enhancement. Chem. Biochem. Eng. Q. 2014, 28, 247–258. [Google Scholar] [CrossRef]
- Salish, K.; So, C.; Jeong, S.H.; Hou, H.H.; Mao, C. A Refined Thin-Film Model for Drug Dissolution Considering Radial Diffusion–Simulating Powder Dissolution. Pharm. Res. 2024, 41, 947–958. [Google Scholar] [CrossRef]
- D’Arcy, D.M.; Persoons, T. Mechanistic Modelling and Mechanistic Monitoring: Simulation and Shadowgraph Imaging of Particulate Dissolution in the Flow-Through Apparatus. J. Pharm. Sci. 2011, 100, 1102–1115. [Google Scholar] [CrossRef]
- D’Arcy, D.M.; Persoons, T. Understanding the Potential for Dissolution Simulation to Explore the Effects of Medium Viscosity on Particulate Dissolution. AAPS PharmSciTech 2019, 20, 47. [Google Scholar] [CrossRef]
- Abrami, M.; Grassi, M.; Masiello, D.; Pontrelli, G. Dissolution of irregularly-shaped drug particles: Mathematical modelling. Europ. J. Pharm. Biopharm. 2022, 177, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Grassi, M.; Colombo, I.; Lapasin, R. Experimental determination of the theophylline diffusion coefficient in swollen sodium-alginate membranes. J. Contr. Rel. 2001, 76, 93–105. [Google Scholar] [CrossRef] [PubMed]
- Zanolla, D.; Perissutti, B.; Passerini, N.; Chierotti, M.R.; Hasa, D.; Voinovich, D.; Gigli, L.; Demitri, N.; Geremia, S.; Keiser, J.; et al. A new soluble and bioactive polymorph of praziquantel. Eur. J. Pharm. Biopharm. 2018, 127, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Biasin, A.; Pribac, F.; Milcovich, G.; Franceschinis, E.; Hasa, D.; Voinovich, D.; Grassi, G.; Grassi, M.; Abrami, M. Wettability and hydrodynamics key hallmarks on drugs’ dissolution rate. In Proceedings of the XXIII Simposio ADRITELF, Trieste, Italy, 11–13 September 2023; Poster 46. p. 155. [Google Scholar]
- Grüßer, M.; Waugh, D.G.; Lawrence, J.; Langer, N.; Scholz, D. On the Droplet Size and Application of Wettability Analysis for the Development of Ink and Printing Substrates. Langmuir 2019, 35, 12356–12365. [Google Scholar] [CrossRef]
- Bergese, P.; Colombo, I.; Federici, S. Thermodynamics of (nano)interfaces. In Colloidal Foundations of Nanoscience, 2nd ed.; Berti, D., Palazzo, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 12–56. [Google Scholar]
- Wu, S.J. Calculation of interfacial tension in polymer systems. Polym. Sci. C 1971, 34, 19–30. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Neumann, A.W. Contact angle measurement and contact angle interpretation. Adv. Colloid Interface Sci. 1999, 81, 167–249. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Neumann, A.W. Contact angle interpretation in terms of solid surface tension. Colloids Surf. A Physicochem. Eng. Asp. 2000, 161, 31–48. [Google Scholar] [CrossRef]
- de Boer, G.B.J.; de Weerd, C.; Thoenes, D.; Goossens, H.W.J. Laser Diffraction Spectrome-try: Fraunhofer Diffraction Versus Mie Scattering. Part. Charact. 1987, 4, 14–15. [Google Scholar] [CrossRef]
- Tenchov, B.G.; Yanev, T.K. Weibull distribution of particle sizes obtained by uniform random fragmentation. J. Colloid Interface Sci. 1986, 111, 1–7. [Google Scholar] [CrossRef]
- Nogami, H.; Nagai, T.; Yotsuyanagi, T. Dissolution phenomena of organic medicinals involving simultaneous phase changes. Chem. Pharm. Bull. 1969, 17, 499–509. [Google Scholar] [CrossRef][Green Version]
- Chiarappa, G.; Piccolo, A.; Colombo, I.; Hasa, D.; Voinovich, D.; Moneghini, M.; Grassi, G.; Farra, R.; Abrami, M.P.; Posocco, P.; et al. Exploring the Shape Influence on Melting Temperature, Enthalpy, and Solubility of Organic Drug Nanocrystals by a Thermodynamic Model. Cryst. Growth Des. 2017, 17, 4072–4083. [Google Scholar] [CrossRef]
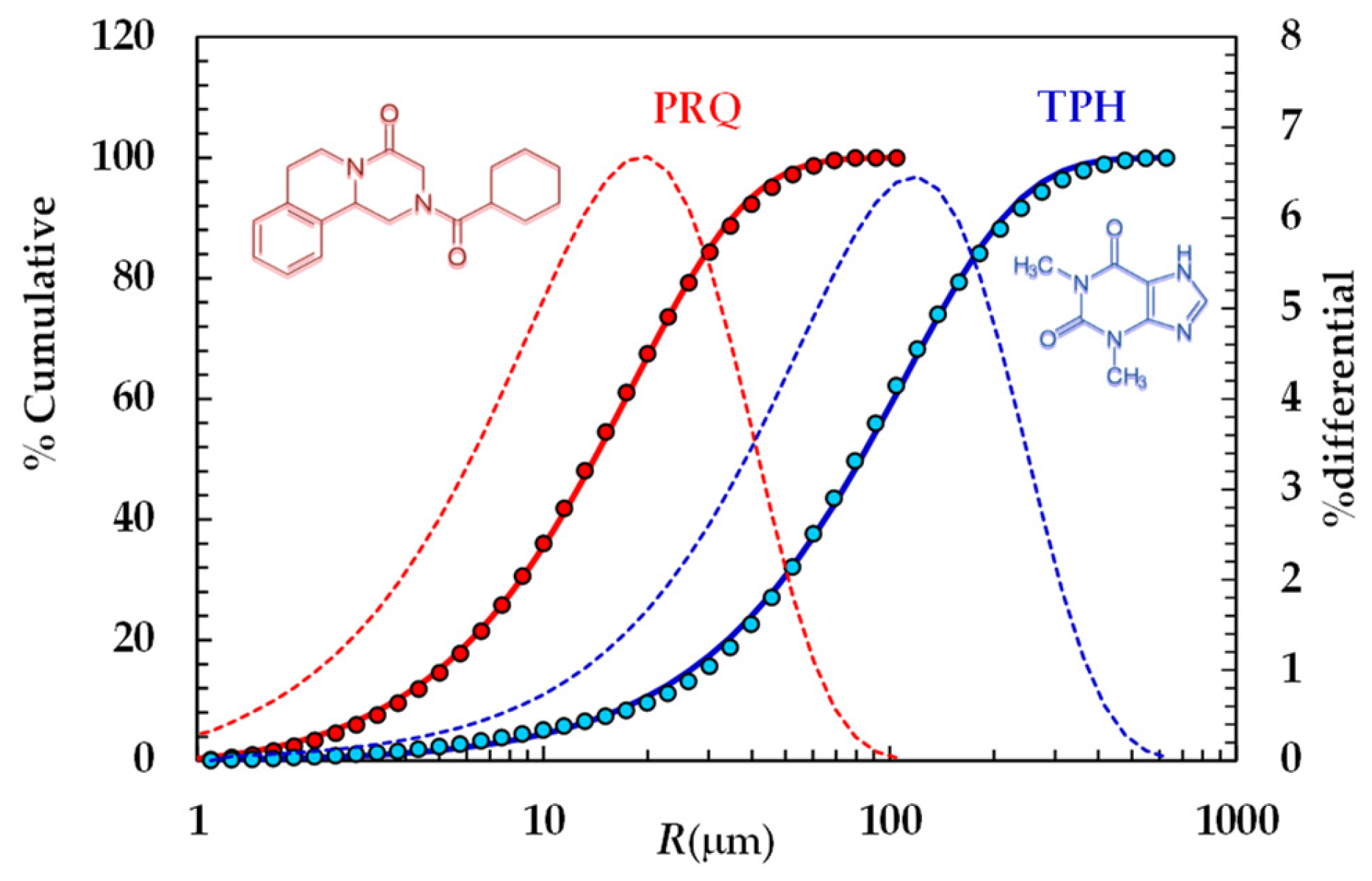



| Liquid | θTPH | θPRQ |
|---|---|---|
| H2O | 49 ± 2.1 | 71.6 ± 1.3 |
| CH3NO | 20.5 ± 4.1 | 41.6 ± 7.6 |
| (CH3)2SO | 14.4 ± 2.2 | 25.7 ± 3.0 |
| CH2I2 | 41.4 ± 1.2 | 18.0 ± 2.3 |
| Liquid | γlv (mJ/m2) | γlvp (mJ/m2) | γlvd (mJ/m2) | Polarity% |
|---|---|---|---|---|
| H2O | 71.8 | 51.0 | 21.8 | 70.0 |
| CH3NO | 68.0 | 19.0 | 39.0 | 32.7 |
| (CH3)2SO | 44.0 | 8.0 | 36.0 | 18.2 |
| CH2I2 | 50.8 | 6.7 | 44.1 | 13.2 |
| Drug | γsv (mJ/m2) | γsvp (mJ/m2) | γsvd (mJ/m2) | Polarity% |
|---|---|---|---|---|
| Theophylline | 55.1 | 27.8 | 27.2 | 50.6 |
| Praziquantel | 50.6 | 38.0 | 12.6 | 24.9 |
| Drug | Rmin (μm) | ϕ (μm) | φ (-) | RA (μm) |
|---|---|---|---|---|
| Theophylline | 0.48 | 218.9 | 1.266 | 109.6 |
| Praziquantel | 0.79 | 35.3 | 1.256 | 18.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biasin, A.; Pribac, F.; Franceschinis, E.; Cortesi, A.; Grassi, L.; Voinovich, D.; Colombo, I.; Grassi, G.; Milcovich, G.; Grassi, M.; et al. The Key Role of Wettability and Boundary Layer in Dissolution Rate Test. Pharmaceutics 2024, 16, 1335. https://doi.org/10.3390/pharmaceutics16101335
Biasin A, Pribac F, Franceschinis E, Cortesi A, Grassi L, Voinovich D, Colombo I, Grassi G, Milcovich G, Grassi M, et al. The Key Role of Wettability and Boundary Layer in Dissolution Rate Test. Pharmaceutics. 2024; 16(10):1335. https://doi.org/10.3390/pharmaceutics16101335
Chicago/Turabian StyleBiasin, Alice, Federico Pribac, Erica Franceschinis, Angelo Cortesi, Lucia Grassi, Dario Voinovich, Italo Colombo, Gabriele Grassi, Gesmi Milcovich, Mario Grassi, and et al. 2024. "The Key Role of Wettability and Boundary Layer in Dissolution Rate Test" Pharmaceutics 16, no. 10: 1335. https://doi.org/10.3390/pharmaceutics16101335
APA StyleBiasin, A., Pribac, F., Franceschinis, E., Cortesi, A., Grassi, L., Voinovich, D., Colombo, I., Grassi, G., Milcovich, G., Grassi, M., & Abrami, M. (2024). The Key Role of Wettability and Boundary Layer in Dissolution Rate Test. Pharmaceutics, 16(10), 1335. https://doi.org/10.3390/pharmaceutics16101335









