Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy
Abstract
:1. Introduction
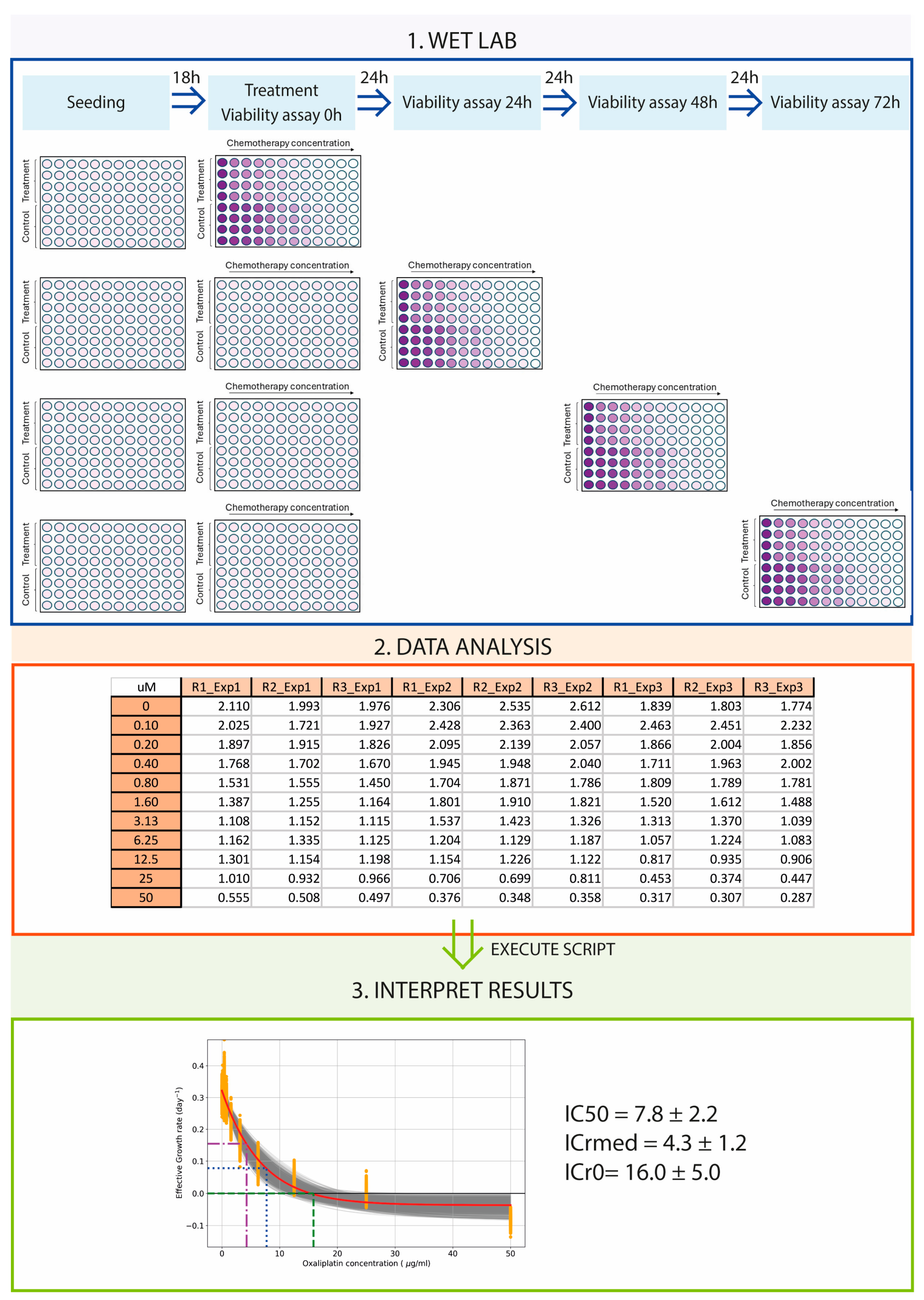
2. Materials and Methods
2.1. Cancer Cell Lines and Cell Culture
2.2. Cell Viability Assay
2.3. Mathematical Model
2.4. Growth Rate Calculation
2.5. Calculation of the IC50, ICr0, and ICrmed Indices
2.6. Statistical Analysis
3. Results
3.1. Viability and IC50 Calculation Are Time and Method Dependent
3.2. Effective Growth Rate Calculation
3.3. Effective Growth Rate Decreases in an Exponential Dose-Dependent Manner
3.4. Parameters to Measure Resistance to Drugs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
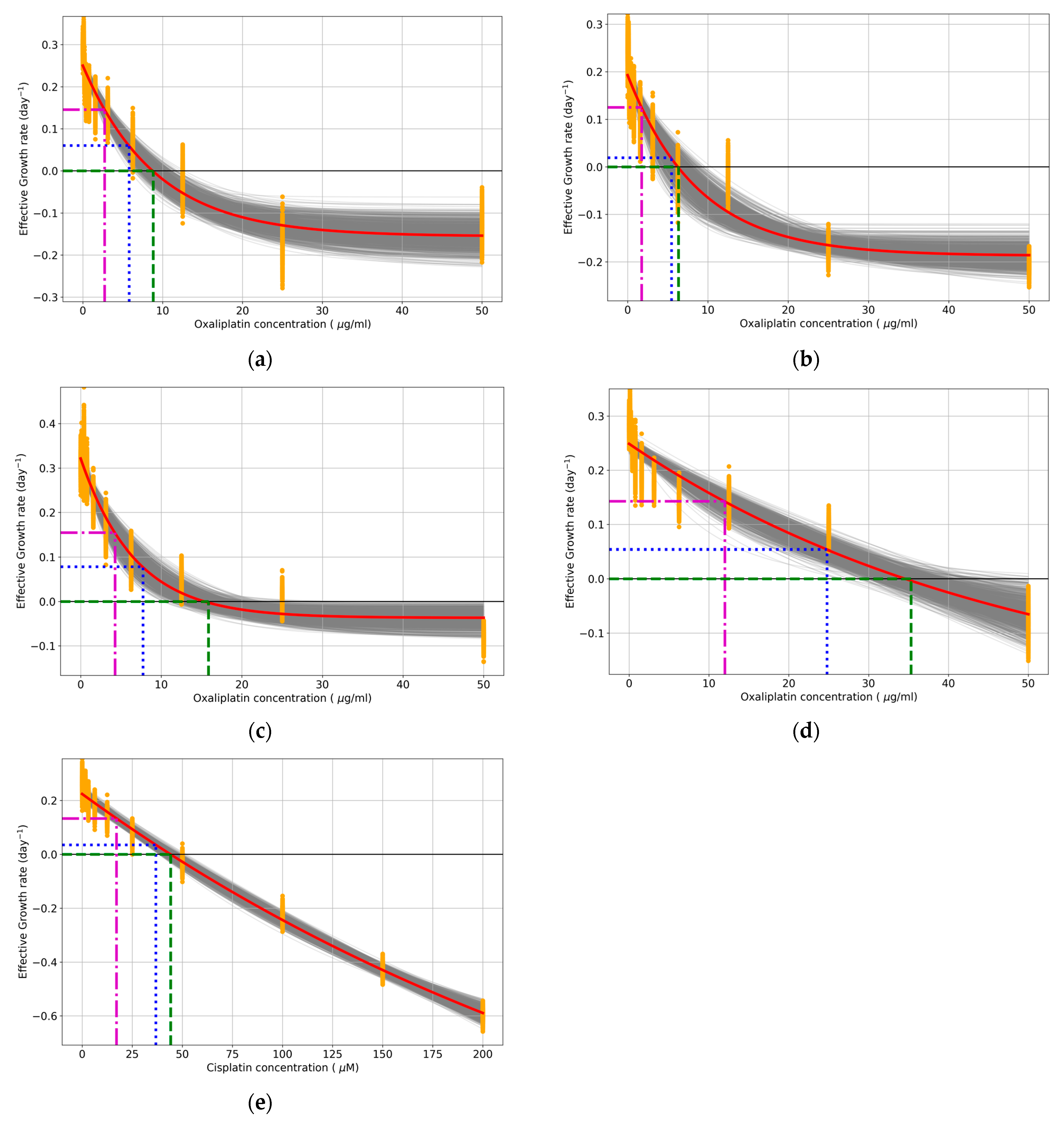
Appendix A.2
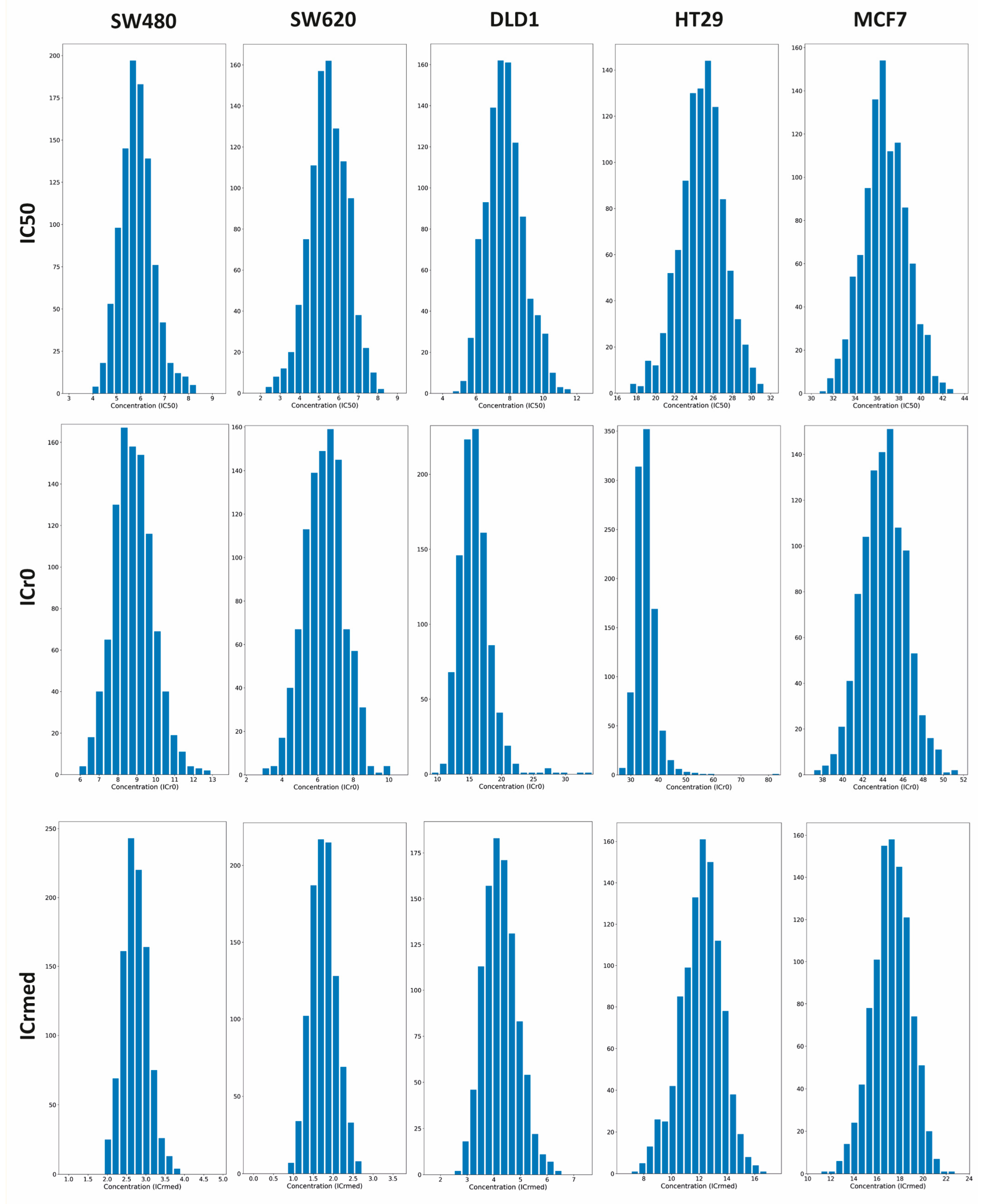
Appendix A.3
References
- World Health Organization. Available online: https://www.who.int/es/news-room/fact-sheets/detail/cancer (accessed on 10 August 2024).
- Ferlay, J.; Colombet, M.; Soerjomataram, I.; Parkin, D.M.; Piñeros, M.; Znaor, A.; Bray, F. Cancer Statistics for the Year 2020: An Overview. Int. J. Cancer 2021, 149, 778–789. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Chan, P.S.; Lok, V.; Chen, X.; Ding, H.; Jin, Y.; Yuan, J.; Lao, X.Q.; Zheng, Z.J.; Wong, M.C. Global Incidence and Mortality of Breast Cancer: A Trend Analysis. Aging 2021, 13, 5748–5803. [Google Scholar] [CrossRef] [PubMed]
- Altobelli, E.; Latella, G.; Morroni, M.; Licini, C.; Tossetta, G.; Mazzucchelli, R.; Profeta, V.F.; Coletti, G.; Leocata, P.; Castellucci, M.; et al. Low HtrA1 Expression in Patients with Long-Standing Ulcerative Colitis and Colorectal Cancer. Oncol. Rep. 2017, 38, 418–426. [Google Scholar] [CrossRef]
- Campagna, R.; Pozzi, V.; Giorgini, S.; Morichetti, D.; Goteri, G.; Sartini, D.; Serritelli, E.N.; Emanuelli, M. Paraoxonase-2 Is Upregulated in Triple Negative Breast Cancer and Contributes to Tumor Progression and Chemoresistance. Hum. Cell 2023, 36, 1108–1119. [Google Scholar] [CrossRef]
- AAT Bioquest. Comprehensive Guide to Cell Health Assays in Flow Cytometry: A Multidimensional Exploration. Available online: https://www.aatbio.com/resources/assaywise/2023-12-1/comprehensive-guide-to-cell-health-assays-in-flow-cytometry-a-multidimensional-exploration (accessed on 5 September 2024).
- van Meerloo, J.; Kaspers, G.J.L.; Cloos, J. Cell Sensitivity Assays: The MTT Assay. In Cancer Cell Culture: Methods and Protocols; Springer: Berlin/Heidelberg, Germany, 2011; pp. 237–245. [Google Scholar]
- Ali-Osman, F.; Maurer, H.R. Comparison of Cytostatic Sensitivities of L 1210 Cells and Human Stimulated Lymphocytes in Three Cell Proliferation Assays; Springer: Berlin/Heidelberg, Germany, 1980; Volume 98. [Google Scholar]
- Tobiiren, D. Differential Survival of Cell Subpopulations in Spheroids After Treatment with Bleomycin. J. Cancer Res. Clin. Oncol. 1981, 102, 189–193. [Google Scholar] [CrossRef]
- Ng, C.E.; Lnch, W.R. Comparison of the Densities of Clonogenic Cells From EMT6 Fibrosarcoma Monolayer Cultures, Multicell Spheroids, and Solid Tumors in Ficoll Density Gradients. J. Natl. Cancer Inst. 1978, 60, 1017–1022. [Google Scholar] [CrossRef]
- Karnes, R.J.; MacKintosh, F.R.; Morrell, C.H.; Rawson, L.; Sprenkle, P.C.; Kattan, M.W.; Colicchia, M.; Neville, T.B. Prostate-Specific Antigen Trends Predict the Probability of Prostate Cancer in a Very Large U.S. Veterans Affairs Cohort. Front. Oncol. 2018, 8, 296. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef]
- Sebaugh, J.L. Guidelines for Accurate EC50/IC50 Estimation. Pharm. Stat. 2011, 10, 128–134. [Google Scholar] [CrossRef]
- Adile, A.A.; Bakhshinyan, D.; Venugopal, C.; Singh, S.K. In Vitro Assays for Screening Small Molecules. In Methods in Molecular Biology; Humana Press Inc.: Totowa, NJ, USA, 2019; Volume 1869, pp. 189–196. [Google Scholar]
- Islam, M.T.; Aktaruzzaman, M.; Saif, A.; Hasan, A.R.; Sourov, M.M.H.; Sikdar, B.; Rehman, S.; Tabassum, A.; Abeed-Ul-Haque, S.; Sakib, M.H.; et al. Identification of Acetylcholinesterase Inhibitors from Traditional Medicinal Plants for Alzheimer’s Disease Using in Silico and Machine Learning Approaches. RSC Adv. 2024, 14, 34620–34636. [Google Scholar] [CrossRef]
- Lyles, R.H.; Poindexter, C.; Evans, A.; Brown, M.; Cooper, C.R. Nonlinear model-based estimates of ic50 for studies involving continuous therapeutic dose-response data. Contemp. Clin. Trials 2008, 29, 878. [Google Scholar] [CrossRef] [PubMed]
- Motulsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting Contents at a Glance; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Freshney, R.I. Culture of Animal Cells; Wiley: Hoboken, NJ, USA, 2010; Biology of Cultured Cells. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: Boca Raton, FL, USA, 1998; ISBN 0412042312. [Google Scholar]
- Cheng, R.C.H. Chapter 14 Resampling Methods. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands, 2006; Volume 13, pp. 415–453. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Pandas Development Team. Pandas-Dev/Pandas. 2024. Available online: https://pandas.pydata.org/about/citing.html (accessed on 12 January 2025).
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Sánchez-Díez, M.; Alegría-Aravena, N.; López-Montes, M.; Quiroz-Troncoso, J.; González-Martos, R.; Menéndez-Rey, A.; Sánchez-Sánchez, J.L.; Pastor, J.M.; Ramírez-Castillejo, C. Implication of Different Tumor Biomarkers in Drug Resistance and Invasiveness in Primary and Metastatic Colorectal Cancer Cell Lines. Biomedicines 2022, 10, 1083. [Google Scholar] [CrossRef]
- Chalak, M.; Hesaraki, M.; Mirbahari, S.N.; Yeganeh, M.; Abdi, S.; Rajabi, S.; Hemmatzadeh, F. Cell Immortality: In Vitro Effective Techniques to Achieve and Investigate Its Applications and Challenges. Life 2024, 14, 417. [Google Scholar] [CrossRef]
- Park, J.H.; Pyun, W.Y.; Park, H.H. Cancer Metabolism: Phenotype, Signaling and Therapeutic Targets. Cells 2 2020, 9, 2308. [Google Scholar] [CrossRef]
- Sharma, A.; Boise, L.H.; Shanmugam, M. Cancer Metabolism and the Evasion of Apoptotic Cell Death. Cancers 2019, 11, 1144. [Google Scholar] [CrossRef]
- Gordon, J.L.; Brown, M.A.; Reynolds, M.M. Cell-Based Methods for Determination of Efficacy for Candidate Therapeutics in the Clinical Management of Cancer. Diseases 2018, 6, 85. [Google Scholar] [CrossRef]
- Murali, V.S.; Chang, B.J.; Fiolka, R.; Danuser, G.; Cobanoglu, M.C.; Welf, E.S. An Image-Based Assay to Quantify Changes in Proliferation and Viability upon Drug Treatment in 3D Microenvironments. BMC Cancer 2019, 19, 502. [Google Scholar] [CrossRef]
- Felmlee, M.A.; Morris, M.E.; Mager, D.E. Mechanism-Based Pharmacodynamic Modeling. In Computational Toxicology; Brad, R., Mayeno, A.N., Eds.; Humana Press: Totowa, NJ, USA, 2012; Volume I, pp. 583–600. ISBN 978-1-62703-050-2. [Google Scholar]
- Cheng, Y.-C.; Prusoff, W.H. Relationship between the Inhibition Constant (KI) and the Concentration of Inhibitor Which Causes 50 per Cent Inhibition (I50) of an Enzymatic Reaction. Biochem. Pharmacol. 1973, 22, 3099–3108. [Google Scholar] [CrossRef]
- Gil-Gas, C.; Sánchez-Díez, M.; Honrubia-Gómez, P.; Sánchez-Sánchez, J.L.; Alvarez-Simón, C.B.; Sabater, S.; Sánchez-Sánchez, F.; Ramírez-Castillejo, C. Self-Renewal Inhibition in Breast Cancer Stem Cells: Moonlight Role of PEDF in Breast Cancer. Cancers 2023, 15, 5422. [Google Scholar] [CrossRef] [PubMed]
- Berrouet, C.; Dorilas, N.; Rejniak, K.A.; Tuncer, N. Comparison of Drug Inhibitory Effects (IC50) in Monolayer and Spheroid Cultures. Bull. Math. Biol. 2020, 82, 68. [Google Scholar] [CrossRef]
- González-Larraza, P.G.; López-Goerne, T.M.; Padilla-Godínez, F.J.; González-López, M.A.; Hamdan-Partida, A.; Gómez, E. IC50Evaluation of Platinum Nanocatalysts for Cancer Treatment in Fibroblast, HeLa, and DU-145 Cell Lines. ACS Omega 2020, 5, 25381–25389. [Google Scholar] [CrossRef] [PubMed]
- McDermott, M.; Eustace, A.J.; Busschots, S.; Breen, L.; Crown, J.; Clynes, M.; O’Donovan, N.; Stordal, B. In Vitro Development of Chemotherapy and Targeted Therapy Drug-Resistant Cancer Cell Lines: A Practical Guide with Case Studies. Front. Oncol. 2014, 4, 79768. [Google Scholar] [CrossRef]
- Yu, H.; Kim, D.J.; Choi, H.Y.; Kim, S.M.; Rahaman, M.I.; Kim, Y.H.; Kim, S.W. Prospective Pharmacological Methodology for Establishing and Evaluating Anti-Cancer Drug Resistant Cell Lines. BMC Cancer 2021, 21, 1049. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Pachnikova, G.; Wang, H.; Wu, Y.; Przybilla, D.; Schäfer, R.; Chen, Z.; Zhu, S.; Keilholz, U. IC50: An Unsuitable Measure for Large-Sized Prostate Cancer Spheroids in Drug Sensitivity Evaluation. Biomol. Biomed. 2022, 22, 580–592. [Google Scholar] [CrossRef]
- Hafner, M.; Niepel, M.; Chung, M.; Sorger, P.K. Growth Rate Inhibition Metrics Correct for Confounders in Measuring Sensitivity to Cancer Drugs. Nat. Methods 2016, 13, 521–527. [Google Scholar] [CrossRef]
- Larsson, P.; Engqvist, H.; Biermann, J.; Werner Rönnerman, E.; Forssell-Aronsson, E.; Kovács, A.; Karlsson, P.; Helou, K.; Parris, T.Z. Optimization of Cell Viability Assays to Improve Replicability and Reproducibility of Cancer Drug Sensitivity Screens. Sci. Rep. 2020, 10, 5798. [Google Scholar] [CrossRef]
- Hazekawa, M.; Nishinakagawa, T.; Kawakubo-Yasukochi, T.; Nakashima, M. Evaluation of IC50 Levels Immediately after Treatment with Anticancer Reagents Using a Real-time Cell Monitoring Device. Exp. Ther. Med. 2019, 18, 3197–3205. [Google Scholar] [CrossRef]
- Murphy, H.; McCarthy, G.; Dobrovolny, H.M. Understanding the Effect of Measurement Time on Drug Characterization. PLoS ONE 2020, 15, e0233031. [Google Scholar] [CrossRef]
- Lindström, H.J.G.; Friedman, R. Inferring Time-Dependent Population Growth Rates in Cell Cultures Undergoing Adaptation. BMC Bioinform. 2020, 21, 583. [Google Scholar] [CrossRef] [PubMed]
- Vandermeer, J. How Populations Grow: The Exponential and Logistic Equations|Learn Science at Scitable. Available online: https://www.nature.com/scitable/knowledge/library/how-populations-grow-the-exponential-and-logistic-13240157/ (accessed on 10 September 2024).
- GraphPad. How to Determine an IC50-FAQ 1859. Available online: https://www.graphpad.com/support/faq/how-to-determine-an-icsub50sub/ (accessed on 10 September 2024).
- AAT Bioquest. IC50 Calculator. Available online: https://www.aatbio.com/tools/ic50-calculator (accessed on 10 September 2024).
- Özkaya, A.B.; Geyik, C. From Viability to Cell Death: Claims with Insufficient Evidence in High-Impact Cell Culture Studies. PLoS ONE 2022, 17, e0250754. [Google Scholar] [CrossRef] [PubMed]
- Niepel, M.; Hafner, M.; Mills, C.E.; Subramanian, K.; Williams, E.H.; Chung, M.; Gaudio, B.; Barrette, A.M.; Stern, A.D.; Hu, B.; et al. A Multi-Center Study on the Reproducibility of Drug-Response Assays in Mammalian Cell Lines. Cell Syst. 2019, 9, 35–48.e5. [Google Scholar] [CrossRef] [PubMed]
- Linares, J.; Sallent-Aragay, A.; Badia-Ramentol, J.; Recort-Bascuas, A.; Méndez, A.; Manero-Rupérez, N.; Re, D.L.; Rivas, E.I.; Guiu, M.; Zwick, M.; et al. Long-Term Platinum-Based Drug Accumulation in Cancer-Associated Fibroblasts Promotes Colorectal Cancer Progression and Resistance to Therapy. Nat. Commun. 2023, 14, 746. [Google Scholar] [CrossRef]
- Rottenberg, S.; Disler, C.; Perego, P. The Rediscovery of Platinum-Based Cancer Therapy. Nat. Rev. Cancer 2020, 21, 37–50. [Google Scholar] [CrossRef]
- Hewitt, R.E.; McMarlin, A.; Kleiner, D.; Wersto, R.; Martin, P.; Tsokos, M.; Stamp, G.W.; Stetler-Stevenson, W.G. Validation of a Model of Colon Cancer Progression. J. Pathol. 2000, 192, 446–454. [Google Scholar] [CrossRef]
- Chenxi, Y.I.N.; Wenhua, L.U.; Mingzhe, M.A.; Yang, Q.; Wenzhuo, H.E.; Yumin, H.U.; Liangping, X.I.A. Efficacy and Mechanism of Combination of Oxaliplatin with PKM2 Knockdown in Colorectal Cancer. Oncol. Lett. 2020, 20, 312. [Google Scholar] [CrossRef]
- Zheng, Z.; Wu, M.; Li, H.; Xu, W.; Yang, M.; Pan, K.; Ni, Y.; Jiang, T.; Zheng, H.; Jin, X.; et al. Downregulation of AC092894.1 Promotes Oxaliplatin Resistance in Colorectal Cancer via the USP3/AR/RASGRP3 Axis. BMC Med. 2023, 21, 132. [Google Scholar] [CrossRef]
- Landrum, G.A.; Riniker, S. Combining IC50 or Ki Values from Different Sources Is a Source of Significant Noise. J. Chem. Inf. Model. 2024, 64, 1560–1567. [Google Scholar] [CrossRef]
- Cai, C.; Yuan, Y.; Ji, Y. A Bayesian Dose Finding Design for Oncology Clinical Trials of Combinational Biological Agents. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 63, 159–173. [Google Scholar] [CrossRef]
- Ritz, C.; Baty, F.; Streibig, J.C.; Gerhard, D. Dose-Response Analysis Using R. PLoS ONE 2015, 10, e0146021. [Google Scholar] [CrossRef] [PubMed]
- King, T.C.; Schlessinger, D.; Krogstad, D.J.; Kacian, D.L.; Longo, D.; Medoff, G.; Moellering, R.C.; Murray, P.R.; Storch, G.A. The Assessment of Antimicrobial Combinations. Rev. Infect. Dis. 1981, 3, 627–633. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Hwang, S. Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance. Pharmaceuticals 2021, 14, 1324. [Google Scholar] [CrossRef] [PubMed]

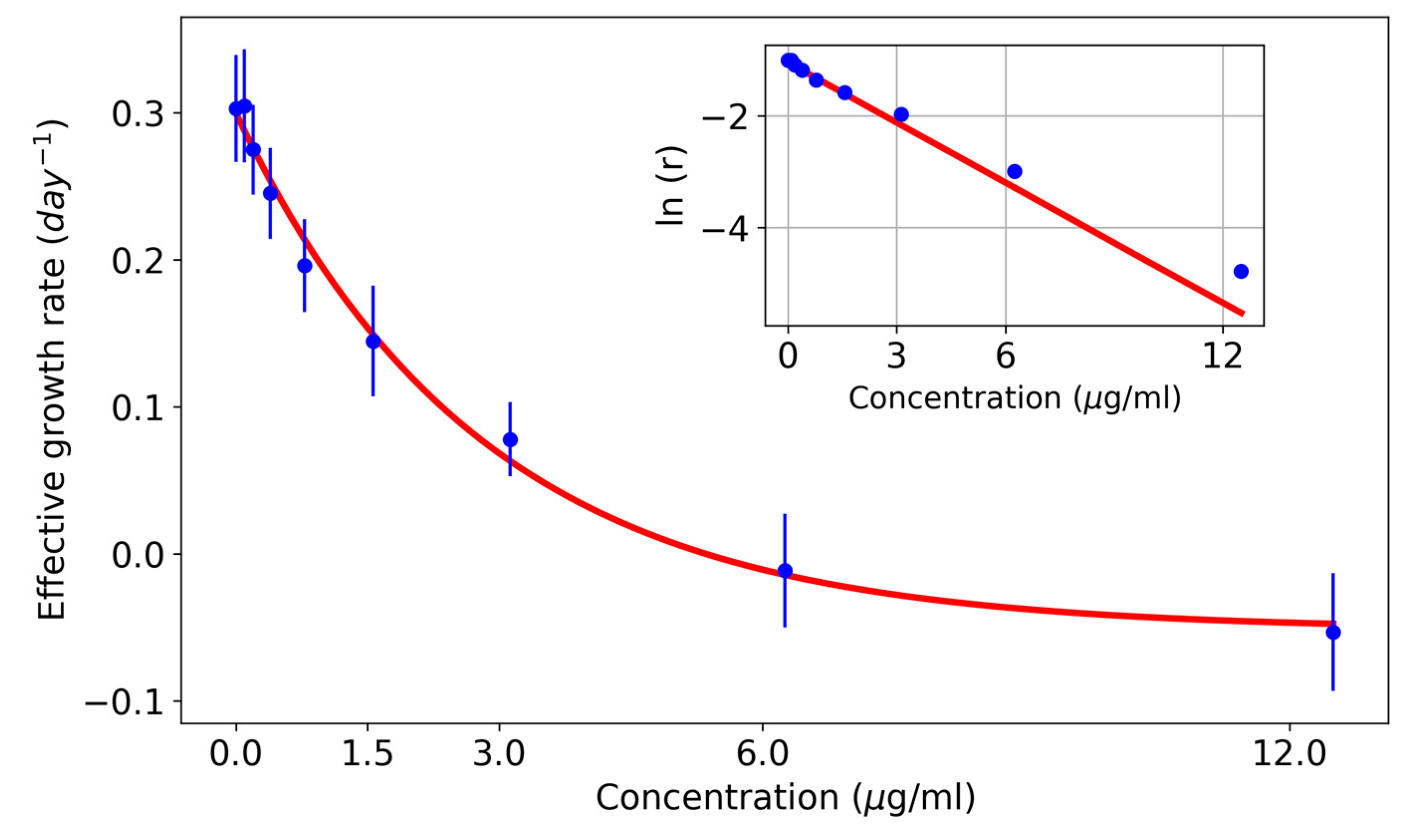



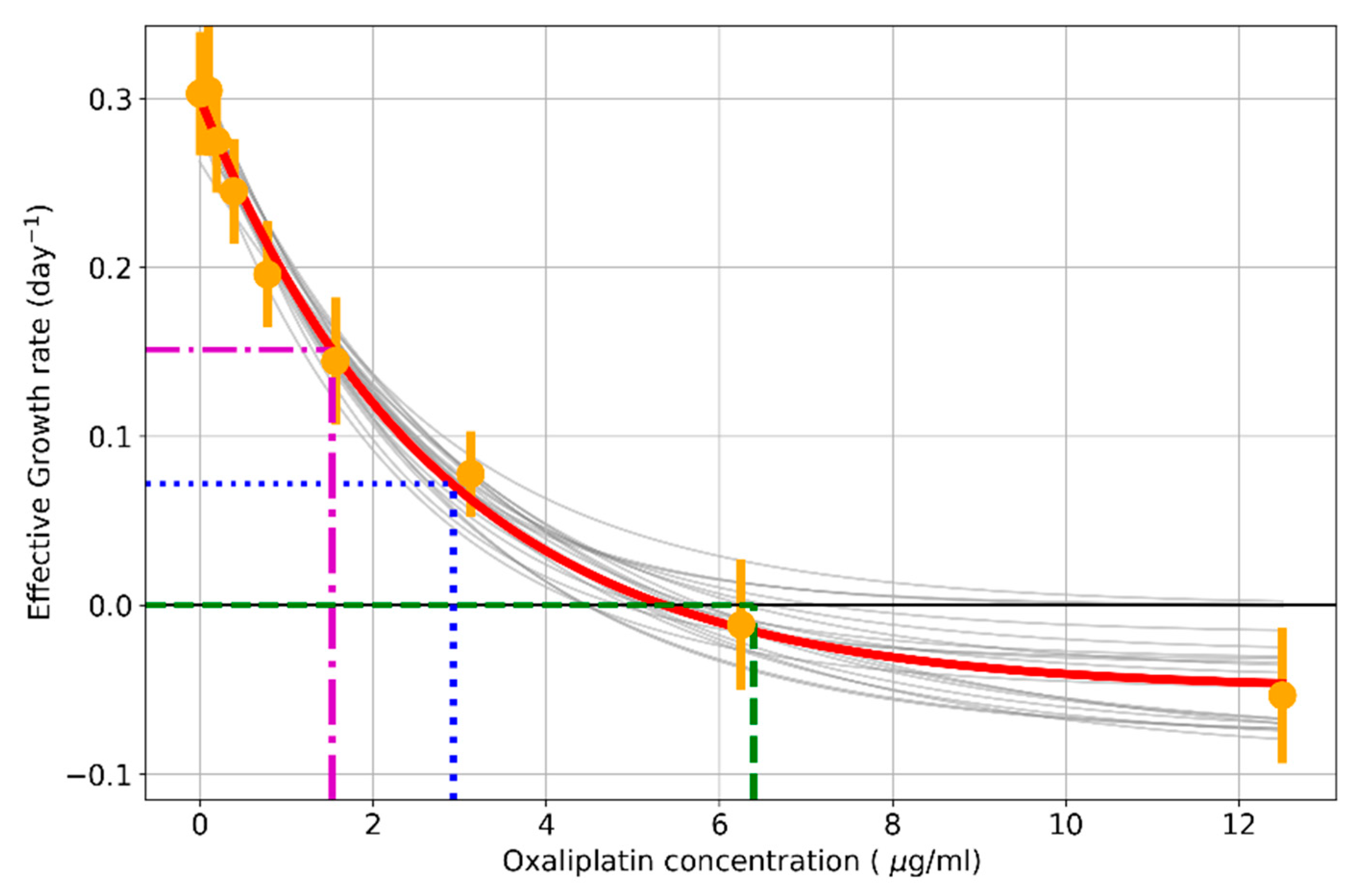

| Concentration (µg/mL) | Effective Growth Rate (Days−1) | Standard Error |
|---|---|---|
| 0 | 0.30 | 0.04 |
| 0.1 | 0.30 | 0.04 |
| 0.2 | 0.27 | 0.03 |
| 0.4 | 0.25 | 0.03 |
| 0.8 | 0.20 | 0.03 |
| 1.6 | 0.14 | 0.04 |
| 3.13 | 0.08 | 0.03 |
| 6.25 | −0.01 | 0.04 |
| 12.5 | −0.05 | 0.04 |
| 25 | −0.21 | 0.06 |
| 50 | −0.44 | 0.04 |
| Cell Line | IC50 GraphPad Prism (µg/mL) | IC50 Calculator (µg/mL) | IC50 New Method (µg/mL) |
|---|---|---|---|
| SW480 | 7.89 [5.61–11.11] | 13.52 | 5.8 ± 1.3 |
| SW620 | 5.83 [3.90–8.71] | 11.26 | 5.5 ± 2.1 |
| DLD1 | 10.85 [8.57–13.76] | 10.92 | 7.8 ± 2.2 |
| HCT116 | 5.37 [3.95–7.29] | 8.22 | 5.5 ± 1.0 |
| HT29 | 22.88 [15.90–33.31] | 31.54 | 25.5 ± 4.7 |
| MCF7 | 8.44 [7.21–9.87] | 8.97 | 11.1 ± 1.1 |
| Cell Line | IC50 (µg/mL) | ICr0 (µg/mL) | ICrmed (µg/mL) |
|---|---|---|---|
| SW480 | 5.8 ± 1.3 | 8.9 ± 2.0 | 2.7 ± 0.6 |
| SW620 | 5.5 ± 2.1 | 6.3 ± 2.4 | 1.8 ± 0.7 |
| DLD1 | 7.8 ± 2.2 | 16.0 ± 5.0 | 4.3 ± 1.2 |
| HCT116 | 5.5 ± 1.0 | 8.3 ± 1.5 | 2.9 ± 0.5 |
| HT29 | 25.5 ± 4.7 | 37.0 ± 10.0 | 12.0 ± 3.0 |
| MCF7 | 11.1 ± 1.1 | 13.3 ± 1.3 | 5.2 ± 0.9 |
| Cell Line | Endpoints | IC50 (µg/mL) | ICr0 (µg/mL) | ICrmed (µg/mL) |
|---|---|---|---|---|
| SW480 | 0 h, 24 h, 48 h, and 72 h | 5.8 ± 1.3 | 8.9 ± 2.0 | 2.7 ± 0.6 |
| 0 h and 72 h | 5.9 ± 1.4 | 8.7 ± 2.1 | 2.7 ± 0.6 | |
| SW620 | 0 h, 24 h, 48 h, and 72 h | 5.5 ± 2.1 | 6.3 ± 2.4 | 1.8 ± 0.7 |
| 0 h and 72 h | 6.0 ± 1.8 | 6.7 ± 2.0 | 1.9 ± 0.6 | |
| DLD1 | 0 h, 24 h, 48 h, and 72 h | 7.8 ± 2.2 | 16.0 ± 5.0 | 4.3 ± 1.2 |
| 0 h and 72 h | 7.7 ± 2.2 | 15.8 ± 4.3 | 4.3 ± 1.2 | |
| HCT116 | 0 h, 24 h, 48 h, and 72 h | 5.5 ± 1.0 | 8.3 ± 1.5 | 2.9 ± 0.5 |
| 0 h and 72 h | 5.6 ± 0.8 | 8.3 ± 1.2 | 2.9 ± 0.4 | |
| HT29 | 0 h, 24 h, 48 h, and 72 h | 25.5 ± 4.7 | 37.0 ± 10.0 | 12.0 ± 3.0 |
| 0 h and 72 h | 23.7 ± 4.4 | 34.4 ± 10.3 | 10.6 ± 2.9 | |
| MCF7 | 0 h, 24 h, 48 h, and 72 h | 11.1 ± 1.1 | 13.3 ± 1.3 | 5.2 ± 0.9 |
| 0 h and 72 h | 11.5 ± 1.1 | 12.9 ± 1.1 | 5.0 ± 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Díez, M.; Romero-Jiménez, P.; Alegría-Aravena, N.; Gavira-O’Neill, C.E.; Vicente-García, E.; Quiroz-Troncoso, J.; González-Martos, R.; Ramírez-Castillejo, C.; Pastor, J.M. Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy. Pharmaceutics 2025, 17, 247. https://doi.org/10.3390/pharmaceutics17020247
Sánchez-Díez M, Romero-Jiménez P, Alegría-Aravena N, Gavira-O’Neill CE, Vicente-García E, Quiroz-Troncoso J, González-Martos R, Ramírez-Castillejo C, Pastor JM. Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy. Pharmaceutics. 2025; 17(2):247. https://doi.org/10.3390/pharmaceutics17020247
Chicago/Turabian StyleSánchez-Díez, Marta, Paula Romero-Jiménez, Nicolás Alegría-Aravena, Clara E. Gavira-O’Neill, Elena Vicente-García, Josefa Quiroz-Troncoso, Raquel González-Martos, Carmen Ramírez-Castillejo, and Juan Manuel Pastor. 2025. "Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy" Pharmaceutics 17, no. 2: 247. https://doi.org/10.3390/pharmaceutics17020247
APA StyleSánchez-Díez, M., Romero-Jiménez, P., Alegría-Aravena, N., Gavira-O’Neill, C. E., Vicente-García, E., Quiroz-Troncoso, J., González-Martos, R., Ramírez-Castillejo, C., & Pastor, J. M. (2025). Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy. Pharmaceutics, 17(2), 247. https://doi.org/10.3390/pharmaceutics17020247










