Secure Communication for Uplink Cellular Networks Assisted with Full-Duplex Device-to-Device User

Abstract

In this paper, the secure communication based on the full-duplex (FD) device-to-device (D2D) in cellular networks is proposed. For the proposed scheme, the novel model is established, in which a D2D user is played as a relay operating in FD mode to assist in the secure transmission of uplink information. Considering that the D2D user as a relay is untrusted, D2D link rate maximization is formulated with the constraint of secrecy rate, which ensures the security of uplink cellular networks. To cope with the optimization problem, the optimal power allocation factors of the cellular user (CU) and the D2D user are jointly optimized. Firstly, by using the monotonicity of the objective function, the optimal solution of the power allocation factor at the D2D user can be obtained. Subsequently, the closed-form expression of the optimal power allocation factor at the CU is derived and verified that the solution is the global minimum point. Simulation results verify that the proposed scheme has better output performance than the conventional scheme.

1. Introduction

The increasing use of wireless devices has led to explosive growth in data traffic, so wireless spectrum resources are becoming increasingly scarce [1,2,3]. D2D communication as an underlying network can share the cellular communication resources to realize information transmission between D2D users, which improves the utilization of spectrum resources [4,5]. At the same time, the D2D cellular network has reliable synchronism by using the joint detection method [6]. In [7], the power control problem is studied by using a game-theoretic method based on sigmoid cost function for the underlying D2D network. Furthermore, when the distance between the CU and the base station (BS) is very long, the D2D user can act as a relay to assist the cellular link transmission. By using cooperative protocols, such as amplify and forward (AF), decode and forward (DF) and quantize and forward (QF), the cooperative D2D communication not only ensures reliable and effective information transmission [8,9], but also reduces the performance degradation of the CUs caused by the D2D users reusing the cellular networks spectrums. Therefore, both the CUs and the D2D users can benefit from the cooperation, and some existing studies have shown that D2D-assisted cellular networks can better improve system performance. In [10], a two-way communication scheme between BS and CU in two time slots based on D2D assistance is proposed. On this basis, considering the interference caused by the D2D reuse of cellular network resources, a superposition coding scheme [11] is proposed at the D2D transmitter and the power allocated to assist the downlink transmission of the cellular is minimized. Considering multiple D2D pairs and CUs, the weighted sum energy efficiency [12] of the D2D user is maximized through bandwidth allocation, power allocation, and selection of the optimal D2D user as a relay. In addition, Kim et al. propose a half-duplex (HD) D2D-assisted cooperative relay system [13] using non-orthogonal multiple access which can achieve maximum total capacity scaling.

The aforementioned studies have focused on D2D cooperation in HD mode, which lose spectrum resources. The combination of FD technology and D2D communication underlaying cellular networks can effectively improve the spectrum efficiency of the system [14,15]. However, the FD technology causes self-interference, which restricts the performance improvement of the FD wireless communication system to a certain extent. In fact, the current self-interference cancellation technology (SIC) has made a huge breakthrough [16,17,18], and D2D in FD mode to assist cellular transmission becomes practical. A beam-based analog SIC scheme for FD MIMO systems is proposed in [14], which can effectively eliminate self-interference. However, there is still residual self-interference after analog SIC, and digital SIC is a supplement to the previous analog cancellation. The nonlinear digital SIC [15] is achieved by pre-calibrating at the transmitter. A more general technique is studied in [16], and a framework that combines digital SIC and analog SIC is established to adaptively eliminate various interferences in dynamic environments. For D2D communication using FD technology, the feasibility of the FD function of D2D communication is proven in a heterogeneous network and a solution is obtained to reduce interference in an FD D2D network [19]. In [20], a virtual carrier scheme is proposed to solve the problem of intercarrier interference in V2V networks.

Nevertheless, the inherent openness of wireless communication threatens the security of wireless networks [21,22]. For D2D user-assisted cellular communication, since the D2D user as a relay may try to decode the signal to be forwarded, it is vital to protect the secure transmission of cellular link information. However, conventional encryption technology is difficult to implement in cooperative communication networks because of its complexity and a huge amount of calculation. From the perspective of the physical layer, physical layer security technology uses channel characteristics to protect information transmission, which can greatly enhance the security of the communication system [23,24,25]. Thus, physical layer security technology in this paper is adopted to increase the security of cellular networks based on D2D in FD mode.

The main contributions of our proposed scheme can be summarized as follows:

(1)

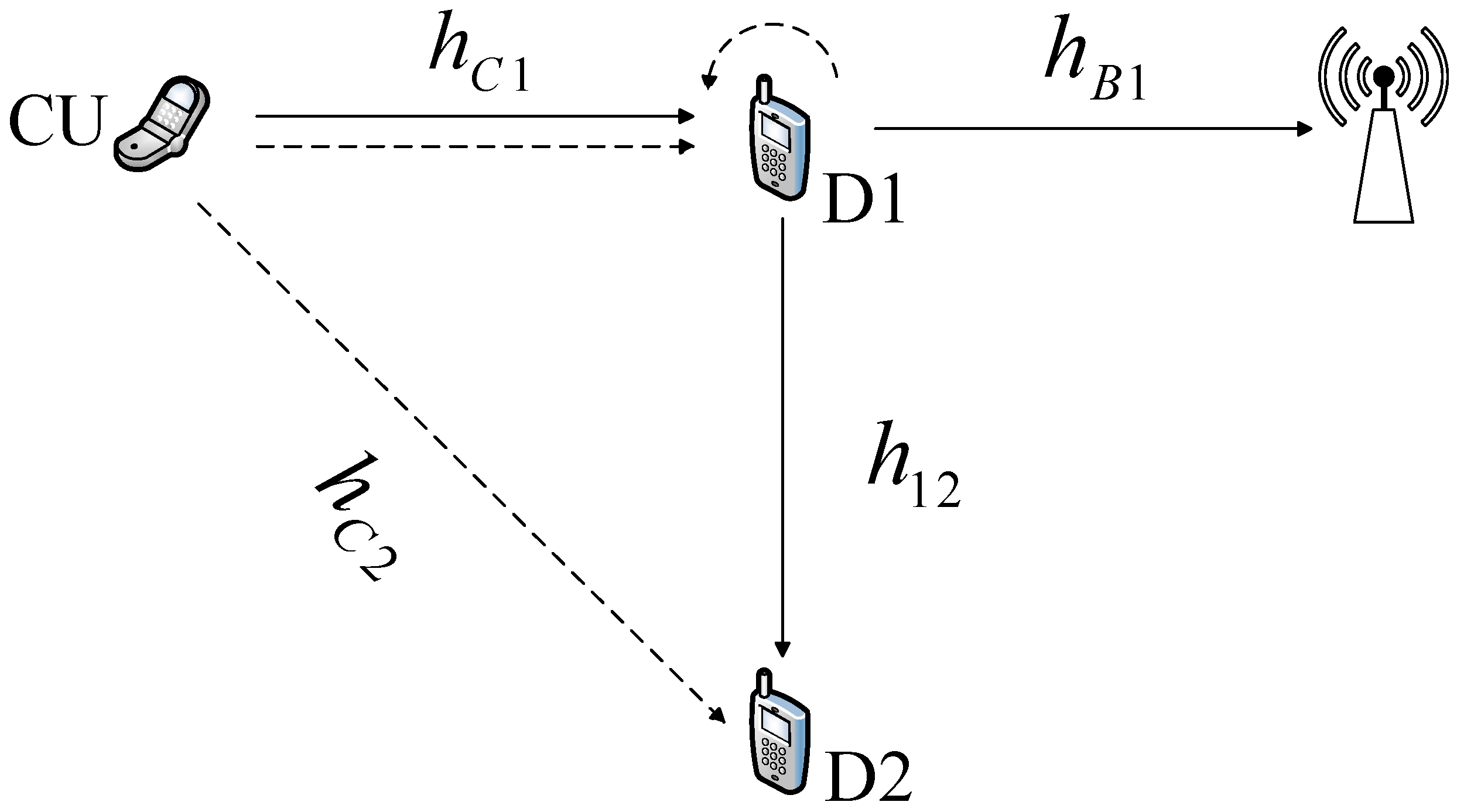
A novel secure cooperative communication model is proposed to simultaneously solve the problems of long-distance cellular uplink transmission and reliability of auxiliary transmission. In the established system model, the D2D user can play the role of relay to assist in the information transmission from CU to BS. As the low spectrum efficiency of HD, the relay in this paper is operated in FD mode to shorten the transmission time slot, which is not involved in [9,10,11,12]. Unlike the existing works, we consider the reliability of D2D user-assisted transmission, which means that the relay is untrusted at the data level. Alternatively, the relay may decode confidential information from the received signal. In order to ensure secure communication between the CU and the BS, the CU transmits a signal that combines a confidential signal and an interference signal to reduce the signal to noise ratio (SNR) of the untrusted relay.

(2)

Based on physical layer security, the secrecy rate is defined as the rate difference between the legal link and wiretapping link. Therefore, we first derive the expression of the secrecy rate of the cellular uplink for the untrusted relay. If the secrecy rate is greater than a positive threshold, it indicates that the D2D user cannot successfully decode the confidential information. Considering the interference of the CU to the D2D user, the instantaneous rate expression of D2D is obtained. Subsequently, an optimization problem to maximize the D2D link rate is formulated.

(3)

For the optimization problem formulated, we jointly optimized the power allocation factors of the CU and the D2D user. Specifically, the optimal power allocation factor at the D2D user is obtained based on the monotonicity of the objective function. Then we prove that the power allocation factor at CU is optimal.

The remainder of this paper is organized as follows. Section 2 describes the considered system model of cellular networks based on the relay played by D2D in FD mode. In Section 3, we formulate the D2D link rate maximization problem with the constraint of cellular secrecy rate. Moreover, the power allocation factors at CU and the D2D user is optimized. In Section 4, simulation results verify the performance of our proposed scheme compared with the conventional scheme. Finally, Section 5 concludes this paper.

2. System Model

The system model is shown in Figure 1. We consider a network composed of a BS, a CU and a pair of D2D users (D1, D2). Among them, D1 is operated in FD and equipped with a transmitting antenna and a receiving antenna, CU and D2 are equipped with a single antenna. Due to long-distance transmission, CU and BS cannot communicate directly, and only an untrusted D2D device (D1) is relay assisted in communication.

From Figure 1, CU and D2 can send their communication requests to BS with the assistance of D1. BS sends the control message to D1, and control information can be obtained by CU and D2 from D1. Initially, a signal combined with the confidential signal and the jamming signal is transmitted from the CU to D1. Then D1 forwards the signal from the CU to the BS, and at the same time communicates with D2. Since D2D reuses the spectrum resources of the cellular uplink, interference occurs between the D2D link and the cellular uplink.

In addition, the channel gain model is adopted as follows:

$$h_{ij}=g_{ij}{d}_{ij}^{-\theta }$$

(1)

where $i\in (C,1,B)$, $j\in (1,2)$, $g_{ij}$ is the channel coefficient, $d_{ij}$ is the distance between node $i$ and node $j$, and $\theta$ denotes the path loss exponent. All the channels are assumed to be narrow-band quasi-static and frequency flat fading.

First, CU transmits the confidential signal $x_s$ with power $\beta P$ and the jamming signal $x_z$ with power $(1-\beta )P$, inhere $\beta$ represents the power allocation factor between $x_s$ and $x_z$ at CU. The signal $y_{D1}$ received at the D1 can be written as:

$$y_{D1}=\sqrt{\beta P_C}{h}_{C1}{x}_s+\sqrt{(1-\beta )P_C}{h}_{C1}{x}_z+\sqrt{\kappa P_D}{f}_1{x}_D+n_{D1}$$

(2)

where $P_C$ and $P_D$ are the transmit power from CU and D1, respectively, $f_1$ is the self-interference channel, the parameter $\kappa \in [0,1]$ is the cancellation coefficient, which is used to characterize the influence of self-interference on FD communication, $x_D$ is the signal from D1, and $n_{D1}~CN(0,{\sigma }^2)$ is the additive noise at D1.

Subsequently, D1 receives the signal from CU, and assigns part fraction $\alpha$ of the available power to amplify and forward the signal to the BS, inhere $\alpha$ is the power allocation factor at D1. The remaining $1-\alpha$ is used for D2D communication. We assume that the BS can eliminate the interference from D2D communication through successive interference cancellation technology when $0\le \alpha \le 1/2$ [26,27]. The signal $y_B$ received at the BS can be written as:

$$\begin{array}{ll}{y}_B\hfill & =G{h}_{B1}{y}_{D1}+n_B\hfill \\ \hfill & =\sqrt{\beta P_C}G{h}_{C1}{h}_{B1}{x}_s+\sqrt{(1-\beta )P_C}G{h}_{C1}{h}_{B1}{x}_z+\sqrt{\kappa P_D}G{h}_{B1}{f}_1{x}_D+G{h}_{B1}{n}_{D1}+n_B\hfill \end{array}$$

(3)

where $n_B~CN(0,{\sigma }^2)$ is the additive noise at BS, and the parameter $G$ is denoted as the amplifying gain at D1, which can be considered by normalization of the received signal, i.e.,

$$G=\sqrt{\frac{\alpha P_D}{P_C{\left|h_{C1}\right|}^2+\kappa P_D{\left|f_1\right|}^2+{\sigma }^2}}$$

(4)

The signal $y_{D2}$ received at the D2 can be written as:

$$y_{D2}=\sqrt{\left(1-\alpha \right)P_D}{h}_{12}{x}_D+\sqrt{\beta P_C}{h}_{C2}{x}_s+\sqrt{(1-\beta )P_C}{h}_{C2}{x}_z+\sqrt{\alpha P_D}{h}_{12}{x}_D+n_{D2}$$

(5)

where $n_{D2}~CN(0,{\sigma }^2)$ is the additive noise at D2.

3. Problem Formulation and Analysis

In this section, we propose a secure communication scheme that maximizes the achievable rate of the D2D link with the constraint of the secrecy rate of the cellular uplink. The optimization problem is solved by deriving the power allocation factors of CU and D1. First of all, the optimal power allocation factor of D1 is obtained according to the monotonicity of the objective function. Then after verifying that the solution is the global minimum point, the closed-form solution of the optimal power allocation factor of the CU is derived.

The instantaneous SINR at D1 can be described as:

$${\gamma }_{D1}=\frac{\beta P_C{\gamma }_{C1}}{(1-\beta )P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}$$

(6)

where ${\gamma }_{C1}$ and ${\gamma }_1$ are channel-to-noise ratios (CNRs) of the link from CU to D1 and the self-interference channel, respectively, defined as:

$${\gamma }_{C1}={\left|h_{C1}\right|}^2/{\sigma }^2$$

(7)

$${\gamma }_1={\left|f_1\right|}^2/{\sigma }^2$$

(8)

The achievable rate of D1 is given by:

$$R_1=W{\log }_2\left(1+\frac{\beta P_C{\gamma }_{C1}}{(1-\beta )P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}\right)$$

(9)

where the parameter $W$ is the system bandwidth.

D1 employs the FD AF protocol to assist the cellular uplink transmission. The jamming signal is assumed to be known in advance by the BS, so that the BS is able to cancel out the jamming signal from the received signal. Then the instantaneous SINR at BS is expressed as:

$${\gamma }_B=\frac{\alpha \beta P_C{P}_D{\gamma }_{C1}{\gamma }_{B1}}{\kappa \alpha P_D^2{\gamma }_1{\gamma }_{B1}+\alpha P_D{\gamma }_{B1}+P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}$$

(10)

where ${\gamma }_{B1}$ is CNRs of the link from D1 to BS, defined as:

$${\gamma }_{B1}={\left|h_{B1}\right|}^2/{\sigma }^2$$

(11)

The achievable rate of cellular uplink communication is given by:

$$R_C=W{\log }_2\left(1+\frac{\alpha \beta P_C{P}_D{\gamma }_{C1}{\gamma }_{B1}}{\kappa \alpha P_D^2{\gamma }_1{\gamma }_{B1}+\alpha P_D{\gamma }_{B1}+P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}\right)$$

(12)

Due to the reuse of the cellular uplink spectrum, the cellular uplink will cause interference to D2. So the instantaneous SINR at D2 can be described as:

$${\gamma }_{D2}=\frac{\left(1-\alpha \right)P_D{\gamma }_{12}}{P_C{\gamma }_{C2}+\alpha P_D{\gamma }_{12}+1}$$

(13)

where ${\gamma }_{C2}$ and ${\gamma }_{12}$ are the CNRs of the links from CU and D1 to D2, respectively, defined as:

$${\gamma }_{C2}={\left|h_{C2}\right|}^2/{\sigma }^2$$

(14)

$${\gamma }_{12}={\left|h_{12}\right|}^2/{\sigma }^2$$

(15)

The achievable rate of D2D communication is given by:

$$R_D=W{\log }_2\left(1+\frac{\left(1-\alpha \right)P_D{\gamma }_{12}}{P_C{\gamma }_{C2}+\alpha P_D{\gamma }_{12}+1}\right)$$

(16)

For simplicity, $R_D$ can be rewritten as:

$$R_D=W{\log }_2\left(1+F\left(\alpha \right)\right)$$

(17)

where the parameter $F\left(\alpha \right)$ is given by:

$$F\left(\alpha \right)=\frac{\left(1-\alpha \right)P_D{\gamma }_{12}}{P_C{\gamma }_{C2}+\alpha P_D{\gamma }_{12}+1}$$

(18)

Therefore, the optimization function of the proposed scheme can be expressed as:

$$\underset{\alpha ,\beta }{\arg \max }{R}_D(\alpha ,\beta )$$

(19a)

$$\mathrm{s}.\mathrm{t}.{[R_C-R_1]}^{+}\ge R_{th}$$

(19b)

$$0\le \alpha \le 1/2$$

(19c)

$$0\le \beta \le 1$$

(19d)

where $R_{th}$ represents the secrecy rate threshold of the cellular uplink.

Then, substituting (9) and (12) into the constraint (19a) with secrecy rate, as follows:

$$\frac{1+\frac{\alpha \beta P_C{P}_D{\gamma }_{C1}{\gamma }_{B1}}{\kappa \alpha P_D^2{\gamma }_1{\gamma }_{B1}+\alpha P_D{\gamma }_{B1}+P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}}{1+\frac{\beta P_C{\gamma }_{C1}}{(1-\beta )P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1}}\ge \eta$$

(20)

where the parameter $\eta$ is given as:

$$\eta =2^{R_{th}/W}$$

(21)

According to (20), we can derive that:

$$\alpha \ge \frac{(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\left[(\eta -1+\beta )P_C{\gamma }_{C1}+(\kappa P_D{\gamma }_1+1)(\eta -1)\right]}{P_D{\gamma }_{B1}\left[\beta (1-\beta )P_C^2{\gamma }_{C1}^2-(\kappa P_D{\gamma }_1+1)(\eta -1)(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\right]}$$

(22)

From (17), we can easily see that $R_D$ is a monotonically increasing function with respect to $F\left(\alpha \right)$, so we obtain the optimal object $R_D$ (19) by solving the maximum value of $F\left(\alpha \right)$. The derivative of $F\left(\alpha \right)$ (18) with respect to $\alpha$ can be derived as follows:

$$\frac{\partial F\left(\alpha \right)}{\partial \alpha }=\frac{-\left(P_C{P}_D{\gamma }_{C2}{\gamma }_{12}+P_D{\gamma }_{12}+P_D^2{\gamma }_{12}^2\right)}{{\left(P_C{\gamma }_{C2}+\alpha P_D{\gamma }_{12}+1\right)}^2}<0$$

(23)

We note that $F\left(\alpha \right)$ is a monotonically decreasing function with respect to $\alpha$, so according to the range of ${\alpha }^{\ast }$ derived in (22), the optimal power allocation factor ${\alpha }^{\ast }$ with respect to $\beta$ that maximizes $F\left(\alpha \right)$ can be obtained:

$${\alpha }^{\ast }=\frac{(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\left[(\eta -1+\beta )P_C{\gamma }_{C1}+(\kappa P_D{\gamma }_1+1)(\eta -1)\right]}{P_D{\gamma }_{B1}\left[\beta (1-\beta )P_C^2{\gamma }_{C1}^2-(\kappa P_D{\gamma }_1+1)(\eta -1)(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\right]}$$

(24)

Furthermore, in order to obtain the optimal value of power allocation factor $\beta$ at CU that minimizes ${\alpha }^{\ast }$, we calculate the derivative of ${\alpha }^{\ast }$ with respect to $\beta$ and set it to 0, as follows:

$$\frac{\partial {\alpha }^{\ast }}{\partial \beta }=\frac{bc{\beta }^2+2ac\beta -(ac+bd)}{{\left[c\beta \left(1-\beta \right)-d\right]}^2}=0$$

(25)

where,

$$\begin{array}{c}a={(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)}^2(\eta -1)\hfill \\ b=(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)P_C{\gamma }_{C1}\hfill \\ c=P_C^2{\gamma }_{C1}^2{P}_D{\gamma }_{B1}\hfill \\ d=P_D{\gamma }_{B1}(\kappa P_D{\gamma }_1+1)(\eta -1)(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\hfill \end{array}$$

(26)

It can be observed that the optimal value of $\beta$ is obtained by solving the Equation (25). From (25), we derive that:

$$bc{\beta }^2+2ac\beta -(ac+bd)=0$$

(27)

According to the properties of the quadratic equation, we can calculate that the root discriminant $\Delta ={(2ac)}^2+4bc(ac+bd)>0$ of the Equation (27). Since the coefficient $bc$ of the quadratic term (27) is greater than zero, so there are two solutions to the Equation (27), denoted by ${\beta }_1$ and ${\beta }_2$, which can be obtained as follows:

$${\beta }_1=\frac{-2ac-\sqrt{\Delta }}{2bc}$$

(28)

and

$${\beta }_2=\frac{-2ac+\sqrt{\Delta }}{2bc}$$

(29)

As $\beta \in (-\infty ,{\beta }_1)$ and $\beta \in ({\beta }_2,+\infty )$, we obtain that the derivative $\frac{\partial {\alpha }^{\ast }}{\partial \beta }$ is greater than 0 according to the properties of the quadratic equation, then ${\alpha }^{\ast }$ is a monotonically increasing function of $\beta$. The derivative $\frac{\partial {\alpha }^{\ast }}{\partial \beta }$ is less than 0 as $\beta \in ({\beta }_1,{\beta }_2)$, that is, ${\alpha }^{\ast }$ is a monotonic decreasing function of $\beta$. Obviously, ${\beta }_2$ is the minimum point. Moreover, since ${\beta }_1<0$ and ${\beta }_2>0$, ${\beta }_2$ is the global minimum point. Therefore, the optimal power allocation factor ${\beta }^{\ast }$ at CU can be expressed as:

$${\beta }^{\ast }={\beta }_2=\frac{-2ac+\sqrt{△}}{2bc}=\frac{(P_C{\gamma }_{C1}+\kappa P_D{\gamma }_1+1)\left[\sqrt{\eta (\eta -1)}-(\eta -1)\right]}{P_C{\gamma }_{C1}}$$

(30)

Thus, the optimization object $R_D$ in Equation (19) can be obtained by the optimal power allocation factor ${\alpha }^{\ast }$ of CU and the optimal power allocation factor ${\beta }^{\ast }$ of D1.

4. Simulation Results and Analysis

In this section, simulation results can present the performance of two different schemes, including the proposed FD scheme and the conventional HD scheme. For the conventional HD scheme, we still consider that the D2D user as a relay is untrusted, but the D2D user is operated in HD mode to assist cellular uplink transmission while reusing the cellular spectrum to achieve D2D communication. The instantaneous SINRs at D1, BS and D2 can be formulated as:

$${\gamma }_{D1}^{HD}=\frac{\beta P_C{\gamma }_{C1}}{(1-\beta )P_C{\gamma }_{C1}+1}$$

(31)

$${\gamma }_B^{HD}=\frac{\alpha \beta P_C{P}_D{\gamma }_{C1}{\gamma }_{B1}}{\alpha P_D{\gamma }_{B1}+P_C{\gamma }_{C1}+1}$$

(32)

$${\gamma }_{D2}^{HD}=\frac{\left(1-\alpha \right)P_D{\gamma }_{12}}{P_C{\gamma }_{C2}+\alpha P_D{\gamma }_{12}+1}$$

(33)

The optimal power allocation factors at D1 and CU in the HD scheme can be expressed as:

$${\alpha }_{HD}^{\ast }=\frac{(P_C{\gamma }_{C1}+1)\left[({\eta }^2-1)(P_C{\gamma }_{C1}+1)+\beta P_C{\gamma }_{C1}\right]}{P_D{\gamma }_{B1}\left[\beta (1-\beta )P_C^2{\gamma }_{C1}^2-({\eta }^2-1)(P_C{\gamma }_{C1}+1)\right]}$$

(34)

$${\beta }_{HD}^{\ast }=\frac{(P_C{\gamma }_{C1}+1)\left[\sqrt{{\eta }^2({\eta }^2-1)}-({\eta }^2-1)\right]}{P_C{\gamma }_{C1}}$$

(35)

For the Monte Carlo experiment, the simulation results are averaged over 1000 independent channel realizations. Simulation parameters are elaborated in

Table 1. Simulation parameters.

Parameter	Value
Bandwidth	5 Hz
Noise power	−70 dBm
Path loss exponent	2
The distance between CU and D1	200 m
The distance between CU and D2	200 m
The distance between D1 and D2	200 m
The distance between D1 and BS	300 m
Power of CU	1 W
Power of D1	1 W

.

Figure 2 shows the optimal power allocation factor ${\beta }^{\ast }$ at CU versus various secrecy rate threshold $R_{th}$. We set cancellation coefficients $\kappa$ as 0.001, 0.005 and 0.01, respectively. As shown in Figure 2, the optimal power allocation factor at CU will monotonically increase as the secrecy rate threshold increases. The reason is that the CU allocates more power to transmit the confidential signal to increase the cellular link rate, which can improve the security of the relay. In addition, the larger ${\beta }^{\ast }$ can be obtained, as the cancellation coefficient $\kappa$ is bigger.

The optimal power allocation factor ${\alpha }^{\ast }$ at D1 versus $R_{th}$ under different SIC levels is shown in Figure 3. From Figure 3, when the secrecy rate threshold is 1, the optimal power factor ${\alpha }^{\ast }$ with $\kappa =0.01$ is approximately 0.48, the optimal power factor ${\alpha }^{\ast }$ with $\kappa =0.008$ is about 0.39, and the optimal power factor ${\alpha }^{\ast }$ with $\kappa =0.005$ is only 0.3. That is because the smaller cellular uplink rates can be obtained, as the cancellation coefficient is greater. In order to ensure that the cellular communication can achieve a secrecy rate, D1 must allocate more power to assist in transmission, which also causes the D2D link rate to drop.

The D2D link rate $R_D$ versus secrecy rate threshold $R_{th}$ in the proposed FD scheme and the conventional HD scheme is shown in Figure 4. As can be seen from Figure 4, the output performance of the proposed FD scheme is better than the HD scheme, and the D2D link rate decreases as the secrecy rate threshold $R_{th}$ increases. Furthermore, the D2D link rate with $\kappa =0.01$ in the proposed FD scheme is less than with $\kappa =0.005$.

Figure 5 displays the optimal allocation factor versus the cancellation coefficient $\kappa$, in which the secrecy rate thresholds are set as 0.1, 0.5 and 1, respectively. From Figure 5, when the secrecy rate threshold is 1, the optimal power allocation factor ${\beta }^{\ast }$ is greater than that when the secrecy rate threshold is 0.1 and 0.5. Specifically, when the cancellation coefficient $\kappa$ is 0.008, the power allocation factor ${\beta }^{\ast }$ with $R_{th}=1$ is greater than that with $R_{th}=0.5$, and about 0.2 larger than that with $R_{th}=0.1$.

The curves of the optimal allocation factor ${\alpha }^{\ast }$ versus various cancellation coefficient are plotted in Figure 6. The optimal power allocation factor ${\alpha }^{\ast }$ is a monotonically increasing function with respect to the cancellation coefficient $\kappa$.

Figure 7 compares the optimal D2D link rates of our proposed FD scheme and the conventional HD scheme with various cancellation coefficient $\kappa$. Obviously, the performance of the conventional HD scheme where the cancellation coefficient $\kappa$ ranges from 0.005 to 0.01 is worse than the proposed FD scheme. When the cancellation coefficient $\kappa$ is 0.005, the D2D link rate $R_{th}=0.5$ in the proposed FD scheme is approximately 1.8 bps larger than that of the conventional HD scheme. Moreover, the D2D link rate $R_{th}=0.5$ is better than that $R_{th}=1$ in the proposed FD scheme.

Figure 8 compares the optimal D2D link rates of two schemes, which concludes the scheme with the optimal power allocation factor ${\alpha }^{\ast }$ at D1 and the scheme with fixed power allocation factor $\alpha$ versus various power of D1. The fixed power allocation factor is set as 0.4. It can be seen that the optimal power allocation factor scheme can achieve a larger D2D link rate as compared to the scheme with the fixed $\alpha$. In the proposed scheme, the D2D rate is about 6.9 bps, while in the fixed power allocation factor scheme, the D2D rate can only achieve approximately 4.2 bps. In addition, the optimal D2D link rates become good with the increase of the power of D1.

5. Conclusions

We propose a secure communication scheme suitable for FD D2D user-assisted cellular uplink transmission. In this scheme, the cooperative D2D communication model is built for realizing long-distance cellular uplink transmission and reliable cooperative transmission. In particular, the D2D user as a relay is operated in FD mode to improve the spectrum efficiency of the system, and the combination of the confidential signal and the interference signal is transmitted by the CU so that the untrusted relay cannot successfully decode the information to be forwarded to the BS. We formulate our problem in order to maximize the D2D link rate while achieving a secrecy rate for the cellular uplink. The closed-form expressions of the power allocation factors at the D2D user and the CU are derived. The simulation results show that the D2D link rate of the proposed FD scheme is significantly improved compared with the conventional HD scheme.